Multiple imputation to account for measurement error in marginal structural models

Abstract

Background

Marginal structural models are an important tool for observational studies. These models typically assume that variables are measured without error. We describe a method to account for differential and non-differential measurement error in a marginal structural model.

Methods

We illustrate the method estimating the joint effects of antiretroviral therapy initiation and current smoking on all-cause mortality in a United States cohort of 12,290 patients with HIV followed for up to 5 years between 1998 and 2011. Smoking status was likely measured with error, but a subset of 3686 patients who reported smoking status on separate questionnaires composed an internal validation subgroup. We compared a standard joint marginal structural model fit using inverse probability weights to a model that also accounted for misclassification of smoking status using multiple imputation.

Results

In the standard analysis, current smoking was not associated with increased risk of mortality. After accounting for misclassification, current smoking without therapy was associated with increased mortality [hazard ratio (HR): 1.2 (95% CI: 0.6, 2.3)]. The HR for current smoking and therapy (0.4 (95% CI: 0.2, 0.7)) was similar to the HR for no smoking and therapy (0.4; 95% CI: 0.2, 0.6).

Conclusions

Multiple imputation can be used to account for measurement error in concert with methods for causal inference to strengthen results from observational studies.

Marginal structural models have become widely used tools to estimate the effects of exposures in the presence of time-varying confounding and selection bias¹. These models have been essential in HIV, where time-varying confounding by biomarkers limits the use of standard methods when estimating the effects of antiretroviral therapy and other exposures in observational studies^2–6. Similarly, joint marginal structural models have been proposed⁷ and applied^8,9 to estimate the joint effects of two or more exposures when one or more exposures are subject to time-varying confounding affected by prior exposure.

With few exceptions^10–12, most implementations of both standard and joint marginal structural models assume that exposures are measured without error, but exposure measurement is often imperfect. Here, we estimate the joint effects of therapy initiation and current smoking (a known risk factor for death among patients in treatment for HIV^13,14) on all-cause mortality in the Centers for AIDS Research Network of Integrated Clinical Systems (CNICS), a large clinical cohort of patients infected with HIV in the United States. In this cohort, smoking status reported by health care providers in the medical record was prone to measurement error, but information on smoking status was also available from a subgroup of patients who completed a clinical assessment of smoking status using detailed self-report instruments. We estimate the joint effects of therapy initiation and current smoking by combining multiple imputation to account for misclassification of smoking status with inverse probability weighted estimation of a joint marginal structural model. We also illustrate the finite sample properties of the proposed method using a limited Monte Carlo simulation.

METHODS

We are interested in the joint effects of initiation of antiretroviral therapy and current smoking on mortality, as parameterized by a set of three hazard ratios. This set of parameters can be identified using a 2-by-2 factorial randomized trial in which therapy-naïve patients were randomized to 1 of 4 arms: 1) initiate therapy and smoke; 2) initiate therapy and do not smoke; 3) do not initiate therapy and smoke; and 4) do not initiate therapy and do not smoke. The three hazard ratios of interest compare arms 1–3 above with arm 4. Because the prevalence of smoking among patients with HIV is high, many patients recruited for such a trial would likely have smoked prior to study entry, but the trial would estimate the effect of smoking only during the study period. Of course, if trial participants had exposure to smoking prior to randomization, then there would be interest in exploring how smoking history possibly modifies the effect of current smoking.

To consistently estimate these parameters using observational data, we must additionally assume that we can adequately account for confounding of both exposures, including confounding by smoking history at study entry.

Study population

CNICS was developed to support population-based HIV research in the United States¹⁵. The CNICS cohort includes over 29,000 HIV-positive adults engaged in clinical care from January 1, 1995 to the present (2014) at 8 Centers for AIDS Research sites (Case Western Reserve University; Fenway Community Health Center of Harvard University; Johns Hopkins University; University of Alabama at Birmingham; University of California, San Diego; University of California, San Francisco; University of North Carolina; and University of Washington). All patients attending two primary HIV medical care visits at one of the eight study sites are eligible for CNICS and followed for clinical events, lab measurements, and medications while they remain in care at study sites. Institutional review boards at each site approved study protocols. Participants provided written informed consent to be included in the CNICS cohort or contributed administrative and/or clinical data with a waiver of written informed consent where approved by local Institutional Review Boards.

CNICS includes 13,241 patients who entered care at a CNICS site prior to initiation of antiretroviral therapy and had a viral load of at least 500 copies/mL at cohort entry between January 1, 1998 and December 31, 2011. We excluded patients who did not have both CD4 cell count and viral load recorded within one year of study entry (n=152), and who were missing information on race (n=438) or transmission risk factor (n=361). The remaining 12,290 patients were included in this analysis.

Therapy initiation and smoking status

Therapy initiation was defined as the date on which patients were first prescribed three or more antiretroviral agents. After therapy initiation, patients were assumed to be on therapy throughout follow-up under an observational analog to the intention-to-treat assumption⁴. As in prior observational analyses^3,16, we estimate the effect of initiating therapy rather than being on therapy.

Patients classified as current smokers at any time during the study period were considered current smokers for the entire study period. Information on smoking status was available for all patients through provider documentation on patient medical records. However, smoking status as documented in the medical records was likely measured with error, and the absence of a positive report was assumed to imply nonsmoking. Moreover the validity of health care provider-reported smoking status was possibly influenced by predictors of mortality.

A subset of 3686 patients from five sites self-reported smoking status on the CNICS clinical assessment using a web-based survey software application implemented during clinical care. These patients composed an internal validation subgroup. Patient-reported current smoking status was considered less error-prone and used as a “gold standard” measure of smoking classification¹⁷.

Mortality ascertainment

The outcome of interest was all-cause mortality. Deaths were obtained through clinic sources, death certificates, and the United States vital status databases. Each CNICS site maintains a registry of deaths among patients at that site and regularly queries the Social Security Death Index and/or National Death Index to confirm mortality data.

Statistical methods

The 12,290 patients were followed from study entry until death, loss to follow-up, December 31, 2011, or 5 years after study entry. Patients were considered to be lost to follow-up after 12 consecutive months without a documented clinic visit including a CD4 cell count or viral load measurement.

We aim to estimate the joint effects of current smoking and therapy initiation using the joint marginal structural Cox model

$${\lambda }_{T^{s,a}}(t)={\lambda }_0(t)\text{exp}\{{\beta }_{1}s+{\beta }_{2}a(t)+{\beta }_{3}sa(t)\},$$ (1)

where the effects of interest are the hazard ratios exp(β₁), exp(β₂), and exp(β₁ + β₂ + β₃) for the joint effects of no therapy and smoking, therapy and no smoking, and therapy and smoking on mortality, respectively, relative to the hazard among nonsmoking patients not on therapy. S represents the gold standard (patient-reported) smoking status and A(t) is an indicator of therapy initiation by time t.

Because gold-standard smoking status S is not available for all patients, we must classify patients according to provider-reported smoking status if we do not wish to limit our analysis to the subset of patients who filled out detailed smoking status information on the electronic questionnaires. The standard analysis estimates the parameters β = {β₁, β₂, β₃}of equation 1 as θ = {θ₁, θ₂, θ₃} in equation 2 by fitting the marginal structural Cox model

$${\lambda }_{T^{s^{*},a}}(t)={\lambda }_0(t)\text{exp}\{{\theta }_1{s}^{*}+{\theta }_{2}a(t)+{\theta }_3{s}^{*}a(t)\},$$ (2)

where smoking is measured by provider-reported smoking status (S*) rather than the gold-standard, patient reported smoking status (S). We fit the marginal structural model using inverse-probability weights to create a pseudo-population in which neither exposure is associated with the confounders measured prior to the exposure^2,3,18,19. Details on the implementation of the standard marginal structural model shown above are provided in section A of the eAppendix.

Analysis accounting for measurement error

To estimate hazard ratios for the joint effects of current smoking and therapy initiation that were not biased by misclassification of provider-reported smoking status, we used multiple imputation to impute S, the patient-reported measure of current smoking status, prior to fitting the marginal structural model. Multiple imputation is a technique to account for missing data^21–24. Viewing misclassification of current smoking status as a missing data problem in which S is missing for patients outside the validation subgroup facilitates the use of missing data methods, like multiple imputation, to account for measurement error^25,26.

We used information on the relationship between variables that were measured for all patients and patient-reported current smoking status in the validation subgroup to impute S for all other patients in each of M imputations. Details are provided in the Appendix.

In each of the M imputations, we fit the marginal structural Cox model

$${\lambda }_{T^{s,a}}^m(t)={\lambda }_0^m(t)\text{exp}\{{\gamma }_1^m{s}^m+{\gamma }_2^{m}a(t)+{\gamma }_3^m{s}^{m}a(t)\}$$ (6)

by maximizing the weighted partial likelihood in each imputation

$$L({\mathit{\gamma }}^{\mathit{m}})=\prod _{i=1}^N{\left\{\frac{\text{exp}\{{\gamma }_1^m{s}^m+{\gamma }_2^{m}a(y_i)+{\gamma }_3^m{s}^{m}a(y_i)\}}{{\sum }_{j=1}^{N}I(y_j\ge y_i)\times \text{exp}\{{\gamma }_1^m{s}^m+{\gamma }_2^{m}a(y_i)+{\gamma }_3^m{s}^{m}a(y_i)\}\times w_j^m(y_i)}\right\}}^{{\delta }_i\times w_i^m(y_i)}$$ (7)

where Y_i represents the time to the first of mortality or censoring and δ_i is an event indicator for patient i. Note that distinct values of the parameters γ are estimated in each imputation m.

Weights were estimated for each month in each imputation as W^m(t) = W_S^mW_A(S^m)(t). Smoking weights were estimated as W_S^m = f(S^m)/f(S^m|L) and treatment weights were estimated as

$$W_{A(S^m)}(t)=\prod _{k=0}^{\lfloor t\rfloor }\frac{f\{A(k)|Ā(k-1),S^m\}}{f\{A(k)|Ā(k-1),\mathit{L},\overline{\mathit{Z}}(\mathit{k}),S^m\}},$$ (8)

where ⌊t⌋ is the count of completed months from study entry to time t and L is a vector of time-fixed covariates including age, sex, race, ethnicity, and year, HIV transmission risk factor (indicators of being a man who has sex with men and injection drug use), CD4 cell count, and viral load at study entry.

Assuming that inclusion in the subset of patients with detailed smoking information depends only on the observed covariates, the parameters of interest, exp(β₁), exp(β₂), and exp(β₁ + β₂ + β₃) can be consistently estimated by exp(γ̄₁), exp(γ̄₂), and exp(γ̄₁ + γ̄₂ + γ̄₃), respectively, where γ̄_p is the average γ_p across all imputations,

$$\text{exp}({\overline{\gamma }}_p)=\text{exp}\left(M^{-1}\sum _{m=1}^M{\hat{\gamma }}_p^m\right);p\in (1,2,3).$$ (9)

A large-sample estimate of the variance for γ̄_p is given by

$$V({\overline{\gamma }}_p)=M^{-1}\sum _{m=1}^{M}V({\hat{\gamma }}_p^m)+(1+M^{-1}){(M-1)}^{-1}\sum _{m=1}^M{({\hat{\gamma }}_p^m-{\overline{\gamma }}_p)}^2,$$ (10)

where the within imputation variance, $V({\hat{\gamma }}_p^m)$, is the robust variance for ${\hat{\gamma }}_p^m$^3,27. In this example, we set M = 20.

We also graphically present the cumulative incidence of mortality for patients in each of the four groups in the standard analysis and analysis accounting for measurement error^19,28. Statistical analyses were performed using SAS version 9.3 (SAS Institute, Inc., Cary, NC), and SAS code is provided in Section B of the eAppendix.

We further explored the finite-sample properties of multiple imputation to account for measurement error in marginal structural models using simulations. The bias, 95% confidence interval coverage, power, and mean squared error were evaluated for the standard marginal structural model and the marginal structural model using multiple imputation to account for measurement error that is non-differential (scenario 1) and differential (scenario 2) with respect to the outcome. Details about the simulations are provided in Section C of the eAppendix.

RESULTS

Table 1 describes the characteristics of the study population at study entry and over 36,418 person-years of follow-up. Of the 12,290 patients included in the study, 82% were male, 39% were black, and 60% were men who have sex with men. At study entry 19% had been diagnosed with AIDS. Provider diagnoses identified 39% of the cohort as current smokers, and 69% of the patients initiated antiretroviral therapy before the end of follow-up. Over the 5 years of follow-up, 935 patients died, and 5137 were lost to follow-up.

Table 1.

Demographics and clinical characteristics at study entry of 12,290 patients who were linked to care at a CNICS site between January 1, 1998 and December 30, 2011 at eight US clinical sites and followed for death up to 5 years

Characteristics	All patients at study entry (n=12,290)		All patients over 36,418 person-years	Validation subgroup at study entry (n=3686)		Validation subgroup over 12,157 person-years
	n	%	%	n	%	%
Male sex	10034	82	81	3217	87	87
Black race	4841	39	39	1044	28	28
Hispanic ethnicity	1342	11	11	533	14	14
Injection drug user	2295	19	18	538	15	15
MSM	7340	60	60	2652	72	71
AIDS	2132	19	26	487	13	21
CD4 cell count
<250	5131	42	26	1461	40	23
250 – 500	4235	34	40	1344	36	41
>500	2924	24	34	881	24	36
Suppressed viral load b	0	0	52	0	0	40
Physician-reported current smoker c	4823	39	42	1596	43	45
Patient-reported current smoker d	- e	- e	- e	1687	46	44
On therapy	0	0	67	0	0	73
No therapy, nonsmoker f	7467	61	20	1999	54	13
No therapy, smokerf	4823	39	14	1687	46	14
On therapy, nonsmokerf	0	0	39	0	0	42
On therapy, smokerf	0	0	28	0	0	31

^aCNICS: Centers for AIDS Research Network of Integrated Clinical Systems; MSM: men who have sex with men

^b<500 copies/mL; only patients with unsuppressed viral load at cohort entry were included in the study

^cProvider-reported smoking was likely measured with error

^dPatient-reported smoking was the gold-standard measure of smoking status

^ePatient-reported smoking status was not available for patients outside the validation subgroup

^fSmoking status is provider-reported smoking status for all patients and patient-reported smoking status for patients in the validation subgroup

A subset of 3686 patients completed detailed self-reported smoking status as part of the CNICS clinical assessment of patient reported outcomes during the study period and were included in the validation subgroup. Patients in the validation subgroup were similar to all patients at the sites where they were enrolled but more likely to be male and/or men who have sex with men, and less likely to be black, injection drug users, or have AIDS at baseline than patients in the main cohort. In the validation subgroup, 43% of patients had a provider diagnosis as a current smoker, while 46% reported themselves that they were current smokers. Using self-reported current smoking status as the gold standard, the sensitivity of provider-diagnosed smoking was 74% (95% CI: 72%, 76%) and the specificity was 83% (95% CI: 81%, 85%) in the validation subgroup. Of the 3686 patients in the validation subgroup, 52 died and 855 were lost to follow-up over 5 years.

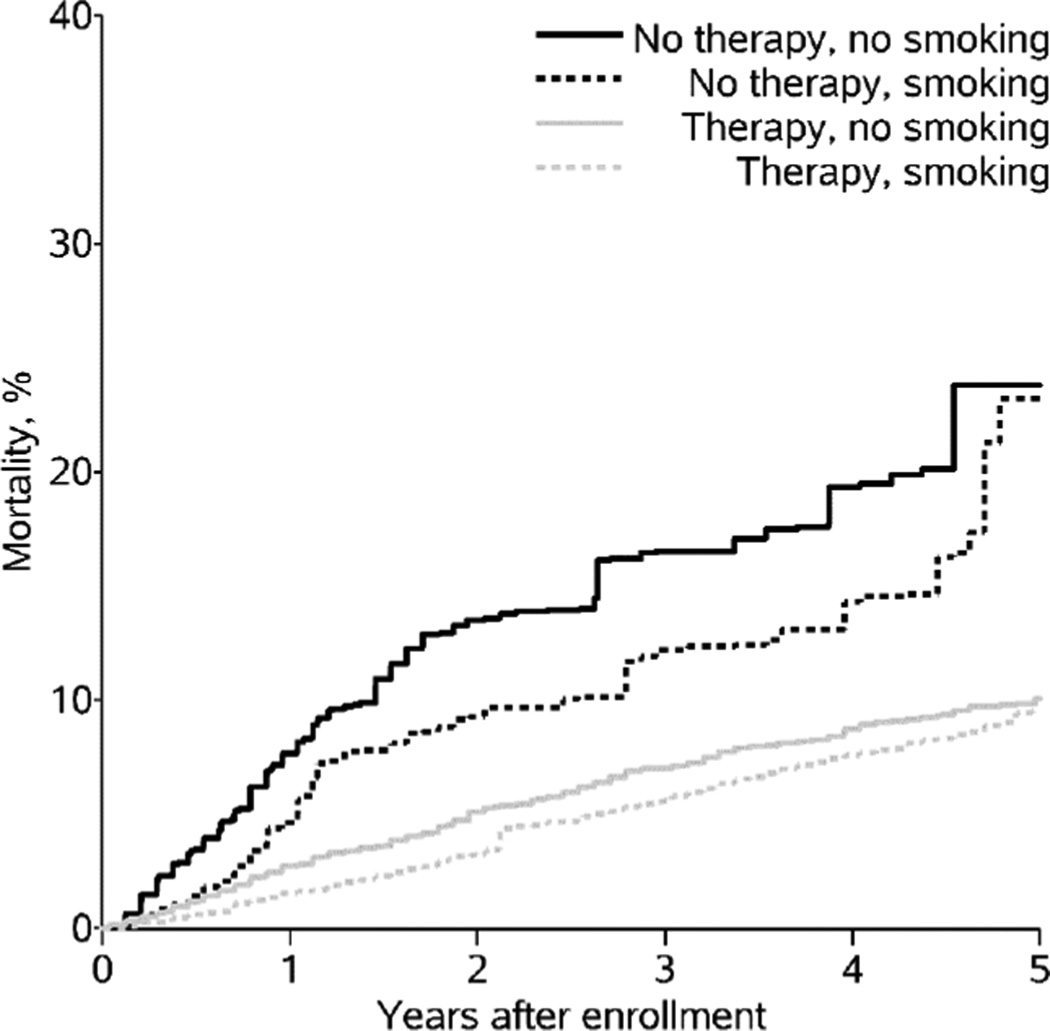
Table 2 presents hazard ratios comparing mortality between exposure groups in the standard analysis and in the analysis accounting for measurement error of smoking status. In the standard joint marginal structural model, the hazard ratio (HR) comparing smoking and not initiating therapy to not smoking and not initiating therapy was a counterintuitive 0.6 (95% CI: 0.6, 0.8). The HR for not smoking and initiating therapy was 0.3 (95% CI: 0.3, 0.4), and the HR for smoking and initiating therapy was 0.3 (95% CI: 0.2, 0.3). These results suggest that smoking (with and without therapy) was protective of 5-year total mortality. Figure 1 presents the risk of mortality over time for each exposure group in the standard analysis.

Table 2.

5-year cumulative incidence of mortality, standard hazard ratios (based on provider-reported smoking), and hazard ratios accounting for misclassification of smoking status comparing patients in each of four groups defined by therapy initiation and current smoking status between January 1, 1998 and December 30, 2011 at eight US clinical sites and followed for death up to 5 years

Model	Standard			Accounting for measurement error
	Mortality	HR	95% CI	Mortality	HR	95% CI
Crude
No therapy, no smoking	10.5	1		11.6	1
No therapy, smoking	10.8	0.8	0.7, 1.0	12.3	1.2	0.6, 2.5
Therapy, no smoking	13.6	0.9	0.8, 1.1	10.8	1.1	0.7, 1.5
Therapy, smoking	11.8	0.9	0.8, 1.2	11.8	1.2	0.6, 2.2
Marginal Structural Model
No therapy, no smoking	22.6	1		22.4	1
No therapy, smoking	22.1	0.6	0.6, 0.8	22.9	1.2	0.6, 2.3
Therapy, no smoking	10.0	0.3	0.3, 0.4	9.3	0.4	0.2, 0.6
Therapy, smoking	9.6	0.3	0.2, 0.3	10.4	0.4	0.2, 0.7

HR: hazard ratio; CI: confidence interval

Figure 1.

Weighted cumulative incidence of mortality by provider-reported smoking status and therapy initiation among 12,290 patients in the CNICS cohort at 8 sites in the United States, 1998 – 2012.

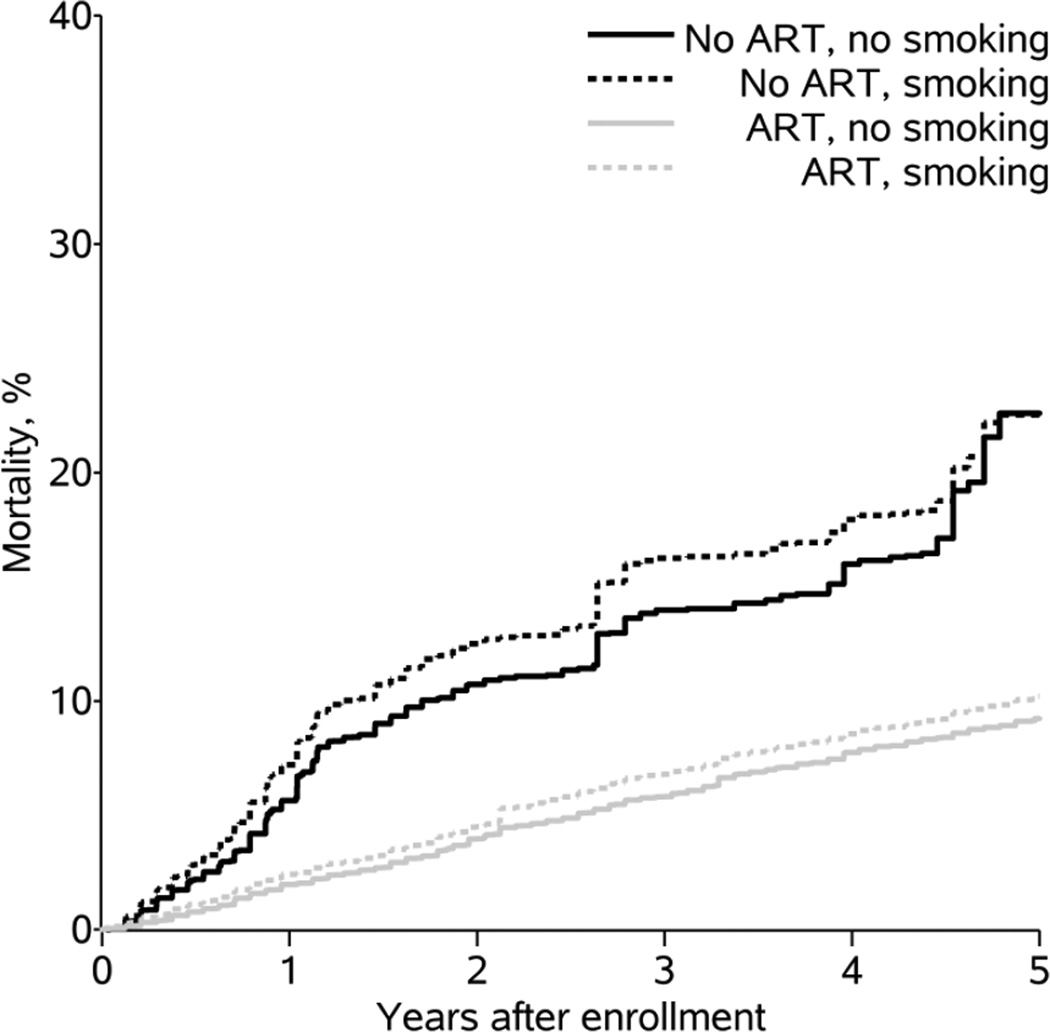
After accounting for the measurement error in current smoking status, the prevalence of smoking in the entire cohort was 50%. Compared to not smoking and not initiating therapy, the mortality hazard ratio for smoking and not initiating therapy was 1.2 (95% CI: 0.6, 2.3). Compared to not smoking and not initiating therapy, the HR for not smoking and initiating therapy was 0.4 (95% CI: 0.2, 0.6), and the HR for smoking and initiating therapy was similar at 0.4 (95% CI: 0.2, 0.7). Figure 2 presents the risk of mortality over time for each exposure group after accounting for measurement error. The HR for smoking and initiating therapy was similar to the expected HR under multiplicativity of the effects of smoking and therapy (0.4) and farther from the null than the expected HR under additivity (0.6).

Figure 2.

Weighted cumulative incidence of mortality by patient-reported smoking status and therapy initiation among 12,290 patients in the CNICS cohort at 8 sites in the United States, 1998 – 2012.

Table 3 presents the results from Monte Carlo simulations. In 2000 simulated cohorts each of 2000 patients, the multiple imputation approach produced an HR with little bias and appropriate coverage under conditions mimicking the data used in this analysis. When exposure misclassification was differential with respect to the outcome, the multiple imputation approach that assumed non-differential misclassification yielded results with more bias than the multiple imputation approach accounting for the differential misclassification, but much less bias than the standard marginal structural model.

Table 3.

Results from 2000 simulated cohorts of 2000 patients with a 30% validation subgroup^a

Method	Sensitivity	Specificity	Average HR	Biasb	SD c (Bias)	Coverage d	Power e	MSE f
Scenario 1 g
Truth	1	1	1.73
Standard MSM	0.7	0.8	1.15	41.00	4	0	70	1162
MSM with MI	0.7	0.8	1.73	0.09	12	97	99	137
Scenario 2 h
Truth	1	1	1.73
Standard MSM	0.6 (noncases) 0.95 (cases)	0.7 (noncases) 0.9 (cases)	1.45	17.00	5	22	99	314
MSM with MI (nondifferential)	0.6 (noncases) 0.95 (cases)	0.7 (noncases) 0.9 (cases)	1.74	0.70	12	96	99	139
MSM with MI (differential)	0.6 (noncases) 0.95 (cases)	0.7 (noncases) 0.9 (cases)	1.73	0.36	11	97	99	121

^aSe: Sensitivity; Sp: Specificity; MSM: Marginal structural model; MI: Multiple Imputation; CI: Confidence interval

^bBias was defined as the average of the difference between the true ln(HR) and the estimated ln(HR) in each simulated scenario times 100

^cStandard deviation of the bias

^e95% confidence interval coverage was the proportion of iterations in which the estimated 95% confidence interval contained the true value

^ePower was the proportion of simulations in which the estimated 95% confidence interval excluded the null value

^fMean squared error was the sum of the square of the bias and the square of the standard deviation of the bias

^gIn the first scenario, exposure misclassification was nondifferential with respect to the outcome

^hIn the second scenario, exposure misclassification was differential with respect to the outcome

DISCUSSION

Results from a joint marginal structural model that accounted for misclassification of current smoking status suggested that patients who smoked had slightly higher risk of mortality under no therapy initiation (23% vs. 22%) and under therapy initiation (10% vs. 9%) over 5 years. These findings are consistent with existing literature on risks of smoking among individuals in care for HIV^13,14,29,30. In the standard joint marginal structural model, which did not account for measurement error of smoking status, current smoking (counter to expectations) appeared to decrease the risk of mortality.

As in existing studies highlighting the discrepancies between electronic health records and patient report outcomes¹⁷, provider classification of current smoking status on electronic health records was a poor proxy for self-reported smoking. After accounting for measurement error of smoking status, the prevalence of current smoking in the CNICS was similar to the prevalence of self-reported smoking reported in other cohorts of patients with HIV^13,29,31. Existing studies conducted among therapy initiators report that smoking sometimes is associated with poorer adherence to therapy^29,32,33, inferior immunological markers^29,34, and increased risk of mortality²⁹, leading investigators to suggest that smoking may make therapy less effective^29,34,35. Studies in the era prior to effective therapy found no effect of smoking on mortality^36–38. In this analysis, conducted in the current HIV treatment era, we report somewhat increased mortality for smokers under no therapy initiation, which has not been examined in previous studies.

Here, we have described a method to estimate the joint effects of therapy and current smoking from observational data when smoking status may be misclassified. These joint effects can be conceptualized as the effects of joint interventions on therapy and current smoking. Estimating these joint effects in observational data requires accounting for confounding of both therapy initiation and current smoking. Because CNICS is based on data collected at routine clinic visits, we were unable to include information not routinely collected at an HIV patient visit, meaning that we may have residual confounding by unmeasured covariates. In addition, CNICS does not include information for most patients on smoking prior to study entry, which is likely to affect both smoking during the study and mortality. However, in analyses conducted among only patients who completed detailed questionnaires, the effect of smoking on mortality was similar when estimated using weights that included prior smoking (HR: 1.6; 95% CI: 0.8, 3.3) and when estimated using weights that did not include prior smoking (HR: 1.6; 95% CI: 0.9, 2.8), lending support to our results despite possible residual confounding by prior smoking status.

Alternatively, we could consider current smoking as a modifier of the effect of therapy on mortality. Because a modifier is not required to be unconfounded, we could examine modification by current smoking status by fitting the structural model proposed above with only the treatment weights. Numerical results are similar when smoking is considered to be an effect modifier, though we interpret the results as stratum specific effects of therapy, rather than joint effects. The HR for the effect of treatment on mortality was not modified by smoking status; the HR was 0.4 (95% CI: 0.2, 0.6) for nonsmokers and 0.4 (95% CI: 0.2, 0.6) for smokers.

We also assume non-informative censoring. Over the 5-year study period, 5137 of the 12,290 patients in the cohort were lost to follow-up. Note that, when one includes potential confounders in an outcome regression survival model, one simultaneously accounts for confounding and informative censoring based on those variables. Here, because we accounted for confounding using inverse probability weights instead of including confounders in the structural model, we would need inverse probability of censoring weights to produce consistent estimates of the hazard ratios in the presence of covariates that predict both loss to follow-up and death. However, while the proportion of patients lost to follow-up was high, no measured covariates were strongly associated with loss to follow-up. In addition, previous work has shown that loss to follow-up in the CNICS cohort does not predict mortality³⁹, indicating that selection bias resulting from the high proportion of patients lost to follow-up is likely to be modest. As expected, when we applied inverse probability of censoring weights in unpublished analyses, results were unchanged.

We used multiple imputation to account for misclassification of current smoking status using self-reported smoking as the gold standard. However, if patients did not accurately report their smoking status, we could have residual measurement error. Similarly, if patients changed their smoking behaviors over follow-up, we would have misclassified their smoking status for at least some of the study period. Unfortunately, smoking behaviors have changed very slowly among patients with HIV, which is one reason smoking rates among patients with HIV are still over twice as high as among the general population^40–44. Finally, we assume all other variables, including date of therapy initiation, are measured without error, though the multiple imputation approach could be extended to account for measurement error of multiple variables.

Multiple imputation is a method to handle missing data that is familiar to epidemiologists and has been previously applied to account for measurement error of exposures²⁵ and outcomes²⁶. For multiple imputation to produce consistent estimates in the presence of exposure measurement error, we must assume transportability of the misclassification probabilities; that is, we assume that inclusion in the validation subgroup is independent of the gold-standard exposure, given the observed exposure and covariates included in the imputation model⁴⁵. Just as we must assume that a variable is missing at random given the observed data to use multiple imputation for missing data, we must assume that information on the gold standard exposure is missing at random (conditional on observed data) to use multiple imputation to account for measurement error.

The gold standard exposure is guaranteed to be missing at random when the validation subgroup is randomly selected from the study population (or randomly selected within strata of covariates) and participation is perfect. In our example, the validation subgroup was not randomly selected, but gold standard exposure information may still be missing at random if we measured all predictors of being included in the validation subgroup that also affect the misclassification probabilities and included these variables in the imputation model. However, we were not able to include study site as a predictor of patient-reported smoking in the imputation model because the patient-reported outcomes were collected at only 5 of the 8 study sites during the study period. If study site predicted smoking status, we may have residual bias due to measurement error. Finally, the validity of the estimates from the multiple imputation procedure depends not only on including all relevant covariates in the imputation model but also on correctly specifying their functional forms and including all relevant interactions between covariates.

One may wish to estimate the effect of exposure on outcome using patients in the validation subgroup alone. However, if a covariate influences both selection into the validation sample and the outcome, effects estimated from the validation sample alone may not be generalizable to the entire study sample, even if they are internally valid (e.g., not subject to measurement bias or selection bias) for the participants in the validation sample. In this case, multiple imputation can estimate the effect of exposure on outcome that is generalizable to the entire study sample because it allows the investigator to use information from all study participants. On the other hand, if the validation sample is randomly selected from the main study data, we would expect the estimate of effect from the validation sample to be generalizable to the entire study sample. In this case, multiple imputation still offers an advantage over using validation sample alone in terms of precision, though this advantage diminishes as the size of the validation sample relative to the main study increases.

Several alternative methods to account for measurement error are available. Regression calibration has been proposed to account for nondifferential measurement error in marginal structural models¹¹ and can be applied in studies with internal or external validation data, but regression calibration does not appear to work well with differential measurement error⁴⁶. Differential measurement error is possible if the provider’s classification of smoking status depends on predictors of mortality, a situation that is possible if health care providers are more likely to ask a sick patient about tobacco use, and therefore correctly classify that patient as a smoker or nonsmoker, than a healthy patient. Multiple imputation allows for differential exposure measurement error by including a term for the product between the misclassified exposure and the outcome in the imputation model. Alternatively, Bayesian methods can be used to account for measurement error in studies both with and without internal validation data^45,47–49.

We used multiple imputation to account for measurement error in a marginal structural model to estimate the joint effects of current smoking and therapy. These analyses were feasible in a large observational database due to improved measurement of smoking status for a subset of patients leveraging patient reported outcomes collected in addition to information from the electronic health record. Using Monte Carlo simulations, we showed that multiple imputation can be combined with a marginal structural model to produce consistent estimates of the hazard ratio in the presence of confounding and measurement error similar in magnitude to the measurement error of smoking seen in the CNICS cohort.

When estimating causal effects from observational data, with few notable exceptions^11,50,51 epidemiologists and biostatisticians have predominantly focused on accounting for bias due to confounding and selection, limiting consideration of measurement error to speculation in the Discussion sections of manuscripts. We have illustrated a technique to account for measurement error quantitatively that can be combined with modern methods to control confounding in observational settings.

Appendix

Imputation details

We used the monotone logistic method for multiple imputation to impute the smoking status S for each patient²³. In the validation sample, we fit the logistic regression

$$\text{logit}P(S=1|S^{*},\mathit{L},\delta ,\text{log}(Y),A,\text{log}(H))={\alpha }_0+{\alpha }_1{S}^{*}+{\alpha }_2\delta +{\alpha }_3\text{log}(Y)+{\alpha }_4\delta \text{log}(Y)+{\alpha }_5\delta S^{*}+{\mathit{\alpha }}_{\mathbf{6}}\mathit{L}+{\alpha }_{7}A+{\alpha }_8\text{log}(H)+{\alpha }_{9}A{S}^{*},$$

where S* is the provider-reported smoking status, δ is an indicator of death during the study period, Y is the time to death or censoring, L is a vector of time-fixed covariates, A is an indicator of initiating therapy during the study period, and H is the time from study entry to the first of therapy initiation, death, or censoring. We included interactions δS* and AS* to allow for differential measurement error of smoking with respect to mortality and therapy, respectively.

Next, for each of M imputations, we draw a set of regression coefficients α^m from a multivariate normal distribution with mean vector (α̂₀, α̂₁, α̂₂, α̂₃, α̂₄, α̂₅, α̂₆, α̂₇, α̂₈, α̂₉) and covariance matrix Σ̂_{S*,δ,log(Y),L,A,log (H)} estimated from the logistic regression above. In each imputation m, we draw the imputed smoking status S^m for patients not in the validation subgroup from a Bernoulli distribution with probability p^m, where $p^m=\text{expit}\{{\hat{\alpha }}_0^m+{\hat{\alpha }}_1^m{S}^{*}+{\hat{\alpha }}_2^m\delta +{\hat{\alpha }}_3^m\text{log}(Y)+{\hat{\alpha }}_4^m\delta \text{log}(Y)+{\hat{\alpha }}_5^m\delta S^{*}+{\hat{\mathit{\alpha }}}_{\mathbf{6}}^{\mathit{m}}\mathit{L}+{\hat{\alpha }}_7^{m}A+{\hat{\alpha }}_8^m\text{log}(H)+{\hat{\alpha }}_9^{m}A{S}^{*}\}$ and expit(·) = exp(·)/{1 + exp(·)}. For patients in the validation subgroup, S^m = S for all m.