Hyperspectral time-resolved wide-field fluorescence molecular tomography based on structured light and single-pixel detection

Abstract

We present a time-resolved fluorescence diffuse optical tomography platform that is based on wide-field structured illumination, single-pixel detection, and hyperspectral acquisition. Two spatial light modulators (digital micro-mirror devices) are employed to generate independently wide-field illumination and detection patterns, coupled with a 16-channel spectrophotometer detection module to capture hyperspectral time-resolved tomographic data sets. The main system characteristics are reported, and we demonstrate the feasibility of acquiring dense 4D tomographic data sets (space, time, spectra) for time domain 3D quantitative multiplexed fluorophore concentration mapping in turbid media.

Diffuse optical tomography (DOT) has been the focus of significant research endeavors over the last two decades, motivated by its noninvasive, nonionizing nature and high sensitivity for functional and/or molecular contrast in turbid media. DOT has been widely applied in breast tumor detection [1,2], brain activity monitoring [3,4], and preclinical small animal imaging [5,6]. The later application has been powered by the advances in molecular optical probes and focuses mainly, to date, in imaging fluorescence signals.

The performance of fluorescence DOT or fluorescence molecular tomography (FMT) system is determined by various factors such as spatial density of data collected, data type employed, forward model accuracy, and methods adopted to solve the inverse problem. It is well established that time-resolved (TD) DOT/FMT systems provide the most information-enriched data sets, enabling the imaging of tissue absorption/scattering with minimal crosstalk and the imaging of multiple molecular probes via fluorescence lifetime multiplexing [7,8]. In addition, the combination of early-arriving photons and late-arriving photons offers complementary information for improved resolution and quantification [9,10]. However, TD FMT’s advantages are traded off by its significantly longer data acquisition time compared to its continuous wave (CW) counterpart. For instance, typical TD FMT studies are limited to 2D cross-section imaging and mono wavelength acquisition but still require in the order of 30–45 min acquisition times [11,12]. Such lengthy and spatially limited imaging capability has hampered the wide spread dissemination of TD FMT for in vivo applications.

Recently, wide-field optical tomography techniques that rely on time-resolved structured illumination strategies have been proposed for small animal imaging [13–15]. These new approaches are poised to become the gold-standard as they offer the potential to image large volume at fast acquisition speed. By reducing the number of measurements required via spatially modulated illumination and decreasing the acquisition integration times, thanks to active illumination [16], whole body preclinical imaging is feasible in a few minutes, still with the high resolution, lifetime multiplexing, and quantitative accuracy offered by TD FMT [17]. However, such implementations still rely on monospectral excitation and detection. Herein, we expand on our previous spatial modulation single-pixel detection channel scheme for real time CW DOT [18], to time-resolved hyperspectral single-pixel acquisition. Specifically, we combine wide-field spatial modulation in illumination and detection with two digital micro-mirror devices (DMDs) to generate independently wide-field illumination and detection patterns to capture time-resolved tomographic data sets over large volumes. Our wide-field spatial modulated method was validated in time domain [19] by spatially integrating the ICCD camera measurements. Herein we employ a “single-pixel camera” instrumental approach. Moreover, it is well established that spectrally rich measurements can improve reconstruction accuracy and robustness of both DOT and FMT [20,21]. Hence, our DMD detection channel is coupled with a 16-channel time-resolved multi-anode photomultiplier tube (PMT) to capture hyperspectral time resolved tomographic data sets.

The instrumental layout of the proposed imaging platform is depicted in Fig. 1. Transmittance geometry is used for the sake of tomographic performances. The illumination source employed in the system is a Ti:sapphire laser (Spectra-Physics, Newport Corporation, CA) with 100-fs pulse-width, tunable in the spectrum from 690 to 1020 nm. The output power of the laser is controlled via a closed-loop power control system before being coupled into a multimode fiber. Then the light is focused into a DMD-based spatial light modulator (PK101 projector, Optoma, California) for shining time-resolved spatial patterns coded over 256 gray levels on the illumination area. Transmitted fluorescent signals after the turbid media are spatially integrated and modulated by a second DMD-based spatial light modulator (D4110 with S2+ optics module, Texas Instruments, Texas) with excitation light filtered by a bandpass or longpass filter. The spatially integrated light is then fed into a time-resolved multispectral PMT detector that is the combination of a polychromator (MS125, Oriel Instruments, Newport, Connecticut, US) and multi-anode PMT with 16 detection channels (PML-16-1-C, Becker and Hickl, Germany). A lightguide with converted cross-sections from circular to linear shape is applied for matching the output of spatial light modulator and the input of the polychromator. Time-correlated single photon counting (TCSPC) technique is employed for data acquisition (SPC-150, Becker and Hickl, Germany). The experimental intensity distributions of the patterns are recorded by a near-infrared (NIR) CCD camera, and the temporal instrument response functions (IRFs) are acquired for each experiments. These spatial and temporal calibrations are incorporated in our Monte Carlo forward model to ensure an accurate match between experimental data and simulation for optimal quantitative reconstructions.

Fig. 1.

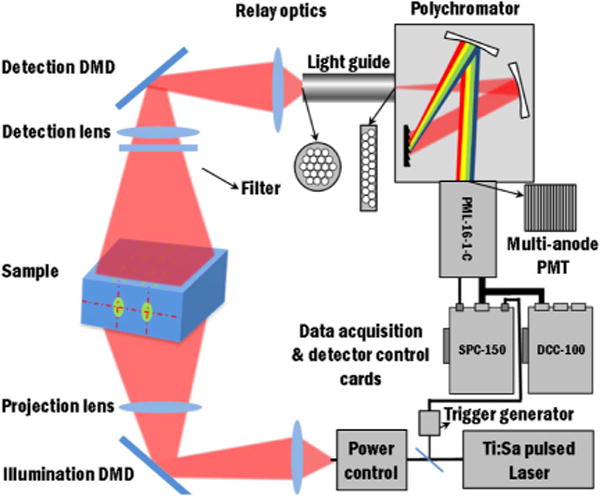
Schematic of the hyperspectral time-resolved wide-field DOT instrumental implementation.

To perform tomographic imaging, we employed the reconstruction methodology described in Ref. [10], but extended to multispectral data sets. Briefly, the forward-adjoint Monte Carlo (aMC) method is implemented to formulate the forward model, where the Jacobian matrix is obtained by calculating the product of illumination field and detection field. The time-gated fluorescence intensity measured for L lifetime components at the kth spectral channel (suppose data from N wavelength channels are used for reconstruction) is written as

$$U_k^f(r_s,r_d,t)={\displaystyle \sum _{n=1}^L{\displaystyle {\int }_{\mathrm{\Omega }}{W}_{n,k}(r_s,r_d,r,t){\eta }_{n,k}(r){\mathrm{d}}^{3}r}}$$ (1)

and

$$\begin{array}{l}{W}_{n,k}(r_s,r_d,r,t)={\displaystyle {\int }_0^t\mathrm{d}{t}^{\prime }{e}^{-(t-t^{\prime })/{\tau }_n}}\\ {\displaystyle {\int }_0^{t^{\prime }}\mathrm{d}{t}^{″}{G}^x}(r_s,r,t^{\prime }-t^{″})G_k^m(r,r_d,t^{″}),\end{array}$$ (2)

where r_s, r_d defines the illumination and detection location. Ω is defined as the entire imaging volume, and η_n,k (r) is the effective quantum yield distribution of the nth fluorophore at the kth wavelength channel. G^x and $G_k^m$ are Green’s functions for light propagation at excitation (x) and the kth emission wavelengths (m, k). τ_n is the lifetime of the nth fluorophore. Under the commonly employed assumption that the scattering coefficients are identical at excitation/emission wavelengths, thus

$$\begin{array}{l}{W}_{n,k}(r_s,r_d,r,t)=W_n(r_s,r_d,r,t)\\ ={\displaystyle {\int }_0^t\mathrm{d}{t}^{\prime }{e}^{-(t-t^{\prime })/{\tau }_n}}{\displaystyle {\int }_0^{t^{\prime }}\mathrm{d}{t}^{″}G}(r_s,r,t^{\prime }-t^{″})G(r,r_d,t^{″}).\end{array}$$ (3)

In addition, we employ a Born formulation where time-domain emission measurements are normalized by continuous wave excitation flux at the same position [10], to mitigate the dependence of the detected fluorescent signal on background optical properties. Therefore

$$\begin{array}{l}\frac{M_k^m(r_s,r_d,t)}{M^x(r_s,r_d)}=\frac{{\alpha }_k}{U^x(r_s,r_d)}\\ •{\displaystyle \sum _{n=1}^L{\displaystyle {\int }_{\mathrm{\Omega }}{\mathrm{d}}^{3}r{W}_n(r_s,r_d,r,t){\eta }_{n,k}(r)}},\end{array}$$ (4)

where α_k is wavelength dependent coefficient that incorporate unknown constants associated with the imaging system response and can be calibrated through controlled experiments. M^x (r_s, r_d) and U^x (r_s, r_d) are measured and simulated total excitation flux of a source-detector pair, and $M_k^m(r_s,r_d,t)$ is time domain fluorescence measurement from the kth wavelength channel. Then a system of linear equation is generated to cast the inverse problem using multiple time gates. This system, for multiple spectral channels can be expressed as

$$\left[\begin{array}{c}{\gamma }_{1,1}\\ \cdots \\ {\gamma }_{PG,1}\\ \cdots \\ {\gamma }_{1,N}\\ \cdots \\ {\gamma }_{PG,N}\end{array}\right]=\left[\begin{array}{ccc}{c}_{1,1}{\beta }_1{W}_{1,1}^{\mathrm{\Omega }}& \cdots & c_{L,1}{\beta }_1{W}_{1,L}^{\mathrm{\Omega }}\\ \cdots & \cdots & \cdots \\ c_{1,1}{\beta }_p{W}_{PG,1}^{\mathrm{\Omega }}& \cdots & c_{L,1}{\beta }_p{W}_{PG,L}^{\mathrm{\Omega }}\\ \cdots & \cdots & \cdots \\ c_{1,N}{\beta }_1{W}_{1,1}^{\mathrm{\Omega }}& \cdots & c_{L,N}{\beta }_1{W}_{1,L}^{\mathrm{\Omega }}\\ \cdots & \cdots & \cdots \\ c_{1,N}{\beta }_p{W}_{PG,1}^{\mathrm{\Omega }}& \cdots & c_{L,N}{\beta }_p{W}_{PG,L}^{\mathrm{\Omega }}\end{array}\right]\left[\begin{array}{c}{C}_1^{\mathrm{\Omega }}\\ \cdots \\ C_L^{\mathrm{\Omega }}\end{array}\right],$$ (5)

where the measurements of P source-detector pairs and G time gates in N wavelength channels are arranged in the left, and c_n,k = α_kε_n,kϕ_n,k is the overall coefficient for the nth dye under the kth channel, which is calibrated experimentally. ɛ_n,k and ϕ_n,k represent the extinction coefficients and quantum yields of the nth fluorophore at kth channel, and C_n (r) represents the concentration of the nth fluorophore. The 3D fluorophore concentration distribution is obtained through solving the inverse problem with L₁ regularization [22] using least square reconstruction as the initial guess.

The system tomographic capabilities are established through a solid phantom study aiming at mapping the relative concentration of two fluorescence dyes with lifetime contrast: Alexa Fluor 750 (Life Technologies, New York, buffered by phosphate buffered saline solution, lifetime: 0.52 ns) and 3; 3′-diethylthiatricarbocyanine iodide (DTTCI) (Sigma-Aldrich Corporation, Missouri, buffered by 100% ethanol, lifetime: 1.23 ns). Two tubes (3.0-mm inner diameter; 15.5-mm center-to-center distance) with dye inclusions (left: AF750 2.40 μM; right: DTTCI 12.24 μM) are suspended at 10-mm depth in the 20-mm-thick medium $({\mu }_a=0.1{\text{cm}}^{-1},{{\mu }^{\prime }}_s=9.6{\text{cm}}^{-1})$. The sample is excited at 750 nm, and hyperspectral data sets span to 10 wavelength channels centered in the 770–820 nm range. The transmitted light is encoded over 40 mm × 30 mm area on the sample with 36 bar-shape patterns [see Fig 2(a)] in both illumination and detection to yield a 36 × 36 measurements combination, the spatial distribution of illumination intensity for the full-field pattern is shown in Fig. 2(b). The ADC resolution of the TCSPC module is set as 256, resulting in a 48.9-ps temporal channel width over a 12.5-ns time window. The acquisition time for each illumination-detection pair is <10 s. An example of the hyperspectral datasets acquired is show in Fig. 2(c). The Monte Carlo simulation is performed using our extended hybrid parallel version mMC code [23], with 10⁹ photons launched for each illumination and detection pattern. The simulation for one pattern can be done in about 3.6 min with 128 nodes on CCNI at RPI.

Fig. 2.

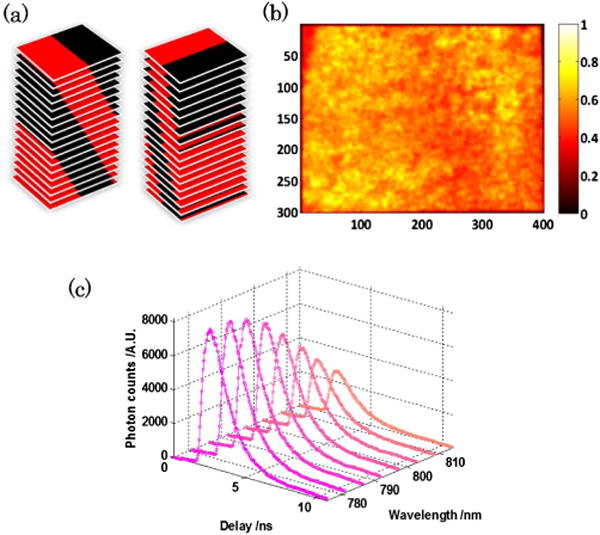
(a) The 36 bar-shape patterns used for generating 36 × 36 illumination-detection pairs. (b) Spatial intensity distribution of the full-field illumination pattern. (c) Hyperspectral dataset acquired for the 1st illumination-detection pair (only eight spectral channels are shown here).

The instrument response functions (IRFs) of the system under all wavelengths have a full-width at half maximum (FWHM) of ∼200 ps, indicating that the addition of DMDs in the optical chain and the integration of photons over large areas do not compromise the time-resolved characteristics of the measurements. The spatial and temporal IRFs are experimentally collected and employed within our wide-field mesh-based Monte Carlo forward model [23]. A comparison between experiment data sets both at excitation and emission with their counterpart from Monte Carlo simulations are provided in Figs. 3(a) and 3(b). The incorporation of spatial and temporal characteristics of the experimental patterns into simulation ensures an admirable agreement between simulations and measurements at all temporal points. In addition, the excellent agreement at early time gates shows the accuracy of our MC model in simulating minimally scattered photon propagation, which cannot be achieved through the diffusion equation.

Fig. 3.

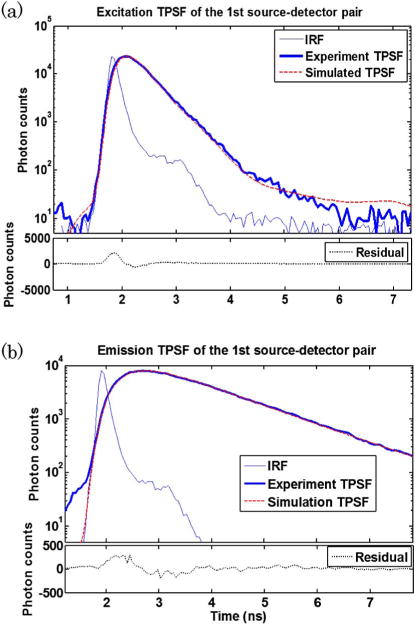
Comparison between experimental TPSF curves and simulated TPSF curves of (a) excitation measurement and (b) fluorescence emission measurement. The 1st illumination-detection pair is used as an example.

To cast the inverse problem, the temporal data set was reduced to eight temporal gates (peak gate and 75%, 60%, 50%, 40%, 35%, 30%, and 25% late gates) per channel and pattern combinations (CW data were obtained via time integration of the full TPSFs). Such reduction in temporal sampling allows casting a tractable inverse problem in terms of computational burden (memory) without compromising the multiplexing accuracy [24]. Second, three spectral channels were considered herein for reconstructions based on SNR considerations. The examples of the reconstruction results using CW measurements and time domain measurements with different wavelength channel combinations are shown in Figs. 4(a)–4(d) (red: AF750, blue: DTTCI). The stopping criteria of least square were set to 5 × 10⁻⁴ for CW and 1 × 10⁻³ for TD data set. And for each case, we selected the best regularization parameter based on the L-curve [see Fig. 4(e)].

Fig. 4.

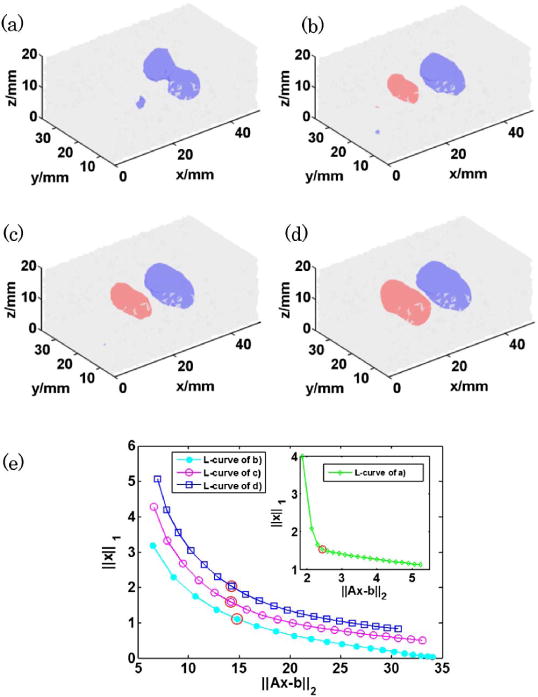
3D reconstruction from (a) CW measurements (792 nm channel), (b) TD measurements (792 nm channel), (c) TD measurements (786 nm + 792 nm channels), and (d) TD measurements (781 nm + 786 nm + 792 nm channels). (isovolume = 0.5 for all the reconstructions) (e) L-curves used for selecting the optimal L1 regularization parameter λ (highlighted with red circles).

As expected, TD reconstructions outperformed CW reconstructions by resolving spatially both inclusions and unmixing the two fluorophores. The addition of multiple spectral channels did increase the quantitative fidelity of the reconstructions. Especially, the higher crosstalk seen (AF750) was reduced by 20% when using multispectral versus using monospectral data sets. Similarly, the quantitative ratio of concentration between DTTCI and AF750 was improved by ∼17%.

In summary, a novel design of DOT system based on structured illumination and structured hyperspectral detection is presented. Two digital light processors (DMDs) are employed to code light into bar-shape patterns in illumination and single-pixel detection sides, respectively. The multi-channel PMT detector is applied to acquire multiplexing data sets in 16 wavelength channels simultaneously. The structured light encoding allows capturing hyperspectral time-resolved data sets for optical tomography. We are currently optimizing the optical chain and data acquisition workflow to achieve acquisition time less than 30 min. First, both temporal sampling and integration times can be significantly reduced without compromising reconstructions results. The inverse problem is typically cast with less than 10 temporal data, and time gates with as less as 100 photons can be employed reliably, whereas 256 temporal data for 16 wavelengths were acquired at very high signal-to-noise ratio (typically peak counts above 5 k per channel) in this work. Second, we are optimizing the system overall power efficiency to further enable fast imaging in low light conditions and implementing active wide-field optimization strategies based on compressive sensing theory [22] and subject-driven optimal dynamic data acquisition [25]. Last, we are still refining our reconstruction strategies as well as investigating the optimal combination of temporal, spectral and spatial sampling.