Current Issues in the Design and Analysis of Stepped Wedge Trials

Abstract

The use of stepped wedge designs in cluster-randomized trials and implementation studies has increased rapidly in recent years but there remains considerable debate regarding the merits of the design. We discuss three key issues in the design and analysis of stepped wedge trials - time-on-treatment effects, treatment effect heterogeneity and cohort studies.

1. Introduction

The use of stepped wedge designs in cluster-randomized trials and implementation studies has become increasingly common in recent years. In the first comprehensive literature review on this topic, Brown & Lilford (2007) found 12 references to papers incorporating stepped wedge designs. Four years later, Mdege et al. (2011) reported 25 citations. More recently, an informal PubMed search encompassing just the 7 month period August, 2014 – February, 2015 found 18 studies reporting use of the stepped wedge design, as well as additional methodological papers. In spite of this rapid increase in use, there remains considerable debate regarding the merits of the stepped wedge design.

Figure 1 illustrates a classic stepped wedge cluster randomized design compared to a standard parallel cluster randomized trial design. In general, a stepped wedge cluster randomized trial is any design in which the clusters cross over unidirectionally (in a randomized order) from the control or standard of care condition to the intervention condition in a staggered fashion such that the intervention effect is partly, but not completely, confounded with time. Outcome data collection must be synchronized in time between clusters. See Hemming et al. (2015) figures 1–3 for some variations of this design. Note that this relatively broad definition of the stepped wedge design includes some designs that Kotz et al. (2012b) include as variations of parallel designs. Nonetheless, we choose this definition to emphasize the unique features of this design – the unidirectional crossover and the partial confounding of intervention effect and time. Note that a before-after trial does not qualify as a stepped wedge design since the intervention effect is completely confounded with time in that design.

Figure 1.

Schematic representation of parallel versus stepped wedge cluster randomized designs with 8 clusters. Each row represents a cluster. C = Control condition, T = Treatment condition

An informative series of papers and letters (Mdege et al., 2011; Kotz et al., 2012b; Mdege et al., 2012; Kotz et al., 2012a; Hemming et al., 2013; Kotz et al., 2013; Hemming et al., 2015) lays out many of the strengths and weaknesses of the stepped wedge design. Table 1 summarizes key issues raised in these papers and others. In this manuscript we provide more detailed comments on three key issues relevant to the design and analysis of stepped wedge trials - delayed treatment effects, heterogeneous treatment effects, and cohort studies.

Table 1.

Summary of key issues regarding stepped wedge designs

Issue	Comments
Feasibility	No need to provide intervention to many communities at once Allows intervention to be rolled out in systematic manner
Social/Political	Provides intervention to all clusters/communities Intervention never removed once introduced Randomized order of introduction of the intervention perceived as “fair”
Duration	If step length fully adjustable, the trial duration can be fixed and steps added as convienent Likely longer duration than parallel design trial if steps have minimum length due to measurement of outcome data or need to wait for intervention to take effect Longer duration trials are more susceptible to contamination, external events
Delayed rollout/effects	Delayed rollout and/or intervention effect can reduce power Accounting for delayed rollout and estimation of time-on-treatment effects possible (see section 3)
Size	Requires fewer clusters than a parallel design but more measurements per cluster See discussion in Woertman et al. (2013), Hemming & Girling (2013) and de Hoop et al. (2013)
Participant burden	High, if longitudinal data collection on a cohort of participants; low, if repeated cross-sectional samples
Power	Insensitive to intracluster correlation Greater sensitivity to treatment heterogeneity (see section 4)
Analysis	Use modeling to separate time and intervention effects (see section 2) Typical methods are generalized linear mixed models and generalized estimating equations

2. Power calculation and analysis of stepped wedge trials

In this section we introduce notation and briefly review standard approaches for analyzing data and computing power in stepped wedge trials based on repeated cross-sectional samples (see section 5 for remarks on cohort-based trials).

Any analysis of data from a stepped wedge design must account for the intentional confounding of time and treatment as well as the correlation between repeated observations in the same cluster. Model based approaches include generalized linear mixed models (glmm) (Hussey & Hughes, 2007) or generalized estimating equations (gee) (Scott et al., 2015).

Hussey & Hughes (2007) propose the following model for data from a stepped wedge trial:

$$Y_{ijk}=\mu +{\alpha }_i+{\beta }_j+X_{ij}\theta +e_{ijk}$$ (1)

where Y_ijk denotes the response corresponding to individual k at time j from cluster i (i = 1 … I, j = 1 … T, k = 1 … m_ij), β_j are fixed time effects corresponding to interval j (β_T = 0 for identifiability), X_ij is an indicator of the treatment mode in cluster i at time j, θ is the treatment effect, μ is the mean of Y_ijk in the control or standard of care condition at time T, α_i is a random intercept for cluster i such that α_i ~ N(0, τ²), and $e_{ijk}~N(0,{\sigma }_e^2)$. Typically, X_ij = 1 if the intervention is provided in cluster i at time j and 0 otherwise. If m_ij = m for all i and j then an analysis of the cluster-level means (Ȳ_ij) is possible; however, if the cluster sizes vary then an analysis of individual-level data provides increased efficiency.

An important assumption of model (1) is that the underlying time effect is the same for each cluster. This assumption could be relaxed somewhat to allow groups of clusters (strata) to have different underlying time trends by adding a stratum main effect and a strata by time interaction. However, it is not possible to allow each cluster to have a separate time trend; such a model would be unidentifiable (unless one assumes a parametric form for the time trend).

The approximate power for testing the hypothesis H_o : θ = 0 versus H_a : θ = θ_A may be determined from the formula

$$\mathit{\text{power}}=\mathrm{\Phi }(\frac{{\theta }_A}{\sqrt{\text{Var}(\hat{\theta })}}-Z_{1-\alpha /2}).$$ (2)

For the special case were the X_ij are all 0 or 1 and m_ij = m, a closed form formula for Var(θ̂) based on model (1) is given in Hussey & Hughes (2007). For a “balanced” stepped wedge design (one with T time periods, I clusters (all of equal size m), all clusters starting in the control condition and h = I/(T − 1) (an integer) clusters crossing over from control to intervention at each time) Rhoda et al. (2011) show that

$$\text{Var}(\hat{\theta })=\frac{6(T-1)(1-\rho )({\sigma }_e^2+{\tau }^2)(1+(mT-1)\rho )}{mIT(T-2)(1+[\frac{m(T+1)}{2}-1\left]\rho \right)}$$ (3)

where $\rho ={\tau }^2/({\sigma }_e^2+{\tau }^2)$. For binary outcomes, one may set ${\sigma }_e^2=\mu *(1-\mu )$. Woertman et al. (2013) provide a formula for direct calculation of sample size by deriving a design effect for balanced stepped wedge cluster randomized trials (see also Hemming & Girling (2013) and de Hoop et al. (2013)).

More generally, for situations were the above do not apply (i.e. X_ij not 0 or 1, or all m_ij not equal), Var(θ̂) may be computed using basic results from generalized least squares (Draper & Smith, 1998). Specifically, let D be the design matrix from model (1) and V be the covariance matrix of Y. Then the appropriate diagonal element of (D′V⁻¹D)⁻¹ gives the variance of θ̂ (see appendix for details).

3. Delayed treatment effects

An important consideration in designing stepped wedge studies is the potential for loss of power associated with delayed intervention effects. Specifically, if the intervention is not fully effective in the time interval in which it is introduced then substantial reductions in power are possible, even for minor delays (Hussey & Hughes, 2007). Such delays can occur due to a slower than expected intervention rollout or due to an intrinsic lag between introduction of the intervention and its effect on the outcome.

The most effective approach to avoiding this loss of power is through careful study design. For instance, in a stepped wedge design the time intervals between steps should be long enough for the intervention to be rolled out and become fully effective (and for the outcome to be measured) within the time step in which the intervention is introduced. In some cases this may require a “wash-out” period between steps that allows enrolled individuals to provide outcome data but during which no new individuals are enrolled in the trial (Hemming et al., 2015). For example, in a clinic-based trial of approaches to providing antiretroviral (ART) medications to HIV-infected women to prevent mother-to-child transmission of HIV, Killiam et al. (2010) enrolled women during pregnancy but the endpoint (ART uptake) could occur anytime until delivery. A transition period was needed between the stepped wedge time steps to allow the women enrolled in the control condition to deliver their infants before introducing the intervention in the clinic. Women initiating clinic care during the transition period were not included in the analysis.

In other cases, there may be an intrinsic delay between provision of the intervention and realization of its effect and this may lead to an unacceptably long trial duration. For example, suppose one were interested in implementing a program of male circumcision to reduce HIV incidence in a community. Previous randomized trials (Auvert et al., 2005; Gray et al., 2007; Bailey et al., 2007) have shown that male circumcision reduces the risk of acquiring HIV by approximately 60% in heterosexual men. However, the effect of implementing a large-scale male circumcision program on community-wide HIV incidence (i.e. incidence among both women and men, circumsized or not) is unknown. Since implementation of a mass circumcision campaign would take time and be extremely resource intensive, an argument might be made to use a stepped wedge design to measure the program effect during rollout. Nonetheless, a stepped wedge would be a poor design choice in such a situation. The effect of male circumcision on community-level HIV incidence depends not only on direct effects (protecting the circumcised men) but also on indirect effects (protecting partners, and partners of partners, of the circumcised men by breaking chains of infection). Modeling predicts that the full effect of a mass circumcision intervention would take years to be realized (Alsallaq et al., 2013), but a stepped wedge design with multi-year time steps is likely impractical. As an alternative, a stepped wedge design that measured a process outcome, such as number of men circumcised in each interval, would be feasible. Of course, additional modeling work and assumptions would be needed to relate this outcome to community-level HIV incidence.

In some cases, clever design can overcome a delay between provision of an intervention and its effect. The Gambia Hepatitis Intervention Study (Hall et al., 1987) used a stepped wedge design to roll out a Hepatitis B vaccination program to infants in 17 districts in The Gambia over a 4 year period. One objective for the trial was to show an increase in HBV titers due to the intervention. This endpoint is highly amenable to the stepped wedge design as there is little delay between vaccination and development of a detectable HBV titer. However, the primary objective of the trial was to show a decrease in hepatocellular cancer and other chronic liver disease due to the vaccination program. Since a reduction in hepatocellular cancer and liver disease due to infant HBV vaccination would take many years to be realized, it would appear as though this objective is incompatible with the trial design. However, during the rollout of the vaccination program a national registry to record all cases of hepatocellular cancer and other chronic liver diseases was created in The Gambia. When a case is entered in the registry, the birthdate and birthplace of the affected individual is also recorded. Over the years, as individuals born during the HBV vaccination program rollout enter the registry, the birthdate/birthplace information can be used to assign each case of disease to the appropriate cluster and time step in the stepped wedge design, thereby making an analysis of the long-term effects of infant HBV vaccination possible (Viviani et al., 2008). In contrast, if one were to simply measure incidence of liver disease over time, without the ability to explicitly link cases back to the original cluster-time steps, it is highly unlikely that changes in incidence 30 years after the (4 year) rollout of vaccination would yield interpretable information about the intervention effect due to the variable time of disease onset, migration, etc.

3.1. Estimation of time-on-treatment effects

In spite of the best efforts of investigators, however, unexpected delays in the intervention rollout or effect may occur. Although model (1) assumes complete rollout of the intervention in the time step when it is introduced and a constant intervention effect, these assumptions can be relaxed. If a delay in realizing the full effectiveness of the intervention is due to a slower than expected or incomplete rollout of the intervention, and if a measure of the completeness of the intervention rollout in a given interval is available, then this measure can be included in the analysis by setting the X_ij in model (1) to fractional values between 0 and 1 (Hussey & Hughes, 2007). This is effectively an “as-treated” analysis (while the use of X_ij equal to 0 or 1 is comparable to an intent-to-treat analysis). For example, in a stepped wedge trial to access the impect of expedited partner treatment trial (EPT) on gonorrhea and chlamydia prevalence in Washington state (Golden et al., 2015) an estimate of the proportion of STI patients who were offered EPT was obtained through a random survey of individuals diagnosed with gonorrhea or chlamydia. This information could be used in the analysis to adjust for less than complete provision of the intervention. Note, however, that this approach assumes that the effect of the intervention on the outcome is directly proportional to the amount of the intervention provided.

A similar approach can also be used to account for delayed treatment effects (time-on-treatment effects). Suppose prior modelling or theory predicts that the intervention will only be 50% effective in the time interval in which it is introduced and 100% effective thereafter. Then, as above, the X_ij may be set to fractional values to incorporate this (prior) knowledge into the analysis.

If the completeness of the intervention rollout or the expected fractional treatment effect in each interval is unknown, then the time-on-treatment intervention effect can be estimated from the data. This can be accomplished by extending model (1) to

$$Y_{ijk}=\mu +{\alpha }_i+{\beta }_j+L_{ij\ell }{\theta }_{\ell }+e_{ijk}$$ (4)

where ℓ is the number of time steps since the intervention was introduced (ℓ = 0 for control intervals, ℓ = 1 in the time step in which the intervention is introduced, ℓ ≤ T − 1) (Scott et al., 2015). Setting L_ijℓ = 1 if the j^th time interval in the i^th cluster is ℓ (≥ 1) intervals since the introduction of the intervention and 0 otherwise provides an estimate of the time-on-treatment effects, θ_ℓ. The global hypothesis H_o : θ₁ = θ₂ = … = θ_T−1 can be used to test for a time-on-treatment effect. Parametric functional forms for the time-on-treatment effect that are linear in θ_ℓ (e.g. L_ijℓ = ℓ and θ_ℓ = θ) may be directly incorporated in equation (4) and estimated using standard statistical methods (glmm or gee).

Alternatively, a nonlinear model for time-on-treatment may be of interest. For example, the following model would be appropriate for an intervention that is thought to increase to a long-term maximum effect over time following introduction

$${\theta }_{\ell }={\theta }_0(1-e^{-\ell /d})$$ (5)

where d indexes the rate with which the intervention approaches its full long-term effect, θ₀ (which may be positive or negative). Granston (2013) proposes using a two-stage estimation procedure to fit this model:

1. Fit model (4)

2. Use the θ̂_ℓ from step 1 and nonlinear weighted least squares to fit model (5) with weights given by the covariance matrix of the θ̂_ℓ from step 1.

A bootstrap procedure is used to obtain standard errors of the parameters.

3.2. Effect of delayed treatment effects on power

The generalized least squares framework (section 2 and appendix) can be used to predict the expected attenuation in the estimated treatment effect and associated loss of power due to a delay in the treatment effect or incomplete rollout of the intervention. Let D^a be a design matrix that is identical to D except that the last column (corresponding to the X_ij) contains fractional numbers that represent the the expected fractional rollout of the intervention or the expected fractional treatment effect in each cluster at each time point. Let b be the vector (of length T + 1) of expected parameters under the alternative hypothesis, (μ, β₁ … β_T−1, θ_A). Then, if the data are analyzed without accounting for the delayed treatment effect (i.e. using D instead of D^a in the analysis),

$$E(\hat{b})={(D\prime V^{-1}D)}^{-1}D\prime V^{-1}{D}^{a}b.$$ (6)

The (T +1)’st element of E(b̂) is ${\theta }_A^a$, the adjusted treatment effect under the delayed effect/rollout scenario. ${\theta }_A^a$ can be substituted for θ_A in equation (2) to determine the power of an analysis that fails to account for the delayed rollout/effect.

A correct analysis would incorporate the delayed treatment effect as described in section 3.1. If the delay is expressed using fractional treatment effects then the power may be computed using equation (2) with the original value of the treatment effect, θ_A, and with Var(θ̂) computed from (D^a′V⁻¹D^a)⁻¹. Note that this approach is appropriate for computing power when known fractional values are used for the X_ij but not when the delayed treatment effect is estimated from the data. The latter is an area of ongoing research.

4. Treatment Effect Heterogeneity

Hussey & Hughes (2007) argue that variations in the mean response from cluster to cluster in model (1) (as quantified by τ² or ρ) have little effect on power when designing a stepped wedge trial. Intuitively, this is because part of the information on the intervention effect is coming from the within-cluster comparisons (adjusted for time trends) in which each cluster serves as its own control. In a within-cluster comparison the α_i in model (1) effectively cancels out when taking the difference between the intervention and control time periods, making variations in this term irrelevant.

However, model (1) assumes that the intervention effect, θ, is constant across clusters. In many circum-stances it is plausible that the effect of the intervention may vary from cluster to cluster due to variation in the quality of implementation or other factors. Thus, model (1) may be extended to include treatment heterogeneity:

$$Y_{ijk}=\mu +{\alpha }_i+{\beta }_j+X_{ij}\theta +X_{ij}{\gamma }_i+e_{ijk}$$ (7)

where γ_i ~ N(0, η²) is a random treatment effect for cluster i. Powering a stepped wedge design trial based on model (7) can still use equation (2) but now requires specification of three variance components: τ², η², and ${\sigma }_e^2$ to compute Var(θ̂). In this situation, no simple formula for Var(θ̂), analogous to equation (3), is possible; rather, Var(θ̂) must be obtained by computing (D′V⁻¹D)⁻¹ as described in section 3.2 and the appendix.

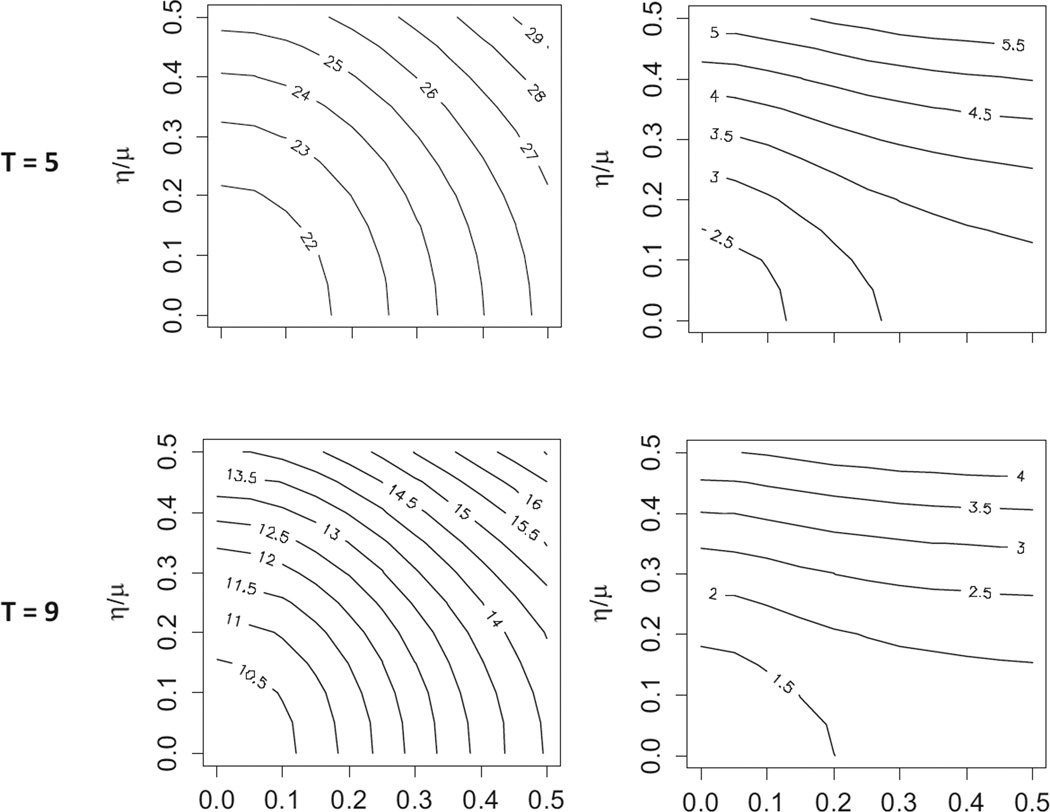
Importantly, the magnitude of η² can have a significant effect on power. Figure 2 shows the effect of variations in the magnitude of τ² and η² on Var(θ̂) for various choices of T and m in a balanced stepped wedge trial (we ignore I since, in a balanced stepped wedge trial, the number of clusters affects only the magnitude, but not the shape, of the contours shown in figure 2). In these examples, variation in T has minimal effect on the shape of the contours, although, of course, Var(θ̂) declines as T increases. However, variation in m has a significant effect on the shape of the contours. Specifically, for small m, variations in both τ² and η² have a significant effect on Var(θ̂). However, for large m (such that ${\sigma }_e^2/m\ll {\tau }^2$) the value of τ² has little effect on Var(θ̂) and, hence, little effect on power but variations in η² continue to have a significant effect on Var(θ̂), regardless of the size of m. As seen in the figure, increases in η² result in increases in Var(θ̂) and, hence, decreases in power.

Figure 2.

Contours of Var(θ̂) × 10⁵ as a function of τ and η for selected m and T using the Washington State Expedited Treatment Trial (??) balanced stepped wedge design: μ = 0.05, σ² = 0.05 * 0.95, 24 clusters and h = 6 (T = 5) or h = 3 (T = 9)

The preceding observations suggest that a reasonable estimate of treatment effect heterogeneity, as quantified by η, should be included in power calculations when designing a stepped wedge trial. If preliminary data are available then these can be used to estimate η (and τ). However, if no such data are available then we have found that conducting the following thought experiment with knowledgeable investigators can be useful in deriving reasonable values of η and τ. We first orient the discussion by identifying reasonable values for the overall mean of the outcome (or prevalence for a binary outcome), μ, and the average intervention effect, θ. Then we explain that the “true” mean of each cluster may vary around μ, where variations in the true mean reflect underlying differences between the clusters, not sampling variability. We ask the investigators to specify a range around μ that should include the true mean response for “almost all” the clusters. We take this range to represent an interval that includes 95% of the cluster means (i.e. ±2τ), so τ = (range in means)/4. Similarly, we ask the investigators to specify the cluster to cluster variation in intervention effects as a range of possible intervention effects, centered around θ. Then, η = (range in intervention effects)/4.

An R package, swCRTdesign, containing functions for power computation (accommodating treatment heterogeneity) and summarizing data from a stepped wedge design, is available at http://faculty.washington.edu/jphughes. A Stata package for doing power calculations is described by Hemming & Girling (2014).

5. Cohort Studies

The discussion above has focused primarily on data collected cross-sectionally at each time point. Although there have been fewer examples and less methodological development for stepped wedge studies in which cohorts of individuals are enrolled and followed for multiple time periods, the THRio study (Duronvi et al., 2013) provides one such example. The THRio trial was designed to evaluate a program for increasing provision of isoniazid prophylaxis therapy to prevent tuberculosis in HIV-infected individuals. Moulton et al. (2007) used a simulation approach to determine power and the final analysis of the trial used a Cox proportional hazard model in calendar time (so the baseline hazard incorporated any underlying time trends in incidence), a gamma-distributed random effect to control for clustering, and a time-varying covariate to capture the intervention effect (Duronvi et al., 2013).

This example illustrates some of the key issues that must be considered in the design and analysis of a cohort-based stepped wedge design, including i) individuals, as well as clusters, may cross over from the control to the intervention condition, ii) repeated measures may be collected on individuals leading to two levels of correlation (cluster and individual), and iii) loss-to-followup. Additional issues, not illustrated in the THRio study, but that may be relevant to cohort trials include iv) healthy survivor bias, where occurrence of the outcome removes individuals from the risk set (i.e. death, HIV, etc), and v) interval-censoring, in which the event time for a participant may only be known to occur within a period that overlaps the transition from control to intervention. Some results on the analysis of stepped wedge studies with time-to-event data and interval-censoring are provided in Granston (2013) but additional research is needed on power calculations and analytic approaches for stepped wedge studies using repeated measures and cohort data.

6. Conclusion

In summary, the stepped wedge design is a useful tool for clinical and implementation science research, particularly in situations where a parallel design study is viewed as infeasible, unethical or otherwise unacceptable. However, those contemplating use of a stepped wedge design must be aware of the limitations of the design, particularly with respect to issues around modeling assumptions, delayed effects, and treatment effect heterogeneity.

Appendix

In this appendix we give a detailed description of the construction of the design and covariance matricies that can be used for power calculations in non-standard designs. We use the notation introduced with equation 1.

Let M = (∑_ij m_ij) be the total number of observations across clusters and time periods. In general, the design matrix, D, and the covariance matrix, V, have dimension M × (T + 1) and M × M, respectively, if the analysis is at the individual-level and dimension IT × (T +1) and IT × IT, respectively, if the analysis uses cluster-time summaries.

Consider a stepped wedge design with 3 clusters and 4 time periods:

$$\begin{array}{cc}\hfill \hfill & \hfill \text{time}\hfill \\ \hfill \begin{array}{c}\hfill \text{cluster}\hfill \\ \hfill 1\hfill \\ \hfill 2\hfill \\ \hfill 3\hfill \end{array}\hfill & \hfill \begin{array}{cccc}\hfill 1\hfill & \hfill 2\hfill & \hfill 3\hfill & \hfill 4\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\hfill \end{array}$$

where 0 indicates the control condition and 1 indicates the intervention condition.

Assuming model (7) with the analysis at the cluster-time level and parameter vector (μ, β₁, β₂, β₃, θ), then

$$D=\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ (8)

Notice that the last column of D corresponds to the X_ij. V is given by

$$V=\left(\begin{array}{ccc}\hfill V_1\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill V_2\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill V_3\hfill \end{array}\right)$$ (9)

where

$$V_1=\left(\begin{array}{cccc}\hfill {\sigma }_e^2/m+{\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill \end{array}\right),$$

$$V_2=\left(\begin{array}{cccc}\hfill {\sigma }_e^2/m+{\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2+{\eta }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill \end{array}\right),$$

$$V_3=\left(\begin{array}{cccc}\hfill {\sigma }_e^2/m+{\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\eta }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\eta }^2\hfill & \hfill {\tau }^2\hfill \\ \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\tau }^2\hfill & \hfill {\sigma }_e^2/m+{\tau }^2+{\eta }^2\hfill \end{array}\right),$$

and 0 is a 4 × 4 matrix of 0’s. Note that if η = 0 (no variation in the intervention effect among clusters) then V₁ = V₂ = V₃ and V is the block diagonal covariance matrix used by Hussey & Hughes (2007). The variance of θ̂, which is used for power calculations, is given by the [T + 1, T + 1] element of (D′V⁻¹D)⁻¹).