Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Nov 10;5:16345. doi: 10.1038/srep16345

Electron Beam Induced Artifacts During in situ TEM Deformation of Nanostructured Metals

Rohit Sarkar 1, Christian Rentenberger 2, Jagannathan Rajagopalan 1,a
PMCID: PMC4639785  PMID: 26552934

Abstract

A critical assumption underlying in situ transmission electron microscopy studies is that the electron beam (e-beam) exposure does not fundamentally alter the intrinsic deformation behavior of the materials being probed. Here, we show that e-beam exposure causes increased dislocation activation and marked stress relaxation in aluminum and gold films spanning a range of thicknesses (80–400 nanometers) and grain sizes (50–220 nanometers). Furthermore, the e-beam induces anomalous sample necking, which unusually depends more on the e-beam diameter than intensity. Notably, the stress relaxation in both aluminum and gold occurs at beam energies well below their damage thresholds. More remarkably, the stress relaxation and/or sample necking is significantly more pronounced at lower accelerating voltages (120 kV versus 200 kV) in both the metals. These observations in aluminum and gold, two metals with highly dissimilar atomic weights and properties, indicate that e-beam exposure can cause anomalous behavior in a broad spectrum of nanostructured materials, and simultaneously suggest a strategy to minimize such artifacts.

Metallic materials with sub micrometer microstructural or sample dimensions exhibit mechanical properties that are distinct from their bulk, coarse-grained counterparts1,2,3,4,5,6,7,8,9,10. Transmission electron microscopy (TEM), because of its atomic scale resolution and the capability to measure crystal rotations and lattice strains using diffraction, has been extensively used to understand the deformation behavior of such materials11,12,13,14,15,16,17. In particular, in situ TEM straining experiments have provided insights into the deformation mechanisms18,19,20, inelastic strain recovery21,22, grain rotation and growth23,24,25, and generation and motion of dislocations26,27,28 in nanocrystalline and ultrafine-grained metals. More recently, a combination of conventional TEM and automated crystal orientation mapping has enabled further insights into the mechanisms of grain growth and deformation29,30,31.

While TEM is a fundamental technique to characterize nanoscale materials, it is also well known that the high energy of the electron beam (e-beam) used in TEM can cause radiation damage in the materials being probed32. In addition, the e-beam can activate dislocations, and defects generated by e-beam exposure can lead to additional deformation processes. For example, low to moderate intensity e-beam has been used to induce superplastic deformation in nanoscale silica particles and nanowires that are usually brittle at low temperatures33. Since nanocrystalline and ultrafine-grained metals have a high density of crystal defects (non-equilibrium grain boundaries and associated extrinsic dislocations) that can be activated by the e-beam, it is quite conceivable that e-beam exposure will alter the mechanical behavior of such materials during in situ experiments. However, the e-beam effect on the in situ deformation response of nanostructured materials remains unknown.

Here, using quantitative in situ TEM tensile straining of aluminum and gold films with a range of thicknesses (80–400 nm) and mean grain sizes (d ~ 50–220 nm) we provide direct evidence that e-beam exposure causes increased dislocation activation, significant stress relaxation and anomalous changes in sample geometry. By systematically controlling the beam conditions (accelerating voltage, intensity and beam diameter) during cyclic deformation and stress relaxation experiments we show that, contrary to expectation, beam-induced artifacts are much more pronounced at lower accelerating voltages (120 kV compared to 200 kV). In addition, the experiments reveal that e-beam exposure causes an unexpected necking of the samples along their width, which depends more on the beam diameter than intensity. These observations in two metals with highly dissimilar atomic weights and properties strongly suggest that the e-beam can significantly alter the deformation response of a broad spectrum of nanostructured materials. At the same time, the results also point to strategies that can be adopted to minimize beam-induced artifacts during in situ TEM testing.

Experimental

Two Al films, 225 nm and 400 nm thick, respectively, and one Au film, 80 nm thick, were deposited on 200-μm thick, 100 mm diameter, (100) silicon (Si) wafers using DC magnetron sputtering. Before deposition, the Si wafers were etched with hydrofluoric acid to remove the native silicon dioxide layer. The 225 nm thick Al film (from here on referred to as Al-225 film) and Au film were deposited immediately after the removal of the silicon dioxide layer at base pressures of 1.5 × 10−8 Torr and 5 × 10−8 Torr respectively. The 400 nm thick Al film (from here on referred to as Al-400 film) film was deposited at a base pressure of 1.5 × 10−7 Torr about 1.5 hours after the removal of the oxide layer. For all depositions, the argon pressure was 3 mTorr and the deposition rate was between 4–5 nm/minute. Dog-bone shaped freestanding samples were then co-fabricated with micro-electro-mechanical systems (MEMS) based tensile testing devices (Fig. 1) using photolithography and plasma etching techniques described in34. The MEMS devices, with a width of 2.5 mm and length of 9 mm, have built-in force and displacement sensing gauges to measure the stress and strain during in situ TEM straining. The effective gauge length of all the samples was 395 μm, whereas the width was 30 μm.

Figure 1. MEMS device and experimental setup:

Figure 1

Open in a new tab

(a) Optical micrograph of a typical MEMS device mounted on the TEM straining holder. (b) Optical micrograph of the MEMS device showing the force sensing beams. (c) Optical micrograph showing the freestanding Al sample and the strain and force measuring gauges. (d) Zoomed in image of the two strain sensing gauges x and y and the stationary force sensing gauge, z. The change in distance between gauges x and y gives the deformation on the sample while the change in distance between gauges x and z multiplied by the stiffness of the force sensing beams gives the force acting on the sample.

The MEMS devices with the freestanding film samples were mounted on a displacement controlled single tilt straining holder and the films were subjected to cyclic deformation inside a Philips CM200 TEM equipped with a LaB6 cathode. In each of the straining cycles the beam condition was systematically controlled as follows. The beam intensity was varied for a given beam area by changing the e-beam current. The beam current was controlled by altering the Wehnelt bias, the filament heating current of the TEM and the size of the condenser aperture. In all the experiments the microstructure was observed under TEM bright field conditions and recorded using an Orius GatanTM CCD camera.

Strain pulses (typically corresponding to <0.1% strain) were applied to the sample, following which the sample was allowed to relax for a period of 5 minutes and the stress-strain data was then recorded. Two types of experiments were performed to quantify the effect of e-beam exposure. In the first set of experiments, the stress-strain response of the Al-225, Al-400 and Au film during the first cycle was measured without e-beam exposure to serve as a reference. In the subsequent cycles, the films were exposed to the e-beam at different accelerating voltages and the beam diameter (area) and intensity were systematically varied. In the second set of experiments on the Al-225 film, the sample was exposed to the e-beam only at two points during each loading to quantify beam-induced stress relaxation. At both these points, stress-strain data was recorded for a period of 15 minutes, typically at 5-minute intervals. Table 1 and 2 show the beam conditions for all the experiments.

Table 1. Beam conditions and stress response of Al-225, Al-400 and Au film during cyclic deformation.

Al-225 Cycle Voltage (kV) Area (μm2) Current (nA) Intensity (A/cm2) σ1% (MPa)
  1 0 0 0 0 380
  2 80 12.5 44 0.352 358
  3 120 201 103 0.051 362
  4 200 201 61 0.03 408
  5 200 804 61 0.007 419
  6 120 804 103 0.012 445
Al-400 Cycle Voltage (kV) Area (μm2) Current (nA) Intensity (A/cm2) σ0.75% (MPa)
  1 0 0 0 0 120
  2 120 201 14 0.0069 109
  3 200 201 10 0.0049 167
Au Cycle Voltage (kV) Area (μm2) Current (nA) Intensity (A/cm2) σ1% (MPa)
  1 0 0 0 0 443
  2 120 7 95 1.357 395
  3 200 7 95 1.357 464
Open in a new tab

Table 2. Beam conditions and stress response of Al-225 film during relaxation experiments.

Cycle Voltage (kV) Area (μm2) Current (nA) Intensity (A/cm2) 1st Stress Drop (%) 2nd Stress Drop (%)
1 120 201 71 0.035 8.06 7.79
2 200 201 71 0.035 2.88 6.24
3 120 804 61 0.0075 7.37 10.63
4 200 804 66 0.0082 4.32 7.79
Open in a new tab

The stress-strain response of the films was obtained by analyzing images of the built-in force and displacement gauges during deformation, using a custom MATLABTM program. The program tracks prescribed features using cross-correlation techniques across a series of images to calculate the displacement of the gauges. Using this process, stress and strain resolutions better than 2 MPa and 0.005%, respectively, were obtained for both Al and Au films.

Once the raw stress-strain data was obtained, the data was fitted with polynomial functions to obtain the stress at a given strain. To avoid over fitting, for both loading and unloading the polynomial order was chosen so that there were at least three data points for each coefficient. Typically, fourth order polynomials were used to fit the stress-strain data for loading and third order polynomials were used for unloading. For stress-relaxation, for which only four or fewer data points were measured, a linear fit was chosen. The R2 value was higher than 0.995 for all the loading and unloading fits. Similarly, the R2 value for fits to the stress relaxation data exceeded 0.98 except for the first stress drop in the 2nd cycle (R2 = 0.804), when the relaxation was very small (Table 2). The equations of the fitted curves were then used to extract the stress at 1% strain (σ1%) for the Al-225 and Au films, the stress at 0.75% strain (σ0.75%) for the Al-400 film and the stress drop for relaxation experiments on the Al-225 film. σ1% and σ0.75% were calculated for a particular cycle after offsetting the stress-strain curve to account for residual plastic strain from previous cycles. To ensure robustness of the analysis we also calculated σ1% and σ0.75% from higher order and lower order polynomial fits, but observed no meaningful changes.

Results

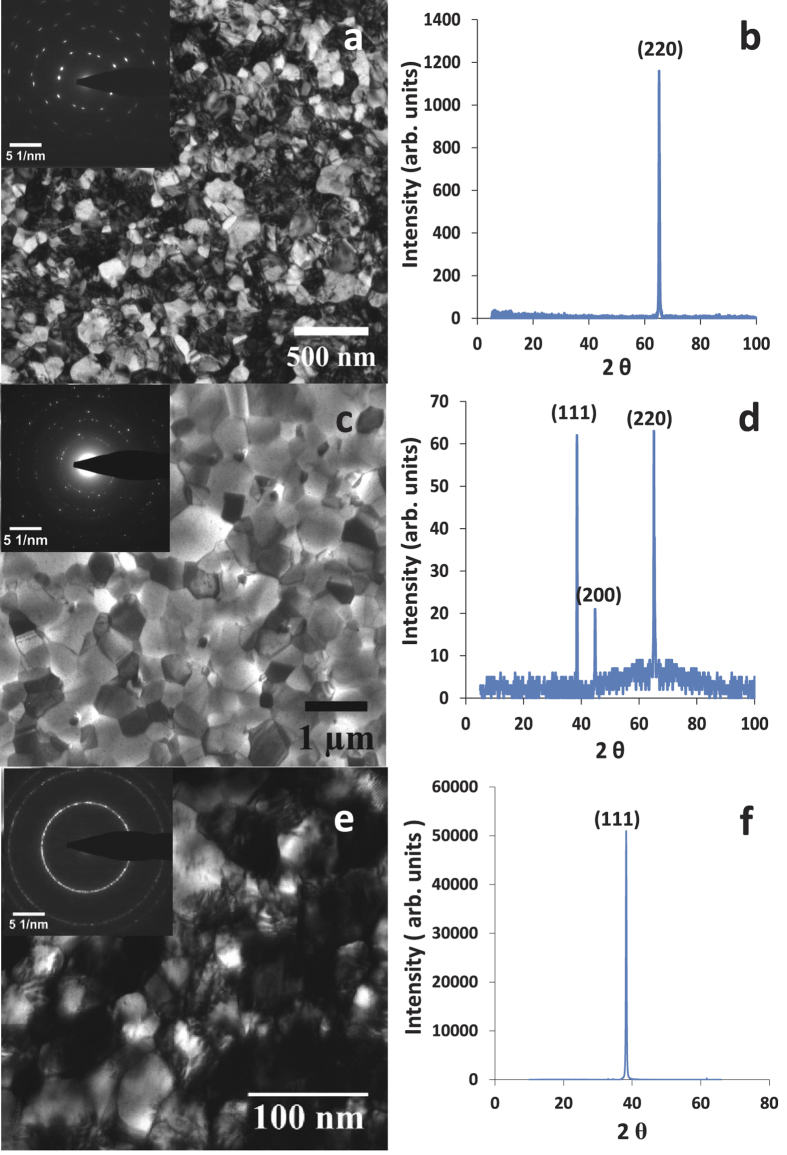
The microstructure of the films was characterized by TEM and x-ray diffraction (XRD). The analyses (Fig. 2a,b) revealed a d of 120 nm and an (110) out-of-plane texture with only two in-plane grain variants (bicrystalline microstructure) for the Al-225 film. The Al-400 film had a higher d of 220 nm and a mild (110) out-of-plane texture with random in-plane grain orientations (Fig. 2c,d), whereas the Au film had a d of 50 nm and a strong (111) out-of-plane texture with random in-plane grain orientations (Fig. 2e,f).

Figure 2. Microstructure of Al and Au films:

Figure 2

Open in a new tab

(a) Bright-field TEM image and selected area diffraction (SAD) pattern (inset) of the undeformed Al-225 film (d = 120 nm). The SAD pattern shows an (110) out-of-plane texture with two in-plane grain variants rotated 900 with respect to each other. (b) XRD scan of the Al-225 film. (c) Bright-field TEM image of the undeformed Al-400 film (d = 220 nm). The ring like SAD pattern (inset) reveals random in-plane grain orientations. (d) XRD scan of the Al-400 film. The (111) and (220) peaks have similar intensities, whereas in random polycrystalline Al their ratio is 10:3, which shows a mild (110) out-of-plane texture. (e) Bright-field TEM image and SAD pattern (inset) of the undeformed Au film (d = 50 nm). (f) XRD scan of the Au film showing an (111) out-of-plane texture.

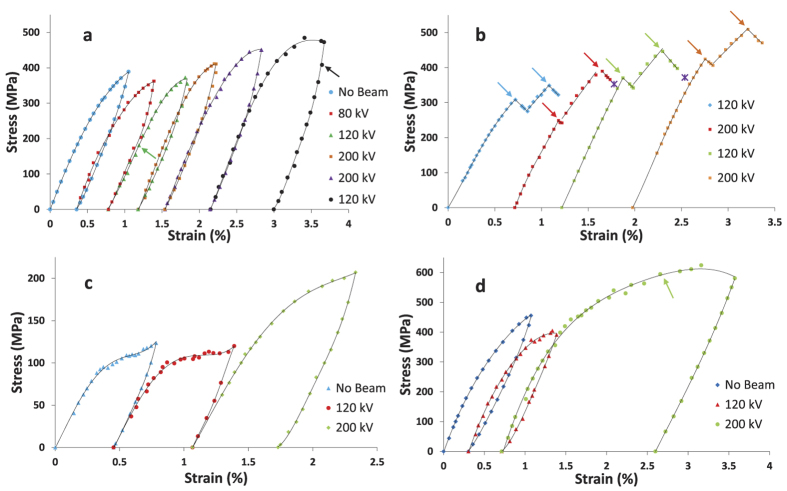
Figure 3 shows the stress-strain response of the films for the cyclic loading and stress relaxation experiments under different beam conditions. To quantify the e-beam effect on the stress-strain response during the cyclic loading experiments, we compare the stress at the same strain level during each cycle, after offsetting the stress-strain curve to account for residual plastic strain from previous cycles. For the Al-225 and Au film, σ1% is used for comparison. The overall trend is very similar even if we use the stress at a lower strain level for comparison. The Al-400 film started deforming plastically at lower strain and hence was subjected to smaller strains during each cycle. Therefore, we compare the σ0.75% during each cycle. σ1% for the Al-225 and Au film and σ0.75% for the Al-400 film during each cycle is summarized in Table 1.

Figure 3. Cyclic stress-strain response and stress relaxation of Al and Au films:

Figure 3

Open in a new tab

(a) Stress-strain response of the Al-225 film over six cycles under different beam conditions. A reduction in stress can be observed for the 2nd and 3rd cycle with respect to the 1st cycle. The imaging conditions for the different deformation cycles are summarized in Table 1. The green and black arrows correspond to Fig. 4 and supplementary video 2 (videoS2), respectively. (b) Beam induced stress relaxation in the Al-225 film. The film was exposed to the e-beam only at two points during each loading (indicated by arrows). At the end of the 2nd and 3rd cycles, the e-beam was moved to a new location, which led to significant additional relaxation (indicated by the violet cross). (c) Stress-strain response of the Al-400 film over three cycles with different beam conditions. (d) Stress-strain response of the Au film over three cycles with different beam conditions. The green arrow in (d) corresponds to supplementary video 4 (videoS4). In all the figures, the black lines correspond to fitted polynomials while the individual points indicate raw data.

In cyclic loading of metal films, the stress for a given strain is usually higher in the later cycles due to strain hardening. However, σ1% for the Al-225 film (Table 1, Fig. 3a) decreased from 380 MPa in the 1st cycle (no e-beam exposure) to 358 MPa in the 2nd cycle (80 kV beam). Notably, σ1% for the 3rd cycle (120 kV beam) was still ~5% lower than the 1st cycle despite the significant plastic deformation induced in the film during the first two cycles. This clearly shows the effect of e-beam exposure on the stress-strain response of the Al-225 film. When the accelerating voltage was increased to 200 kV in the 4th cycle, σ1% was markedly higher (408 MPa) compared to both the 3rd and 1st cycle. Between the 4th and 5th cycle, the accelerating voltage and beam current (area times intensity) were kept constant but intensity was reduced 4-fold, which resulted in a slight increase of σ1% to 419 MPa. In the 6th cycle, the accelerating voltage (120 kV) and beam current were made identical to the 3rd cycle but the intensity was reduced 4-fold by spreading the beam. In addition, the e-beam was shifted to a previously unexposed region of the sample. This led to an increase in σ1% to 445 MPa.

The marked increase in σ1% of the Al-225 film between the 3rd and 4th cycle (Table 1) suggested that beam-induced stress relaxation is higher at 120 kV compared to 200 kV. However, the e-beam intensity and current were different for those cycles and hence a definitive conclusion could not be made. To unambiguously verify if stress relaxation is higher at 120 kV, we performed stress relaxation experiments on a different sample of the Al-225 film (Fig. 3b) at 120 kV and 200 kV. In the first two cycles, we kept the e-beam area, intensity and current identical and just varied the accelerating voltage. We loaded the sample without e-beam exposure and irradiated the sample with the e-beam at only two points during loading and measured the percentage stress drop (decrease in stress/initial stress) on each occasion. As evident from the data (Fig. 3b, Table 2), stress relaxation was significantly higher at 120 kV. In the 3rd and 4th cycle we increased the beam area and decreased the intensity while keeping the beam current close to its value in the 1st and 2nd cycle. Again, the stress relaxation was higher at 120 kV (3rd cycle), even though the intensity was slightly larger in the 4th cycle (200 kV).

To ensure that the larger stress relaxation observed in the Al-225 film at lower voltages is not unique to a particular grain size, sample texture or thickness, we repeated the cyclic load-unload experiments on a thicker Al film (Al-400). This film had a notably larger mean grain size (d = 220 nm) compared to the Al-225 film (d = 120 nm) and the texture was also different (Fig. 2). Despite these differences, the Al-400 film also showed a significantly larger stress relaxation at 120 kV (Fig. 3c, Table 1) compared to 200 kV. In fact, the percentage decrease in σ0.75% for the Al-400 film at 120 kV was even higher compared to the percentage decrease in σ1% for the Al-225 film at the same voltage (3rd cycle in Fig. 3a).

We further verified if this trend (higher stress relaxation at lower voltages) was consistent across different materials by performing cyclic load-unload experiments on an Au film. The Au film had a considerably different texture and a much smaller mean grain size (Fig. 2) and thickness compared to both the Al-225 and Al-400 film. Nevertheless, the e-beam effect on the stress-strain response of the Au film (Fig. 3d) was fully consistent with the effect on the Al films, leading to significantly higher stress relaxation at 120 kV compared to 200 kV.

In addition to the stress-strain response, the evolution of the microstructure during and after deformation was also monitored. The Al-225 film showed a small increase in d from 120 nm to 135 nm after six cycles whereas the Al-400 and Au film did not show any grain growth. In all the films dislocation activity was seen even at small strains where the stress-strain curve showed little deviation from linearity. Figure 4 shows an example of such dislocation activity in the Al-225 film during the third deformation cycle when the strain was ~0.41% (indicated by the green arrow in Fig. 3a). The video corresponding to these images (videoS1) is available as supplementary material. Notably, significant dislocation activity was also seen during the initial stages of unloading (videoS2), when the macroscopic stress-strain response was elastic. The stress corresponding to videoS2 is about 408 MPa (indicated by the black arrow in Fig. 3a), 76 MPa lower than the peak stress during the cycle. These observations suggest that dislocations are activated by e-beam exposure, leading to localized plastic deformation.

Figure 4. Dislocation motion during straining:

Figure 4

Open in a new tab

TEM bright-field images of the Al-225 film after the application of a set of displacement pulses during the 3rd cycle. The approximate stress and strain at this point was 225 MPa and 0.41%, respectively (green arrow in Fig. 3a). The red arrows point to locations of dislocation activity. The video corresponding to these images (videoS1) is available as supplementary material.

To confirm this, during the stress relaxation experiments on the Al-225 film (Fig. 3b) we shifted the e-beam to a different region of the sample at the end of 2nd loading cycle for approximately 2 minutes. Immediately upon e-beam exposure, substantial dislocation activity (videoS3) was observed in the new region, which was accompanied by further stress relaxation (violet cross at the end of 2nd cycle). Note that this additional stress relaxation occurred even though the sample had been exposed to the e-beam for 15 minutes in the previous observational area and significant stress relaxation (>6%) had already occurred. We similarly shifted the beam to a new location at the end of the 3rd cycle and again observed significant additional relaxation (violet cross at the end of 3rd cycle). To verify if the same e-beam induced mechanism is active in the Au film, we temporarily shifted the beam to a new location during the 3rd loading cycle (indicated by green arrow in Fig. 3d). Once again, this led to enhanced dislocation activation in the new location (videoS4).

Apart from microstructural changes, significant necking along the sample width was seen in the Al-225 film (Fig. 5). This localized necking exactly corresponded to the location of the e-beam on the sample (indicated by a red circle or rectangle), which strongly suggests that the necking is a direct consequence of e-beam exposure. In the Al-225 film, the width reduced from 30 μm to 27.54 μm, an 8.2% reduction, after 5 deformation cycles. To understand the effect of beam conditions on necking, we analyzed the changes in sample width (Δw) from the 2nd to 5th cycle. Since the initial sample width (at the beam location) was different for each cycle, we first calculated the percentage width reduction (Δw/w) for each cycle. We then normalized Δw/w by the plastic strain (εp) imposed in that cycle. After this normalization, we found a clear dependence of necking on both the beam area as well as accelerating voltage (Table 3).

Figure 5. Anomalous necking of films:

Figure 5

Open in a new tab

(a–f) TEM images of the Al-225 sample at the locations where it was exposed to the e-beam, with scale bar shown in (e). The left edge of the sample is aligned so that changes in width after each cycle can be easily seen. The red circles in (a–c) are the areas exposed to the e-beam. In (d) and (f), the entire width of the sample was exposed as indicated by the red rectangles. The center of the e-beam was approximately at the same location from the 2nd to 5th cycle. The imaging location was changed before the 6th cycle. The image in (e) corresponds to a previously unexposed region of the sample before the 6th cycle. The image in (f) corresponds to the region in (e) after exposure to the e-beam during the 6th cycle. The necking of the sample is clearly visible in (d) and (f). (g) TEM image of the 400 nm sample after the 2nd cycle, with the arrows pointing to the necked region.

Table 3. Beam conditions and necking parameters of Al-225 film during cyclic deformation.

Cycle Voltage (kV) Area (μm2) Intensity (A/cm2) εp (%) w (μm) Δw(μm) Δw/w(%) r =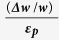Inline graphic
2 80 12.5 0.352 0.426 30 0.00 0.00 0.00
3 120 201 0.051 0.399 30 1 3.33 8.35
4 200 201 0.03 0.357 29 0.34 1.17 3.28
5 200 804 0.007 0.606 28.66 1.12 3.91 6.45
6 120 804 0.012 0.848 30 2.46 8.20 9.67
Open in a new tab

When the beam area was very small (2nd cycle) there was no notable decrease in the sample width. For a given accelerating voltage and beam current (4th and 5th cycle), the normalized width reduction (r = (Δw/w)/εp) was significantly larger when the beam area was larger. This suggests that the extent of necking is more dependent on the beam area than intensity. Similar to stress relaxation, necking was also more pronounced at 120 kV. For example, in the 3rd cycle (120 kV beam) r = 8.35, which is higher by a factor of 2.5 compared to the 4th cycle (200 kV beam, r = 3.28), even though the beam area was the same and beam intensity was only 1.7 times larger. Interestingly, when the e-beam was shifted to a new region for the 6th cycle (120 kV), a new neck appeared in that region and there was no further reduction in width of the previously necked region, which confirms that necking results from e-beam exposure. Furthermore, the specimen width decreased from 30 μm to 27.54 μm (8.2% reduction) in a single cycle.

Similar sample necking was seen in the Al-400 film as well (Fig. 5g) but the reduction in width was even more pronounced. The sample width reduced from 30 μm to 26.85 μm (10.5% reduction) after just one cycle of deformation at 120 kV, even though the imposed plastic strain was only 0.6% and the beam intensity was also quite low (Table 1). In the Au film no obvious necking was observed, presumably because the beam area was much smaller (Table 1).

Discussion

Radiolysis, caused by the inelastic scattering of incident beam electrons, and knock-on displacement, due to elastic scattering of beam electrons, are the two main radiation damage mechanisms in TEM. However, in conducting materials such as metals, radiolysis is mostly suppressed because of the high density of delocalized electrons32, which leaves knock-on displacement as the primary damage mechanism. Since knock-on displacement typically increases with accelerating voltage, a maximum voltage of 200 kV is used in most in situ TEM deformation experiments on metals to mitigate radiation damage. Nevertheless, recent studies have shown that even low to moderate e-beam exposure in a TEM can affect the mechanical behavior of nanoscale materials such as nanoparticles and nanowires33,35.

Our experiments demonstrate that the mechanical behavior of nanocrystalline and ultrafine-grained metals is also significantly affected by electron irradiation. In particular, the experiments reveal two unexpected trends as discussed below. First, beam-induced artifacts in nanostructured metals occur at beam energies far below the radiation damage (knock-on displacement) thresholds of these materials. Second, the beam-induced artifacts are more pronounced at lower accelerating voltages.

Knock-on displacement occurs when the beam energy exceeds a threshold, and may either result in the formation of vacancy-interstitial pairs in the bulk or lead to sputtering at the surfaces. However, the threshold energy for knock-on displacement in the bulk is usually larger than at the surface. For Al, the bulk displacement threshold energy exceeds 100 kV36 but the surface sputtering threshold energy is only 65 kV37. Since substantial stress relaxation is observed at 80 kV for the Al-225 sample (Fig. 3a), it is conceivable that surface sputtering could be partly responsible for the observed relaxation. However, the experiments on the Al-400 film (Fig. 3c) strongly suggest otherwise. If surface sputtering were a primary damage mechanism, the e-beam effect would be much smaller on the Al-400 film because of its higher thickness. In contrast, stress relaxation as well as necking in the Al-400 film (at 120 kV) was more pronounced compared to the Al-225 film.

The experiments on the Au film provide even stronger evidence that knock-on displacement is not responsible for the observed stress relaxation. The estimated surface sputtering threshold energy for Au is around 400 kV37 and the threshold for knock-on displacement in the bulk exceeds 1000 kV. Therefore, no e-beam effect would be expected at 120 kV. Still, considerable stress relaxation (>10%) was observed when the film was exposed to the 120 kV beam (Fig. 3d and Table 1).

The experiments also reveal that the e-beam effects are more pronounced at 120 kV compared to 200 kV for all three films and the results are consistent across both cyclic loading as well as stress relaxation experiments (Fig. 2, Table 1). For example, in the Al-400 film σ0.75% decreased by 9% in the 2nd cycle compared to the 1st cycle (no beam) due to irradiation by 120 keV electrons, whereas σ0.75% increased by ~40% when 200 keV electrons were used to image the sample in the 3rd cycle. Thus, there was a qualitative change in the stress-strain response when the accelerating voltage was changed, even though the beam areas were identical and beam intensities were comparable. The stress-strain behavior of the Au film (Fig. 3d, Table 1) provides even more convincing evidence that the e-beam effect is higher at lower voltages since in this case the beam conditions (area, intensity and current) were identical. While σ1% decreased by 11% between the 1st cycle (no beam) and 2nd cycle (120 kV beam), it was 5% higher in the 3rd cycle (200 kV beam) compared to the 1st cycle.

The trends in stress relaxation strongly indicate that knock-on displacement cannot explain the observations, which suggests that other processes are responsible for the changes in stress-strain behavior and sample geometry. It is well known that conduction electrons interact with lattice defects such as grain boundaries and dislocations and this leads to an increase in electrical resistivity38 compared to a perfect crystal. Furthermore, it has been shown that an electric current pulse of high density (104 A/cm2) can assist dislocations in overcoming obstacles causing electroplasticity39.

In the present case, the incident beam electrons play a role analogous to the electric current pulse. The beam electrons scatter inelastically near lattice defects and generate local lattice vibrations (phonons) either by scattering-induced phonon generation or via the excitation and damping of plasmons40,41. The interaction of the phonons and dislocations leads to depinning of dislocations pinned at the grain boundaries. This phonon-assisted depinning increases dislocation mobility and consequently results in stress relaxation. For a given beam area, the number of inelastic scattering events increases with increasing beam intensity. Therefore, stress relaxation caused by phonon assisted depinning of dislocations increases with increasing beam intensity. Similarly, if the intensity is constant and the beam area increases, stress relaxation is again higher because dislocation activation is enhanced in a larger fraction of grains across the sample width.

Notably, this mechanism is consistent with the observation that when the beam is shifted to a new location there is increased dislocation activity in both the Al-225 film (videoS3) and the Au film (videoS4). In this context, it is also worth noting that the cross-section of inelastic processes typically decreases with increasing beam energy42. Therefore, the probability for phonon generation and dislocation activation would be higher at 120 kV compared to 200 kV, which can explain the higher e-beam effect at 120 kV. However, it is important to note that these phonons generated by inelastic scattering of beam electrons do not lead to a sustained increase in the overall sample temperature. Both Al and Au have high thermal conductivity (>200 W/m/K) and even the largest beam currents used in our experiments are not expected to raise the sample temperature by more than 1 K42. This remains the case even when we account for the lower thermal conductivity of nanocrystalline materials43.

In addition to stress relaxation, the e-beam also caused considerable necking of the films (Fig. 5). This necking along the width is highly unusual because in thin film samples with a relatively large width, the thickness tends to decrease more during uniaxial loading due to geometrical constraints (Supplementary Fig. 1). Similar to stress relaxation, the necking was also more pronounced at a lower accelerating voltage. But somewhat surprisingly the extent of necking was more sensitive to the beam area than beam intensity (compare 4th and 5th cycles or 3rd and 6th cycles of the Al-225 film). One possible explanation is that when the beam area is large, dislocation activation is increased in a higher fraction of grains across the sample width and these grains collectively deform to form a neck. When the beam area is small, plastic relaxation is enhanced in only a small fraction of grains across the sample. So even if the extent of relaxation in these grains is higher (because of higher beam intensity), their deformation is constrained by the surrounding grains that undergo no relaxation. Thus, there is less macroscopic necking of the sample.

Overall, these results unambiguously show that the beam energy required to induce stress relaxation in nanostructured metals is substantially lower than their radiation damage threshold and that the relaxation is more pronounced at lower beam energies. It is important to note that these beam-induced artifacts are observed in two metals (Al and Au) that have highly dissimilar atomic weights and substantial differences in material properties (stacking fault energy, for example). The observations are also consistent across a range of sample thicknesses and grain sizes. This strongly suggests that e-beam exposure is likely to alter the deformation behavior in a broad spectrum of nanostructured metals, including commonly studied metals such as nickel and copper.

Furthermore, our results show that e-beam exposure causes anomalous changes in geometry when a larger cross-sectional area of the sample is exposed. Therefore, materials with sub micrometer dimensions (nanowires, nano pillars), which typically have their entire cross-section illuminated by the e-beam during in situ deformation experiments, are likely to be more susceptible to e-beam induced artifacts. Hence, caution needs to be exercised in interpreting the stress-strain response of such materials from in situ experiments.

While the observations clearly demonstrate the e-beam effect on the deformation response of nanocrystalline and ultrafine-grained metals, they also suggest a strategy to minimize beam-induced artifacts during in situ testing. The results indicate that beam-assisted dislocation activation is far more important in these materials compared to radiolysis or knock-on damage. And since dislocation activation is reduced at higher beam energies, it may be prudent to employ higher accelerating voltages during in situ testing of nanostructured materials. However, it should be noted that the e-beam intensities used in this study are quite low (<1.5 A/cm2). When higher intensities (for high resolution imaging or spectroscopy applications) are employed, knock-on damage could become significant at higher accelerating voltages. Therefore, careful studies are required to establish appropriate imaging conditions to minimize beam-induced artifacts during in situ TEM deformation of nanocrystalline and ultrafine-grained metals.

Additional Information

How to cite this article: Sarkar, R. et al. Electron Beam Induced Artifacts During in situ TEM Deformation of Nanostructured Metals. Sci. Rep. 5, 16345; doi: 10.1038/srep16345 (2015).

Supplementary Material

Supplementary Figure
srep16345-s1.doc (28.5KB, doc)
Supplementary Video Captions
srep16345-s2.doc (22.5KB, doc)
Supplementary Video 1
Download video file (1.4MB, avi)
Supplementary Video 2
Download video file (2.7MB, avi)
Supplementary Video 3
Download video file (7.8MB, avi)
Supplementary Video 4
Download video file (7.1MB, avi)

Acknowledgments

This project was funded by the National Science Foundation (NSF) grants ECCS 1102201, CMMI 1400505 and DMR 1454109. The authors would like to gratefully acknowledge the use of facilities at the John M. Cowley Centre for High Resolution Electron Microscopy and the Centre for Solid State Electronics Research at Arizona State University and at the Faculty of Physics of the University of Vienna. Financial support from the Austrian Science Fund (FWF): [P22440, I1309] is acknowledged.

Footnotes

Author Contributions C.R. and J.R. conceived the study. R.S. and J.R. fabricated the MEMS devices. R.S., C. R. and J.R. performed the experiments, analyzed the data and wrote the manuscript. All authors reviewed the manuscript.

References

  1. Kumar K., Van Swygenhoven H. & Suresh S. Mechanical behavior of nanocrystalline metals and alloys Acta Mater. 51, 5743–5774 (2003). [Google Scholar]
  2. Uchic M. D., Shade P. A. & Dimiduk D. M. Plasticity of Micrometer-Scale Single Crystals in Compression. Annu. Rev. Mater. Res. 39, 361–386 (2009). [Google Scholar]
  3. Greer J. R. & De Hosson J. T. M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 56, 654–724 (2011). [Google Scholar]
  4. Schwaiger R., Moser B., Dao M., Chollacoop N. & Suresh S. Some critical experiments on the strain-rate sensitivity of nanocrystalline nickel. Acta Mater. 51, 5159–5172 (2003). [Google Scholar]
  5. Wang Y., Hamza A. & Ma E. Temperature-dependent strain rate sensitivity and activation volume of nanocrystalline Ni. Acta Mater. 54, 2715–2726 (2006). [Google Scholar]
  6. Wei Y., Bower A. F. & Gao H. Enhanced strain-rate sensitivity in fcc nanocrystals due to grain-boundary diffusion and sliding. Acta Mater. 56, 1741–1752 (2008). [Google Scholar]
  7. McFadden S. X., Mishra R. S., Valiev R. Z., Zhilyaev A. P. & Mukherjee A. K. Low-temperature superplasticity in nanostructured nickel and metal alloys. Nature 398, 684–686 (1999). [Google Scholar]
  8. Rajagopalan J., Han J. H. & Saif M. T. A. Plastic Deformation Recovery in Freestanding Nanocrystalline Aluminum and Gold Thin Films. Science 315, 1831–1834 (2007). [DOI] [PubMed] [Google Scholar]
  9. Wei X. & Kysar J. W. Residual plastic strain recovery driven by grain boundary diffusion in nanocrystalline thin films. Acta Mater. 59, 3937–3945 (2011). [Google Scholar]
  10. Rajagopalan J., Han J. H. & Saif M. T. A. Bauschinger effect in unpassivated freestanding nanoscale metal films. Scr. Mater. 59, 734–737 (2008). [Google Scholar]
  11. Espinosa H. D., Bernal R. A. & Filleter T. In situ TEM Electromechanical Testing of Nanowires and Nanotubes. Small 8, 3233–3252 (2012). [DOI] [PubMed] [Google Scholar]
  12. Shan Z. et al. Grain Boundary-Mediated Plasticity in Nanocrystalline Nickel. Science 305, 654–657 (2004). [DOI] [PubMed] [Google Scholar]
  13. Shan Z. W., Mishra R. K., Syed Asif S. A., Warren O. L. & Minor A. M. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 7, 115–119 (2008). [DOI] [PubMed] [Google Scholar]
  14. Oh S. H., Legros M., Kiener D. & Dehm G. In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mater. 8, 95–100 (2009). [DOI] [PubMed] [Google Scholar]
  15. Legros M., Gianola D. S. & Motz C. Quantitative In situ mechanical testing in electron microscopes. MRS Bull. 35, 354–360 (2010). [Google Scholar]
  16. Yu Q., Legros M. & Minor A. M. In situ TEM nanomechanics. MRS Bull. 40, 62–70 (2015). [Google Scholar]
  17. Oh S. H. et al. Dislocation plasticity of Al film on polyimide investigated by cross-sectional In situ transmission electron microscopy straining. Scr. Mater. 65, 456–459 (2011). [Google Scholar]
  18. Hugo R. C. et al. In-situ TEM tensile testing of DC magnetron sputtered and pulsed laser deposited Ni thin films. Acta Mater. 51, 1937–1943 (2003). [Google Scholar]
  19. Kumar K. S., Suresh S., Chisholm M. F., Horton J. A. & Wang P. Deformation of electrodeposited nanocrystalline nickel. Acta Mater. 51, 387–405 (2003). [Google Scholar]
  20. Hattar K., Han J., Saif M. T. A. & Robertson I. M. In situ Transmission Electron Microscopy Observations of Toughening Mechanisms in Ultra-fine Grained Columnar Aluminum Thin Films. J. Mater. Res. 20, 1869–1877 (2005). [Google Scholar]
  21. Rajagopalan J., Rentenberger C., Peter Karnthaler H., Dehm G. & Saif M. T. A. In situ TEM study of microplasticity and Bauschinger effect in nanocrystalline metals. Acta Mater. 58, 4772–4782 (2010). [Google Scholar]
  22. Mompiou F., Caillard D., Legros M. & Mughrabi H. In situ TEM observations of reverse dislocation motion upon unloading in tensile-deformed UFG aluminium. Acta Mater. 60, 3402–3414 (2012). [Google Scholar]
  23. Wang Y. B., Li B. Q., Sui M. L. & Mao S. X. Deformation-induced grain rotation and growth in nanocrystalline Ni. Appl. Phys. Lett. 92, 011903 (2008). [Google Scholar]
  24. Shan Z. et al. Large lattice strain in individual grains of deformed nanocrystalline Ni. Appl. Phys. Lett. 92, 091917 (2008). [Google Scholar]
  25. Legros M., Gianola D. S. & Hemker K. J. In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films. Acta Mater. 56, 3380–3393 (2008). [Google Scholar]
  26. Shan Z. et al. Dislocation Dynamics in Nanocrystalline Nickel. Phys. Rev. Lett. 98, (2007). [DOI] [PubMed] [Google Scholar]
  27. Wang L. et al. Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum. Nat. Commun. 5, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mompiou F. et al. Inter- and intragranular plasticity mechanisms in ultrafine-grained Al thin films: An In situ TEM study. Acta Mater. 61, 205–216 (2013). [Google Scholar]
  29. Kobler A., Kashiwar A., Hahn H. & Kübel C. Combination of In situ straining and ACOM TEM: A novel method for analysis of plastic deformation of nanocrystalline metals. Ultramicroscopy 128, 68–81 (2013). [DOI] [PubMed] [Google Scholar]
  30. Rauch E. F. & Véron M. Automated crystal orientation and phase mapping in TEM. Mater. Charact. 98, 1–9 (2014). [Google Scholar]
  31. Idrissi H. et al. Plasticity mechanisms in ultrafine grained freestanding aluminum thin films revealed by in-situ transmission electron microscopy nanomechanical testing. Appl. Phys. Lett. 104, 101903 (2014). [Google Scholar]
  32. Egerton R. F., Li P. & Malac M. Radiation damage in the TEM and SEM. Micron 35, 399–409 (2004). [DOI] [PubMed] [Google Scholar]
  33. Zheng K. et al. Electron-beam-assisted superplastic shaping of nanoscale amorphous silica. Nat. Commun. 1, 1–8 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Han J. H., Rajagopalan J. & Saif M. T. A. MEMS-based testing stage to study electrical and mechanical properties of nanocrystalline metal films. Proc. SPIE, 64640C–64640C–8 (2007). [Google Scholar]
  35. Dai S. et al. Electron-Beam-Induced Elastic–Plastic Transition in Si Nanowires. Nano Lett. 12, 2379–2385 (2012). [DOI] [PubMed] [Google Scholar]
  36. Mingler B. & Karnthaler H. P. Radiation damage during HRTEM studies in pure Al and Al alloys. Int. J. Mater. Res. 97, 1041–1045 (2006). [Google Scholar]
  37. Egerton R. F., McLeod R., Wang F. & Malac M. Basic questions related to electron-induced sputtering in the TEM. Ultramicroscopy 110, 991–997 (2010). [Google Scholar]
  38. Bross H. & Haberlen O. The scattering of electrons by edge dislocations in Al. J. Phys. Condens. Matter 5, 7687 (1993). [Google Scholar]
  39. Sprecher A. F., Mannan S. L. & Conrad H. Overview no. 49: On the mechanisms for the electroplastic effect in metals. Acta Metall. 34, 1145–1162 (1986). [Google Scholar]
  40. Wang Z. Elastic and Inelastic Scattering in Electron Diffraction and Imaging. (Springer Science & Business Media, 2013). [Google Scholar]
  41. Egerton R. F. Control of radiation damage in the TEM. Ultramicroscopy 127, 100–108 (2013). [DOI] [PubMed] [Google Scholar]
  42. Williams D. B. & Carter C. B. Transmission Electron Microscopy: A Textbook for Materials Science. (Springer Science & Business Media, 2009). [Google Scholar]
  43. Dong H., Wen B. & Melnik R. Relative importance of grain boundaries and size effects in thermal conductivity of nanocrystalline materials. Sci. Rep. 4, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure
srep16345-s1.doc (28.5KB, doc)
Supplementary Video Captions
srep16345-s2.doc (22.5KB, doc)
Supplementary Video 1
Download video file (1.4MB, avi)
Supplementary Video 2
Download video file (2.7MB, avi)
Supplementary Video 3
Download video file (7.8MB, avi)
Supplementary Video 4
Download video file (7.1MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES