Protrusive waves guide 3D cell migration along nanofibers

Reductionist approaches based on 3D fibers reveal that single-cell migration along fibers is driven by lateral actin-based waves for various cell types.

Abstract

In vivo, cells migrate on complex three-dimensional (3D) fibrous matrices, which has made investigation of the key molecular and physical mechanisms that drive cell migration difficult. Using reductionist approaches based on 3D electrospun fibers, we report for various cell types that single-cell migration along fibronectin-coated nanofibers is associated with lateral actin-based waves. These cyclical waves have a fin-like shape and propagate up to several hundred micrometers from the cell body, extending the leading edge and promoting highly persistent directional movement. Cells generate these waves through balanced activation of the Rac1/N-WASP/Arp2/3 and Rho/formins pathways. The waves originate from one major adhesion site at leading end of the cell body, which is linked through actomyosin contractility to another site at the back of the cell, allowing force generation, matrix deformation and cell translocation. By combining experimental and modeling data, we demonstrate that cell migration in a fibrous environment requires the formation and propagation of dynamic, actin based fin-like protrusions.

Introduction

Cell migration is essential for fundamental phases of development and adult life, including embryogenesis, wound healing, and inflammatory responses (Li et al., 2004; Even-Ram and Yamada, 2005; Abreu-Blanco et al., 2011). Deregulation of cell migration can lead to pathological conditions, such as developmental defects, impaired healing, and cancer metastasis (Thiery, 2003). Understanding the mechanisms underlying cell migration is thus crucial to develop novel clinical strategies in regenerative medicine, tissue repair, and cancer therapies. To date, most of the research has focused on cell migration on 2D surfaces for experimental convenience. In this context, cellular protrusion has been described as an essential step for cell migration, which starts with the extension of membrane protrusions that include needle-like filopodia and flat leaf-like lamellipodia (Ladoux and Nicolas, 2012). These protrusions are driven by actin filament polymerization against the plasma membrane (Mogilner, 2006; Sykes and Plastino, 2010) and are assisted by activation, capping, branching, and cross-linking protein complexes such as N-WASP or Arp2/3 (Pollard and Borisy, 2003). Arp2/3-based lamellipodia protrusion is also crucial for directional persistence (Wu et al., 2012; Krause and Gautreau, 2014). The leading edge of the cell is then stabilized by the formation of cellular adhesions to the substrate (Lauffenburger and Horwitz, 1996).

These 2D-based studies have been crucial in establishing our current understanding of cell migration (Sheetz et al., 1998). However, in vivo cell migration occurs within complex 3D environments (Doyle et al., 2013). During tumor formation (Friedl and Wolf, 2003; Sahai, 2005), immune response (Muller, 2003; Rabodzey et al., 2008), or tissue repair (Martin and Parkhurst, 2004; Ghosh and Ingber, 2007), cells exist in a 3D environment and may encounter matrices that have different physical properties in terms of stiffness, topography, protein composition, ligand density, and pore size (Zaman et al., 2006; Wolf et al., 2013; Charras and Sahai, 2014). These heterogeneous environments undergo remodeling, which affects cell shape, migration, and the organization of protrusive activity (Lämmermann and Sixt, 2009; Bergert et al., 2012; Petrie et al., 2012; Sharma et al., 2013), raising questions on how motility modules studied in 2D are combined and altered or present during 3D cell migration (Vogel and Sheetz, 2006).

Within in vivo 3D environments, directional migration is determined by various cell protrusions and the modulation of small GTPase activity, such as Rac1 and Rho (Carmona-Fontaine et al., 2008; Matthews et al., 2008), as well as actomyosin-based contractility (Poincloux et al., 2011; Petrie et al., 2014). Single cells, such as fibroblasts or neutrophils, use various protrusions simultaneously or sequentially to face changes in environmental cues (Wolf and Friedl, 2009; Doyle et al., 2013; Tomba et al., 2014). These protrusions include lamellipodia and filopodia, as observed in 2D environments, but also lobopodia (Petrie et al., 2012), blebs (Charras and Paluch, 2008), pseudopodia (Baumann, 2010), and invadopodia (Yamaguchi et al., 2005). In addition, during axonogenesis in vitro and in vivo, neurons respond to external cues using an original mode of protrusion with propagative waves (Ruthel and Banker, 1999). These waves transport actin and associated proteins along the extending neurites and play a crucial role in breaking cellular symmetry to induce neuronal polarization (Flynn et al., 2009). Wave translocation along the neurite has recently been shown to be driven by directional assembly and disassembly of actin filaments and their anchorage to the substrate, with actin-associated proteins comigrating with the actin filament by interacting with them (Katsuno et al., 2015).

The various mechanisms underlying in vivo 3D migration are therefore far from being comprehensively understood. The 3D environment is highly complex, with optical properties that make spatial and temporal high-resolution imaging difficult (Even-Ram and Yamada, 2005). To shed light on cell motility in in vivo–like conditions, we studied cell migration on controlled arrays of fibronectin-coated electro-spun nanofibers that mimic 3D fibrillar environments. Our nanofiber approach allows high-resolution spatiotemporal live cell microscopy, along with the ability to finely control nanofiber size, density, and orientation (Li et al., 2004; Zhang et al., 2007). We demonstrate that cell migration along nanofibers relies on the formation and propagation of wave-like cellular protrusions. Such protrusions were observed in many different cell types, including fibroblasts, epithelial, endothelial, and brain-derived cell lines, and thus represent widely used dynamic structures, which cells use to travel within fibrillar environments. These highly periodic and dynamic waves resemble thin fins and are predominantly driven by Arp2/3-mediated actin polymerization and Rac 1 activity. However, regulation of cell contractility through Rho and formins pathways is also required for fin nucleation. Inhibition of contractility led to the formation of oversized fins, whereas overactivation of contractility impaired fin formation and instead favored the formation of a distinct type of protrusion, known as lobopodia (Petrie et al., 2012). Because both modifications affect cell migration, our study clearly highlights that attaining the right balance between contractility and protrusion is a prerequisite for efficient migration in 3D.

Results

Cells migrate rapidly and persistently on suspended nanofibers mimicking fibrillar environment

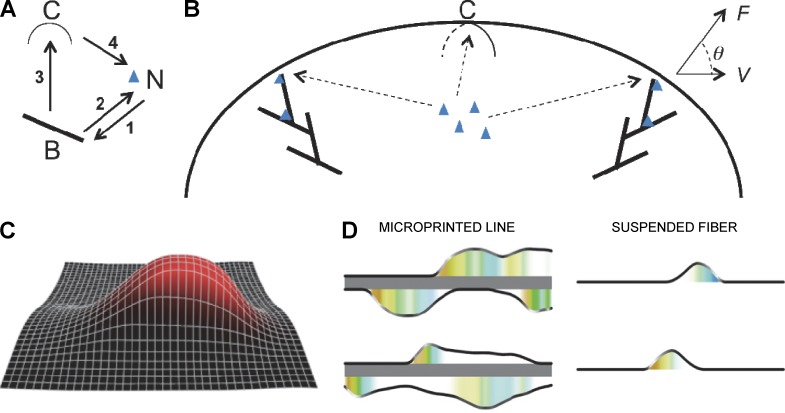
We developed an in vitro model mimicking the interaction of cells with a single fiber to investigate how cell migration occurs in vivo on fibrous environments. Arrays of polycaprolactone (PCL) aligned suspended fibers were produced by electrospinning (Fig. 1 A and Fig. S1 A). In brief, high voltage was applied to the surface of the polymer solution, which caused the ejection of a thin jet of polymer. During the process, the diameter and orientation of the fibers could be controlled (Li et al., 2004; Chew et al., 2006b). The deposition process also allowed for the alignment of nanofibers (Li et al., 2003; Chew et al., 2006a; Fig. S1, A and B).

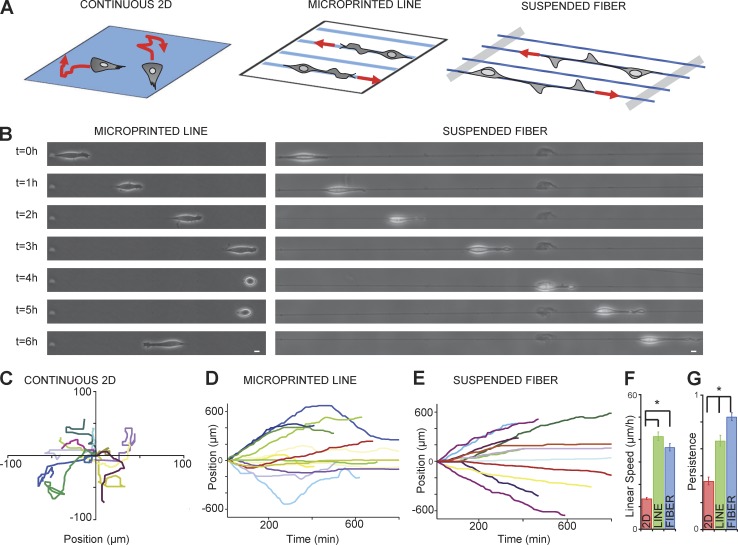
Figure 1.

Cells migrate faster and harbor higher persistence on suspended nanofibers mimicking a fibrillar environment. (A) Drawing of cells plated on fibronectin for continuous surface, microprinted lines or suspended fibers. (B) Snapshots of 3T3 cell movement over 6 h (1 frame/h) on line (left) or fiber (right). Bar, 10 µm. (C–E) Typical trajectories of 13 3T3 fibroblasts on continuous surface (C), lines (D), and fibers (E) for 6 h. Each colored trajectory is one single cell. (F) Quantification of linear speed and (G) persistence: continuous surface (red), line (green), and fiber (blue). Error bar, SEM, from four independent experiments; *, P < 0.001 (Student's t test); number of cells (NB), 203 (2D), 211 (line), and 222 (fiber).

Previous studies based on micropatterned lines have revealed that 1D cell migration could recapitulate 3D modes of cell migration (Doyle et al., 2009, 2012; Petrie et al., 2012), although cells on 1D lines can undergo undesired nonspecific interactions with the surrounding substrate. In contrast, our 3D nanofiber assay allows cells to interact with real life-size fibers, without complications from nonspecific interactions. As opposed to 3T3 fibroblasts on 2D flat substrates (Fig. 1 A and Fig. S1 B), cells on fibers coated with fibronectin (Fig. S1 C) adhered and adopted a robust spindle-shape morphology associated with long protrusions that could span up to several hundred micrometers in length (Fig. 1 B and Fig. S1 B). As a control, cells on uncoated or poly-l-lysine–coated fiber could only weakly attached to the fibers (Fig. S1, E and F; and Video 1).

We then compared 3T3 migration on micro-patterned lines and suspended fibers, under similar fibronectin-coated conditions (Fig. 1, A and B; Fig. S1 B; and Video 2). At low microscopic resolution, the cellular morphology appeared similar between cells adhering on micropatterned lines and on fibers (Fig. 1 B and Fig. S1 B). We quantified the cell linear speed (v_s: total trajectory length of the cell body divided by the total time) and the migration persistence (p_s: track length from initial to last position divided by the total displacement of the cell). On 4-µm-wide lines and on fibers 1.3 µm in diameter that presented adhesive areas of similar size, we obtained similar values of cell linear speed of around 40 µm/h (Fig. 1 F). However, we observed that the persistence on fibers (p_s = 0.92 ± 0.02) was significantly enhanced compared with lines (p_s = 0.63 ± 0.02; Fig. 1 G). This was confirmed by observing cell trajectories because cells on fibers displayed high directionality (Fig. 1 E) compared with cells on lines, which often changed direction (Fig. 1 D). As a control, cells on planar surfaces exhibited random walk behavior, rapidly changing direction (p_s = 0.35 ± 0.02) with a linear speed of around v_s = 10 µm/h (Fig. 1, C, F, and G). We then varied the fibronectin concentrations (from 12.5 to 100 µg/ml) and the fiber diameters (from 0.3 to 1.3 µm). We did not observe significant changes in the cell linear speed within these ranges of variation (Fig. S1 D). However, those diameters remain below the size of a single cell and thus other cell behaviors may be observed on larger diameters, as recently reported for collective epithelial migration (Yevick et al., 2015).

Cells exhibit waves of fin-like protrusions on fibers

Cell migration is often quantified as the net movement of the cell body over long time periods (several hours, as described in the preceding section). However, movement of the cell body relies on events that occur over a shorter time scale, such as protrusion-retraction cycles at the leading edge (Giannone et al., 2004; Krause and Gautreau, 2014). The integration of such numerous cycles within a range of seconds or at most minutes provides the basis for efficient long-term cell migration (Sheetz et al., 1998; Small et al., 1998; Giannone et al., 2004). For 3T3 fibroblasts on printed lines, cycles have been reported at the leading edge, with a frequency of approximately one event per minute and a protrusion extension capacity of 2–3 µm (Doyle et al., 2012). Because we observed that persistence was increased on suspended fibers, we anticipated that cellular protrusive activity and cell body translocation could be achieved by different mechanisms than the ones previously described in 2D or on printed lines.

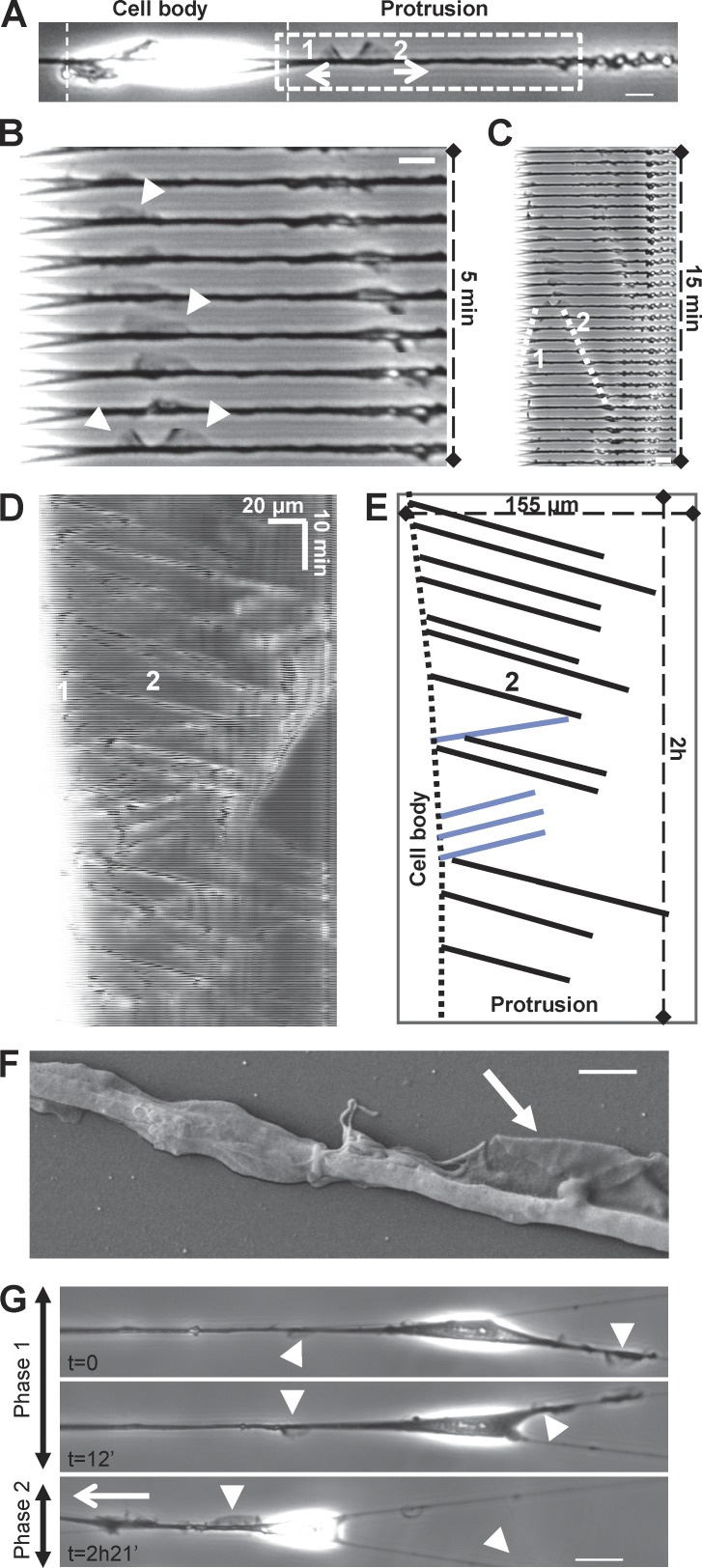
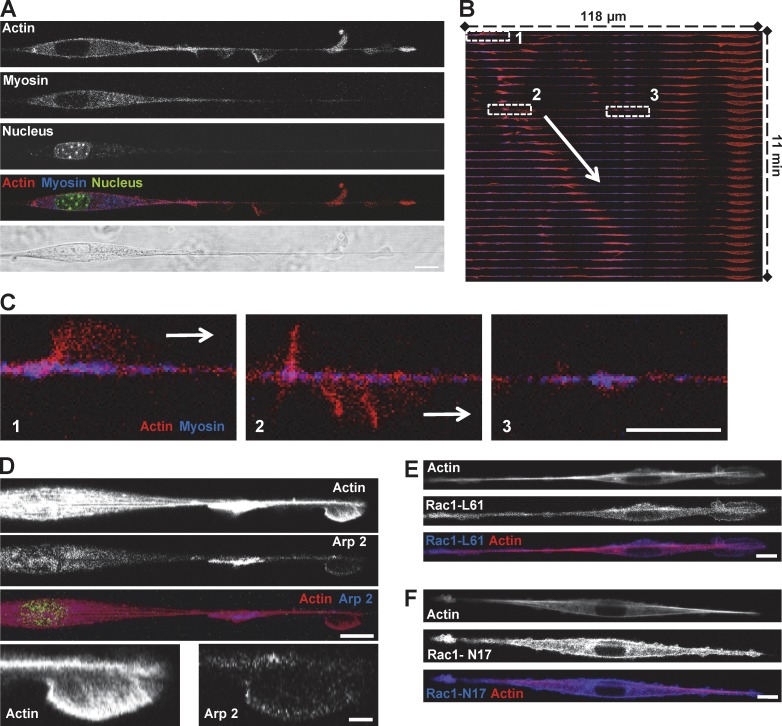
By increasing time-lapse resolution to seconds, we observed that cells migrating on fibers formed thin protrusions, normal to the fiber axis, which shared morphologic similarities with lamellipodial extensions or membrane ruffles (Fig. 2, A–C; and Video 3). This was confirmed with scanning electron microscopy (Fig. 2 F). While propagating along the fiber, these protrusions exhibited a characteristic fin-like shape with a thin and curved leading edge toward the direction of propagation and a straight denser zone at the back (Fig. 2 A, arrow 2; and Video 3). Remarkably, these protrusions were solely born at the end of the spindle-shaped cell body. From there, they traveled along the fiber on the long and thin extended part of the cell up to the leading edge (Fig. 2, C–E). As cells could freely wrap around the fiber as opposed to when platted on patterned surfaces, those protrusions were probably also rotating and spending most of the time out of the focal plane, but they continued to be easily identified as a thicker and more optically refractive zone (Fig. 2 D). Kymographs revealed their cyclic propagation (frequency of 10 per hour, independent of fiber diameters; Fig. 2, D and E; and Fig. S2 B) and fast and robust speed (around 400–500 µm/h; Fig. 2 E and Fig. S2 A). They preferentially moved toward the leading edge, but some were able to turn back once they reached the edge or they separated in two when formed near the cell body (Fig. 2, A–C). As the protrusions returned toward the cell body, they adopted a shape with opposite polarity but similar speed (Fig. 2 A, fin 1 compared with fin 2; Fig. 2 E, blue lines). Interestingly, the speed of protrusions (around 400 µm/h) is compatible with the maximum velocity of actin polymerization, as reported for lamellipodia extension in mouse embryonic fibroblasts (around 120–150 nm/s or 432–524 µm/h; Giannone et al., 2007).

Figure 2.

Fibroblasts display cyclical “fin-like protrusion” on nanofibers. (A) 3T3 fibroblast on fiber presenting two fin-like protrusions. Bar, 10 µm. (B and C) Time-sequenced zooms of the leading edge during fin propagation. Bar, 10 µm. (D) Kymograph of fin motion along the fiber. The white zone (left) corresponds to the end of the cell body where fins are born before propagating. (E) Schematic analysis of kymograph (D) showing properties of fin-like protrusion including robust speed and propagation between cell body and cell tip. Black lines, forward-moving fins; blue lines, backward-moving fins. (F) Scanning electronic microscopic image of the fin-like protrusion (arrow). Bar, 2 µm. (G) 3T3 in a multiple fiber situation. Two phases: phase 1, no net migration with fins on both fibers; phase 2, fins only in one fiber leading to the migration of the cell along this fiber. Arrowheads, fin-like protrusions; white arrow, direction of migration. Bar, 20 µm.

To further investigate the specificity of cell migration along nanofibers, we compared our fibers with microprinted lines, which have been proposed to mimic cell migration in 3D (Doyle et al., 2009, 2012, 2013). Most of the protrusions observed on microprinted lines did not propagate along the line but rather formed large and flat lateral extensions over the nonadherent area (Fig. S2, C and D; and Video 4). “Cuttlefish-like” shapes were observed with the entire cell surrounded by a continuous flat lamellipodium-like structure (Video 4). In the rare case of fin-like protrusion formation on microprinted lines, they failed to propagate over long distances (Fig. S2 C and Video 4). Often, the lamellipodia expanded cyclically—from one side as they retracted from the other side—in a “tug of war”–like mechanism, without an effect on the overall cell migration (Fig. S2 D, bottom; and Video 4). The only region generating protrusions beneficial for effective migration was located near the leading edge on the adhesive part of the surface, as shown in the kymograph (Fig. S2 C) and as reported elsewhere (Doyle et al., 2012). Altogether, these results show distinct roles of cellular protrusions on fibers and 2D micropatterned lines highlighting the specificity of fin-like protrusions during cell migration on suspended fibrillar matrices.

We then hypothesized that the fin-like protrusions could direct cell movement within more complex fibrous environments. We thus analyzed cellular interactions with multiple fibers. Under such conditions, fins were also observed to simultaneously protrude on adjacent fibers and extend the cell body (Fig. 2 G and Video 5). As fins encountered crossed fibers, they first started to protrude in all directions. As fins became predominant in one direction, this set the direction of migration (Fig. 2 G and Video 5). These protrusive structures not only contribute to cell body extension but also to cell polarity and migration. Consequently, these fins might help cells find their way within complex 3D matrices by dynamically probing the environment and controlling the cell’s capacity to change direction.

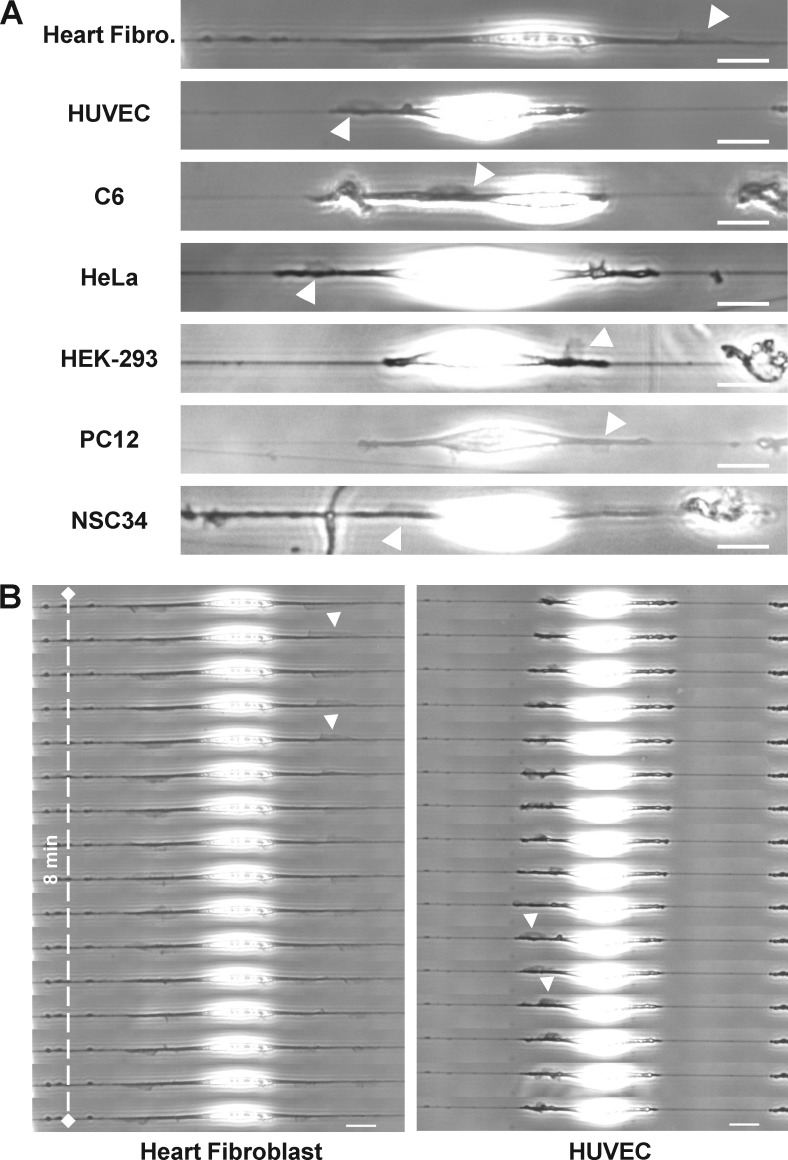
We next wondered whether the waves were cell type specific or potentially a more generic mode of extension used by cells within fibrous environments. Waves of fin-like protrusions were observed in 11 of 13 cell types studied (Table S1 and Fig. 3 A). The four fibroblast types investigated generated fin-like protrusions, including primary fibroblasts directly extracted from rat heart (Fig. 3 B, left). The three epithelial and three brain-derived cell types investigated also exhibited this type of protrusion. Finally, the primary human umbilical vein endothelial cells (HUVEC) also harbored very clear waves of fin-like protrusions (Fig. 3 B, right). Among all the cell lines tested, only one epithelial cell type (MDCK) and one macrophage-like type (THP1) did not harbor the fin-like structures or migrate along the fibers. MDCK cells spread slowly and remained nonmotile (Fig. S5 A), whereas THP1 cells were unable to spread (Video 3). Altogether, these results suggest that such protrusions are an important and generic mechanism for cell migration in vivo.

Figure 3.

Fin-like protrusions are a universal feature harbored by different cell lines. (A) Fin-like protrusions (arrowheads) for different cell types on fiber. Bar, 20 µm. (B) Time sequence of fin propagation (arrowheads) for heart fibroblast and HUVEC. Bar, 20 µm.

Waves extend the leading edge and correlate with cell motility

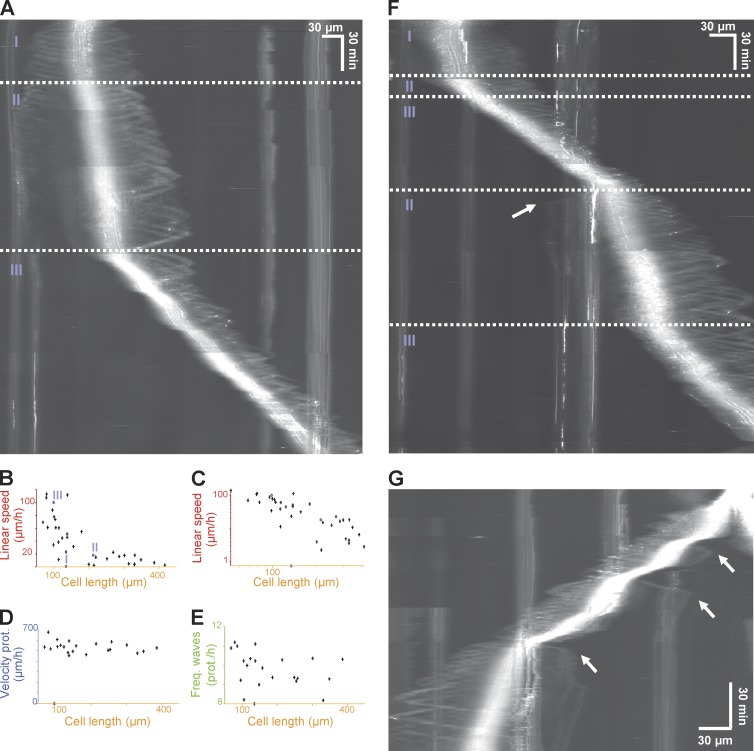
We analyzed the correlation between effective cell migration (i.e., cell body translocation) and fin-like waves. Migrating cells, as explained in the previous paragraph, established a long extension from the cell body, defined as the protrusive region, on one side during migration. Because our single fiber assay allows for long-term cell tracking, we investigated how cells broke symmetry to initiate the transition from a spreading and nonmigrating state to migrating state (Fig. 4 A and Video 6, showing 10 examples). The kymograph showed that a stationary symmetric cell had two equal extensions on the opposite sides of the cell body, and waves traveled with equal frequency and speed on both sides (Fig. 4 A, state I). The breaking of symmetry was always characterized by the gradual fading of the waves on one side, which coincided with the strengthening of the waves and cell body migration on the opposite side (Fig. 4 A, state II; and Video 6, showing 10 examples from spreading to polarized fast migration). Transition to a faster migratory regimen (from ∼20 to ∼100 µm/h) was characterized by the disengagement and disappearance of the tail at the back, after which the cell migrated steadily (Fig. 4 A, state III; and Video 6, all examples).

Figure 4.

Fin-like protrusive waves are correlated with cell polarity. (A) Kymograph of 3T3 on fiber. Three distinct states were observed: a spreading-immobile state (I), a migrating state (II), and a faster migrating state (III). (B and C) Linear speed as a function of cell length (normal and log-log plot). Number of cells (NB), 35. (D) Velocity of protrusion as a function of cell length. NB, 22. (E) Frequency of protrusion as a function of cell length. NB, 22. (F) Kymograph of 3T3 switching behavior on fiber. (G) Kymograph of 3T3 cell during postmitotic spreading switching behavior as in F. White arrows in F and G show new fin generation at the trailing edge.

We then investigated whether cell body extension and protrusion dynamics were correlated. It could be observed from Fig. 4 A that the leading edge was elongated by a few micrometer steps when the fin-like protrusions were arriving, increasing the overall cell length. On average, given the wave frequency (10 per hour) and the cell linear speed (∼40 µm/h), each fin-like protrusion added ∼4 µm of cell length at each cycle. Meanwhile, cell shortening was occurring continuously (via sliding) or by micrometer-step retraction at the trailing edge. The kymograph also showed that the faster the cell migrated, the more each fin-like protrusion extended the leading edge. After the waves were nucleated, their major function was to travel for up to hundreds of micrometers along the protrusive region. We recorded cells during early spreading to confirm that fins participated in the extension of the leading edge on fiber. We observed that fins created and extended the leading edge (Fig. S1 H), with each fin-like wave depositing up to 20 µm of new cell length at a time (Fig. S1 H). To further quantify the relationship between fin protrusions and cell movement, we analyzed various parameters during the steady migratory state, such as (a) cell body linear speed, (b) velocity of protrusion, and (c) frequency of protrusion as a function of cell length (Fig. 4, B–D). Interestingly, we observed an inverse relation between cell velocity and cell length (Fig. 4, B and C, log-log plot). In addition, the velocity of protrusions as well as the frequency of protrusions remained almost constant with the cell length (Fig. 4, D and E). This suggests that the smaller the cells, the faster they migrate, as fins only have to propagate over shorter distance to extend the leading edge.

Altogether, these results highlighted the role of fins as a critical structure to extend the leading edge. In addition, the imbalance in fins’ generation, associated with cell contractility, helped polarity acquisition, cell translocation, and persistence. This was further illustrated by cells presenting fluctuations in speed during normal migration or postmitotic spreading/migration (Fig. 4, F and G; and Video 6). Kymographs and movies of those cells showed that a single event of fin extension was capable of depositing tens of micrometers of new material at the trailing edge, simultaneously slowing down migration (Fig. 4, F and G, arrows). In agreement with our observation on polarity acquisition after spreading, as soon as this counterproductive protrusion disappeared by breaking or retracting, the cell restarted the fast migration mode, repeating cyclically the states II and III (Fig. 4, F and G).

Fin-like waves are driven by Arp2/3 mediated actin polymerization

We hypothesized that the cells use specific molecular mechanisms to drive the generation of fin-like protrusions, which enable free rotational movement along the suspended fiber. Because the actomyosin network has been shown to play a key role in various modes of cell migration (Even-Ram and Yamada, 2005; Charras and Paluch, 2008; Ladoux and Nicolas, 2012), we sought to determine its role in the formation and propagation of the fin protrusions. By following cells coexpressing tagged actin and myosin light chain (MLC), we observed that the fins were composed of an actin meshwork (Fig. 5 A). Most of the myosin was concentrated in the spindle-shaped cell body, with only discrete myosin spots observable along the fiber (Fig. 5, A–C). Whereas the actin-rich fin moved toward the leading edge of the cell (Fig. 5, B and C, zones 1 and 2), those myosin spots remained stationary (Fig. 5, B and C, zone 3). Examination of the fin structure showed that actin density was higher at the back of the fin (identified as the straight, denser zone, observed by phase-contrast microscopy; Fig. 2) than at the front, unveiling a possible polarity mechanism with a fast polymerizing leading front and a retracting or crushing zone at the back. This experiment also confirmed that fins rotate around the fiber while propagating (Fig. 5, B and C, zones 1 and 2). Because the velocity of fin propagation is compatible with the velocity of polymerizing actin-based structures (Giannone et al., 2007), we hypothesized that these structures would contain actin-polymerizing machineries. Cotransfection with actin or immunostaining demonstrated that the fin was enriched in Arp2 (Fig. 5 D, Fig. S3 A, and Video 7), whereas the cell body was poorly stained for Arp2, in clear contrast with the myosin staining (Fig. 5 A). In contrast, endogenous formin mDia1 or overexpressed mDia1 or mDia2, the two most classic formins reported to be implicated in cell migration, were absent from the fins (Fig. S3), as opposed to Arp2/3 (Fig. 5 D). Microtubule staining also did not colocalize with actin at the protrusion but colocalized at the end of the spindle-shaped cell body (Fig. S5 B).

Figure 5.

Fin-like protrusion is driven by Arp2/3 mediated actin polymerization. (A–C) 3T3 cells transfected with GFP-Actin and RFP-MLC on fiber. Bar, 10 µm. (A) Fins contained actin whereas myosin was concentrated in the cell body. Bar, 10 µm. (B) Kymograph of the merge color (actin in red, myosin in blue) showing propagation of the fin (arrow). (C) 3-Zoom image from B. 1, fin; 2, same fin from 1 after turning around the fiber; 3, myosin patches on fiber. Bars, 10 µm. (D) 3T3 cells were transfected with GFP-Actin and mCherry-Arp2/3 on fiber. Bars: (main) 10 µm; (zooms) 2 µm. (E and F) 3T3 cells were transfected with YFP-Rac1-L61 (Rac dominant positive, oversized fins) or YFP-Rac1-N17 (Rac dominant negative, no fin-like protrusion) and RFP-Actin and plated on fiber. Bars, 10 µm.

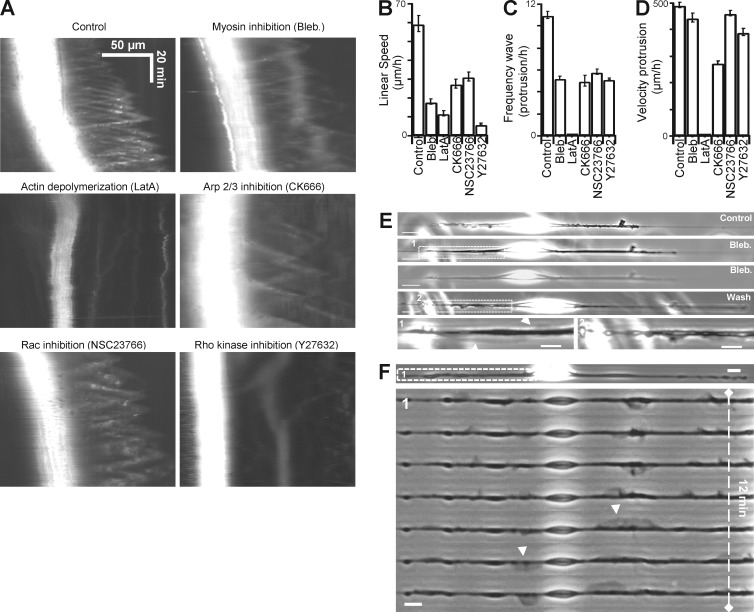
Using inhibitors for actin (latrunculin), myosin II (blebbistatin), and Arp2/3 complex (CK666), we demonstrated that those three molecules were critical for cell motility (Fig. 6 B), as well as for protrusion formation and dynamics (Fig. 6 A). Inhibition of actin and myosin slowed down the average cell body velocity to a greater extent than did inhibition of Arp2/3 (Fig. 6 B). Depolymerizing of actin completely suppressed the wave (Fig. 6, A–D), whereas myosin inhibition modified only wave frequency (Fig. 6 C) without affecting velocity (Fig. 6 D) and led to overextended fins spanning along the entire leading edge (Fig. 6 E, blebbistatin washout experiment). In contrast, Arp2/3 inhibition significantly reduced wave frequency and was, apart of actin depolymerization, the treatment that most affected protrusion velocity (Fig. 6, C and D; and Fig. S4 for washout experiments). We then tested the importance of Rac1 activity in fin generation and propagation by inhibition of Rac1 (Fig. 6, B–D) and overexpression of its dominant negative form Rac1 N17 (Fig. 5 F). Both treatments resulted in a strong reduction of fin propagation. Through inhibition-washout experiments with wiskostatin, we confirmed that N-WASP activity upstream of Arp2/3 was crucial for protrusion formation and propagation, further highlighting the importance of Arp2/3-based actin polymerization in fin dynamics (Fig. S4).

Figure 6.

Effects of inhibitors on fin-like protrusion properties. (A) Kymographs from cells treated with different inhibitors showing the effects on the formation and propagation of fins. (B and D) Quantification of the (B) linear speed (error bar, SEM from a typical experiment; NB, 33 [control], 32 [blebbistatin (Bleb)], 30 [latrunculin A.], 38 [CK666], 33 [NSC23766], 37 [Y27632]); (C) frequency of the protrusions (NB, 14 [control], 10 [blebbistatin], 10 [latrunculin A.], 10 [CK666], 12 [NSC23766], 12 [Y27632]); and (D) velocity of the protrusions (NB, 59 [control], 49 [blebbistatin], 27 [CK666], 59 [NSC23766], 54 [Y27632]) in different conditions tested. (E and F) Cells were incubated with blebbistatin or Y27632 inhibitor. Oversized and normal fins were formed (arrowheads). Bar, 10 µm.

Even though myosin was not enriched in the fin-like protrusions, inhibition of myosin altered fin dynamics. This suggested a possible link between actomyosin contractility and fin generation. Because actin and myosin were enriched at the end of the spindle-shaped cell body (Fig. 5 A), where fin-like structures are generated, it stands to reason that actomyosin contractility may play a role in the initial steps of protrusion assembly. The signaling cascades that lead to myosin II–mediated contractility are mostly under the upstream control of RhoA-ROCK pathway, whereas the Arp2/3 pathway is under the control of the small GTPase Rac1 and N-WASP-WAVE complex. By decreasing cell contractility through ROCK inhibition (Fig. 6 F and Fig. S4 for washout experiments) or Rac1 overexpression (Fig. 5 E), we observed the formation of oversized fins. Altogether, these data suggest that contractile forces generated through actomyosin activity are predominantly exerted at the two poles of the spindle-shaped cell body, where actin waves are initiated. Besides, the protrusive region where actin waves are propagating relies on Rac1-Arp2/3-actin pathway.

Cells apply contractile forces at the edges of the spindle-shaped cell body

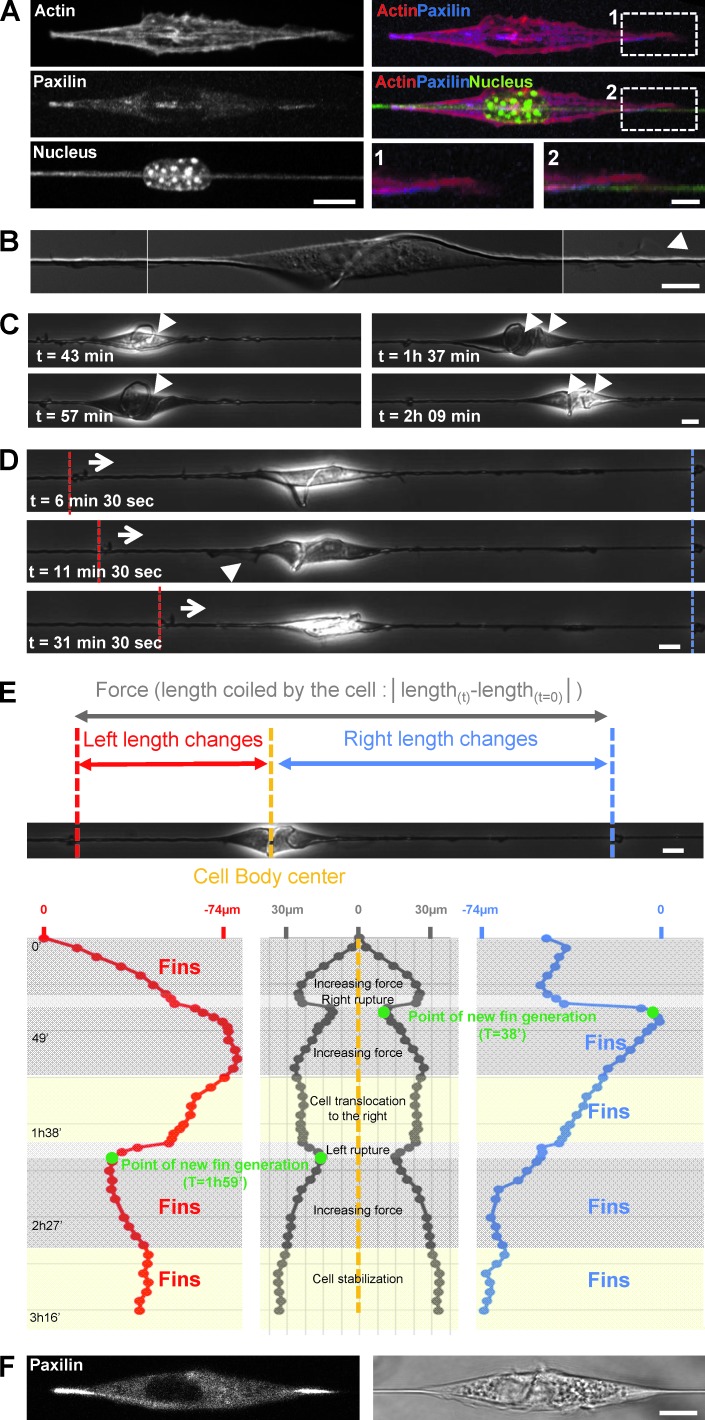
To further define the interconnection between actomyosin contractility and wave-based migration, we explored the distribution of adhesion complexes from cells on fibers. Cells expressing fluorescent paxillin formed focal adhesions on the fibers, located under the cell body with two major deposition sites at the end of the spindle shape (Fig. 7 A). Interestingly, we did not observe detectable adhesion complexes along the extended protrusions (Fig. 7 A, panel 1 versus 2). This was in sharp contrast to the cells on microprinted lines that harbored focal adhesions all along the cell, except on the extreme lamellipodia tip (Fig. S5 A), as reported elsewhere (Doyle et al., 2012). Contractile sites were localized at the extremities of the spindle-cell body, where wave protrusions were generated. This finding confirmed that actomyosin contractility plays an important role in the formation and dynamic regulation of the protrusions. These data suggested that this coupling was required for efficient cell migration along the fibers. However, the localization of the contractile pattern alone was not sufficient to promote cell migration. Indeed, MDCK cells that did not exhibit fin-like protrusions were found to harbor two major adhesion sites at the poles of the cell body but were unable to migrate on fiber (Fig. S5, A and B).

Figure 7.

Paxilin-containing adhesions on fiber are the anchorage point for force application and matrix deformation. (A) 3T3 cells transfected with GFP-Actin (red) and RFP-Paxilin (blue) with nucleus and fiber labeled with DAPI staining (green). Bars, 10 µm and 2 µm (zooms). (B) Combined high-resolution DIC images showing the torsion of fiber and a fin (arrowhead). Bar, 10 µm. (C) Time sequence extracted from Video 8 showing fiber deformation and coiling (arrowheads, number of coils). Bar, 10 µm. (D) Fin appearance was correlated with the pulling direction (see also Video 8). In the time sequence presented, fins were on the left when the fiber was pulled inward from the left (arrows and dashed white lines) as opposed to the right (dashed red lines). Bar, 10 µm. (E) Quantitative analysis of fiber deformation by the cell presented in C and D and in Video 8. On each side of the cell the presence of small particles immobile on the fiber allowed accurate tracking of the fiber deformation induced by the cell. The red track depicts tracking of the left side deformation, the blue track the right side. In the middle panel, the overall length change between the two reference points was calculated and is an indirect estimation of the forces applied by the cell while coiling the fiber. (F) Paxillin location during fiber coiling. Bar, 10 µm.

These results suggested that forces generated by cells on fiber were localized at these two focal adhesion sites connected by the actomyosin contractile network. Observing and quantifying cellular forces in vivo are technically challenging because of complexities of the 3D environment. Our nanofiber assay offers a unique opportunity to investigate how fibrous matrices are deformed under forces generated by cells. We focused on the analysis of particular events in which cells were able to actively deform the fibers (Fig. 7, B–D; and Video 8). This deformation was induced by pulling forces exerted by the cells (Fig. 7, D and E; and Video 8). Interestingly, it appeared that these forces were mainly applied at both extremities of the cell body, where the adhesion sites were localized (Fig. 7 F), as shown by the coiling and deformation profile of the fiber (Fig. 7, B–F). An estimate of the pulling forces leads to the following formula: F = SEε where S is the fiber cross-sectional area (πR²; R = 350 nm), E is the Young modulus of the material (≈120 MPa), and ε represents the deformation (ΔL/L₀ = 100 µm/20 mm). On the basis of this approximation, we obtained a force of around 200 nN, which is compatible with previous measurements at the cellular scale (Mitrossilis et al., 2009; Ghibaudo et al., 2011). Remarkably, after analysis of the fiber deformation by tracking the length changes on both side of the cell, it appeared that fin-like protrusions were generated only on the side of the cell where the fiber was being pulled inward. Fins were first generated on the left side (Fig. 7, D and E; and Video 8), then on the right side after partial cell detachment on the right and force relaxation (Fig. 7 E). Finally, they were generated from both sides (Fig. 7 E, last increase in force, both side being pulled inward; and Video 8). This observation reinforces the important role of protrusions in extending the leading edge and subsequently cell body translocation. Interestingly, we also observed that the first fin nucleation and protrusion preceded the large increase in force, both on the right side (38-min time point on Fig. 7 E and Video 8) or the left side (1-h 59-min time point in Fig. 7 E and Video 8). This indicates that fin generation is an early event, followed by the building up of tension and translocation of the adhesion along the fiber on the side where these cyclic fins are observed.

Alternative mode of protrusion by lobopodia formation

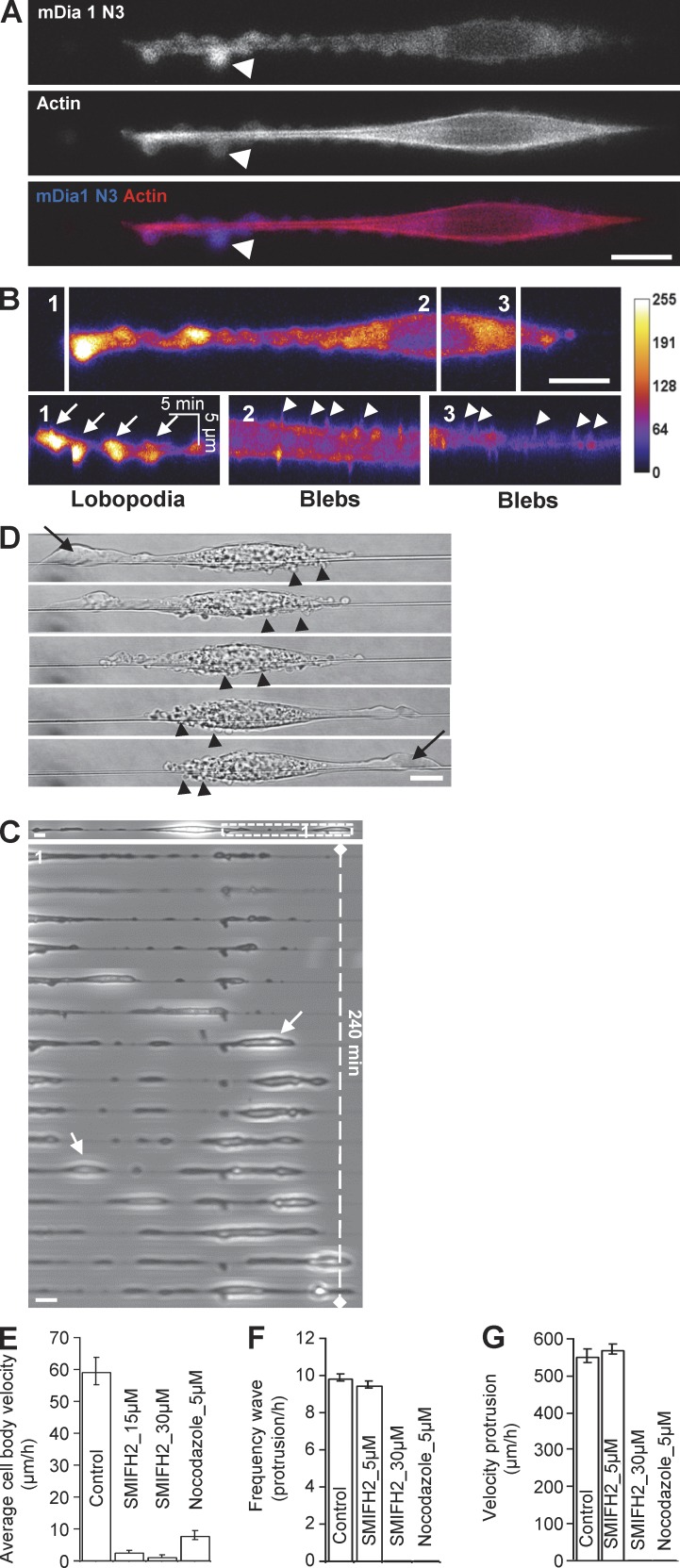
Our results demonstrate that on 3D fibers, cells finely tune contractility and actin polymerization to generate actin-based wave protrusions. However, cells occasionally exhibited a different kind of protrusions, such as large ones that shifted over time from one side of the cell to the other, leading to another mode of migration. The morphology of these protrusions was very distinct from the fins but reminiscent of lobopodia-type protrusions, as described elsewhere (Petrie et al., 2012; Fig. 8). We observed that this mode of protrusion was enhanced by a variety of treatments, namely overexpression of the active formin mDia1(DeltaN3) (Fig. 8 A), inhibition of microtubule polymerization with nocodazole (Fig. 8 C), a treatment known to also enhance contractility (Kolodney and Elson, 1995), or by increasing expression of the adhesive molecules talin and paxillin (Fig. 8 D and Video 9).

Figure 8.

Alternative mode of protrusions is explained by lobopodia formation. (A) 3T3 cell transfected with GFP-mDia1 ΔN3 (dominant positive) and RFP-Actin. Lobopodia (arrows) are at the leading edge, and the trailing edge presented strong blebbing. Bar, 10 µm. (B) 3 kymographs of mDia1 ΔN3 intensity map. 1, lobopodia slow dynamic (arrows); 2 and 3, blebs fast dynamic (arrowheads). (C) An image and a zoomed time sequence of a Nocodazole-treated 3T3 cell plated on fiber. Increasing contractility led to the formation of large structures resembling lobopodia (arrows). Bars, 10 µm. (D) 3T3 cell transfected with GFP-Talin and RFP-Paxilin (see also Video 9) showing shifting polarity of a large lobopodia (arrow) and the mirror changes for the blebbing region (arrowheads). Bar, 10 µm. (E) Quantification of the mean linear speed for cells. Error bar, SEM from a typical experiment; NB, 33 (control), 27 and 31 (SMIFH2), 30 (nocodazole). (F) Frequency of protrusions (NB, 13 [control] 6 [SMIFH2], 6 [nocodazole]). (G) Velocity of protrusions (NB, 39 [control], 41 [SMIFH2]), under different conditions.

The appearance of lobopodia-like protrusions was associated with a lack of persistence (Fig. 8, C and D), as cells kept alternating their polarization from one side to the other (Fig. 8 D and Video 9). In addition, the formation of lobopodia was associated with the presence of blebs localized along the cell body (Fig. 8, B and D), as reported elsewhere (Petrie et al., 2012). In contrast with blebs, lobopodia were enriched in mDia1(DeltaN3) and exhibited slower dynamics than blebs (Fig. 8 B) or fins (Fig. 8 C compared with Figs. 2 D and 8 D). Blebs appeared at the rear of the cell back, whereas lobopodia formed at the font, although this polarity swapped when the cell changed direction (Fig. 8 D and Video 9). The appearance of blebs is associated with variations in hydrostatic pressure (Charras and Paluch, 2008), pointing toward a major role of these forces for lobopodia formation. The plausible effect of hydrostatic pressure was also illustrated by organelle movement during lobopodia extension (Video 9). Because actomyosin-based contractility is a major motor for generating hydrostatic pressure, this could explain why lobopodia appeared when contractibility was at the highest level, such as during overexpression of mDia1(DeltaN3) or adhesion molecules, or after nocodazole treatment.

Our findings suggest that the balance between formin/Arp2/3 activities regulates lobopodia/fins appearance, respectively. Because formins are present in the lobopodia but absent in the fins, we hypothesized that inhibition of formins could shift the balance toward Arp2/3-fins pathway. Surprisingly, treatment with the formin family inhibitor SMIFH2 dramatically stopped cell migration and prevented the generation of any form of protrusion (Fig. 8, E–G; and Fig. S4 for washout experiments). This result shows that formins, although implicated in lobopodia formation, are also actin polymerizing machineries that are required for wave generation but not propagation.

In silico model for actin dynamics and cell behaviors on fibers

After our experimental findings, we developed a computational model to better understand the observed phenotypes displayed by cells migrating in a 3D environment. Our model is based on the following positive feedback loops (Fig. 9 A). We hypothesize that growing barbed ends of actin filaments in the Arp2/3-mediated branched network impinge on the membrane and drive it outward, creating a curvy membrane region protruding away from the fiber (Atilgan et al., 2005). Furthermore, we hypothesize that at the leading edge of this protrusion, nucleation promoting factors (NPFs) bind to certain membrane proteins with a spontaneous curvature so that they effectively prefer binding to the curved region of the membrane (Gov and Gopinathan, 2006; Shlomovitz and Gov, 2007; Liu et al., 2009; Peleg et al., 2011). Previously, Shlomovitz and Gov (2007) proposed that myosin contractility could be the main element behind the formation of curvature-actin waves, whereas Peleg et al. (2011) proposed that a combination of several curved proteins is key for membrane wave propagation. Our data show that myosin inhibition does not affect wave propagation. Therefore, we assume that membrane proteins with a spontaneous curvature are responsible for the protrusion-curvature feedback, although the identity of these proteins is yet to be elucidated. In the study by Peleg et al. (2011), a decrease in the actin polymerization force that deforms the membrane reduced the wave velocity. We also find that perturbations of the actin machinery slow the waves down, which reinforces our model assumptions.

Figure 9.

Computational model of actin protrusive array. (A) Positive feedbacks in the model: (1) actin filament branching (stick, B) needs NPFs (blue chevron, N); (2) NPF binding needs barbed ends; (3) actin pushing increases the membrane curvature (arc, C); (4) NPFs are attracted to the regions of higher membrane curvature. (B) Protrusive actin arrays impinge on the membrane at various angles (q) and generate force (F). The membrane ridge travels with velocity V of the order of actin polymerization rate. The arrays compete for the common pools of NPFs in the cytoplasm. (C) Model predicts that the membrane deforms in a ridge-like shape; barbed end density is shown in red. (D) The left/right column depicts simulated protrusion on microprinted line/fiber; upper and lower rows show snapshots from two different time points. (right) On fiber, the traveling wave of actin organized in a fin-like protrusion evolves. The black curve shows the outline of the actin ridge, white/gray shading indicates the NPF density at the leading edge. The colored shading below the membrane protrusion encodes the orientation of the local dominating actin array (warm colors, barbed ends grow to the left; cold colors, to the right). (left) as at the right but the parameters characterizing the total NPF amount and membrane tension are increased.

These assumptions lead to the self-organization of the fin if two additional feedback loops are present: Actin branching requires binding of the growing barbed ends to NPFs, whereas NPFs are recruited to the leading edge by the growing barbed ends (see Online supplemental material for details). Similar to a previous study (Kabaso et al., 2011), our study demonstrate that these four feedback loops cause the actin ridge to evolve with Arp2/3 and growing barbed ends at the leading edge (Fig. 9 C and Online supplemental material). We also show in the supplemental material that if a fluctuation results in a specific Arp2/3-actin array (distinguished from other arrays by growing at certain angle) becoming denser, this subsequently enhances the recruitment of additional NPFs and actin filaments to this location (Fig. 9 B). As a result, this dense array becomes even denser and will eventually incorporate most NPFs into its leading edge, thereby depleting the NPF pool and effectively outcompeting the actin arrays growing in other directions. Our simulations suggest that the resulting actin-driven fins can maintain a fixed shape and travel at a steady speed along the fiber with the ability to reflect between the boundaries at the cell body and the cell tip (Fig. 9 D and Video 10) and that the fin travels with a speed roughly equal to the actin polymerization rate, both findings that were observed experimentally.

Cells on adhesive lines displayed protrusive, lamellipodia-like extensions on both sides of the stripes. These extensions, unlike the fins, did not travel persistently along the stripes, and the lateral length of their combined leading edge was an order of magnitude greater than that of the fin. These differences can be explained by the fact that the actin-membrane protrusive ridge evolves on the solid flat surface because weak, nascent adhesions on the solid surface adjacent to the adhesive strip are likely to be engaged in synergistic dynamics with both the flat branching actin network (Choi et al., 2008) and Arp2/3 complexes (DeMali et al., 2002; Case and Waterman, 2011). This explains why the lamellipodia evolve on the solid surface rather than protrude up away from the surface, as observed on fiber. Finally, because the cell can spread more widely on the solid flat surface, the membrane tension in 2D is probably higher than that on the fiber (Even-Ram and Yamada, 2005). In our computer simulations, we demonstrate that by altering two model parameters—increasing the NPF concentration and the membrane tension—it is possible to reproduce the experimentally observed broad and dynamic protrusions at both sides of the adhesive strip (Fig. 9 D and Video 10; see Online supplemental material for details). Further discussion of how our model can explain the switching behavior between fin-like and lobopodia-like protrusions can be found in the Supplemental Material.

Discussion

Because of a large variety of physical properties that are being encountered by cells in 3D environments, various modes of migration have been described depending on ECM organization and composition (Even-Ram and Yamada, 2005; Doyle et al., 2013). Using a reductionist approach, we provide evidence that dynamic wave-like structures are crucial to promote cell migration along fibers. We observed that along these fibronectin-coated suspended fibers, the cell generates fin-like protrusive waves, built from the flat actin network through the activity of Arp2/3, N-WASP, and Rac1. Whereas these fin-like protrusions lead to cell migration, cells can generate other protrusions, such as lobopodia, which are formed because of higher cell contractility, but these do not promote cell body translocation. Our data show that fin-like protrusions are a very robust mechanism that are created at the cell body but act distally by propagating up to hundreds of micrometers away from the cell body, extending the leading edge. Similar actin-based waves have been observed during neuron extension and axonogenesis in vivo (Edmondson and Hatten, 1987; Flynn et al., 2009; Govek et al., 2011). By observing these fin-like protrusions at a high spatio-temporal resolution, we were able to determine that these fins guide cell migration along fibers but also analyze their dynamics, a finding that has not been reported in previous studies (Lee et al., 2013; Sharma et al., 2013; Xue et al., 2014; Higgins et al., 2015). Importantly, our study demonstrated that these waves of fin-like protrusions are exhibited and used by a variety of cell types, including endothelial, glioma, and fibroblast cell lines (Table S1), suggesting that is a widely used mechanism for fibrillar migration. In addition, this mechanism is also required when cells encounter multiple fibers. We anticipate that these fin-like protrusions can be used to guide cell migration within 3D matrices by dynamically probing the environment and facilitating changes in direction. As such, it appears to be a highly robust and versatile actin-based mechanism for cell migration.

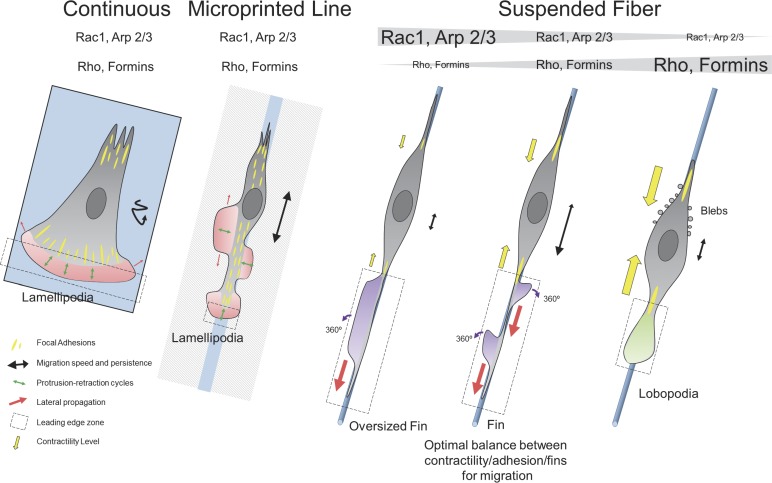
Although such fin-like protrusions may be reminiscent of lamellipodial structures observed from cells on flat surfaces (Borisy and Svitkina, 2000; Rottner and Stradal, 2011; Fig. 10), there are striking differences in shape and dynamics. These fin-like protrusions usually extend laterally over a much longer distance (up to hundreds of micrometers) than lamellipodia (Figs. 2 A and 10). However, their height is remarkably similar to the persistent width of lamellipodia (∼5 µm), and this is probably determined by the balance between actin polymerization-depolymerization rates (see also the cofilin staining in Fig. S3 B) and membrane resistance, as recently reported for neurons in 2D surface (Katsuno et al., 2015). The fin extension protruding along suspended fibers is, as opposed to the lamellipodia, perpendicular to the main cell-motion axis. This illustrates the main difference between the two structures: Cells on fibers rely on the lateral propagation of the fins as opposed to cells on flat substrates (2D or 1D lines) that rely on lamellipodia protrusion in the axis of cell migration (Fig. 10). It is worth noticing that this capacity to laterally propagate has been observed in numerous cases in cells on flat substrates; however, although this is linked to cell motility, it is not associated with migration efficiency (Döbereiner et al., 2006; Allard and Mogilner, 2013). We demonstrate that these fin-like protrusions assemble at the spindle cell body and mainly propagate toward the leading edge of the cell, allowing cell membrane extension and, as such, the progression of the cell’s front. Remarkably, the length of the protrusive region that extends from focal adhesion site to the leading edge on 3D fibers is an order of magnitude longer than on 2D surfaces.

Figure 10.

Schematic representation. On continuous substrate, the leading edge (dashed black box) is narrow in the axis of migration and determined by lamellipodia width and is very large in the transverse axis. Protrusion-retraction cycles of this region, along the axis of migration, promote cell motion, whereas lateral diffusion of the lamellipodia (red arrows) does not assist in migration. Migration is slow and poorly persistent (black track). On microprinted lines, the leading edge of the cell is now restricted by the width of the line, and short protrusion-retraction cycles in this zone are responsible for leading edge advancement. Focal adhesions are distributed over the entire cell length, resulting in the nucleation of new lamellipodia sites that do not promote effective migration. The lateral propagation could help migration, but the supportive nature of the substrate around the lines promotes lateral extension rather than propagation. Migration is fast and moderately persistent as the cell can easily nucleate new leading edge at the back of the cell. On suspended fibers, the leading edge is long in the axis of migration but narrow in the other axis. The lamellipodia-like actin under Rac1-Arp2/3 signaling cascade forms fin-like protrusions at the focal adhesion site. The lateral diffusion of fins is the leading cause for edge extension and cell migration. No protrusion retraction cycles are observed, as the fins are moving forward or backward. The fins are rotating and capable of changing direction and polarity once reaching the extreme end of the leading edge. Migration is fast and highly persistent. There is an optimal balance between contractility, adhesion and fins to promote the migration (contribution of contractility showed by yellow arrows). The Rho-formin pathway is important for fin creation but does not participate in their propagation. If the Rac1-Arp2/3 pathway becomes predominant, the cell shifts behavior and harbors oversized fins. If the Rho-formin pathway becomes predominant, the cell shifts behavior and harbors large lobopodia protruding at the front and lateral blebs at the back. Those cells are poorly persistent as lobopodia can change direction, in part because of strong hydrostatic pressure in the cell.

We show that the propagation of these fin-like structures that drive cell migration depends on Arp2/3 polymerization and Rac1 activity. Our modeling suggests that a positive feedback loop between the membrane curvature at the leading edge of such protrusions and Arp2/3 polymerization machinery may be sufficient to maintain small protrusions extending away from the fiber, without the need for adhesions. Moreover, simple competition for nucleation/branching regulators can lead to one actin array growing away, dominating resource use, and further extending in parallel to the fiber, creating traveling actin pulses. Our modeling predicts that the velocity of these traveling pulses is close to the actin polymerization rate, which agrees with the experimental data. However, the mechanisms behind actin transport and turnover, as well as the precise organization of the rear of the thin, dynamic, fin-like protrusions, remain to be elucidated. Our results show that the fins rely on actin assembly through Rac and Arp2/3 activity and disassembly through cofilin (as shown by immunostaining in Fig. S3 B), which suggests that the fins exhibit shared properties as lamellipodial fragments, which also travel without the need for a nucleus and other organelles, and move with a speed, shape, and actin organization that are strikingly similar (Ofer et al., 2011; Online supplemental material).

Intriguingly, we observed that another mode of round, bleb-like protrusions occasionally emerge at the leading edge of the cells on a fiber. These lobopodia-like protrusions (Petrie and Yamada, 2012) contain actin and are associated with formins. Small blebs in the cell body region accompanying the formin-associated lobopodia and the fact that strengthening of contractility enhanced this mode of protrusion suggest that this mechanism is associated with a higher hydrostatic pressure of the cytoplasm. On the basis of our modeling, we propose that Arp2/3-mediated and formin-mediated networks compete for the common limiting resource on fiber (i.e., the actin pool; Burke et al., 2014). Other relevant phenomena have been reported in recent studies on cell migration in confined environments (Wilson et al., 2013; Bergert et al., 2015; Liu et al., 2015; Ruprecht et al., 2015). Distinct actin networks were observed depending on the boundary conditions, with the freely growing network against the cell membrane being driven by Arp2/3 (Wilson et al., 2013). Yet the cell switched to bleb formation when this pathway was inhibited (Wilson et al., 2013).

The emergence of cell migration modes relies on internal and external mechanical signals, such as nuclear deformation, cytoskeleton dynamics, cytoplasmic and external osmotic pressure, scaffold porosity, and stiffness (Zaman et al., 2006; Ilina and Friedl, 2009; Wolf et al., 2013; Petrie et al., 2014). Depending on the external physical constraints, cells probably have to switch from one mode of migration to another (Wilson et al., 2013; Bergert et al., 2015; Liu et al., 2015; Ruprecht et al., 2015). It is possible that when the fibrous environment is less porous and the cell nucleus becomes confined, upregulation of contractility induces the formation of lobopodia, which are able to push out the surrounding matrix, creating pores to allow the nucleus through, whereas in a more porous environment, the cell embraces individual fibers and generates long, polarized protrusions along the fibers for fast migration. The fins traveling along these long protrusions deliver cytoskeletal and polymerization machinery to the protrusion tips from the cell body. The formation of the fin-like protrusions is thus crucial for effective cell polarization and highly persistent cell migration along the fibers.

In this study, by reducing the complexity of cell migration using a nanofiber approach, we show that cells in a 3D environment generate a unique organization of protrusions, where fin-like structures allow proper migration. This work opens the way for further studies based on similar substrates incorporating increased but well-defined complexities, as well as allowing the direct measurement of forces exerted by cells within 3D environments.

Materials and methods

Cell culture and transfections

NIH-3T3 fibroblasts (ATCC), immortalized mouse embryonic fibroblasts RPTPα (Giannone et al., 2004), REF52 fibroblasts (ATCC), HeLA cells (ATCC), HEK-293 cells (ATCC), NSC34 cells (Cellutions Biosystems), MDCK cell lines (ATCC), C6 rat glioma cells (ATCC), and HUVEC (PromoCell) were cultured in high glucose DMEM supplemented with 10% heat-inactivated FBS (Hi-FBS; Invitrogen) at 37°C with 5% CO₂. THP1 human monocytic leukemia cell line was obtained from Health Protection Agency Culture Collections and cultured using Roswell Park Memorial Institute medium 1640 (Life Technologies) media supplemented with 10% Hi-FBS (Life Technologies) and 2 mM glutamine (Life Technologies) with 50 µg/ml mercaptoethanol (Sigma-Aldrich) at 37°C with 5% CO₂. PC12 cells (ATCC) were cultured in DMEM supplemented with 5% FBS and 10% horse serum (Life Technologies) at 37°C with 5% CO₂.

Neonatal cardiac fibroblasts were isolated from 1–3-day-old Sprague-Dawley rats (Nagy et al., 2006). In brief, ventricles were minced and digested with 0.3–0.5 mg/ml collagenase type II (Worthington Biochemical Corp.) in 37°C water bath with 250 rpm linear shaking. Tissues were digested three to four times, and cell suspensions from each digestion were combined for Percoll (GE Healthcare) density gradient centrifugation to separation. With Percoll (1.06 g/ml stock) density of the top layer (10 ml mixed with 2.5 ml ADS + 12.1 ml dH₂O) and the bottom layer (9 ml mixed with 1 ml ADS), fibroblasts and cardiomyocytes were separated on the top and bottom of the lower-density Percoll layer, respectively. Fibroblasts were recovered for further study.

Purified cardiac fibroblasts were seeded onto collagen type I–coated culture dishes (5 µg/cm²; Sigma-Aldrich). The culture medium was DMEM containing low glucose (1 g/l), 10% FBS, 100 U/ml penicillin, 100 µg/ml streptomycin, and 250 ng/ml amphotericin B (Thermo Fisher Scientific). Fresh medium was replaced after overnight attachment. Cells were then grown to subconfluency before passaging with 0.25% trypsin-EDTA (Thermo Fisher Scientific).

Plasmids were transfected into NIH-3T3 fibroblasts by electroporation using a neon electroporator (Invitrogen) as per manufacturer’s recommendations.

Reagents

Plasmids used in this study were RFP-actin, YFP-Rac1L61, and YFP Rac1N17 (from Lemichez’s group, C3M University of Nice Sophia Antipolis, Nice, France); RFP-MLC (from M. Tamada, Memorial Sloan Kettering, New York, NY); mCherry-Arp2, GFP-mDiaN3, and mCherry-Paxilin cDNAs (Addgene); GFP-mDia1 full-length and GFP-mDia2 full-length cDNAs (Addgene); peYFP-α tubulin (Clontech); and GFP-Tallin (from Critchley’s group, University of Leicester, Leicester, UK). Fibronectin was obtained from Roche Applied Science. Poly-l-lysine (0.01%), blebbistatin, latrunculin A, nocodazole, CK666, and wiskostatin were obtained from Sigma-Aldrich. Formin inhibitor SMIFH2 was obtained from Hit2Lead.com. Y27632 dihydrochloride and NSC23766 were obtained from Tocris Bioscience. For experiments with inhibitor, cells were first seeded in a normal media and, after 3 h, inhibitor was added. For washout experiments, the same protocol was followed; after 3 h with inhibitor, the media was switched to a normal one.

Electrospinning: preparation of fibers

PCL (mol wt, 80,000) and 2,2,2-tetrafluoroethanol (≥99%) were obtained from Sigma-Aldrich. PCL fibers were produced by electrospinning (Cao et al., 2009). Different parameters were used to produce 300-nm, 700-nm, and 1.3-µm fibers, as reported in Table S2. PCL fibers were coated with fibronectin for 1 h at 37°C and washed with PBS. All experiments were performed with 25 µg/ml of fibronectin unless otherwise specified.

Micropatterning

4-µm lines were printed on plastic dishes using microcontact printing: Polydimethylsiloxane stamps for microcontact printing were prepared as described elsewhere (Vedula et al., 2012). Molds of the pattern were prepared using standard lithography methods. Polydimethylsiloxane (Sylgard 184; Dow Corning) was prepared by mixing the base and curing agent in a ratio of 1:10 (wt/wt) and degassed. It was poured over the mold, degassed, and cured for 2 h at 80°C. Stamps were peeled off the molds and plasma cleaned to make their surface hydrophilic. Fibronectin (25 µg/ml) was added immediately over the stamps and was allowed to be absorbed for 30 min at 37°C. The excess fibronectin was removed and the stamps were air blow-dried. They were gently pressed against the bottom of a non–culture-treated Petri dish for ∼1 min. The stamps were then carefully lifted up and the Petri dishes were treated with a solution of 0.2% Pluronic F127 (Sigma-Aldrich) for 1 h to prevent cell attachment on the unstamped areas. After the incubation, the dishes were thoroughly rinsed several times with PBS to remove excess Pluronic F127. 3T3 cells were seeded on the patterns and incubated at 37°C. The medium was removed 30–60 min later to wash off the unattached cells, and the Petri dishes were rinsed again with culture medium to remove floating cells.

Fluorescent labeling of ECM proteins

Fibronectin was conjugated with Alexa 568 Fluor–based dyes as per manufacturer recommendations (Invitrogen).

Immunofluorescence staining

Antibodies

The following antibodies were used: mouse anti-Arp3 (Abcam), mouse anti-mDia1 (BD Biosciences), rabbit anti-Cofilin (Abcam), and rabbit anti-Paxilin (Abcam).

Fixation and immunofluorescence

Before fixation, fibers were coated with fibronectin as described previously and cells were seeded for 2 h. For analysis of Cofilin and mDia1, 3T3 cells were fixed in 4% paraformaldehyde in PBS and then neutralized using 10 mM NH₄Cl in PBS for 15 min. Cells were subsequently washed three times with PBS, blocked, and permeabilized using PBS containing 0.1% Triton X-100 and 0.5% BSA for 15 min at room temperature for 15 min. Then, cells were incubated with primary antibodies for 1 h at room temperature. After washes, they were incubated with Alexa 488-conjugated goat anti-mouse or anti-rabbit and rhodamine phalloidin (Sigma-Aldrich) for 45 min at room temperature. For analysis of Arp3, cells were fixed with methanol for 5 min at −20°C. For analysis of Arp3, cells were fixed with methanol for 5 min at −20°C before immunostaining according to the above protocol except that phalloidin staining was omitted. MDCK cells were immunostained according to the protocol used for 3T3 cells.

Imaging

The fixed cells were imaged using the confocal microscope LSM70 (Observor Z1; Carl Zeiss) with a 63× (NA 1.2, water) objective.

Microscopy

Long-term imaging was done using a microscope equipped with temperature, humidity, and CO₂ control (Olympus IX81 inverted microscope) or a BioStation (Nikon). Phase contrast images were acquired every 2 min or 30 s using a 10× (NA, 0.3, Ph1) or 20× (NA, 0.45, Ph2) objective. Acquisitions were typically obtained over a period varying from 4 to 24 h. Short-term imaging was performed using an Olympus IX81 inverted microscope with a 20× or 60× differential interference contrast (DIC; NA, 1.2, DIC1, water) with an acquisition every 2 s for a few hours. For high-resolution microscopy, spinning disk confocal microscopy was performed with a Perkin-Elmer confocal spinning unit connected to an IX 81 microscope body (Olympus). Images were acquired through a 60× (NA, 1.2, water) objective with a C9100-13 electron multiplying charge coupled device camera (Hamamatsu Photonics). A confocal LSM70 Observor Z1 (Carl Zeiss) with a 63× (NA, 1.2, water) objective was also used for image acquisition. MetaMorph software (for Olympus microscope; Molecular Devices), Nikon software (for BioStation), and ZEN 2006 software (for Carl Zeiss microscope) were used. For life cell imaging, all images were acquired with cells in high glucose DMEM supplemented with 10% Hi-FBS (Invitrogen) at 37°C with 5% CO₂.

Tracking

Cell bodies were tracked using the manual tracking plugin for Fiji software over 6 h of migration. Only single cells were tracked. Once the position of the cell body was recorded over time, different parameters were calculated: total trajectory length (sum of the displacement at each time point), track lengths (the last position minus the initial position), cell body linear speed (total trajectory length over total time), and persistence p_s (track length [the last position minus the initial position] divided by the total displacement of the cell).

Modeling

Aggregation of barbed ends and NPFs and emergence of ridge-like membrane protrusion

Barbed ends (density B), NPFs (density N), and fluid membrane characterized by local elevation above the base plane are the major players in the formation of the protrusions. All densities and membrane elevation are the functions of time and spatial coordinates x and y. If N accumulates at places where local membrane curvature is high (convex being positive), the increased N will activate more B, which pushes against the membrane and deforms it further. Then, dynamics of N and B is coupled to the mechanics of the membrane through a positive feedback. We introduce the following model:

$$\frac{\partial B}{\partial t}=D_B{\nabla }^{2}B+k_1\frac{NB}{1+k_{2}B}-k_{3}B$$ (1)

$$\frac{\partial N}{\partial t}=D_N{\nabla }^{2}N+k_{4}B\left(1-\frac{1}{N_0}{{\displaystyle \int }}^{\text{}}NdA\right)-k_{5}N$$

Here, the first terms in the right side for both equations describe diffusion where D_B is the effective diffusion constant of barbed ends (because of growth at various angles along the membrane; Lacayo et al., 2007) and D_N is the effective diffusion constant of NPFs. The second term in the first equation describes the branching rate of barbed ends, which is proportional to the local concentration of NPFs and to the local barbed end density at low B. At higher branched end density the rate saturates. The last term in the first equation describes the disassembly and/or capping. The second term in the second equation describes recruitment of the NPFs to the leading edge by the barbed ends with the rate proportional to both barbed end density and concentration of the NPFs in the cytoplasm and/or plasma membrane. The last term in the last equation describes removal of the NPFs by the actin centripetal flow. We use nondimensional units for the barbed end and NPF densities. The unit of time is 1 s, and the unit of length is 1 µm. The model is not sensitive to the exact values of the diffusion coefficients as far as they are smaller than 1 µm²/s, which is always the case: characteristic diffusion coefficient for membrane protein is at least an order of magnitude less than a micrometer squared per second (Jacobson et al., 1987), and the effective diffusion of the barbed ends can be estimated as the rate of actin growth (∼0.1 µm/s) squared divided by the rate of capping (∼1/s), which is two orders of magnitude <1 µm²/s.

The characteristic rates of capping, retraction from the leading edge by the centripetal flow and disassembly are all of the order of 1/s (Mogilner and Edelstein-Keshet, 2002), and so we use the nondimensional values k₃ = 0.5 and k₅ = 1. Similarly, the rate of branching is of the order of the capping rate, and we assume that the rate of NPF recruitment to the barbed end (which is unknown) is of the same order. Thus, nondimensional values of parameters k₁ and k₄ are of the order of 1; we use k₁ = 2 and k₄ = 1. Finally, we assume that the nondimensional value of the unknown parameter k₂ = 1 and the value of parameter N₀ = 10A, where A is the simulated area of the membrane. The model predictions are valid in the wide range of parameters k₁, k₂, k₃, k₄, and k₅ as far as they are of the order of 1.

Eq. 1 for B and N were solved using the explicit “forward time-centered space” finite difference method (Garcia, 2000). The result is the steady-state distribution on a 20 × 20-µm² surface with periodic boundary condition shown in Fig. S5 F. This result shows that a steady-state aggregation of the barbed ends and NPFs self-organizes in the model.

In our model, the cell membrane is assumed to be in the x-y plane and subject to pushing forces by actin filaments in the z-direction. We use an orthogonal mesh with fixed x- and y-coordinates and variable z-coordinate to describe the contour of the membrane. Because the membrane is fluid, the mesh does not represent the positions of specific lipids in the membrane but rather the height of the membrane at given x- and y-locations. We calculate the forces on each membrane grid point and then obtain the z-coordinate of the grid as follows. The force along the z-direction on each grid is the sum of bending, tension, osmotic/hydrostatic pressure and filament pushing forces:

$$F=\left[k_b{\nabla }^{4}z+\lambda {\nabla }^{2}z+p_0\left(1-V/V_0\right)+f_{0}B\right]\Delta A$$ (2)

where k_b is the bending stiffness of the membrane, λ is the membrane tension, ­p₀ is a pressure factor stabilizing the volume inside the membrane, $V=\int zdA$ is the volume of the underneath membrane, V₀ is the target volume at which the pressure is zero, f₀ is the protrusion force per barbed end, and ΔA is the area per grid. The motion of each grid in the z-direction in each time is assumed to approach the position of force equilibrium. The displacement in z-direction is Δz = F/k₅, where $k_{\mathrm{5}}=\lambda \sqrt{\Delta A}$ is the effective spring constant for each membrane grid estimated by dimension analysis. We used the values k_b = 0.1 pN × µm (Diz-Muñoz et al., 2013), λ = 100 pN/µm (Lieber et al., 2013), unknown factor p₀ = 10³ Pa, the target volume V₀ = 100 µm³, the force per filament f₀ = 1 pN (Prass et al., 2006), and the unit of the barbed end density 10³/µm³ (Prass et al., 2006).

We simulated the model as follows. The projected area of the membrane in our simulations is 10 × 10 µm with a periodic boundary condition. The mesh has 40 grid points along each direction (total number of grid points, 1,600). At the beginning of the simulation, the membrane is flat and lies in the x-y plane. The initial values of B, N, and ${\overline{n}}_B$(${\overline{n}}_B$ is the outward normal to the membrane) are randomly assigned with $\overline{\overline{B}}=1/k_2$ and $\overline{N}=N_0/A$. The time step Δt is chosen so that the numeric scheme for equations for B and N are stable, which requires: (1) $\mathrm{ }\Delta t<min\left(\Delta x^2,\Delta y^2\right)/\left[2max\left(D_B,D_N\right)+k_6/min\left(\Delta x^2,\Delta y^2\right)\right]$, (2) $\Delta t<\left(1+k_2\overline{B}\right)/k_1\overline{NB}$, (3) $\Delta t<min\left(k_3,k_5\right)$, and (4) $\Delta t<\overline{N}/k_4\overline{B}$.

We describe the additional term that requires coefficient k₆ below. At each time step, values of B and N are updated, the force on the membrane is calculated, and the membrane grid points are moved accordingly.

The coupling energy between an elastic membrane and membrane proteins with nonzero spontaneous curvature has been proposed to be proportional to the local curvature of the membrane (Ramaswamy et al., 2000; Shlomovitz and Gov, 2007). Because the curvature-driven force on a membrane protein is the spatial derivative of the coupling energy, we assume that NPFs associate with asymmetric membrane proteins and drift with the curvature-dependent rate ${\overline{v}}_N$ given by the following expression:

$${\overline{v}}_N=k_6{\left(\frac{\partial C_x}{\partial x},\frac{\partial C_y}{\partial y}\right)}^T,$$

where k₆ is a constant, and C_x = ∂²z/∂x² and C_y = ∂²z/∂y² are the membrane curvatures along the x and y directions, respectively. The value of the coefficient k₆ is unknown; we use k₆ = 0.01 µm³/s, which accounts for the slow drift, with a rate of 0.01 µm/s providing a small curvature gradient of 1/ µm per 1 µm. Then, the equation for density N is changed as follows:

$$\frac{\partial N}{\partial t}=D_N{\nabla }^{2}N-\nabla \cdot \left({\overline{v}}_{N}N\right)+k_{4}B\left(1-\frac{1}{N_0}{{\displaystyle \int }}^{\text{}}NdA\right)-k_{5}N\mathrm{.}$$ (3)

Simulation of this model (Eqs. 1–3) shows that the barbed ends deform the membrane into the ridge-like shape (Fig. S5 G) rather than an axisymmetric bulge.

Model of the actin sheet with variable orientations of actin arrays

The ridge of protrusion that is observed in the experiment is not stationary but behaves like a traveling wave along the membrane. To simulate this effect, we have to incorporate the orientation of actin filament arrays into the model. It is computationally too expensive to formulate a full 3D model, so we formulate the model in 2D, in the plane of the ridge-like protrusion, so that the barbed end and NPFs are now located at the leading edge defined by the curve y(x), where x − axis is the baseline (surface of the fiber in the 3D case and edge of the adhesive strip in the 2D case) and y is the magnitude of the membrane protrusion.

We describe the distribution of growing actin filaments arrays by the barbed-end density B (x,θ), which grows on the membrane at x with orientation θ (Fig. S5 G).

New actin filaments are assumed to be created by branching, which requires both existing filaments and membrane-bound NPFs. Therefore, as noted above, the creation rate of barbed ends is assumed to be proportional to both B and the local density of membrane-bound NPFs (N (x)):

$$\frac{\partial B}{\partial t}=k_1\frac{NB\cos \phi }{1+k_{2}B}-k_{3}B-v_x\frac{\partial B}{\partial x}.$$ (4)

Here, the first two terms are the same as respective terms in the first equation in (1), other than that we assume that the branching rate depends on the angle ϕ at which the actin array impinges on the membrane. Note that we do not consider individual actin filaments but rather branching trees of filaments where successive "mother" and "daughter" filaments grow at angles of 75° relative to each other. The array is perpendicular to the leading edge if the individual filaments approach the membrane at ±35°. Following the idea and experimental results in Maly and Borisy (2001), we assume that the more perpendicular the whole array is to the membrane, the more effective is the branching. In Maly and Borisy (2001), the assumption was that effective capping decreases for perpendicular angles, but mathematically their and our assumptions are equivalent. The last term accounts for the propagation of the actin array with the rate v_x = v­₀ cosθ along the x-axis, where v­₀ is the growth speed of the filaments. We use v­₀ = 0.1 µm/s (Mogilner and Edelstein-Keshet, 2002).

After growing filaments are capped with rate k₃, they stop elongating but still provide structural stability to the lamellipodia until they are fully disassembled. The density of capped filaments is denoted as C (x,θ) and we describe it with the following equation:

$$\frac{\partial C}{\partial t}=k_{3}B-k_{7}C,$$ (5)

where k₇ (we use k₇ = 0.05/s; Mogilner and Edelstein-Keshet, 2002) is the disassembly rate of actin filaments.

We adjust the model for the NPF dynamics to the 2D geometry of the model as:

$$\frac{\partial N}{\partial t}=k_4\frac{N_{tot}-{{\displaystyle \int }}^{\text{}}Ndx}{L}{{\displaystyle \int }}^{\text{}}Bd\theta -k_{5}N,$$ (6)

where L is the length of the leading edge projection onto the x-axis.

The membrane is modeled as a chain of M evenly spaced nodes, each of which has a fixed x-coordinate with a constant spacing Δx = L/M between neighboring nodes. Each node has a variable y-coordinate to denote the local displacement of the membrane. These nodes do not represent material points of the membrane but serve as markers to show the membrane contour. The motion of these nodes is obtained by minimizing the Helfrich free energy of the membrane (Zhong-can and Helfrich, 1987) in the presence of the pushing forces from actin filaments. We neglect the bending stiffness of the membrane in this model because the curvature in the direction parallel to the leading edge is much smaller than that in the perpendicular direction and calculate the total energy of the membrane as follows:

$$E=\lambda {{\displaystyle \int }}^{\text{}}dl+p_0{\left({{\displaystyle \int }}^{\text{}}ydx-A_0\right)}^2+{{\displaystyle \int }}^{\text{}}{E}_{B}dx+{{\displaystyle \int }}^{\text{}}{E}_{C}dx,$$ (7)

where λ and p₀ have the same meaning as membrane tension and pressure parameters of the 3D model and A₀ has the same meaning as V₀, E_B, and E_C in that the last two terms are the linear density of mechanical work from pushing and capped filaments, respectively. E_B is calculated as

$$E_B=\underset{0}{\overset{\delta y}{{\displaystyle \int }}}{F}_{B}dy,$$ (8)

where δy = y − y_B is the distance between the membrane (y) and the barbed ends (y_B) at the same x, and F_B is the y-component of force from the growing filaments to the membrane. We assume that that each filament generates a pushing force f₀ against the membrane. Magnitude of F_B is assumed to be proportional to the number of growing filaments that grow along the normal direction of local membrane:

$$F_B=f_0{n}_{y}max\left[1-max\left(\delta y/y_o,0\right),0\right]\underset{\phi <\pi /2}{\overset{}{{\displaystyle \int }}}B\cos \phi d\theta ,$$ (9)

where n_y = sin α projects the normal force on the membrane to the y-direction and y_{0 =} f_0/k₀ is the maximum deformation of each growing filament. The term in the square brackets describes the linear reduction and the maximum range of the pushing force as a function of δy because of spring relaxation. Similarly, work from capped filaments is nonzero only if capped filaments are compressed by the membrane (δy < 0):

$$E_c=\underset{0}{\overset{\delta y}{{\displaystyle \int }}}{F}_{C}dy,$$ (10)

where F_C is the resisting force from the capped filaments satisfying

$$F_C=H(-\delta y)k_0{n}_y\delta y\underset{\phi <\pi /2}{\overset{}{{\displaystyle \int }}}C\cos \phi d\theta .$$ (11)

H(x) in Eq. 11 is the Heaviside step function with H(x) = 1 if x ≥ 0 and H(x) = 0 if x < 0. In the simulation, we find the equilibrium geometry of the membrane by minimizing the total energy of membrane in Eq. 7.

At the beginning of each simulation time step Δt, we assume that all B, C, and N are located at the local membrane. We calculate the change in B, C, and N using a finite difference method according to Eqs. 4–7. After the values of B, C, and N are obtained, we fix the positions of barbed ends y_B at each x and vary the y-coordinate of the corresponding nodes as y(x) = y_B(x) + δy, where δy = k_BTU/f_oB₀Δx is the height variation, U is a random number with a uniform distribution between −1 and 1, and

$$B_0=\left(\frac{c_0{N}_{tot}}{c_{2}L}-1\right)/c_1$$

is the estimated steady-state concentration of barbed ends from Eq. 1. We then calculate the change in the total energy (ΔE) from Eq. 7. The new position of each membrane node is accepted if ΔE ≤ 0 or a random number with a uniform distribution between 0 and 1 is less than exp(−ΔE/k_BT) when ΔE > 0. Otherwise, the membrane node reverts to its previous position. We repeat the membrane relaxation multiple times for each Δt until values of ΔE between two sequential runs differ by less than 1%. After the membrane is relaxed, we define the y-position of barbed ends at each x to be the same as that of the membrane: yB = y. We then repeat the preceding steps with time increased by Δt. In the calculations, L = 20 µm; A₀ = 20 µm²; M = 60; and other parameters values are as above. When we simulate the case of the fiber, we use λ = 50 pN and p₀ = 50 pN/µm. For the case of the adhesive strip, we use increase these parameters to λ = 300 pN and p₀ = 400 pN/µm, and we increase the total number of units of NPFs from 10 to 40. The results of the simulations are shown in the main text.

Model of competition of Arp2/3- and formin-mediated actin networks

The model can explain the switching behavior between the fin-like and lobopodia-like protrusions as follows. We hypothesize that in the case of lobopodia formation, higher myosin contractility induces an increase in the internal hydrostatic pressure, and that this pressure balances a greater fraction of the opposing membrane tension-relieving resistance to growth of actin filaments impinging on the membrane. This allows formin-associated filaments to grow more easily in regions not colocalized with flat, mechanically robust and Arp2/3-governed actin sheets. As a result of this relative advantage of the formin-governed actin polymerization, competition for a limiting molecular resource needed in both Arp2/3- and formin-actin networks can lead to the "winner-takes-all" transition from the flat fin-like traveling actin waves to the stationary lobopodia-like formin-governed protrusions (see Online supplemental material). Conversely, lowering myosin contractility and relieving the hydrostatic pressure disadvantages the isotropic and formin-governed network, allowing all actin resources to concentrate in the fins.

The branched and formin-generated filaments are likely to compete for the common G-actin pool. (This is a hypothesis based on Burke et al. [2014]; competition for any other limiting molecular resource leads to the same conclusions.) We consider the following conceptual model:

$$\frac{dB}{dt}={\tilde{k}}_1\frac{B}{1+k_{2}B}\left(\overline{G}-{\beta }_{1}B-{\beta }_{2}F\right)-k_{3}B$$ (12)

$$\frac{dF}{dt}={\tilde{k}}_8\frac{F}{1+k_{9}F}\left(\overline{G}-{\beta }_{1}B-{\beta }_{2}F\right)-k_{10}F$$ (13)

Here, B and F are the densities of the branched and formin-generated F-actin, respectively (we consider just temporal dynamics, not spatial distributions, in this simplified model), densities of which are measured in units of a characteristic scale. The last terms in the right hand sides of Eqs. 12 and 13 describe disassembly of respective networks; for simplicity we consider equal disassembly rates k₃ = 1/min and k₁₀ = 1/min. The first terms in the right hand sides of Eqs. 12 and 13 describe growth rates of the branched and formin-generated F-actin because of branching and elongation and nucleation and elongation of the filaments, respectively. Note that in the equation for B (compare with Eq. 1) we incorporated the factor proportional to the NPF (Arp2/3) concentration into the growth rate. We also use the assumption that both branching rate and filament elongation rate are proportional to the G-actin concentration. For the elongation rate, this is well established (Mogilner and Edelstein-Keshet, 2002); for the branching rate, see Kelly et al. (2006). Similarly, we assume that for formin-associated filaments, both nucleation rate and elongation rate are proportional to the G-actin concentration (Scott et al., 2011). We also assume that the rate of increase of the formin-associated Factin has the same functional dependence on the formin concentration as that for branched actin on the Arp2/3 concentration; these exact functional dependencies are not crucial for the qualitative model conclusion. Finally, the available G-actin pool is proportional to the total actin amount $\overline{G}$ minus the amounts of F-actin associated with branching and formin-derived networks; β₁ and β₂ are respective proportionality coefficients.

Lastly, we assume that if contractility and so hydrostatic pressure in the cell increases, the cell membrane is tended to be inflated into bubble-like protrusions rather than flat lamellipodia-like protrusions with curvy leading edges. Because of that, the curvature effect does not assist Arp2/3 aggregation, effectively diminishing the growth rate of the branching network ${\tilde{k}}_1$.

We use the following parameter values: $\overline{G}$ = 3 units, k₂ = k₉ = 1/unit, β₁ = β₂ = 3, ${\tilde{k}}_8$ = 1/(unit × min), and ${\tilde{k}}_1$ ≈ 1/(unit × min). Exact values of the parameters are not important for the qualitative outcome of the model, as long as the parameters are of the given order of magnitude.

We simulated the model given by Eqs. 12 and 13 and found that there is a phase transition when the effective growth rate of the branched network becomes greater or smaller than that of the formin-associated actin network (Fig. S5 H). Assuming that in control the effective growth rate of the branched network is greater than that of the formin-associated actin network, the branched actin density is much higher than density of formin-associated actin filaments. However, when contractility and thus hydrostatic pressure in the cell increase, the formin-generated network becomes much denser than the branched network.

Notes on actin transport and membrane tension

In the model, we focused in detail on the self-organization of the leading edge. Of course, this is but a part of the whole picture. The most pressing question, which is beyond the scope of this study, is how transport, turnover, and recycling of actin in the traveling actin band are organized. Here, we briefly discuss theoretical hypotheses relevant for this topic. We hypothesize that the mechanics of the actin fin traveling on a fiber is largely similar to that of the keratocyte lamellipodial fragment (Ofer et al., 2011), which also migrates without the cell body, and with similar shape, speed, size, and distributions of actin and Arp2/3. In keratocyte fragments, actin monomers are transported with the fragment; there are theoretical demonstrations that G-actin can be transported by diffusion (moving forward down the gradient providing the G-actin concentration is lower at the leading edge) within the protruding F-actin band (most recent relevant study is Vitriol et al. [2015]). In the case of the actin fin traveling on a fiber, in principle, monomers could be delivered to the fin from the cell body. However, in this case, the diffusive flux is approximately equal to D (ΔG/L), where D is the monomer diffusion coefficient, L is the distance between the cell body and traveling fin, and ΔG is the difference between the G-actin concentration in the cell body and in the fin. This flux has to be equal to the drift of F-actin forward, which is VF, where V is the traveling speed and F is the F-actin concentration in the fin. Thus, (ΔG/L = VF → ΔG = (VL/D)F. V ≈ 0.15 μm/s (this study), L ≈ 200 µm (this study), D ≈ 15 µm² (Ofer et al., 2011), F ≈ 500 µm (Ofer et al., 2011), so ΔG ≈ 1 mM, which is an order of magnitude greater than even the greatest existent estimate (Koestler et al., 2009). Thus, delivery of actin from the cell body is highly unlikely. The reason is that the distance from the cell body is too great for diffusion to work.

Similarly to keratocyte fragments, actin network is likely to gradually disassemble behind the leading edge in a cofilin-assisted process, so by the time the rear of the fin reaches a certain point, the actin network at this point could be almost completely disassembled (Ofer et al., 2011). Membrane tension at the rear could assist in crushing remaining weak actin network, thus actin accumulating at the rear is likely a dense gel of disconnected, rapidly disassembling short actin filaments. According to the model, the speed of propagation at the front is equal to filament elongation rate at the front, which is the free polymerization rate, slowed down by the membrane tension. Lastly, we hypothesize that the result of photo-ablation experiment, which showed that the actin ridge cannot propagate autonomously, can be explained as follows. As we already noted, transport of actin and actin-related proteins from the cell body to the fin is unlikely. Membrane tension, however, is crucial for the fin propagation: according to the model, it both enables one dominant actin array to win, polarizing the protrusion, and crushes the weak actin network at the rear. After ablation, the membrane tension in the part of the cell disconnected from the cell body is likely to drop drastically, disabling the protrusion.

Online supplemental material

Fig. S1 shows the experimental system and some complementary results on cell speed and spreading. Fig. S2 shows analysis of cell behavior on fibers of different diameters and on printed lines. Fig. S3 shows fluorescent staining for different actin-polymerizing machineries. Fig. S4 shows kymographs of washout experiments for 3T3 cells seeded on fiber. Fig. S5 shows complementary experiments with MDCK cells on fiber and 3T3 cells on line and fiber as well as figures from the mathematical modeling. Table S1 summarizes the different cell types tested and Table S2 summarizes the parameters used for electrospinning. Video 1 shows a comparison of 3T3 behavior in different coating of fiber. Video 2 shows a comparison of migration behavior on different substrates. Video 3 shows a 3T3 migration on suspended fiber, formation of fin-like protrusion vs TPH1 on suspended fiber, no fin-like protrusion. Video 4 shows 3T3 migration on microprinted-line. Video 5 shows Fin-like protrusion in a cell spanning between multiple fibers. Video 6 shows 3T3 migration on suspended fiber: correlation between fin and polarization. Video 7 shows Arp2/3-mediated cell polarization. Video 8 shows force application and matric deformation on fiber. Video 9 shows an alternative mode of protrusion. Video 10 shows a simulation of protrusion dynamics on line and fiber. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.201501106/DC1.