Abstract
An image-based 3D–2D registration method is presented using radiographs acquired in the uncalibrated, unconstrained geometry of mobile radiography. The approach extends a previous method for six degree-of-freedom (DOF) registration in C-arm fluoroscopy (namely ‘LevelCheck’) to solve the 9-DOF estimate of geometry in which the position of the source and detector are unconstrained. The method was implemented using a gradient correlation similarity metric and stochastic derivative-free optimization on a GPU. Development and evaluation were conducted in three steps. First, simulation studies were performed that involved a CT scan of an anthropomorphic body phantom and 1000 randomly generated digitally reconstructed radiographs in posterior–anterior and lateral views. A median projection distance error (PDE) of 0.007 mm was achieved with 9-DOF registration compared to 0.767 mm for 6-DOF. Second, cadaver studies were conducted using mobile radiographs acquired in three anatomical regions (thorax, abdomen and pelvis) and three levels of source-detector distance (~800, ~1000 and ~1200 mm). The 9-DOF method achieved a median PDE of 0.49 mm (compared to 2.53 mm for the 6-DOF method) and demonstrated robustness in the unconstrained imaging geometry. Finally, a retrospective clinical study was conducted with intraoperative radiographs of the spine exhibiting real anatomical deformation and image content mismatch (e.g. interventional devices in the radiograph that were not in the CT), demonstrating a PDE = 1.1 mm for the 9-DOF approach. Average computation time was 48.5 s, involving 687 701 function evaluations on average, compared to 18.2 s for the 6-DOF method. Despite the greater computational load, the 9-DOF method may offer a valuable tool for target localization (e.g. decision support in level counting) as well as safety and quality assurance checks at the conclusion of a procedure (e.g. overlay of planning data on the radiograph for verification of the surgical product) in a manner consistent with natural surgical workflow.
Keywords: image-based 3D, 2D registration, geometric calibration, global optimization, image-guided interventions, image-guided surgery, mobile radiography, quality assurance, patient safety
1. Introduction
Mobile digital radiography (DR) is widely used in the operating room (OR), intensive care unit (ICU) and in various bedside applications for diagnosis, target localization and/or verification of interventional device placement and surgical product. A mobile DR system consists of an x-ray source and (in recent systems, a wireless digital) detector that are somewhat unconstrained in their geometric relationship. The flexibility in imaging geometry facilitates the use of mobile radiography in challenging setups about the OR table, ICU bed, etc, though it can also challenge the radiographer in placing the detector at a suitable position with respect to the source and patient. For 3D–2D registration, a mobile system entails nine degrees of freedom (9-DOF) to be solved in estimating the source-detector geometry, compared to 6-DOF associated with a C-arm (in which the source–detector relationship is constrained by the C-arm gantry and can be well calibrated).
Intraoperative mobile radiography is often employed at both the beginning of a case (e.g. for level counting in spine surgery) and at the end of a case (as verification of surgical product and a check against retained foreign bodies). Analysis of the radiograph is primarily visual and qualitative—for example, visual confirmation that a target structure is correctly localized by placing a radio-opaque tool on the patient, or assessing the placement of implants (e.g. pedicle screws) visually with respect to their relative position to the surrounding anatomy. The work reported below aims to extend the utility of mobile intraoperative radiography via accurate 3D–2D registration to preoperative CT and planning data for more rigorous and quantitative localization and verification. For example, registration to a mobile radiograph acquired at the beginning of a case could provide decision support in vertebral level counting analogous to the LevelCheck method (Otake et al 2013b) and registration at the end of a case could provide more rigorous quality assurance of the surgical product in direct comparison to (registered) planning data.
Registration of a prior 3D volume using 3D–2D registration has been applied in mobile radiographs for intraoperative guidance, such as in hip implant surgery (Zheng et al 2009) and 3D reconstruction of the spine (Moura et al 2011, Zhang et al 2013) and hip (Schumann et al 2013). These studies employed either a one-time calibration (Zhang et al 2013), a geometry approximated from the knowledge of the source–detector distance (SDD) (also known as focal-film distance) recorded in the DICOM header (Zheng 2010), or a geometry measured by a built-in measuring device (e.g. laser rangefinder) (Moura et al 2010). Another approach to geometric calibration in an unconstrained geometry is to image the patient together with a calibration fiducial of known shape, such as a ‘calibration jacket’ (Moura et al 2011) or a custom-made phantom (Otake et al 2010, Schumann et al 2013). However, such approaches introduce additional complexity in workflow and require the fiducial/phantom to be present in both the 3D and 2D image. In addition to one-time calibration, (Otake et al 2010) used an alternating optimization between the geometry and the patient pose parameters to improve registration accuracy. The method used multiple pre-calibrated projection images acquired by a C-arm and demonstrated the challenge associated with local optima. An analogous method with a known fiducial marker was shown to provide automatic image-to-world registration in C-arm cone-beam CT for surgical navigation (Dang et al 2012).
This paper develops and evaluates a method to solve the geometric calibration and patient registration simultaneously in a single optimization using a single uncalibrated projection image of the patient. The approach is based on the notion common to many forms of 3D–2D registration in which the patient anatomy itself acts as the fiducial tying the preoperative 3D image to the intraoperative 2D image. The algorithm models the projection geometry according to a 9-DOF configuration of the 3-DOF source position (x, y, z)s and 6-DOF patient position (x, y, z, η, θ, ϕ)obj, both with respect to the detector coordinate system. The method is equivalent to an alternative 9-DOF representation of the source–detector geometry (x, y, z)s and (x, y, z, η, θ, ϕ)d. The algorithm simultaneously seeks all the model parameters that maximize similarity between the acquired projection and a digitally reconstructed radiograph (DRR) computed from a preoperative CT. Previous work has not addressed the joint optimization framework of the geometry and the patient pose parameters. The contributions of this paper include: (1) to extend previous work to a novel optimization framework well suited to the 9-DOF problem; (2) to experimentally validate performance of the method to perturbation in a certain degree of freedom; and (3) to demonstrate its application in the context of mobile intraoperative radiographs. Key to the method is a robust optimization facilitated by performing a large number of function evaluations in an efficiently parallelized GPU implementation. The focus of application in studies reported below is orthopaedic or neurosurgical spine intervention, where 3D–2D registration could provide decision support in target localization and postoperative assessment.
2. Method
2.1. Projection geometry
The projection geometry is illustrated in figure 1. The world coordinate frame is located at the center of the detector with the X and Y axes parallel to the detector edge and the Z axis formed by their cross product. The coordinate frame of the CT volume was defined at the center of the volume and its position and orientation with respect the world coordinate frame was represented as a 6-element vector of translations and rotations (x, y, z, η, θ, ϕ)obj using the ZYX Euler angle. The projection geometry was parameterized by the source position with respect to the world coordinate (x, y, z)s, where zs represents the length of the perpendicular line from the source to the detector (SDD). These nine parameters formed the following projection matrix relating a 3D point and its projection in the 2D detector plane:
| (1) |
where (x, y, z)T is the 3D point in the CT coordinate frame, (u,v)T is the projected location in the detector coordinate frame, R3 × 3 is the rotation matrix for the CT frame with respect to the detector frame parameterized by (η, θ, ϕ)obj, PM3 × 4 is the resulting projection matrix and the ~symbol denotes that the left and right sides are equal to within scalar multiplication—i.e. (a b)T ~ (A B C)T implying a = A/C and b= B/C.
Figure 1.
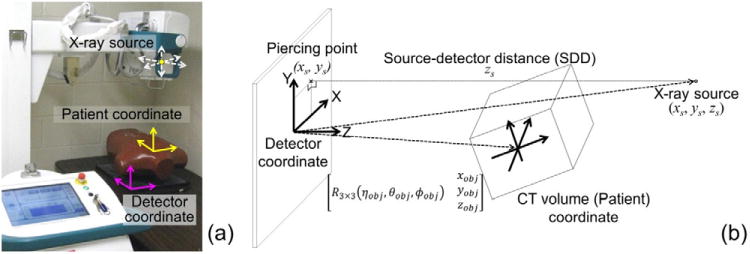
Projection geometry. (a) Setup of a mobile radiography system and chest phantom placed prone on the detector. (b) Parameters associated with the source, CT and detector coordinate frames.
2.2. 3D–2D registration with 9-DOF
The framework underlying the 3D–2D registration method follows that of Otake et al (2013b) in which an optimization algorithm seeks model parameters that maximize the similarity between the radiograph and DRR, extended in this work to a 9-DOF representation of the projection geometry that does not require geometric calibration of the imaging system. The optimization algorithm was implemented on a CPU for flexibility in parameter selection. DRRs and similarity metric were computed on a GPU as in previous publications (Otake et al 2012, Tornai et al 2012) to improve computational performance. Data transfer between the CPU and the GPU was minimized by transferring only nine model parameters and one similarity value back to the CPU in each function evaluation—i.e. copy of 9 × 4 = 36 N bytes from the CPU to the GPU and 4 N bytes from the GPU to the CPU for N function evaluations with single-precision floating point values. Prior to registration, the CT and radiograph were cropped to a consistent region of support and the collimated regions of the radiograph were cropped. The CT image was also thresholded to remove low-density structure, with voxels below a threshold (T) set to 0. A nominal value of T = 100 HU was used in all studies, selected between typical values of soft tissue (typically <80 HU) and bone (typically >150 HU). The results were verified to be insensitive to threshold selection across a fairly broad range of 0–200 HU.
2.2.1. Similarity metric
The best choice of similarity metric depends on the application, though comparative studies (Russakoff et al 2003, Birkfellner et al 2009) show that metrics based on local intensity correspondence tend to outperform those based on global intensity (e.g. mutual information, MI) in 3D–2D registration. A previous study (Otake et al 2013b) used the gradient information (GI) similarity metric, which compares the gradient magnitude at each pixel and ignores gradients appearing only in one of the images. Since GI relies on the absolute value of the gradient magnitude, registration of images with different dynamic ranges (e.g. mobile radiographs of fixed bit depth [0 4095] for 12 bit format) can be a challenge. We therefore employed the gradient correlation (GC) (Penney et al 1998) similarity metric, since it is independent of the image dynamic range. The GC averages the normalized cross correlation (NCC) between the X- and Y-gradients of the fixed (I0) and moving (I1) images as follows:
| (2) |
| (3) |
where Ω denotes the entire image domain. The GC was calculated on a GPU by treating one image as a column vector and using matrix multiplication in CUBLAS (nVidia, Santa Clara, CA) to simultaneously evaluate multiple moving images against a single fixed image. Therefore, m moving images were represented as an n × m matrix, M, where n is the number of pixels in an image and the fixed image was represented as an n × 1 vector, F. For example, the numerator in equation (3) (pixel-wise multiplication and summation) for all moving images was computed by MTF using the cublasSgbmv matrix-vector multiplication function.
2.2.2. Initialization
Initialization of the optimization used basic knowledge of the imaging protocol but did not rely on calibration of the imaging geometry. For example, in acquisition of a mobile radiograph, the operator places the source and detector manually in a desired orientation (e.g. view) posterior–anterior (PA) or lateral (LAT) with the source roughly centered on the detector (Varnavas et al 2013). A tape measure is sometimes used to estimate the SDD, which is governed largely by the physical constraints of bedside imaging (e.g. the bed, rails and film stand) and a desired level of geometric magnification. We assumed such basic, coarse knowledge in setting the initialization and allowed a broad capture range in the optimization. In each case, source position was initialized to (x, y, z)s = (0, 0, 1000) mm to emulate clinical practice (at our institution) in which the radiography technician typically sets the geometry such that the SDD is approximately 1000 mm and the approximate orientation of the patient with respect to the detector (PA or LAT, prone or supine) was derived from the acquisition protocol to initialize the volume data at (η, θ, ϕ)obj = (0, 0, 0) degrees. The distance from patient to detector assumed the detector to be placed as close to the patient as possible (to maximize radiographic field-of-view, FOV), giving initial translation along the Z axis, zobj, equal to half the size of the volume (sometimes termed ‘patient separation’). Initialization of the translation in X and Y directions, xobj, yobj, involved the selection of a landmark in the volume coordinate frame, p3D and a roughly corresponding point in the radiograph coordinate frame, p2D. The initial xobj and yobj were defined such that the projection of p3D yielded p2D using equation (1). Such manual initialization is currently being implemented in a simple graphical interface suitable for use by a radiographer to specify the approximate position of the radiograph in the superior–inferior direction. Robustness over a broad range of initialization error was evaluated in the simulation study described in the next section.
2.2.3. Optimization
The covariance matrix adaptation-evolutionary strategy (CMA-ES) (Hansen 2006) was used to solve the optimization problem:
| (4) |
where Φ = {xs, ys, zs, xobj, yobj, zobj, ηobj, _θobj, _ϕobj}, and S represents the solution space (i.e. search range). CMA-ES calculations were performed on a CPU in Matlab (The Mathworks, Natick, MA) with function calls to an externally compiled C++ library for computing DRRs and similarity metric on a GPU using CUDA (nVidia, Santa Clara, CA).
CMA-ES generates multiple sample solutions (population size λ) in each generation to be independently evaluated, allowing parallelization of λ function evaluations. A multi-start optimization strategy (Otake et al 2013b) was employed to divide the search space into N smaller subspaces by the kD-tree partitioning algorithm (Bentley 1975), perform local optimization in each partition, and select the best of the resulting converged solutions (i.e. local optima). The number of multi-starts was 100 in this study, improving global search performance and parallelization by allowing λ × N concurrent function evaluations. In each generation, λ × N projection matrices were computed based on the nine parameters at the sample solutions in the current generation using equation (1), with DRRs and similarity metric for λ × N samples simultaneously computed on the GPU. A two-level multi-resolution pyramid (Munbodh et al 2009) with 1252 and 5002 pixels was used to improve robustness against local optima and improve the convergence rate.
2.3. Experiments
2.3.1. Simulation study
Simulation studies were conducted to evaluate the accuracy of the registration and robustness against initialization error by using a CT scan of an anthropomorphic torso phantom containing a natural human skeleton in soft-tissue-equivalent plastic (Rando™, The Phantom Laboratory, Greenwich, NY). One thousand random geometries were generated by perturbing the default geometry parameters ((x, y, z)s = (0, 0, 1000) mm, (x, y, z)obj = (0, 0, 300) mm and (η, θ, ϕ)obj = (0, 0, 0) degrees) according to three standard deviations in the normal distributions about each parameter as detailed in table 1. Simulated PA and LAT radiographs with each random geometry were generated using Siddon’s ray-tracing algorithm (Siddon 1985). The perturbation thus represents the initial misalignment (i.e. the error in mobile x-ray system setup compared to the first view with the default geometry in the optimization) and is illustrated graphically in figure 2.
Table 1.
Summary of experimental and algorithmic parameters.
| Simulation study | ||
|---|---|---|
| CT | Dimension | 512 × 512 × 894 voxels |
| Voxel size | 0.73 × 0.73 × 0.50 mm3 | |
| Perturbation range (3σ) | (x, y, z)s | (±100, ±100, ±200 mm) |
| (x, y, z)obj | (±100, ±100, ±200 mm) | |
| (η, θ, ϕ)obj | (±10°, ±10°, ±10°) | |
| Simulated radiograph | Dimension | 2560 × 3072 pixels |
| Pixel size | 0.139 × 0.139 mm2 | |
|
| ||
| Cadaver study | ||
|
| ||
| CT | Dimension | 512 × 512 × 1427 voxels |
| Voxel size | 0.67 × 0.67 × 0.60 mm3 | |
| Mobile radiograph | Dimension | 2560 × 3072 pixels |
| Pixel size | 0.139 × 0.139 mm2 | |
| Regions | thoracic, abdominal, pelvic | |
| SDD | ~800, ~1000, ~1200 mm | |
|
| ||
| Optimization parameters | ||
|
| ||
| Population size | λ = 50 | |
| Number of multi-starts | N = 100 | |
| Image dimensions in | Level1 | 1252 pixels |
| multi-resolution pyramid | Level2 | 5002 pixels |
| Upper/lower bound of the | (x,y,z)s | (±100, ±100, ±200 mm) |
| search space | (x,y,z)obj | (±100, ±100, ±200 mm) |
| (η, θ, ϕ)obj | (±10°, ±10°, ±10°) | |
Figure 2.
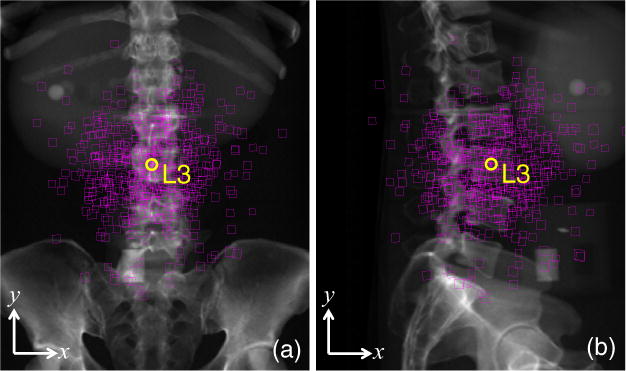
Illustration of the distribution in initialization errors in the simulation study superimposed on (a) PA and (b) LAT radiographs. Each square indicates one initial pose estimate of the L3 vertebra (with the true position shown as a yellow circle). Close inspection of the corners of each square shows not only the error in (x, y) placement but also a skew imparted by rotational errors in the initialization.
Registration accuracy was evaluated in terms of projection distance error (PDE) (van de Kraats et al 2005) defined as:
| (5) |
where is the projection of the ith target point computed by a projection matrix (equation (1)) estimated by the registration and is the projection computed by the true projection matrix. Target points were manually defined in the CT volume at the approximate centroid of each vertebra. The 9-DOF registration was compared against a conventional 6-DOF registration, the latter assuming a fixed source position (x, y, z)s = (0, 0, 1000) mm. All calculations were performed on a desktop Windows 7 64 bit workstation with an Intel Xeon 2 processor (2.4 GHz) and GeForce TITAN GPU (nVidia, Santa Clara, CA).
2.3.2. Cadaver study
A fresh (unfrozen, unfixed) cadaver torso from neck to mid-femur without arms was prepared and immobilized on a carbon fiber fluoroscopy tabletop and ten BB markers were placed on its surface. The specimen was imaged in CT (SOMATOM Definition Flash, Siemens Healthcare) (120 kVp, 100 mAs, CARE Dose B20 s kernel) and carefully transported on the carbon fiber tabletop to a mobile radiography system (Sedecal SM-40, Madrid, Spain) equipped with a 35 × 43 cm2 wireless flat-panel detector (DRX-1, Carestream Health, Rochester, NY). Deformation of the specimen between CT and radiography is believed to be minimal. Nine mobile radiographs were acquired (100 kVp, 5 mAs) across three ROIs (thoracic, abdominal and pelvic) and three SDDs (~800, ~1000, ~1200 mm) as illustrated in figure 3. One hundred registration trials initialized at the ‘default geometry’ explained above ((x, y, z)s = (0, 0, 1000) mm, (x, y, z)obj = (0, 0, 300) mm and (η, θ, ϕ)obj = (0, 0, 0) degrees) were performed with the 6- and 9-DOF algorithms. For the 6-DOF algorithm, SDD = 800 and 1200 mm were also tested to explore dependency on the SDD (which is fixed in 6-DOF). For each radiograph, a geometric calibration phantom (Cho et al 2005) was placed above the cadaver to define the ground truth of the system geometry (figure 3(a)). The phantom was then removed for acquisition of a radiograph to be used in 3D–2D registration. Each radiograph contained 3–7 BBs depending on the ROI. Each BB was manually segmented in both CT and mobile radiographs and the center of each BB was quantitatively defined by the Hough transform (Hough 1962) as the target point and registration accuracy was evaluated in terms of the PDE as described above.
Figure 3.
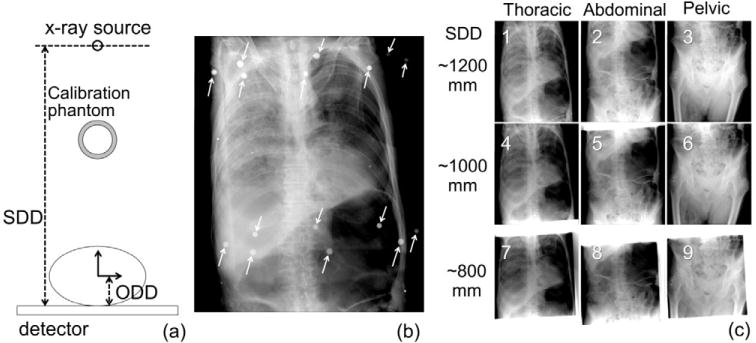
Experimental setup for the cadaver study. (a) Illustration of projection geometry showing SDD, ODD (object-to-detector distance) and placement of the calibration phantom for truth definition. (b) Example radiograph with arrows marking the location of fiducials in the calibration phantom). The small target BBs placed on the cadaver are visible upon close inspection. (c) Radiographs acquired in three anatomical regions at three values of SDD.
In addition, to evaluate robustness of the proposed method against the initialization error in the real image, an experiment with random initializations similar to the simulation study was performed. The nine parameters were randomly perturbed from the ground truth registration by (±50, ±50, ±100) mm in patient translation, (±5, ±5, ±5) degrees in patient rotation and (±50, ±50, ±100) mm in source position, which produced the maximum PDE of 168.5 mm (mean: 36.2 mm, standard deviation: 19.4 mm). One thousand random trials were performed on each image (i.e. 9000 trials in total).
2.3.3. Patient study
An IRB-approved retrospective study was performed using preoperative CT and intraoperative mobile radiographs acquired for two patients undergoing spinal intervention (one image per patient) at our institution to further test and validate the robustness of 3D–2D registration under conditions of realistic imaging protocols, anatomical deformation and placement of interventional devices. The inferior edge of the spinous process on each vertebra served as anatomical landmarks manually localized in both the CT and mobile radiograph by a fellowship-trained radiologist for quantitative evaluation of accuracy. As in the other two experiments, the registration was initialized with the ‘default geometry’ ((x, y, z)s = (0, 0, 1000) mm, (x, y, z)obj = (0, 0, 300) mm and (η, θ, ϕ)obj = (0, 0, 0) degrees).
3. Results
3.1. Simulation study
Figure 4 summarizes the results of the simulation study, demonstrating an improvement in the registration accuracy achieved by the 9-DOF optimization in comparison to 6-DOF. For each case (i.e. LAT or PA views registered via 9-DOF or 6-DOF), performance was assessed in terms of the error in each of nine geometric parameters (xs, ys, zs, xobj, yobj, zobj, ηobj, _θobj, _ϕobj) as well as PDE. The median PDE at initialization over all cases was ~120 mm, corresponding to a broad range of initialization error equivalent to ~3 vertebral levels (and therefore raising the distinct possibility of vertebra mis-localization). Such coarse initialization is believed to be achieved with relative ease by a capable radiographer using basic setup tools (e.g. measuring tape) as mentioned in section 2.2.2. The 9-DOF registration resulted in a median PDE of 0.007 mm (0.006 mm for LAT and 0.009 mm for PA) whereas the 6-DOF registration was 0.767 mm (0.566 mm for LAT and 1.044 mm for PA). The larger error in 6-DOF registration was due to the mismatch of the source position between the real and assumed geometries. The median PDE is therefore within a clinically acceptable range (<5 mm) for vertebral level location using either registration scheme, but the 9-DOF method also demonstrated reduced variability in the registration result, with one case exhibiting a PDE of 1.105 mm and all other cases giving PDE < 1 mm, compared to 725/2000 cases giving a PDE > 1 mm (and one outlier with PDE > 10 mm) for the 6-DOF method. Average computation time was 48.5 s (687, 701 function evaluations) for 9-DOF registration and 18.2 s (233, 851 function evaluations) for 6-DOF registration, each potentially within the workflow requirements of safety checks and QA in a mobile radiograph acquired at the beginning and/or end of a case.
Figure 4.
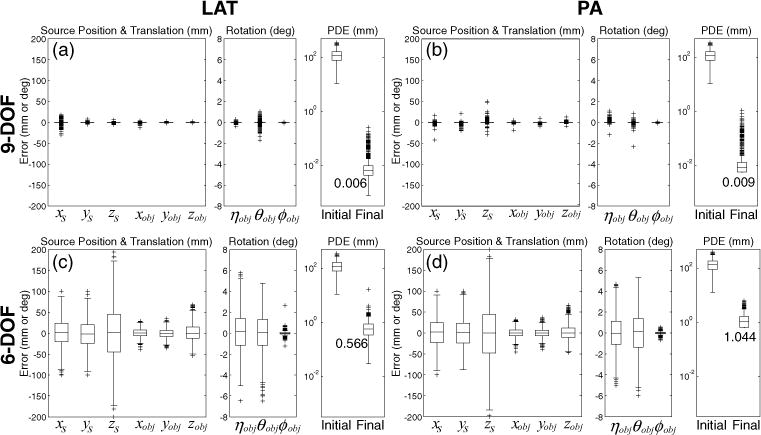
Registration accuracy for 9- and 6-DOF registration of LAT and PA views of the body phantom over 1000 simulation trials with randomly perturbed initialization. Details of the steps to generate the random initialization and its range were explained in section 2.3.1. In each case (a)–(d), the error in each of nine system parameters is shown along with the resulting PDE before and after the registration. Box and whisker plots denote the first/third quartiles and min/max values, respectively, with the median marked by the horizontal line and outliers by crosses. For 6-DOF registration, the error in (x, y, z)s is the same as the initialization error since these parameters were not solved.
The plots in figures 4(c) and (d) illustrate that the 6-DOF registration attempted to partially compensate for the error in source position by translating and rotating the CT volume to generate a similar view as the radiograph. For example, the error in zs (SDD) was partially compensated by adjusting zobj (out-of-plane translation of the volume) and the error in xs (horizontal translation of the piercing point) was partially compensated by adjusting xobj and θobj (horizontal translation and rotation about the vertical axis) and so on. Thus, the ratio between the absolute errors in these coupled parameters (i.e. xs and xobj, ys and yobj, zs and zobj) was approximately equal to the ratio between the SDD and object-to-detector distance (ODD) (i.e. 1000:300 in this study). On the other hand, the 9-DOF registration correctly estimated the source position and yielded greater accuracy in the translation and rotation parameters.
Interestingly, PA projections resulted in a slightly elevated PDE and a greater number of outliers than LAT projections. This finding is attributed to the ambiguity between the SDD and ODD for planar objects, i.e. a reduced magnification effect in the shorter PA extent of the pelvis (cf its lateral extent). Conversely, the larger depth of the pelvis in the LAT view yielded a more distinct global optimum in the objective function and improving robustness of the optimization.
3.2. Cadaver study
The cadaver study also demonstrated the advantage of 9-DOF registration over the 6-DOF. Figure 5(a) shows the BB target positions projected by the true and estimated projection matrix with the zoomed-in views of figure 5(b) illustrating the increased error associated with 6-DOF registration although both methods demonstrated a PDE < 5 mm, which may be suitable for various applications. A quantitative comparison of the nine images illustrated in figure 3(c) (thorax, abdomen and pelvis at three values of SDD) is shown in figure 5(c). The actual SDD of images #1–#3, #4–#6 and #7–#9 was approximately 1200, 1000, and 800 mm respectively. Whereas the 9-DOF registration was able to achieve sub-mm PDE across all nine scenarios irrespective of initialization across the range examined, the performance of the 6-DOF registration was susceptible to error if poorly initialized. Specifically, although each 6-DOF case performed reasonably well (PDE < 2 mm) if initialized at an SDD matching the (approximate) true SDD, each was subject to errors of ~4–10 mm if the SDD initialization was poor.
Figure 5.
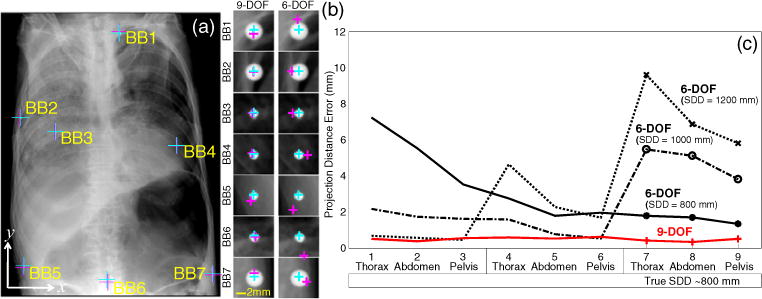
(a) Example registration for the thoracic radiograph acquired with an SDD of ~1200 mm with the true and estimated position of seven target BBs overlaid. (b) Zoomed-in views of the each target BB, showing the true (cyan) and estimated (magenta) locations for the 9- and 6-DOF registration methods. (c) Median PDE (over 100 trials) for each image in the nine cases in the cadaver study (three anatomical regions and three values of SDD).
Over all cadaver studies, the average PDE of the 9-DOF registration was 0.49 mm with a maximum of 0.62 mm whereas the best case 6-DOF registration (source position of (0, 0, 1000) mm with correct initialization of the SDD) achieved a mean PDE of 2.53 mm (and range up to 5.50 mm).
The evaluation of robustness with 9000 random trials (1000 for each image) demonstrated a PDE of 1.29 ± 0.54 mm (mean ± std) after registration (figure 6) with one failure case (33.3 mm final PDE). Considering the large initial perturbation (and the large initial PDE), this result suggests a fairly high degree of robustness in real data.
Figure 6.
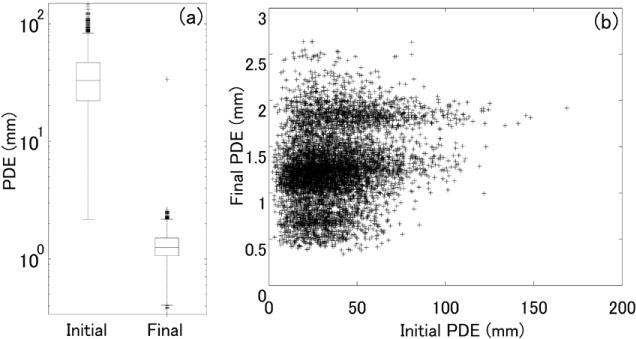
Robustness evaluation in 9000 random trials with real images from the cadaver study. (a) Initial and final PDE. Box and whisker plots denote the first/third quartiles and min/max values, respectively, with the median marked by the horizontal line and outliers by crosses. (b) Scatter plot of the final PDE as a function of the initial PDE.
3.3. Patient study
Figure 7 illustrates 3D–2D registration of anatomical landmarks (inferior aspect of the spinous process) in patient images analyzed retrospectively from real preoperative CT and intraoperative mobile radiographs. Using 9-DOF 3D–2D registration, the average PDE at the spinous processes was 1.13 mm for both patients whereas, using 6-DOF registration, it was 1.41 mm for patient #1 and 1.22 mm for patient #2. Due to a lack of highly accurate landmarks (e.g. radioopaque fiducial BBs), the manual truth definition involved a degree of uncertainty upwards of ~1–5 pixels or ~0.14–0.70 mm. Thus, despite the slightly larger error in 6-DOF than 9-DOF, further investigation with a larger cohort is needed to reveal statistically significant differences in accuracy. Since the ground-truth registration (including the source position) is not available, and the anatomical landmarks for target definition also involved a degree of uncertainty in the patient study, it is not straightforward to draw a definitive conclusion from those two cases. However, one possible reason why the 6-DOF algorithm gave a comparatively good result was that the actual SDD happened to be closer to the assumed value (1000 mm) in those two cases. In patient #2, two of the lumbar landmarks (marked by arrows in figure 7(d)) exhibited the largest error due to deformation around the sacrum and L5 vertebra as discussed below. The GC images (figures 7(c) and (f)) show the contributions of each pixel to the GC metric (equation (2)). Note that the GC was computed such that the summation occurs at the end of the process to improve parallelization; the images in figures 7(c) and (f) show the GC at each pixel before summation. The GC image therefore illustrates edges that were well matched between the DRR and radiograph with regions of higher intensity indicating structures that were consistent with the preoperative CT.
Figure 7.
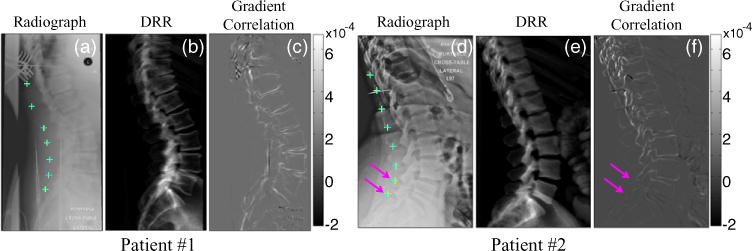
9-DOF 3D–2D registration of anatomical landmarks (spinous processes) in patients undergoing spinal intervention. (a,d) Intraoperative radiographs superimposed by true (defined by a radiologist, cyan) and estimated (via 3D–2D registration, yellow) landmark locations. (b,e) DRRs computed at the registration result, shown for side-by-side comparison to the true radiograph. (c,f) GC similarity metric image at the registration solution. Overall, the registration result agreed with the true locations, with slight error (<2 mm) noted in the lumbar spine of patient #2 due to an anatomical deformation marked by pink arrows. The color-bars indicate the grayscale window of the GC image (c,f). The windows of a, b, d, e were adjusted manually.
The various annotations burned into the radiograph are evident in figures 7(a) and (d) and could not be removed without explicit post-processing. The gradients associated with annotation were fairly minor and did not challenge the registration process (in part due to the intrinsic robustness of the GC in ignoring inconsistent gradients and the robust optimization in avoiding converging to the false local optima), so no post-processing was applied. (One could alternatively apply a simple mask function to the annotation as in Otake et al (2013b)). With respect to interventional tools, patient #1 (figure 7(a)) included retractors, an inserted K-wire and structure associated with OR table and patient #2 (figure 7(d)) included a K-wire, wires associated with monitoring devices and intubation. However, the presence of such strong gradients did not appear to degrade the registration results again attributable, in part, to the intrinsic robustness of the GC against mismatched gradients and the robust optimization. A strong degree of anatomical deformation, however, was seen to cause potential errors in the registration. For example, patient #2 (figures 7(d)–(f)) exhibited fairly strong deformation in the lumbar spine and pelvis relative to the preoperative CT. The reduced GC in that region of the image is associated with a noticeable discrepancy in the registration of target points. One method to mitigate such mismatches from contributing to the similarity metric is to apply a weighting mask to down-weight regions suspected to exhibit deformation (or instrumentation) as proposed in Otake et al (2013b). Such masks could potentially be created manually or automatically by detecting objects that create artificially strong gradients.
4. Discussion
A 3D–2D registration method was presented that specifically addresses the challenge of 2D projections acquired in an uncalibrated geometry as common in mobile radiography systems. The algorithm models the complete projection geometry using 9-DOF and estimates each geometric parameter based on fast DRR calculations, GC similarity and CMA-ES optimization. The primary contribution of the current work is the extension of 3D–2D registration to 9-DOF compared to previous work that assumed a rigid relationship (6-DOF) of the source and detector as common to a C-arm. Experiments in phantoms, cadavers and patients demonstrated a robust and accurate estimation of the nine parameters (PDE <5 mm in all cases and typically <1 mm) in a reasonable computation time (<60 s) using a parallelized GPU implementation. The 9-DOF method demonstrated a PDE of 0.007 mm in the phantom study (compared to 0.767 mm for 6-DOF method) and 0.49 mm in the cadaver study (compared to 2.53 mm for the 6-DOF method). Similarly, the 9-DOF method demonstrated a PDE of ~1.1 mm in patient images (compared to 1.2–1.4 mm for the 6-DOF method).
A clinically relevant performance requirement varies depending on the application. Previous work defined criteria to determine possible registration failure in application to spine level localization in terms of PDE within the approximate spatial extent of a single vertebra (e.g. a conservative range of ~5–10 mm). The current study aims to achieve accuracy as high as possible for purposes of quality assurance beyond level localization. For example, application to surgical navigation requires a much higher accuracy (e.g. <2 mm) for purposes of registering the image with respect to an interventional tool.
In the clinical study, there was no attempt to control or limit the quality of the images or patient setup. Therefore, the images are believed to exhibit real, presumably typical, challenges presented by (in possibly increasing order of importance) image quality, annotations burned into the DICOM images, the presence of surgical tools and anatomical deformation. With respect to image quality, the images in this study were acquired using standard clinical protocols and other work has examined the possible effects associated with coarser voxel and pixel size (Uneri et al 2013) and reduced radiation dose (Uneri et al 2014).
Two potential applications of the method are: (1) an assistant to decision support in localization of vertebrae in spine surgery (cf conventional level counting), especially in the mid-thoracic area where the lack of clear anatomical landmarks can challenge confident localization even by an expert surgeon or radiologist and presents a known source of wrong-site error (Palumbo et al 2013); and (2) verification, QA and documentation of the surgical product whereby planning data can be accurately registered to the postoperative radiograph. Such registration could provide a more quantitative assessment of the quality of surgical products, conformity to intended device locations and trajectories and a check against instrumentation of the wrong (or additional) levels. In addition, Otake et al posited a method by which the registration could be used to increase the conspicuity of retained foreign bodies through subtraction (or other comparative analysis) of the registered DRR and true radiograph (Otake et al 2013a).
It is worth noting, however, that the 3D–2D registration is subject to possible local optima in the objective functions associated with the somewhat periodic nature of the spinal column. For example, one of the failure modes includes a vertical shift by exactly one level of vertebra due to the similarities between the neighboring vertebrae. However, even though the vertebrae are almost periodic in the 2D projection, surrounding structures (e.g. rib cage, abdominal organs) exhibit non-periodic appearances, which discourage the false local optima and help the optimization converge at the true optimum. Extensive validations of robustness against local optima in the 6-DOF 3D–2D registration were reported in Otake et al (2013b), suggesting more than 99.99% success (<5 mm PDE) in various scenarios with local optima were caused by the periodicity and deformation. It is also worth noting, of course, that the process is not robust against human error in labeling structures of interest—e.g. human errors in vertebral labels in preoperative CT would be faithfully reproduced in the registered radiograph.
Since the method involves a rigid 9-DOF (or 6-DOF) transform, large anatomical deformations can challenge the registration process. The GC similarity metric carries a degree of robustness to such gradient mismatch and previous work (Otake et al 2013b) specifically investigated the effect of deformation, the potential benefit of a weighting mask applied to strongly deforming regions (e.g. the diaphragm or skinline) and the ability to accurately register the spine despite strong deformations. The patient study reported above suggests the ability to accommodate realistic deformation, though in a very small cohort (N = 2), and future studies are required to more fully understand the overall reliability and potential failure modes as well as methods to mitigate the effects of deformation (e.g. a mask function applied to the skinline). Another possible solution is to estimate the deformation simultaneously in the optimization by parameterizing potential modes of deformation by a small number of parameters. For example, deformation of the spine could be modeled as articulated rigid vertebrae whose deformation can be constrained within statistical variations found in patient population studies (Boisvert et al 2008).
The accuracy of the DRR calculation can be further improved by introducing more realistic forward projection models such as inclusion of a polyenergetic x-ray spectrum, x-ray scatter and a finite focal spot size, which may improve the similarity with the real radiograph and thus improve the registration accuracy. Robustness of the registration can be further improved by increasing the number of multi-starts at the expense of computation time as shown in previous work (Otake et al 2013b). Assuming an ongoing increase in the number of GPU processor cores, the parallelization efficiency is a key factor in improving robustness by methods that increase computation time (e.g. number of multi-starts and population size). The stochastic derivative-free approach is especially beneficial in this regard compared to inherently sequential algorithms such as the Newton-type gradient-based algorithms or the classic derivative-free approach such as Powell’s method (Powell 1964), downhill simplex (Nelder and Mead 1965) and simulated annealing (Kirkpatrick et al 1983) where the next sampled solution is dependent on the completion of all previous function evaluations.
Acknowledgments
This research was supported by academic-industry partnership with Siemens Healthcare (XP Division, Erlangen Germany). The authors extend their thanks to Ronn Wade (University of Maryland Anatomy Board) for assistance with cadaver specimens. The authors gratefully acknowledge the contributions of Dr A J Khanna (Johns Hopkins University) in development and evaluation of the 6-DOF registration method in previous work. The mobile radiography system used in the phantom and cadaver studies was provided by Carestream Health (Rochester NY) with thanks to Dr John Yorkston and Dr David Foos.
References
- Bentley JL. Multidimensional binary search trees used for associative searching. Commun ACM. 1975;18:509–17. [Google Scholar]
- Birkfellner W, Stock M, Figl M, Gendrin C, Hummel J, Dong S, Bergmann H. Stochastic rank correlation: a robust merit function for 2D/3D registration of image data obtained at different energies. Med Phys. 2009;36:3420–8. doi: 10.1118/1.3157111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boisvert J, Cheriet F, Pennec X, Labelle H, Ayache N. Geometric variability of the scoliotic spine using statistics on articulated shape models. IEEE Trans Med Imaging. 2008;27:557–68. doi: 10.1109/TMI.2007.911474. [DOI] [PubMed] [Google Scholar]
- Cho Y, Moseley DJ, Siewerdsen JH, Jaffray DA. Accurate technique for complete geometric calibration of cone-beam computed tomography systems. Med Phys. 2005;32:968–83. doi: 10.1118/1.1869652. [DOI] [PubMed] [Google Scholar]
- Dang H, Otake Y, Schafer S, Stayman JW, Kleinszig G, Siewerdsen JH. Robust methods for automatic image-to-world registration in cone-beam CT interventional guidance. Med Phys. 2012;39:6484–98. doi: 10.1118/1.4754589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen N. The CMA evolution strategy: a comparing review. In: Lozano J, et al., editors. Towards a New Evolutionary Computation. Vol. 192. Berlin: Springer; 2006. pp. 75–102. [Google Scholar]
- Hough P. Method and means for recognizing complex patterns. 3069654 US Patent. 1962
- Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–80. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Moura DC, Barbosa JG, Reis AM, Tavares JMR. A flexible approach for the calibration of biplanar radiography of the spine on conventional radiological systems. Comput Model Eng Sci. 2010;60:115–38. [Google Scholar]
- Moura DC, Boisvert J, Barbosa JG, Labelle H, Tavares JM. Fast 3D reconstruction of the spine from biplanar radiographs using a deformable articulated model. Med Eng Phys. 2011;33:924–33. doi: 10.1016/j.medengphy.2011.03.007. [DOI] [PubMed] [Google Scholar]
- Munbodh R, Tagare HD, Chen Z, Jaffray DA, Moseley DJ, Knisely JP, Duncan JS. 2D–3D registration for prostate radiation therapy based on a statistical model of transmission images. Med Phys. 2009;36:4555–68. doi: 10.1118/1.3213531. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–13. [Google Scholar]
- Otake Y, Armand M, Armiger RS, Kutzer MD, Basafa E, Kazanzides P, Taylor RH. Intraoperative image-based multiview 2D/3D registration for image-guided orthopaedic surgery: incorporation of fiducial-based C-arm tracking and GPU-acceleration. IEEE Trans Med Imaging. 2012;31:948–62. doi: 10.1109/TMI.2011.2176555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otake Y, Armand M, Sadowsky O, Armiger R, Kazanzides P, Taylor R. An iterative framework for improving the accuracy of intraoperative intensity-based 2D/3D registration for image-guided orthopedic surgery. In: Navab N, Jannin P, editors. Information Processing in Computer-Assisted Interventions. Vol. 6135. Berlin: Springer; 2010. pp. 23–33. [Google Scholar]
- Otake Y, Wang AS, Stayman JW, Kleinszig G, Vogt S, Khanna AJ, Siewerdsen JH. Verification of surgical product and detection of retained foreign bodies using 3D–2D registration in intraoperative mobile radiographs. Proc Computer Assisted Radiology Surgery (26–29 June 2013, Heidelberg, Germany) 2013a:185–6. paper presented at the. [Google Scholar]
- Otake Y, Wang AS, Webster Stayman J, Uneri A, Kleinszig G, Vogt S, Siewerdsen JH. Robust 3D–2D image registration: application to spine interventions and vertebral labeling in the presence of anatomical deformation. Phys Med Biol. 2013b;58:8535–53. doi: 10.1088/0031-9155/58/23/8535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palumbo MA, Bianco AJ, Esmende S, Daniels AH. Wrong-site spine surgery. J Am Acad Orthop Surg. 2013;21:312–20. doi: 10.5435/JAAOS-21-05-312. [DOI] [PubMed] [Google Scholar]
- Penney GP, Weese J, Little JA, Desmedt P, Hill DL, Hawkes DJ. A comparison of similarity measures for use in 2D–3D medical image registration. IEEE Trans Med Imaging. 1998;17:586–95. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
- Powell MJD. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput J. 1964;7:155–62. [Google Scholar]
- Russakoff D, Rohlfing T, Ho A, Kim D, Shahidi R, Adler J, Jr, Maurer C., Jr . Evaluation of intensity-based 2D–3D spine image registration using clinical gold-standard data. In: Gee J, et al., editors. Biomedical Image Registration. Vol. 2717. Berlin: Springer; 2003. pp. 151–60. [Google Scholar]
- Schumann S, Liu L, Tannast M, Bergmann M, Nolte L-P, Zheng G. An integrated system for 3D hip joint reconstruction from 2D x-rays: a preliminary validation study. Ann Biomed Eng. 2013;41:2077–87. doi: 10.1007/s10439-013-0822-6. [DOI] [PubMed] [Google Scholar]
- Siddon RL. Fast calculation of the exact radiological path for a 3D CT array. Med Phys. 1985;12:252–5. doi: 10.1118/1.595715. [DOI] [PubMed] [Google Scholar]
- Tornai GJ, Cserey G, Pappas I. Fast DRR generation for 2D to 3D registration on GPUs. Med Phys. 2012;39:4795–9. doi: 10.1118/1.4736827. [DOI] [PubMed] [Google Scholar]
- Uneri A, Otake Y, Wang AS, Kleinszig G, Vogt S, Khanna AJ, Siewerdsen JH. 3D–2D registration for surgical guidance: effect of projection view angles on registration accuracy. Phys Med Biol. 2013;59:271–87. doi: 10.1088/0031-9155/59/2/271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A, Wang S, Otake Y, Kleinszig G, Vogt S, Khanna A, Siewerdsen J. Evaluation of low-dose limits in 3D–2D registration for surgical guidance. Phys Med Biol. 2014;59:5329–45. doi: 10.1088/0031-9155/59/18/5329. [DOI] [PubMed] [Google Scholar]
- van de Kraats EB, Penney GP, Tomazevic D, van Walsum T, Niessen WJ. Standardized evaluation methodology for 2D–3D registration. IEEE Trans Med Imaging. 2005;24:1177–89. doi: 10.1109/TMI.2005.853240. [DOI] [PubMed] [Google Scholar]
- Varnavas A, Carrell T, Penney G. Increasing the automation of a 2D–3D registration system. IEEE Trans Med Imaging. 2013;32:387–99. doi: 10.1109/TMI.2012.2227337. [DOI] [PubMed] [Google Scholar]
- Zhang J, Lv L, Shi X, Wang Y, Guo F, Zhang Y, Li H. 3D reconstruction of the spine from biplanar radiographs based on contour matching using the Hough transform. IEEE Trans Biomed Eng. 2013;60:1954–64. doi: 10.1109/TBME.2013.2246788. [DOI] [PubMed] [Google Scholar]
- Zheng G. Statistical shape model-based reconstruction of a scaled, patient-specific surface model of the pelvis from a single standard AP x-ray radiograph. Med Phys. 2010;37:1424–39. doi: 10.1118/1.3327453. [DOI] [PubMed] [Google Scholar]
- Zheng G, Zhang X, Steppacher SD, Murphy SB, Siebenrock KA, Tannast M. HipMatch: an object-oriented cross-platform program for accurate determination of cup orientation using 2D–3D registration of single standard x-ray radiograph and a CT volume. Comput Methods Programs Biomed. 2009;95:236–48. doi: 10.1016/j.cmpb.2009.02.009. [DOI] [PubMed] [Google Scholar]


