Implicit treatment of solvent dispersion forces in protein simulations

Abstract

A model is proposed for the evaluation of dispersive forces in a continuum solvent representation for use in large-scale computer simulations. It captures the short and long-range effects of water-exclusion in conditions of partial and anisotropic hydration. The model introduces three parameters, one of which represents the degree of hydration (water occupancy) at any point in the system, which depends on the solute conformation, and two that represent the strength of water-water and water-solute dispersive interactions. It is optimized for proteins, using hydration data of a sub-optimally hydrated binding site and results from dynamics simulations in explicit water. The model is applied to a series of aliphatic-alcohol/protein complexes and a set of binary and ternary complexes of various sizes. Implications for weak and ultra-weak protein-protein association and for simulation in crowded media are discussed.

I. Introduction

When a solute approaches another solute in an aqueous solution the water displaced is reorganized structurally and dynamically. The overall effect of water removal and reorganization can be divided into electrostatic and non-electrostatic forces. A continuum solvent representation for use in large-scale (i.e., long-time, big-size) simulations requires both effects to be properly incorporated into the force field, and to be computationally efficient as well. To this end, effective potentials have been developed that represent the solvent effects implicitly,^1–5 but these have focused mainly on the treatment of electrostatics. Non-electrostatic effects include solvent-induced forces (SIF) and dispersion forces (DF), both essential components of the hydration process. SIF are short-ranged, non-pairwise forces that originate in the rearrangements of the solute-water and water-water hydrogen-bond network in the solute hydration shells,^6–9 and thus modulate molecular interactions at close proximity. In purely nonpolar solutes, SIF are hydrophobic forces, for which several continuum theories have been proposed.^10–13 For polar/charged solutes the treatment of SIF is more complicated, especially if the surfaces are topographically irregular, as most proteins are.^14,15 SIF make important contributions to the intermolecular potentials of mean force,¹⁶ and partially determine the height of the desolvation barriers and the strength of hydrogen bonds (HB) between hydrated groups.⁵ A model has been proposed to account for HB modulation by SIF in protein simulations,^5,17 and an algorithm developed to incorporate the non-pairwise nature of SIF in Langevin dynamics.¹⁸

The focus here is on the implicit treatment of DF. These forces are weak but pervasive,¹⁹ and their importance in implicit solvation has long been recognized.^20–23 The fundamental role of DF in protein hydration energies,^21,24 protein-ligand interactions,^21,25–28 thermal stability of proteins,^29,30 and preferential hydration/binding underlying protein denaturation by cosolutes³¹ have been probed experimentally and computationally. Increasing awareness of the importance of water-mediated DF has led to a number of extensions of implicit solvent models (ISMs) to incorporated DF in protein simulations.^32,33

Because DF are attractive at all distances, failure to account for solvent DF may lead to overly compact structures of peptides and proteins, over-stabilization of non-native conformers, unphysical orientations and reduced fluctuations of side chains at protein surfaces, and stronger protein/ligand binding. In the latter case the problem is typically circumvented by neglecting the direct protein-protein dispersive energy altogether. This ad hoc solution is based on the notion that proteins and the water they displace upon association make equal contributions to the dispersive energy, and thus cancel out. This assumption is not always justified because the density of interfacial water varies substantially throughout the protein surface, and range from mild over-hydration,³⁴ to partial dewetting,³⁵ to significant dehydration in crevices and narrow pockets.²⁶ Indeed, it has been shown that dispersive interactions are the main contributions to the binding energy in sub-optimally hydrated binding sites as a result of uncompensated dispersive attraction upon binding.^26,27 In addition, DF between large solutes have a long-range, shape-dependent component³⁶ (e.g., ~1/L for spheres, and ~1/L² for planes, where L is the separation between the surfaces), which may result in an effective attraction or repulsion between the solutes in an aqueous solution,^28,37 depending on their densities and materials, as determined by the relative values of the Hamaker constants.³⁸ The strength of protein-water dispersion interactions has been estimated by computer simulations,²¹ and it was shown that a significant contribution is made by atoms in the interior of the protein (for ubiquitin, a rather small protein, the protein-water van der Waals energy was estimated at ~45 kcal/mol²¹). Other simulation studies have shown similar results.²⁴ Although water and proteins are arguably similar organic substances, small differences in dispersive energies could rapidly add up as the system size increases, and could conceivably make a measurable contribution in multimeric complexes and assemblies. Such effective attraction may even exist between proteins and small molecules, as shown in μs-length simulations of urea binding to hen lysozyme.³¹ The implications for the behavior of crowded, anisotropic media, such as those in the interior of a living cell could be far reaching, possibly affecting subcellular organization and molecular translocation.

The model introduced here corrects the aforementioned limitations of current ISMs, and is designed for large-scale simulations. Parameterization is based on results from dynamic simulations of barnase/barstar and cytochrome C peroxidase/cytochrome C complexes in explicit water, and on calorimetric data of a sub-optimally hydrated protein binding site. Results are presented for a set of binary and ternary complexes of different sizes, and for a series of aliphatic alcohol/MUP-I complexes.

II. Model

The simplest treatment of electrostatic and non-electrostatic forces in a continuum solvent representation is through a local, position-dependent permittivity ε and density ρ.^18,39 The dependence of these functions at the solute/liquid interface is complicated, but suitable approximations based on classical theories of dielectrics⁴⁰ and liquid structure⁴¹ can provide practical expressions for both.^3,18,39 In this case each element of liquid exerts a force on the solute, and the total force is obtained by integration over the space occupied by the liquid.¹⁸ Improvements can be introduced empirically by incorporating non-local and other non-linear effects in ε and ρ.^39,42,43 Most ISMs used in macromolecular simulations assume ρ = 0, so the solute-solute DF tend to be stronger, especially for atoms close to the interface, where uncompensated forces are more apparent. The model proposed here adopts an intermediate approach, in which ρ ≠ 0 only at critical points, thus correcting for solvent DF at a fraction of computational cost.

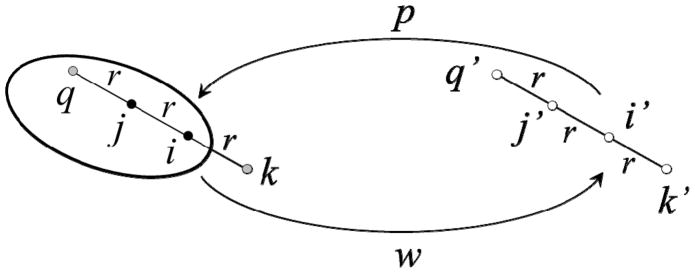
A solute atom i in a liquid is subject to an average dispersion force f = |f|r/r towards atoms within a volume dv at a position r (relative to i); an element dv at −r exerts an average force f′ = −|f′|r/r in the opposite direction. If both elements of volume are in average occupied by the same kind of substance, both forces cancel out. An imbalance of forces can result from different substances occupying r and −r or by different water densities in either position. In the absence of explicit water a major imbalance of forces will systematically occur throughout the system, which must be corrected. In addition, when a solute is assembled in solution the (dispersion) work necessary to move an atom i from bulk water to its final position in the solute is partially compensated by the work of removing water from the site in the opposite direction. These two independent processes are summarized in the cycle of fig. 1. A solute element p is moved from i′ in bulk water to i in the solute, whereas a water element w is moved from i to i′. The position j is occupied by another solute element, and site k is occupied by water with an occupancy s_k dependent on the solute conformation (s → 1 in bulk water, and s → 0 within the solute); positions j′ and k′ are both occupied by bulk water. If the dispersive energy between two elements of volume separated a distance r is V^d = −2εσ⁶/r⁶ (with ε > 0) the energy change upon transfer, $\mathrm{\Delta }{V}_{ij}^d=V_{ij}^d(p\text{in}i;w\text{in}{i}^{\prime })-V_{ij}^d(w\text{in}i;p\text{in}{i}^{\prime })$, is given by

Figure 1.

Formation of a solute in water. A solute element p is transferred from bulk water (site i′) to its final position (i) in the growing solute, while water w is moved from i to i′. Site j at a distance r from i is occupied by solute; sites k and k′ contain water with occupancies s_k ≤ 1 and s_k′ = 1; likewise for q and q′; s_i and s_j are assumed to be unity.

$$\mathrm{\Delta }{V}_{ij}^d=-2({\mathrm{\epsilon }}_{ij}{\mathrm{\sigma }}_{ij}^6+{\mathrm{\epsilon }}_{ik}{\mathrm{\sigma }}_{ik}^6+{\mathrm{\epsilon }}_{w{j}^{\prime }}{\mathrm{\sigma }}_{w{j}^{\prime }}^6+{\mathrm{\epsilon }}_{w{k}^{\prime }}{\mathrm{\sigma }}_{w{k}^{\prime }}^6-{\mathrm{\epsilon }}_{wj}{\mathrm{\sigma }}_{wj}^6-{\mathrm{\epsilon }}_{wk}{\mathrm{\sigma }}_{wk}^6-{\mathrm{\epsilon }}_{i^{\prime }{j}^{\prime }}{\mathrm{\sigma }}_{i^{\prime }{j}^{\prime }}^6-{\mathrm{\epsilon }}_{i^{\prime }{k}^{\prime }}{\mathrm{\sigma }}_{i^{\prime }{k}^{\prime }}^6)/r^6$$ (1)

which is probably the simplest way to incorporate the dependence of the solvent dispersion energy on the solute conformation. All the σ’s are here set equal to σ_ij, so water-exclusion effects are incorporated only through ε’s. By setting ε_ik = ε_iw s_k, ε_wj = ε_wj s_i, and ε_wk = ε_ww s_k s_i, and because ε_wj′ = ε_wk′ = ε_ww and ε_i′j′ = ε_i′k′ = ε_iw, the term in parenthesis in eq 1 can be cast into a single effective dispersive factor ${\mathrm{\epsilon }}_{ij}^s{\mathrm{\sigma }}_{ij}^6$, where

$${\mathrm{\epsilon }}_{ij}^s={\mathrm{\epsilon }}_{ij}+{{\mathrm{\epsilon }}^{\prime }}_{ij}={\mathrm{\epsilon }}_{ij}+\left\{-{\mathrm{\epsilon }}_{wj}+({\mathrm{\epsilon }}_{ww}-{\mathrm{\epsilon }}_{iw})[2-s_k]\right\}$$ (2)

is the solvent-corrected strength of the direct (ε_ij) dispersive interaction between the two solute elements (s_i was set to unity, i.e., the site is assumed to be occupied by water prior to transferring the atom). Similar calculation for j in the presence of i yields (cf. fig. 1)

$${\mathrm{\epsilon }}_{ji}^s={\mathrm{\epsilon }}_{ji}+{{\mathrm{\epsilon }}^{\prime }}_{ji}={\mathrm{\epsilon }}_{ji}+\left\{-{\mathrm{\epsilon }}_{iw}+({\mathrm{\epsilon }}_{ww}-{\mathrm{\epsilon }}_{wj})[2-s_q]\right\}$$ (2′)

where s_q is the water occupancy at site q. To preserve the symmetry of the potential the effective strength of the pair (ε̃_ij) is obtained as the arithmetic mean of ${\mathrm{\epsilon }}_{ij}^s$ and ${\mathrm{\epsilon }}_{ji}^s$, i.e.,

$${\stackrel{\sim }{\mathrm{\epsilon }}}_{ij}={\mathrm{\epsilon }}_{ij}+{{\stackrel{\sim }{\mathrm{\epsilon }}}^{\prime }}_{ij}$$ (3)

where the solvent-corrected interaction is determined by ε̃′_ij = [ε′_ij + ε′_ij]/2. Because ε̃_ij is symmetrical upon permutation of indexes i and j, the total van der Waals energy of a solute composed of N atoms is

$$E_{\mathit{vdw}}=E_{\mathit{vdw}}^0+V_{\mathit{disp}}=\frac{1}{2}\sum _{i\ne j}^N{\mathrm{\epsilon }}_{ij}\{{({\mathrm{\sigma }}_{ij}/r_{ij})}^{12}-2{({\mathrm{\sigma }}_{ij}/r_{ij})}^6\}-\sum _{i\ne j}^N{{\stackrel{\sim }{\mathrm{\epsilon }}}^{\prime }}_{ij}(\mathbf{r}){({\mathrm{\sigma }}_{ij}/r_{ij})}^6$$ (4)

where $E_{\mathit{vdw}}^0$ is the direct solute-solute van der Waals energy and V_disp is the correction to the dispersive energy due to the solvent. The dependence on the solute conformation, represented by r ≡ {r₁, r₂, …, r_N}, where r_i is the position of atom i, is made explicit in the last term.

An obvious choice for s(r) in eqs 2 and 2′ is a function proportional to the local water density ρ(r), for which any of the common approximations in liquid theory, including a simple barometric law probably suffices. For computational efficiency the approach used here is based on a contact model similar to that used in the development of the SCP implicit model of electrostatics,^5,44 namely,

$$s_k(\mathbf{r})=1-s_0^{-1}\sum _{l=1}^{N}exp(-r_{kl}/\mathrm{\lambda })$$ (5)

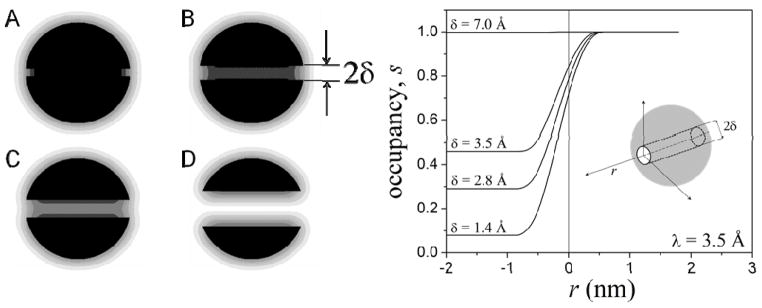
where r_kl ≡|r_l + r_j − 2r_i| is the distance between an atom l of the solute and the off-solute site r_k = 2r_i − r_j determined by the (i, j) pair; a similar equation holds for s_q, with r_ql = |r_l + r_i − 2r_j|. Thus, s → 1 for a point far from the solute (bulk water), and s₀ is chosen so that s → 0 for a point in the interior of the solute. For proteins, s₀ can be estimated analytically⁵ as s₀ ≈ 3(ζ + 2ζ² + 2ζ³)exp(−1/ζ), where ζ = λ/p_a and p_a = (3V_p/4πN_p)^1/3 ~1.4 Å is the average radius of a protein atom, and V_p ~183 ų and N_P ~15 are the average volume and average number of atoms per residue, respectively, estimated from the PDB. The behavior of eq 5 is illustrated in fig. 2 for a sphere with a radius of 2 nm containing a cylindrical cavity of radius δ along its major axis. The sphere is composed of atoms distributed uniformly in a cubic lattice, with a number density N_P/residue. To illustrate the effects of cavity size on water occupancy, δ is varied from 1.4 Å (radius of a water molecule) to 7 Å (effective diameter of an amino acid). Figure 2 shows a grey-scale representation of s(r) on a plane containing the cavity axis (left panel), along with the values of water occupancy along the axis (right panel) for λ = 3.5 Å. For a narrow cavity only its openings are partially accessible to water, while the interior remains fully dehydrated (s ~ 0). As the cavity size increases the level of hydration increases from sub-optimal (0 < s < 1) to optimal (s ~1). In the current implementation the level of hydration is represented by the single parameter λ, which must be optimized using experimental or simulation data (cf. Section III). The extent of hydration inside the cavity depends not only on the thermodynamic conditions, the size and the topology of the pocket, but also on the chemical properties of the lining atoms. Improvement of the parameterization (not pursued here) would then require at least two λ’s, one for non-polar groups and one for polar/charged groups.

Figure 2.

Left panel: gray-scale representation of water occupancy s (eq 5) in a sphere containing a cylindrical cavity of radius δ along one of its major axes (black: s = 0; white: s = 1). The system mimics a typical globular protein with a diameter of ~4 nm, containing a binding site with varying degrees of water accessibility. The sphere is formed by identical atoms distributed in a cubic lattice with a constant of 1.4 Å; λ in eq 5 is 3.5 Å. (A) δ = 1.4 Å (radius of a water molecule); only the openings of the cavity are accessible to water; (B) δ = 2.8 Å; hydration at the center of the cavity remains significantly reduced; (C) δ = 3.5 Å (effective radius of an amino acid in a protein); hydration reaches half the value of bulk water; (D) δ = 7 Å; near optimal hydration. Right panel: water occupancy as a function of the distance r along the cavity axis for different cavity radii δ; r = 0 is at the entrance of the cavity (inset).

Introducing the expression of s_k and s_q into eq 3 yields ε̃′_ij = a_ij + b_iΣexp(−r_kl/λ) + b_jΣexp(−r_ql/λ) where a_ij = ε_ww − ε_iw − ε_wj; b_i = (ε_ww − ε_iw)/2s₀; and b_j = (ε_ww − ε_wj)/2s₀. For proteins, an additional simplification is introduced in which a single dispersion strength is assigned to all the atoms (represented by a generic index p), i.e., ε_iw = ε_pw. Given the known sensitivity of simulation results to Lennard-Jones parameters, as evidenced by the continuous effort in force field parameterizations based on chemical atom types,⁴⁵ this simplification may require revision. In addition, water occupancy at a given off-solute site is largely determined by the solute atoms close to the site, so the summation in eq 5 can be restricted to a subset N_k of atoms l within a distance d_c from k; likewise for a subset N_q around q. Finally, the parameter λ is made independent of k, so the final expression for ε̃′_ij is

$${{\stackrel{\sim }{\mathrm{\epsilon }}}^{\prime }}_{ij}(\mathbf{r})=a+b\sum _{l=1}^{N_k}exp(-r_{kl}/\mathrm{\lambda })+b\sum _{l=1}^{N_q}exp(-r_{ql}/\mathrm{\lambda })$$ (6)

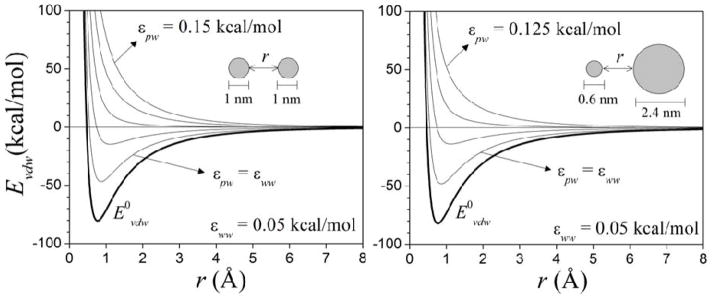
This expression contains three parameters to be determined, either a, b, and λ; or ε_ww, ε_pw, and λ. In the latter approach, which is followed here, ε_ww and ε_pw have a physical meaning. In particular, these are positive quantities, and their values are expected to be close to those of LJ parameters in the protein force field. Their relative values determine whether the effective interactions between hydrated solutes are attractive or repulsive, as illustrated in fig. 3. All the potentials show a long-range decay.

Figure 3.

van der Waals interaction energy E_vdw (eq 4) between two spheres in water, as a function of the distance r between their surfaces, and for different values ε_ww and ε_pw (eq 6). The spheres are composed of identical atoms distributed uniformly on a cubic lattice with a constant of 1.4 Å. Lennard-Jones parameters are ε_ij = 0.15 kcal/mol and σ_ij = 2.5 Å (LB mixing rules used). The energies at equilibrium are similar (within ~2 kcal/mol) in both systems for the same values of ε_ww and ε_pw. The direct potentials (E⁰_vdw; for ε_ww = ε_pw = 0) corresponding to the uncorrected interactions are also shown.

The van der Waals force F_vdw,i on an atom i is calculated as F_vdw,i = −∇_iE_vdw, where the gradient is taken with respect to r_i while keeping all the off-solute positions r_k fixed in the calculation of the partial derivatives. From eq 4 ${\mathbf{F}}_{\mathit{vdw},i}=-{\nabla }_i{E}_{\mathit{vdw}}^0+{\mathbf{F}}_{\mathit{disp},i}$, where the first term is the direct van der Waals force ( ${\mathbf{F}}_{\mathit{vdw},i}^0$) and the second term is the correction of the total dispersion force on i due to the solvent, given by

$${\mathbf{F}}_{\mathit{disp},i}=12\sum _{j\ne i}^N{{\stackrel{\sim }{\mathrm{\epsilon }}}^{\prime }}_{ij}(\mathbf{r})r_{ij}^{-1}{({\mathrm{\sigma }}_{ij}/r_{ij})}^6{\widehat{\mathbf{r}}}_{ij}+\sum _{k=1}^{N(N-1)}{\mathrm{\eta }}_{ik}{\widehat{\mathbf{r}}}_{ik}$$ (7)

where r̂_ij = (r_j − r_i)/|r_j − r_i| is the unit vector in the direction determined by the pair (i, j), and r̂_ik = (r_k − r_i)/|r_k − r_i| is the unit vector determined by i and the off-solute site k. The first term in eq 7 has the usual pairwise form of a dispersion force determined by ε̃′_ij, and originates in the presence of solvent at sites k and q. The quantity η in the second sum of eq 7 is given by

$${\mathrm{\eta }}_{ik}=(2b/\mathrm{\lambda }){({\mathrm{\sigma }}_k/r_k)}^6\mathrm{\theta }(d_c-r_{ik})exp(-r_{ik}/\mathrm{\lambda })$$ (8)

and originates in the changes of solvent occupancy at site k due to changes in the position of atom i; θ is the Heaviside step function, and the index k is determined by the corresponding (m, n) atom pairs, i.e., r_k = 2r_m − r_n, and r_ik = r_k − r_i, so σ_k ≡ σ_nm and r_k ≡ r_nm. In practice, the cutoff distance d_c can be made rather small, so most of the N(N−1) terms in eq 7 vanish.

III. Results

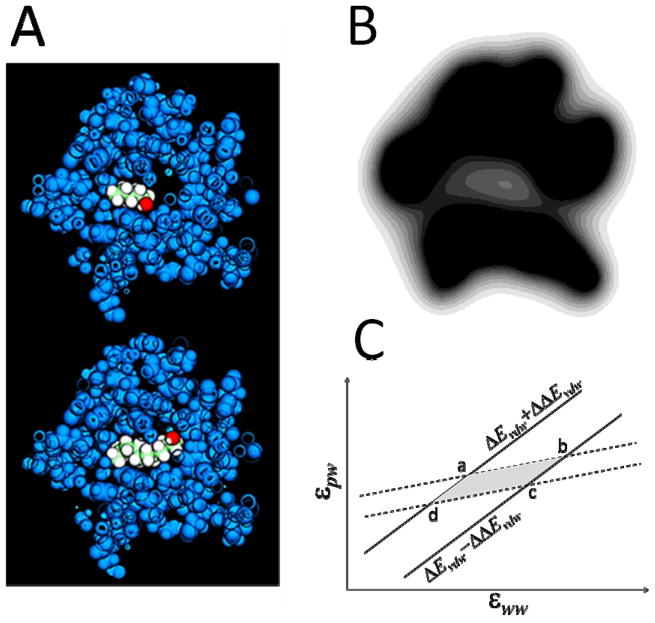
Isothermal titration calorimetry (ITC) of a series of aliphatic alcohols bound to the major urinary protein (MUP-I) showed that the binding enthalpy is determined mainly by ligand-protein dispersive interactions.^26,27 This is an example of suboptimal hydration, hence an ideal system for optimization of λ in eq 5. The crystal structures of the complexes (cf. caption fig. 7) show a narrow binding pocket located deep into MUP-I (fig. 4A) and lined mostly with nonpolar residues. These structures are used here to calculate the average water occupancy within the binding pocket and the binding enthalpies of the complexes. For computational efficiency the summation in eq 5 is restricted to C_α atoms only, so s₀ is determined by p_a = 3.5 Å. This simplification was used previously to treat long-range water-exclusion effects on electrostatics.⁵ The protein is immersed into a cubic lattice with a cell length of 1.4 Å, and s calculated with eq 5 at each point of the lattice. The density of water within the binding pocket was estimated²⁶ at ~0.21 g/cm³. An average occupancy <s> ~0.2 is well reproduced by eq 5 with λ = 2 Å, although s is heterogeneous throughout the pocket (fig. 4B). In general, increasing λ lowers s. This value of λ was estimated with no cutoffs in eq 5, but <s> remains unchanged with d_c as small as ~12 Å.

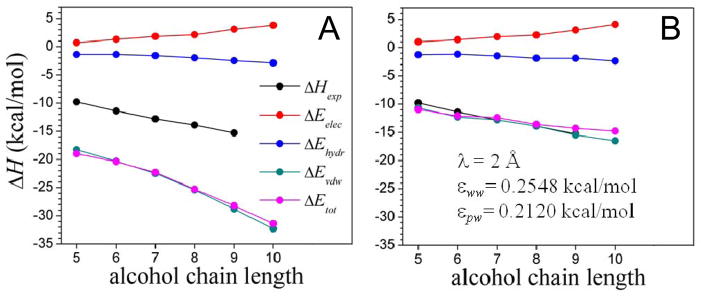
Figure 7.

Energy contributions to the binding energy of the MUP-I protein to a series of aliphatic alcohols as a function of the chain length, calculated with the implicit solvent model (E_elec given by eq 10; E_vdw by eq 4, and E_hydr is the cavity-formation energy). (A) Uncorrected dispersion energy ( $E_{\mathit{vdw}}=E_{\mathit{vdw}}^0$ in eq 4); and (B) solvent-dispersion corrected energy ( $E_{\mathit{vdw}}=E_{\mathit{vdw}}^0+V_{\mathit{disp}}$). The structures of the complexes are taken from the PDB; accession codes 1znd, 1zne, 1zng, 1znh, 1znk, 1znl, for pentan-, hexan-, heptan-, octan-, nonan-, and decan-1-ol, respectively. The experimental binding enthalpy²⁶ (ΔH_exp) is also shown (ITC data for decan-1-ol not available). Binding is dominated by dispersive forces, as determined by the extent of sub-optimal hydration of the binding pocket.

Figure 4.

(A) Cross section of the pentan-1-ol/MUP-I (upper) and decan-1-ol/MUP-I (lower) complexes, showing the buried cavity and the alcohol molecules filling the space (PDB 1znd used). (B) Gray-scale representation of water occupancy s on a (arbitrary) plane across the sub-optimally hydrated binding cavity. To be compared with fig. 2. Water occupancy was calculated with λ = 2 Å in eq 5, which yields <s> ~0.2 inside the binding pocket, based on reported results.²⁷ (C) Iso-energy lines of the van der Waals dissociation energies of barnase/barstar (dashed lines) and cytochrome C peroxidase/cytochrome C (solid) complexes in the ε_ww−ε_pw plane, determined by the statistical errors (~2 kcal/mol) estimated from MD simulation in explicit water. The overlapping section is defined by the following (ε_ww, ε_pw) pairs: a = (0.2252, 0.2501); b = (0.4313, 0.4074); c = (0.2824, 0.2898); d = (0.0763, 0.1325); all in kcal/mol.

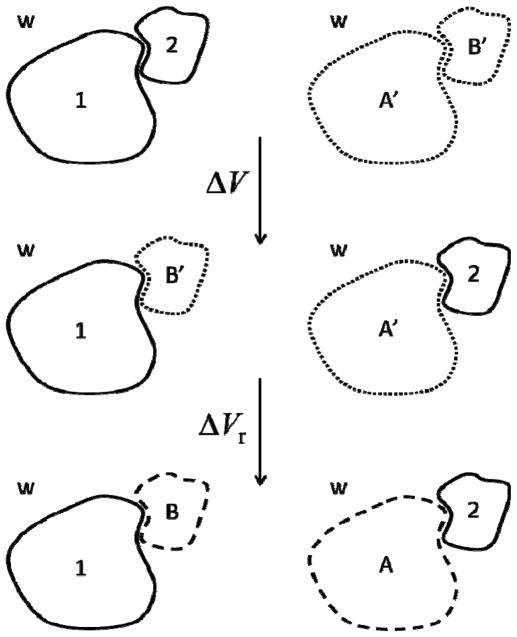
The optimized λ is used next to obtain ε_ww and ε_pw in eq 6. Figure 5 depicts a generalization of the cycle of fig. 1, in which two proteins (1 and 2) are dissociated from their bound state. The van der Waals contribution to the total dissociation energy is ΔE_vdw = ΔV + ΔV_r, where ΔV is the energy required to separate the proteins without affecting the behavior of water (an ideal process), and ΔV_r is the reorganization energy of water in contact with the protein. A′ and B′ are regions of bulk water with the same shapes and volumes as proteins 1 and 2, whereas A and B are the same regions of (non-bulk) water in contact with the proteins. After evaluating ΔV and ΔV_r the energy change can be approximated as

Figure 5.

Thermodynamic cycle used to estimate the total van der Waals contribution to protein-protein binding in water used in the molecular dynamics simulations. A′ and B′ are regions of bulk water with the same sizes and shapes of proteins 1 and 2, respectively; whereas A and B are the same regions of water in contact with the proteins 2 and 1 upon structural and dynamic reorganization (see text).

$$\mathit{\Delta }{E}_{\mathit{vdw}}=(E_{BB}-E_{B^{\prime }{B}^{\prime }})+(E_{AA}-E_{A^{\prime }{A}^{\prime }})+E_{1B}+E_{2A}-E_{A^{\prime }{B}^{\prime }}-E_{12}$$ (9)

where E_IJ is the van der Waals interaction energy between subsystems I and J, and the terms with I = J are self-energies; all the terms corresponding to interactions of the proteins with bulk water (E_1w and E_2w) cancel out, and the differences (E_Aw − E_A′w) and (E_Bw − E_B′w) are small compared to the other terms in eq 9, thus neglected. A system in which the protein interfaces are well hydrated prior to binding appears to be the barnase/barstar complex, for which the binding enthalpy at 25 °C and pH 7 has been measured⁴⁶ at ~19.3 kcal/mol. Each term of eq 9 is here calculated for this complex using molecular dynamic simulations in explicit water, so ΔE_vdw and the individual contributions can be estimated directly. The all-atom representation of the CHARMM protein force field⁴⁵ (version c35b5) with default protonation states (pH 7) was used, resulting in an electrically neutral system. The simulations were carried out in the canonical ensemble at 25 °C and 1 atm, using periodic boundary conditions and the CHARMM-optimized TIP3P water model. A cubic simulation cell with a side length of ~9.33 nm was used, large enough to accommodate both bulk and non-bulk (interfacial) water around the complex and the unbound proteins. Long-range electrostatics was treated with PME summations,⁴⁷ with specifications reported previously.¹⁶ Bond lengths and angles were constrained with SHAKE, and a 2-fs time step was used (leapfrog integrator). Pressure was maintained with the Langevin piston method,⁴⁸ with a mass of 400 amu and a collision frequency of 20 ps⁻¹; temperature was fixed with the Hoover thermostat,⁴⁹ using a mass of 10³ kcal mol⁻¹ ps². NPT-equilibration of pure water yielded an average density of ~0.993 g/cm³.

The conformations of the proteins were taken from the crystal structure of the complex (PDB id 1brs). To calculate E₁₂ (1 = barnase; 2 = barstar) the complex was initially centered in the simulation cell and water molecules overlapping protein atoms were removed. To calculate E_1B, E_2A, E_AA, and E_BB the unbound proteins were positioned within the simulation cell in the same positions they occupied in the simulation of the complex. Throughout the simulations all the C_α atoms were constrained at fixed positions, and the system equilibrated for 5 ns. To calculate E_A′A′, E_B′B′ and E_A′B′ only the dynamics of water was simulated. The regions of non-bulk (A, B) and bulk (A′, B′) water were defined by the molecular surfaces of the corresponding proteins, using the Lee-Richards algorithm (probe radius set to zero). The error in the estimate of ΔE_vdw is chosen to be ΔΔE_vdw ~2 kcal/mol, which is the expected accuracy of the force field. Therefore, each term in eq 9 was evaluated with a statistical error ΔE = σ/n^1/2 ~0.25 kcal/mol, where σ is the standard deviation of the corresponding term E_IJ obtained from the fluctuating energy E_IJ(t), and n is the number of uncorrelated steps given by n = τ/τ_c, where τ is the total simulation time and τ_c the correlation time estimated from the autocorrelation function C(t) ~ ∫E_IJ(t′)E_IJ(t+t′)dt′. To decrease the errors to the required values each term in eq 9 required a different simulation length τ, ranging from 10 to 20 ns. For the calculation of the energies from the trajectories PME was abandoned, and all the non-bonded terms were calculated directly without truncation. All the energies reported below are in kcal/mol. The changes in water self-energies upon reorganization were practically identical despite the different amounts of water in each region: E_AA − E_A′A′ = 12.5 ± 0.8 and E_BB − E_B′B′ = 12.7 ± 0.8. Both energies are also positive, implying unfavorable rehydration. The similarity of self-energies appears to be related to the number of water molecules “in contact” with the protein surfaces, which are the ones affected the most by the reorganization at the interfaces. Thus, region A has a number of water molecules in contact with protein 2, which is similar to the number of water molecules in B in contact with 1. However, this similarity is not expected to be a general feature, and larger differences would likely be observed in the presence of more complex surfaces. There is also a slight increase in the average number of water molecules within each region: n_A = 668 ± 10 and n_A′ = 663 ± 10; and n_B = 544 ± 9 and n_B′ = 542 ± 9, where Δn are now standard deviations. From a thermodynamic standpoint, these changes are related to the differences in chemical potential (μ) induced by the surfaces. Thus, μ of water in A′ cannot be equal to μ_w of the bulk water, but μ in A becomes equal to μ_w once all the structural rearrangements (including water absorption) set in; similar for B and B′. The changes in self-energies within each region can be partially explained by an increase in water packing induced by the protein surfaces. The interaction terms are: E_2A = −38.5 ± 0.1, E_1B = −41.2 ± 0.1, E_A′B′ = 7.3 ± 0.1, and E₁₂ = −62.9 ± 0.1. The resulting van der Waals contribution is thus ΔE_vdw = 1.1 ± 2 kcal/mol, a small attraction but within the statistical error of the calculation. Therefore, in this case where water reorganization at the interface is modest and the proteins are relatively small, ΔE_vdw ~ 0 is justified.

The parameterization requires a second protein complex. To partially incorporate the effect of protein size, the complex is chosen on the basis of the following criteria: One of the proteins must be similar in size to barnase (or barstar) and the second protein must be larger than barstar; in addition, the proteins must be globular and relatively rigid, with a topographically simple protein/protein interface to also expect near-optimal pre-binding hydration. Cytochrome C peroxidase contains the same number of residues than barnase; and its ligand, cytochrome C, is ~3.5 times larger than barstar. The binding enthalpy of this complex (PDB id: 2pcc) has been measured at ~2.6 kcal/mol. Dynamic simulations were performed using the same protocol described above. The van der Waals contribution to dissociation was estimated at ΔE_vdw = 0.5 ± 2 kcal/mol, also weakly attractive but still within the statistical error.

The dispersive contributions to the dissociation energies are now calculated using eqs 4 and 6 with the optimized λ. Robust methods exist to evaluate the relative binding affinities of small ligands for a rigid binding site,⁵⁰ including free energy perturbation and thermodynamic integration. Accurate estimates of absolute free energies are more challenging, even for small system, and no reliable methods are yet available for proteins, although progress is being made.⁵¹ The method employed here is simple, yet robust enough for the purpose of parameterization. The conformations of the complexes are first relaxed using canonical MC simulations of the proteins in the bound state at 25 °C. The average energy is calculated⁵² as <E_b> = Z⁻¹Σ_i E_i exp(−E_i/kT) ≈ Σ_i E_i/n, where E_i and n in the last sum are the energy of the accepted conformation i and the number of accepted conformations, respectively. The energy is given by E_i = E_elec,i + E_vdw,i + E_hydr,i, each term corresponding, respectively, to electrostatic, van der Waals, and hydrophobic contributions. Electrostatic interactions are calculated with the SCP model.^5,53 In this model the electrostatic energy E_elec of a solute composed of N atoms is given by,

$$E_{\mathit{elec}}=\frac{1}{2}\sum _{i\ne j}^N\frac{q_i{q}_j}{r_{ij}{D}_{ij}(r_{ij};\mathbf{r})}+\frac{1}{2}\sum _{i=1}^N\frac{q_i^2}{R_i(q_i;\mathbf{r})}\left\{\frac{1}{D_i[R_i(q_i;\mathbf{r});\mathbf{r}]}-1\right\}$$ (10)

where r denotes the conformation of the system, and q are the atomic charges. In the partition of eq 10 the first sum is the interaction energy term, and the second sum is the self-energy term. The dependence of E_elec on the conformation is through the screening functions D and the effective radii R, as both of these quantities account for solvent-exclusion effects at different length scales.⁵ The effects of SIF on HB energies are introduced⁵ through a suitable modification of R, whereas the hydrophobic energy is given by a cavity term E_hydr = aγ, where γ is the solute solvent-accessible surface-area, and a is a parameter obtained from hydration energies of small alkanes.⁵³ The functions D, R, and γ are all estimated with a contact model similar to eq 5.

Optimization of the model requires adjusting ε_ww and ε_pw in such a way that the association energy ΔE_d = <E_b> − E_∞ equals the experimental binding enthalpy at same temperature. This procedure would require a fully-converged MC simulation for each parameter set over the course of the optimization. To simplify the computational demand only one structure in the bound state is used, which is chosen from a MC simulation carried out with the non-corrected model ( $E_{\mathit{vdw}}=E_{\mathit{vdw}}^0$ in eq 4). A member k of the canonical ensemble is selected such that E_k is closest to the average <E_b> of the ensemble. The representative structure k is subjected to a short minimization to relax it with the dispersion-corrected force field. For each values of ε_ww and ε_pw the dissociation energy is calculated simply as ΔE_d = E_k − E_∞, a major simplification but good enough for the optimization. Then, for each (ε_ww, ε_pw) pair, the van deer Waals dissociation energy ΔE_vdw = E_vdw,k − E_vdw,∞ is compared to ΔE_vdw obtained from the explicit-water simulations. Calculations are also carried out with the all-atom CHARMM force field,⁴⁵ using standard protonation states, and no truncations of the non-bonded interactions.

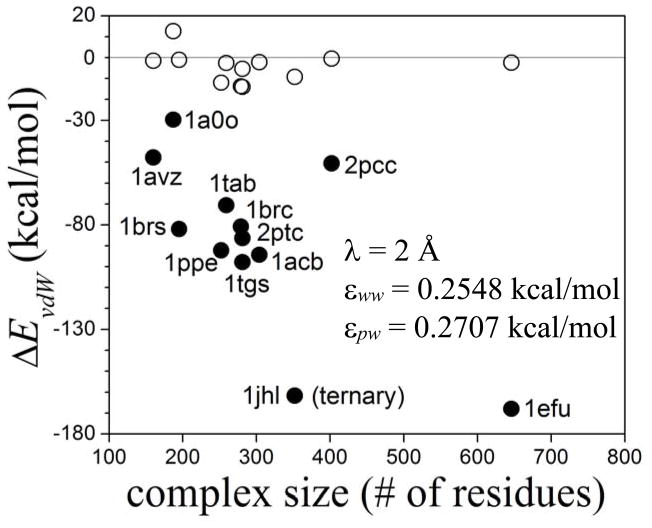
Figure 4C shows the region in the ε_ww−ε_pw plane within which ΔE_vdw (in kcal/mol) equals the dissociation energies. For each complex the iso-energy contour plots are straight lines, and lines corresponding to different complexes intersect, forming an extended rhomboid-shaped region. Any combination of ε_ww and ε_pw within this region can be chosen as optimized parameters; in particular the values at the center, namely, ε_ww ~0.2548 kcal/mol and ε_pw ~0.2707 kcal/mol. These values make physical sense as they are within the order of magnitude of the LJ parameters of the CHARMM force field. These values are used to estimate the van der Waals contributions to the binding energies of a set of binary and ternary protein complexes of varying sizes. The procedure is the same as described above for 1brs and 2pcc; for the ternary complex the dissociated state corresponds to the three components separated from one another. Results are shown in fig. 6. The uncorrected energies (solid circles) are large in all cases, but correction by water dispersion destabilize the complexes significantly (open circles). Yet, in all but one of the complexes the corrected van der Waals contributions are attractive. The degree of stabilization does not correlate with complex size (at least within this range of sizes considered here) but appears to be related more closely to the structural details of the protein/protein interfaces. For the binary complexes the contribution is negative (ΔE_vdW < − 2 kcal/mol) for complexes in which a specificity-conferring residue (Arg or Lys) in one protein is buried in the other protein (1tgs, 2pts, 1brc, 1ppe). The interfaces of the other complexes are less tight, including 1a0o, which shows a rather low degree of complementarity. This reinforces the notion that dispersion in the presence of topographically complex interfaces characterized by crevices and narrow pockets could make important contributions to binding. This is illustrated by the aliphatic-alcohols/MUP-I protein complexes. Binding energies are calculated with the ISM at T = 27 °C, using the same protocol used for the protein complexes. Figure 7A shows the components of the binding energy without corrections for water dispersion effects. The hydrophobic attraction increases with chain length, as expected, but it is compensated by an unfavorable electrostatic energy. This leaves only the direct van der Waals interaction ( $E_{\mathit{vdw}}^0$ in eq 4) as the main contribution to the binding energy. This energy, however, is almost twice as large as the experimental enthalpy²⁷ ΔH_exp, a consequence of uncompensated dispersive interaction. The partial weakening of the binding energy is due to the solvent dispersion correction (V_disp in eq 4), as shown in fig. 7B. To reproduce the experimental enthalpy within ~2 kcal/mol accuracy the parameter ε_pw for the alcohol atoms has to be adjusted to ~0.2120 kcal/mol. Using the same value of ε_pw obtained for proteins, the van der Waals contribution is underestimated by ~6 kcal/mol, which demonstrates the sensitivity of the results to the LJ parameters; nonetheless, the linear behavior with the chain length is still reproduced. As mentioned, a single ε_pw is unlikely to be optimal for all chemical species, and different values are needed for amino acids, nucleic acids, alcohols, fatty acids, and other basic units. Ultimately, an atom-type-based parameterization would probably be required, in line with the parameterization of the LJ potential in the force field. Another reason to recalibrate ε_wp for alcohols is that the C_α-based calculation of s can no longer be used; in this case the sum in eq 5 included all the C atoms of the aliphatic chain, which underestimates the values of s if the same λ is used.

Figure 6.

Water-dispersion effects of the binding energies of a number of binary and ternary protein complexes of varying sizes (identified by PDB id) as estimated with the ISM. Van der Waals energy of binding (ΔE_vdw); solid symbols: uncorrected dispersive interactions ( $E_{\mathit{vdw}}=E_{\mathit{vdw}}^0$ in eq 4); open: corrected dispersion ( $E_{\mathit{vdw}}=E_{\mathit{vdw}}^0+V_{\mathit{disp}}$). Barnase/barstar (1brs) and cytochrome C peroxidase/cytochrome C (2pcc) used in the optimization are also shown. The proteins include enzymes bound to substrates, inhibitors, or activators; and an antigen-antibody complex.

IV. Discussion and Conclusions

Dispersion forces have been shown to play a role in protein-ligand interactions,^25–28 the conformational stability of proteins,^29,30 and the preferential hydration/binding mechanism underlying denaturation by cosolutes.³¹ The importance of incorporating DF in an implicit solvent model has been established.^20,22,23 Progress has been made in recent years, and models have been proposed that incorporate solvent DF empirically.^32,33 The treatment of long-range effects and the dependence on the solute conformation are important physical features that still need careful consideration.

In this paper a model was proposed which incorporates solvent-corrected DF through effective interactions between the solute atoms. The model captures the short- and long-range effects of water-exclusion in conditions of partial and anisotropic hydration. It was developed in the context of a classical (molecular mechanics) force field, where electrostatics and van der Waals interactions are treated independently³⁶ (although both are electrostatic in origin). The solvent correction is introduced through the LJ coefficients ε (eq 6). The extent of water exclusion is represented in ε through a conformation-dependent water-occupancy function s(r) (eq 5), using a contact model similar to that used earlier in the treatment of water-exclusion in electrostatics.^5,44 In the current implementation ε are made independent of temperature; such dependence can eventually be incorporated through s. The model is simple yet general, as its formulation does not depend on the nature of the solute. In combination with the implicit electrostatic model developed previously^5,44,53 (which includes effects of SIF) it forms a complete ISM, as it captures the main physical effects of partial, anisotropic hydration common in real biological systems. Improvements are probably needed both in the treatment of s and in the parameterization. The current implementation uses only three parameters, one of which (λ) represents the degree of hydration and two others that represent the strength of water-water (ε_ww) and solute-water (ε_pw) dispersive interactions. These parameters were optimized for proteins, using hydration data of a sub-optimally hydrated binding site (MUP-I), and results from explicit-water MD simulations of two medium-sized complexes (barnase/barstar and cytochrome C peroxidase/cytochrome C).

The model was applied to a series of aliphatic-alcohol/MUP-I complexes for which ITC data suggest dispersive interactions to be the major contributions to the binding enthalpy. The model reproduces the linear increase of affinity with chain length. It was found, however, that (favorable) hydrophobic and (unfavorable) electrostatic energies are not negligible, but compensate each other for all the chain lengths, thus leaving dispersion as the main contribution. The model was also used to estimate the binding energies of several protein complexes of various sizes, demonstrating that a significant reduction of the dispersive attraction is achieved with the current implementation. Need for improvements can only be determined by MD simulations in explicit water, and accomplished through atom-type-based parameterization of ε_pw.

To account for long-range interactions no cutoffs were used to evaluate either eq 4 or eq 5, so the computational cost of the current implementation makes the model more suitable for peptides and small proteins. However, several strategies can be used to speed up computation of the long-range contributions, in line with the treatment of long-range electrostatics in the SCP model.⁵ These include suitable truncations of eqs 4 and 5; the use of Hamaker-like potentials between distant residues; infrequent updates of eq 3 during Langevin dynamics; and neglect of the 3-body terms in eq. 7. Depending on how these approximations are implemented the CPU time can be improved substantially, to a maximum of about ~2–4 times the computational cost required in the gas phase; these approximations, however, require careful re-parameterization, and will be the topic of a future study.

In general, aqueous interfaces display non-bulk behavior that can extend up to a few nanometers into the bulk, depending on the surface size, topography, and charge distribution.⁵ In particular, the density of interfacial water can vary from mild over-hydration,³⁴ to partial dewetting,³⁵ to significant dehydration in crevices and narrow pockets.²⁶ The imbalance of DF introduced by density variations at the interface could affect the association/dissociation mechanism. Furthermore, dispersive interactions have a long-range component that may lead to effective attraction/repulsion between proteins in large complexes and assemblies. Small differences in the strength of protein-protein and protein-water DF could make significant contributions in weak and ultra-weak protein association.^52,54 The implications in crowded, anisotropic environments, such as those in the interior of a living cell, can be far reaching. Evidence suggests that a large proportion of biologically active molecules in the cell do not diffuse freely in the bulk medium despite their high solubility, but are transiently bound to one another, to membranes, or to the cytoskeleton.⁵⁵ In addition to electrostatics, long-range uncompensated DF may play a role in such non-specific interactions, possibly affecting subcellular organization and molecular translocation.