Effective dimension reduction for sparse functional data

Summary

We propose a method of effective dimension reduction for functional data, emphasizing the sparse design where one observes only a few noisy and irregular measurements for some or all of the subjects. The proposed method borrows strength across the entire sample and provides a way to characterize the effective dimension reduction space, via functional cumulative slicing. Our theoretical study reveals a bias-variance trade-off associated with the regularizing truncation and decaying structures of the predictor process and the effective dimension reduction space. A simulation study and an application illustrate the superior finite-sample performance of the method.

1. Introduction

In functional data analysis, one is often interested in how a scalar response $Y\in \mathbb{R}$ varies with a smooth trajectory X(t), where t is an index variable defined on a closed interval $\mathcal{T}$; see Ramsay & Silverman (2005). To be specific, one seeks to model the relationship Y = M(X; ϵ), where M is a smooth functional and the error process ϵ has zeromean and finite variance σ² and is independent of X. Although modelling M parametrically can be restrictive in many applications, modelling M nonparametrically is infeasible in practice due to slow convergence rates associated with the curse of dimensionality. Therefore a class of semiparametric index models has been proposed to approximate M(X; ϵ) with an unknown link function $g:{\mathbb{R}}^{K+1}\to \mathbb{R}$; that is,

$$Y=g(\langle {\beta }_1,X\rangle ,\dots ,\langle {\beta }_K,X\rangle ;ϵ),$$ (1)

where K is the reduced dimension of the model, β₁, … , β_K are linearly independent index functions, and ⟨u, v⟩ = ∫ u(t)v(t) dt is the usual L² inner product. The functional linear model Y = β₀ + ∫ β₁(t)X(t) dt + ϵ is a special case and has been studied extensively (Cardot et al., 1999; Müller & Stadtmüller, 2005; Yao et al., 2005b; Cai & Hall, 2006; Hall & Horowitz, 2007; Yuan & Cai, 2010).

In this article, we tackle the index model (1) from the perspective of effective dimension reduction, in the sense that the K linear projections ⟨β₁, X⟩, … , ⟨β_K , X⟩ form a sufficient statistic. This is particularly useful when the process X is infinite-dimensional. Our primary goal is to discuss dimension reduction for functional data, especially when the trajectories are corrupted by noise and are sparsely observed with only a few observations for some, or even all, of the subjects. Pioneered by Li (1991) for multivariate data, effective dimension reduction methods are typically link-free, requiring neither specification nor estimation of the link function (Duan & Li, 1991), and aim to characterize the K-dimensional effective dimension reduction space S_Y∣X = span(β₁, … , β_K ) onto which X is projected. Such index functions β_k are called effective dimension reduction directions, K is the structural dimension, and S_Y∣X is also known as the central subspace (Cook, 1998). Li (1991) characterized S_Y∣X via the inversemean E(X ∣ Y) by sliced inverse regression, which has motivated much work for multivariate data. For instance, Cook & Weisberg (1991) estimated var(X ∣ Y), Li (1992) dealt with the Hessian matrix of the regression curve, Xia et al. (2002) proposed minimum average variance estimation as an adaptive approach based on kernel methods, Chiaromonte et al. (2002) modified sliced inverse regression for categorical predictors, Li & Wang (2007) worked with empirical directions, and Zhu et al. (2010) proposed cumulative slicing estimation to improve on sliced inverse regression.

The literature on effective dimension reduction for functional data is relatively sparse. Ferré & Yao (2003) proposed functional sliced inverse regression for completely observed functional data, and Li & Hsing (2010) developed sequential χ² testing procedures to decide the structural dimension of functional sliced inverse regression. Apart from effective dimension reduction approaches, James & Silverman (2005) estimated the index and link functions jointly for an additive form $g(\langle {\beta }_1,X\rangle ,\dots ,\langle {\beta }_K,X\rangle ;ϵ)={\beta }_0+{\sum }_{k=1}^K{g}_k(\langle {\beta }_k,X\rangle )+ϵ$, assuming that the trajectories are densely or completely observed and that the index and link functions are elements of a finite-dimensional spline space. Chen et al. (2011) estimated the index and additive link functions nonparametrically and relaxed the finite-dimensional assumption for theoretical analysis but retained the dense design.

Jiang et al. (2014) proposed an inverse regression method for sparse functional data by estimating the conditional mean $E\left\{X\right(t)\mid Y=\tilde{y}\}$ with a two-dimensional smoother applied to pooled observed values of X in a local neighbourhood of $(t,\tilde{y})$. The computation associated with a two-dimensional smoother is considerable and further increased by the need to select two different bandwidths. In contrast, we aim to estimate the effective dimension reduction space by drawing inspiration from cumulative slicing for multivariate data (Zhu et al., 2010). When adapted to the functional setting, cumulative slicing offers a novel and computationally simple way of borrowing strength across subjects to handle sparsely observed trajectories. This advantage has not been exploited elsewhere. As we will demonstrate later, although extending cumulative slicing to completely observed functional data is straightforward, it adopts a different strategy for the sparse design via a one-dimensional smoother, with potentially effective usage of the data.

2. Methodology

2·1. Dimension reduction for functional data

Let $\mathcal{T}$ be a compact interval, and let X be a random variable defined on the real separable Hilbert space $H\equiv L^2\left(\mathcal{T}\right)$ endowed with inner product $\langle f,g\rangle ={\int }_{\mathcal{T}}f\left(t\right)g\left(t\right)\mathrm{d}t$ and norm ‖f‖ = ⟨f, f⟩^1/2. We assume that:

Assumption 1

X is centred and has a finite fourth moment, ∫_τ E{X⁴(t)} dt < ∞.

Under Assumption 1, the covariance surface of X is ∑(s, t) = E{X(s)X(t)}, which generates a Hilbert–Schmidt operator ∑ on H that maps f to (∑f)(t) = ∫_τ ∑(s, t) f (s) ds. This operator can be written succinctly as ∑ = E(X ⊗ X), where the tensor product u ⊗ v denotes the rank-one operator on H that maps w to (u ⊗ v)w = ⟨u, w⟩v. By Mercer’s theorem, ∑ admits a spectral decomposition $\Sigma ={\sum }_{j=1}^{\infty }{\alpha }_j{\varphi }_j\otimes {\varphi }_j$, where the eigenfunctions {ϕ_j}_j=1,2,… form a complete orthonormal system in H and the eigenvalues {α_j}_j=1,2,… are strictly decreasing and positive such that ${\sum }_{j=1}^{\infty }{\alpha }_j<\infty$. Finally, recall that the effective dimension reduction directions β₁, … , β_K in model (1) are linearly independent functions in H, and the response $Y\in \mathbb{R}$ is assumed to be conditionally independent of X given the K projections ⟨β₁, X⟩, … , ⟨β_K , X⟩.

Zhu et al. (2010) observed that for a fixed $\tilde{y}\in \mathbb{R}$, using two slices $I_1=(-\infty ,\tilde{y}]$ and $I_2=(\tilde{y},+\infty )$ would maximize the use of data and minimize the variability in each slice. The kernel of the sliced inverse regression operator var{E(X ∣ Y)} is estimated by the two-slice version ${\Lambda }_0(s,t;\tilde{y})\propto m(s,\tilde{y})m(t,\tilde{y})$, where $m(t,\tilde{y})=E\left\{X\right(t\left)1\right(Y\le \tilde{y}\left)\right\}$ is an unconditional expectation, in contrast to the conditional expectation E{X(t) ∣ Y} of functional sliced inverse regression. Since Λ₀ with a fixed $\tilde{y}$ spans at most one direction of S_Y∣X, it is necessary to combine all possible estimates of $m(t,\tilde{y})$ by letting $\tilde{y}$ run across the support of $\tilde{Y}$, an independent copy of Y. Therefore, the kernel of the proposed functional cumulative slicing is

$$\Lambda (s,t)=E\left\{m\right(s,\tilde{Y}\left)m\right(t,\tilde{Y}\left)w\right(\tilde{Y}\left)\right\},$$ (2)

where $w\left(\tilde{y}\right)$ is a known nonnegative weight function. Denote the corresponding integral operator of Λ(s, t) by Λ also. The following theorem establishes the validity of our proposal. Analogous to the multivariate case, a linearity assumption is needed.

Assumption 2

For any function b ∈ H, there exist constants $c_0,\dots ,c_K\in \mathbb{R}$ such that

$$E(\langle b,X\rangle \mid \langle {\beta }_1,X\rangle ,\dots ,\langle {\beta }_K,X\rangle )=c_0+\sum _{k=1}^K{c}_k\langle {\beta }_k,X\rangle .$$

This assumption is satisfied when X has an elliptically contoured distribution, which is more general than, but has a close connection to, a Gaussian process (Cambanis et al., 1981; Li & Hsing, 2010).

Theorem 1

If Assumptions 1 and 2 hold for model (1), then the linear space spanned by $\left\{m\right(t,\tilde{y}):\tilde{y}\in \mathbb{R}\}$ is contained in the linear space spanned by {∑β₁, … , ∑β_K}, i.e., $\text{span}\left(\right\{m(t,\tilde{y}):\tilde{y}\in \mathbb{R}\left\}\right)\subseteq \text{span}(\Sigma {\beta }_1,\dots ,\Sigma {\beta }_K)$.

An important observation from Theorem 1 is that for any b ∈ H orthogonal to the space spanned by {∑β₁, … , ∑β_K} and for any x ∈ H, we have ⟨b, Λx⟩ = 0, implying that range(Λ) ⊆ span(∑β₁, … , ∑β_K). If has K nonzero eigenvalues, the space spanned by its eigenfunctions is precisely span(∑β₁, … , ∑β_K). Recall that our goal is to estimate the central subspace S_Y∣X, even though the effective dimension reduction directions themselves are not identifiable. For specificity, we regard these eigenfunctions of ∑⁻¹Λ associated with the K largest nonzero eigenvalues as the index functions β₁, … , β_K, unless stated otherwise.

As the covariance operator ∑ is Hilbert–Schmidt, it is not invertible when defined from H to H. Similarly to Ferré & Yao (2005), let R_∑ denote the range of ∑, and let $R_{\Sigma }^{-1}=\{b\in H:{\sum }_{j=1}^{\infty }{\alpha }_j^{-1}\langle b,{\varphi }_j\rangle {\varphi }_j,b\in R_{\Sigma }\}$. Then ∑ is a one-to-one mapping from $R_{\Sigma }^{-1}\subset H$ onto R_∑, with inverse ${\Sigma }^{-1}={\sum }_{j=1}^{\infty }{\alpha }_j^{-1}{\varphi }_j\otimes {\varphi }_j$. This is reminiscent of finding a generalized inverse of a matrix. Let ξ_j = ⟨X, ϕ_j⟩ denote the jth principal component, or generalized Fourier coefficient, of X, and assume that:

Assumption 3

${\sum }_{j=1}^{\infty }{\sum }_{l=1}^{\infty }{\alpha }_j^{-2}{\alpha }_l^{-1}{E}^2\left[E\right\{{\xi }_{j}1(Y\le \tilde{Y})\mid \tilde{Y}\left\}E\right\{{\xi }_{l}1(Y\le \tilde{Y})\mid \tilde{Y}\left\}\right]<\infty$.

Proposition 1

Under Assumptions 1–3, the eigenspace associated with the K nonnull eigenvalues of ∑⁻¹ Λ is well-defined in H.

This is a direct analogue of Theorem 4.8 in He et al. (2003) and Theorem 2.1 in Ferré & Yao (2005).

2·2. Functional cumulative slicing for sparse functional data

For the data {(X_i, Y_i) : i = 1, … , n}, independent and identically distributed as (X, Y), the predictor trajectories X_i are observed intermittently, contaminated with noise, and collected in the form of repeated measurements {(T_ij, U_ij) : i = 1, … , n; j = 1, … , N_i}, where U_ij = X_i (T_ij) + ε_ij with measurement error ε_ij that is independent and identically distributed as ε with zero mean and constant variance ${\sigma }_x^2$, and independent of all other random variables. When only a few observations are available for some or even all subjects, individual smoothing to recover X_i is infeasible and one must pool data across subjects for consistent estimation.

To estimate the functional cumulative slicing kernel Λ in (2), the key quantity is the unconditional mean $m(t,\tilde{y})=E\left\{X\right(t\left)1\right(Y\le \tilde{y}\left)\right\}$. For sparsely and irregularly observed X_i, cross-sectional estimation as used in multivariate cumulative slicing is inapplicable. To maximize the use of available data, we propose to pool the repeated measurements across subjects via a scatterplot smoother, which works in conjunction with the strategy of cumulative slicing. We use a local linear estimator $\widehat{m}(t,\tilde{y})={\widehat{a}}_0$ (Fan & Gijbels, 1996), solving

$$\underset{(a_0,a_1)}{\text{min}}\sum _{i=1}^n\sum _{j=1}^{N_i}{\left\{U_{\mathit{ij}}1\right(Y_i\le \tilde{y})-a_0-a_1(T_{\mathit{ij}}-t\left)\right\}}^2{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right),$$ (3)

where K₁ is a nonnegative and symmetric univariate kernel density and h₁ = h₁(n) is the bandwidth to control the amount of smoothing. We ignore the dependence among data from the same individual (Lin & Carroll, 2000) and use leave-one-curve-out crossvalidation to select h₁ (Rice & Silverman, 1991). Then an estimator of the kernel function Λ(s, t) is its sample moment

$$\widehat{\Lambda }(s,t)=\frac{1}{n}\sum _{i=1}^n\widehat{m}(s,Y_i)\widehat{m}(t,Y_i)w\left(Y_i\right).$$ (4)

The distinction between our method and that of Jiang et al. (2014) lies in the inverse function m(t, y) which forms the effective dimension reduction space. It is notable that (4) is a univariate smoother that includes the effective data satisfying {T_ij ∈ (t − h₁, t + h₁), Y_i ≤ y}, roughly at an order of (nh₁)^1/2 for estimating m(t, y) = E{X(t)1(Y ≤ y)} for a sparse design with E(N_n) < ∞, where N_n is the expected number of repeated observations per subject. By contrast, equation (2·4) in Jiang et al. (2014) uses the data satisfying {T_ij ∈ (t − h_t, t + h_t), Y_i ∈ (y − h_y, y + h_y)} for estimating m(t, y)= E{X(t) ∣ Y = y}, roughly at an order of (nh_th_y)^1/2. This is reflected in the faster convergence of the estimated operator $\widehat{\Lambda }$ compared with ${\widehat{\Gamma }}_e$ in Jiang et al. (2014), indicating potentially effective usage of the data based on univariate smoothing. The computation associated with a two-dimensional smoother is considerable and further exacerbated by the need to select different bandwidths h_t and h_y.

For the covariance operator ∑, following Yao et al. (2005a), denote the observed raw covariances by G_i(T_ij, T_il) = U_ijU_il. Since E{G_i(T_ij, T_il) ∣ T_ij, T_il} = cov{X(T_ij), X(T_il)} + σ²δ_jl, where δ_jl is 1 if j = l and 0 otherwise, the diagonal of the raw covariances should be removed. Solving

$$\underset{(b_0,b_1,b_2)}{\text{min}}\sum _{i=1}^n\sum _{j\ne l}^{N_i}{\left\{G_i\right(T_{\mathit{ij}},T_{\mathit{il}})-b_0-b_1(T_{\mathit{ij}}-s)-b_2(T_{\mathit{il}}-t\left)\right\}}^2{K}_2\left(\frac{T_{\mathit{ij}}-s}{h_2},\frac{T_{\mathit{il}}-t}{h_2}\right)$$ (5)

yields $\widehat{\Sigma }(s,t)={\widehat{b}}_0$, where K₂ is a nonnegative bivariate kernel density and h₂ = h₂(n) is the bandwidth chosen by leave-one-curve-out crossvalidation; see Yao et al. (2005a) for details on the implementation. Since the inverse operator ∑⁻¹ is unbounded, we regularize by projection onto a truncated subspace. To be precise, let s_n be a possibly divergent sequence and let ${\Pi }_{s_n}={\sum }_{j=1}^{s_n}{\varphi }_j\otimes {\varphi }_j$ and ${\widehat{\Pi }}_{s_n}={\sum }_{j=1}^{s_n}{\widehat{\varphi }}_j\otimes {\widehat{\varphi }}_j$ denote the orthogonal projectors onto the eigensubspaces associated with the s_n largest eigenvalues of ∑ and $\widehat{\Sigma }$, respectively. Then ∑_sn = π_sn∑π_sn and ${\widehat{\Sigma }}_{s_n}={\widehat{\Pi }}_{s_n}\widehat{\Sigma }{\widehat{\Pi }}_{s_n}$ are two sequences of finite-rank operators converging to ∑ and $\widehat{\Sigma }$ as n → ∞, with bounded inverses ${\Sigma }_{s_n}^{-1}={\sum }_{j=1}^{s_n}{\alpha }_j^{-1}{\varphi }_j\otimes {\varphi }_j$ and ${\widehat{\Sigma }}_{s_n}^{-1}={\sum }_{j=1}^{s_n}{\widehat{\alpha }}_j^{-1}{\widehat{\varphi }}_j\otimes {\widehat{\varphi }}_j$, respectively. Finally, we obtain the eigenfunctions associated with the K largest nonzero eigenvalues of ${\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }$ as the estimates of the effective dimension reduction directions ${\left\{{\widehat{\beta }}_{k,s_n}\right\}}_{k=1,\dots ,K}$.

The situation for completely observed X_i is similar to the multivariate case and considerably simpler. The quantities $m(t,\tilde{y})$ and ∑(s, t) are easily estimated by their respective samplemoments $\widehat{m}(t,\tilde{y})=n^{-1}{\sum }_{i=1}^n{X}_i\left(t\right)1(Y_i\le \tilde{y})$ and $\widehat{\Sigma }(s,t)=n^{-1}{\sum }_{i=1}^n{X}_i\left(s\right)X_i\left(t\right)$, while the estimate of Λ remains the same as (4). For densely observed X_i, individual smoothing can be used as a pre-processing step to recover smooth trajectories, and the estimation error introduced in this step can be shown to be asymptotically negligible under certain design conditions, i.e., it is equivalent to the ideal situation of the completely observed X_i (Hall et al., 2006).

For small values of $Y_i,\widehat{m}(t,Y_i)$ obtained by (3) may be unstable due to the smaller number of pooled observations in the slice. A suitable weight function w may be used to refine the estimator $\widehat{\Lambda }(s,t)$. In our numerical studies, the naive choice of w ≡ 1 performed fairly well compared to other methods. Analogous to the multivariate case, choosing an optimal w remains an open question.

Ferré & Yao (2005) avoided inverting ∑ with the claim that for a finite-rank operator Λ, range(Λ⁻¹∑) = range(∑⁻¹ Λ); however, Cook et al. (2010) showed that this requires more stringent conditions that are not easily fulfilled.

The selection of K_n and s_n deserves further study. For selecting the structural dimension K, the only relevant work to date is Li & Hsing (2010), where sequential χ² tests are used to determine K for the method of Ferré & Yao (2003). How to extend such tests to sparse functional data, if feasible at all, is worthy of further exploration. It is also important to tune the truncation parameter s_n that contributes to the variance-bias trade-off of the resulting estimator, although analytical guidance for this is not yet available.

3. Asymptotic properties

In this section we present asymptotic properties of the functional cumulative slicing kernel operator and the effective dimension reduction directions for sparse functional data. The numbers of measurements N_i and the observation times T_ij are considered to be random, to reflect a sparse and irregular design. Specifically, we make the following assumption.

Assumption 4

The N_i are independent and identically distributed as a positive discrete random variable N_n, where E(N_n) < ∞, pr(N_n ≥ 2) > 0 and pr(N_n ≤ M_n) = 1 for some constant sequence M_n that is allowed to diverge, i.e., M_n → ∞ as n → ∞. Moreover, ({T_ij, j ∈ J_i}, {U_ij, j ∈ J_i}) are independent of N_i for J_i ⊆ {1, … , N_i}.

Writing T_i = (T_i1, … , T_iNi)^T and U_i = (U_i1, … , U_iNi)^T, the data quadruplets Z_i = {T_i, U_i, Y_i, N_i} are thus independent and identically distributed. Extremely sparse designs are also covered, with only a few measurements for each subject. Other regularity conditions are standard and listed in the Appendix, including assumptions on the smoothness of themean and covariance functions of X, the distributions of the observation times, and the bandwidths and kernel functions used in the smoothing steps. Write ${\Vert A\Vert }_{\mathrm{H}}^2={\int }_{\mathcal{T}}{\int }_{\mathcal{T}}{A}^2(s,t)\mathrm{d}s\mathrm{d}t$ for $A\in L^2(\mathcal{T}\times \mathcal{T})$.

Theorem 2

Under Assumptions 1, 4 and A1–A4 in the Appendix, we have

$${\Vert \widehat{\Lambda }-\Lambda \Vert }_{\mathrm{H}}=O_{\mathrm{p}}\left(n^{-1∕2}{h}_1^{-1∕2}+h_1^2\right),{\Vert \widehat{\Sigma }-\Sigma \Vert }_{\mathrm{H}}=O_{\mathrm{p}}\left(n^{-1∕2}{h}_2^{-1}+h_2^2\right).$$

The key result here is the L² convergence of the estimated operator $\widehat{\Lambda }$, in which we exploit the projections of nonparametric U-statistics together with a decomposition of $\widehat{m}(t,\tilde{y})$ to overcome the difficulty caused by the dependence among irregularly spaced measurements. The estimator $\widehat{\Lambda }$ is obtained by averaging the smoothers $\widehat{m}(t,Y_i)$ over Y_i, which is crucial in order to achieve the univariate convergence rate for this bivariate estimator. The convergence of the covariance operator ∑ is presented for completeness, given in Theorem 2 of Yao & Müller (2010).

We are now ready to characterize the estimation of the central subspace S_Y∣X = span(β₁, … , β_K). Unlike the multivariate or finite-dimensional case, where the convergence of ${\widehat{S}}_{Y\mid X}$ follows immediately from the convergence of $\widehat{\Sigma }$ and $\widehat{\Lambda }$ given a bounded ∑⁻¹, we have to approximate ∑⁻¹ with a sequence of truncated estimates ${\widehat{\Sigma }}_{s_n}^{-1}$, which introduces additional variability and bias inherent in a functional inverse problem. Since we specifically regarded the index functions {β₁, … , β_K} as the eigenfunctions associated with the K largest eigenvalues of ∑⁻¹Λ, their estimates are thus equivalent to ${\widehat{S}}_{Y\mid X}$. For some constant C > 0, we require the eigenvalues of ∑ to satisfy the following condition:

Assumption 5

α_j > α_j+1 > 0, $E\left({\xi }_j^4\right)\le C{\alpha }_j^2$, and α_j − α_j+1 ≥ C⁻¹ j^−a−1 for j ≥ 1.

This condition on the decaying speed of the eigenvalues α_j prevents the spacings between consecutive eigenvalues from being too small, and also implies that α_j ≥ Cj^−a with a > 1 given the boundedness of ∑. Expressing the index functions as ${\beta }_k={\sum }_{j=1}^{\infty }{b}_{\mathit{kj}}{\varphi }_j$ (k = 1, … , K), we impose a decaying structure on the generalized Fourier coefficients b_kj = ⟨β_k, ϕ_j⟩:

Assumption 6

∣b_kj∣ ≤ Cj^−b for j ≥ 1 and k = 1, … , K, where b > 1/2.

In order to accurately estimate the eigenfunctions ϕ_j from $\widehat{\Sigma }$, one requires $j\le \sup \{\ell :{\alpha }_{\ell }-{\alpha }_{\ell +1}>2{\Vert \widehat{\Sigma }-\Sigma \Vert }_{\mathrm{H}}\}$, i.e., that the distance to α_j from the nearest eigenvalue does not fall below $2{\Vert \widehat{\Sigma }-\Sigma \Vert }_{\mathrm{H}}$ (Hall & Hosseini-Nasab, 2006); this implicitly places an upper bound on the truncation parameter s_n. Given Assumption 5 and Theorem 2, we provide a sufficient condition on s_n. Here we write c_1n ≍ c_2n when c_1n = O(c_2n) and c_2n = O(c_1n).

Assumption 7

As n → ∞, $s_n^{a+1}(n^{-1∕2}{h}_2^{-1}+h_2^2)\to 0$; moreover, if h₂ ≍ n^−1/6, s_n = o{n^1/(3a+3)}.

Theorem 3

Under Assumptions 1–7 and A1–A4 in the Appendix, for all k = 1, … , K,

$$\Vert {\widehat{\beta }}_{k,s_n}-{\beta }_k\Vert =O_{\mathrm{p}}\left\{s_n^{3a∕2+1}\left(n^{-1∕2}{h}_1^{-1∕2}+h_1^2\right)+s_n^{2a+3∕2}\left(n^{-1∕2}{h}_2^{-1}+h_2^2\right)+s_n^{-b+1∕2}\right\}.$$ (6)

This result associates the convergence of ${\widehat{\beta }}_{k,s_n}$ with the truncation parameter s_n and the decay rates of α_j and b_kj, indicating a bias-variance trade-off with respect to s_n. One can view s_n as a tuning parameter that is allowed to diverge slowly and which controls the resolution of the covariance estimation. Specifically, the first two terms on the right-hand side of (6) are attributed to the variability of estimating ${\Sigma }_{s_n}^{-1}\Lambda$ with ${\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }$, and the last term corresponds to the approximation bias of ${\Sigma }_{s_n}^{-1}\Lambda$. The first term of the variance is due to ${\Vert {\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\widehat{\Sigma }}_{s_n}^{-1}\Lambda {\widehat{\Sigma }}_{s_n}^{-1∕2}\Vert }_{\mathrm{H}}$ and becomes increasingly unstable with a larger truncation. The second part of the variance is due to ${\Vert ({\Sigma }_{s_n}^{-1}-{\widehat{\Sigma }}_{s_n}^{-1})\Lambda {\Sigma }_{s_n}^{-1∕2}\Vert }_{\mathrm{H}}$, and the approximation bias is determined by the smoothness of β_k; for instance, a smoother β_k with a larger b leads to a smaller bias.

4. Simulations

In this section we illustrate the performance of the proposed functional cumulative slicing method in terms of estimation and prediction. Although our proposal is link-free for estimating index functions β_k, a general index model (1) may lead to model predictions with high variability, especially given the relatively small sample sizes frequently encountered in functional data analysis. Thus we follow Chen et al. (2011) in assuming an additive structure for the link function g in (1), i.e., $Y={\beta }_0+{\sum }_{k=1}^K{g}_k(\langle {\beta }_k,X\rangle )+ϵ$. In each Monte Carlo run, a sample of n = 200 functional trajectories is generated from the process $X_i\left(t\right)={\sum }_{j=1}^{50}{\xi }_{\mathit{ij}}{\varphi }_j\left(t\right)$, where ϕ_j(t) = sin(πtj/5)/ √5 for j even and ϕ_j(t)=cos(πtj/5)/ √5 for j odd, the functional principal component scores ξ_ij are independent and identically distributed as N(0, j^−1·5), and $\mathcal{T}=[0,10]$. For the setting of sparsely observed functional data, the number of observations per subject, N_i, is chosen uniformly from {5, … , 10}, the observational times T_ij are independent and identically distributed as Un[0, 10], and the measurement error ε_ij is independent and identically distributed as N(0, 0·1). The effective dimension reduction directions are generated by ${\beta }_1\left(t\right)={\sum }_{j=1}^{50}{b}_j{\varphi }_j\left(t\right)$, where b_j = 1 for j = 1, 2, 3 and b_j = 4(j − 2)⁻³ for j = 4, … , 50, and β₂(t)=0·3^1/2(t/5 − 1), which cannot be represented with finite Fourier terms. The following single- and multiple-index models are considered:

$$\begin{array}{cc}\hfill \text{Model I}:Y& =\sin (\pi \langle {\beta }_1,X\rangle ∕4)+ϵ,\hfill \\ \hfill \text{Model II}:Y& =\text{arctan}(\pi \langle {\beta }_1,X\rangle ∕2)+ϵ,\hfill \\ \hfill \text{Model III}:Y& =\sin (\pi \langle {\beta }_1,X\rangle ∕3)+\text{exp}(\langle {\beta }_2,X\rangle ∕3)+ϵ,\hfill \\ \hfill \text{Model IV}:Y& =\text{arctan}(\pi \langle {\beta }_1,X\rangle )+\sin (\pi \langle {\beta }_2,X\rangle ∕6)∕2+ϵ,\hfill \end{array}$$

where the regression error ϵ is independent and identically distributed as N(0, 1) for all models.

We compare our method with that of Jiang et al. (2014) for sparse functional data in terms of estimation and prediction. Denote the true structural dimension by K₀. Due to the nonidentifiability of the β_k, we examine the projection operator of the effective dimension space, i.e., $P={\sum }_{k=1}^{K_0}{\beta }_k\otimes {\beta }_k$ and ${\widehat{P}}_{K,s_n}={\sum }_{k=1}^K{\widehat{\beta }}_{K,s_n}\otimes {\widehat{\beta }}_{K,s_n}$. To assess the estimation of the effective dimension reduction space, we calculate ${\Vert {\widehat{P}}_{K,s_n}-P\Vert }_{\mathrm{H}}$ as the estimation error. To assess model prediction, we estimate the link functions g_k nonparametrically by fitting a generalized additive model $Y_i={\beta }_0+{\sum }_{k=1}^K{g}_k\left(Z_{\mathit{ik}}\right)+{ϵ}_i$ (Hastie & Tibshirani, 1990), where $Z_{\mathit{ik}}=\langle {\widehat{\beta }}_{k,s_n},{\tilde{X}}_i\rangle$ with ${\tilde{X}}_i$ being the best linear unbiased predictor of X_i (Yao et al., 2005a). We generate a validation sample of size 500 in each Monte Carlo run and calculate the average of the relative prediction errors, 500⁻¹ ${\sum }_{i=1}^{500}{({\widehat{Y}}_i^{\ast }-Y_i^{\ast })}^2∕{\sigma }^2$, over different values of (K, s_n), where σ² = 1 and ${\widehat{Y}}_i^{\ast }={\widehat{\beta }}_0+{\sum }_{k=1}^K{\widehat{g}}_k\left(Z_{\mathit{ik}}^{\ast }\right)$ with $Z_{\mathit{ik}}^{\ast }=\langle {\widehat{\beta }}_{k,s_n},X_i^{\ast }\rangle$, the $X_i^{\ast }$ being the underlying trajectories in the testing sample. We report in Table 1 the average estimation and prediction errors, minimized over (K, s_n), along with their standard errors over 100 Monte Carlo repetitions. For estimation and prediction, both methods selected (K, s_n) = (1, 3) for the single-index models I and II, and selected (K, s_n) = (2, 2) for the multiple-index models III and IV. The two approaches perform comparably in this sparse setting, which could be due to the inverse covariance estimation that dominates the overall performance. Our method takes one-third of the computation time of the method of Jiang et al. (2014) for this sparse design.

Table 1.

Estimation error and relative prediction error, multiplied by 100, obtained from 100 Monte Carlo repetitions (with standard errors in parentheses) for sparse functional data

Model	Metric	FCS	IRLD	Metric	FCS	IRLD
I	Estimation error	61·1 (1·1)	61·3 (1·1)	Prediction error	17·7 (0·6)	17·9 (0·5)
II		59·3 (1·0)	59·5 (1·0)		19·6 (0·6)	19·4 (0·5)
III		63·7 (0·8)	63·9 (0·9)		18·8 (0·5)	19·5 (0·4)
IV		63·8 (0·8)	63·9 (0·9)		45·2 (1·1)	45·4 (1·1)

FCS, functional cumulative slicing; IRLD, the method of Jiang et al. (2014), where (K, s_n) is selected by minimizing the estimation and prediction errors.

We also present simulation results for dense functional data, where N_i = 50 and the T_ij are sampled independently and identically from Un[0, 10]. With (K, s_n) selected so as to minimize the estimation and prediction errors, we compare our proposal with the method of Jiang et al. (2014), functional sliced inverse regression (Ferré & Yao, 2003) using five or ten slices, and the functional index model of Chen et al. (2011). Table 2 indicates that our method slightly outperforms the method of Jiang et al. (2014), followed by the method of Chen et al. (2011), while functional sliced inverse regression (Ferré & Yao, 2003) is seen to be suboptimal. Our method takes only one-sixth of the time required by Jiang et al. (2014) for this setting.

Table 2.

Estimation error and relative prediction error, multiplied by 100, obtained from 100 Monte Carlo repetitions (with standard errors in parentheses) for dense functional data

Metric	Model	FCS	IRLD	FSIR5	FSIR10	FIND
Estimation error	I	39·2 (1·6)	45·5 (1·5)	59·4 (2·1)	61·7 (2·2)	47·1 (1·6)
	II	35·5 (1·4)	38·1 (1·3)	56·1 (1·8)	57·8 (1·9)	44·5 (1·5)
	III	59·6 (0·8)	63·1 (0·8)	72·6 (1·1)	74·1 (1·3)	63·6 (0·9)
	IV	57·2 (0·6)	59·0 (0·6)	69·3 (1·0)	68·9 (0·9)	61·0 (0·8)
Prediction error	I	11·1 (0·6)	12·7 (0·5)	17·1 (0·7)	16·7 (0·6)	16·1 (1·1)
	II	9·8 (0·5)	10·5 (0·4)	15·5 (0·7)	16·9 (1·0)	14·9 (0·8)
	III	13·5 (0·5)	15·2 (0·5)	15·8 (0·6)	16·6 (0·5)	14·7 (0·6)
	IV	19·9 (0·7)	21·9 (0·7)	31·1 (1·4)	32·2 (1·4)	24·2 (1·2)

FCS, functional cumulative slicing; IRLD, inverse regression for longitudinal data (Jiang et al., 2014); FSIR5, functional sliced inverse regression (Ferré & Yao, 2003) with five slices; FSIR10, functional sliced inverse regression (Ferré & Yao, 2003) with ten slices; FIND, functional index model (Chen et al., 2011).

5. Data application

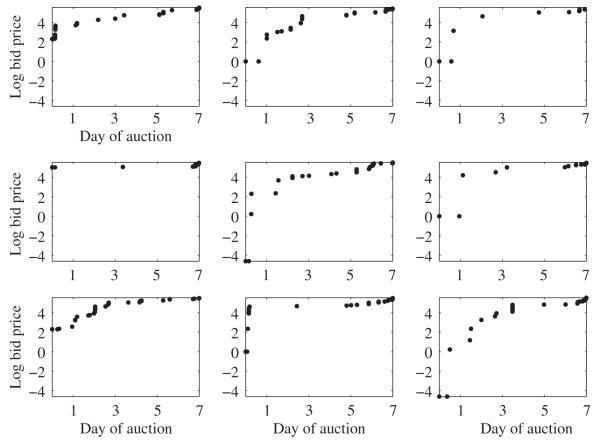
In this application, we study the relationship between the winning bid price of 156 Palm M515 PDA devices auctioned on eBay between March and May of 2003 and the bidding history over the seven-day period of each auction. Each observation from a bidding history represents a live bid, the actual price a winning bidder would pay for the device, known as the willingness-to-pay price. Further details on the bidding mechanism can be found in Liu & Müller (2009). We adopt the view that the bidding histories are independent and identically distributed realizations of a smooth underlying price process. Due to the nature of online auctions, the jth bid of the ith auction usually arrives irregularly at time T_ij, and the number of bids N_i can vary widely, from nine to 52 for this dataset. As is usual in modelling prices, we take the log-transform of the bid prices. Figure 1 shows a sample of nine randomly selected bid histories over the seven-day period of the respective auction. Typically, the bid histories are sparse until the final hours of each auction, when bid sniping occurs. At this point, snipers place their bids at the last possible moment to try to deny competing bidders the chance of placing a higher bid.

Fig. 1.

Observed bid prices over the seven-day auction period of nine randomly selected auctions, after log-transform.

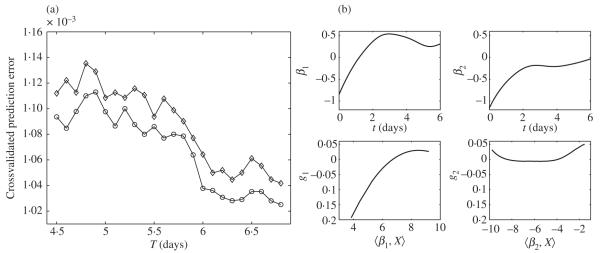
Since our main interest is in the predictive power of price histories up to time T for the winning bid prices, we consider the regression of the winning price on the history trajectory X(t) (t ∈ [0, T]), and set T = 4·5, 4·6, 4·7, … , 6·8 days. For each analysis on the domain [0, T], we select the optimal structural dimension K and the truncation parameter s_n by minimizing the average five-fold crossvalidated prediction error over 20 random partitions. Figure 2(a) shows the minimized average crossvalidated prediction errors, compared with those obtained using the method of Jiang et al. (2014). With the increasing prediction power as the bidding histories encompass more data, the proposed method appears to yield more favourable prediction across different time domains.

Fig. 2.

(a) Average five-fold crossvalidated prediction errors for functional cumulative slicing (circles) and the method of Jiang et al. (2014) (diamonds) over 20 random partitions across different time domains [0, T], for sparse eBay auction data. (b) Estimated model components for eBay auction data using functional cumulative slicing with K = 2 and s_n = 2; the upper panels show the estimated index functions, i.e., the effective dimension reduction directions, and the lower panels show the additive link functions.

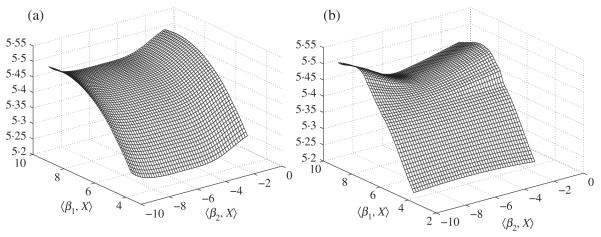
As an illustration, we present the analysis for T = 6. The estimated model components using the proposed method are shown in Fig. 2(b), with the parameters chosen as K = 2 and s_n = 2. The first index function assigns contrasting weights to bids made before and after the first day, indicating that some bidders tend to underbid at the beginning only to quickly overbid relative to the mean. The second index represents a cautious type of bidding behaviour, entering at a lower price and slowly increasing towards the average level. These features contribute most towards the prediction of the winning bid prices. Also seen are the nonlinear patterns in the estimated additive link functions. Using these estimated model components, we display in Fig. 3(a) the additive surface ${\widehat{\beta }}_0+{\widehat{g}}_1(\langle {\widehat{\beta }}_1,X\rangle )+{\widehat{g}}_2(\langle {\widehat{\beta }}_2,X\rangle )$. We also fit an unstructured index model g(⟨β₁, X⟩, ⟨β₂, X⟩), where g is nonparametrically estimated using a bivariate local linear smoother; this is shown in Fig. 3(b), and is seen to agree reasonably well with the additive regression surface.

Fig. 3.

Fitted regression surfaces for the eBay data: (a) additive; (b) unstructured.

Appendix

Regularity conditions and auxiliary lemmas

Without loss of generality, we assume that the known weight function is w(·) = 1. Write $\mathcal{T}=[a,b]$ and ${\mathcal{T}}^{\delta }=[a-\delta ,b+\delta ]$ for some δ > 0; denote a single observation time by T and a pair of observation times by (T₁, T₂)^T, with densities f(t) and f₂(s, t), respectively. Recall the unconditional mean function m(t, y) = E{X(t)1(Y ≤ y)}. The regularity conditions for the underlying moment functions and design densities are as follows, where ℓ₁ and ℓ₂ are nonnegative integers. We assume that:

Assumption A1

∂²∑/(∂s^ℓ₁∂t^ℓ₂) is continuous on ${\mathcal{T}}^{\delta }\times {\mathcal{T}}^{\delta }$ for ℓ₁ + ℓ₂ = 2, and ∂²m/∂t² is bounded and continuous with respect to $t\in \mathcal{T}$ for all $y\in \mathbb{R}$.

Assumption A2

$f_1^{\left(1\right)}\left(t\right)$ is continuous on ${\mathcal{T}}^{\delta }$ with f₁(t) > 0, and ∂f₂/(∂s^ℓ₁∂t^ℓ₂) f₂ is continuous on ${\mathcal{T}}^{\delta }\times {\mathcal{T}}^{\delta }$ for ℓ₁ + ℓ₂ = 1 with f₂(s, t) > 0.

Assumption A1 can be guaranteed by a twice-differentiable process, and Assumption A2 is standard and implies the boundedness and Lipschitz continuity of f. Recall the bandwidths h₁ and h₂ used in the smoothing steps for $\widehat{m}$ in (3) and $\widehat{\Sigma }$ in (5), respectively; we assume that:

Assumption A3

h₁ → 0, h₂ → 0, ${\mathit{nh}}_1^3∕\log n\to \infty$, and ${\mathit{nh}}_2^2\to \infty$.

We say that a bivariate kernel function K₂ is of order (ν, ℓ), where ν is a multi-index ν = (ν₁, ν₂)^T, if

$$\int \int u^{{\ell }_1}{v}^{{\ell }_2}{K}_2(u,v)\mathrm{d}u\mathrm{d}v\{\begin{array}{cc}=0,\hfill & 0\le {\ell }_1+{\ell }_2<\ell ,{\ell }_1\ne {\nu }_1,{\ell }_2\ne {\nu }_2,\hfill \\ ={(-1)}^{\mid \nu \mid }{\nu }_1!{\nu }_2!,\hfill & {\ell }_1={\nu }_1,{\ell }_2={\nu }_2,\hfill \\ \ne 0,\hfill & {\ell }_1+{\ell }_2=\ell ,\hfill \end{array}\phantom{\}}$$

where ∣ν∣ = ν₁ + ν₂ < ℓ. The univariate kernel K is said to be of order (ν, ℓ) for a univariate ν = ν₁ if this definition holds with ℓ₂ = 0 on the right-hand side, integrating only over the argument u on the left-hand side. The following standard conditions on the kernel densities are required.

Assumption A4

The kernel functions K₁ and K₂ are nonnegative with compact supports, bounded, and of order (0, 2) and {(0, 0)^T, 2}, respectively.

Lemma A1 is a mean-squared version of Theorem 1 in Martins-Filho & Yao (2006), which asserts the asymptotic equivalence of a nonparametric V-statistic to the projection of the corresponding U-statistic. Lemma A2 is a restatement of Lemma 1(b) of Martins-Filho & Yao (2007) adapted to sparse functional data.

Lemma A1

Let ${\left\{Z_i\right\}}_{i=1}^n$ be a sequence of independent and identically distributed random variables, and let u_n and v_n be U- and V-statistics with kernel function ψ_n(Z₁, … , Z_k). In addition, let ${\widehat{u}}_n=n^{-1}k{\sum }_{i=1}^n\left\{{\psi }_{1n}\right(Z_i)-{\varphi }_n\}+{\varphi }_n$, where ψ_1n(Z_i)= E{ψ_n(Z_i1, … , Z_ik) ∣ Z_i} for i ∈ {i₁, … , i_k} and ϕ_n = E{ψ_n(Z₁, … , Z_k)}. If $E\left\{{\psi }_n^2\right(Z_1,\dots ,Z_k\left)\right\}=o\left(n\right)$, then $nE\left\{{(v_n-{\widehat{u}}_n)}^2\right\}=o\left(1\right)$.

Lemma A2

Given Assumptions 1–4 and A1–A4, let

$$s_k\left(t\right)=\sum _{i=1}^n\sum _{j=1}^{M_n}\frac{1(N_i\ge j)}{{\mathit{nh}}_1}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right){\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)}^k.$$

Then ${\sup }_{t\in \mathcal{T}}{h}_1^{-1}\mid s_k\left(t\right)-E\left\{s_k\right(t\left)\right\}\mid =O_{\mathrm{p}}\left(1\right)$ for k = 0, 1, 2.

Proofs of the theorems

Proof of Theorem 1

This theorem is an analogue of Theorem 1 in Zhu et al. (2010); thus its proof is omitted.

Proof of Theorem 2

For brevity, we write M_n and N_n as M and N, respectively. Let

$$\begin{array}{cc}\hfill S_n\left(t\right)& =\sum _{i=1}^n\sum _{j=1}^M\frac{1(N_i\ge j)}{{\mathit{nh}}_{1}E\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)\left(\begin{array}{cc}\hfill 1\hfill & \hfill (T_{\mathit{ij}}-t)∕h_1\hfill \\ \hfill (T_{\mathit{ij}}-t)∕h_1\hfill & \hfill {\left\{\right(T_{\mathit{ij}}-t)∕h_1\}}^2\hfill \end{array}\right),\hfill \\ \hfill S\left(t\right)& =\left(\begin{array}{cc}\hfill f_T\left(t\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill f_T\left(t\right){\sigma }_K^2\hfill \end{array}\right),\hfill \end{array}$$

where ${\sigma }_K^2=\int u^{2}K\left(u\right)\mathrm{d}u$. The local linear estimator of $m(t,\tilde{y})$ with kernel K₁ is

$$\begin{array}{cc}\hfill \widehat{m}& (t,\tilde{y})\hfill \\ \hfill & =(1,0)S_n^{-1}\left(t\right)\left(\begin{array}{c}\hfill {\Sigma }_i{\Sigma }_{j}1(N_i\ge j){\left\{{\mathit{nh}}_{1}E\right(N\left)\right\}}^{-1}{K}_1\left\{\right(T_{\mathit{ij}}-t)∕h_1\}{U}_{\mathit{ij}}1(Y_i\le \tilde{y})\hfill \\ \hfill {\Sigma }_i{\Sigma }_{j}1(N_i\ge j){\left\{{\mathit{nh}}_{1}E\right(N\left)\right\}}^{-1}{K}_1\left\{\right(T_{\mathit{ij}}-t)∕h_1\}\left\{\right(T_{\mathit{ij}}-t)∕h_1\}{U}_{\mathit{ij}}1(Y_i\le \tilde{y})\hfill \end{array}\right).\hfill \end{array}$$

Let $U_{\mathit{ij}}^{\ast }(t,\tilde{y})=U_{\mathit{ij}}1(Y_i\le \tilde{y})-m(t,\tilde{y})-m^{\left(1\right)}(t,\tilde{y})(T_{\mathit{ij}}-t),W_n(z,t)=(1,0)S_n^{-1}\left(t\right){(1,z)}^{\mathrm{T}}{K}_1\left(z\right)$. Then

$$\widehat{m}(t,\tilde{y})-m(t,\tilde{y})=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^M\frac{1(N_i\ge j)}{h_{1}E\left(N\right)}{W}_n\left(\frac{T_{\mathit{ij}}-t}{h_1},t\right)U_{\mathit{ij}}^{\ast }(t,\tilde{y}).$$

Denote a point between T_ij and t by $t_{\mathit{ij}}^{\ast }$; by Taylor expansion, $U_{\mathit{ij}}^{\ast }\left(\tilde{y}\right)=U_{\mathit{ij}}1(Y_i\le \tilde{y})-m(T_{\mathit{ij}},\tilde{y})+m^{\left(2\right)}(t_{\mathit{ij}}^{\ast },\tilde{y}){(T_{\mathit{ij}}-t)}^2∕2$. Finally, let $e_{\mathit{ij}}\left(\tilde{y}\right)=U_{\mathit{ij}}1(Y_i\le \tilde{y})-m(T_{\mathit{ij}},\tilde{y})$. Then

$$\begin{array}{cc}\hfill \widehat{m}(t,\tilde{y})-m(t,\tilde{y})=& \frac{1}{n}\sum _{i=1}^n\sum _{j=1}^M\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)e_{\mathit{ij}}\left(\tilde{y}\right)\hfill \\ \hfill & +\frac{1}{2n}\sum _{i=1}^n\sum _{j=1}^M\frac{h_{1}1(N_i\ge j)}{E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right){\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)}^2{m}^{\left(2\right)}(t_{\mathit{ij}}^{\ast },\tilde{y})+A_n(t,\tilde{y}),\hfill \end{array}$$

where

$$A_n(t,\tilde{y})=\widehat{m}(t,\tilde{y})-m(t,\tilde{y})-{\left\{{\mathit{nh}}_{1}E\right(N\left)f_T\right(t\left)\right\}}^{-1}\sum _i\sum _{j}1(N_i\ge j)K_1\left\{\right(T_{\mathit{ij}}-t)∕h_1\}{U}_{\mathit{ij}}^{\ast }(t,\tilde{y}).$$

This allows us to write $\widehat{\Lambda }(s,t)-\Lambda (s,t)=I_{1n}(s,t)+I_{2n}(s,t)+I_{3n}(s,t)$, where

$$\begin{array}{cc}\hfill I_{1n}(s,t)& =\frac{1}{n}\sum _{k=1}^n\left[m(s,Y_k)\left\{\widehat{m}\right(t,Y_k)-m(t,Y_k\left)\right\}+m(t,Y_k)\left\{\widehat{m}\right(s,Y_k)-m(s,Y_k\left)\right\}\right],\hfill \\ \hfill I_{2n}(s,t)& =\frac{1}{n}\sum _{k=1}^n\left\{\widehat{m}\right(s,Y_k)-m(s,Y_k\left)\right\}\left\{\widehat{m}\right(t,Y_k)-m(t,Y_k\left)\right\},\hfill \\ \hfill I_{3n}(s,t)& =\frac{1}{n}\sum _{k=1}^{n}m(s,Y_k)m(t,Y_k)-\Lambda (s,t),\hfill \end{array}$$

which implies, by the Cauchy–Schwarz inequality, that ${\Vert \tilde{\Lambda }-\Lambda \Vert }_{\mathrm{H}}^2=O_{\mathrm{p}}({\Vert I_{1n}\Vert }_{\mathrm{H}}^2+{\Vert I_{2n}\Vert }_{\mathrm{H}}^2+{\Vert I_{3n}\Vert }_{\mathrm{H}}^2)$. In the rest of the proofs, we drop the subscript H and the dummy variable in integrals for brevity. Recall that we defined Z_i as the underlying data quadruplet (T_i, U_i, Y_i, N_i). Further, let ∑_(p) h_i1,…,ip denote the sum of h_i1,…,ip over the permutations of i₁, … , i_p. Finally, by Assumptions A1, A2 and A4, write $0<B_T^{\mathrm{L}}\le f\left(t\right)\le B_T^{\mathrm{U}}<\infty$ for the lower and upper bounds of the density function of T, ∣K₁(x)∣ ≤ B_K < ∞ for the bound on the kernel function K₁, and ∣∂²m/∂t²∣ ≤ B_2m < ∞ for the bound on the second partial derivative of $m(t,\tilde{y})$ with respect to t.

(a) We further decompose I_1n(s, t) into I_1n(s, t) = I_11n(s, t) + I_12n(s, t) + I_13n(s, t), where

$$\begin{array}{cc}\hfill I_{11n}(s,t)=\frac{1}{n^2}\sum _{k=1}^n\sum _{i=1}^n\sum _{j=1}^M& \{\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right)m(s,Y_k)\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(s\right)}{K}_1\left(\frac{T_{\mathit{ij}}-s}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right)m(t,Y_k)\}\hfill \\ \hfill I_{12n}(s,t)=\frac{1}{2n^2}\sum _{k=1}^n\sum _{i=1}^n\sum _{j=1}^M& \{\frac{h_{1}1(N_i\ge j)}{E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right){\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)}^2{m}^{\left(2\right)}(t_{\mathit{ij}}^{\ast },Y_k)m(s,Y_k)\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{h_{1}1(N_i\ge j)}{E\left(N\right)f_T\left(s\right)}{K}_1\left(\frac{T_{\mathit{ij}}-s}{h_1}\right){\left(\frac{T_{\mathit{ij}}-s}{h_1}\right)}^2{m}^{\left(2\right)}(t_{\mathit{ij}}^{\ast },Y_k)m(t,Y_k)\}\hfill \\ \hfill I_{13n}(s,t)=\frac{1}{n}\sum _{k=1}^n\left\{m\right(s,Y_k)A_n& (t,Y_k)+m(t,Y_k)A_n(s,Y_k)\},\hfill \end{array}$$

which we analyse individually below.

We first show that $E{\Vert I_{11n}\Vert }^2=O\left(n^{-1}{h}_1^{-1}\right)$. We write I_11n(s, t) as

$$I_{11n}(s,t)=\frac{1}{2n^2}\sum _{k=1}^n\sum _{i=1}^n\sum _{\left(2\right)}\left\{h_{\mathit{ik}}\right(s,t)+h_{\mathit{ik}}(t,s\left)\right\}=\frac{1}{2n^2}\sum _{k=1}^n\sum _{i=1}^n{\psi }_n(Z_i,Z_k;s,t)=\frac{1}{2}{v}_n(s,t),$$

where v_n(s, t) is a V-statistic with symmetric kernel ψ_n(Z_i, Z_k; s, t) and

$$h_{\mathit{ik}}(s,t)=\sum _{j=1}^M\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right)m(s,Y_k).$$

Since E{e_ij(Y_k) ∣ T_ij, Y_k} = 0, it is easy to show that E{h_ik(s, t)} = E{h_ik(t, s)} = E{h_ki(s, t)} = E{h_ki(t, s)} = 0. Thus θ_n(s, t) = E{ψ_n(Z_i, Z_k; s, t)} = 0. Additionally,

$$\begin{array}{cc}\hfill {\psi }_{1n}(Z_i;s,t)=& E\left\{{\psi }_n\right(Z_i,Z_k;s,t)\mid Z_i\}\hfill \\ \hfill =& \sum _{j=1}^M\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(t\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)E\left\{e_{\mathit{ij}}\right(Y_k\left)m\right(s,Y_k)\mid Z_i\}\hfill \\ \hfill & +\sum _{j=1}^M\frac{1(N_i\ge j)}{h_{1}E\left(N\right)f_T\left(s\right)}{K}_1\left(\frac{T_{\mathit{ij}}-s}{h_1}\right)E\left\{e_{\mathit{ij}}\right(Y_k\left)m\right(t,Y_k)\mid Z_i\}.\hfill \end{array}$$

If $E\left\{{\psi }_n^2\right(Z_i,Z_k;s,t\left)\right\}=o\left(n\right)$, Lemma A1 gives $nE{\left\{v_n\right(s,t)-{\tilde{u}}_n(s,t\left)\right\}}^2=o\left(1\right)$, where ${\tilde{u}}_n(s,t)=2n^{-1}{\sum }_{i=1}^n{\psi }_{1n}(Z_i;s,t)$ is the projection of the corresponding U-statistic. Since the projection of a U-statistic is a sum of independent and identically distributed random variables ψ_1n(Z_i; s, t), E‖I_11n‖² ≤ 2n⁻¹ ∫∫ var[E{h_ik(s, t) ∣ Z_i}] + 2n⁻¹ ∫∫ var[E{h_ik(t, s) ∣ Z_i}] + o(n⁻¹), where

$$\begin{array}{cc}\hfill \frac{2}{n}\int \int \text{var}[& E\left\{h_{\mathit{ik}}\right(s,t)\mid Z_i\}]\mathrm{d}s\mathrm{d}t\hfill \\ \hfill & \le \sum _{j=1}^M\frac{2P(N_i\ge j)}{{\mathit{nh}}_1^{2}E\left(N\right)}\int \int f_T^{-2}\left(t\right)E\left[K_1^2\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)E^2\left\{e_{\mathit{ij}}\right(Y_k\left)m\right(s,Y_k)\mid Z_i\}\right]\mathrm{d}s\mathrm{d}t\hfill \\ \hfill & =\sum _{j=1}^M\frac{2P(N_i\ge j)}{{\mathit{nh}}_{1}E\left(N\right)}\int \int \int f_T^{-2}\left(t\right)K_1^2\left(u\right)\hfill \\ \hfill & \times E_{X_i,Y_i,{\epsilon }_i}\left[E_{Y_k}^2\left\{e_{\mathit{ij}}\right(Y_k\left)m\right(s,Y_k)\mid T_{\mathit{ij}}=t+{\mathit{uh}}_1\}\right]f_T(t+{\mathit{uh}}_1)\mathrm{d}u\mathrm{d}s\mathrm{d}t\hfill \\ \hfill & \to \sum _{j=1}^M\frac{2{\Vert K_1\Vert }^{2}P(N_i\ge j)}{{\mathit{nh}}_{1}E\left(N\right)}\int \int f_T^{-1}\left(t\right)E_{X_i,Y_i,{\epsilon }_i}\left[E_{Y_k}^2\left\{e_{\mathit{ij}}\right(Y_k\left)m\right(s,Y_k)\mid T_{\mathit{ij}}=t\}\right]\hfill \\ \hfill & \le \frac{8{\Vert K_1\Vert }^2}{{\mathit{nh}}_1{B}_T^{\mathrm{L}}E\left(N\right)}E\Vert X^4\Vert +\frac{4{\Vert K_1\Vert }^2{\sigma }^2}{{\mathit{nh}}_1{B}_T^{\mathrm{L}}E\left(N\right)}E\Vert X^2\Vert =O\left(\frac{1}{{\mathit{nh}}_1}\right),\hfill \end{array}$$

where the first line follows from the Cauchy–Schwarz inequality, the second line is obtained by letting $u=h_1^{-1}(T_{\mathit{ij}}-t)$ and observing that T_ij is independent of X_i, Y_i and ε_i, and the third line follows from a variant of the dominated convergence theorem (Prakasa Rao, 1983, p. 35) that allows us to derive rates of convergence for nonparametric regression estimators. Thus $E{\Vert I_{11n}\Vert }^2=O\left(n^{-1}{h}_1^{-1}\right)$, provided that $E\left\{{\psi }_n^2\right(Z_i,Z_k;s,t\left)\right\}=o\left(n\right)$ for all i and k, which we will show below. For i ≠ k,

$$\begin{array}{cc}\hfill E\left\{{\psi }_n^2\right(Z_i,Z_k;s,t\left)\right\}=& 2E\left\{h_{\mathit{ik}}^2\right(s,t\left)\right\}+2E\left\{h_{\mathit{ik}}^2\right(t,s\left)\right\}+4E\left\{h_{\mathit{ik}}\right(s,t\left)h_{\mathit{ik}}\right(t,s\left)\right\}\hfill \\ \hfill & +4E\left\{h_{\mathit{ik}}\right(s,t\left)h_{\mathit{ki}}\right(s,t\left)\right\}+4E\left\{h_{\mathit{ik}}\right(s,t\left)h_{\mathit{ki}}\right(t,s\left)\right\}.\hfill \end{array}$$

Observe that

$$\frac{1}{n}E\left\{h_{\mathit{ik}}^2\right(s,t\left)\right\}=\sum _{j=l}^M\sum _{l=1}^M\frac{P\{N_i\ge \text{max}(j,l\left)\right\}}{E^2\left(N\right)f_T^2\left(t\right)}\times E\left\{{\left({\mathit{nh}}_1^2\right)}^{-1}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)K_1\left(\frac{T_{\mathit{il}}-t}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right)e_{\mathit{il}}\left(Y_k\right)m^2(s,Y_k)\right\}.$$

For j = l, applying the dominated convergence theorem to the expectation on the right-hand side gives $n^{-1}{h}_1^{-1}{\Vert K_1\Vert }^2{f}_T\left(t\right)E\left\{e_{\mathit{ij}}^2\right(Y_k\left)m^2\right(s,Y_k)\mid T_{\mathit{ij}}=t\}$, and hence $n^{-1}E\left\{h_{\mathit{ik}}^2\right(s,t\left)\right\}=o\left(1\right)$ by Assumption A3. For j ≠ l, a similar argument gives n⁻¹ $f_T^2\left(t\right)E\left\{e_{\mathit{ij}}\right(Y_k\left)e_{\mathit{il}}\right(Y_k\left)m^2\right(s,Y_k)\mid T_{\mathit{ij}}=T_{\mathit{il}}=t\}$. The next two terms, $E\left\{h_{\mathit{ik}}^2\right(t,s\left)\right\}$ and E{h_ik(s, t)h_ik(t, s)}, can be handled similarly, as well as E{h_ik(s, t)h_ki(s, t)} = o(n) and the case of i = k. Thus $E\left\{{\psi }_n^2\right(Z_i,Z_k;s,t\left)\right\}=o\left(n\right)$.

Using similar derivations, one can show that $E{\Vert I_{12n}\Vert }^2=O\left(h_1^4\right)+o\left(n^{-1}\right)$.

We next show that ${\Vert I_{13n}\Vert }^2=O_{\mathrm{p}}(n^{-1}{h}_1+h_1^6)$. Following Lemma 2 of Martins-Filho & Yao (2007),

$$\begin{array}{cc}\hfill \mid A_n(t,Y_k)\mid =& \mid \sum _{j=1}^M\sum _{i=1}^n\frac{1(N_i\ge j)}{{\mathit{nh}}_{1}E\left(N\right)}\left\{W_n\left(\frac{T_{\mathit{ij}}-t}{h_1},t\right)-f_T^{-1}\left(t\right)K_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)\right\}{U}_{\mathit{ij}}^{\ast }(t,Y_k)\mid \hfill \\ \hfill \le & h_1^{-1}{\left[(1,0){\left\{S_n^{-1}\right(t)-S^{-1}(t\left)\right\}}^2{(1,0)}^{\mathrm{T}}\right]}^{1∕2}\hfill \\ \hfill & \times \{\mid \sum _j\sum _i\frac{1(N_i\ge j)}{nE\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)U_{\mathit{ij}}^{\ast }(t,Y_k)\mid \phantom{\}}\hfill \\ \hfill & +\phantom{\{}\mid \sum _j\sum _i\frac{1(N_i\ge j)}{\mathit{nE}\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)U_{\mathit{ij}}^{\ast }(t,Y_k)\mid \}\hfill \\ \hfill =& h_1^{-1}{\left[(1,0){\left\{S_n^{-1}\right(t)-S^{-1}(t\left)\right\}}^2{(1,0)}^{\mathrm{T}}\right]}^{1∕2}{R}_n(t,Y_k).\hfill \end{array}$$

Lemma A2 gives ${\sup }_{t\in \mathcal{T}}{h}_1^{-1}\mid {\left[\right(1,0\left){\left\{S_n^{-1}\right(t)-S^{-1}(t\left)\right\}}^2{(1,0)}^{\mathrm{T}}\right]}^{1∕2}\mid =O_{\mathrm{p}}\left(1\right)$. Next, R_n(t, Y_k) ≤ ∣R_n1(t, Y_k)∣ + ∣R_n2(t, Y_k)∣ + ∣R_n3(t, Y_k)∣ + ∣R_n4(t, Y_k)∣, where

$$\begin{array}{cc}\hfill R_{n1}(t,Y_k)& =\sum _{j=1}^M\sum _{i=1}^n\frac{1(N_i\ge j)}{\mathit{nE}\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right),\hfill \\ \hfill R_{n2}(t,Y_k)& =\sum _{j=1}^M\sum _{i=1}^n\frac{h_1^{2}1(N_i\ge j)}{2nE\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right){\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)}^2{m}^{\left(2\right)}(t_{\mathit{ij}}^{\ast },Y_k),\hfill \\ \hfill R_{n3}(t,Y_k)& =\sum _{j=1}^M\sum _{i=1}^n\frac{1(N_i\ge j)}{nE\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)e_{\mathit{ij}}\left(Y_k\right),\hfill \\ \hfill R_{n4}(t,Y_k)& =\sum _{j=1}^M\sum _{i=1}^n\frac{h_1^{2}1(N_i\ge j)}{2nE\left(N\right)}{K}_1\left(\frac{T_{\mathit{ij}}-t}{h_1}\right){\left(\frac{T_{\mathit{ij}}-t}{h_1}\right)}^3{m}^{\left(2\right)}(t_{\mathit{ij}}^{\ast },Y_k).\hfill \end{array}$$

Thus n⁻¹ ∑_k m(s, Y_k) R_n1(t, Y_k) = h₁f_T(t)I_11n(s, t) leads to ‖h₁ f_T I_11n‖² = O_p(n⁻¹h₁), and n⁻¹ ∑_k m(s, Y_k)R_n2(t, Y_k) = h₁ f_T(t)I_12n(s, t) leads to ${\Vert h_1{f}_T{I}_{12n}\Vert }^2=O_{\mathrm{p}}\left(h_1^6\right)$. It follows similarly that the third and fourth terms are O_p(n⁻¹h₁) and $O_{\mathrm{p}}\left(h_1^6\right)$, respectively. Hence, ${\Vert I_{13n}\Vert }^2=O_{\mathrm{p}}(n^{-1}{h}_1+h_1^6)$. Combining the previous results gives ${\Vert I_{1n}\Vert }^2=O_{\mathrm{p}}\{{\left({\mathit{nh}}_1\right)}^{-1}+h_1^4\}$.

(b) These terms are of higher order and are omitted for brevity.

(c) By the law of large numbers, ${\Vert n^{-1}{\sum }_{i=1}^{n}m(\cdot ,Y_i)m(\cdot ,Y_i)-\Lambda \Vert }^2=O_{\mathrm{p}}\left(n^{-1}\right)$.

Combining the above results leads to ${\Vert \widehat{\Lambda }-\Lambda \Vert }^2=O_{\mathrm{p}}(n^{-1}{h}_1^{-1}+h_1^4)$.

Proof of Theorem 3

To facilitate the theoretical derivation, for each k = 1, … , K let η_k = ∑^1/2 β_k and ${\widehat{\eta }}_{k,s_n}={\widehat{\Sigma }}_{s_n}^{1∕2}{\widehat{\beta }}_{k,s_n}$ be, respectively, the normalized eigenvectors of the equations ∑⁻¹ Λ ∑^−1/2η_k = λ_kβ_k and ${\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}{\widehat{\eta }}_{k,s_n}={\widehat{\lambda }}_{k,s_n}{\widehat{\beta }}_{k,s_n}$. Then

$$\begin{array}{cc}\hfill \Vert {\widehat{\beta }}_{k,s_n}-{\beta }_k\Vert & \le \Vert {\widehat{\lambda }}_{k,s_n}^{-1}{\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\lambda }_k^{-1}{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert +{\lambda }_k^{-1}\Vert {\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert \Vert {\widehat{\eta }}_{k,s_n}-{\eta }_k\Vert \hfill \\ \hfill & \le {\widehat{\lambda }}_{k,s_n}^{-1}\Vert {\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert +\Vert {\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert \left(\mid {\widehat{\lambda }}_{k,s_n}^{-1}-{\lambda }_k^{-1}\mid +{\lambda }_k^{-1}\Vert {\widehat{\eta }}_{k,s_n}-{\eta }_k\Vert \right),\hfill \end{array}$$

using the fact that ${\widehat{\lambda }}_{k,s_n}^{-1}\le {\lambda }_k^{-1}+\mid {\widehat{\lambda }}_{k,s_n}^{-1}-{\lambda }_k^{-1}\mid$. Applying standard theory for self-adjoint compact operators (Bosq, 2000) gives

$$\begin{array}{cc}\hfill \mid {\widehat{\lambda }}_{k,s_n}-{\lambda }_k\mid & \le \Vert {\widehat{\Sigma }}_{s_n}^{-1∕2}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }^{-1∕2}\Lambda {\Sigma }^{-1∕2}\Vert ,\hfill \\ \hfill \Vert {\widehat{\eta }}_{k,s_n}-{\eta }_k\Vert & \le C\Vert {\widehat{\Sigma }}_{s_n}^{-1∕2}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }^{-1∕2}\Lambda {\Sigma }^{-1∕2}\Vert (k=1,\dots ,K),\hfill \end{array}$$

where C > 0 is a generic positive constant. Thus ${{\widehat{\beta }}_{k,s_n}-{\beta }_k\Vert }^2=O_{\mathrm{p}}(I_{1n}+I_{2n})$, where

$$I_{1n}={\Vert {\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert }^2,I_{2n}={\Vert {\widehat{\Sigma }}_{s_n}^{-1∕2}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }^{-1∕2}\Lambda {\Sigma }^{-1∕2}\Vert }^2.$$

It suffices to show that $I_{1n}=O_{\mathrm{p}}\left\{s_n^{3a+2}\right(n^{-1∕2}{h}_1^{-1∕2}+h_1^2)+s_n^{(4a+3)}(n^{-1∕2}{h}_2^{-1}+h_2^2)+s_n^{-2b+1}\}$. The calculations for I_2n are similar and yield that I_2n = o_p(I_1n).

Observe that I_1n ≤ 3I_11n + 3I_12n + 3I_13n, where $I_{11n}={\Vert {\Sigma }_{s_n}^{-1}\Lambda {\Sigma }_{s_n}^{-1∕2}-{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert }^2,I_{12n}={\Vert {\widehat{\Sigma }}_{s_n}^{-1}\Lambda {\widehat{\Sigma }}_{s_n}^{-1∕2}-{\Sigma }_{s_n}^{-1}\Lambda {\Sigma }_{s_n}^{-1∕2}\Vert }^2$ and $I_{13n}={\Vert {\widehat{\Sigma }}_{s_n}^{-1}\widehat{\Lambda }{\widehat{\Sigma }}_{s_n}^{-1∕2}-{\widehat{\Sigma }}_{s_n}^{-1}\Lambda {\widehat{\Sigma }}_{s_n}^{-1∕2}\Vert }^2$. Recall that ${\Pi }_{s_n}={\sum }_{j=1}^{s_n}{\varphi }_j\otimes {\varphi }_j$ is the orthogonal projector onto the eigenspace associated with the s_n largest eigenvalues of ∑. Let I denote the identity operator and ${\Pi }_{s_n}^{\perp }=I-{\Pi }_{s_n}$ the operator perpendicular to π_sn, i.e., ${\Pi }_{s_n}^{\perp }$ is the orthogonal projector onto the eigenspace associated with eigenvalues of ∑ that are less than α_sn. Thus ${\Sigma }_{s_n}^{-1}\Lambda {\Sigma }_{s_n}^{-1∕2}={\Pi }_{s_n}{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}{\Pi }_{s_n}$ allows us to write $I_{11n}\le \Vert {\Pi }_{s_n}^{\perp }{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert +\Vert {\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}{\Pi }_{s_n}^{\perp }\Vert$. Since ∑⁻¹Λ ∑^−1/2η_k = λ_kβ_k,

$$\begin{array}{cc}\hfill {\Vert {\Pi }_{s_n}^{\perp }{\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}\Vert }^2& \le \sum _{k=1}^K{\lambda }_k^2{\Vert \sum _{i>s_n}\sum _{j=1}^{\infty }{b}_{kj}\langle {\varphi }_i,{\varphi }_j\rangle {\varphi }_i\Vert }^2\le \sum _{k=1}^K{\lambda }_k^2\sum _{i>s_n}{b}_{ki}^2\hfill \\ \hfill & \le C\sum _{k=1}^K{\lambda }_k^2\sum _{i>s_n}{i}^{-2b}=O\left(s_n^{-2b+1}\right);\hfill \end{array}$$

similarly, ${\Vert {\Sigma }^{-1}\Lambda {\Sigma }^{-1∕2}{\Pi }_{s_n}^{\perp }\Vert }^2=O\left(s_n^{-2b+1}\right)$.

We decompose I_12n as I_12n ≤ 3I_121n + 3I_122n + 3I_123n, where $I_{121n}={\Vert ({\Sigma }_{s_n}^{-1}-{\widehat{\Sigma }}_{s_n}^{-1})\Lambda {\Sigma }_{s_n}^{-1∕2}\Vert }^2,I_{122n}={\Vert \left({\Sigma }_{s_n}^{-1}\Lambda \right({\Sigma }_{s_n}^{-1∕2}-{\widehat{\Sigma }}_{s_n}^{-1∕2})\Vert }^2$ and $I_{123n}={\Vert ({\Sigma }_{s_n}^{-1}-{\widehat{\Sigma }}_{s_n}^{-1})\Lambda ({\Sigma }_{s_n}^{-1∕2}-{\widehat{\Sigma }}_{s_n}^{-1∕2})\Vert }^2$. Note that I_121n ≤ 6‖Λ∑^−1/2π_sn‖²(I_1211n + I_1212n), where

$$I_{1211n}={\Vert \sum _{j=1}^{s_n}({\alpha }_j^{-1}-{\widehat{\alpha }}_j^{-1}){\widehat{\varphi }}_j\otimes {\widehat{\varphi }}_j\Vert }^2,I_{1212n}={\Vert \sum _{j=1}^{s_n}{\alpha }_j^{-1}({\widehat{\varphi }}_j\otimes {\widehat{\varphi }}_j-{\varphi }_j\otimes {\varphi }_j)\Vert }^2.$$

Under Assumption 7, for all 1 ≤ j ≤ s_n, $\mid {\widehat{\alpha }}_j-{\alpha }_j\mid \le \Vert \widehat{\Sigma }-\Sigma \Vert \le 2^{-1}({\alpha }_j-{\alpha }_{j+1})$ implies that ${\widehat{\alpha }}_j\ge 2^{-1}({\alpha }_j+{\alpha }_{j+1})\ge C^{-1}{j}^{-a}$, i.e., ${\widehat{\alpha }}_j^{-1}\le C{j}^a$ for some C > 0. Thus

$$I_{1211n}\le \sum _{j=1}^{s_n}{({\widehat{\alpha }}_j-{\alpha }_j)}^2{\left({\alpha }_j{\widehat{\alpha }}_j\right)}^{-2}\le C{\Vert \widehat{\Sigma }-\Sigma \Vert }^2\sum _{j=1}^{s_n}{j}^{4a}=O_{\mathrm{p}}\left\{s_n^{4a+1}\right(n^{-1}{h}_2^{-2}+h_2^4\left)\right\}.$$

For I_1212n, using the fact that $\Vert {\widehat{\varphi }}_j-{\varphi }_j\Vert \le 2\surd 2{\delta }_j^{-1}\Vert \widehat{\Sigma }-\Sigma \Vert$ (Bosq, 2000), where δ₁ = α₁ − α₂ and δ_j = min_2≤ℓ≤j (α_ℓ−1 − α_ℓ, α_ℓ − α_ℓ+1) for j > 1, we have that ${\delta }_j^{-1}\le j^{a+1}$ and

$$I_{1212n}\le 2\sum _{j=1}^{s_n}{\alpha }_j^{-2}{\Vert {\widehat{\varphi }}_j-{\varphi }_j\Vert }^2\le C{\Vert \widehat{\Sigma }-\Sigma \Vert }^2\sum _{j=1}^{s_n}{j}^{4a+2}=O_{\mathrm{p}}\left\{s_n^{4a+3}\right(n^{-1}{h}_2^{-2}+h_2^4\left)\right\}.$$

Using Λ∑^−1/2η_k = λ_k∑β_k, we obtain ${\Vert \Lambda {\Sigma }^{-1∕2}{\Pi }_{s_n}\Vert }^2\le {\sum }_{k=1}^K{\lambda }_k^2{\Vert {\sum }_{i=1}^{s_n}{\alpha }_i{\sum }_{j=1}^{\infty }{b}_{\mathit{kj}}\langle {\varphi }_i,{\varphi }_j\rangle {\varphi }_i\Vert }^2\le {\sum }_{k=1}^K{\lambda }_k^2{\sum }_{i=1}^{s_n}{\alpha }_i^2{b}_{\mathit{ki}}^2<\infty$. Thus $I_{121n}=O_{\mathrm{p}}\left\{s_n^{4a+3}\right(n^{-1}{h}_2^{-2}+h_2^4\left)\right\}$. Using decompositions similar to the one for I_121n, both I_122n and I_123n can be shown to be $o_p\left\{s_n^{4a+3}\right(n^{-1}{h}_2^{-2}+h_2^4\left)\right\}$. This leads to $I_{12n}=O_{\mathrm{p}}\left\{s_n^{4a+3}\right(n^{-1}{h}_2^{-2}+h_2^4\left)\right\}$.

Note that $I_{13n}\le {\Vert {\widehat{\Sigma }}_{s_n}^{-1}\Vert }^2{\Vert \widehat{\Lambda }-\Lambda \Vert }^2{\Vert {\widehat{\Sigma }}_{s_n}^{-1∕2}\Vert }^2$, where ${\Vert {\widehat{\Sigma }}_{s_n}^{-1}\Vert }^2\le {\sum }_{j=1}^{s_n}{\widehat{\alpha }}_j^{-2}\le C{\sum }_{j=1}^{s_n}{j}^{2a}=O_{\mathrm{p}}\left(s_n^{2a+1}\right)$ and, similarly, ${\Vert {\widehat{\Sigma }}_{s_n}^{-1∕2}\Vert }^2=O_{\mathrm{p}}\left(s_n^{a+1}\right)$. From Theorem 2, we have $I_{13n}=O_{\mathrm{p}}\left\{s_n^{3a+2}\right(n^{-1}{h}_1^{-1}+h_1^4\left)\right\}$. Combining the above results leads to (6).