Topological RPdBi half-Heusler semimetals: A new family of noncentrosymmetric magnetic superconductors

Tunable superconductivity and magnetism in noncentrosymmetric RPdBi provide a new route to exotic topological excitations.

Abstract

We report superconductivity and magnetism in a new family of topological semimetals, the ternary half-Heusler compound RPdBi (R: rare earth). In this series, tuning of the rare earth f-electron component allows for simultaneous control of both lattice density via lanthanide contraction and the strength of magnetic interaction via de Gennes scaling, allowing for a unique tuning of the normal-state band inversion strength, superconducting pairing, and magnetically ordered ground states. Antiferromagnetism with ordering vector (½,½,½) occurs below a Néel temperature that scales with de Gennes factor dG, whereas a superconducting transition is simultaneously supressed with increasing dG. With superconductivity appearing in a system with noncentrosymmetric crystallographic symmetry, the possibility of spin-triplet Cooper pairing with nontrivial topology analogous to that predicted for the normal-state electronic structure provides a unique and rich opportunity to realize both predicted and new exotic excitations in topological materials.

Topological insulators (TIs) have recently caused a paradigm shift in the traditional classification of quantum phases of matter (1, 2). Compared to condensed-matter states well understood using the concept of spontaneous symmetry breaking, the lack of symmetry breaking in insulators with topological order, including the integer quantum Hall states, is now understood to arise from the presence of nontrivial topological components and to lead to gapless boundary modes with chirality. In the so-called Z2 two-dimensional (2D) and 3D systems, these topologically protected metallic states carry extreme interest because of their potential for realizing new technologies in spintronics and quantum computation. Combined with symmetry-breaking ordered states, TI states can give rise to unusual collective modes, such as Majorana fermions (3) with superconductivity and axions (4) with magnetic order occurring in the topologically nontrivial materials. Besides the exotic collective modes, antiferromagnetism breaks time reversal and translational symmetries but preserves the combination of both symmetries, leading to a different type of TI, the antiferromagnetic TI (5). Despite extensive studies on bismuth-based TI materials (1), only a few materials that may harbor an interplay of symmetry-breaking and topological phases have been identified (6–8).

The large family of ternary half-Heusler compounds (9) is a prime candidate for combining topological and symmetry-breaking phases to explore new collective behavior. These compounds straddle the border between topologically trivial and nontrivial electronic structures because of a strong tuning of the s- and p-like band inversion via atomic number, lattice density, and spin-orbit coupling strength (10–12). In addition, the stabilization of magnetic and superconducting ground states in these materials allows for a controlled interplay of symmetry and topology to be put to use. In particular, the rare earth–based RPdBi half-Heusler series is ideal for this purpose. Antiferromagnetic long-range order has been observed in polycrystalline RPdBi at low temperatures (13), promising emergence of antiferromagnetic topological states (5, 14). Moreover, in relation to the discovery of superconductivity in the related platinum-based compounds YPtBi (15) and LuPtBi (16), recent reports of superconductivity in ErPdBi (17) and LuPdBi (18) suggest that this family hosts an interesting interplay of ground states.

Here, we report a systematic study of superconductivity and magnetism in single crystals of the half-Heusler series RPdBi (R = Y, Sm, Gd, Tb, Dy, Ho, Er, Tm, and Lu) grown using a Bi self-flux technique as described in Methods. We find that tuning the de Gennes factor dG scales local-moment Néel order while simultaneously suppressing the superconducting transition temperature T_c. Aspects of the superconducting state, including a possible spin-triplet pairing symmetry, confirm RPdBi as a new noncentrosymmetric magnetic superconductor family. Overall, the combination of magnetism and superconductivity, together with the lack of crystallographic inversion symmetry and tunable band inversion strength in this system, provides a promising route to achieving new quantum states of matter.

The MgAgAs-type crystallographic unit cell of the RPdBi family is readily tuned in size by using the lanthanide contraction effect, whereby the cubic lattice parameter is continuously reduced as heavier R elements are substituted. The lattice spacing has been predicted as a key parameter that divides the RPdBi system into trivial and nontrivial materials at the critical value of ~6.62 Å, where the calculated band inversion strength ΔE = E_Γ8 − E_Γ6 crosses from positive to negative (E_Γi is the energy of the bands with Γ_i symmetry, with Γ₆ twofold and Γ₈ fourfold degenerate with total momentum J = 3/2) (12). As shown in Fig. 1, whereas Sm, Y, Dy, Tb, and Gd are expected to have ΔE <0 and therefore trivial band topologies, the Ho, Er, Tm, and Lu systems with ΔE >0 are expected to be nontrivial, with increasing band inversion strength as the lattice constant is further reduced.

Fig. 1. Evolution of lattice constants as a function of rare earth species R in RPdBi determined by x-ray diffraction, showing the lanthanide contraction effect on the half-Heusler cubic ($\mathit{F}\overline{4}3\mathit{m}$) crystal structure (inset).

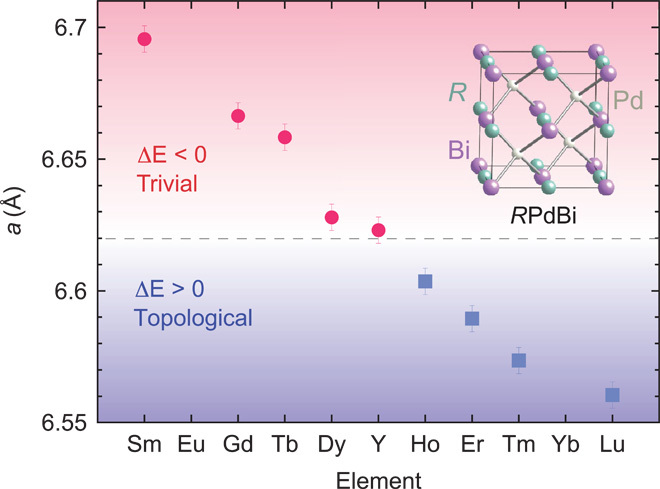
The dashed line indicates the critical lattice constant a_c = 6.62 Å demarcation between positive and negative electronic band inversion strength ΔE = E_Γ8 − E_Γ6 (12), and, therefore, between RPdBi members with predicted topologically nontrivial (squares) and trivial (circles) band structure.

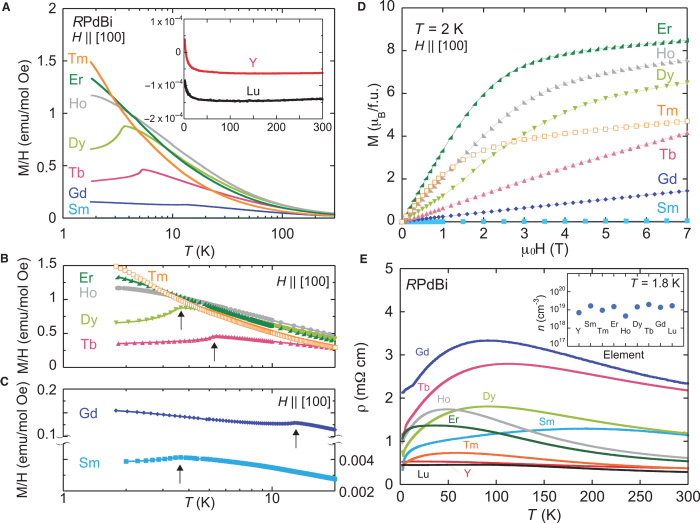
At the same time, substitution of different rare earth species allows fine tuning of the magnetic properties, which are rather simple and well described by the presence (or absence) of localized 4f rare earth moments. As shown in Fig. 2A, typical Curie-Weiss behavior is observed in the magnetic susceptibility, indicating that the effective moments in the magnetic compounds are close to those expected for free R³⁺ ion moments (see table S1), with the exception of R = Sm, where the J-multiplet lying just above the ground state is very close in energy. The field dependence of the magnetization as shown in Fig.2D saturates at high field, which also indicates that the f-electrons are well localized. In contrast, the nonmagnetic members YPdBi and LuPdBi exhibit diamagnetic behavior as shown in the inset of Fig.2A.

Fig. 2. Physical properties of RPdBi single crystals, focusing on evolution of magnetic order with rare earth species R = Sm, Gd, Tb, Dy, Ho, Er, and Tm.

(A) Magnetic susceptibility M/H of RPdBi members with magnetic R species, showing Curie-Weiss behavior and clear, abrupt decreases in M/H denoting antiferromagnetic (AFM) transitions. Inset: Data for nonmagnetic YPdBi and LuPdBi, exhibiting diamagnetic behavior. (B and C) Low-temperature zoom of M/H for Tb, Dy, Ho, Er, and Tm (B) and for Gd and Sm (C), with arrows indicating Néel temperatures. (Note: 1 emu/mol Oe = 4π × 10⁻⁶ m³/mol.) (D) Magnetization M at 2 K for magnetic rare earth members R = Sm, Gd, Tb, Dy, Ho, Er, and Tm. f.u., formula unit. (E) Electrical resistivity of all members in the temperature range of 2 to 300 K, showing nonmonotonic temperature dependence in all species. Inset: Charge carrier density n_H obtained from single-band analysis of Hall effect measurements performed at 1.8 K (see text). The sign of all carriers is positive.

The R local-moment sublattice leads to long-range antiferromagnetic order in R = Sm, Gd, Tb, and Dy, as evidenced by abrupt drops in susceptibility shown in Fig. 2 (B and C), with transition temperatures consistent with previous work on polycrystalline samples (13). Low-temperature specific heat measurements confirm the thermodynamic antiferromagnetic transitions (see the Supplementary Materials) and reveal low-temperature ordering in HoPdBi and ErPdBi at 1.9 and 1.0 K, respectively (13, 17). We also observe a precursor of magnetic order in TmPdBi, as evidenced by a huge divergence of heat capacity reaching ~10 J/mol K² at the lowest measured temperatures.

The ordered magnetic structure for DyPdBi was determined by neutron diffraction measurements on a sample of randomly oriented crushed single crystals and clearly reveals magnetic Bragg peaks corresponding to half-integral reflections of a face-centered cubic (fcc) type II antiferromagnet as shown in Fig. 3A. This magnetic structure is characterized by a doubling of the simple fcc Dy unit cell along all three crystallographic directions as illustrated in the inset of Fig.3B, suggesting a similar structure proposed for topological antiferromagnetism (5, 14). We note that for R = Tb and Ho, we obtain the same spin structure as DyPdBi. A mean-field fit of the temperature dependence of the intensity of the Q = (½,½,½) Bragg peak (Fig. 3B) results in T_N = 4.9 K for single crystal TbPdBi, in agreement with the magnetic, transport, and thermodynamic measurements.

Fig. 3. Characterization of antiferromagnetic order with elastic neutron diffraction.

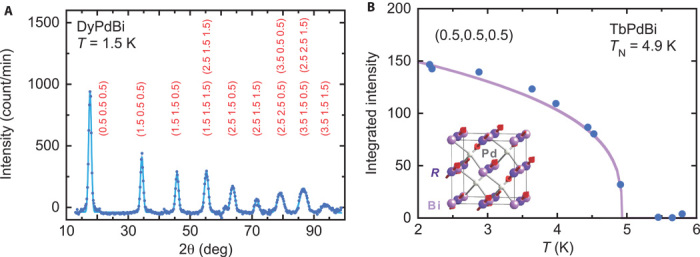
(A) Low-temperature magnetic diffraction pattern of DyPdBi obtained by subtracting 18-K data from 1.5-K data. Labels indicate the series of half-integer antiferromagnetic peaks. deg, degree. (B) Antiferromagnetic order parameter of single-crystal TbPdBi obtained from the intensity of the (0.5,0.5,0.5) magnetic Bragg peak. The solid curve is a mean-field fit to the data, and the inset presents a schematic of the antiferromagnetic spin structure.

Charge transport measurements at higher temperatures reveal the normal-state band structure and magnetic nature of RPdBi. Figure 2E presents the semimetallic nature of the temperature dependence of the resistivity ρ(T) for RPdBi, whereas the Hall effect carrier density n at 1.8 K is very small (n ~10¹⁹ cm⁻³) and consistent with band calculations (10–12). For R = Sm, Gd, Tb, Dy, and Ho, an anomaly associated with magnetic order is observed in the resistivity at temperatures consistent with the thermodynamic measurements. Except for R = Gd, all heavy R members of the RPdBi series undergo a superconducting transition at low temperatures, as evidenced in the low-temperature resistivity measurements presented in Fig. 4A. We observe a rather high transition temperature (~1.6 K) for nonmagnetic YPdBi and LuPdBi, whereas no trace of superconductivity is found for GdPdBi down to 20 mK. As plotted in Fig. 4C, we confirm a large diamagnetic screening in AC susceptibility measurements that onsets below T_c , consistent with the resistive transition temperature and with an estimated full volume fraction of the sample as determined by calibrations using aluminum. The large but nonsaturating diamagnetic screening has also been observed in other superconducting half-Heusler compounds (15–17), attributed to the extremely long penetration depth (19). Note that very small traces of an impurity superconducting phase with T_c ~1.5 K but very different magnetic properties are mostly removed with proper crystal synthesis methods (see the Supplementary Materials for details).

Fig. 4. Superconducting state properties of RPdBi single crystals.

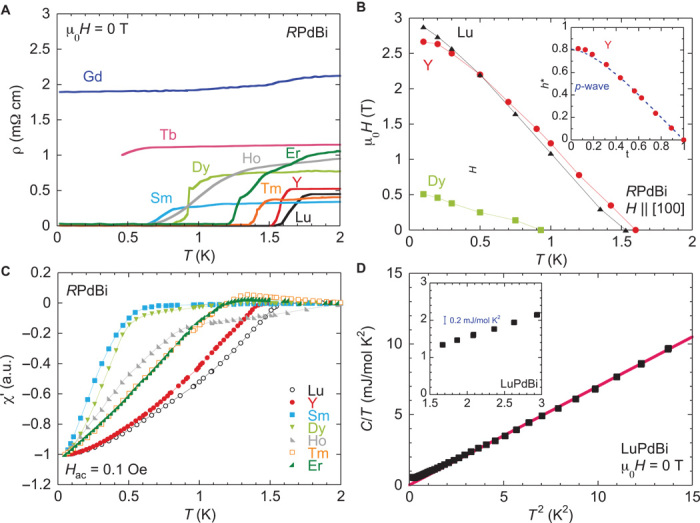
(A) Resistivity of RPdBi at temperatures below 2 K, showing superconducting transitions for each compound. (B) Temperature dependence of upper critical field H_c2 obtained from the resistive transition for YPdBi, LuPdBi, and DyPdBi. Inset: Normalized upper critical field h^* = H_c2/T_cdH_c2/dT|_{T = Tc} as a function of normalized temperature t = T/T_c for YPdBi, with the dashed line indicating the expectation for a polar p-wave state. (C) AC susceptibility of single-crystal samples of RPdBi. The magnitude of the screening below the superconducting transition is comparable to a test sample of superconducting aluminum, confirming bulk diamagnetic screening (see text). a.u., arbitrary unit. (D) Heat capacity C/T as a function of T² for LuPdBi. The solid line is a fit to the data using C/T = γ + βT², where γT is the electronic and βT³ is the phonon contribution to the specific heat. Inset: Enlarged view of the C/T versus T² near T_c ~1.5 K, with estimated size of jump at the superconducting transition based on BCS expectation shown as an error bar (see text).

Specific heat measurements for nonmagnetic LuPdBi and YPdBi do not reveal a discernible signature of T_c within the present experimental resolution, as shown in Fig. 4D. With strong evidence for the bulk nature of superconductivity in the half-Heuslers (15–18), the absence of a jump in C(T) can presumably be explained by the peculiar superconductivity in this system: low carrier density, noncentrosymmetric structure, and coexistence of magnetism and superconductivity. The measured electronic component γ_n, obtained from fits to C/T = γ_n + βT², where βT² is a phonon contribution, is found to be 0.0 ± 0.5 mJ/mol K² (Fig. 4D), attributed to the low carrier density and very small effective mass (15). An estimate of γ_n based on the carrier density n = 10¹⁹ cm⁻³ and effective mass ~0.09m_e, where m_e is electron mass (20), and assuming ΔC/γ_nT_c = 1.43 for the Bardeen-Cooper-Schrieffer (BCS) weak coupling limit, yields an expected jump at T_c of <0.2 mJ/mol K beyond the resolution of our experiment (inset of Fig. 4D).

Because noncentrosymmetry requires a mixing of singlet and triplet pairing states (21), the absence of a jump in C(T_c) may actually be considered evidence for the presence of a dominant triplet component, in analogy with the tiny heat capacity jump measured in the A₁ phase of ³He (22). This is corroborated by the behavior of the upper critical field H_c2, which suggests an unusual superconducting state. We plot H_c2 for YPdBi, LuPdBi, and DyPdBi obtained from resistive transitions as a function of T in Fig. 4B. H_c2 linearly increases with decreasing temperature down to ~T_c/5, in contrast with H_c2(T) in conventional type II superconductors determined by orbital depairing as described by the Werthamer-Helfand-Hohenberg theory, H_c2(0) = −αT_cdH_c2/dT|_{T = Tc}, where α is 0.69 in the dirty limit and 0.74 in the clean limit (23). However, H_c2(0) values of 2.7 T (α = 0.82), 2.9 T (α = 0.91), and 0.52 T (α = 0.93) for Y, Lu, and Dy, respectively, all exceed the conventional orbital limit, which can occur for several reasons. Multiband effects and Fermi surface topology (24–26) can give rise to an exceedingly large orbital depairing field, but this is not supported by the calculated (10–12) and observed (15, 27) simple band structures. As previously shown for YPtBi (15), the observed H_c2 curve is close in form to that of a polar p-wave (triplet) state (28) as plotted in the inset of Fig. 4C. Together with the superconductivity in the clean limit ℓ > ξ obtained from experimental parameters ℓ = 70 nm and ξ = 10 nm, the quasilinear H_c2 is suggestive of the finite triplet contribution to the pairing state because of the noncentrosymmetric nature. We note that H_c2(0) is comparable to the Pauli paramagnetic limiting field H_p (Tesla) = 1.84T_c (K) obtained from a simple estimation within the weak-coupling BCS theory with Δ = 1.76k_BT_c.

As shown in the phase diagram (Fig. 5), the evolution of magnetism and superconductivity as a function of local-moment exchange strength reveals a well-behaved tradeoff and coexistence from one ground state to the other. We plot T_c and T_N as a function of the de Gennes factor dG = (g_J − 1)²J (J + 1), where g_J is the Landé factor and J is the total angular momentum of the R³⁺ ion Hund’s rule ground state. T_N scales well with dG for RPdBi, which indicates that the coupling between the conduction electrons and the local magnetic moments giving rise to the long-range magnetic order is due to the RKKY (Ruderman-Kittel-Kasuya-Yosida) interaction. T_c is suppressed almost linearly with dG, which indicates that magnetic rare earth R³⁺ ions are a source of magnetic pair breaking (29). The superconductivity found in RPdBi has several peculiar features that may give rise to novel phenomena involving topological surface states or excitations. First, these superconductors derive from a band structure with extremely low carrier density of ~10¹⁹ cm⁻³, rivaled only by SrTiO_3−x (30) and FeSe (31). In the superconducting state, this, together with a very light effective mass of 0.09m_e (20), leads to an extreme long penetration depth λ ~1 μm; this situation can give rise to anomalous vortex states and also proximity effect to the topological surface states if present. More fundamentally, the low carrier density translates to a very small Fermi energy (about several hundred kelvin), putting the usual Frohlich approximation (T_F ≫ Θ_D), and thus expected BCS superconducting properties, into question. This breakdown of the Frohlich approximation may explain the anomalous estimate of Δ = ħυ_F/πξ ~210 K, obtained from experimental parameters ξ = 10 nm and υ_F = 8.6 × 10⁵ m/s.

Fig. 5. Phase diagram of RPdBi series, indicating evolution of superconducting and antiferromagnetic ground states as a function of de Gennes factor dG = (g_J − 1)²J(J + 1).

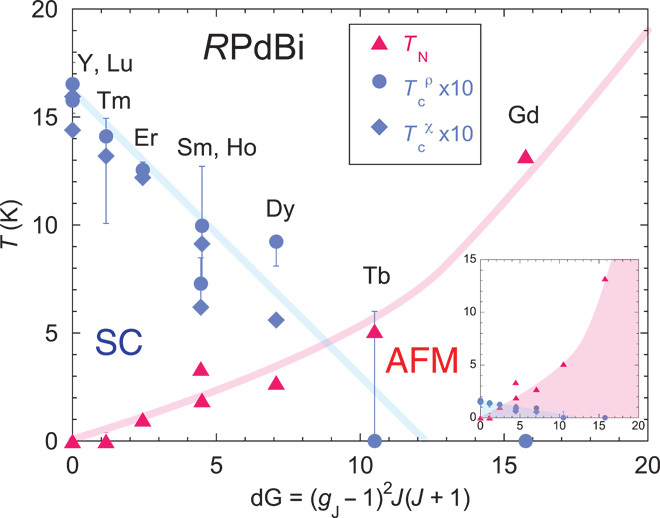
The superconducting transition T_c (blue) is obtained from the midpoint of the resistive transition (circles; upper and lower error bars indicate onset and zero resistance) and the onset of diamagnetism in AC susceptibility (diamonds), and Néel temperature T_N (red triangles) is obtained from DC magnetic susceptibility. The plotted T_c is scaled by a factor of 10, and solid lines are guides to the eye. Note that T_c (T_N) for SmPdBi is lower (higher) than that for HoPdBi. Inset: Unscaled T_c and T_N as a function of dG.

Second, noncentrosymmetry of the half-Heusler crystal structure forces an automatic mixing of singlet and triplet pairing states in the superconductivity, resulting in not only complex superconducting gap functions but also very unique excitations involved in the Majorana fermions in topological superconductors by controlling the singlet and triplet contributions. Indeed, in the noncentrosymmetric superconductor Li₂(Pt,Pd)₃B, by changing the relative concentrations of Pt and Pd, one can tune the spin parity of the gap function from singlet dominant to triplet dominant (32).

Third, the coexistence of magnetism and superconductivity in this system not only adds another of only a few canonical magnetic superconductor platforms such as the borocarbide (29) and Chevrel phases (33) but may also serve as a unique platform to investigate topological orders with multisymmetry breaking states.

Finally, we note that the tunability of the band structure via chemical means provides an ideal platform for traversing the quantum phase transition between trivial and nontrivial topological states, traversing the critical lattice parameter and tuning the interplay between antiferromagnetic and superconducting ground states continuously and controllably. Our transport measurements are quite consistent with band calculations, which reveal that RPdBi is a promising candidate for a topological semimetal. Photoemission studies of the related compound RPtBi (R = Lu, Dy, and Gd) have observed metallic surface states not inconsistent with TI properties predicted by band calculations (27).

In summary, we have investigated the coexistence of magnetism and superconductivity in the single-crystal RPdBi series. The magnetic rare earth members of this series exhibit an antiferromagnetic ordered state with Q = (½,½,½) due to RKKY interaction between conduction electrons and localized moments. Except for GdPdBi, all RPdBi members exhibit bulk superconductivity with an unusual upper critical field behavior that suggests odd-parity superconductivity, likely due to the lack of inversion symmetry in the crystal structure. The scaling of both magnetic order and superconductivity with de Gennes factor indicates RPdBi to be a new family of magnetic superconductors, which, together with the proposed topological properties, provide a unique platform to investigate the emergence of novel quantum states of matter.

METHODS

Single crystals of RPdBi were grown using a Bi self-flux technique in a ratio of R/Pd/Bi = 1:1:5–10. The typical size of resulting crystals is ~3 × 3 × 3 mm³. We confirmed the RPdBi phase with powder x-ray diffraction, without any measurable impurity phase except a very small traces of Bi flux (see the Supplementary Materials for more information). Low-temperature resistivity and AC susceptibility measurements were performed in a dilution refrigerator. The AC susceptibility signal was obtained in a driving field H_ac = 0.1 Oe. We measured high-temperature transport and heat capacity using the ³He option of a physical property measurement system. DC magnetization was obtained using a magnetic property measurement system. In the transport and magnetization measurements, we applied field along the [100] orientation. The neutron measurements were carried out on the BT-7 spectrometer (34) using collimations of 80′ full-width-at-half-maximum before and after the pyrolytic graphite (PG) monochromator and 80′ radial collimator after the sample, with the 1D position-sensitive detector. An incident monochromatic beam of λ = 2.359 Å was used with a PG filter to suppress higher-order wavelengths. A pumped helium cryostat was used to control the sample temperature.

SUPPLEMENTARY MATERIALS

Supplementary materials for this article are available at http://advances.sciencemag.org/cgi/content/full/1/5/e1500242/DC1

Table S1. Néel temperature T_N obtained from the heat capacity and magnetization, Weiss temperature Θ_W, and the effective moments μ_eff for RPdBi obtained from a fit to the Curie-Weiss expression.

Fig. S1. X-ray diffraction patterns for RPdBi with Cu Kα radiation.

Fig. S2. Transport properties of PdBi₂.

Fig. S3. Specific heat as a function of temperature for RPdBi.

References (35–38)