Crowdsourced earthquake early warning

Consumer devices and real and simulated earthquake data demonstrate that earthquake early warning can be achieved via crowdsourcing.

Abstract

Earthquake early warning (EEW) can reduce harm to people and infrastructure from earthquakes and tsunamis, but it has not been implemented in most high earthquake-risk regions because of prohibitive cost. Common consumer devices such as smartphones contain low-cost versions of the sensors used in EEW. Although less accurate than scientific-grade instruments, these sensors are globally ubiquitous. Through controlled tests of consumer devices, simulation of an M_w (moment magnitude) 7 earthquake on California’s Hayward fault, and real data from the M_w 9 Tohoku-oki earthquake, we demonstrate that EEW could be achieved via crowdsourcing.

INTRODUCTION

Earthquake early warning (EEW) strives to detect an earthquake’s initiation, estimate its location and magnitude, and alert people and automated systems to imminent shaking (1, 2). EEW has had encouraging initial results (3), although two issues impede performance and wider implementation. First, magnitude estimates are unreliable for larger earthquakes [moment magnitude (M_w) >7] when based solely on brief observations of the earliest seismic waves (4). This can be overcome by using observations from Global Navigation Satellite Systems (GNSS) such as the Global Positioning System (GPS) (5). Second, it is expensive to install and operate the required dense seismic and GNSS networks. Nevertheless, even well-monitored regions such as California, Oregon, and Washington require extensive expansion and upgrade of existing instrumentation, including installing hundreds of new instruments, to implement EEW (6). Consequently, seismic EEW is operational in a handful of regions, and only a few of those (Japan, Mexico, and the United States) are incorporating GNSS data into their systems (Fig. 1) (7). Much of the global population exposed to high seismic risk, especially in poorer countries, does not benefit from EEW.

Fig. 1. Global seismic hazard and extent of EEW.

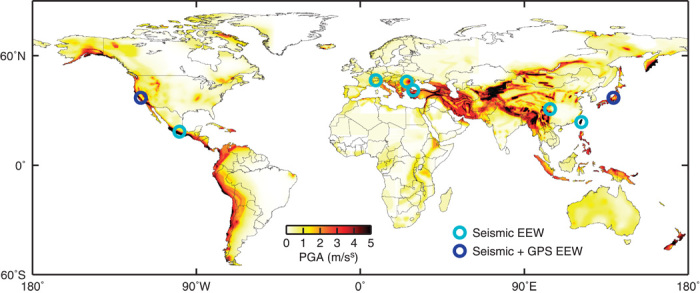
Symbols show the few regions of the world where public citizens and organizations currently receive earthquake warnings and the types of data used to generate those warnings (7). Background color is peak ground acceleration with 10% probability of exceedance in 50 years from the Global Seismic Hazard Assessment Program.

Commercial demand for personal mobile navigation has led to a proliferation of devices that use the same, albeit lower-quality, GNSS and Inertial Navigation Systems (INS) sensors used for EEW (8). Smartphones alone currently number 1 billion worldwide and will increase to ~5.9 billion by 2019 (9). The ubiquity of consumer devices raises the possibility that operational EEW could be achieved via crowdsourcing (10–12). For a global population exposed to ever-increasing earthquake risk (13), the significantly reduced costs associated with crowdsourcing could facilitate widespread EEW implementation and substantially reduce the impact of future earthquakes.

Although there has already been exploration of the potential of scientific seismic and GPS data (14), as well as consumer-quality accelerometers (15), for EEW and tsunami early warning, the potential of consumer-quality GNSS receivers remains untapped (16–18). As we will show, these data are rapidly improving in quality and are much less noisy than consumer-quality accelerometers, at only a fraction of the cost of scientific-quality instruments. Furthermore, GNSS data, which are displacement observations, are particularly well suited to monitoring large earthquakes and to produce magnitudes that do not saturate. Finally, we present a conceptual strategy for a crowdsourced EEW system that includes device use, data processing and quality control, earthquake detection, false alarm suppression, earthquake location, and magnitude determination that could be used to extend the benefits of EEW worldwide.

We assess the potential performance of smartphones and a crowdsourced EEW system in three ways. First, we perform controlled tests on a variety of consumer devices to determine their noise character and displacement detection capability. Second, for a scenario M_w 7 rupture on northern California’s Hayward fault, we generate synthetic smartphone accelerometer and GNSS time series for different data types we might obtain from crowdsourcing at random locations based on census population data. Finally, we consider GPS position time series of an actual earthquake, the M_w 9.0 Tohoku-Oki event, obtained using positioning data of the type found on consumer devices.

RESULTS

To obtain surface displacement observations for EEW, it is the instrument’s change in position that must be measured accurately; absolute position is used only for spatial reference. Consumer devices typically use single-frequency, C/A (coarse acquisition) code methods for GNSS positioning rather than the more precise and accurate locations derived from dual-frequency, carrier phase–based algorithms used in scientific applications (19). These C/A code positions can be substantially improved by using differential corrections via satellite-based augmentation systems (SBAS) (19), tracking the more precise GNSS carrier phase and using it to filter the C/A code data (“phase smoothing”) (20), or by combination with independent INS data in a Kalman filter (21). Today’s smartphones have some or all of these capabilities.

Two data types represent the range of data most likely for crowdsourced EEW. First, we investigated the least-precise data recorded by consumer devices: raw C/A code positions and low-quality accelerometer time series. These data can be used alone or in combination using a Kalman filtering approach (21). The Kalman filter takes advantage of the fact that the accelerometer is recording the second derivative of the same displacement time series that the GNSS receiver is recording, and from these two data sources produces a unified estimate of displacement with much less noise and bias than either of the original time series. Second, we considered the most sophisticated GNSS receiver commonly found in consumer devices: one capable of recording raw C/A data as well as real-time SBAS differential corrections while applying phase smoothing. To represent these scenarios (a poor GNSS receiver supplemented by a poor accelerometer, and a good GNSS receiver), we studied a latest-generation smartphone (Google Nexus 5) that contains a C/A code receiver and accelerometer, and a u-blox consumer GNSS receiver that is capable of recording SBAS and performing phase smoothing. We then subjected these two devices, along with a scientific-grade INS, to a series of displacements ranging from ~0.1 to 2.0 m (Fig. 2). The displacement time series from the scientific-grade INS system may be considered to be the true motion. Figure 2A shows the response of these two data types, as well as the twice-integrated acceleration and C/A code time series input to the Kalman filter, to a simple time series of motion. Both data types reproduce the time history of displacement with very high fidelity.

Fig. 2. Device tests.

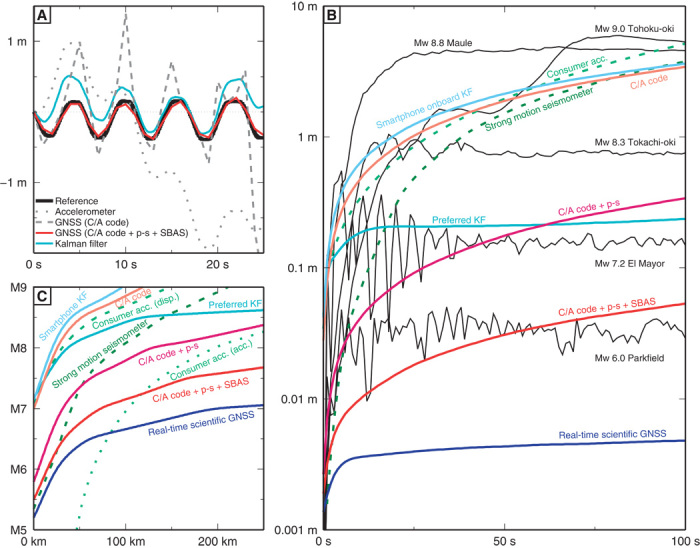
(A) Comparison of displacements obtained from consumer GNSS receivers with and without phase smoothing (p-s) and SBAS, by twice integrating smartphone acceleration and by Kalman filtering acceleration and GNSS data. Almost any smartphone or similar consumer device would generate the displacement and acceleration data shown with gray lines. Although these time series individually do a poor job of reproducing the true time history of motion (shown in black), they can be combined using a Kalman filter. This process produces one unified estimate of displacement (cyan) that is much less noisy than the original acceleration and displacement data used as inputs to the filter. However, the best GNSS hardware found in consumer devices (shown in red) is such high quality that there is no need to supplement the data with acceleration observations, and in fact, the displacement time series could be degraded by doing so. (B) Drift of position obtained from various devices (GNSS, double-integrated accelerometers, and Kalman filtering thereof) compared to observed earthquake displacements (7). Neither GNSS displacement observations nor acceleration data double integrated to displacement are stable over long periods. For GNSS data, this is because the inherent noise in the observations is not white noise. For acceleration data, this is because small tilts or steps in the observed acceleration cause large drifts when integrated. Thus, over time, the apparent position of sensors drifts, obscuring the true displacement of the instrument. The color curves show the apparent drift expected for each sensor and data type based on controlled tests. The black lines are observed displacement time series for earthquakes of different magnitudes. Thus, anywhere that a colored line is below a black line, the signal-to-noise ratio for that data type is greater than 1. In a crowdsourced setting, we expect to obtain data ranging in quality from a Kalman filter of C/A code data with acceleration data (cyan line created by combining data from light blue line with light green line), to C/A code data that have been phase-smoothed (“C/A code + p-s,” magenta line), to C/A code data that have been phase-smoothed and supplemented with SBAS (“C/A code + p-s + SBAS,” red line). Although all of these data types are significantly noisier than scientific-quality GNSS data (blue line), they are sensitive enough to record M6-7 earthquakes. (C) Using the drift curves shown in (B) and the peak ground displacement expected as function of magnitude and distance from the source (27), we can calculate the minimum magnitude earthquake observable with a signal-to-noise ratio of 10. Dotted line shows sensitivity of acceleration recorded on a smartphone. Dashed lines show sensitivity of displacement data obtained by twice integrating consumer and scientific acceleration data. At very close distances, the highest-quality consumer devices can observe earthquakes as small as M6 with a signal-to-noise ratio of at least 10.

To demonstrate the capability of consumer-quality sensors to record earthquake ground motions, we compare the noise from various instruments to observed displacement time series for recent earthquakes (Fig. 2B) (22–24). Raw C/A code positions alone recorded by any GNSS-equipped consumer device (light pink curve) are capable of recovering displacements from great earthquakes. The light blue curve represents observations from typical smartphones; generally, smartphones do not report positions from raw C/A code data, but instead use a Kalman filter to combine raw C/A code positions with the device’s accelerometer. The filter operates on the GNSS chipset and is optimized for consumer navigational needs, such as vehicular and urban canyon positioning, rather than recording higher-frequency earthquake motions. If the same raw C/A code positions and acceleration data recorded by a smartphone were combined in a Kalman filter tuned to optimize earthquake surface displacements, the noise level would be reduced to that shown by the cyan curve. Some consumer devices are now beginning to use better GNSS positioning hardware (SBAS-capable receivers, red curve) and algorithms (such as phase smoothing, magenta curve). Either of these improvements reduces noise so significantly that Kalman filtering is no longer required and the detection threshold approaches smaller (M6-7) earthquakes.

We compute the minimum magnitude earthquake observable with a signal-to-noise ratio of at least 10 for all data types at different source-receiver distances (Fig. 2C). These results show that consumer C/A code GNSS data augmented by phase smoothing, SBAS, or Kalman filtering with twice-integrated acceleration data could be used for measuring ground displacement from ~M_w ≥6 earthquakes within ~100 km of the source (7). Data from consumer accelerometers could be used to detect smaller earthquakes but not to recover their associated ground displacement (Fig. 2, B and C). This is because twice-integrated acceleration records from both consumer and scientific devices are subject to drifts (usually from tilting) that could render them useless for larger earthquakes after a small number of seconds. However, Kalman filtering accelerometer data with consumer C/A code-data yield displacement time series with much less drift (Fig. 2B).

To assess the performance of a crowdsourced EEW system composed of consumer devices, we consider two events: an M_w 7 scenario rupture on the Hayward fault, and the 2011 M_w 9 Tohoku-Oki earthquake. For the Hayward fault scenario, we assume that a device is triggered if it and its four nearest neighbors record displacements greater than 5 cm. If at least 100 devices are triggered, we declare that an event has been detected. In practice, the availability and noise characteristics of crowdsourced observations will vary greatly depending on the device and how it is used. For example, at any time, a fraction of all smartphones are turned off, out of communication, or subject to anthropogenic motion. These devices, however, produce enough information about data quality, connectivity, and background motion to permit discrimination of sensors suitable for EEW. For example, using this system information, it may be desirable to only include observations from devices that are not otherwise being used by their owners (and thus not subject to anthropogenic noise), are not operating on battery power, have a large-bandwidth telemetry connection, and whose GNSS position is derived from a sufficient number of satellites. Therefore, we assume that only a very small subset of potential consumer devices will be useful during the event. With 0.2% (n = 4696) of the population reporting, the earthquake could be detected in 5 s, a sufficient amount of time to issue a warning to major population centers (San Francisco and San Jose) before damaging S waves arrive (Fig. 3). These data are sufficient to estimate the epicentral location to within 5 km (using a power law fit to the observed displacements) as soon as the system is triggered, and to estimate the real-time magnitude evolution with high accuracy and very little latency (using an analytical finite fault slip inversion) (Fig. 3, D and E) (7, 25). Note that although the earthquake epicenter is a property of the rupture initiation, moment release evolves over the duration of the rupture. Thus, the performance of an EEW approach should be evaluated on how quickly after origin and how accurately the epicenter is obtained, and how accurately and with how little latency the methodology infers the moment release of the earthquake as a function of time (7, 25). By both of these metrics, the crowdsource-derived epicenter and moment estimates are extremely good. Decreasing the participation rate to as little as 0.0125% (n = 294) of the population does not degrade the quality of the source parameter estimates, although sparser observation sets require more time to accumulate 100 triggers (Fig. 3C). Additionally, it is important to note that these results hold whether the simulated observations are from Kalman-filtered GNSS and INS data (Fig. 3) or from phase-smoothed GNSS data with SBAS corrections (fig. S4) (7).

Fig. 3. Hayward fault earthquake scenario.

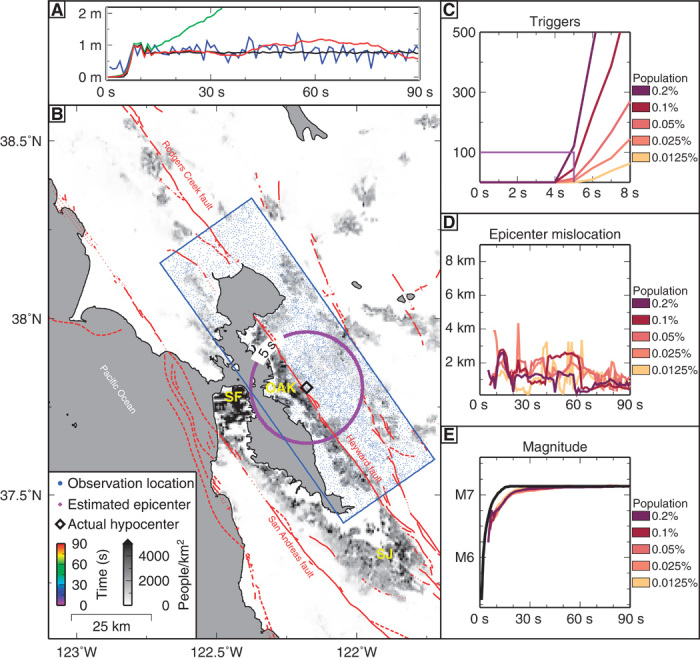
(A) Representative displacement time series from Hayward fault rupture scenario. Black line: true displacement. Blue line: simulated smartphone C/A code GNSS. Green line: simulated smartphone accelerometer, twice integrated. Red line: Kalman filter combining GNSS and accelerometer. The red line is representative of the data we expect to observe with the least sophisticated consumer devices, yet it still does a good job of recovering the true ground motion shown in black. (B) Diamonds showing estimated epicentral location colored by time after origin. As soon as the earthquake is detected (at 5 s after origin), its epicenter can be estimated with an error of less than 5 km using consumer-quality data. Contour: S wave position when detection criterion is satisfied. Yellow text denotes major cities: SF, San Francisco; SJ, San Jose; OK, Oakland. Blue dots denote observer locations assuming 0.2% of the population within the blue box contribute data. (C) Number of observers who have detected a potential earthquake trigger as a function of time. The higher the density of observations, the sooner the detection criteria of a hundred triggers is reached. With just 0.2% of the population contributing data, the earthquake can be detected in 5 s. (D) Epicenter location error as a function of time. The error on the epicenter location is always <5 km even with very small percentages of the population contributing observations. (E) Estimated moment magnitude as a function of time for different participation levels. Black line: true magnitude. The estimated magnitude release almost perfectly reproduced the actual time history of moment release with very little latency, even for very low participation rates. The accuracy and low latency of the detection, location, and magnitude estimate of the earthquake based on very small numbers of consumer-quality observations suggest that a crowdsourced EEW system is feasible.

We assess the feasibility of crowdsourced EEW for an actual earthquake by analyzing C/A code positions for the 2011 M_w 9 Tohoku-Oki event obtained from data recorded by the GPS Earth Observation Network (GEONET) (24) (Fig. 4A). The data from these 462 GEONET stations represent the scenario of collecting crowdsourced observations from ~0.0004% of the population of Japan. Although the C/A code positioning technique is identical to that which is used in the consumer devices, it should be noted that these data were recorded at scientific GPS stations equipped with more sophisticated antennas than consumer electronics. The better hardware decreases multipath noise effects, and so, the C/A code positions obtained from the GEONET stations should be less noisy than C/A code time series from consumer electronics. Figure S2, however, shows that the observed noise level on the GEONET C/A code time series is equivalent to that obtained from a consumer device when the C/A code position is supplemented by phase smoothing, and the GEONET C/A positions are significantly noisier than consumer time series with both phase smoothing and SBAS. Thus, the Tohoku time series are, in fact, representative of the data quality that we might obtain from consumer devices. In addition to the C/A code positioning, we also compute position time series using scientific-grade processing. The estimated static displacements from these two processing methods compare well, following a 1:1 relationship over a range of horizontal displacements from ~0.5 to 4 m, further demonstrating that consumer-quality GNSS data are sufficient for EEW (7) (fig. S6). We use similar detection and location criteria and the same magnitude estimation approach as for the Hayward fault scenario earthquake. However, in this case, we examine pre-event C/A code time series to determine how often a device might trigger due to noise. We then express the number of triggers as SDs from the background triggering rate and use the very conservative criterion that we will not issue a warning until the number of triggers exceeds 5σ of the background triggering rate, which would, theoretically, restrict the chances of issuing a false alarm to about one in 2 million. With the use of this conservative detection criterion, the earthquake is detected at 77 s after the origin time (Fig. 4). At ~100 s, the solution yields a location of comparable accuracy to one obtained by scientific-grade instruments. The M_w estimate follows the best estimate of the actual moment release for the earthquake obtained from an independent kinematic rupture model (24), quickly growing to a final maximum value of ~M_w 8.8 instead of saturating near M_w 8 like the seismic-only EEW estimate. Although not fast enough to provide a warning for cities closest to the offshore rupture, this information would have permitted a warning to be issued before the earthquake’s damaging S waves reached metropolitan Tokyo, and a tsunami warning could have been issued minutes before the tsunami made landfall.

Fig. 4. Tohoku-oki earthquake example.

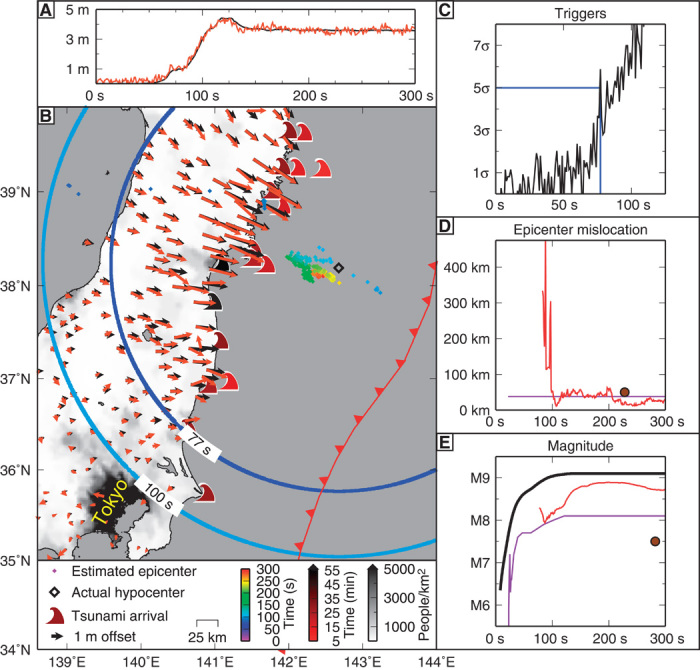
(A) Representative displacement time series observed for Tohoku-oki earthquake. Black line: scientific-grade GPS. Red line: consumer-grade (C/A code) GPS. C/A code GPS positions are the worst type of data we expect to obtain from consumer devices. However, even these data do a good job of recovering the actual displacement time series as shown by the scientific-grade GPS data. (B) Diamonds showing estimated epicentral location colored by time after origin. Waves indicate tsunami arrival times (28). Blue contour: S wave position when detection criterion is satisfied. Cyan contour: S wave position when S wave reaches Tokyo. Although there is higher latency in this example than the Hayward fault example due to the offshore location of the earthquake and the noisier data used, the proposed crowdsourcing approach could detect and locate the Tohoku earthquake before strong shaking reaches Tokyo and before the tsunami makes landfall. (C) Number of potential earthquake triggers versus time. We looked at the time series of C/A code positions before the earthquake to determine the frequency with which a trigger might be observed due to noise. We then expressed the number of triggers as SDs from that background triggering rate and then, to be very conservative, do not issue a warning until the number of observed triggers exceeds 5σ of the background triggering rate. (D) Red: location error of our estimated epicenter relative to the epicenter of (29). Purple: error associated with locations reported by Japan Meteorological Agency (JMA) EEW system. Brown: first location available from global monitoring (30). Although significantly slower than scientific-quality EEW (which includes offshore near-source observations from ocean-bottom seismometers), the consumer-quality data are capable of determining the earthquake’s location just as accurately as the scientific-quality JMA EEW system and do so significantly faster than an epicenter could be obtained from global scientific seismic data. (E) Red: estimated magnitude release as a function of time. Purple: M_j values reported by JMA’s EEW system. Brown: first M_w estimate available from global monitoring (30). Black: true magnitude from independent kinematic rupture model (24). Again, although there is more latency in the magnitude estimated using only onshore consumer-quality data than offshore scientific-quality data, the proposed crowdsourced EEW system is significantly faster than the global response to the earthquake. Also, note that the consumer-quality magnitude, which is based on GNSS data, does not saturate like the seismic magnitudes estimated from scientific-quality seismic data.

DISCUSSION

Our results demonstrate that the GNSS and INS navigational sensors built into consumer devices such as smartphones are capable of detecting surface displacements from moderate and larger earthquakes. This economical approach warrants further development, although we do not suggest that it is a substitute where monitoring of smaller, but still potentially destructive, earthquakes is required. In regions where resources cannot be allocated for scientific-grade EEW due to limited financial resources or less frequent occurrence of destructive earthquakes, crowdsourced EEW may be the best option. For example, large regions of central and south America, the Caribbean, the Pacific rim, and south Asia have high seismic hazard but no early warning capabilities (Fig. 1). Whether the data from consumer devices are retrievable from participants in a crowdsourced monitoring system, however, depends on each device’s operating system and the levels of access to raw data permitted by device vendors. This is a challenge, in fact, germane to many crowdsourcing endeavors, where the crowdsource observational objective may not align with the original commercial intent of the device.

How close are we, then, to operational crowdsourced EEW? As we have shown, current smartphones could be used immediately to provide warnings for the largest earthquakes, such as those associated with subduction zones, worldwide. Additionally, because of the enormous number of potentially available devices, a crowdsourced approach could be very conservative in terms of data quality control (for example, excluding devices with poor sky view or subject to unwanted accelerations such as from automobile usage) without sacrificing performance. Ultimately, to detect a wider range of earthquakes, access to unfiltered raw C/A code data through these devices’ application programming interfaces will be necessary. This is a trivial technical task requiring only a software change and no hardware changes. However, this change would need to be made in cooperation with device manufacturers because it could have commercial ramifications.

Because we have shown that inexpensive additions, such as adding SBAS or phase smoothing capability, permit smartphones to detect moderate to large earthquakes, an interim solution would be to deploy these sensors in extremely low-cost monitoring networks. Although this would require some capital investment for installation and maintenance, these costs are markedly less than would be required to build a similar network of scientific instruments. A crowdsourced EEW system would, of course, have almost zero hardware and maintenance cost because the participants would purchase and care for the sensors (26). However, a formal monitoring system built on consumer sensors would not only cost much less than an equivalent scientific network but also cost less than the public would spend on a crowdsourced system because the monitoring network could be built from the hardware components found within consumer devices. These components constitute only a small part of the cost of a smartphone or similar device. Further, this low-cost network strategy has several attractive aspects in common with scientific-grade networks, including the ability to concentrate sensors near hazardous faults.

Crowdsourcing is an important phenomenon that has only begun to be used across the sciences and must be considered seriously. Given the long repeat times between earthquakes and tsunamis and limited budgets with which to take preventive measures, crowdsourcing may be an important part of building, maintaining, and operating warning systems. Crowdsourcing drastically reduces the marginal costs associated with EEW because sensor and communication costs would be assumed by the system’s beneficiaries. Further, the commercial push for ever-greater positioning performance would ensure that a crowdsourced EEW network would always incorporate the latest technology without need for large periodic capital outlays for equipment upgrades. Finally, by encouraging inclusion of consumer devices into EEW, the devices can be used not only to gather the observations used to issue warnings but also to deliver these warnings to the public. This will permit alerts to be customized according to a user’s location and should enhance system efficacy via a feedback process: The more that users engage with the system, the more effective it becomes at reducing the future impact from earthquakes and tsunamis.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/3/e1500036/DC1

Text

Fig. S1. Background position noise for various GNSS receivers found on consumer devices.

Fig. S2. Spectra of drift of position time series for various GNSS receivers found on consumer devices.

Fig. S3. Observed time series from consumer accelerometers and GNSS receivers.

Fig. S4. Hayward fault earthquake scenario.

Fig. S5. Epicenter location uncertainty for Hayward fault scenario rupture.

Fig. S6. Tohoku-oki earthquake example.

Fig. S7. Epicenter location uncertainty for Tohoku-oki earthquake.

Table S1. Description of observed GPS earthquake displacement time series shown in Fig. 2B.

Table S2. Number of data used and detection response times for Hayward fault simulation.

Table S3. Locations of GEONET GPS stations used in analysis of Tohoku-oki earthquake.

References (31–34)