Topographic representations of object size and relationships with numerosity reveal generalized quantity processing in human parietal cortex

Significance

Processing of quantities such as object sizes and numbers relies on analyses of sensory information and informs cognitive tasks such as decision making and mathematics. Whereas sensory processing is organized into topographic maps reflecting sensory organ structure, organization of cognitive processing is poorly understood. We demonstrate topographic representation of object size-tuned responses. This arises separately from object number tuning, but these two quantities are associated in overlapping maps. This generalized quantity representation may allow us to consider object size and number together when making decisions. Optimization of cognitive processing using topographic maps may be a common organizing principle in association cortex, as it is in sensory processing. Linking cognitive representations in maps of related features may support increasingly abstract cognition.

Abstract

Humans and many animals analyze sensory information to estimate quantities that guide behavior and decisions. These quantities include numerosity (object number) and object size. Having recently demonstrated topographic maps of numerosity, we ask whether the brain also contains maps of object size. Using ultra-high-field (7T) functional MRI and population receptive field modeling, we describe tuned responses to visual object size in bilateral human posterior parietal cortex. Tuning follows linear Gaussian functions and shows surround suppression, and tuning width narrows with increasing preferred object size. Object size-tuned responses are organized in bilateral topographic maps, with similar cortical extents responding to large and small objects. These properties of object size tuning and map organization all differ from the numerosity representation, suggesting that object size and numerosity tuning result from distinct mechanisms. However, their maps largely overlap and object size preferences correlate with numerosity preferences, suggesting associated representations of these two quantities. Object size preferences here show no discernable relation to visual position preferences found in visuospatial receptive fields. As such, object size maps (much like numerosity maps) do not reflect sensory organ structure but instead emerge within the brain. We speculate that, as in sensory processing, optimization of cognitive processing using topographic maps may be a common organizing principle in association cortex. Interactions between object size and numerosity maps may associate cognitive representations of these related features, potentially allowing consideration of both quantities together when making decisions.

Humans and animals share a sense of numerosity (object number) that guides behavior and decisions (1, 2), for example choosing numerous objects when foraging or shopping. As such, numbers and numerical processing are fundamental to cognitive neuroscience and are linked to mathematics, value judgments, and economics (1, 3). Because aspects of numerosity perception mirror primary sensory perception, it has been referred to as a “number sense” (4). However, another theory (5) sees numerosity as one aspect of a more generalized quantity system. Here we investigate the representation of another quantity: object size.

Behaviorally, object size and numerosity perception interfere with each other (6). At the neural level, single neurons in macaque parietal cortex can be tuned to numerosity (7), line length (a measure of object size), or both (8). However, it is unclear whether numerosity and object size preferences are related, either in the same neurons or in nearby neurons (8). Using human neuroimaging, we have shown that numerosity-tuned neural populations in human posterior parietal lobe are topographically organized (9): Similar numerosity preferences are grouped together, changing gradually across the cortical surface. Visual features of the presented stimuli affect numerosity preferences, which may reflect preferences for particular object sizes (9, 10).

Here we ask whether object size-tuned responses are found in the same area, whether these are topographically organized, and how tuning and organization relate to representations of numerosity and visual space in the same area. We find topographically organized object size-tuned responses that largely overlap with numerosity maps and show correlated tuning preferences. However, many differences between object size and numerosity tuning and map organization suggest that responses arise from distinct mechanisms.

These intermingled neuronal representations of object number and size may allow generalization and abstraction in quantity processing and consideration of related quantities when making decisions. Optimization of cognitive processing using topographic maps may be a common organizing principle in association cortex, particularly in quantity processing, as it is in sensory processing.

Materials and Methods

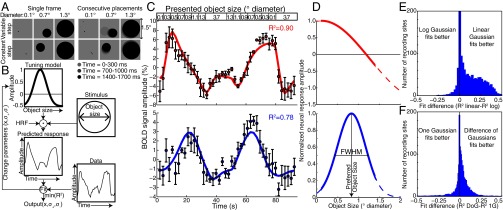
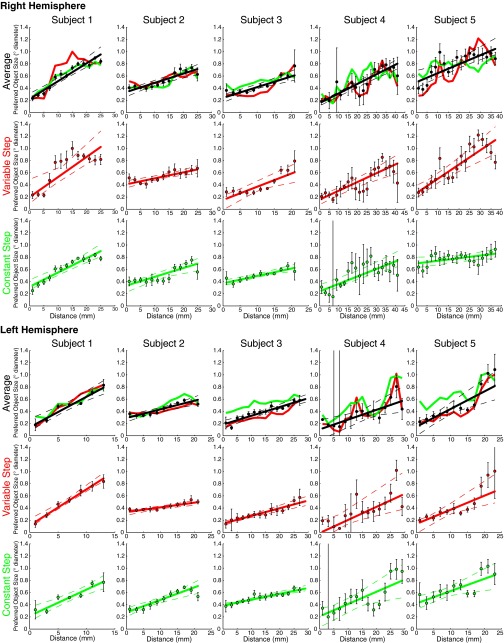
We showed a single object (a circle) whose size varied systematically within a 7T functional (f)MRI scan (Fig. 1A, Fig. 1C, Top, and SI Materials and Methods). We recorded responses to two different stimulus sets on different days. The first (“variable step”) allowed any object placement where the entire object lay within 0.75° of fixation. Here, larger objects had a more limited range of possible positions, and so took smaller average steps between consecutive placements (Fig. 1A). The second condition (“constant step”) always used the same step length between consecutive object locations, in random directions. These two conditions gave very similar responses, demonstrating repeatability, and are averaged for most analyses. Subjects reported when objects were shown in white rather than black (10% of presentations, mean performance 89% correct). No object size judgments were required. Written informed consent was obtained before every scanning session. All experimental procedures were approved by the ethics committee of University Medical Center Utrecht.

Fig. 1.

Stimuli and pRF modeling. (A) Example stimuli. Objects were placed either randomly or pseudorandomly to lie entirely within 0.75° of fixation. Using purely random placements, smaller objects can take larger steps between consecutive placements (variable step condition). Therefore, we introduced a condition where objects always made steps of the same length in random directions (constant step condition). These two conditions gave very similar responses. (B) pRF modeling procedure (9, 11). A candidate neural tuning model describes a tuning function of an fMRI recording site, characterized by a preferred object size, tuning width, and suppressive surround width. Convolving the tuning model’s response amplitude with the time course of presented object sizes and the hemodynamic response function (HRF) predicts the fMRI response for this tuning model. For each recording site, we find the best-fitting tuning model parameters by minimizing the squared difference between the predicted fMRI response and the recorded data. (C) Two example fMRI time courses from sites in right posterior parietal cortex, about 2 cm apart, elicited by the presented object size time course (Top). Points represent mean response amplitudes; error bars represent the SE over repeated runs. In the Upper panel, the largest responses occur after presentation of small objects, whereas in the Lower panel the largest responses occur for larger objects, considering the hemodynamic response delay. The tuning model predictions (colored lines) capture over 75% of the variance (R²) in the time courses. BOLD, blood oxygen level-dependent. (D) The tuning models that explain the most variance in each time course. The model describes a linear Gaussian tuning function with a suppressive surround, characterized by two parameters: preferred object size and tuning width summarized by the function’s full width at half maximum (FWHM). Different tuning model parameters explain the different responses seen in C, capturing similar amounts of variance. Dashed lines show the continuation of tuning functions outside the presented object size range. (E) Linear one-Gaussian object size tuning models explain more response variance in most recording sites than logarithmic tuning models. Goodness of fit is evaluated by twofold cross-validation. Comparisons of difference of Gaussian tuning models give similar results. (F) Linear DoG object size tuning models explain more response variance in most recording sites than linear one-Gaussian models.

SI Materials and Methods

Subjects.

We present data from five subjects (all male, age range 25–39 y). One was left-handed. All were well-educated, with good mathematical abilities. All had normal or corrected-to-normal visual acuity. All were trained on tasks requiring numerosity judgments before scanning. All experimental procedures were cleared by the ethics committee of University Medical Center Utrecht.

A total of seven subjects was recruited. However, two subjects were excluded from analysis and no complete dataset was recorded, because the first scanning session revealed that the position of the superior sagittal sinus prevented imaging of the numerosity map (9).

Object Size and Numerosity Stimuli.

Visual stimuli were presented by back-projection onto a 15.0 × 7.9-cm screen inside the MRI bore. The subject viewed the display through prisms and mirrors, and the total distance from the subject’s eyes (in the scanner) to the display screen was 41 cm. Visible display resolution was 1,024 × 538 pixels.

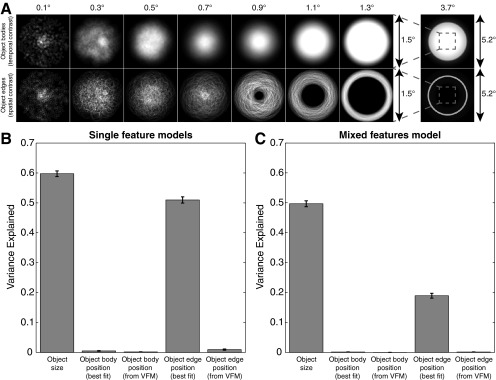
The stimuli were generated in MATLAB using the Psychophysics Toolbox (22). A large diagonal cross, composed of thin red lines, crossed the entire display, a design that facilitates accurate fixation. Subjects were asked to fixate the intersection of the cross. Stimuli consisted of single circles or groups of circles presented in the central 0.75° (radius) of the visual field, with the exception of the largest circle presented when characterizing object size selectivity, which reached a maximum eccentricity of 2.6°. This small central stimulus area decreased the need to make eye movements to view the circles. It also minimized the cortical surface extent of the visually responsive part of the brain activated by presentation of the stimulus, avoiding confusion between spatially tuned responses and object size- or numerosity-tuned responses.

Circles were randomly positioned at each presentation so that each circle fell entirely within the central 0.75° (except for the largest circle in the object size selectivity experiment, whose center was randomly positioned in the same area). Each of the many presentations (384 presentations for each object size or numerosity in each condition) contained circles placed in a new, random position. Averaging these responses to different visual positions minimized links between particular visual field positions and particular numerosities or object sizes (9). To prevent perceptual grouping, individual items in the numerosity experiments were distributed roughly homogeneously across the stimulus area (except for the high-density condition described below).

To characterize object size tuning, we varied the size of a single circle. Again, circles were randomly placed in the first condition (variable step condition) (Fig. 1A). However, because circles were always constrained to fit within the central 0.75° of the display, larger circles would take a shorter average step between consecutive presentations. As such, a second stimulus configuration (constant step) kept this step size constant at 0.06° across different circle sizes, with the direction of steps varied randomly.

To characterize numerosity tuning, we used various stimulus configurations (9) to ensure that responses to low-level visual features of the stimulus did not follow the same time course in different conditions. The first stimulus configuration (“constant area” condition) kept the total surface area of all of the circles combined constant across numerosities, ensuring equal luminance across conditions. The second (“constant object size”) kept individual circle size constant. The third (“constant circumference”) kept the total circumference constant, ensuring equal edge density. The fourth condition (“high density”) contained the same circles as the constant area condition but at higher density, with all circles falling entirely within a 0.375°-radius area that was randomly placed inside the stimulus area.

All patterns were presented as black circles on a gray background. Patterns were presented briefly (300 ms) to ensure subjects did not have time to sequentially count the objects. This was repeated every 700 ms, each time with a new random pattern presented, with a 400-ms presentation of a uniform gray background between pattern presentations. For object size tuning experiments, this was repeated three times, over 2,100 ms [one repetition time (TR), fMRI volume acquisition], before the size changed. For numerosity tuning experiments, this was repeated six times, over 4,200 ms (two TRs), before the numerosity changed. This allowed a slow progression through the numerosity range while only presenting whole numbers of objects. On 10% of pattern presentations, the circles were shown in white instead of black. Subjects were instructed to press a button when this happened to ensure they were paying attention to the patterns during fMRI acquisition. No object size or numerosity judgments were required. Subjects responded on 80–100% of white circle presentations within each scanning run.

In the object size tuning experiments, circles with diameters of 0.1°–0.7° were shown as the main stimulus (Fig. 1C, Top), first presented in linearly increasing order. This was followed by a longer period (16.8 s) where the circle was 3.7°-diameter, followed by the same object sizes in descending order, followed by another long period of 3.7° diameter.

In the numerosity experiments, the numerosities 1–7 were shown as the main stimulus (9), first presented in ascending order, followed by a longer period (16.8 s) where the stimulus contained 20 circles, followed by the numerosities in descending order, followed by another long period of 20 circles.

This sequence was repeated four times in each scanning run. The long period of 20 circles or a 3.7°-diameter circle had a similar function to the blank periods used in visual field mapping stimuli in population receptive field experiments, allowing us to distinguish between very small and very large tuning widths, that is, between populations that responded at all times and those that never responded (9, 11). During this period, little neural response was expected from neurons with small preferred object sizes or numerosities, because such a large object size or numerosity should be well outside of the range that elicits strong responses. This allows hemodynamic responses to return back to baseline between blocks of changing object size or numerosity. However, using numerous or large objects (rather than no objects) provides a stronger visual stimulus than the other stimuli. As such, neural populations responding to the contrast energy of the stimulus should respond most strongly during presentation of large or numerous circles, avoiding confusion with populations preferring a specific large object size or numerosity.

Stimuli were presented many times between changes (three times for object size tuning and six times for numerosity tuning measurements), ensuring strong fMRI responses and facilitating measurements of response preferences. As in many fMRI experiments, these stimuli likely cause some adaptation to the presented object sizes and numerosities (4, 23). We aim to minimize effects of adaptation on tuning estimates by modeling responses to stimuli with both ascending and descending changes. We thus counterbalance adaptation effects by presenting stimuli that give both higher and lower responses before presentation of any object size or numerosity. Because the tuning model must fit both of these response sequences with one set of tuning parameters, the resulting tuning parameters reflect the preferred stimulus without strong dependence on preceding stimuli.

MRI Acquisition.

Anatomical MRI data for subjects 2, 3, and 4 were acquired on a Philips Achieva 3T scanner with a Quasar dual gradient set. T1-weighted anatomical MRI data were acquired at a resolution of 0.75 × 0.75 × 0.8 mm. Repetition time was 10.029 ms, echo time (TE) was 4.6 ms, and flip angle was 8°.

Anatomical MRI data for subjects 1 and 5 were acquired on a Philips 7T scanner using a 32-channel head coil. T1-weighted anatomical MRI data were acquired at a resolution of 0.5 × 0.5 × 0.8 mm. TR was 7 ms, TE was 2.84 ms, and flip angle was 8°.

Functional T2*-weighted multislice echo planar images were acquired on a Philips 7T scanner using a 32-channel head coil at a resolution of 1.77 × 1.77 × 1.75 mm, with a field of view of 227 × 227 × 71.75 mm. TR was 2,100 ms, TE was 25 ms, and flip angle was 70°. We used a single-shot gradient echo sequence with SENSE acceleration factor 3.0 in the anterior–posterior (AP) encoding direction and 41 interleaved slices. Maximum gradient strength was 26 mT/m, and maximum slew rate was 140 T⋅m⁻¹⋅s⁻¹. We used a third-order image-based B0 shim of the field of view of the functional scans (in-house IDL software, version 6.3; RSI). Functional runs were each 182 time frames (382.2 s) in duration, of which the first six time frames (12.6 s) were discarded to ensure the signal was at steady state. Eight repeated runs were acquired within the same session for each stimulus condition. All stimulus conditions were acquired on different days.

We used 7T data acquisition because it produces better signal strength at high scanning resolutions than 3T, reducing required scan times. Because of extensive comparisons between responses to different stimulus sets, experiments required a total of 10.5 h of scanning per subject. 3T scanning would have required approximately twice as much scanning to produce similar data quality.

Preprocessing of Anatomical and Functional Images.

Functional MRI analysis was performed in the mrVista software package, which is freely available at white.stanford.edu/software. T1-weighted anatomical scans were automatically segmented using FreeSurfer (freesurfer.net) and then hand-edited to minimize segmentation errors (24) using ITK-SNAP (www.itksnap.org). This provided a highly accurate description of the cortical surface and white matter, an anatomical segmentation space used for analysis of cortical organization. The cortical surface was reconstructed at the gray–white matter border and rendered as a smoothed 3D surface (25). Head movement and motion artifacts between and within functional scans were measured and corrected for (26). Functional data were aligned to the anatomical scans (26) and interpolated to the anatomical segmentation space. Data from several sessions, resulting from all stimulus conditions, were imported into the same anatomical segmentation space. fMRI time-series data from all stimulus conditions (for numerosity and object size separately) were averaged together to produce datasets with very high signal-to-noise ratios. Reconstruction of gray matter depth was stopped 4 mm from the gray–white matter border, or where recording points were outside the gray matter. Across cortical thickness, data from all vertices in the gray matter thickness were collapsed and averaged onto the nearest point on the gray–white matter surface (27). This increased signal strength and formed a (folded) 2D representation of the gray matter. All data were also analyzed using the same methods without collapsing onto a 2D surface, with very similar results. Note that the acquired data were averaged, rather than the model parameters. Data from each individual condition were also analyzed separately.

Exclusion of Vein Artifacts.

A large draining venous system, consisting of the superior sagittal sinus and its branches, runs over medial posterior parietal lobe. Draining veins spatially and temporally distort the fMRI signal around this vein (21). Measurements from high-field MRI scanners (we used 7T here) are less susceptible to signals originating in large veins (28). Nevertheless, we identified these locations by the mean signal intensity of the BOLD signal averaged over all sessions (28, 29) and excluded these from further analysis (Fig. S3). Because we used the mean BOLD signal across all sessions to identify these vein artifacts, anatomically equivalent recording points were excluded from all conditions. Similar results are found if these vein regions are included in the analysis. However, this procedure excludes regions where the topographic representation and tuning width measurements are distorted.

Fig. S3.

BOLD signal strength at each recording point in the average data across all object size and numerosity stimulus conditions, rendered on inflated cortical surfaces showing the same views as used in all other figures and supporting figures. Large draining veins on the pial surface and the superior sagittal sinus and its branches can be seen as areas of low signal strength. These are outlined with dashed lines, which correspond to the red dashed lines seen in other renderings of the cortical surface. Data from these areas are distorted, and the blood flow and oxygenation here result from neural activity elsewhere. Based on a subject-specific threshold of minimum signal strength in the average data, such recording points are excluded from analysis of preferred number and tuning width. The lines highlighting these areas are for illustration only. AU, arbitrary units.

fMRI Data Analysis.

Object size and numerosity tuning models were estimated from the fMRI data and stimulus time course as previously described for numerosity tuning (9). This approach is based on methods we developed to estimate visuospatial population receptive field properties in human visual cortex (11).

Population receptive field models describe the aggregate tuning of the neural population within each fMRI recording site. A forward model predicts neural responses at each time point depending on which stimulus was shown (Fig. 1B). The models describe tuning to object size or numerosity using Gaussian functions characterized by (i) a preferred object size or numerosity (mean of the Gaussian distribution); (ii) a tuning width (SD of the Gaussian); (iii) and an inhibitory surround width (SD of a negative Gaussian with the same mean). By examining the overlap of the stimulus at each time point with this tuning model, a prediction of the neuronal response time course is generated. By convolving this with a hemodynamic response function (HRF), a predicted fMRI time course is generated. The predicted fMRI time courses were generated for all combinations of a large range of candidate preferred object size (or numerosity), tuning width, and inhibitory surround width parameters. For each recording point, the parameters were chosen from the prediction that fit the data most closely by minimizing the sum of squared errors (R², variance explained) between the predicted and observed fMRI time series. To convert these R²s to probabilities of observing these model fits by chance, we generated a null distribution by fitting tuning models to recordings from 191,000 white matter recording points in the same scans. We then determine the proportion of fits exceeding any particular R². We correct these probabilities for multiple comparisons using false discovery rate correction (30), taking all gray matter voxels in the scanning volume into account.

The candidate preferred object sizes and numerosities extend beyond the range shown, allowing model fit parameters beyond this range. This allows us to be confident that returned parameters within the stimulus range are reported accurately, rather than the best fit of a limited set. However, recording points with preferences modeled outside the stimulus range must be treated with caution. In such recording points, response amplitude monotonically increases or decreases across the stimulus range. As such, we have little confidence that the preferred tuning estimate is correct here, so these recording points were not labeled on cortical surface renderings and were excluded from further analyses.

We estimate the HRF parameters across the whole acquired fMRI volume from the data using a near-identical procedure we use in visual cortex (29). Briefly, by having the stimulus pass through the stimulus range in both ascending and descending directions, we can derive the HRF properties. We estimated the HRF parameters by comparing predicted and measured time series and chose the HRF parameters that minimized the difference between prediction and measurements over the entire volume for each stimulus condition, including all object size and numerosity tuning conditions. Next, we averaged the HRF parameters determined from each condition’s data and used those HRF parameters to reestimate the tuning models. This procedure improved the goodness of fit and ensured that the same HRF is used in modeling responses to all conditions and at every point in the brain. Very similar results, although with not as good model fits, were obtained by fitting the data using a canonical HRF (31). We have reported analogous effects of fitting subject-specific HRFs in visual cortex (29).

Comparisons Between Tuning Models.

For both object size and numerosity tuning, we compared different tuning functions describing the distribution of response selectivity, namely different relationships between the range of displayed stimuli and the measured response amplitudes. Here we split our repeated scanning runs into two halves of odd or even scans and, for each half, fit tuning as a logarithmic Gaussian function, linear Gaussian function, and logarithmic and linear difference of Gaussian functions. To compare object size tuning models, we also split our object size response data into two halves acquired in different sessions, finding very similar results. Because numerosity tuning parameters differ slightly between the stimulus conditions used in different scan sessions (9), we split numerosity response data into two halves from the first and second halves of each scan session. Again, this produces very similar results to an odd–even scan split. To evaluate the fits of these models, we quantified the variance each model explained in the fMRI signal from the complementary half of scans (Fig. 1 E and F). This split-scan cross-validation approach allows us to compare the goodness of fit of different models without biases that would arise from additional free parameters in the DoG models: DoG models will only achieve better fits when the fit inhibitory surround captures repeatable signals.

Region of Interest Definitions.

Because we aim to examine relationships between object size tuning and numerosity tuning, we focus on the area around the previously defined numerosity map in posterior parietal cortex (9). As previously described, numerosity tuning models fit the recordings from this area well in all stimulus conditions and participants.

Starting with a tuning model from the average of all numerosity stimulus conditions, we first rendered the preferred numerosities of each recording site on the cortical surface (Fig. 3A and Fig. S7). From this, we define our numerosity map region of interest (ROI). Medial and lateral borders of the ROI (the “ends”) each followed lines of equal preferred numerosity at the low and high ends, respectively, of the preferred numerosity range seen in each hemisphere. Anterior and posterior borders (the “sides”) describe the edges of the topographic organization, which coincided with decreases in the goodness of model fits.

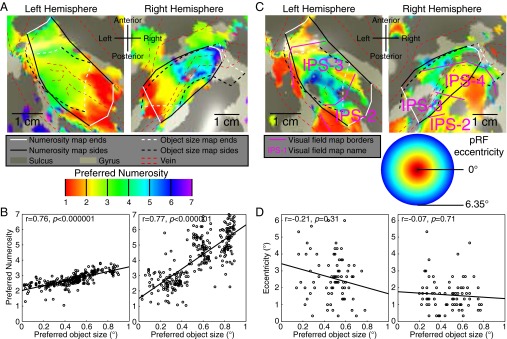
Fig. 3.

Relationships between object size maps, numerosity maps, and visual field maps. (A) Numerosity preferences in the same areas as Fig. 2 form numerosity maps (solid black and white lines) that largely overlap with object size maps (dashed black and white lines). Left hemisphere numerosity maps are less clear than right, and represent a smaller numerosity range. Object size maps are similar bilaterally. (B) Among recording sites that lie in both maps, object size and numerosity preferences are correlated. The ratio of these preferences differs between hemispheres. (C) IPS visual field maps partially overlap with object size and numerosity maps. Object size- and numerosity-tuned responses were not limited to the central visual field positions where their stimuli were presented. Visual field map borders did not coincide with object size or numerosity map borders. (D) Among the fewer recording sites that lie in both visual field maps and object size or numerosity maps, neither object size nor numerosity preferences were correlated with pRF eccentricity or pRF size.

Fig. S7.

Maps of preferred numerosity. (A) Preferred numerosity varies across the cortical surface, in data averaged over all numerosity stimulus conditions. Topographic organization is clearer in the right hemisphere than in the left. Colors represent different preferred numerosities rendered on an inflated back view of the cortical surface, in the same area of cortex shown in Fig. S4. An area of clear topographic representation is defined in black and white. The borders of this area representing minimum and maximum equal preferred numerosities are shown as white lines at the medial and lateral ends of the map. The posterior and anterior borders of this topographic representation are shown as black lines. Data are thresholded based on goodness of fit: In the average data, only recording points where R² is above 0.3 (P < 0.007) are shown; for all individual conditions the R² threshold is 0.25 (P < 0.015). Recording points where the model fits a preferred numerosity outside of the stimulus range are not shown. Dashed red lines outline distortions in the data caused by the presence of large veins on the pial surface (Fig. S3). The object size maps described in Fig. S4 are shown as black and white dashed lines. (B) Progression of preferred numerosity with distance along the maps shown in A in the average data for each subject. Different stimulus conditions are represented as colored lines joining the condition-specific bin means. In the left hemisphere, the rate of change of preferred numerosity across the cortical surface is less than in the right hemisphere, as is the interquartile range of preferred numerosities present in the map. Map organization in the right hemisphere is also more consistent between conditions. Points represent the mean preferred numerosity in each distance bin, with error bars representing the SE. Solid lines are the fit to the bin means. These fit lines are straight in logarithmic space. Dashed lines represent 95% confidence intervals determined by bootstrapping fits to the binned points. For the average of all stimulus conditions, numerosity preferences increase significantly across the map, at P < 0.0001 in each hemisphere (permutation analysis).

Using a similar approach, we rendered onto the same area of the same cortical surface model the preferred object sizes from tuning models fit to the average of both object size stimulus conditions. Medial and lateral borders of object size map ROIs (the ends) each followed lines of equal preferred object size, again at the low and high ends, respectively, of the preferred object size range seen in each hemisphere. Again, anterior and posterior borders (the sides) describe the edges of the topographic organization, which coincided with decreases in the goodness of model fits.

Analysis of Changes Across the ROI.

Having defined lines following the lowest and highest preferred object sizes or numerosities seen in each map ROI, we then calculated the distance along the cortical surface from each point in each ROI to the nearest point on each of these lines. The ratio between the distances to each end line gives a normalized distance along the ROI in the primary direction of change of object size or numerosity preferences. We multiplied this normalized distance by the mean length of the ROI in this direction.

For every 2-mm increase in distance along the ROI, we formed a bin of recording points and then calculated the mean and SE of the preferred object sizes or numerosities of the sites within the bin. We fit lines to bootstrapped samples of the bin means that were the best-fitting straight lines (for object size maps) or logarithmic functions (for numerosity maps); for the progression of numerosity preferences, but not object size preferences, logarithmic functions fit better than straight lines. In both cases, the fits were described by a slope and an intercept term. From the set of bootstrapped fits, we took the median of each fit parameter as the best fit. We determined 95% confidence intervals by plotting all lines generated during bootstrapping iterations and finding the 2.5% and 97.5% percentiles on values for these fits. To determine the statistical significance of these topographic progressions, we tested whether the 95% confidence intervals of the slopes were above zero.

We also performed a permutation analysis to determine the significance of these slopes. We repeatedly (10,000 times) randomize which preferred object size or numerosity was associated with each distance bin and fit the slope of each of these permutations. We then determined the percentage of these permutations with equal or greater slopes than the observed data, giving a probability of observing this slope by chance.

Tuning Widths.

To determine how tuning width changed with preferred object size, we followed the procedure previously used to examine relationships between preferred numerosity and tuning width (9). For each recording site within the map ROI, we first reconstructed the DoG function describing the relationship between presented object size and response amplitude. We measured the width of this function at half its maximum amplitude, the FWHM, and used this measure of tuning width. We then binned recording sites by their preferred object sizes, with preferred object size increments of 0.05° diameter between bins, up to a maximum of 0.9° diameter. Few recording sites with preferred object size above 0.9° diameter were seen, and near the edge of the stimulus range unstable fits are common, as there is little information to distinguish between different tuning widths (11, 29). Where the ROI did not contain recording sites with preferred object sizes over this whole range, fits were limited to the range of preferred object sizes seen. Lines and confidence intervals were fit as described above for the progression of preferences across the ROI. Again, we tested for significant relationships between preferred object size and tuning width by testing whether bootstrapped confidence intervals of these fits included zero slopes. Again, we also performed a permutation analysis.

Fig. 4 shows a set of example tuning functions for a range of object size preferences. To produce these tuning functions, we took tuning model parameters of all recording points in all hemispheres, specifically the widths and amplitudes of the best-fitting positive and negative (suppressive) Gaussian tuning functions. For each of these parameters, we took the best-fitting straight line describing how that parameter changes with preferred object size. We then evaluated these fit lines at values from zero to 1°, using the resulting parameters to plot the example tuning functions shown.

Fig. 4.

Object size tuning functions for a range of object size preferences, following average tuning parameters found across all hemispheres.

Visual Field Mapping Stimuli.

Because posterior parietal cortex contains several visual field maps (32), we also acquired visual field mapping responses to ensure that we did not confuse visual field position-specific responses with object size- or numerosity-specific responses and to examine the relationship between these maps. The mapping paradigm was almost identical to that described in previous studies (11, 12, 29). The stimulus consisted of drifting bar apertures at various orientations, which exposed a moving checkerboard pattern. The stimulus had a radius of 6.35°, larger than the object size or numerosity mapping stimuli (0.75° radius). Two diagonal red lines, which intersected at the center of the display, were also presented throughout the entire scanning run to provide a target for accurate fixation even when the subject was not performing the task.

fMRI Analysis for Visual Field Mapping.

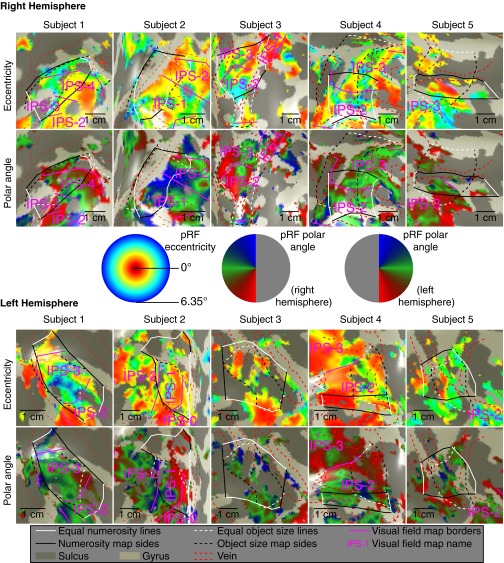
Visual field mapping data were analyzed following a standard population receptive field analysis, as described elsewhere (11, 29). We identified visual field map borders based on reversals in polar angle of visual field position preference and identified particular visual field maps in parietal lobe with reference to previous studies (32) (Fig. S9).

Fig. S9.

Visual field map representations around the object size and numerosity maps, showing the same views seen in Figs. S4, S7, and S8. Borders between visual field maps are marked by purple lines. Dashed red lines show locations of veins, solid black and white lines show the borders of numerosity maps, and dashed black and white lines show the borders of object size maps, as in previous figures. Although visual field maps overlap with the object size numerosity maps, their borders do not correspond and there is no clear relationship between them. (Middle) Relationship between displayed color and preferred visual field position in visual field eccentricity and polar angle.

Relationships Between Object Size, Numerosity, and Visual Field Position Preferences.

Object size-, numerosity-, and visual field position-tuned responses were found in partially overlapping maps. To examine the relationship between any two of these response preferences in each subject, we first selected recording points that lay in both map ROIs. This yielded an ROI intersecting both maps. Across the recording points in this intersection ROI, we determined the Pearson’s correlation between object size and numerosity preferences, and between both of these and visual field position tuned pRF eccentricity and pRF size. Because these data were resampled to higher resolution when interpolating to the common anatomical space, we used the number of acquired recording sites within the intersection ROI to give the degrees of freedom in this statistical test.

To quantify the relationship between the directions of change of numerosity and object size preferences across the cortex, we first computationally flattened the area of cortex surrounding the center of the intersection ROI. Such computational flattening introduces slight spatial distortions into the cortical surface model, and so was not used in other analyses. However, using a 2D representation of the cortex makes calculation and comparison of directions far simpler. We then interpolated the numerosity map, object size map, and intersection ROIs onto this flattened surface.

For every recording site within the intersection ROI, we determined the largest circle that stayed entirely within the ROI. We determined the angle between the vector joining maximum and minimum object size preferences and the vector joining maximum and minimum numerosity preferences. This gave a set of differences between directions of greatest numerosity and size preference changes.

To demonstrate that this difference between map directions was greater than differences between repeated measures, we then computed a set of direction differences between numerosity maps measured in different sessions, computed in the same way. For the set of recording sites remaining in both sets of direction differences, we compared the absolute magnitude of the direction differences using paired t tests in each hemisphere.

To determine whether tuning for visual field positions presented in our stimuli contributed to the responses to our object size stimuli, we first determined the cumulative positions of the object bodies and their edges shown for each presented object size (Fig. S11A). We then used these as inputs to conventional visual field mapping pRF models. We allowed the models to find the best-fitting possible pRF and also constrained the models taking the pRF properties already determined from visual field mapping experiments. For each of the resulting pRF models, we compared the variance explained by each model with the variance explained by object size tuning (Fig. S11B). We then used the best-fitting predictions of each of these models as regressors in a single general linear model to ask whether visual field stimulation parameters explained additional response variance that was not captured by the object size tuning model. We quantified the response variance predicted by components tuned to object size and visual field position (Fig. S11C).

Fig. S11.

Distribution of visual field stimulation for different object sizes, and the potential predictive accuracy of retinotopic stimulation in explaining recorded responses. (A) Stimuli are designed to place object bodies randomly in the same stimulus area for all object sizes, minimizing links between particular visual field positions and particular object sizes. Furthermore, the largest object shown (3.7°) completely covers the area where other object sizes could be presented. This stimulates all these visual field positions but reduces response amplitudes. However, the positions of object edges are unavoidably linked to object size: Larger object sizes tend to have edges at higher eccentricities. Furthermore, the largest object has no edges in the central visual field, consistent with a decrease in response amplitude. Light intensities show positions where object bodies or edges are most likely to appear for a particular object size. (B) Response variance explained by separate models tuned to object size or visual field positions responding to object bodies or edges. Object size tuning predicts responses most closely, but tuned responses to object edge position can predict response well if allowed to choose any position tuning parameters. Here, pRF preferred positions are consistently at the visual field center, with position tuning widths (i.e., pRF sizes) increasing with preferred object size. Responses to conventional visual field mapping (VFM) stimuli, on the other hand, demonstrate that these recording sites prefer visual field positions outside the visual field center. If visual field position tuning properties are taken from VFM models, they predict responses poorly. (C) Response variance explained by the same response predictions when used as components of a single general linear model. Object size tuning continues to predict responses well, but any visual field position tuning captures little additional response variance. Error bars show 95% confidence intervals.

Results

Neural Populations in Parietal Cortex Are Tuned to Object Size.

These stimuli elicited very different fMRI responses at different recording sites (Fig. 1C), which we summarize using object size-tuned population receptive field (pRF) models (Fig. 1 B–D and SI Materials and Methods) (9, 11, 12). We fit object size tuning as linear difference of Gaussian (DoG) functions that include below-baseline suppressive surround responses. These explained more response variance than logarithmic Gaussian functions (Wilcoxon signed-rank test, P < 10⁻¹⁰) or one-Gaussian functions without suppressive surrounds (P < 10⁻¹⁰) (Fig. 1 E and F and Fig. S1A) using twofold cross-validation. Nevertheless, our results do not depend greatly on the tuning model chosen.

Fig. S1.

Stimuli varying in object size and numerosity over time yield different responses captured by different tuning models. (A) Two example fMRI time courses from sites in right posterior parietal cortex, about 2 cm apart, elicited by the presented object size sequence (Top). Points represent mean response amplitudes; error bars represent the SE over repeated runs. In the Upper panel, the largest response amplitude occurs after the presentation of small objects, whereas in the Lower panel the largest response occurs with larger objects, considering the hemodynamic response delay. The tuning model prediction captures much of the variance (R²) in the time courses, indicated by the colored lines. However, different tuning models capture different amounts of this variance. (B) Representation of the tuning models that best fit each time course. The best-fitting models describe linear Gaussian tuning functions with inhibitory surrounds. Tuning models describing other tuning functions perform less well, failing to capture features of the fMRI time courses in A. (C) fMRI time courses from the same two sites in A, elicited by the presented numerosity sequence (Top). Although these time courses are very different, the largest response amplitude in the Upper panel again occurs after the presentation of small numerosities, whereas in the Lower panel the largest response occurs with larger numerosities, considering the hemodynamic response delay. Again, tuning models capture much of the variance in the time courses, and different models capture different amounts of variance. (D) Representation of the tuning models that best fit each time course. The best-fitting models describe logarithmic Gaussian tuning functions. Tuning models describing linear tuning functions perform less well, failing to capture features of the fMRI time courses in C. Dashed lines show the continuation of tuning functions outside the presented object size range.

Object size tuning models summarize the fMRI responses seen using three parameters: (i) preferred object size, (ii) tuning width, and (iii) width of the suppressive surround. They explained the recorded responses well (mean R² = 0.59, median R² = 0.59, P = 0.0016 after false discovery rate correction) in the posterior parietal area surrounding the previously described numerosity map (9). We only examine tuning properties of recording points with preferred object sizes within the stimulus range. Here, response amplitude decreases on both sides of the preferred object size, demonstrating tuned responses. Recording points with preferred object sizes outside the stimulus range monotonically increase or decrease their response as we move through the range of object sizes, with no clear evidence of tuning.

Because a circle’s area is proportional to its diameter squared, we compare fits from tuning models in linear (diameter, radius, or circumference) and squared (area) space. Tuning functions in linear space explain more response variance than those in square space (Wilcoxon signed-rank test, P < 10⁻¹⁰).

Because all objects had the same contrast, display luminance covaried with object size. To distinguish tuning for object size and luminance, we used a control stimulus where the luminance of the object size stimulus was distributed evenly across the largest object in the stimulus set. Responses differed considerably from responses to object size varying stimuli (Fig. S2), so object size-tuned responses do not reflect responses to display luminance.

Fig. S2.

Responses to luminance-varying stimuli from the example recording sites shown in Fig. 1C and Fig. S1 (Upper and Lower panels here correspond to Upper and Lower panels of Fig. 1C and Fig. S1 A and C). To distinguish object size tuning from tuning to mean display luminance, we recorded responses to a stimulus where the mean luminance of the object size stimulus was distributed evenly across the largest object in the stimulus set, 1.3° diameter. During the long period that contained a 3.7°-diameter circle in the object size stimuli, the sequence also contained a 3.7°-diameter circle. Responses differed considerably from responses to stimuli of varying object size: They did not show tuned responses to a specific, low luminance, and response amplitudes increased when a larger circle was shown, which covered visual field positions that were not stimulated by the rest of the stimulus sequence.

Topographic Maps of Object Size.

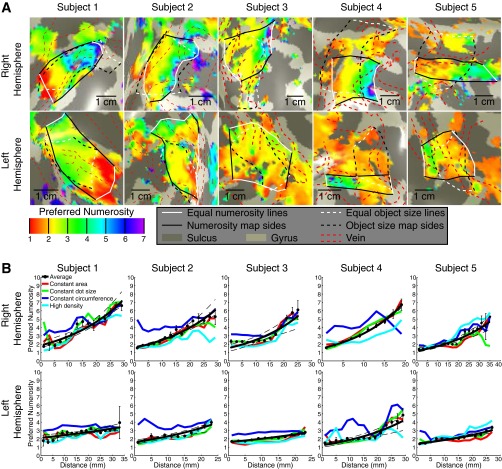
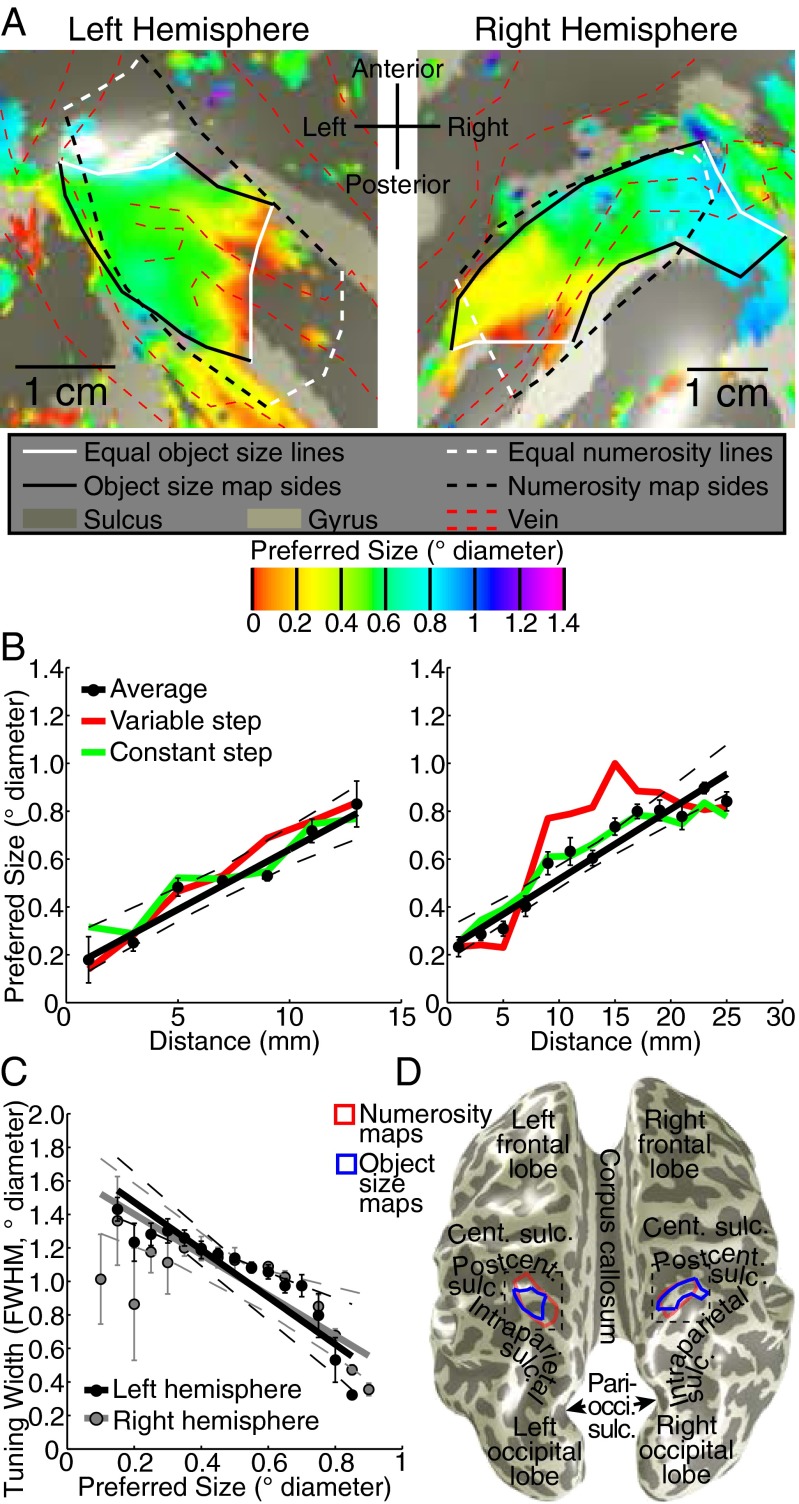
We projected each recording site’s preferred object size onto the cortical surface around the previously identified numerosity map (SI Materials and Methods) (9). This revealed orderly topographic object size preference maps (Fig. 2A and Figs. S3 and S4). These were consistently found in similar locations bilaterally on the medial superior parietal lobule (Fig. 2D), centered at mean (SD) Montreal Neurological Institute (MNI) x,y,z coordinates −23 (4), −57 (6), 55 (9) and 23 (3), −60 (7), 59 (6) in the left and right hemispheres, respectively.

Fig. 2.

Topographic representation of object size. (A) Object size preferences surrounding the previously described numerosity map (white and black dashed lines) (9) for data averaged from both stimulus conditions. Preferred object size changes gradually between lines of equal minimal and maximal preferred object size (white lines) in both hemispheres, forming topographic maps (black and white solid lines). Areas of low signal intensity, corresponding to pial veins (red dashed lines) (Fig. S3), were excluded from further analysis (21). (B) Object size preferences progress approximately linearly along the map. Recording sites were organized by their distances from the white lines in A. The two stimulus conditions are shown as colored lines joining condition-specific bin means. (C) Tuning width decreases as preferred object size increases. (D) Locations of object size and numerosity maps on an inflated cortical surface, relative to nearby major anatomical landmarks. Dashed boxes show the areas detailed in A. Cent., central; Pari-occi., parieto-occipital; Postcent, postcentral; Sulc., sulcus. In B and C, all dots represent the mean in each bin. Error bars represent SEs. All dashed lines represent 95% confidence intervals of the fit (solid line) to the bin means.

Fig. S4.

Preferred object size varies across the cortical surface of right and left posterior parietal lobes in both stimulus conditions. Colors represent different object size preferences rendered on an inflated back view of the cortical surface. An area of clear topographic organization in all stimulus conditions is defined in black and white. The borders of this area representing minimum and maximum equal preferred object sizes are shown as white lines at the medial and lateral ends of the map. The posterior and anterior borders of this topographic representation are shown as black lines. Data are thresholded based on goodness of fit: In the average data, only recording points where R² is above 0.3 (P < 0.018 after false discovery rate correction) are shown; for all individual conditions the R² threshold is 0.25 (P < 0.031). Recording points where the model fits a preferred object size outside of the stimulus range are not shown. Dashed red lines outline distortions in the data caused by the presence of large veins on the pial surface (Fig. S3). This shows the areas around the previously described numerosity maps, whose borders are shown as black and white dashed lines.

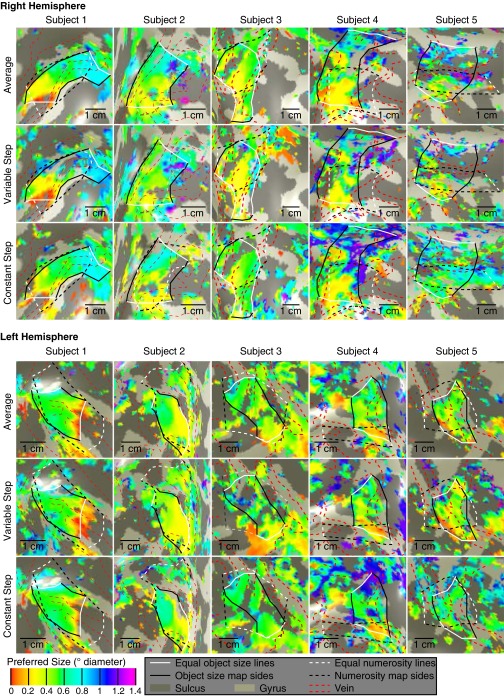
To quantify this organization, we sorted recording sites within each hemisphere’s map by their cortical surface distance from lines of the minimum and maximum object size preferences found in that map. We plotted preferred object size against this distance for each stimulus condition and their average (Fig. 2B and Fig. S5). In all subjects, preferred object size increases significantly and repeatedly across both hemispheres’ cortical surfaces, with similar object size preferences found in separate scanning sessions.

Fig. S5.

Progression of preferred object size with distance along the map (shown in Fig. S4) for both stimulus conditions and the average data for each subject. Points represent the mean preferred object size in each distance bin, with error bars representing the SE. Solid lines are the best linear fit to the bin means. Dashed lines represent 95% confidence intervals determined by bootstrapping fits to the bin means. Object size preferences increase significantly across the map, at P = 0.01 or less in each hemisphere (permutation analysis).

Cortical Magnification and Tuning Widths.

In these maps, preferred object size increases approximately linearly along the cortical surface (Fig. 2B and Fig. S5): Linear functions capture the variance of size preferences with distance as well as more complex logarithmic functions. Tuning widths for object size decrease as preferred object size increases (Fig. 2C and Fig. S6).

Fig. S6.

Tuning width changes across the cortical surface with preferred object size. (A) Change in tuning width across the cortical surface for average data, showing the same views seen in Fig. S4, with the same threshold criteria. Tuning width decreases from the medial to the lateral ends of the map. (B) Tuning width shown as a function of preferred object size: Tuning width decreases as preferred object size increases. Recording points are binned based on preferred object size. Points represent the mean tuning width in each bin; error bars represent the SE. Solid lines are the best linear fit to the bins. Dashed lines represent 95% confidence intervals determined by bootstrapping fits to the bin means. Tuning widths decrease significantly with preferred object size, all at P = 0.007 or less in each hemisphere (permutation analysis).

As such, small object sizes are not overrepresented in comparison with larger sizes, neither by the larger cortical representations nor by the smaller tuning widths seen in the representations of small numerosities, central vision, sensitive somatosensory areas, or dexterous motor areas. Nevertheless, there is a systematic relationship between tuning width and preferred object size.

Relationship to Numerosity Tuning.

We measured responses to stimuli of varying numerosity in the same subjects as previously described (SI Materials and Methods) (9). These yield very different response time courses than stimuli of varying object size (Fig. S1): The tuning functions that explain most response variance differed considerably between numerosity- and object size-tuned responses. First, object size tuning models describing linear Gaussian functions explain more variance than those describing logarithmic Gaussian functions (Fig. 1E). Conversely, numerosity tuning models describing logarithmic Gaussian functions explain more variance than those describing linear Gaussian functions (9). Second, object size tuning models describing DoG functions explain more variance than single-Gaussian functions (Fig. 1F). Conversely, numerosity-tuned models describing single-Gaussian functions explain more variance than DoG functions (Wilcoxon signed-rank test, P < 10⁻¹⁰). So although we find both numerosity- and object size-tuned responses, the underlying tuning functions are quite different.

Relationship to Numerosity Maps and Visual Field Maps.

We found topographic organization of numerosity preferences as previously described (9) (Fig. 3A). Numerosity maps were also consistently found in similar locations bilaterally on the medial superior parietal lobule (Fig. 2D), centered at mean (SD) MNI x,y,z coordinates of −26 (4), −56 (6), 58 (8) and 22 (2), −61 (3), 60 (6) in the left and right hemispheres, respectively. We quantify our previous finding that numerosity maps were right-lateralized, with less-clear maps in the left hemisphere (Fig. 3A and Fig. S7). In all subjects, both the rate of change of numerosity preferences with cortical distance and the interquartile range of numerosity preferences were greater in the right hemisphere than the left (paired t tests, P = 0.023 and P = 0.006, respectively). For object size preferences, neither the rate of change nor the interquartile range differed significantly between hemispheres (P = 0.21 and P = 0.19). As such, numerosity maps are significantly right-lateralized, whereas object size maps are similar in both hemispheres.

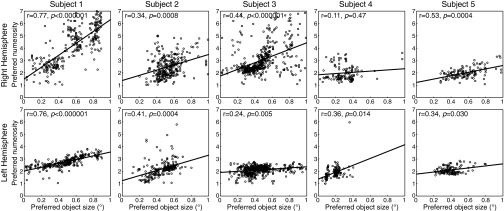
Although object size and numerosity maps were not coextensive, they partially overlapped in each hemisphere (Fig. 2A and Fig. 3A). Among recording sites within both maps, numerosity and size preferences are consistently positively correlated (Fig. 3B and Fig. S8) in 9 of our 10 hemispheres (Pearson’s correlation; Spearman’s rank correlation gave similar results). Although smaller object size and numerosity preferences are consistently associated, the ratio of these preferences differs between hemispheres: Any object size is not consistently associated with a particular numerosity.

Fig. S8.

Among recording sites that lie in both numerosity and object size maps, numerosity and object size preferences are correlated in both hemispheres. Although smaller numerosities are consistently found with smaller object sizes, the slope of this relationship differs between hemispheres. Significant correlation was absent in one hemisphere where the overlap of object size and numerosity maps covers little of the range of object size or numerosity preferences. r values are Pearson’s correlation coefficients. When calculating corresponding P values, the number of recording sites is adjusted to compensate for upsampling of data during transformation to cortical surface models. Lines represent the best-fitting linear relationship between object size and numerosity preferences.

The direction of greatest object size and numerosity preference change (i.e., direction of map progression) also differed in many hemispheres. In 7 of our 10 hemispheres, the direction of change differed significantly more between object size and numerosity maps than between numerosity maps measured in different sessions. Here, object size preferences increased more posterior-to-anterior than numerosity preferences. However, in the other hemispheres, map directions were very similar.

We characterized the intraparietal sulcus (IPS) visual field maps that partially overlap both object size and numerosity maps(SI Materials and Methods) (9) (Fig. 3C and Fig. S9). Several results distinguish object size and numerosity preferences from visuospatial preferences. (i) Object size- and numerosity-tuned responses were not limited to the central visual field positions where we presented their stimuli. (ii) Preferred object size is far smaller than pRF size (σ) at the same sites (paired t test, P < 10⁻⁵ in each hemisphere). (iii) IPS visual field map borders did not coincide with object size or numerosity map borders (Fig. 3C). (iv) Visual field map positions relative to object size and numerosity maps varied considerably between subjects and hemispheres. (v) Among recording sites within both visual field maps and object size or numerosity maps, neither object size nor numerosity preferences were consistently correlated with visuospatial pRF size or eccentricity (Fig. 3D and Fig. S10). However, in the same recording sites, both pRF size and eccentricity are consistently correlated between complementary halves of the visual field mapping data (P < 0.01 in 9/10 and 8/10 hemispheres, respectively), demonstrating sufficient data quality to reveal correlations here. (vi) Tuning models fit to the presented visual field positions predict responses to our object size stimuli poorly (Fig. S11). As such, object size and numerosity preferences here are not associated with visual field position preferences, pRF sizes, or visual field map locations.

Fig. S10.

Among recording sites that lie in both object size maps and visual field maps, object size preferences and pRF properties of recording sites are not consistently correlated. (A) Preferred object size is not significantly correlated with pRF eccentricity. (B) Preferred object size is not significantly correlated with pRF size. (C) Preferred numerosity is not significantly correlated with pRF eccentricity. (D) Preferred numerosity is not significantly correlated with pRF size. r values are Pearson’s correlation coefficients, although Spearman’s rank correlation gives similar results. When calculating corresponding P values, the number of recording sites is adjusted to compensate for upsampling of data during transformation to cortical surface models. Lines represent the best-fitting linear relationship between object size preferences and pRF properties. Although some P values do reach significance at P < 0.05 in individual hemispheres, the directions of these correlations are not consistent between hemispheres, and only 1 of 40 remains significant after Bonferroni correction for multiple comparisons.

Discussion

We find object size-tuned responses in fMRI recording sites in bilateral human posterior parietal cortex. These show that surround suppression and tuning widths decrease as preferred object size increases. Object size-tuned neural populations form bilateral topographic maps: Object size preferences progress gradually and approximately linearly across the cortical surface. We characterize numerosity tuning and maps in the same subjects (9). These overlap largely but not completely with the object size maps. Many properties of object size and numerosity representations differ, suggesting they result from distinct mechanisms. However, object size and numerosity preferences were correlated among recording sites within both maps. Although IPS visual field maps partially overlapped with object size and numerosity maps, neither visual field eccentricity nor pRF size correlated with preferred object size or numerosity. As such, this object size tuning is separated from visual field map structure, so its topographic organization emerges within the brain. Object size representations are instead associated with numerosity representations, suggesting that neural processing generalizes across quantities.

Differences Between Object Size and Numerosity Representations.

Despite similarities between representations of object size and numerosity, we find many differences in both tuning and cortical organization. First, object size tuning is better-described by linear Gaussian functions, whereas logarithmic Gaussian functions characterize numerosity tuning (7, 9, 13–15). Second, object size tuning widths decrease as preferred object size increases. This contrasts with numerosity tuning widths, which increase with increasing preferred numerosity (7, 9, 14).

What is the functional significance of these differences? Logarithmic numerosity tuning functions have long tails that carry some information about high numerosities, although numerosity preferences above five are rarely seen (9, 15). Object size tuning narrows as preferred size increases, bringing all responses to zero at the top of the presented size range (Fig. 4). Modeled tuning functions can also extend below zero, predicting responses to negative object sizes, which cannot exist. More likely, presenting no object (i.e., zero size) produces no response, truncating the tuning function at zero. So, object size tuning functions seem to be limited at both ends of the presented size range, suggesting that tuning properties might change if different size ranges were presented. Such adaptability may allow us to process a broader range of sizes, much like logarithmic tuning functions increase the effective range of numerosity processing.

A third difference is that object size preferences change approximately linearly with cortical distance, whereas numerosity preferences change more gradually for small numerosities (9). These first three properties of the numerosity representation likely underlie better discriminability of small than large numerosities (14, 15). The properties of the object size representation differ considerably from those of the numerosity representation, suggesting that small object sizes may not be far more discriminable than large object sizes. However, visuospatial receptive fields and neural populations with monotonically changing responses to object size (which we do not examine here, and may carry very different information) may also contribute to object size perception. Furthermore, neural populations with broader tuning functions do not necessarily hold less-detailed information (16).

Fourth, presentation of objects far from the preferred size suppresses object size-tuned responses below baseline. Such surround suppression is common in visuospatial responses (12). Although we find no similar surround suppression for numerosity-tuned responses, we interpret this distinction with caution. The presented numerosities did not cover the entire tuning function, so responses to larger numerosities may reveal suppressive surrounds. However, macaque studies have covered narrower single-neuron numerosity tuning functions more completely without finding surround suppression (15).

Fifth, object size maps were similar in posterior parietal areas of both hemispheres. On the other hand, numerosity maps were far less clear in the left than right hemisphere. However, we did find some left hemisphere numerosity map organization, and numerosity preferences here were also correlated with object size preferences. As such, we find no evidence of lateralization of object size processing but evidence of partial lateralization of numerosity processing, as reported previously (17). However, given the relatively small numbers of subjects tested in these studies and the few left-handed subjects tested [one in this study, two in our previous study (9)], this lateralization of numerosity processing may not generalize to the entire population.

Finally, object size and numerosity preferences were correlated where they overlapped. However, the two maps are not coextensive and preferences often changed in different directions along the cortical surface, so these maps are distinct structures.

These differences suggest that distinct mechanisms produce object size- and numerosity-tuned responses. They also demonstrate that the properties of tuning and organization we describe do not result from our methods: Very similar methods can produce different results from different neural populations.

Generalization Across Quantities.

We find overlapping maps of object size and numerosity, with correlated response preferences across recording sites. Macaque recordings reveal neurons tuned for numerosity only, line length only, or both quantities together in parietal cortex (8, 18). Although we examine tuning for object size rather than line length, similar mechanisms are likely to be involved here. Although neurons tuned for numerosity and line length do not show correlated preferences, only 14 such neurons were recorded (8, 18). We use 35–145 recording sites per hemisphere, giving far greater statistical power. We do not show whether the same neurons or nearby neurons have correlated object size and numerosity preferences. It is not necessary for the same neurons to process both quantities for their representations to interact.

Associated object size and numerosity representations are evident in perception. Participants cannot independently choose larger or more numerous objects when objects vary in both dimensions (6): Larger objects are seen as more numerous and vice versa.

Object size and numerosity represent different aspects of quantity. Grouping these neural representations may allow cognitive processing to link different aspects of quantity and generalize subsequent quantity processing (5). In that sense, object size and numerosity maps may be considered subdivisions of a general nonsymbolic quantity representation (5, 9). Other quantities may have similarly organized and linked neural representations.

Mechanisms and Models of Quantity Tuning.

Several mechanisms might produce responses like those we report. Here we examine possible interpretations of our findings.

Could tuning for both object size and numerosity reflect tuning to a single feature that covaries with both quantities? For example, the area surrounding the dot patterns (the convex hull) increases with object size and often, although not always, increases with numerosity, so could tuning for both features reflect tuning for the convex hull extent or the attentional window needed to attend the stimulus? This alternative hypothesis does not fit our results: Our high-density numerosity stimulus condition groups objects in a dense pattern with a much smaller convex hull yet gives very similar responses to less-dense patterns (9). Similarly, object size changes with numerosity in some numerosity stimuli, so could numerosity tuning and correlated quantity preferences both reflect tuning for object size only? Again, this does not fit our results: Numerosity tuning and maps are found even where either individual object size or total object size does not change with numerosity. Where object size does change with numerosity, it decreases with increasing numerosity, predicting negative correlations between numerosity and object size preferences rather than the positive correlations observed.

Furthermore, the many differences in tuning and map organization suggest that different mechanisms are involved. The ratio of object size and numerosity preferences also differs between hemispheres (even in the same subject), whereas any relationship between tuning and stimulus features would not. Therefore, tuning for a single feature cannot explain both responses.

We have previously shown that numerosity tuning is stable across stimulus features but not completely invariant (9): Changing relationships between object size and numerosity influence numerosity estimates. This led to the suggestion that numerosity-tuned responses might reflect tuning for a feature that covaries with numerosity in our stimuli (10). We now show correlated object size preferences at the same sites. Therefore, neural populations preferring small numerosities and small sizes may respond more to larger numbers of small objects than smaller numbers of large objects. As such, effects of object size on numerosity estimates do not reflect a covarying feature but rather related tuning preferences for both quantities in the same neural populations.

“Object size” might describe one of several specific features. We do not find similar responses when varying display luminance without changing object size (Fig. S2). We also show that tuning for linear object size (radius, diameter, or circumference) predicts responses better than tuning for areal object size (area or luminance). We do not distinguish tuning for diameter, radius, circumference (which are directly proportional in the circles we use), and spatial frequency. This distinction does not affect our conclusions: All are measures of object size.

Could visuospatial tuning explain object size tuning? Early visual neurons (and voxels) have spatially limited receptive fields and so prefer particular stimulus sizes. However, we find many differences between our object size preferences and visuospatial tuning of earlier size-tuned responses. First, our stimuli present many objects of the same size at different locations, evenly spread across the same stimulus area. Second, most recording sites’ visuospatial pRFs are outside our size and numerosity stimulus area. Third, preferred object sizes are far smaller than pRF sizes at the same sites. Last, pRF sizes do not correlate with preferred object sizes.

We also show that our maps do not reflect eccentricity changes (or associated pRF size changes) across a visual field map. First, pRF eccentricities are not correlated with preferred object sizes. Second, object size maps do not share borders with IPS visual field maps. Third, relative positions of object size maps and visual field maps differ between subjects and hemispheres.

Quantity-tuned and visuospatially tuned responses in the same cortical area seem independent. This is in line with macaque results, where about 80% of neurons in quantity-tuned areas show no quantity tuning (8). So, independent intermingled representations of quantity and visual space may exist. On the other hand, interactions between quantity-tuned and visuospatially tuned responses may underlie the cognitive spatial “number line” (5).

Several mechanisms have been proposed to derive numerosity tuning from visuospatial responses (13, 19). We hypothesize that object size tuning could be separated from visuospatial tuning through mechanisms that associate similar receptive field sizes across different visual field positions.

Recent studies show that the numerosity of enumerated patterns affects visual short-term memory capacity, suggesting that the numerosity representation guides attention spread between multiple objects (20). This is in line with the parietal and frontal locations of attention and numerosity processing. The object size representation may similarly guide attention spread within single objects. As visual stimuli attract attention, numerosity- and size-tuned responses may reflect properties of the stimulus or the spread of attention the stimulus generates. Because visual processing guides attention and vice versa, attention may be an inherent component of higher-level visual feature representations.

Conclusions

Because object size and numerosity information help guide human and animal behavior (1–3), straightforward mechanisms to derive these metrics may be selectively advantageous. Extending topographic organization into quantity processing suggests that the computational benefits of topographic wiring efficiency (9) apply to both sensory and cognitive systems, providing common organizing principles. Linking cognitive representations in related feature maps may support increasingly abstract cognition and share processing resources between related cognitive concepts.