El Niño−Southern Oscillation frequency cascade

Significance

This study identifies a mechanism to generate atmospheric variability on near-annual and subannual timescales. Responding nonlinearly to both the El Niño−Southern Oscillation (ENSO) and the annual cycle in sea surface temperatures, the atmosphere develops a wide range of deterministic spectral peaks and corresponding spatial patterns. It is demonstrated that the resulting deterministic variability, which projects onto one of the major modes of East Asian Monsoon variability, exhibits similar predictability as ENSO.

Abstract

The El Niño−Southern Oscillation (ENSO) phenomenon, the most pronounced feature of internally generated climate variability, occurs on interannual timescales and impacts the global climate system through an interaction with the annual cycle. The tight coupling between ENSO and the annual cycle is particularly pronounced over the tropical Western Pacific. Here we show that this nonlinear interaction results in a frequency cascade in the atmospheric circulation, which is characterized by deterministic high-frequency variability on near-annual and subannual timescales. Through climate model experiments and observational analysis, it is documented that a substantial fraction of the anomalous Northwest Pacific anticyclone variability, which is the main atmospheric link between ENSO and the East Asian Monsoon system, can be explained by these interactions and is thus deterministic and potentially predictable.

The El Niño−Southern Oscillation (ENSO) phenomenon is a coupled air−sea mode, and its irregular occurring extreme phases El Niño and La Niña alternate on timescales of several years (1–8). The global atmospheric response to the corresponding eastern tropical Pacific sea surface temperature (SST) anomalies (SSTA) causes large disruptions in weather, ecosystems, and human society (3, 5, 9).

One of the main properties of ENSO is its synchronization with the annual cycle: El Niño events tend to grow during boreal summer and fall and terminate quite rapidly in late boreal winter (9–18). The underlying dynamics of this seasonal pacemaking can be understood in terms of the El Niño/annual cycle combination mode (C-mode) concept (19), which interprets the Western Pacific wind response during the growth and termination phase of El Niño events as a seasonally modulated interannual phenomenon. This response includes a weakening of the equatorial wind anomalies, which causes the rapid termination of El Niño events after boreal winter and thus contributes to the seasonal synchronization of ENSO (17). Mathematically, the modulation corresponds to a product between the interannual ENSO phenomenon (ENSO frequency: $f_E$) and the annual cycle (annual frequency: 1 y^-1), which generates near-annual frequencies at periods of $\sim$ 10 mo (1 + $f_E$) and $\sim$ 15 mo (1 − $f_E$) (19).

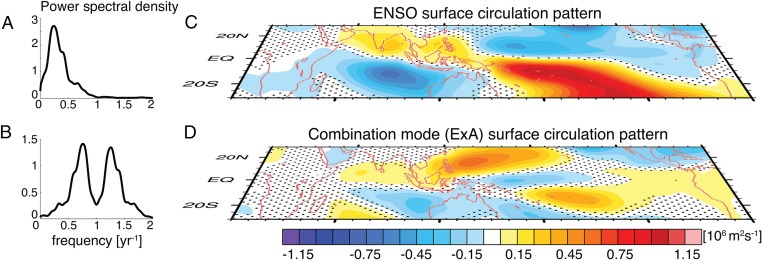
In nature, a wide variety of nonlinear processes exist in the climate system. Atmospheric examples include convection and low-level moisture advection (19). An example for a quadratic nonlinearity is the dissipation of momentum in the planetary boundary layer, which includes a product between ENSO (E) and the annual cycle (A) due to the windspeed nonlinearity: v_E⋅ v_A (17, 19). In the frequency domain, this product results in the near-annual sum (1 + $f_E$) and difference (1 − $f_E$) tones (19). The commonly used Niño 3.4 (N3.4) SSTA index (details in SI Appendix, SI Materials and Methods) exhibits most power at interannual frequencies (Fig. 1A). In contrast, the near-annual combination tones ($1\pm f_E$) are the defining characteristic of the C-mode (Fig. 1B).

Fig. 1.

Schematic for the ENSO (E) and combination mode (ExA) anomalous surface circulation pattern and corresponding spectral characteristics. (A) Power spectral density for the normalized N3.4 index of the Hadley Centre Sea Ice and Sea Surface Temperature data set version 1 (HadISST1) 1958–2013 SSTA using the Welch method. (B) As in A but for the theoretical quadratic combination mode (ExA). (C) Regression coefficient of the normalized N3.4 index and the anomalous JRA-55 surface stream function for the same period (ENSO response pattern). (D) Regression coefficient of the normalized combination mode (ExA) index and the anomalous JRA-55 surface stream function (combination mode response pattern). Areas where the anomalous circulation regression coefficient is significant above the 95% confidence level are nonstippled.

Physically, the dominant near-annual combination mode comprises a meridionally antisymmetric circulation pattern (Fig. 1D). It features a strong cyclonic circulation in the South Pacific Convergence Zone, with a much weaker counterpart cyclone in the Northern Hemisphere Central Pacific. The most pronounced feature of the C-mode circulation pattern is the anomalous low-level Northwest Pacific anticyclone (NWP-AC). This important large-scale atmospheric feature links ENSO impacts to the Asian Monsoon systems (20–25) by shifting rainfall patterns (SI Appendix, Fig. S1B), and it drives sea level changes in the tropical Western Pacific that impact coastal systems (26). It has been demonstrated using spectral analysis methods and numerical model experiments that the C-mode is predominantly caused by nonlinear atmospheric interactions between ENSO and the warm pool annual cycle (19, 20). Local and remote thermodynamic air−sea coupling amplify the signal but are not the main drivers for the phase transition of the C-mode and its associated local phenomena (e.g., the NWP-AC) (20).

Even though ENSO and the C-mode are not independent, their patterns and spectral characteristics are fundamentally different, which has important implications when assessing the amplitude and timing of their regional climate impacts (Fig. 1). Here we set out to study the role of nonlinear interactions between ENSO and the annual cycle (10) in the context of C-mode dynamics. Such nonlinearities can, in principle, generate a suite of higher-order combination modes, which would contribute to the high-frequency variability of the atmosphere—in a deterministic and predictable way.

Idealized Frequency Experiments

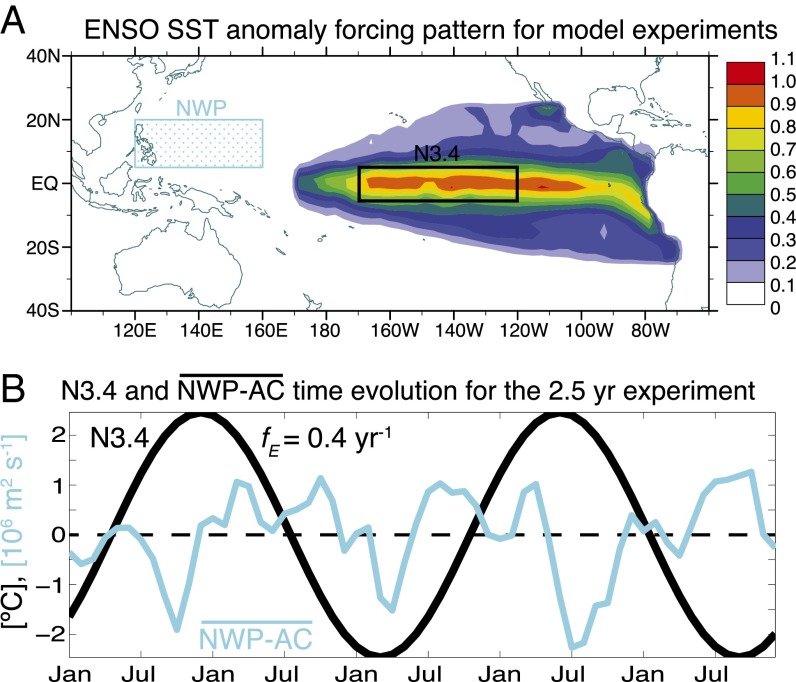
To investigate the nonlinear atmospheric response to interannual ENSO SSTA, in the presence of the annual cycle, we use a similar experimental setup as in ref. 20. The eastern tropical Pacific SSTA pattern (Fig. 2A) is multiplied by a sinusoidal interannual time series (e.g., Fig. 2B for one experiment example) to derive the spatiotemporal evolution of the anomalous boundary forcing for a suite of atmospheric general circulation model (AGCM) experiments using the Community Earth System Model (CESM) Community Atmosphere Model version 4 (CAM4) (27) in a T42 horizontal resolution with 26 vertical levels (details in SI Appendix, SI Materials and Methods). The total boundary forcing comprises the observed SST annual cycle additional to the aforementioned ENSO anomalies. In the following, the warm pool annual cycle time evolution is given the variable A(t), and the ENSO time evolution is given the variable E(t).

Fig. 2.

(A) ENSO SST anomaly forcing pattern for the AGCM experiments. The amplitude of the anomaly pattern is given by the colored shading (no units). The N3.4 (black) and NWP (cyan) regions are marked by two boxes. (B) The time evolution of the N3.4 SST anomaly index (black) and the anomalous ensemble mean circulation index $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ (cyan) for the 2.5-y experiment.

The aforementioned nonlinear processes are an essential part of general circulation models such as CESM CAM4. For an SST boundary forcing that includes only ENSO (E) and the annual cycle (A), the nonlinear interaction during these processes can be expanded with a Taylor expansion, as a sum of terms ${\displaystyle {\sum }_{n=0}^k{\alpha }_{n\left(k-n\right)}{E}^n{A}^{k-n}}$. If we consider only the linear response ($k=1$) as well as quadratic ($k=2$) and cubic ($k=3$) interactions, the following frequencies are generated in the atmospheric response to the SST forcing: the ENSO forcing frequency ($f_E$), its noninteraction overtones ($2f_E$ and $3f_E$), and the quadratic interaction terms ($1\pm f_E$), as well as the cubic interaction terms ($1\pm 2f_E$ and $2\pm f_E$). Here 1 denotes the annual (A) cycle frequency (f = 1 y^-1) and 2 denotes the semiannual (SA) cycle frequency (f = 2 y^-1).

For our experiments, we chose five different discrete idealized ENSO SSTA forcing frequencies ($f_E$) spanning the observed interannual band (Fig. 1A): 3/7 y^-1, 2/5 y^-1, 3/10 y^-1, 3/13 y^-1, and 3/16 y^-1. These choices were motivated by an intended separation of all ENSO forcing frequencies and the resulting ENSO/annual cycle nonlinear interaction frequencies (SI Appendix, Table S1). We also added additional sinusoidal frequency experiments that have some overlapping forcing and interaction frequencies, $f_E$ = 1/2 y^-1, 1/3 y^-1, and 1/4 y^-1, to investigate the role of frequency overlapping in estimating the functional form of the atmospheric response. The expected response frequencies for these experiments, as well as the respective number of ensemble members for each experiment, are listed in SI Appendix, Table S1. The cubic ENSO noninteraction term (frequency $3f_E$) is omitted in the following analysis, as its amplitude is near zero.

When analyzing the nonlinear atmospheric response to the combined ENSO/annual cycle forcing, we focus here on the anomalous low-level NWP-AC because it acts as the crucial bridge between ENSO variability and the East Asian Monsoon system (20). To characterize this anomalous circulation, we define the anomalous surface wind stream function averaged over the NWP region (120°E−160°E, 5°N−20°N, Fig. 2) as our circulation index NWP-AC(t) for each experiment (as in ref. 20). To remove the noise (unforced internal atmospheric variability), the ensemble mean indices are calculated and reduplicated to give a time series of the same length as the original indices, which is labeled $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$. This time series can be considered as the deterministic atmospheric response in the region to the combined ENSO/annual cycle SST boundary forcing.

Higher-Order Combination Modes

The power spectra for the $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ indices for a selected number of experiments (blue lines in SI Appendix, Figs. S2A, S3A, and S4A) show that most of the variance can be attributed to the quadratic combination tone peaks ($1\pm f_E$). However, clear deterministic peaks are also evident for the ENSO noninteraction frequencies ($f_E$, $2f_E$) as well as for the higher-order combination tones. The ensemble averaging has removed nearly all of the internally generated atmospheric noise from the circulation indices, leaving only the modes that originate from the ENSO/annual cycle interactions for our analysis.

Distinctively different anomalous low-level atmospheric circulation patterns (Fig. 3 G−K) are associated with the individual frequency components (Fig. 3 A−E), adding together to the full response pattern (Fig. 3L). Most of the meridionally antisymmetric response can be attributed to the ENSO interactions with either the annual or semiannual cycle. These distinct pattern and associated timescales demonstrate that ENSO’s impact extends far beyond its interannual timescale and canonical response pattern (Fig. 1 A and C).

Fig. 3.

(A−E) Power spectral density for the individual reconstruction components for the 2.5-y Sine ENSO AGCM experiment using the averaged coefficients using the fast Fourier transform (FFT) method. (F) Power spectral density for the anomalous ensemble mean circulation index $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ for this experiment (light blue lines) and the full reconstruction (red lines) using all of the terms depicted in A−E. (G−K) Regression coefficient of the normalized respective reconstruction component and the anomalous surface stream function of this experiment: (G) E, (H) E², (I) ExA, (J) E²xA, and (K) ExSA. (L) Regression coefficient of the normalized full reconstruction time series and the anomalous surface stream function of this experiment.

The very clearly identifiable peaks (SI Appendix, Figs. S2A, S3A, and S4A) at the theoretically expected frequencies (SI Appendix, Table S1) motivate us to use a least square optimization approach to determine the following amplitude (${\alpha }_{n\left(k-n\right)}$) and phase (${\varphi }_m$) coefficients for each experiment. The reconstruction ${\mathrm{\Psi }}_c\left(\text{t}\right)$ is based on the linear, quadratic, and cubic Taylor expansion (the curly brackets indicate the associated frequencies with each term),

$${\mathrm{\Psi }}_c\left(\text{t}\right)=\stackrel{f_E}{\overbrace{{\alpha }_{10}\times \text{E}\left(\text{t}\right)}}+\stackrel{2f_E}{\overbrace{{\alpha }_{20}\times \widehat{\text{E}}{\left(\text{t}\right)}^2}}+\stackrel{1\pm f_E}{\overbrace{{\alpha }_{11}\times \text{E}\left(\text{t}\right)\times \text{cos}\left({\omega }_{A}t-2\pi {\varphi }_1\right)}}+\underset{1\pm 2f_E}{\underbrace{{\alpha }_{21}\times \widehat{\text{E}}{\left(\text{t}\right)}^2\times \text{cos}\left({\omega }_{A}t-2\pi {\varphi }_1\right)}}+\underset{2\pm f_E}{\underbrace{{\alpha }_{12}\times \text{E}\left(\text{t}\right)\times \text{cos}\left({\omega }_{SA}t-2\pi {\varphi }_2\right)}},$$

where ${\omega }_A$ denotes the angular frequency of the annual cycle and ${\omega }_{SA}$ denotes the angular frequency of the semiannual cycle. Because of the single sinusoidal ENSO frequency forcing (${\omega }_E$) with a given phase (${\varphi }_E$), we can write the ENSO time series E(t) with a given amplitude (${\alpha }_E$) in the following form (the second equation has been adjusted to guarantee a zero mean):

$$\text{E}\left(\text{t}\right)={\alpha }_E\times \text{cos}\left({\omega }_{E}t-2\pi {\varphi }_E\right),$$

$$\widehat{\text{E}}{\left(\text{t}\right)}^2=\text{E}{\left(\text{t}\right)}^2-0.5={\alpha }_E^2\times 0.5\cos \left[2\left({\omega }_{E}t-2\pi {\varphi }_E\right)\right].$$

We find that for the cases with nonoverlapping response frequencies, the estimated regression coefficients agree very well (SI Appendix, Table S2). We use these five experiments to calculate the averaged coefficients. The estimates clearly diverge for the experiments with 1/2 y^-1 and 1/3 y^-1 forcing frequencies, as the frequencies from different terms overlap (SI Appendix, Table S1). Using the averaged coefficients ${\alpha }_{n\left(k-n\right)}$ and ${\varphi }_m$ (last line in SI Appendix, Table S2), we now reconstruct our theoretical index time series for each experiment, which includes all of the terms (linear, quadratic, and cubic) listed in the equations above. We find very high correlations (R$>$ 0.9), high spectral coherence, and phase relationships between our reconstructions ${\mathrm{\Psi }}_c$ (refer to Materials and Methods for the reconstruction nomenclature) and the ensemble mean indices (SI Appendix, Figs. S2, S3, and S4 and Table S3), with the largest contribution to the correlation coming from the quadratic combination tones. Furthermore, we see that the full reconstruction captures well the $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ spectrum (Fig. 3F).

Application of the Concept

These results motivate us to test if we are also able to identify these higher-order combination tones in (i) an AGCM experiment with observed nonsinusoidal (broad spectral peak) ENSO forcing and (ii) the Japanese 55-year reanalysis (JRA-55) for the period 1958–2013 (28).

Consistent with the previous idealized frequency experiments, we find that the linear correlation coefficient (R) between the AGCM ensemble mean $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ and the reconstruction using the linear ENSO term is only 0.27. Adding the quadratic and cubic terms increases the correlation significantly to 0.66 and 0.71, respectively. This confirms that our estimated coefficients also hold for a realistic ENSO temporal evolution with a broad spectral peak.

The JRA-55 index comprises, in addition to the fixed pattern ENSO response, attributions from different SSTA patterns as well as internal unforced variability that is not accounted for in our idealized AGCM experiments. Using a multiple linear regression approach, we calculate the amplitude regression coefficients ${\alpha }_{n\left(k-n\right)}$ between the individual response components and the 4-mo low-pass filtered JRA-55 NWP-AC(t) index (SI Appendix, Table S4). The contribution of the quadratic C-mode term is larger in the reanalysis than in the model experiments, most likely because of the C-mode amplification due to thermodynamic air−sea coupling (20). Furthermore, the estimated coefficients agree very well with our previous estimates (from the individual frequency experiments) for both the linear ENSO term and the ENSO interaction term with the semiannual cycle. It is important to note that the JRA-55 reanalysis exhibits a different skewness (caused mostly by the quadratic noninteraction ENSO term) in the NWP circulation than estimated from the AGCM experiments. This is explained by model biases, specifically by a too-strong cyclonic response in the NWP region during the El Niño developing phase.

Using the linear ENSO term alone, we find a correlation coefficient of only 0.04 between the filtered JRA-55 NWP-AC(t) index and our reconstruction (${\mathrm{\Psi }}_a$*). This confirms the negligible direct impact of ENSO on the anomalous NWP circulation. In contrast, when adding the quadratic (quadratic + cubic) term(s), the correlation increases to 0.52 (0.53). Considering only ENSO conditions (when N3.4 is above 0.5°C or below −0.5°), R(JRA-55,$\mathrm{\Psi }$*) values of 0.71 (0.72) can be obtained for El Niño conditions and 0.60 (0.60) for La Niña conditions. These correlations increase even more when considering only strong El Niño and La Niña events.

Our spectral analysis (SI Appendix, Fig. S5) shows a clear cross-spectral coherence between reanalysis, model experiment, and the theoretical reconstruction at the near-annual quadratic combination tone frequencies ($1\pm f_E$). We find statistically significant coherence (above the 95% confidence level) for the frequency bands associated with the quadratic combination tones ($1\pm f_E$) (SI Appendix, Fig. S5C). Furthermore, the phase estimation for the quadratic interaction term between model and theoretical reconstruction is well captured (red line in SI Appendix, Fig. S5B). Additionally, we find significant coherence and phase relationships when comparing the JRA-55 reanalysis with both our model experiment (green line) and the reconstruction ${\mathrm{\Psi }}_c$* (light blue line). No clear coherence or phase signals can be found at higher frequencies associated with cubic interaction terms. Note that in our previous studies (19, 20), we discussed some ambiguity for the quadratic sum tone ($1+f_E$) signal in the observations. Here we can confirm a clear coherence in this frequency range between the JRA-55 reanalysis and our reconstruction (SI Appendix, Fig. S5).

Predictability of the NWP Circulation During ENSO

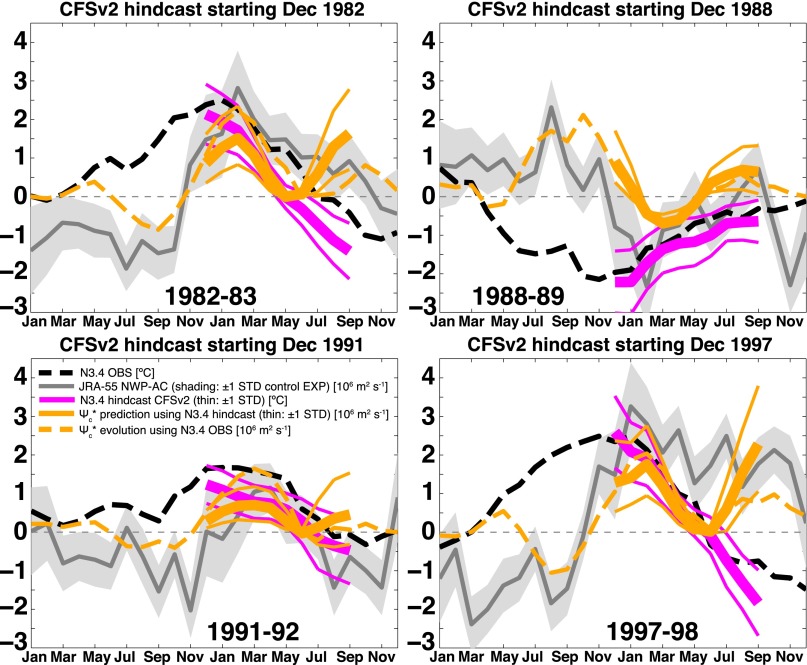
To demonstrate the predictability of the NWP-AC, we use the National Centers for Environmental Prediction coupled forecast system model version 2 (CFSv2) (29) to hindcast the onset (SI Appendix, Fig. S6) and termination (Fig. 4) phases of major ENSO events. All selected termination phase hindcasts begin during the event peak phases in December. As expected from previous studies (17, 19), we see that the N3.4 prediction (thick magenta line for the ensemble mean and thin magenta lines for the 1 SD error) captures the observed evolution of the index (dashed black line) reasonably well. A hindcast of the NWP-AC is performed (thick solid orange line for the mean and thin orange lines for the 1 STD error) using the ${\mathrm{\Psi }}_c$* reconstruction based on the hindcasted N3.4 index. Although large unforced variability is present in the NWP region (gray shading for a conservative estimate using a control AGCM experiment), it is clear that if the N3.4 hindcast (magenta lines) is successful, predictability for the anomalous NWP circulation exists up to 9 mo for both the onset and termination phases of ENSO events, which is a much longer lead time than previous estimates (24).

Fig. 4.

Predictability of the observed NWP-AC circulation during major El Niño and La Niña events. Shown are the observed N3.4 index (dashed black line), the JRA-55 NWP-AC index (solid gray line), and the CFSv2 hindcast for the N3.4 index beginning in December (termination phase) of each event (thick magenta line). The error estimate for the NWP-AC index is 1 SD of the NWP-AC circulation in a 50-y integration of CESM CAM4 with only the annual cycle as forcing (gray shading). The error for the N3.4 hindcast is 1 SD in the ensemble spread (thin magenta lines). The reconstruction ${\mathrm{\Psi }}_c$* is used for predicting the circulation (solid orange line for the prediction and thin orange lines for the 1 SD error) and on the observations (dashed orange line). A small offset between observations and the CFSv2 initialization is explained by both the CFSv2 climatology (1999−2010) and the observational uncertainty of the CFSv2 analysis (the SD of the initial conditions is shown by the range of the thin magenta lines during the first month).

For instance, for the hindcast starting in December 1982, we accurately predicted the NWP-AC in the following boreal summer. Persistence due to thermodynamic air−sea coupling, which is not included in our idealized AGCM experiments, plays a role in sustaining the C-mode response in boreal spring during some El Niño events (e.g., 1982–1983) (20). However, it is the atmospheric response (as captured by our AGCM experiments) that drives the crucial phase reversal of the anomalous NWP circulation and is responsible for the fast near-annual and subannual timescales in this region. For instance, these phase reversals include the rapid transition from cyclonic to anticyclonic circulation starting in October 1982 and the subsequent decay of the anticyclonic anomalies after the peak of the warm pool annual cycle in February 1983 (Fig. 4).

Discussion

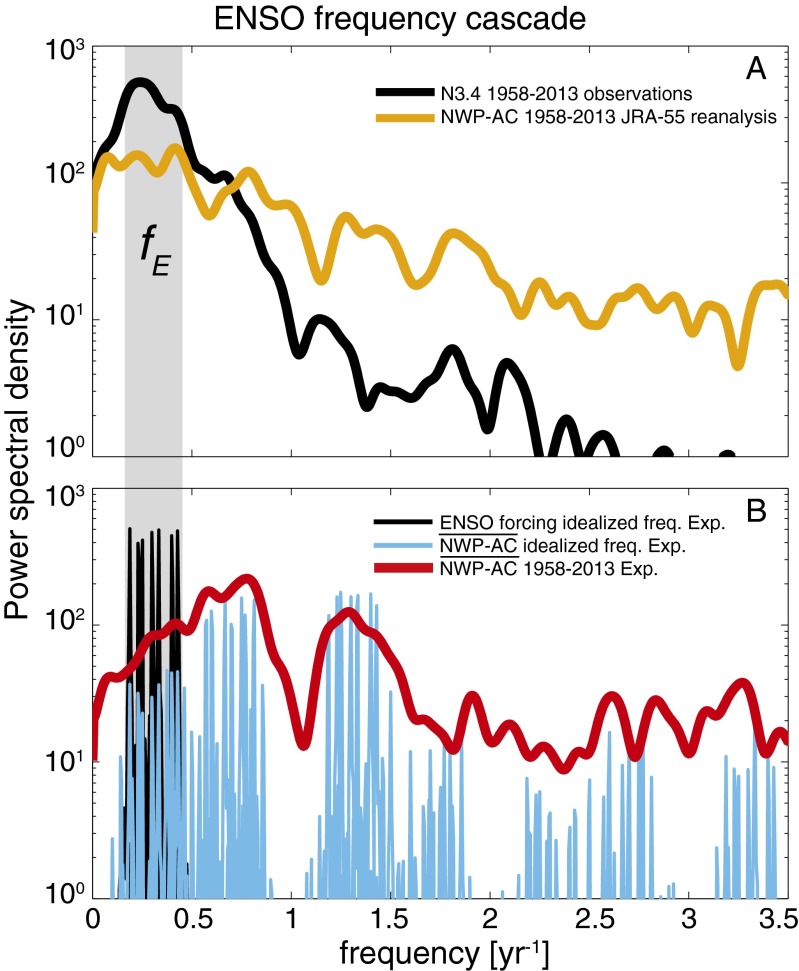
Our results reveal a nonlinear combination mode frequency cascade in the seasonally modulated atmospheric response to ENSO: The nonlinear interaction between interannual ENSO variability and the seasonal cycle results in a wide range of high-frequency variability, with peaks, for instance, at $1\pm f_E$, $2\pm f_E$, $1\pm 2f_E$, and $3\pm f_E$ (Fig. 5). This mechanism changes the fundamental timescales of ENSO’s impacts to predominantly higher frequencies. Hence, a considerable fraction of the atmospheric spectrum beyond the interannual band is purely deterministic and thus potentially predictable during ENSO events. For instance, our estimates from the idealized frequency experiments indicate that up to 50% variance of the anomalous low-level NWP-AC can be attributed to a deterministic signal during ENSO conditions (SI Appendix, Table S5). We conclude that the atmosphere uses the annual cycle as a carrier frequency to effectively transfer power from the interannual ENSO band to higher frequencies.

Fig. 5.

The ENSO frequency cascade: deterministic transfer of power from interannual to higher frequencies. (A) Power spectral density for the normalized 1958–2013 HadISST1 N3.4 index (black line) and the anomalous JRA-55 surface stream function NWP-AC(t) index (orange line) using the Welch method. (B) FFT power spectral density for the ENSO forcing of each individual frequency experiment (thin black lines), and the anomalous ensemble mean circulation index $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ for each individual frequency experiment (thin blue lines). Power spectral density of the anomalous ensemble mean circulation index $\overline{\text{NWP}-\text{AC}\left(\text{t}\right)}$ of the 1958–2013 experiment using the Welch method (red line). All of the Welch power spectra are scaled by the same factor to approximately match the power estimate of the FFT spectra for better visualization.

We outlined a general way to determine the coefficients of this atmospheric response function and to assess the regional importance of the individual frequency components (Fig. 3). Despite evident model biases, we found a remarkable agreement of many of these coefficients between our AGCM and the reanalysis. Further model improvements will allow us to estimate the nonlinear functions with even more confidence. Internal unforced variability and different SSTA forcing pattern play an additional role for the observed anomalous circulation in the NWP region. For instance, the zonal location of the SSTA forcing plays a crucial role in determining the combination mode response (30, 31). The fact that the estimated regression coefficients are largely independent of the forcing frequency indicates a robust atmospheric response to SSTA forcing. This gives us confidence that the proposed methodology can be applied for other climate combination modes. We outlined a very powerful, yet simple, framework to identify any interactions of climate phenomena occurring on different timescales, and showed that a significant part of the atmospheric spectrum in the tropical Western Pacific is due to ENSO/annual cycle interactions and thus is deterministic.

Materials and Methods

To reduce the noise in the JRA-55 index, we first low-pass filtered the index with a 4-mo cutoff Lanczos filter (32). The choice of 4 mo does not interfere with the quadratic and cubic combination tone timescales. Our reconstruction using only the linear ENSO term, labeled ${\mathrm{\Psi }}_a$. ${\mathrm{\Psi }}_b$, includes the linear ENSO term and the quadratic interaction and noninteraction terms. ${\mathrm{\Psi }}_c$ includes all of the aforementioned terms plus the cubic interaction terms. The cross-spectra are calculated using the Welch method. All AGCM experiments use the same SST anomaly forcing pattern (Fig. 2A) with different forcing frequencies and time evolution (e.g., Fig. 2B). The detailed methods can be found in SI Appendix, SI Materials and Methods.