Synaptic circuits and their variations within different columns in the visual system of Drosophila

Significance

Circuit diagrams of brains are generally reported only as absolute or consensus networks; these diagrams fail to identify the accuracy of connections, however, for which multiple circuits of the same neurons must be documented. For this reason, the modular composition of the Drosophila visual system, with many identified neuron classes, is ideal. Using EM, we identified synaptic connections in the fly’s second visual relay neuropil, or medulla, in the 20 neuron classes in a so-called “core connectome,” those neurons present in seven neighboring columns. These connections identify circuits for motion. Their error rates for wiring reveal that <1% of contacts overall are not part of a consensus circuit but incorporate errors of either omission or commission. Autapses are occasionally seen.

Abstract

We reconstructed the synaptic circuits of seven columns in the second neuropil or medulla behind the fly’s compound eye. These neurons embody some of the most stereotyped circuits in one of the most miniaturized of animal brains. The reconstructions allow us, for the first time to our knowledge, to study variations between circuits in the medulla’s neighboring columns. This variation in the number of synapses and the types of their synaptic partners has previously been little addressed because methods that visualize multiple circuits have not resolved detailed connections, and existing connectomic studies, which can see such connections, have not so far examined multiple reconstructions of the same circuit. Here, we address the omission by comparing the circuits common to all seven columns to assess variation in their connection strengths and the resultant rates of several different and distinct types of connection error. Error rates reveal that, overall, <1% of contacts are not part of a consensus circuit, and we classify those contacts that supplement (E+) or are missing from it (E−). Autapses, in which the same cell is both presynaptic and postsynaptic at the same synapse, are occasionally seen; two cells in particular, Dm9 and Mi1, form ≥20-fold more autapses than do other neurons. These results delimit the accuracy of developmental events that establish and normally maintain synaptic circuits with such precision, and thereby address the operation of such circuits. They also establish a precedent for error rates that will be required in the new science of connectomics.

Neuronal networks are widely argued to be highly optimized (e.g., 1, 2), yet few would claim them to be perfect. Existing studies generally fail to address the question of just how perfect they may be because they assume that a network supports specific physiological interactions (3–6) or average the pattern of real connections, or they assume that connections are both exclusive and optimal. However rare, wiring errors violate these assumptions and can only be found by comparing multiple complete examples of the same anatomical wiring diagram. By explicitly documenting synaptic connections using EM, the new approach of connectomics (7) now opens the possibility to study wiring variation more widely. However, existing connectomes (8, 9) have yet to address this issue, and, so far, their accuracy could only be estimated insofar as the underlying circuit was incompletely known. Indeed, only for the nematode Caenorhabditis elegans, a model of determinate cell lineage and complement, is the complete synaptic network known (10, 11). In that case, the probability that a given pair of adult neurons will be connected by chemical synapses if the contralateral homolog is so connected averages 87%, whereas the average probability that a given pair of adult neurons will be connected by chemical synapses is only 75% of the probability that they will be connected in an L4 larva (11).

Few other precedents document the connection accuracy of any nervous system. The task of documenting such accuracy is enabled in the simple nervous systems of many invertebrate animals, in which neurons and their classes are uniquely identifiable from specimen to specimen (12), especially by those systems in which neurons are tiled in parallel repeating pathways, as in the visual system. For example, an early study on the visual system of the crustacean Daphnia (13) reports a roughly threefold range in the number of synapses formed by four specimens of a single neuron, cell D2 left and right, onto each of three types of postsynaptic neuron. The cellular diversity and sheer volume of larger brains or brain regions are profound impediments to comparable studies in most species, but the repeating columnar composition of the optic neuropils of the fruit fly Drosophila, harnessed to the fly’s genetic credentials (14, 15), makes this species propitious for further study, even if its neurons have tiny neurites that are highly branched (16, 17), which are features unfavorable for reconstructing the synaptic circuits to which they contribute. We have therefore developed methods to make such reconstructions semiautomatically (18, 19) and applied these reconstruction methods to the second visual relay station, or optic medulla, the largest neuropil of the fly’s brain (20).

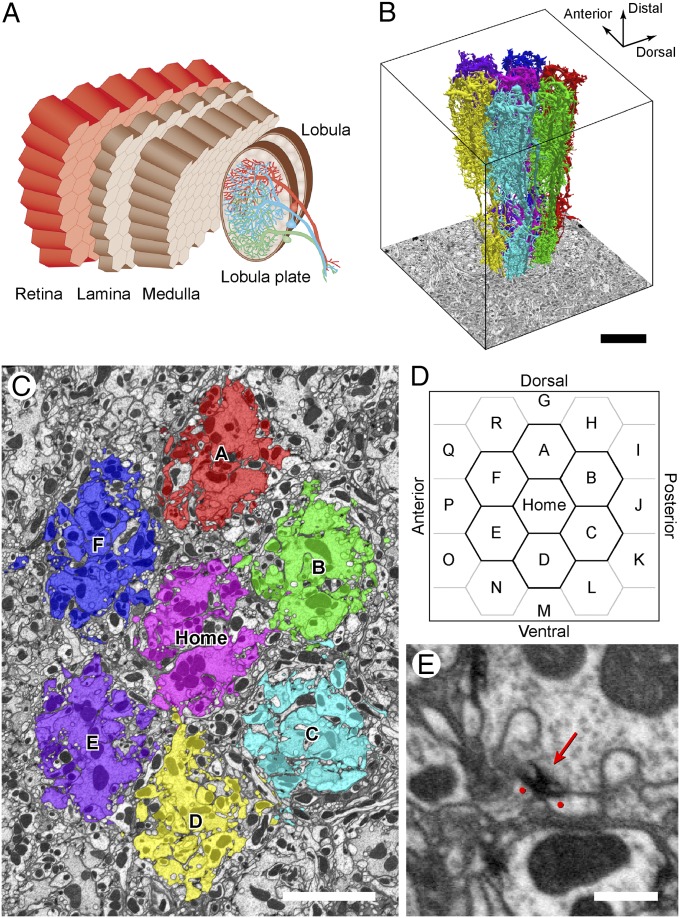
In the fruit fly Drosophila melanogaster, the medulla comprises a retinotopic array of repeating columns (16, 21), each ∼8 μm in diameter and ∼60 μm long (Fig. 1 A–C). Every column contains a fixed group of 27 columnar neurons, 17 medulla cells, and 10 inputs to or from the lamina (two photoreceptor terminals; five lamina terminals; and neurites of T1, C2, and C3) (16, 17, 21) that are morphologically similar from column to column and from animal to animal (16, 21). Together, they constitute what we will define as a module of the medulla’s architecture. The diversity of neuron classes and their packing density have together constituted the major challenge faced by those researchers who would seek to identify wiring specificity in this or other regions of the fly’s brain but are, we suggest, most easily tackled among the repeated neuronal arrays of a visual neuropil. Furthermore, some aspects of the optic lobe’s deeper circuits depend little on the fly’s visual experience (22, 23), indicating that there, at least, the accuracy of synaptic wiring is inbuilt, making the medulla a clear candidate for neuronal stereotypy and an excellent test bed to examine both the accuracy with which neurons contact each other to form synaptic networks and, correspondingly, the accuracy of EM reconstructions used to catalog those networks.

Fig. 1.

Seven-column connectome reconstruction. (A) Overview of the optic lobe of Drosophila, showing the repeating retinotopic architecture of successive neuropils. Modified with permission from ref. 24. (B) Three-dimensional reconstruction of modular medulla cell types in each of seven reconstructed columns. (C) Transverse section in distal medulla stratum M1. Columns (Home and A–F) are colored to conform to B. (D) Plot of a column array. The central Home column is surrounded by its six neighboring columns A–F and 12 more in the outer ring. (E) Focused-ion beam milling (FIB) electron micrograph of neurite profiles with a presynaptic T-bar ribbon (arrow) and two juxtaposed dendrites with PSDs, revealed by membrane densities (dots). (Scale bars: B, 10 μm; C, 5 μm; E, 500 nm.)

Results

Reconstruction of a single circuit cannot differentiate between wiring errors, reconstruction errors, and natural variations. Multiple analyses of identical circuits are needed to determine both the consensus circuit and the accuracy of synaptic connections with respect to this consensus. For this reason, and to analyze multicolumn circuits that we will report elsewhere, we collected and reconstructed an EM image stack of seven medulla columns, a central “Home” column and its six immediate neighbors, columns A to F (Fig. 1 B–D). The completed connectome is among the largest to date for any brain, with ∼900 reconstructed cells, ∼53,500 presynaptic sites, and ∼315,500 postsynaptic sites. Some modular cells are wider than a single column, with their arbors overlapping as opposed to being contained entirely within a single column. As a result, the central Home column, which receives dendrites spreading from its six neighbors, is more completely annotated than the six surrounding columns. Compared with the Home column, which has 2,634 presynaptic sites, the relative completeness percentages of columns A–F are 84.1%, 98.3%, 89.1%, 86.8%, 83.6%, and 83.3%.

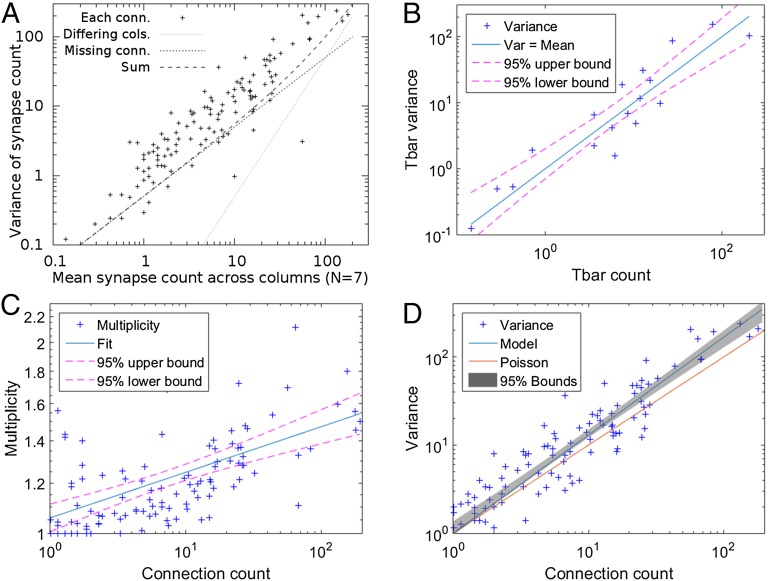
Our analysis addressed the numbers of connections between identified synaptic partners. In the medulla, the sizes of T-bars are relatively uniform, so our estimates used the number of synaptic contacts in parallel, and not their size, as a proxy of pathway strength. “Strong” pathways of more than five synapses, corresponding to those pathways found by serial section electron microscopy (ssEM) in a single column (21), were identical in all columns, although with statistical variation in synaptic strength between columns (Fig. 2 and Table 1).

Fig. 2.

Variation as a function of mean synapse count among connections of the core connectome. (A) Crosses represent the variation in each connection for the seven columns of the core connectome as a function of the mean connection count. Lines represent the two main experimental contributions to this variance, and their sum. “Differing cols.” shows the contribution that would be measured if each column were identical but reported to the estimated completeness. “Missing conn.” shows the variation expected from the incomplete reporting of synaptic contacts, assuming a binomial distribution with P = 0.5. The sum of these experimental artifacts falls well short of the observed variation. (B) Variation in T-bar counts across columns, from medulla stratum M2. A model with variance equal to the mean explains the data to within experimental error. (C) Multiplicity as a function of synapse count. (D) Same data as in A, plus a gray band showing the 95% confidence limits from fitting a straight line to these data. The best fit, not shown, is centered in the gray band. The proposed model from the text, combining the T-bar variance, the multiplicity, and the estimated experimental error, accounts reasonably well for the overall variance. A purely Poisson model, also shown, underpredicts this variance.

Table 1.

Sample data from the core connectome

Pre	Post	Home	A	B	C	D	E	F	Mean	Variance	SD
L1	Mi1	150	158	180	159	161	154	133	156.43	168.82	12.99
L5	Mi1	47	24	46	41	51	45	53	43.86	78.98	8.89
Mi1	L1	26	22	33	31	24	23	24	26.14	15.27	3.91
Mi1	T3	18	23	24	21	17	39	32	24.86	54.12	7.36
Tm2	Mi1	1	0	1	0	2	3	1	1.14	0.98	0.99

Shown are the two strongest presynaptic and postsynaptic partners of Mi1, plus a very weak connection for comparison. Entries at each intercept are the number of synapses between the two cell partners, followed by the mean, variance, and SD of the seven values. The full dataset is given in Dataset S2.

To detect and compare the incidence of different classes of errors, we first extracted a core connectome (Dataset S1), comprising 20 cell types that occurred exactly once in each of the seven columns, and the connections between these cells. The cells were C2, C3, L1, L2, L3, L4, L5, Mi1, Mi4, Mi9, R7, R8, T1, T2, T2a, T3, Tm20, Tm1, Tm2, and Tm9 (16, 21). Of the remaining modular types, T4, Tm3, Tm4, Tm5Ya, and Tm6 could not be unambiguously associated with a column, as required for this analysis. In particular, there are about four motion-sensing T4 cells, of different subtypes, per column. Dm2, Dm8, and Mi15 were missing from one column each, as discussed below, and likewise were omitted. T3 we now believe to be modular; we found one T3 per column in our sample, and an overall count from genetic single-cell labeling is compatible with the number of columns.

Variation Between Columns.

The observed connection strengths among identified modular neurons vary between columns, as shown in Fig. 2A and Table 1. This variation sums true variation and the variation introduced by our reconstruction methods, which has several origins. The largest influences come from the different completeness of the columns in our EM dataset, and the variance introduced by our inability to trace every connection. Making the conservative assumption that we may miss as many as half of the connections, we model this incompleteness by a binomial distribution with P = 0.5. Other sources of human-induced variation, such as differences in the decisions of different proofreaders (the observers who arbitrate profile continuity) and the evolution of tools and procedures that occurred over time during the proofreading, are believed to be less significant, based on repeated reconstructions of subsets of the data by different proofreaders. We conclude that the bulk of the measured variation is biological and, in fact, real (Fig. 2A).

The observed variation in connections cannot be explained by a binomial or Poissonian process involving the likelihood that each pre/post connection exists independently. For such a Poisson distribution, the variance would need to equal the mean, but the observed variation is, in fact, greater (Fig. 2D). All binomial distributions have less variance than Poisson distributions and may also be excluded. The excess variation also cannot be fully explained by variation in T-bar counts, for which the variance equals the mean to within experimental error (Fig. 2B).

One possible way to explain the high variance would be if the likelihood that a connection exists is, in fact, not independent of other connections, such that whenever a single connection is present, multiple other similar connections are also more likely to occur. A possible cause for this multiplication is that single medulla neurons often form multiple postsynaptic densities (PSDs) opposite the same presynaptic site. This duplication differs from the situation in the medulla’s input neuropil, the lamina, where at the tetrad synapses of photoreceptors R1–R6, such multiple contacts are strictly excluded for the dendrites of L1 and L2 (25).

We estimate the “multiplicity” as the average number of PSDs formed by a given postsynaptic cell that contacts a single T-bar (from the total connection count divided by the number of T-bars involved). This multiplicity robustly increases with overall connection count (Fig. 2C). We model this increase with a power law (a linear fit on a log–log scale). Only connections with an average count of at least 1 are considered in the fit, because multiplicity has a lower limit of 1. Combining the known variance in T-bar counts, and the observed multiplicity, with the variance from incomplete reconstruction (as explained in SI Materials and Methods) provides a respectable fit to the observed variance (Fig. 2D).

Contact Area Is Not a Good Predictor of Synapse Number.

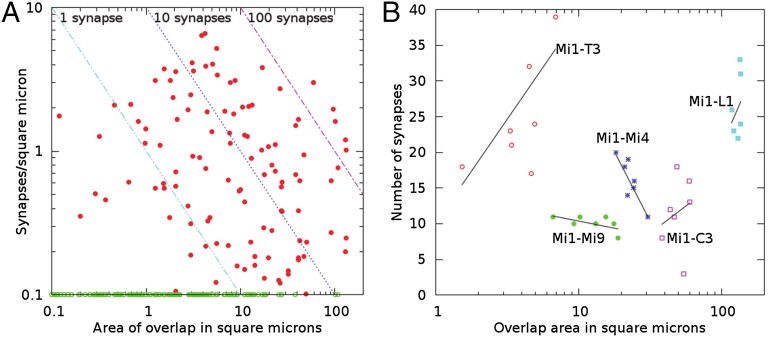
On the grounds that two neurons with extensive contact also have more opportunity to form synapses, a natural supposition might be that synapse count is determined by, or at least correlates with, the area of contact between any pair of neurons. This correlation, known as Peters’ rule, has been established for vertebrate cortical neurons (26), but has so far been of limited application in insect neurons. EM reconstructions provide not only the synapse count but also the area of overlap between neuron partners (Dataset S3) and allow this correlation to be measured directly. The contact area per synapse (square micrometers) varies over almost two orders of magnitude, however, and thus shows little correlation (Fig. 3A).

Fig. 3.

Contact area per synapse within the core connectome. (A) All connections. Cells with overlap but no connections (green) are shown along the bottom axis to appear on a log-scale plot. The diagonal lines represent combinations of area and density that result in the same synapse count between two cells. (B) Contact area and synapse count for the five most numerous outputs of Mi1. Solid lines are least-square fits to the seven examples of each connection.

Even though contact area per synapse varies widely when considered across all connections, it might be possible that the column-to-column count of a particular connection would correlate more closely with contact area. We examined each connection type in the core connectome and calculated the correlation between synapse count and contact area. Even among connections of the same type, contact area was not a good predictor of synapse strength, with fits of opposite signs almost as common as positive correlations. As an illustration, one particular set of connections (Mi1 to its top five partner neurons: T3, Mi4, Mi9, C3, and L1) is shown in Fig. 3B. The same inconsistency between synapse number and contact area that is found among connections in general is also found for specific partners, and for connections in which the overlap measurement is confined to specific medulla strata.

We also found no evidence for strongly conserved ratios of synaptic partners or evidence for area competition (as explained in SI Materials and Methods).

Autapses.

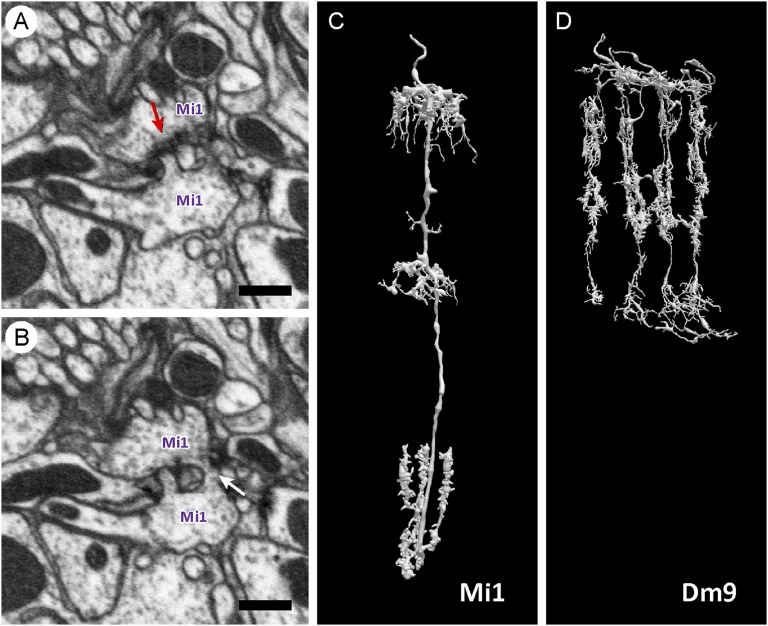
Autapses, at which a neuron synapses upon itself, were identified and double-checked as part of our reconstruction because they are a common reconstruction error. If a significant number of autapses was found for a cell type, each was carefully checked again. We therefore believe that the autapses remaining are not tracing errors but real biological features that constitute a functional part of the connectome. Endorsing their bona fides, they occur at elevated frequencies in just two cell types (Mi1 and Dm9) (Fig. S1). Both cells are postsynaptic at autapses, in 1.96% and 2.6% of cases, respectively, at least 20-fold more frequently than for other cell types, and in both cells, the formation of autapses is consistent in all seven columns.

Fig. S1.

Autapses (self-synapses). (A and B) Mi1 neuron makes a synaptic contact to itself (red arrow). A few sections later, the presynaptic and postsynaptic profiles connect (white arrow in B). (C) Reconstructed Mi1 neuron in the Home column. (D) Dm9 neuron extends between columns. (Scale bars: 500 nm.)

Error Rates of Wiring.

By reconstructing seven complete medulla columns, we could interrogate the synapses of all seven core connectomes. Given the existence of a core connectome, if we find a pathway connecting the same presynaptic to postsynaptic neurons in all seven columns, independent of its strength, then we consider it consistent (Fig. 4A). On average, each synapse we recorded has more than a 99% chance of belonging to such a consistent connection. The few connections that are not reproduced in all seven columns we then consider to be inconsistent connections (ICs). Several lines of evidence lead us to conclude that these ICs are wiring errors, and not biologically deliberate connections or errors of human provenance.

Fig. 4.

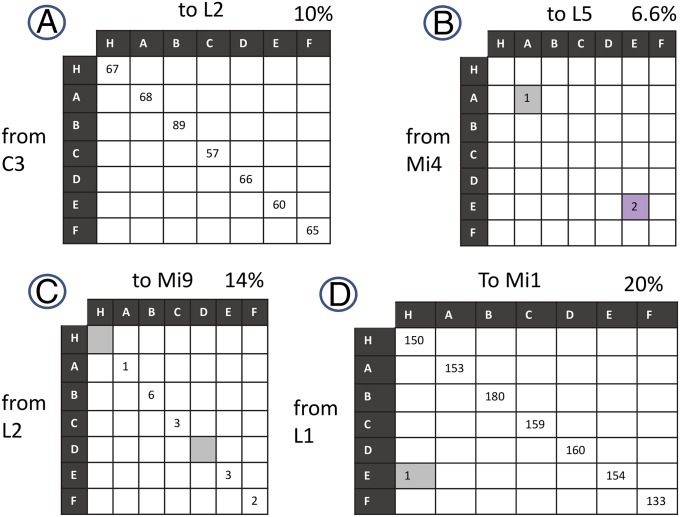
Characterizing connection errors. Plots for each synapse class between presynaptic (vertical columns) and postsynaptic (horizontal rows) partners. Each entry intercept is the number of synaptic contacts from the presynaptic cell (Left) to its postsynaptic partner (Top) for each of the seven columns [Home (H) and A–F]. (A) Completely consistent connection, with seven-column variation in connection strength. (B) Class E + U errors. (C) Class E− errors. (D) Class E + N errors. ICs are shaded throughout. The percentage (of all 400 pre/post pairs) with this pattern is shown at the top right of each matrix. Not shown are examples lacking connections (60%) and connections that did not fall into the patterns shown here (3.5%). The sum exceeds 100% because a single cell pair can have both missing and extra connections.

We classified all ICs into two classes: those ICs that supplement the consensus connection designated as class E+ (Fig. 4 B and D) errors and those ICs missing from it as class E− (Fig. 4C) errors. A third class of error, missing cells, we consider as a limiting case of class E−, in which all connections to a cell are missing. Absent biological intent, a connection found in some but not all columns could be interpreted as either additional or missing connections. For our analysis, we consider a connection found in fewer than half of the columns as an unprogrammed addition (E+) but a connection found in more than half (but not all) of the columns as a biological intent to wire all columns. The remaining connections are classified as missing (E−), and we estimate their strength as the average of the connections that are present.

Different Classes of Errors.

To aid in their analysis, we divide E+ errors into class E + U (the target cell is a target cell type that is normally unconnected by such synapses; Fig. 4B), E + N (the target cell is a normally targeted type, but in the wrong column; Fig. 4D), and AUT (the target cell connects to itself at an autapse) (Table S1). This distinction reflects a commonly proposed mechanism (27), that the cell surface proteins regulating synaptogenesis are specific to particular cell types, and may affect E + U, E + N, and AUT errors differentially. Supporting this hypothesis, we find the two error classes behave very differently as a function of synapse count. E + N errors grow roughly in proportion to the number of synapses, whereas E + U errors decrease for cells with more synapses, suggesting that pathway strength and error rates are governed by different mechanisms.

Table S1.

Biological errors in the core connectome

Type	Inputs	E + U	E + N	E−	Aut	Outputs	E + U	E + N	E−	Aut	Total
R7	178	5	0	0	0	43	6	0	19	0	221
R8	12	0	0	4	0	657	6	4	21	0	669
C2	689	3	0	0	1	795	16	2	35	1	1,484
C3	879	3	1	29	0	2,159	1	5	13	0	3,038
T1	2,474	1	1	12	0	94	9	0	12	0	2,568
T2a	262	1	0	10	0	39	0	0	15	0	301
T2	880	5	8	29	1	91	0	0	5	1	971
T3	502	6	0	0	0	11	0	0	8	0	513
Mi1	2,049	0	38	26	74*	1,255	0	12	0	74*	3,304
Mi4	774	0	10	17	2	718	4	4	18	2	1,492
Mi9	1,304	9	22	22	3	404	10	0	7	3	1,708
Tm20	777	2	10	21	1	131	5	2	16	1	908
Tm1	1,757	2	0	9	7	701	0	0	53	7	2,458
Tm2	1,523	2	0	10	1	685	5	11	19	1	2,208
Tm9	390	14	4	15	0	12	0	0	9	0	402
L1	640	1	2	0	0	3,022	0	9	0	0	3,662
L2	733	4	1	6	4	4,521	4	3	21	4	5,254
L3	56	1	0	25	0	1,103	1	14	1	0	1,159
L4	56	4	0	20	0	223	19	0	4	0	279
L5	2,109	5	20	19	1	1,380	0	36	11	1	3,489
Totals	18,044	68	117	274	21	18,044	86	102	287	21
Percentages, %		0.38	0.65	1.52	0.12		0.48	0.57	1.59	0.12

E−, connections missing from individual cells, although present in the consensus; E + N, connections to normally connected types but in the wrong column; E + U, connections to cell types unconnected in the consensus connectome.

^*These autapses (Aut) are not considered errors; instead, we reason that they are programmed and possibly functional.

Overall, by synapse count, we find 0.43% E + U errors, 0.61% E + N errors, 0.12% AUT errors, and 1.55% E− errors; these rates include those error rates for the most weakly connected neuron partners. We reexamined all E+ errors to verify that they were real and not reconstruction errors (Materials and Methods). This analysis provides a solid lower limit to such errors, but it is possible that additional incorrect connections were missed, so that the true rate could be somewhat higher. By their nature, E− errors are much harder to verify and are naturally generated by typical reconstruction errors, such as the failure to attach correctly a fragment of an arbor to the rest of its neuron. We regard our E− errors as an upper bound and informally suspect that their true rate is closer to the other error rates.

Missing Cells.

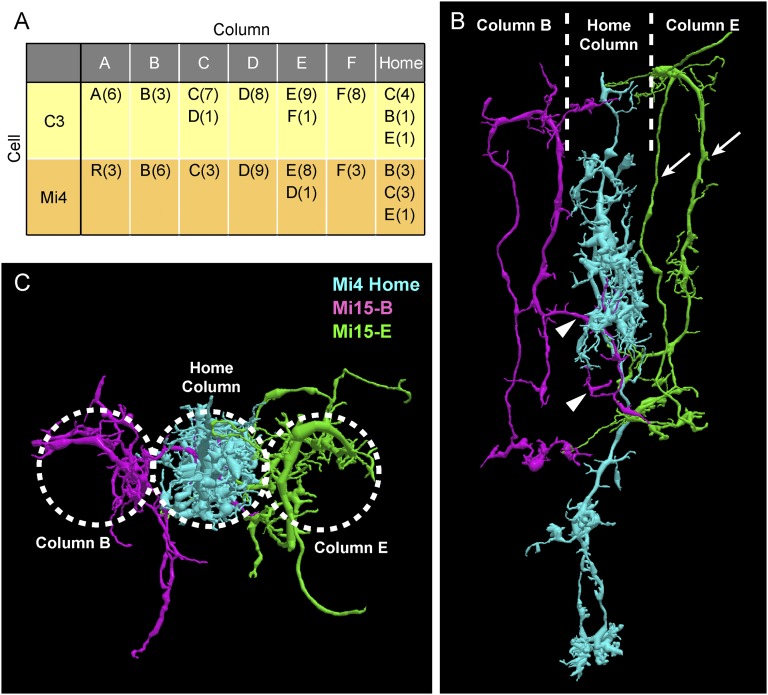
An additional error, missing cells, is only detectable by careful examination of our dense reconstruction of all cells, in which none can hide. From each of three nominally modular cell types, we found one cell missing from the seven columns: distal medulla (Dm) amacrine neurons Dm2 and Dm8, and Medulla intrinsic (Mi) neuron Mi15 (16, 21). We analyzed their potential contribution by adding the three types to the core connectome and then counting all connections to these cells as missing. This analysis raised the incidence of E− errors to 2.5%. The 0.94% increase, unlike the 1.56% base rate, we considered sound because we verified in three different ways that the parent cells were indeed missing (SI Materials and Methods). In particular, Mi15 was missing from the central Home column, making it an especially complete case to analyze in detail. We looked at cells and circuits to which Mi15 would normally contribute and found four qualitative and quantitative changes. Some targets ignored the missing cell, some connected to adjacent cells of the same type, and some extended longer arbors across the gap. More surprisingly, one of the adjacent Mi15s (normally a single-column cell) grew an additional arbor in the missing column, which may well speak to the development process by which these cells organize themselves and find their target connections. These changes are illustrated in Fig. S2 and further discussed in SI Materials and Methods.

Fig. S2.

Missing Mi15 cell in the Home column. (A) Synaptic connections between Mi15 and C3/Mi4. Mi15 is normally presynaptic to both C3 and Mi4 in its own column. However, because the Home column lacks Mi15, the Home C3 and Home Mi4 are instead postsynaptic to Mi15s in the neighboring columns (the number of their contacts is shown in parentheses). (B) Cell in column E (green) is a typical Mi15 with two main branches (arrows). The Mi15 in column B (magenta) extends a branch in the Home column (arrowheads), where the normal Mi15 is missing. This branch connects to Mi4, which is normally postsynaptic to the Mi15 in its own column. (C) Plan view of B. Dotted circles indicate approximate boundaries of columns.

SI Materials and Methods

Tissue Preparation.

The head of an adult Canton-S WT fly, between 5 and 6 d posteclosion, was prepared according to the methods of Takemura et al. (21). This procedure simplified the comparison of the focused-ion beam milling (FIB) SEM imaging methods used here with previous results obtained using thin-section transmission electron microscopy (TEM).

Imaging.

A block face series of 32,000 images was acquired by FIB-SEM at 10 nm per pixel using a Zeiss NVision instrument (47). Between images, a focused ion beam was used to remove 2.5 nm of material from the sample block face. The images were aligned using affine transforms, and consecutive sets of four images were summed to generate isotropic 10-nm voxels.

Annotation, Segmentation, and Proofreading.

Reconstructing synaptic circuits from EM images requires both large amounts of raw data and an intricate network of software and processing tools. The raw data are too large to include as Supporting Information, and the software and processing tools are too complex to describe here in full detail. Therefore, we provide a summary here, and more details can be found in the references; for full datasets and for the software and processing used, please contact the authors.

After images were acquired and aligned, the region of interest was identified and the image set was divided into smaller overlapping cubes. Presynaptic densities were first automatically detected and then annotated on the grayscale images, along with corresponding postsynaptic regions. A watershed algorithm was applied on the pixel-wise predictions to generate the initial oversegmentation of the images within the region of interest. The overfragmented volume was then refined using a context-aware two-stage agglomeration framework (48) to produce the final segmentation. Because errors still persist in the reconstruction after automatic analysis, the segmentation was improved through a manual process of “focused” proofreading, concentrating on the separations between cells that are both biologically improbable and produce important 3D shapes, especially if these boundaries are doubtful (49). An additional inspection concentrated on features thought to be improbable, such as “orphan” fragments that have no cell body and fail to touch the surface of any cube. The cubes were then stitched together using a combination of automatic and manual operations. We assigned cells to previously proposed types by comparing the shapes of reconstructed arbors with the shapes reported from light microscopy using Golgi impregnation (16) or genetic single-cell labeling (figure 2E of ref. 21), as well as from the results of our prior single-column reconstruction (21). Shape matching was undertaken both manually and with the assistance of an automated shape-matching algorithm (50). After the initial proofreading, each synapse had roughly a 98% chance of belonging to the consensus connectome.

Volume Rendering.

Reconstructed neuron bodies were visualized in three dimensions with neuTube software (51). Neuron reconstructions were closely examined to find any proofreading errors. Cell types of reconstructed neurons were identified by matching the shapes of their arbors with the shapes of previously reported neuron reconstructions and from light microscopy.

Verification of Differences Between Columns.

Because the differences between columns are critical to our analysis, they were subject to additional checks. Inspection of the seven-column core connectome was used to generate a list of features not common to all columns. Each connection in this list was rechecked, by one of our two most experienced proofreaders, for the following: that the presynaptic site showed a clear T-bar structure and that the postsynaptic site showed a clear membrane-associated density. The presynaptic site was retraced to verify that it connected to the claimed cell, and the postsynaptic site was similarly traced. Only connections confirmed by all these tests were retained for our analysis. In three cases, a nominally modular cell was present in six of the seven columns but missing from a single column (Dm8 was missing from column B, Dm2 from column D, and Mi15 from the Home column). Because we found these cells in all other columns and our reconstruction is dense, with all elements being traced, an omission should be easily detected. We therefore rechecked in several ways.

First, the six existing examples were rechecked to make sure the identification of cell types was correct. Then, the detailed location of the suspected cell was noted with respect to the main columnar cells in each of the six columns that possessed it. A stratum of the medulla in which the missing cell type has large arbors was selected for this purpose (e.g., stratum M6 for Dm8). The corresponding location in the column missing the cell was reexamined, and every cell profile in the suspected area was checked to verify that it was not part of the cell reported missing.

Finally, seeking further confirmation, we ran two additional tests. First, we found the cell that provides the strongest input to the missing cell in neighboring columns in which that cell exists. For example, Dm8 in all columns receives its strongest input from R7. We found the terminal of R7 in the column lacking an identified Dm8 and checked all of its postsynaptic partners. None of these partners was the missing Dm8. We repeated this analysis for the other missing types. Second, we also ran an experimental shape-matching tool (50) that tried to find cells, or fragments of cells, that could be portions of a specific cell type. In all three cases, this procedure found the six known examples but no other matches in all seven columns.

Combining these multiple tests, we are completely certain that the named cells are indeed missing in the columns we claim to lack them.

Model Combining T-Bar Variation, Multiplicity, and Proofreading Incompleteness.

To estimate the variation we expect to observe for a connection of numerical strength N, we use a model in which the final strength is determined by a three-stage process, with the variation introduced at each stage independent of variation introduced by the others. The first distribution is in the number of T-bars, which we observe has a distribution with the variance equal to the mean (Fig. 2B). In the next step, because many presynaptic T-bar sites incorporate multiple contacts from the same target neuron, the number of presynaptic inputs is multiplied by the mean number of PSDs, or multiplicity (mean m, where m ≥ 1, and variance $V_m$), for each T-bar. Finally, we observe on a probabilistic basis a fraction p < 1 of these connections.

Given that we observe N pre/post connections, we must have started with N/(pm) T-bars. This T-bar count will have a variance equal to the mean (Fig. 2B). So, after stage 1, we have

$${\mathrm{\mu }}_1=N/\left(pm\right),$$

$${\mathrm{\sigma }}_{\mathrm{1}}^2=N/\left(pm\right).$$

Next, we multiply the distribution by m, which has its own variance $V_m$. Because we now have a product of two distributions, we now have a stage 2 distribution with

$${\mathrm{\mu }}_2={\mathrm{\mu }}_{1}m=N/p,$$

$${\mathrm{\sigma }}_{\mathrm{2}}^2={\mathrm{\sigma }}_{\mathrm{1}}^2{m}^2+V_m{\mathrm{\mu }}_{\mathrm{1}}^2=\left(N/\left(pm\right)\right)m^2+V_m{\left(N/\left(pm\right)\right)}^2.$$

Next, we identify synapses from this distribution with a probability p, thus introducing an additional binomial variance ${\mathrm{\sigma }}^2=\left(N/p\right)p\left(1-p\right)$, leading to a final

$${\mathrm{\mu }}_3={\mathrm{\mu }}_{2}p=N,$$

$${\mathrm{\sigma }}_{\mathrm{3}}^2={\mathrm{\sigma }}_{\mathrm{2}}^2{p}^2+\left(N/p\right)p\left(1-p\right)=Npm+V_m{\left(N/m\right)}^2+N\left(1-p\right).$$

The next step is to estimate values for the variable of the model. For each type of connection, say from L1 to Mi1, if there are at least four examples in the seven columns, then we use the connection counts to estimate N, m, and $V_m$ for that specific connection, because these parameters vary by connection type. If there are fewer than four columns with connections, we measure N but assume m = 1 and $V_m=0$. All such connections are very weak. When estimating m and $V_m$, we assume that any untraced connections are statistically identical to the traced connections, and we will connect the same cells in the same proportion as the traced connections of those cells in the same medulla stratum. We use an overall P = 0.5 because this value should not be connection-specific. Using these estimates and the equation above gives the model variance reported in Fig. 2.

Lack of Evidence for Strongly Conserved Ratios.

One option to offset variation in synapse numbers would be to preserve the ratio of connection strengths, even if individual strengths were not preserved. The operation of the circuit might then depend not on the strength of a particular connection but on its ratio with another connection. In this case, the relative strength of two inputs, or the strengths of directly reciprocal connections, could be more tightly controlled as a ratio than the absolute numbers of synapses. Such ratiometric operations have long been used in human-designed circuits (52) and have also been proposed for biological circuits. For example, network operation in a “balanced state” (53) is facilitated by a fixed ratio of excitation to inhibition but does not require a specific synapse count.

We tested the possibility that ratios were preserved by looking for tightly distributed ratios of strengths. We did this analysis across the seven columns for all connections in our core connectome. There are several confounding factors to this analysis. First, the individual connection strengths correlate with an overall column strength that is influenced, in turn, by the column completeness, as discussed in Results. Second, the connection counts in different columns are positively correlated in general, although not to a level at which the ratios are more conserved than the counts that generate the ratios. Because of these correlations, and the large number of potential pairs (160,000), some fraction of tightly conserved ratios would be expected by chance alone, even without any mechanism that explicitly preserves such ratios.

We tried two different forms of analysis, with both giving similar results. In the first and simplest analysis, because a tightly constrained ratio implies a high correlation, we looked at the correlation across connections and recorded those connections with unusually high values. In the second analysis, we expressed the variation in each connection, and the corresponding ratio, as a percentage of the mean and recorded all cases in which the ratio had a tighter relative distribution than either of its parent connections. Using both metrics, we first discarded pairs containing 0 strength connections, for which ratios make no sense. We then looked at three subsets of the remainder: all pairs (5,550 pairs), all pairs with a common cell type (1,338 pairs), and all directly reciprocal pairs (28 of these pairs were found).

We compared our results with a null hypothesis constructed from 10,000 artificial examples in which each connection across all seven columns had the same mean and SD as the real connection, but in which all connection strengths were uncorrelated. Each of these examples was subjected to the analysis above to estimate the range of values expected by chance. This analysis is conservative, because including the known columnar correlations would lead to even more false-positive results in the null examples.

Using the correlation metric, we found in our data an average correlation of −0.007 for all connections, 0.051 for all connections to a single cell type, and 0.047 for reciprocal connections. These values are far short of the level needed to ensure conserved ratios. Looking instead at the strongest correlations (r > 0.9), we found 22 cases in all pairs, four in cell pairs, and none in reciprocal connections. However, the null hypothesis gave 18 ± 6 cases for all pairs, 4 ± 2 cases for cell pairs, and 0.096 ± 0.43 cases for reciprocal connections. We therefore conclude that the number of strongly correlated connections does not significantly exceed the number predicted by chance.

We also looked at the strongest correlations explicitly to see if they were perhaps too strong to be obtained by chance alone. However, each case we examined was also found many times in the null examples. Even the least likely occurred in about 1/3,600 of all trials, which is not convincingly rare, given that we tested more than 5,000 pairs.

In our current reconstruction, we therefore conclude that we have no strong evidence for more, or more strongly, preserved ratios than predicted by chance.

No Evidence for Area Competition.

A related possibility could be that the sum of two connection strengths is preserved. This conservation of the sum could happen, for example, if membrane contact area were a limiting factor, so that if there were more synapses of type A, there must be fewer of type B. To test this possibility, we looked for both strong negative correlation and all examples in which the sum of two connections had smaller variance than either of the numbers of parent synapses (all expressed as a fraction of the mean). As above, similar results were obtained assuming the null hypothesis. This finding is consistent with the observation that very few connections appear close to the physical limit of synapse density.

Adaptations Downstream of Missing Cells.

As reported in the main text, the Home column is missing cell Mi15. We observed four different consequences on downstream cells:

• i)One of the downstream cells is C3. All other C3s connect to the Mi15 in their own column. Lacking the Mi15 in its own column, the Home column C3 connected instead to the Mi15 in three adjacent columns (Fig. S2A).
• ii)Another downstream target cell is Dm7. This cell normally collects input from a large number of Mi15s. It appeared simply to ignore the missing connections.
• iii)Another downstream target cell is Mi15 itself. We cannot, of course, say whether the omission of Mi15 in the Home column should be interpreted as a morphogenetic accident or as part of a normal distribution of Mi15 with omissions from every seven or more columns, but the Mi15s in the neighboring columns would normally be postsynaptic to the missing Mi15 in the Home column. Lacking their normal Mi15 partner, the Mi15s in two neighboring columns B and E instead reached across the gap to Mi15 cells on the far side, extending in the process a far longer neurite than any other Mi15 in the reconstruction.
• iv)The most interesting case, however, is provided by Mi4 (Fig. S2). This cell, which would normally be postsynaptic to the missing Mi15, now connected instead to the Mi15 in neighboring column B. Looking at this connection more closely, the Mi15 in each column is normally centered in its own column. In column B, however, the Mi15 had a horizontal dendrite at the M3/M4 boundary and then formed an additional arbor in the middle of the Home column. No other Mi15 behaved in this manner.

Comparison of Circuits in Two Animals.

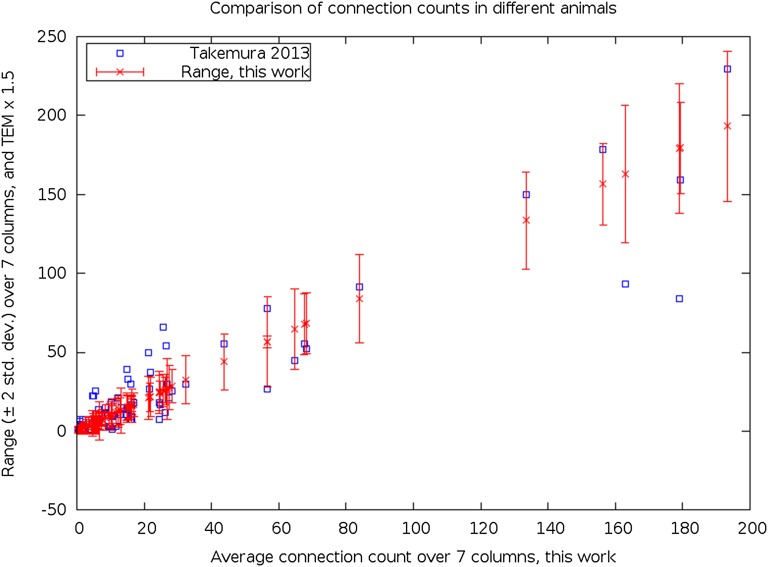
The seven columns analyzed in this study are all from a single WT fly. How closely do its circuits match the circuits in other flies? Takemura et al. (21) reconstructed a single column in a different fly, but complicating the comparison, they used a WT Oregon R female fly, with different techniques having differing resolutions [3.1 × 3.1 × 42 nm using ssEM (21) compared with 10-nm isotropic voxels using FIB-SEM here]. Relative to cells in the first study (21), we identified about 1.5-fold as many T-bars and more PSDs [six (sextads), on average, as opposed to four (tetrads) seen with ssEM]. These differences in detection result from the improved z-axis resolution in our isotropic FIB stack, compared with the z-axis resolution available in ssEM, in which our ability to see T-bars and PSDs in the depth of the stack is limited by section thickness.

Given that there are 1.5-fold as many T-bars in our FIB-SEM data as were found using ssEM (21) if we multiply the reported transmission electron microscopy (TEM) counts by 1.5, the TEM data fall almost entirely within the variation found in the seven columns with FIB-SEM. In Fig. S3, the latter are plotted for each pathway as a range bar showing the mean ±2 SDs relative to the single connection number (key) seen with ssEM (21). The outlier ssEM data to the lower right find a natural explanation because they are the connections to the neuron T1. If this neuron were missing one or more of its branch(es) in stratum M2, we would expect reductions to the many presynaptic sites on T1 seen in TEM. The points to the upper left of the diagonal (TEM counts more numerous than FIB) involve much weaker connections, and predominantly consist of connections to a single cell, C2. All other connections are compatible with the hypothesis that the circuit is the same to within biological variation in the two flies, but reported to 1.5-fold greater completeness in the FIB-SEM data. We additionally conclude that there are no numerical differences between the two different WTs.

Fig. S3.

Comparison of the connection counts in two individual flies.

Discussion

Discrepancies in wiring are informative for three main reasons. First, they are a biological phenomenon, one that defines the function of circuits, such as those circuits for motion, which have high temporal resolution, setting a standard for the accuracy in some cases that we might seek in other networks of neurons. Second, as in genomics (28), knowledge of biological error rates, and the demonstration that analytical tools can attain these rates, is a fundamental prerequisite for the science of connectomics. Third, the quantification of errors reveals the performance limits of the mechanisms that direct the initial wiring. Circuit changes downstream of such errors additionally show the adaptive capacity of network wiring. We refer to such variations as errors, recognizing that our sample represents only core circuits of modular neurons, and these neurons at only a single point in time. The medulla’s circuits formed by nonmodular neurons may differ, whereas connections we consider to be errors may be only transient. Such transient events may represent an avenue for structural plastic changes in the optic lobe, for example, such as those structural plastic changes occurring on a circadian basis among lamina synapses (29). We consider circuit constancy in the context of motion sensing, but many of the synapses must also be the substrate for other sensory circuits. Our reconstructions reveal minor variations in branching patterns of the same cell type in different columns that we interpret as relational, which are required to match reciprocal variations in target neurons so as to establish constancy in pathway strength.

Our results reveal that, on average, only 0.5% of the recorded synapses distributed among all cell types are not part of a consensus circuit and that, at most, 1.5% of the synapses that we might expect to find in any one connection are missing. Compared with recorded variation in the corresponding synapses of the crustacean Daphnia (13) or different specimens of the nematode C. elegans (11), we believe that the fly’s circuits are the most accurate reported to date in the literature. They reveal a clear numerical separation among strong pathways with many parallel synapses that constitute effective network pathways and minor exceptions that may be functionally trivial and perhaps attributable to developmental noise.

Even though these results show impressive stereotypy, they are subject to particular limitations. The seven columns are all from adjacent columns near the center of one eye from a single fly, and hence subject to very similar visual experience as well. Cells elsewhere in the medulla, particularly those cells beneath the dorsal rim (e.g., 30), are known to differ. The difference between individual flies may be greater as well, although our results are consistent with the results from a single-column reconstruction in a different animal (Fig. S3). The possibility for stratum-specific or local microcircuit variations is real, but few models exist for this possibility in the fly. We searched for conserved local microcircuits by performing many of our analyses on a per-stratum basis, but these analyses were even more limited by the statistics of small numbers than our whole-cell analysis, allowing no firm conclusions.

We have examined the issue of wiring accuracy within the context of our analysis of motion-sensing circuits, exploiting the arrangement of parallel pathways typical of visual systems. We now understand that these circuits will emerge, as in the vertebrate retina (31), not from exclusive pathways for each parallel channel but from hitherto unsuspected combinations of interconnected microcircuits, each with an accuracy now defined. Although motion detection circuits in insects (32) have long been modeled from studies on quantitative behavior (33, 34) as a single circuit, their accuracy has never been examined previously, albeit the crystalline composition of the fly’s optic medulla has always offered that prospect.

What significance should we attach to our putative errors, the ICs? Can they improve network performance, and thus be considered in any way functionally adaptive? It is possible that at least some ICs are adaptations to upstream differences in the lamina or photoreceptor neurons, or that they may add noise to a circuit to improve its performance, as is sometimes used in both human-made (35–37) and biological circuits (38). There is also evidence that some nerve cells respond better when their input has a random component (39). These adaptations seem unlikely in the medulla, however, insofar as upstream compensation, or noise injection, would be best served by specific additional connections added at particular points in a network, whereas the observed ICs vary from column to column and include all cell types. Are ICs then simply morphogenetic errors? It may be significant that the projection patterns of R1–R6 photoreceptor terminals in an error-prone region of the fly’s eye also had an error rate of about 1.5% (40), a magnitude similar in larger scale miswiring to the magnitude found here at a very local scale, among synapses. On the other hand, error rates, measured directly for the differentiation and axon targeting of large numbers of Drosophila photoreceptors, show that ∼0.08% of photoreceptors may be missing and that 0.04% of axons innervate the wrong cartridge (41). These rates are thus at least an order of magnitude less inaccurate then the synaptic errors we report here.

If visual pathways have evolved to process information at near-optimal performance, this comparison between morphogenesis and synaptogenesis suggests that the limit to accurate signal transfer may be set at the level of the synaptic populations. It is not clear whether this mismatch reflects the limit set by programming cell adhesion during synaptogenesis, or whether it may reflect that the selective pressure on any one connection in a distributed and redundant network is less than the selective pressure on an entire sensory neuron. Alternatively, it may be functionally important, injecting noise in a programmed network.

We also observe that the largest cells with most synapses, such as L1, L2, and Mi1, have fewer E + U errors than cells with fewer synapses. This counterintuitive finding could be explained by selective pressure to optimize the function of these presumably major input neurons. Combining these lines of evidence (the presence of errors on every cell type, their lack of obvious function, comparability with other error sources, and fewer errors on cells with more synapses) leads us to conclude that ICs simply indicate the accuracy attained by the mechanisms of neuronal synaptogenesis when wiring the medulla. These mechanisms may include the mechanisms of chemoaffinity (42) or those mechanisms involved in exclusion of incorrect connections through self-avoidance (43, 44). These mechanisms, along with other cell surface and secreted molecules, are thought to regulate synaptogenesis between synaptic partners, forming the basis for the accuracy of synaptic connections we report.

Autapses are a special case of synapse found at elevated frequency in two cells, Mi1 and Dm9, and elsewhere at specific sites of various regions of the vertebrate brain (45, 46). Most are thought to be inhibitory, and therefore self-limiting, maintaining the precision with which a neuron fires action potentials (46). Normally, neurites are rigorously excluded from contacting their own neuron; in Drosophila, the cell adhesion molecule Dscam1 promotes the repulsion of processes of the same neuron among axons (43) and synapses (25). We tentatively interpret autapses on cell types Mi1 and Dm9 to reflect the reduced effectiveness at these two specific neurons of DScam1-mediated self-exclusion, which normally prevents the self-contact that occurs at autapses.

The biological error rates shown here set a limit to the accuracy needed in connectome reconstruction, the network simulations these connectomes can support, and the functional analyses they predict, on a cell-by-cell basis. Furthermore, we have shown, for the first time to our knowledge, that EM reconstruction can be sufficiently accurate to expose underlying biological errors in connectivity, even in the most stereotyped circuits known. Combined, these rates provide us with quantitative targets against which other circuits may be compared as we proceed to document yet larger connectomes.

Materials and Methods

We used focused-ion beam milling SEM (47) in Drosophila prepared, as previously reported (21), after high-pressure freezing and freeze substitution (SI Materials and Methods). We imaged a 40 × 40 × 80-μm volume at an isotropic resolution of 10 nm per pixel and reconstructed all columnar and noncolumnar neurons, including tangential fibers, in the seven-column volume. For each neuron, we used semiautomated prediction software to identify presynaptic sites, which are marked by an organelle, the T-bar ribbon, at the release site in Drosophila. Opposite the T-bar, we identified membrane densities (PSDs) at postsynaptic sites (Fig. 1E).