Preventing fibril formation of a protein by selective mutation

Significance

Protein folding intermediates are associated with formation of amyloid fibrils, which are responsible for a number of neurodegenerative disorders, such as Alzheimer’s, Parkinson’s, Huntington’s, and Creutzfeldt-Jakob’s diseases. Alzheimer’s disease is one of the largest problems nowadays, with a significant rise in the number and cost (more than $1 trillion a year by 2050 will be spent in the United States alone unless action is taken to shift current trends; www.alz.org). Therefore, elucidation of the origins of formation of intermediates and finding ways to prevent them are very important. The presented findings may lead to an understanding of the structural mechanisms by which intermediates initiate fibril aggregation.

Abstract

The origins of formation of an intermediate state involved in amyloid formation and ways to prevent it are illustrated with the example of the Formin binding protein 28 (FBP28) WW domain, which folds with biphasic kinetics. Molecular dynamics of protein folding trajectories are used to examine local and global motions and the time dependence of formation of contacts between C^αs and C^βs of selected pairs of residues. Focus is placed on the WT FBP28 WW domain and its six mutants (L26D, L26E, L26W, E27Y, T29D, and T29Y), which have structures that are determined by high-resolution NMR spectroscopy. The origins of formation of an intermediate state are elucidated, viz. as formation of hairpin 1 by a hydrophobic collapse mechanism causing significant delay of formation of both hairpins, especially hairpin 2, which facilitates the emergence of an intermediate state. It seems that three-state folding is a major folding scenario for all six mutants and WT. Additionally, two-state and downhill folding scenarios were identified in ∼15% of the folding trajectories for L26D and L26W, in which both hairpins are formed by the Matheson–Scheraga mechanism much faster than in three-state folding. These results indicate that formation of hairpins connecting two antiparallel β-strands determines overall folding. The correlations between the local and global motions identified for all folding trajectories lead to the identification of the residues making the main contributions in the formation of the intermediate state. The presented findings may provide an understanding of protein folding intermediates in general and lead to a procedure for their prevention.

An intermediate state in protein folding is involved in amyloid fibril formation, which is responsible for a number of neurodegenerative diseases (1–7). Therefore, prevention of the aggregation of folding intermediates is one of the most important problems to surmount. Hence, it is necessary to determine the mechanism by which an intermediate state is formed. For example, one of the members of the WW domain family (8, 9), the triple β-stranded WW domain from the Formin binding protein 28 (FBP28; Protein Data Bank ID code 1E0L) (10) (Fig. 1N), has been shown to fold with biphasic kinetics exhibiting intermediates during folding (3, 5, 6, 11–16). We address this problem here with the design of new FBP28 WW domain mutants and by examining their structural properties and folding kinetics.

Fig. 1.

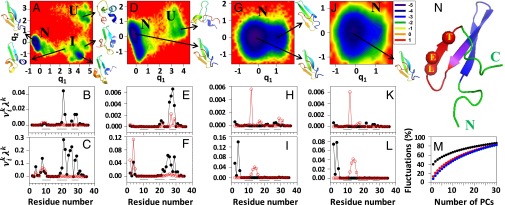
FELs (kilocalories per mole) along the first two PCs with representative structures at the minima, and contributions of the principal modes (defined in SI Materials and Methods) [${\nu }_i^k{\lambda }^k$; black lines with black circles (principal mode 1) and red lines with white circles (principal mode 2)] to the MSFs along the θ- and γ-angles for the (A–C) three-state, (D–F) two-state, and (G–I) downhill folding trajectories of L26D and (J–L) the downhill folding trajectory of L26W. The black lines on the bottoms of B, C, E, F, H, I, K, and L correspond to the β-strand regions. I, intermediate; N, native; U, unfolded. M represents percentages of the total fluctuations captured by the PCs for three-state (black line), two-state (red line), and downhill (blue line) trajectories of L26D and the downhill folding trajectory (green line; indistinguishable from the blue line) of L26W. N represents the experimental structure of FBP28, in which the mutated residues are represented by spheres, and hairpins 1 and 2 are represented by blue and red, respectively (the purple region corresponds to the overlap of these hairpins). C, C terminus; E, glutamic acid; L, leucine; N, N terminus; T, threonine.

Because of the small size, fast folding kinetics, and biological importance, the formation of intermolecular β-sheets is thought to be a crucial event in the initiation and propagation of amyloid diseases, such as Alzheimer’s disease, and spongiform encephalopathy, FBP28, and other WW domain proteins (e.g., Pin1 and FiP35) have been the subjects of extensive experimental (4, 11, 17–23) and theoretical (3, 5, 6, 12–16, 24–27) studies. However, a folding mechanism of the FBP28 was debatable for a long time because of its complexity. There are not only discrepancies between experimental and theoretical results but also, different experiments that reveal different folding scenarios.

In particular, Nguyen et al. (11) studied the folding kinetics of the WT FBP28 and its full-size and truncated mutants by temperature denaturation and laser temperature–jump relaxation experiments. Nguyen et al. (11) found that the folding of the WT FBP28 involves intermediates (three-state folding) below the melting temperature and that the strand-crossing hydrophobic cluster of Tyr11, Tyr19, and Trp30 residues, which were mutated, is not a likely origin of the three-state scenario; also, truncation at the C terminus and an increase of temperature can modulate the two- and three-state folding behavior. The conclusion regarding three-state folding was challenged by Ferguson et al. (4), who observed single-exponential folding kinetics for the FBP28 by using fluorescence measurements and concluded that the biphasic kinetics observed by Nguyen et al. (11) might be related to aggregation and rapidly forming ribbon-like fibrils at physiological temperature and pH, with morphology typical of amyloid fibrils.

Our recent theoretical studies (12–16) of the same systems (11) showed that (i) folding of all of these systems involves intermediates; (ii) the strand-crossing hydrophobic cluster of residues 11, 19, and 30 is not associated with biphasic kinetics; and (iii) neither an increase of temperature nor truncation can alter the folding scenario. Moreover, discrepancies between experimental and theoretical results for some of these mutants caused by experimental limitations were clarified (16).

It also was found (3, 5) that the WT FBP28 folds with biphasic kinetics attributed to independence in the slow formation of turn 2 contacts with respect to the remainder of the protein and identified a key surface-exposed hydrophobic contact (Tyr21 with Leu26) for enforcing the correct registry of the residues of turn 2. To show the importance of the surface-exposed hydrophobic contact (Tyr21 with Leu26) and the involvement of turn 2 in a slow formation phase, the L26A mutant was studied (3). The fast phase (formation of hairpin 1) was not affected by this mutation, whereas the slow phase became even slower, which also was confirmed experimentally (11). These results suggested that the replacement of leucine by alanine actually stabilizes the misregistered turn 2 conformations relative to the WT; hence, it was concluded (3) that the surface-exposed hydrophobic contact (Tyr21 with Leu26) might be responsible for tying down turn 2 with a correctly formed hairpin. It should be noted that this surface-exposed hydrophobic contact is not present in other members of the WW domain family, which fold with monophasic kinetics.

Later theoretical studies (6, 12–16) of the WT FBP28 confirmed the results of ref. 3, showing biphasic folding kinetics with a stable intermediate state. Therefore, to prevent the formation of the intermediate state, it is logical to make mutations in the region of turn 2 and the third β-strand to speed up the formation of hairpin 2 as implemented here. However, based on the results of mutant L26A (3), it is not an easy task to ensure the elimination of intermediates and therefore, requires a detailed understanding of folding/misfolding mechanisms, folding/misfolding pathways, and effect of temperature on folding mechanism, etc., to identify proper sites for mutations.

Based on previous studies (3, 15), Leu26 is one of the main residues in which mutation might speed up the correct registry of turn 2. Moreover, the FBP28 is the only WW domain among 200 WW domain sequences that contains leucine at this position (3). Usually, this position is almost always occupied by a charged residue or glycine; therefore, following the natural tendency of the WW domain family, two mutants were designed, replacing leucine 26 with negatively charged polar amino acids: aspartic acid and glutamic acid (L26D and L26E, respectively). Also, replacement of leucine by alanine (the smallest nonpolar aliphatic amino acid) was found to slow down the process (3, 11); hence, for replacement of leucine 26, we also selected a very nonpolar and larger aromatic amino acid, tryptophan (L26W). It should be noted that leucine at position 26 is not a reflection of negative design by evolution but rather, is a result of pressure to maximize specificity through use of polar residues (3). Based on earlier results on the binding affinity of the WW domain, it was proposed (3) that requirements for ligand specificity have led to a local sequence with a strong propensity for a misregistered turn.

The next mutant was made by substituting a negatively charged polar amino acid, glutamic acid 27, with a nonpolar aromatic amino acid, tyrosine (E27Y). Finally, two more mutants were designed by replacing a neutral polar amino acid, threonine 29, with a negatively charged polar amino acid, aspartic acid (T29D) and a nonpolar aromatic amino acid, tyrosine (T29Y). Both Glu27 and Thr29 are critically placed residues contributing the most to the mean-square fluctuations (MSFs) (15), and mutation of these residues by disfavored amino acids might destabilize the misregistered turn 2 and β-strand 3 and speed up the correct registry.

To characterize the effects of these mutations, the six recombinant proteins carrying a single-point mutation were expressed, and their structures were studied by high-resolution NMR spectroscopy (SI Materials and Methods). All mutants adopt the triple-stranded antiparallel β-sheet characteristic of the WW fold, with slight variations caused by each specific mutation (Fig. S1). The experimental and theoretical melting temperatures (T_m values) for each mutant were determined with differential scanning calorimetry and multiplexed replica exchange molecular dynamics (MD) simulations, respectively (Table S1). We also ran simulations consisting of 120 (for WT and L26D) and 96 (for L26E, L26W, E27Y, T29D, and T29Y) canonical MD trajectories generated with the coarse-grained united residue (UNRES) force field (SI Materials and Methods) (28–30) at five and four different temperatures, respectively (24 MD trajectories, with ∼1.4 μs formal time and effectively ∼1.4 ms of each at each temperature), which were below, very close to, and above (for some mutants) the melting temperatures. The folding dynamics of each system were analyzed in terms of principal component analysis (PCA) (SI Materials and Methods) (12, 15, 31) describing the global motions of the protein, local motions of each residue [free-energy profiles (FEPs) along the amino acid sequence], and distances between the C^αs and C^βs of selected pairs of residues forming hairpins 1 and 2 over time.

Results

We first determined the foldability of the mutant domains in silico. It appeared that all of these mutants can fold, and the percentages of folding trajectories increase with temperature at most times (Fig. S2). The mutants of Leu26 appeared as better foldable systems (the foldability of L26D and L26E was even higher than that of the WT) than the mutants of Thr29 and especially, Glu27, for which the number of nonfolding trajectories exceeded the number of folding trajectories. We interpret this as the replacements of Glu27 and Thr29 by Tyr with a large aromatic side chain may force a reorganization of surrounding side chains and make folding more difficult (details are in SI Materials and Methods).

All systems were examined to determine the number of pathways through which they can fold. By calculating the rmsd of the first and second hairpins for all mutants and WT with respect to the native state, we determined that all systems can fold mainly through two different folding pathways: (i) hairpin 1 forms first, and then, the rest of the protein folds (dominant pathway with 51–100% occurrence); (ii) hairpin 2 forms first, and then, the rest of the protein folds (minor pathway with 0–49% occurrence). However, two mutants, L26D and L26W, and WT can, in addition, fold through a third folding pathway, in which both hairpins form simultaneously. The emergence of the third folding pathway at temperatures lower than the melting points for L26D (13%) and L26W (20%) and the melting temperatures for WT (4%) and L26W (5%) is a first indication that these systems may fold without intermediates; however, detailed analyses of these trajectories are required to validate this observation. Also, the frequency of occurrence of any type of folding pathway does not depend on temperature (details are in Table S2). Our findings regarding two folding pathways and the dominance of the first folding pathway for WT are in agreement with the recent work by Xu et al. (32).

PCA.

Free-energy landscapes (FELs) provide an understanding as to how proteins fold and function (33–35). It is impossible to present an FEL as a function of all degrees of freedom of a protein. Consequently, we have to rely on the coordinates along which the intrinsic folding pathways can be viewed. The folding dynamics of the WT and all mutants are investigated here by constructing FELs along the principal components (PCs) obtained from PCA, which typically capture most of the total displacement from the average protein structure with the first few PCs during a simulation (12–15, 36).

As was expected, a dominant folding scenario for all studied systems is a three-state folding (i.e., WT and all mutants fold through an intermediate state). An illustrative FEL along the first two PCs, $\mu \left(q_1,q_2\right)=-k_{B}T\text{ln}P\left(q_1,q_2\right)$, of one of the mutants, L26D at 305 K, is plotted in Fig. 1A, in which three states (unfolded, intermediate, and native) can be identified. The representative structures of the states indicate that the L26D mutant in this particular trajectory folds through the first, most dominant pathway. Similar FELs but with different representative structures of intermediate states, in which the second hairpin is formed, are characteristic for the MD trajectories, in which the systems fold through the second type pathway (not shown).

The analyses of the MD trajectories, in which the WT and mutants fold through the third type of pathway (both hairpins form simultaneously), show that only two mutants, L26D and L26W, exhibit two-state and downhill folding scenarios. In particular, L26D at 315 K can undergo both a two-state (Fig. 1D) and downhill folding (Fig. 1G), and L26W at 310 K can fold through the downhill folding scenario (Fig. 1J). The representative structure of the unfolded state in Fig. 1D (two-state folding) is not a typical unfolded structure. It is a mixture of representative structures of intermediate and unfolded states with partially formed hairpin 1. In the FEL, in which L26D undergoes downhill folding (Fig. 1G), two minima can be identified, with native and native-like representative structures; however, both minima are located in the native basin, and the barrier between them is <0.3 kcal/mol. Therefore, we consider it as downhill folding. The rest of the trajectories of WT and L26W, in which both hairpins formed simultaneously, did not exhibit two-state or downhill folding, because the rmsd (unlike PCA) was unable to capture a subtle behavior of one of the hairpins inducing an intermediate state (13).

Apart from the FELs, we have calculated the contributions of the two main principal modes [solid lines with filled (principal mode 1) and empty (principal mode 2) circles in Fig. 1] to the MSFs along the θ- (Fig. 1 B, E, H, and K) and γ-angles (Fig. 1 C, F, I, and L) and the percentages of the total fluctuations captured by the PCs (Fig. 1M) for the three-state, two-state, and downhill folding trajectories.

The main contributions to the fluctuations in a three-state folding trajectory come from all three β-strands and the second turn (Fig. 1 B and C). These results are in agreement with our earlier results on WT FBP28 (15). The main contributions to the fluctuations in a two-state folding trajectory come from the N terminus, the third β-strand, and the second turn (Fig. 1 E and F). There is no contribution from the first β-strand and the first turn, and there are minimal contributions from the middle β-strand, which indicate that the largest part of hairpin 1 forms very fast. These results explain why the representative structure of the unfolded state in a two-state folding trajectory (Fig. 1D) differs from a typical unfolded structure. Contributions to the fluctuations in downhill folding trajectories of L26D (Fig. 1 H and I) and L26W (Fig. 1 K and L) are almost identical (i.e., they come from the N terminus, the first β-strand, and the first turn). There is no contribution from the second turn, and there are some minor contributions from the third β-strand, the main “players” in the emergence of the intermediate state, which explains why L26D and L26W fold through the downhill folding scenario (i.e., without an intermediate state).

The percentage of total fluctuations captured by the first PC in the three-state folding trajectory (Fig. 1M, black line) is ∼40% [the same results were obtained for WT FBP28 (13)], whereas the first PCs in two-state and downhill folding trajectories capture only ∼14% and 9% (Fig. 1M, red, blue, and green lines) of total fluctuations, respectively. We have shown previously that the FEL constructed along PCs can describe the folding dynamics correctly if these PCs can capture at least 40% of the total fluctuations (13). Therefore, here, we examined the two-state and downhill folding trajectories in 7D and 8D PC spaces, respectively; however, we could not find any new major basins. Hence, 2D FELs are sufficient in these folding trajectories. A large difference in the percentages of the captured fluctuations between three-state folding trajectories and two-state and downhill folding trajectories can be explained by the fact that the largest contribution to the fluctuations in two-state and downhill folding trajectories comes from the very flexible part of the protein, the N terminus; also, PCA has proven to be an effective tool for the analysis of protein folding trajectories involving concerted motions of many residues, which can be captured by a few PCs with the largest eigenvalues (15). Interestingly, the distribution of the percentages of the total fluctuations captured by the PCs obtained for the B domain of staphylococcal protein A (13), a three-helical bundle, which folds through the two-state or downhill folding scenario, is similar to those for two-state and downhill folding trajectories of L26D and L26W.

Because the L26D and L26W mutants are the only ones exhibiting (with a small percentage) a folding scenario other than three state, we ran an additional 500 MD trajectories for each mutant to eliminate the possibility that two-state or downhill folding was an accidental folding scenario. Indeed, after examining 500 MD trajectories of both mutants, we found that, in ∼15% of all folding trajectories, these mutants fold through either two-state or downhill folding. The rest of this paper will consider only these two mutants.

Before scrutinizing the folding mechanisms of L26D and L26W, we examined the structures of all mutants determined by high-resolution NMR spectroscopy (Fig. S1 and Table S3) to find out the structural basis for the aforementioned theoretical findings.

The NMR data corresponding to L26D reveal the presence of a well-folded domain. However, no NOEs were identified from the D26 side chain to the surrounding residues. The calculated structures revealed that the D26 side chain is consistently oriented toward the Y21 hydroxyl (Fig. S1A). These results suggest the presence of a water-mediated hydrogen bond that stabilizes that specific orientation, which may allow some “flexibility” during the correct registry of turn 2. In other words, it may either speed up (two-state or downhill folding) or slow down (three-state folding) the correct registry of turn 2 in contrast to the WT, in which surface-exposed hydrophobic contact enforces the slow correct registry of turn 2.

In L26E and L26W, the E26 and W26 substitutions presented contacts more similar to the WT, with the orientation of their side chains in the calculated structures resembling that of L26 (Fig. S1 B and C). In L26W, we observed contacts between the indole of W26 and the aromatic ring of Y21, but the calculated structures result in several orientations of the W26 ring that are compatible with the experimental restraints and do not affect the turn structure (Fig. S1C); hence, their correlation with different folding scenarios is not straightforward. Structural properties of the rest of the mutants are provided in SI Materials and Methods.

Mechanisms of Hairpin Folding.

To elucidate the origins of a significant time difference between formation of the first and second hairpins, which is the cause of the induction of the intermediate state, we focus on the folding mechanisms of each hairpin. In particular, we examined the behavior of the distances between the C^αs of selected residues, pertaining to the first and second and the second and third β-strands (Fig. S3), and also, the behavior of the distances between the C^αs and C^βs of nonpolar residues, pertaining to (i) the solvent-exposed hydrophobic cluster (Tyr11, Tyr19, and Trp30), (ii) the delocalized hydrophobic core (Trp8, Tyr20, and Pro33), (iii) the surface-exposed hydrophobic contact (Tyr21 and Leu26), and (iv) the contact (Ala14 and Gly16) over time. It should be noted that the surface-exposed hydrophobic contact is formed by a different pair (Tyr21 and Trp26) in L26W and does not exist in L26D. We also calculated the time when the distances between the C^αs of each selected pair of residues reach (or are very close to) the experimental distance for the first time; we will designate it below as “the first contact time” (black circles connected by black lines in Fig. 2) and the time when the distance between each selected pair of residues gets stabilized (i.e., does not undergo significant changes after that) (red circles connected by red lines in Fig. 2). The same first contact and stabilization time was calculated for the C^βs of nonpolar residues (white circles connected by dashed lines in Fig. 2).

Fig. 2.

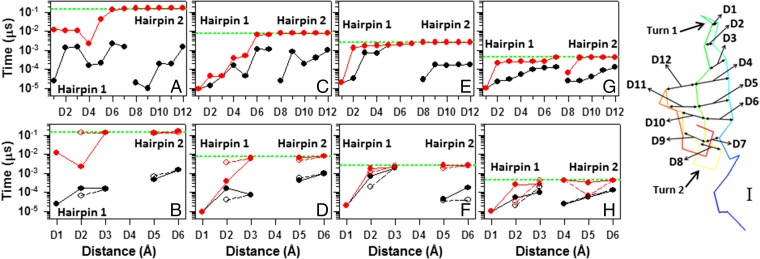
The first contact time (black circles connected by black lines) and stabilization time (red circles connected by red lines) vs. the distances between C^αs of selected pairs of residues of hairpin 1 (D1 → Ala14 and Gly16, D2 → Thr13 and Lys17, D3 → Lys12 and Thr18, D4 → Tyr11 and Tyr19, D5 → Glu10 and Tyr20, D6 → Thr9 and Tyr21, and D7 → Trp8 and Asn22) and hairpin 2 (D8 → Asn23 and Asp26, D9 → Asn22 and Glu27, D10 → Tyr21 and Ser28, D11 → Tyr20 and Thr29, and D12 → Tyr19 and Trp30) and also, vs. the distances between C^αs (C^βs are represented by white circles connected by dashed lines) of only nonpolar residues of hairpin 1 (D1 → Ala14 and Gly16, D2 → Tyr11 and Tyr19, and D3 → Trp8 and Tyr20) and hairpin 2 (D5 → Tyr20 and Pro33 and D6 → Tyr19 and Trp30) for (A and B) three-state, (C and D) two-state, and (E and F) downhill folding trajectories of the L26D mutant and (G and H) the downhill folding trajectory of the L26W mutant (D8 → Asn23 and Trp26 in G and D4 → Tyr21 and Trp26 in H). Structure of L26D is illustrated in I. Horizontal green dashed lines indicate the folding time of L26D and L26W.

By comparing the first contact and stabilization times of the three-state (Fig. 2 A and B), two-state (Fig. 2 C and D), and downhill (Fig. 2 E and F) folding trajectories, we had the following findings. (i) A first contact between C^αs and C^βs of most of the selected pairs of residues occurs within a short time (≤10⁻³ μs) for all trajectories, whereas a stabilization time in the three-state folding trajectory is greater by about one and two orders of magnitude than that in the two-state and downhill trajectories, respectively, which finally causes the emergence of an intermediate state. (ii) There is a correlation between the first contact time and the location of pairs of residues pertaining to the first hairpin in both downhill folding trajectories (Fig. 2 E and G) and partially in the two-state folding trajectory (Fig. 2C). In other words, the first contact time depends on how far a pair of residues is located from the turn and increases with the distance between the turn and the location of pairs of residues. A similar correlation is observed between the first contact time and the location of pairs of residues, pertaining to the second hairpin, in the downhill folding trajectory of L26W (Fig. 2G). There is no such correlation in a three-state folding trajectory (Fig. 2A). (iii) The stabilization time for all selected pairs in the downhill folding trajectories (Fig. 2 E and G) and the two-state trajectory (Fig. 2C) either increases with the distance between the turn and the location of pairs of residues or stays constant. (iv) The first contact time between C^αs and C^βs and the location of pairs of nonpolar residues, pertaining to the second hairpin, are correlated in all trajectories (Fig. 2 B, D, F, and H), whereas the pairs of nonpolar residues, pertaining to the first hairpin, are correlated for both C^αs and C^βs the downhill folding trajectories (Fig. 2 F and H). In three- and two-state folding trajectories, the first contact time between C^αs and C^βs and location of pairs of nonpolar residues, pertaining to the first hairpin, are correlated only for the C^β distances. For some pairs of nonpolar residues, the first contact time between C^αs does not follow the one between C^βs. (v) The stabilization time for the pairs of nonpolar residues in the downhill folding trajectories and the two-state trajectory behaves the same way as described in iii.

The foregoing results indicate that the hairpins of L26D and L26W fold through two different mechanisms. In particular, both hairpins in both downhill folding trajectories fold through the mechanism proposed by Matheson and Scheraga (37), which is based on transient hydrophobic interactions and considers the nucleation process as an initial aspect of folding, converting an extended chain to a collapsed hydrophobic pocket. This method predicts the nucleation regions for protein folding by estimating the free energy of formation of the nucleation sites. This model was later referred to in the literature as a zipper model (38). The first hairpin in a three-state folding trajectory seems to fold through the hydrophobic collapse mechanism proposed by Dinner et al. (39), in which the hydrophobic collapse initiates hairpin formation (Fig. 2A). Two pairs of nonpolar residues, (Tyr11 and Tyr19) and (Trp8 and Tyr20), which make the first contact at the same time (based on the distance between C^αs and almost the same time based on C^βs), are the only driving force for formation of hairpin 1, because the pair (Ala14 and Gly16), responsible for the formation of the first turn, makes the first contact in the early stage of the trajectory but becomes deformed and does not stabilize for a long time (Fig. 2B). The folding of the first hairpin in the two-state folding trajectory is a “mixture” of these two mechanisms (i.e., it does not exhibit the “order”) (Fig. 2D) during formation of nucleation sites proposed by Matheson and Scheraga (37) (i.e., the contact between Trp8 and Tyr20 forms faster than the contact between Tyr11 and Tyr19) and looks more like hydrophobic collapse; however, because of the pair Ala14 and Gly16, which makes a contact in the early stage of the trajectory and remains stabilized (i.e., the first turn is formed), hairpin 1 manages to restore the order (Fig. 2 C and D). Based on the first contact time between the nonpolar residues (Fig. 2 B and D), the second hairpin in both three-state and two-state folding trajectories folds through the model by Matheson and Scheraga (37); however, the order is distorted if we consider all of the selected pairs of hairpin 2 (Fig. 2 A and C). Based on these results, it is crucial when the pairs of nonpolar residues make the first contact and how fast the first turn is formed. If the pair of nonpolar residues, located farther from the turn, makes the first contact faster (or almost at the same time) than the pair of nonpolar residues located closer to the turn and the first turn does not form at the beginning of the trajectory, this order can cause a delay of stabilization of contacts between not only these residues but also, the residues of all selected pairs (especially the pairs of residues pertaining to the second hairpin), which finally induces the emergence of the intermediate state.

It should be noted that we also examined several three-state folding trajectories of the four other mutants examined above and found that the folding mechanisms of the hairpins in these trajectories do not differ from one of those (the three-state folder) presented in this section.

FEPs Along θ_i- and γ_i-Angles of Folding Trajectories.

To explain the origins of three different (downhill, two-state, and three-state) folding scenarios, we studied the local motions of each residue along the sequence. In particular, we investigated the FEPs along the backbone virtual bond angle-θ and backbone virtual bond dihedral angle-γ of each residue (SI Materials and Methods and Fig. S4).

Fig. S5 illustrates the FEPs along the θ_i- (Fig. S5A) and γ_i-angles (Fig. S5B) computed from the above-discussed four MD trajectories. The black, blue, red, and green curves in Fig. S5 correspond to the FEPs of three-state, two-state, and two downhill folding trajectories, respectively. Small red and blue circles at the bottom of each panel in Fig. S5 are the NMR-derived structural data of L26D and L26W, respectively.

By comparing the FEPs along all of the θ- and γ-angles of four trajectories (Fig. S5), we found that the FEPs along most of the θ-angles for all four trajectories are similar to each other; however, there are several θ-angles (θ_i; i = 6, 7, 14, and 19–21) along which the FEPs are different (Fig. S5A). These differences are based on the formation of local minima, which are deepest for the FEP corresponding to the three-state trajectory and gradually become shallow (or disappear) for the FEPs corresponding to two-state and downhill folding trajectories. As was shown previously (15), the γ-angles are more sensitive and correlated to the global motions of the protein than the θ-angles; hence, differences between the FEPs along more γ-angles were found (Fig. S5B). These differences can more or less be observed along almost every γ-angle, except the γ-angles belonging to the C and N termini. They are more complicated than the FEPs along the θ-angles; however, we can identify how gradually the deepness of local minima changes (or vanishes) with the folding scenario. As in the FEPs along the θ-angles, the significant differences between the FEPs occur along the γ-angles consisting of residues pertaining to the solvent-exposed hydrophobic cluster (Tyr11, Tyr19, and Trp30), the delocalized hydrophobic core (Trp8, Tyr20, and Pro33), and the surface-exposed hydrophobic contact (Tyr21 and Leu26).

There is a clear correlation between the FEPs along the θ- and γ-angles and the contributions of the principal modes to the MSF (Fig. 1) (i.e., the θ- and γ-angles, along which the FEPs exhibit one or more local minima, have peaks in the graphs of the principal modes), which is understandable, because an existence of local minima on an FEP is a manifestation of jumps that the angles make, back and forth, between the local and global minima; hence, these angles contribute to the MSF. Contributions to the MSF increase with the deepness of local minima. Therefore, the principal modes of downhill folding trajectories have the least number of peaks. Because the FEPs and principal modes are correlated, we can conclude that the FEPs (Fig. S5) and FELs (Fig. 1) are correlated as well. In other words, the local minima on the FEPs are correlated to the local minima on the FELs. For the three-state trajectory, most of the FEPs along the γ-angles representing the β-strands and their edges exhibit three minima [one (deepest) corresponds to the native state, and the other two (shallow) correspond to the unfolded and intermediate states, respectively], whereas the FEPs along the θ-angles have mainly two minima [one (deepest) corresponds to the native state, and the second (shallow) corresponds to either the unfolded or intermediate state]. By comparing the FEPs along the γ-angles of three-state and two-state trajectories, we can easily identify which local minima of the FEPs along both angles correspond to the unfolded and the intermediate states. The results show that the main contributions in the formation of the intermediate state come from the θ₂₁-, γ₈-, γ₉-, γ₂₁-, γ₂₅-, and γ₂₆-angles pertaining to the surface-exposed hydrophobic contact (Tyr21 and Leu26) and part of the delocalized hydrophobic core (Trp8, Tyr20, and Pro33).

Discussion and Conclusions

One of the important problems in protein folding, the emergence of intermediates implicated in amyloid fibril formation, was addressed in this study in the example of the FBP28, which folds with biphasic kinetics. To understand the origins of biphasic folding kinetics of the FBP28, the structures of six new mutants (L26D, L26E, L26W, E27Y, T29D, and T29Y) have been determined by high-resolution NMR spectroscopy, and extensive MD simulations at different temperatures (below, very close to, and above the melting point) were performed with the coarse-grained UNRES force field. By analyzing the MD trajectories of these six mutants together with the WT in terms of the local motions of each residue and the distances between the C^αs and C^βs of selected pairs of residues over time and by PCA, we made the following findings.

• i)All six mutants fold, maintaining the canonical WW structure as revealed by NMR. Their foldability increases, at most times, with increasing temperature. The mutations of Leu26 create better foldable systems (even better than WT in some cases) than the mutations of Thr29 and especially, Glu27.
• ii)All six mutants and WT can fold through two different folding pathways with a different order of formation of the hairpins. Also, two mutants, L26D and L26W, can fold through a third folding pathway, in which both hairpins form simultaneously.
• iii)Three-state folding is a major folding scenario of all six mutants and WT. However, two other folding scenarios, two-state and downhill folding, have been identified in ∼15% of folding MD trajectories for L26D and L26W.
• iv)For formation of intermediates, it is crucial how each hairpin, especially hairpin 1, folds. If both hairpins are formed by the mechanism by Matheson and Scheraga (37), then the system may fold through a downhill (or two-state) folding scenario. If hairpin 1 is formed by the hydrophobic collapse mechanism, then an intermediate state emerges, and the protein folds through a three-state folding scenario. Apart from the contacts between nonpolar residues, it is also important for a folding scenario when the first contacts occur between selected pairs of polar–polar and polar–nonpolar residues (some of them form hydrogen bonds). In a downhill folding trajectory, the first contacts between all selected pairs of residues occur in order, starting from the pairs closest to the turns. This order is distorted in two-state and three-state folding trajectories.

Previous experimental and theoretical studies (3, 11, 14) have shown that it is not easy to eliminate the intermediate state by mutation. However, the correlations between the local and global motions found here enabled us to identify the residues making the main contribution in the formation of the intermediate state. This approach can be applied to other proteins to identify the residues, mutations of which may help to eliminate intermediates.

Finally, the problems addressed in this study (i.e., elucidation of the origins of formation of intermediates and finding ways to prevent them) are very important for understanding folding/misfolding in general. The findings regarding the folding of the hairpins by different mechanisms, their role in the formation of intermediates, and the correlations between the local and global motions have general importance and can be applied to a broader class of proteins.

Materials and Methods

Canonical MD simulations were carried out with the UNRES force field parameterized (29) on the β-strand protein 1E0L and the α-helical protein 1ENH. The UNRES force field takes the solvent into account implicitly through the mean–force potential of interactions between united side chains (29). The Berendsen thermostat (40) was used to maintain constant temperature. The time step in MD simulations was δt = 0.1 mtu (molecular time unit) [1 mtu = 48.9 fs is the “natural” time unit of MD (41)], and the coupling parameter of the Berendsen thermostat was τ = 1 mtu. In total, ∼3 × 10⁸ MD steps were run for each trajectory, starting from the fully extended structure. Details of the protein purification and structural determination are provided in SI Materials and Methods.