Abstract
Background
Aedes aegypti, the principal vector of dengue fever, have been genetically engineered for use in a sterile insect control programme. To improve our understanding of the dispersal ecology of mosquitoes and to inform appropriate release strategies of ‘genetically sterile’ male Aedes aegypti detailed knowledge of the dispersal ability of the released insects is needed.
Methodology/Principal Findings
The dispersal ability of released ‘genetically sterile’ male Aedes aegypti at a field site in Brazil has been estimated. Dispersal kernels embedded within a generalized linear model framework were used to analyse data collected from three large scale mark release recapture studies. The methodology has been applied to previously published dispersal data to compare the dispersal ability of ‘genetically sterile’ male Aedes aegypti in contrasting environments. We parameterised dispersal kernels and estimated the mean distance travelled for insects in Brazil: 52.8m (95% CI: 49.9m, 56.8m) and Malaysia: 58.0m (95% CI: 51.1m, 71.0m).
Conclusions/Significance
Our results provide specific, detailed estimates of the dispersal characteristics of released ‘genetically sterile’ male Aedes aegypti in the field. The comparative analysis indicates that despite differing environments and recapture rates, key features of the insects’ dispersal kernels are conserved across the two studies. The results can be used to inform both risk assessments and release programmes using ‘genetically sterile’ male Aedes aegypti.
Author Summary
Vector control using releases of sterile insects is a well-known approach. ‘Genetically sterile’ male Aedes aegypti have been developed and released in a modern realisation of the sterile insect technique. Released engineered males seek out and mate with wild females, with the resultant offspring dying before they reach maturity. Control of a wild vector population can therefore be achieved by maintaining sustained releases of sterile males whilst ensuring sufficient distribution and coverage of released males across the target area. In order to efficiently plan releases of these, individuals’ detailed knowledge of how they disperse in the field is required. We present an analysis of the dispersal of these engineered male Aedes aegypti using data from field experiments in Brazil. Our results provide detailed information on how the mosquitoes disperse over their potential flight range.
Introduction
Dengue, an arbovirus, has seen recent re-emergence and spread on a global scale [1] and is now responsible for an estimated 390 million infections annually [2]. The vector of dengue is the Aedes mosquito, with Ae. aegypti and Ae. albopictus responsible for the majority of disease transmission [3]. The release of ‘genetically sterile’ male Aedes mosquitoes has been demonstrated to be a valuable additional tool by which the vector can be controlled [4]. Understanding the ability of the released ‘genetically sterile’ insects to disperse, and their behaviour whilst doing so, is an important step in designing robust, efficient and effective releases. Attaining adequate coverage of released sterile insects across a given area is a major operational challenge of a sterile insect control effort [4]. Knowledge of the distribution of dispersal distances of released insects will improve our ability to target releases, obtain required coverage densities, confidently predict the potential spatial range of a release and is a key element for the assessment of risk.
Independently conceived by Petersen in 1896 and Lincoln in 1930 [5], mark-recapture, capture-recapture or mark-release-recapture studies (hereafter referred to as MRR) have since become a key set of ecological methods. MRR allows inference to be drawn about a number of important ecological factors including the estimation of population size and quantification of dispersal and survival. The methods have been used across a diverse range of species, from whales [6] to fruit flies [7], and have seen extensive use in mosquito ecological studies.
Analysis of the location of recaptured marked insects with respect to the release point allows inference to be made about the dispersal of the released insects. A number of MRR studies have been performed with the aim of assessing the dispersal ability of both lab [8–11] and ‘genetically sterile’ [12] strains of male Ae. aegypti. However, these studies often document only the mean distance travelled (MDT) [8–12] or range [11,12] of dispersal of the released insects. Common measures of range are the flight range 50% and flight range 90% (FR50 and FR90 respectively) which are estimates of the distance within which 50% or 90% of all insects are expected to disperse [12,13]. The MDT and flight range are intuitive summary measures but do not characterise dispersal well when the distribution of dispersal distances is positively skewed with a long tail.
For greater insight, a better understanding of the distribution of dispersal distances can be obtained by incorporating dispersal kernel theory, popular in studies of population spread [14] and seed dispersal [15], into a generalised linear model (GLM) framework [16,17]. Dispersal kernels represent the distribution of dispersal distances over the whole flight range. They can take a wide range of forms with the flexibility to represent dispersal for a diverse range of species [18].
This study attempts improve the characterisation of the dispersal ability of ‘genetically sterile’ male Ae. aegypti mosquitoes using data from large-scale MRR experiments carried out at an urban field site in Brazil. The analysis facilitates the quantification of dispersal through the parameterisation of a dispersal kernel for the released insects. Many summary measures of interest relating to dispersal may be drawn from such a kernel. To enable a comparison of both the biological outcomes and methodology employed, the analytical methods are also used to re-analyse published data on the dispersal of ‘genetically sterile’ male Ae. aegypti at an uninhabited forested site in Pahang, Malaysia [12]. The dispersal ability of the ‘genetically sterile’ insects was previously analysed in the Malaysian study using methods detailed in Morris et al. (1991) [13] and evaluated the MDT to be 52.4m (95% CI: 41.6m, 61.4m) [12]. The aims of the re-assessment of dispersal ability are: i) to assess the robustness of the estimate of dispersal from Brazil data to habitat and locational heterogeneities, ii) to explore potential differences in dispersal behaviour between sites and iii) to assess the applicability of the dispersal kernel method in comparison with more common approaches to estimating and quantifying dispersal.
Methods
Ethics statement
Before establishment of the ‘genetically sterile’ male Ae aegypti line in the mass rearing laboratory and subsequent open releases, regulatory approvals were obtained from the appropriate Brazilian national regulatory body: the Brazilian National Biosafety Technical Commission (CTNBio). Releases were preceded by community engagement with consent and support obtained from regional (Bahia health secretary) and local community leaders (Town Mayor, health secretary and vector control authorities). Prior to sampling, informed consent was received from the landowners.
Study site
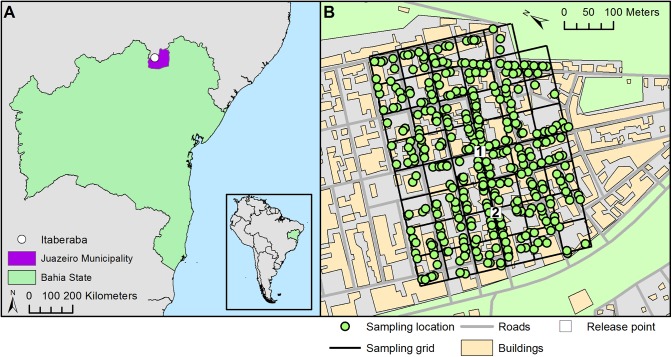
The field site is located in Itaberaba, a suburb of the city of Juazeiro, Bahia, Brazil (Latitude: -9° 26' 59", Longitude: -40° 28' 53") (Fig 1A). The site is located in a semi-arid part of Brazil and consists mainly of low-socioeconomic status residential housing. The majority of houses at the study site were single-story brick and concrete buildings with unscreened windows. The habitat across the sampled region was a homogenous urban environment.
Fig 1. Brazil study site sampling locations.
A) The study site, Itaberaba, a suburb of the city of Juazeiro, Bahia State, Brazil. B) MRR release points (numbered squares) and sampling locations (green circles) within households distributed across the sampling grid at the study site.
Mark-release-recapture
The ‘genetically sterile’ line used was OX513A and was reared according to methodologies given in Carvalho et al. (2014) [19].
A total of 19,164 ‘genetically sterile’ male Ae. aegypti formed three releases. Individuals from each release were marked with the same coloured fluorescent powder (www.dayglo.com). Release 1 (red release) and release 2 (blue release) were performed on 21 February 2011 and consisted of 5,349 and 5,465 individuals released from points 1 and 2 (Fig 1B) respectively. Release 3 (yellow release) was performed on 25 February 2011 with 8,350 individuals released from point 1 (Fig 1B).
Aspiration sampling was used to recapture marked adults. Sampling was conducted using locally made battery powered hand-held aspirators. After obtaining consent from the respective property owner, each building was sampled for a set period of 15 minutes. Sampling locations were distributed across the study site (Fig 1B) and sampling was conducted for up to nine days post release (S1 Data). Sampling locations were chosen by randomly selecting one household from each of the 47 (60m by 60m) grid squares each day (with the exception of day 5 for the red and blue release and day 1 for the yellow release where, for logistical reasons, the number of households sampled was lower). Each mosquito collected was assessed to determine the i) origin (‘genetically sterile’ or wild as indicated by the presence/absence of fluorescent powder respectively), ii) sex and iii) genus (Aedes or non-Aedes). Weather variables (daily maximum temperature and maximum humidity) were recorded from a local weather station (situated approximately 10.2km north-west of Itaberaba).
A secondary analysis of the MRR data from a previously published study in Malaysia [12] was undertaken to obtain a comparative second estimate of the ‘genetically sterile’ insect’s dispersal ability and associated density kernel. In this study a total of 6,045 marked ‘genetically sterile’ males were released at a forested site in Pahang, Malaysia. For a detailed description of the study site and MRR methods please see Lacroix et al. (2012) [12].
Model framework
All multivariable analyses were performed within a GLM framework. In instances where the number of recaptures is small relative to the total releases, the Poisson regression model may be used as an appropriate approximation [20].
We assume that the count response variable (recaptures) is Poisson distributed with mean μ and variance μ
| (1) |
The response must be ≥ 0. Therefore a log link function is used to link the mean to the explanatory variables
| (2) |
where x i β is a linear predictor
| (3) |
where β denotes the unknown parameters to be estimated and x i, the explanatory variables. Parameter estimates were obtained by maximising the log-likelihood () of the data:
| (4) |
In the situation where the response variable is overdispersed (variance>>mean) a Poisson GLM, where the variance is assumed to equal the mean, would be misspecified. In this instance, the negative binomial GLM, detailed below, may be used [21–23].
We assume that the count response variable follows a negative binomial distribution. A Poisson model is used for the count, conditional on the mean value, Z i, which is assumed to have a gamma distribution, with mean, μ i, and constant scale parameter, θ
| (5) |
Therefore the expected value of Y and the variance of Y are as follows
| (6) |
The mean response, μ i, may be linked to a linear combination of explanatory variables using the log link function (Eq (2)) and linear predictor (Eq (3)). Parameters were estimated by maximising the log-likelihood () of the model:
| (7) |
where the gamma function, Γ, is
| (8) |
Dispersal kernels
Considerable inconsistencies abound regarding different interpretations of the term ‘dispersal kernel’ [18,24,25]. Two kernel definitions, often used interchangeably, are i) the probability density function (pdf) of the dispersal distance of each disperser. Referred to as the distance kernel [18] or the distance pdf [25] and ii) the density of probability of a given bearing and dispersal distance from the source. Referred to as the location kernel [18] or the density pdf [25].
We adopt the terminology of Cousens et al. [25], henceforth referring to kernel type 1 as the distance pdf and type 2 as the density pdf. Both kernel types are true pdfs, integrating to 1 (the density pdf is integrated over the whole 2d space). Both kernel types are closely related. The distance pdf can be derived by multiplying the density pdf by 2πd where d is the distance from the source [18] (assuming radial symmetry). Examples of these kernel types are shown in Fig 2.
Fig 2. Dispersal kernels.
Examples of different kernel interpretations for the negative exponential (A, B and C) and exponential power (D, E and F) kernels. The distance pdf is shown in panels A and D. The density with respect to distance is shown in panels B and E and the density pdf is illustrated in panels C and F (after Cousens et al. [25]). Kernels in A, D, C and F integrate to unity (in 1 dimension for the distance pdfs and 2 dimensions for the density pdfs).
The density pdfs, assuming radial symmetry, used in this analysis are defined by the following functions
| (9) |
| (10) |
where d is the distance (metres), a and b are kernel parameters and Γ the gamma function (Eq (8)) [18]. The negative exponential kernel is characterised by the exponential power kernel when b = 1. The associated MDT functions are
| (11) |
| (12) |
Estimates of FR50 and FR90 are made by assessing the cumulative distribution of the distance pdf at the 50% and 90% levels.
Variables
The outcome variable was the number (count) of marked ‘genetically sterile’ male Ae. aegypti recaptured. Potential explanatory variables included in the Brazil analysis were: i) a spatial measure which could either be the measured distance (m) between release and recapture or the density as calculated by a parameterisation of a given density pdf, ii) the number of days post release, the effect of which is assumed to be linear, iii) the number of wild Aedes species collected iv) the number of non-Aedes wild mosquitoes collected, v) the maximum temperature (°C) on the day of collection, vi) the maximum humidity (%) on the day of collection and vii) the directional quadrant, North, South, East or West (relative to release point) that the collection was made in.
Due to the relatively low recapture number, data from all three MRR experiments were combined for analysis.
For the Malaysia analysis the outcome variable was the number (count) of marked ‘genetically sterile’ male Ae. aegypti recaptured. Potential explanatory variables included in the analysis were: i) a spatial measure which could either be the measured distance (m) between release and recapture or the density as calculated by a parameterisation of a given density pdf, ii) the number of days post release, the effect of which is assumed to be linear iii) the number of wild Aedes species (specifically: aegypti, albopictus and togoi) collected, iv) the number of wild Culex collected and v) a categorical variable indicating if the recapture location was uphill or downhill from the release site.
Three models were evaluated to compare different transformations of the distance explanatory variable. Model 1 incorporated all explanatory variable including distance, Model 2 all explanatory variables including distance density (negative exponential kernel) and model 3 all explanatory variable including distance density (exponential power kernel).
For model 1 the full model was fitted using maximum likelihood techniques, utilising the GLM and Negative binomial GLM function of the statistical software package R [26] with the MASS package [21]. All explanatory variables were included in the initial model as well as an interaction term between distance and day post release. Model selection by minimising the Akaike information criterion (AIC), a penalised likelihood score, was then performed using the MASS package [21]. The AIC is calculated as
| (13) |
where k is the number of parameters and the maximised likelihood value.
For models 2 and 3 fitting was performed using the following process. First, the distance density was estimated using the assigned kernel. The GLM was then fitted using the same process as for model 1, as a function of the transformed distance explanatory variable. These steps were then optimised over the kernel parameter space allowing identification of the optimal combination of explanatory variables and kernel parameters as indicated by the AIC. The best overall model was judged to be the one with the minimum AIC value.
For comparison, the estimated survival of released insects in the Brazil study predicted using the GLM was also calculated using a non-linear regression approach [27], that was also used in the original analysis of the Malaysia data [12].
Kernel confidence intervals
Following model estimation, 95% confidence intervals were calculated for the maximum likelihood kernel parameter estimates using the profile likelihood method. The maximised log-likelihood with respect to β, α and b, i.e. that corresponding to the maximum likelihood estimates (MLEs) of β, α and b, is defined as .
First kernel parameter a was increased or decreased in small increments whilst β was held at the MLE and kernel parameter b was optimized conditional on and the assumed value of α (a 0), giving the log-likelihood:
| (14) |
where .
Secondly, kernel parameter b was increased or decreased in small increments whilst β was held at the MLE () and kernel parameter α was optimized conditional on and the assumed value of b(b 0), giving the log-likelihood:
| (15) |
where .
After each change the log-likelihood of the model was recalculated and a corresponding test statistic assessed. For example, evaluating for a, the G 2 statistic was calculated
| (16) |
The G 2 statistic was compared to the χ2 distribution (with 1 degree of freedom) for the (1-α) percentile. Thus for 95% confidence intervals the critical G 2 value is 3.84. The log-likelihood surface was calculated with respect to kernel parameters of the optimal model for exploration and visualisation of the parameter space for both the Brazil and Malaysia analyses.
Results
Primary analysis—Brazil
Recaptures for the three MRR experiments are summarised in Table 1. The locations of recaptures are shown in Fig 3. The mean count of recaptured marked males (the response), per sample, per day was 0.077 (variance = 0.73). Over the recapture period the maximum daily temperature ranged between 25.4°C-34.6°C and the maximum relative humidity between 66%-92%.
Table 1. Summary data of the three MRR experiments in Brazil.
| Release | Release date | Number released | Release point | Number (%) recaptured |
|---|---|---|---|---|
| Red | 21-Feb-2011 | 5,349 | 1 | 22 (0.4) |
| Yellow | 25-Feb-2011 | 8,350 | 1 | 17 (0.2) |
| Blue | 21-Feb-2011 | 5,465 | 2 | 30 (0.5) |
| Total | - | 19,164 | - | 69 (0.36) |
Fig 3. Recaptures for three MRR experiments at the field site in Brazil.
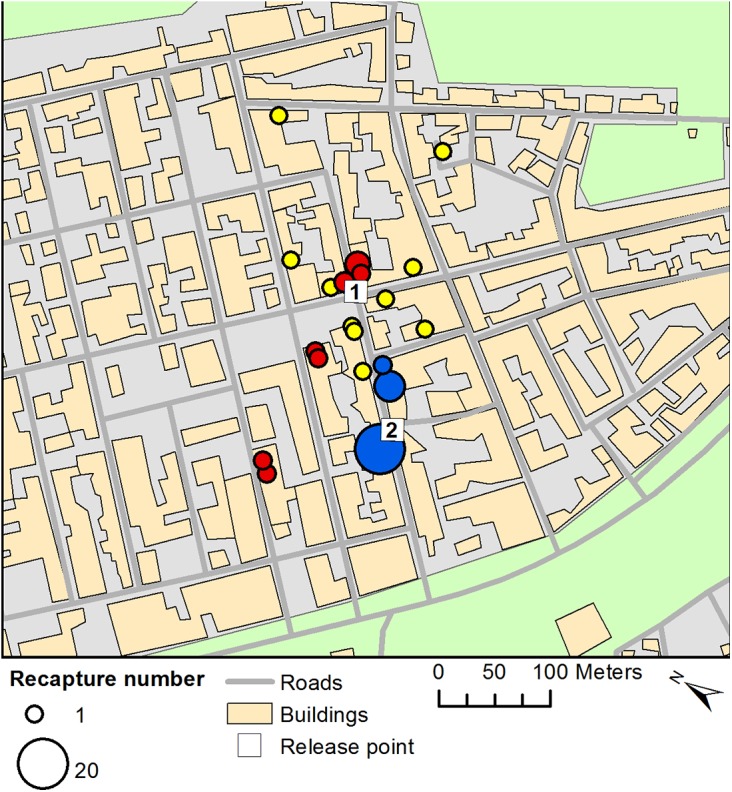
Numbered squares represent the two release points for MRR experiments. Coloured circles indicate the location and size of recaptures for three separate MRR releases (insects marked with red, yellow and blue fluorescent powder).
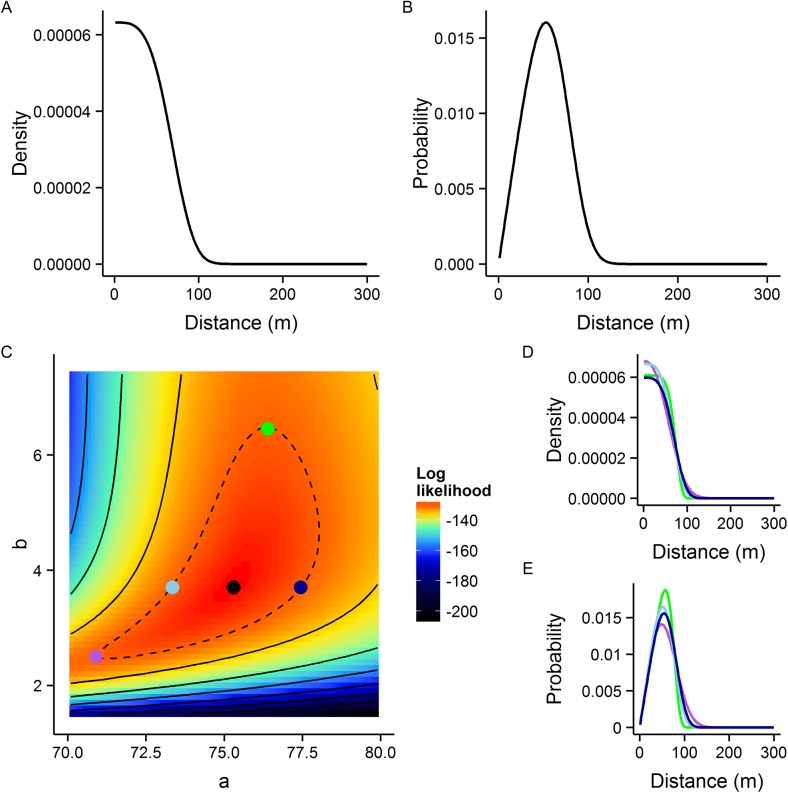
A summary of model performance using the untransformed- and transformed-distance explanatory variable is shown in Table 2. Combining all available data (from the red, yellow and blue releases) the best fitting model (lowest AIC) incorporated the exponential power kernel. The maximum likelihood exponential power density pdf has an associated MDT of 52.8m (95% CI: 49.9m, 56.8m), FR50 of 52.4m (95% CI: 50.6m, 54.7m) and FR90 of 83.0m (95% CI: 74.8m, 93.9m). The MLE kernel, log-likelihood surface and examples of kernels drawn from 95% CI parameter values are shown in Fig 4.
Table 2. Brazil model performance and kernel parameter estimates.
| Distance transformation | AIC | Explained variance (%) | Number of covariates | Kernel parameter estimates (95% CI) | |
|---|---|---|---|---|---|
| a | b | ||||
| Untransformed | 293.5 | 46.7 | 5 | - | - |
| Negative exponential | 286.5 | 48.6 | 6 | 97.8 (57.8,238.3) | - |
| Exponential power | 276.2 | 51.4 | 5 | 75.3 (66.1,85.0) | 3.7 (2.0,7.3) |
The estimated model performance (minimum AIC indicated in bold) and kernel parameters for different transformations of the distance explanatory variable for the Brazil analysis.
Fig 4. Dispersal kernel summary for the Brazil analysis.
A) Maximum likelihood estimate of density with respect to distance for Brazil data. B) Maximum likelihood distance pdf. C) The log-likelihood surface with respect to kernel parameters a and b, coloured points highlight the MLE (black, log-likelihood = -128.1) and examples of extreme 95% CI (green, light blue, dark blue and mauve) kernel parameter combinations. The dotted line demarks the 95% confidence interval contour. Solid black contour lines are at intervals of 10 log-likelihood. Examples of D) distance densities and E) distance pdfs from the 95% confidence interval range corresponding to the coloured points shown in panel C.
For all three models the distance or distance density and the number of days post release were strongly associated with recapture number. There was no evidence of an interaction between distance (untransformed or transformed) and the number of days post release in any of the models considered. Assuming no emigration, the estimated mortality rate of released insects of 0.62 (95% profile likelihood CI: 0.84, 0.42) would equate to a mean average lifespan of 0.62−1 = 1.61 days (95% CI: 1.19 days, 2.38 days). Estimates of the mean average lifespan calculated using the non-linear regression approach [27] were 1.00 days (95% bootstrapped CI: 0.63 days, 1.48 days).
Other significant explanatory variables were the number of non-Aedes mosquitoes recorded from the sample and the maximum humidity. There was evidence of a lack of radial symmetry in dispersal from the release point as the quadrant explanatory variable was also associated with recapture number. A summary of the parameter estimates from the optimal model, using the exponential power transformation of distance as an explanatory variable is shown in Table 3.
Table 3. Brazil model coefficient estimates.
| Coefficient | Estimate | Standard error | z-value | p-value | |
|---|---|---|---|---|---|
| Intercept | -1.35 | 1.18 | -1.16 | 0.25 | |
| Transformed distance | 83,140 | 7,015 | 11.85 | <0.0001 | |
| Number of days post release | -0.62 | 0.11 | -5.84 | <0.0001 | |
| Wild other spp | 0.021 | 0.0079 | 2.62 | 0.0088 | |
| Maximum humidity | -0.035 | 0.016 | -2.22 | 0.027 | |
| Quadrant * | North | 1 | - | - | - |
| South | -1.88 | 0.80 | -2.36 | 0.018 | |
| East | 0.76 | 0.37 | 2.07 | 0.039 | |
| West | 1.40 | 0.35 | 3.97 | 0.00071 | |
GLM coefficient estimates and associated standard errors, z-value and p-values from the optimal model for the Brazil analysis. Distance was transformed using the exponential power kernel.
*Overall significance level p<0.0001 (χ2 = 46.50, 3df).
Secondary analysis—Malaysia
The MRR performed in Malaysia was associated with consistently higher recaptures than the MRR experiments in Brazil. Of 6,045 released ‘genetically sterile’ males 3,034 (50.2%) were recaptured over the 15-day course of the experiment. The count of recaptured, marked males (the response) was very overdispersed (mean = 2.6 per sample per day, variance = 523), and therefore a negative binomial GLM was fitted. A summary of the model performance using the untransformed and transformed distance explanatory variable is shown in Table 4.
Table 4. Malaysia model performance and kernel parameter estimates.
| Model | AIC | Explained variance (%) | Number of covariates* | Kernel parameter estimates (95% CI) | |
|---|---|---|---|---|---|
| a | b | ||||
| Untransformed | 728.7 | 7.9 | 3 | - | - |
| Negative exponential | 668.4 | 54.1 | 3 | 31.3 (27.7,34.9) | - |
| Exponential power | 668.0 | 46.8 | 3 | 48.1 (45.3, 52.1) | 1.4 (1.3,1.5) |
The estimated model performance (minimum AIC indicated in bold) and kernel parameters for different transformations of the distance explanatory variable for the Malaysia analysis.
*Including the interaction term.
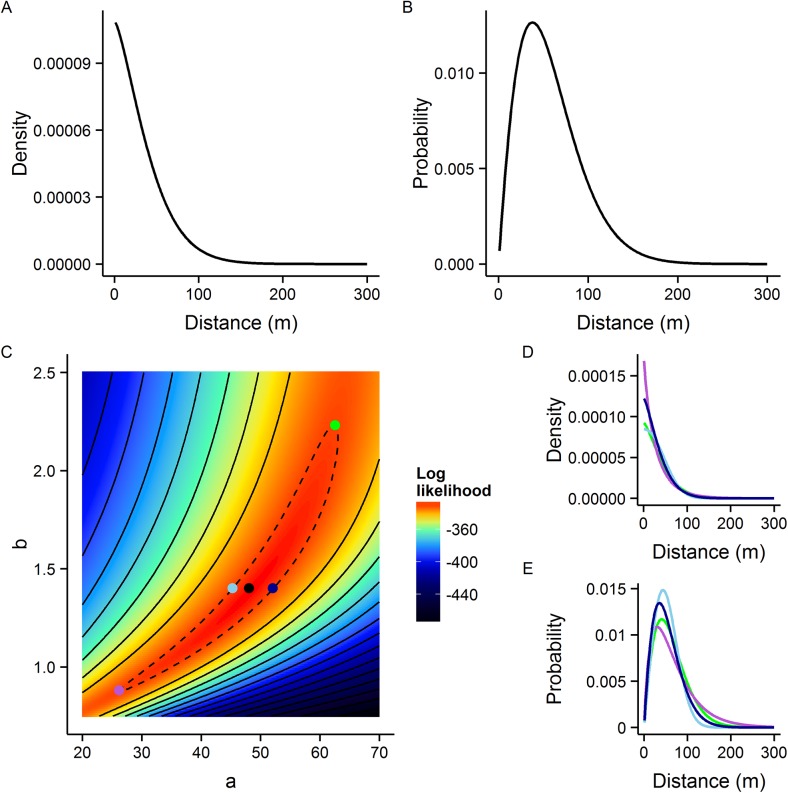
Again, the optimal model, as determined by AIC, used the exponential power density pdf, although the negative exponential density pdf produced only marginally inferior fit (AIC = 668.0 and 668.4 for the exponential power and negative exponential kernels respectively). The MLE exponential power pdf estimates a MDT for the ‘genetically sterile’ release of 58.0m (95% CI: 51.1m, 71.0m), FR50 of 51.8m (95% CI: 47.9m, 58.7m) and FR90 of 105.7m (95% CI: 86.5m, 141.1m). The MLE kernel, log-likelihood surface and examples of kernels drawn from 95% CI parameter values are shown in Fig 5.
Fig 5. Dispersal kernel summary for the Malaysian analysis.
A) Maximum likelihood estimate density with respect to distance for Malaysian data. B) Maximum likelihood distance pdf. C) The log-likelihood surface with respect to kernel parameters a and b, coloured points highlight the MLE (black, log-likelihood = -328) and examples of extreme 95% CI (green, light blue, dark blue and mauve) kernel parameter combinations. The dotted line demarks the 95% confidence interval contour. Solid black contour lines are at intervals of 10 log-likelihood. Examples of D) distance densities and E) distance pdf from the 95% confidence interval range corresponding to the coloured points shown in panel C.
The coefficient summaries from the negative binomial model using the exponential power transformed distance explanatory variable are shown in Table 5. This second analysis again indicates that distance is an important significant predictor of the expected count of recaptures. The number of days post release was also significantly associated with recapture number. Assuming no emigration, the estimated mortality rate of released insects of 0.46 (95% profile likelihood CI: 1.03, 0.13) would equate to a mean average lifespan of 0.46−1 = 2.17 days (95% CI: 0.97 days, 8.85 days). Unlike the analysis for Brazil there was evidence of an association between the distance and the number of days post release explanatory variables.
Table 5. Malaysia model coefficient estimates.
| Coefficient | Estimate | Standard error | t-value | p-value |
|---|---|---|---|---|
| Intercept | -0.013 | 0.79 | -0.016 | 0.98 |
| Transformed distance | 96,300 | 17,500 | 5.50 | <0.0001 |
| Number of days post release | -0.46 | 0.22 | -2.10 | 0.036 |
| Interaction (Transformed distance × Days post release) | -24420 | 6467 | -3.78 | 0.0002 |
GLM coefficient estimates and associated standard errors, t-values and p-values from the optimal model for the Malaysia analysis. Distance was transformed using the exponential power kernel.
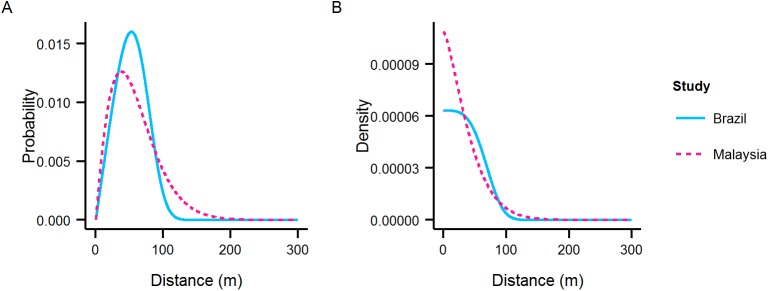
For a direct comparison the distance pdf and density with respect to distance for the optimal kernels estimated from the Itaberaba and Malaysia MRR experiments have been overlaid (Fig 6).
Fig 6. Dispersal kernel comparison.
A comparison of the A) distance pdf and B) density with respect to distance for estimates using MRR data from Brazil (solid blue line) and Malaysia (dashed pink line). The comparison highlights the similarity in estimated kernels for experiments conducted on different continents, in different habitats.
Discussion
An in-depth analysis of the dispersal ability of released ‘genetically sterile’ male Ae. aegypti mosquitoes in the field has been conducted. The primary analysis, of MRR data from Brazil, indicates distance from the release point to be an important predictor of the expected number of recaptures. The relationship between the recapture number and the distance from the release point is highly non-linear. The regression model performed optimally when an exponential power dispersal kernel was used to transform distances. The analysis methodology was also used to re-analyse MRR from Malaysia, where again an exponential power kernel provided best model fit.
The optimal Brazil GLM performed well, explaining around half of the variation observed in the data. Transformed distance and the number of days post release were the most influential, highly significant predictors of recapture number. The decline in numbers temporally after release is considered to be predominantly due to the effect of mortality. The effect of emigration from the study area can be important [28] and would further reduce numbers but was assumed to be small due to the size of the study area and low recaptures at the periphery.
Distance was highly significantly correlated with recapture number in all models considered. The exponential power dispersal kernel provided the optimum model fit. This kernel parametric form is slightly more flexible than the negative exponential. The kernel produced showed a high and consistent level of dispersal from 0-33m from the release site. After this point the density falls fairly steeply, reaching very low levels shortly after 100m (FR90 = 83.0m), indicating that coverage decreases quickly at increasing distances more than 33m from a release point. The MDT estimated using the best-fit kernel parameters was 52.8m (95% CI: 49.9m, 56.8m). This is consistent with a number of published field studies of male Ae. aegypti dispersal which estimate mean distance travelled to range from 10m to 100m (Table 6). There are however, a limited number of studies of male Ae. aegypti dispersal as focus has been on the biting females. It is however, important to note that for skewed distributions of dispersal distances the MDT as a measure of central tendency should be interpreted with some caution.
Table 6. Summary of a literature review of male Ae. aegypti dispersal estimates.
| MDT/MDT range (m) | Location | Notes | Reference |
|---|---|---|---|
| 10–30 | Hainan Island, China | Released in the centre of a village | [8] |
| 15–39 | Sonepat, India | - | [9] |
| 32 | Ilha do Governador, Brazil | Raised on poor diet | [10] |
| 35 | Pentland, Australia | - | [11] |
| 35–60 | Hainan Island, China | Released at the edge of a village | [8] |
| 42 | Ilha do Governador, Brazil | Raised on rich diet | [10] |
| 52 | Jalan Tentera, Malaysia | Transgenic | [12] |
| 100 | Jalan Tentera, Malaysia | Laboratory strain | [12] |
The number of non-Aedes mosquitoes was significantly positively correlated with the number of recaptured ‘genetically sterile’ mosquitoes. This explanatory variable is thought to be a proxy for the house-attractiveness or accessibility of a house to mosquitoes; large numbers of other mosquito species may indicate that the household is situated in a favourable location or particularly amenable or attractive to mosquitoes. Clustering of Aedes mosquitoes at the household level is a commonly observed phenomenon [29–31]. An alternative explanation could also lie in differences in the abilities of operators to sample mosquitoes.
The humidity and directional quadrants were significantly associated with the number of recaptured ‘genetically sterile’ mosquitoes but had small effect sizes. It would be expected that any directional differences are attributable to site- and time-specific heterogeneities in terrain, habitat type, wind direction or other external factors [32–34]. Humidity was positively associated with recapture number, which could be due to an increased tendency for Ae. aegypti to seek shelter with increasing humidity [35]. These explanatory variables must be interpreted with some caution as there is the potential for selection by AIC to overfit models [36,37]. The covariates may therefore be included in the final models despite their relatively small influence on model fit.
One limitation of this study was the low number of recaptures in the Brazil dataset. For this reason there was little power to analyse individual releases separately, necessitating the analysis of the combined datasets and the assumption that influences not accounted for would be similar across all three releases. The proportion of individuals recaptured may have been improved by a more targeted, or higher intensity, sampling effort or increased survival of the released individuals. Alternatively, the absolute number of recaptures could have been increased with larger release numbers. We have assumed throughout that aspiration will not remove all fluorescent dust from the marked individuals [38]. The dataset could also have been further improved with household-specific monitoring of climatic factors to give greater resolution to observations on the relationship between meteorological variables and recapture numbers. The standard errors of the GLM coefficients (Tables 3 and 5) were estimated conditional upon the MLEs for kernel parameters a and b whilst the confidence intervals for the kernel parameters were obtained conditional upon the MLE for the GLM coefficients. Thus the reported standard errors are likely to be smaller than if we had been able to compute the unconditional standard errors and confidence intervals for all of the parameters. Analysis of the residuals indicated little residual spatial autocorrelation with perhaps the exception of some under-estimation of recapture numbers at further distances (>150 m), potentially indicating the influence of long-distance dispersers [39], although, due to the small number of recaptures, this is difficult to verify.
The optimal GLM associated with the Malaysia data also explained approximately 50% of the variation observed in the recapture data. For the optimal model only two covariates, number of days post release and distance, plus their interaction term were included. The optimal model again used the exponential power dispersal kernel, with a corresponding MDT estimate of 58m (95% CI: 51.1m, 71.0m) that corroborated the MDT estimate of 52.4m (95% CI: 41.6m, 61.4m) from the previously published analysis of these data [12]. The FR50 estimate of 51.8m (95% CI: 47.9m, 58.7m) was substantially different from the previously published estimates of 16.2m (95% CI: 10.5m, 22.5m), a product of the different underlying models for dispersal with respect to distance used in each analysis. This deviation further highlights the potential benefits of more accurately characterising dispersal behaviour. The number of days post release covariate, as expected, was significantly negatively associated with recapture number. The associated average lifespan of 2.17 days (95% CI: 0.97 days, 8.85 days) was in good agreement with the previously published estimate of 2 days (95% CI: 1.8 days, 2.2 days). The coefficient indicated a smaller effect size than seen in the Brazil MRR data, implying improved survival, less emigration or a combination of the two for individuals in the Malaysia releases. The recapture rate in the Malaysia MRR experiment was very high, approximately 50% of all individuals released were recaptured. This may bias the results and could violate the underlying assumption that the negative binomial distribution approximates proportions when recapture numbers are small relative to the release size.
The lack of significant interaction between the number of days post release and distance in the Brazil data provides evidence for a single main dispersal event on release (the probability of travelling a given distance is not influenced by the number of days post-release). In the Malaysia analysis the significant interaction term indicates a more continual dispersal process over time, possibly due to the lack of favourable (urban/peri-urban) habitat across the whole range of the study site at this location. However the influence of the interaction term on predicted recaptures is very small; the majority of released individuals have died (or emigrated) before the interaction term becomes influential. For both locations the majority of recaptures are predicted spatially and temporally close to the release location and date respectively. There is published evidence to support either the occurrence of a single dispersal event [40–42] or a more continuous dispersal process upon release [8,9,11].
For experiments carried out in different habitats, on different continents, the estimated dispersal kernels were very similar (Fig 6). The Brazil dispersal kernel is slightly fatter tailed (larger b parameter) but in general there is evidence for a degree of consistency in the dispersal ability of ‘genetically sterile’ male Ae. aegypti across a range of environments. Consistent dispersal may facilitate more generalised release procedures for sterile insect releases across a range of release locations and scenarios.
Accurately measuring and assessing the dispersal of released ‘genetically sterile’ male Ae. aegypti in the field is a vital component necessary to optimise vector control using these genetically sterile individuals. A successful control program using ‘genetically sterile’ male Ae. aegypti would maximise ‘genetically sterile’ insect density over the target area. Knowledge of the released insects’ ability to disperse is vital in predicting their density with respect to specific release points or routes. An ability to predict the coverage of dispersed individuals will facilitate the design and implementation of more efficient control and monitoring programs in the future.
Supporting Information
Georeferenced recapture number with respect to release, time and meteorological variables.
(TXT)
Acknowledgments
We are very grateful to community of Itaberaba, without whose constant support, participation and encouragement the field work evaluations described here would not have been possible. We would like to thank Biofábrica Moscamed Brasil for rearing of the released insects. We thank Dr. Renaud Lacroix for permission to use the data from the Malaysian MRR and discussion of the study.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
PW was funded by the BBSRC (Training Grant, No. BB/I015957/1). PW and CAD thank the Medical Research Council for Centre funding. MLC acknowledges SESAB - Health Secretary of Bahia State 0300110300917-033/2011 for financial support. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.World Health Organization. Dengue. Guidelines for diagnosis, treatment, prevention and control. 2009. [PubMed]
- 2. Bhatt S, Gething PW, Brady OJ, Messina JP, Farlow AW, Moyes CL, et al. The global distribution and burden of dengue. Nature. 2013;496: 504–507. 10.1038/nature12060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Simmons CP, Farrar JJ, Nguyen van VC, Wills B. Dengue. N Engl J Med. 2012;366: 1423–1432. 10.1056/NEJMra1110265 [DOI] [PubMed] [Google Scholar]
- 4. Harris AF, McKemey AR, Nimmo D, Curtis Z, Black I, Morgan SA, et al. Successful suppression of a field mosquito population by sustained release of engineered male mosquitoes. Nat Biotechnol. 2012;30: 828–830. 10.1038/nbt.2350 [DOI] [PubMed] [Google Scholar]
- 5. Southwood TRE, Henderson P. Absolute population estimates using capture-recapture experiments. Ecological methods. 2000. pp. 73–140. [Google Scholar]
- 6. Smith TD, Allen J, Clapham PJ, Hammond PS, Katona S, Larsen F, et al. An ocean-basin-wide mark-recapture study of the North Atlantic humpback whale (Megaptera novaeangliae). Mar Mammal Sci. 1999;15: 1–32. [Google Scholar]
- 7. McKenzie JA. The distribution of vineyard populations of Drosophila melanogaster and Drosophila simulans during vintage and non-vintage periods. Oecologia. 1974;15: 1–16. [DOI] [PubMed] [Google Scholar]
- 8. Tsuda Y, Takagi M, Wang S, Wang Z, Tang L. Movement of Aedes aegypti (Diptera: Culicidae) released in a small isolated village on Hainan Island, China. J Med Entomol. 2001;38: 93–98. [DOI] [PubMed] [Google Scholar]
- 9. Reuben R, Panicker KN, Brooks GD, Ansari MA. Studies on dispersal and loss rate of male Aedes aegypti (L.) in different seasons at Sonepat, India. J Commun Dis. 1975;7: 301–312. [Google Scholar]
- 10. Maciel-De-Freitas R, Codeco CT, Lourenco-De-Oliveira R. Body size-associated survival and dispersal rates of Aedes aegypti in Rio de Janeiro. Med Vet Entomol. 2007;21: 284–292. [DOI] [PubMed] [Google Scholar]
- 11. Muir LE, Kay BH. Aedes aegypti survival and dispersal estimated by mark-release-recapture in northern Australia. Am J Trop Med Hyg. 1998;58: 277–282. [DOI] [PubMed] [Google Scholar]
- 12. Lacroix R, McKemey AR, Raduan N, Kwee Wee L, Hong Ming W, Guat Ney T, et al. Open Field Release of Genetically Engineered Sterile Male Aedes aegypti in Malaysia. PLoS One. 2012;7: e42771 10.1371/journal.pone.0042771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Morris CD, Larson VL, Lounibos LP. Measuring mosquito dispersal for control programs. J Am Mosq Control Assoc. 1991;7: 608–615. [PubMed] [Google Scholar]
- 14. Mollison D. Dependence of epidemic and population velocities on basic parameters. Math Biosci. 1991;107: 255–287. [DOI] [PubMed] [Google Scholar]
- 15. Nathan R, Muller-Landau H. Spatial patterns of seed dispersal, their determinants and consequences for recruitment. Trends Ecol Evol. 2000;15: 278–285. [DOI] [PubMed] [Google Scholar]
- 16. Havel JE, Shurin JB, Jones JR. Estimating Dispersal from Patterns of Spread: Spatial and Local Control of Lake Invasions. Ecology. 2002;83: 3306–3318. [Google Scholar]
- 17. Estep LK, Burkett-Cadena ND, Hill GE, Unnasch RS, Unnasch TR. Estimation of dispersal distances of Culex erraticus in a focus of eastern equine encephalitis virus in the southeastern United States. J Med Entomol. 2010;47: 977–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Clobert J, Baguette M, Benton TG, Bullock JM. Dispersal ecology and evolution. 2012.
- 19. Carvalho DO, Nimmo D, Naish N, McKemey AR, Gray P, Wilke ABB, et al. Mass Production of Genetically Modified Aedes aegypti for Field Releases in Brazil. J Vis Exp. 2014; e3579 10.3791/3579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Faraway JJ. Extending the Linear Model with R. Carlin BP, Chatfield C, Tanner M, Zidek J, editors. Texts in statistical science. 2006.
- 21.Venables WN, Ripley BD. Modern Applied Statistics with S [Internet]. 2002.
- 22. Ismail N, Jemain AA. Handling overdispersion with negative binomial and generalized Poisson regression models. Casualty Actuarial Society Forum. 2007. pp. 103–158. [Google Scholar]
- 23. Lawless J. Negative binomial and mixed Poisson regression. Can J Stat. 1987;15: 209–225. [Google Scholar]
- 24. Peart DR. The Quantitative Representation of Seed and Pollen Dispersal. Ecology. 1985;66: 1081–1083. [Google Scholar]
- 25.Cousens R, Dytham C, Law R. Dispersal in plants. A population perspective. Oxford. 2008.
- 26.R Core Team. R: A Language and Environment for Statistical Computing [Internet]. 2012.
- 27. Buonaccorsi JP, Harrington LC, Edman JD. Estimation and comparison of mosquito survival rates with release-recapture-removal data. J Med Entomol. 2003;40: 6–17. [DOI] [PubMed] [Google Scholar]
- 28. Guerra CA, Reiner RC, Perkins TA, Lindsay SW, Midega JT, Brady OJ, et al. A global assembly of adult female mosquito mark-release-recapture data to inform the control of mosquito-borne pathogens. Parasit Vectors. 2014;7: 276 10.1186/1756-3305-7-276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Regis L, Monteiro AM, Melo-Santos MA, SilveiraJr JC, Furtado AF, Acioli R V, et al. Developing new approaches for detecting and preventing Aedes aegypti population outbreaks: basis for surveillance, alert and control system. Mem Inst Oswaldo Cruz. 2008;103: 50–59. [DOI] [PubMed] [Google Scholar]
- 30. Harrington LC, Scott TW, Lerdthusnee K, Coleman RC, Costero A, Clark GG, et al. Dispersal of the dengue vector Aedes aegypti within and between rural communities. Am J Trop Med Hyg. 2005;72: 209–220. [PubMed] [Google Scholar]
- 31. Getis A, Morrison A, Gray K, Scott T. Characteristics of the spatial pattern of the dengue vector, Aedes aegypti, in Iquitos, Peru. Am J Trop Med Hyg. 2003;69: 494–505. [PubMed] [Google Scholar]
- 32. Nathan R, Getz WM, Revilla E, Holyoak M, Kadmon R, Saltz D, et al. A movement ecology paradigm for unifying organismal movement research. Proc Natl Acad Sci U S A. 2008;105: 19052–19059. 10.1073/pnas.0800375105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Midega JT, Smith DL, Olotu A, Mwangangi JM, Nzovu JG, Wambua J, et al. Wind direction and proximity to larval sites determines malaria risk in Kilifi District in Kenya. Nat Commun. 2012;3: 674 10.1038/ncomms1672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Valerio L, Facchinelli L, Ramsey JM, Bond JG, Scott TW. Dispersal of male Aedes aegypti in a coastal village in southern Mexico. Am J Trop Med Hyg. 2012;86: 665–76. 10.4269/ajtmh.2012.11-0513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Suwannachote N, Grieco J, Achee N, Suwonkerd W, Wongtong S, Chareonviriyaphap T. Effects of environmental conditions on the movement patterns of Aedes aegypti (Diptera: Culicidae) into and out of experimental huts in Thailand. J Vector Ecol. 2009;34: 267–275. 10.1111/j.1948-7134.2009.00035.x [DOI] [PubMed] [Google Scholar]
- 36. Bedrick E, Tsai C- L. Model selection for multivariate regression in small samples. Biometrics. 1994;50: 226–231. [Google Scholar]
- 37. Anderson D, Burnham K, White G. AIC model selection in overdispersed capture-recapture data. Ecology. 1994;75: 1780–1793. [Google Scholar]
- 38. Hagler JR, Jackson CG. Methods for marking insects: current techniques and future prospects. Annu Rev Entomol. 2001;46: 511–543. [DOI] [PubMed] [Google Scholar]
- 39. Service MW. Mosquito (Diptera: Culicidae) Dispersal—The Long and Short of It. Entomol Soc Am. 1997;34: 579–588. [DOI] [PubMed] [Google Scholar]
- 40. McDonald PT. Population characteristics of domestic Aedes aegypti (diptera: Culicidae) in villages on the Kenya coast ii. Dispersal within and between villages. J Med Entomol. 1977;14: 49–53. [DOI] [PubMed] [Google Scholar]
- 41. Sheppard PM, Macdonald WW, Tonn RJ, Grab B. The dynamics of an adult population of Aedes aegypti in relation to Dengue Haemorrhagic Fever in Bangkok. J Anim Ecol. 1969;38: 661–702. [Google Scholar]
- 42. Liew C, Curtis CF. Horizontal and vertical dispersal of dengue vector mosquitoes, Aedes aegypti and Aedes albopictus, in Singapore. Med Vet Entomol. 2004;18: 351–360. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Georeferenced recapture number with respect to release, time and meteorological variables.
(TXT)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.