Abstract
Diverse cell biological processes that involve shaping and remodeling of cell membranes are regulated by membrane lateral tension. Here we focus on the role of tension in driving membrane fusion. We discuss the physics of membrane tension, forces that can generate the tension in plasma membrane of a cell, and the hypothesis that tension powers expansion of membrane fusion pores in late stages of cell-to-cell and exocytotic fusion. We propose that fusion pore expansion can require unusually large membrane tensions or, alternatively, low line tensions of the pore resulting from accumulation in the pore rim of membrane-bending proteins. Increase of the inter-membrane distance facilitates the reaction.
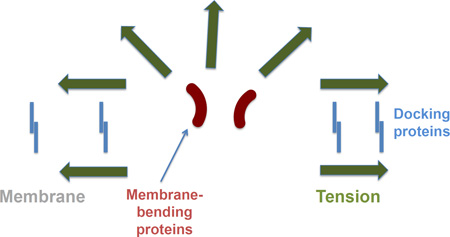
Graphic abstract
Fusion pore expansion in the contact zone between two membranes docked together by the adhesion proteins increases the perimeter of the energy-intensive pore edge and has to be driven by membrane tension. Accumulation of the membrane-bending proteins at the pore rim lowers the pore edge energy (line tension of the pore) and, thus, lowers the membrane tension required for the pore expansion.
Introduction
The notion of membrane tension is widely used in the cell biological literature concerned with membrane deformations and restructuring such as cell spreading on and movement along extracellular substrates, endocytosis, exocytosis, viral infection, cell fusion in development, and propagation of mechanical signals between the cell front and rear. All these diverse processes include transformations of membrane shapes by bending and changes of membrane connectivity by fission and fusion.
While several recent reviews addressed the role of tension in the dynamic changes in membrane shape accompanying cell motion [1–3], fewer attempts have been made to address the effects of tension on membrane remodeling by fission [4,5] and fusion. Here we focus on the latter topic and discuss the current data and hypotheses concerning the role of tension in mechanisms of membrane fusion.
We start with considering the physical meaning of membrane tension, the feasible mechanisms of its generation in cells and the realistic values of tension expected in cell membranes. Then we address the data suggesting that membrane tension plays an important role in fusion and discuss the related hypothetical physical mechanisms.
Membrane tension
Definitions
Tension within a membrane is generated as a response to application to the membrane surface of external forces. Tension develops within lipid bilayers constituting structural bases of all biological membranes. A bilayer can be seen as a continuous two-dimensional film consisting of two lipid monolayers of about 2–3nm thickness. Lipid molecules within the monolayers can be organized in persistent or dynamic domains of diverse lipid compositions and even different physical states (see for recent review [6]).
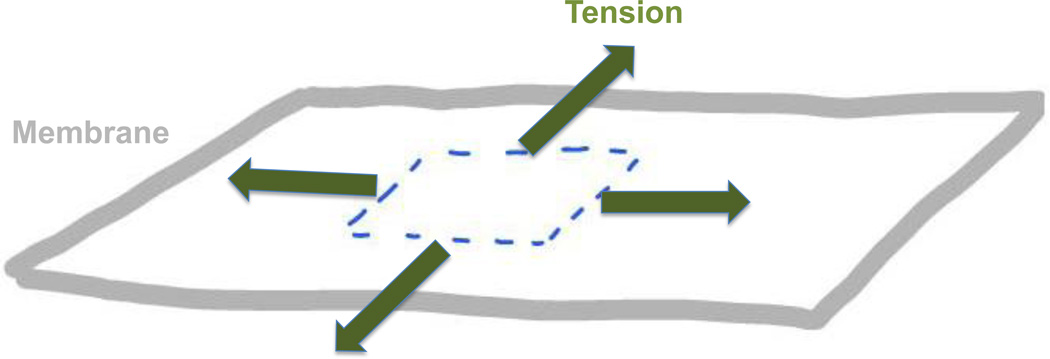
Rigorous definitions of membrane tension, also referred to as the lateral tension, are analogous to those introduced in physical chemistry of interfaces for surface (or interfacial) tension [7]. While several such definitions exist (see for review [8,9]), beginning from the original thermodynamic definition introduced by Gibbs [10], here we will use the most intuitive one, which can be called the mechanical tension (see e.g. [11]). Within this definition, tension is a local characteristic of the membrane describing the stretching-compression elastic stresses at every point along the membrane surface. Definition of tension requires consideration of a small (infinitesimal) element of the membrane plane separated from the rest of the membrane by an imaginary boundary (Fig. 1). The mechanical tension, referred below for brevity as, simply, tension, is a force applied to the unit length of this imaginary boundary by the surrounding membrane in the direction tangential to the membrane plane.
Fig. 1. Definition of membrane tension.
Tension is the force applied to the unit length of the imaginary boundary (dashed line) separating a small membrane region from the rest of the membrane.
Tension distribution
The character of the tension distribution in the membrane plane is determined by the membrane physical properties and the conditions of the intra-membrane mechanical equilibrium. Every membrane domain, each membrane monolayer as a whole, and the entire membrane bilayer have properties of a two-dimensional fluid, which means that lipid molecules diffuse and can undergo two-dimensional flow in the membrane plane (see for recent review [6]). The 2D membrane fluidity determines both the tension dependence on the direction in the membrane plane and the tension distribution along the membrane surface, which are analogous to the orientational and positional dependence of pressure in a regular 3D fluid.
Due to the 2D fluid nature of lipid monolayers, the membrane tension can be presented as consisting of two contributions: static tension, γ, analogous to the hydrostatic pressure in 3D liquid case, and dynamic contribution, γν, representing the tension contribution related to the lipid flow. The dynamic tension, γν, is generally, anisotropic as determined by the direction of the lipid flow shear rate in the membrane plane [11]. In contrast, the static tension, γ, as hydrostatic pressure in 3D fluids, is isotropic. The isotropic tension exists at every point of the membrane surface irrespectively of the lipid flow and represents the tension component most essential for membrane shaping and remodeling.
According to Pascal’s low, the hydrostatic pressure generated in some region of a 3D fluid is transmitted, homogeneously, throughout the whole fluid volume. Hence one would expect also the static tension, γ, to be equal along the whole membrane plane. There are, however, situations where the distribution of γ in the membrane plane is inhomogeneous.
A straightforward reason for inhomogeneity of γ could be related to the sharp boundaries of membrane domains, which represent barriers for lipid lateral diffusion. Indeed, because of the line tension of the domain boundary, βd (see e.g. [12]), the tension within such a domain can be different by an amount, δγ, from the tension in the surrounding membrane. The value of δγ, depends of the domain radius, Dd, according to δγ ≈ βd/Dd. Taking into account that the typical value of the domain line tension constitutes βd ≈ 1pN [12], the tension inside the domain can be smaller than that in the surrounding membrane by a value comparable to a typical cell-membrane tension, δγ ≈ 0.01mN/m (see below), provided that the domain is sufficiently small, Dd ≤ 100nm. For larger domains, the difference between the intra- and extra- domain tension must be negligibly small.
A continuous variation of tension along the membrane plane can be due to the effects of membrane curvature. Thermodynamic consideration or, equivalently, the condition of the membrane mechanical equilibrium in the lateral direction show that the membrane tension depends on the local membrane curvature (see e.g., [13]). Tension adopts larger values in the regions of larger curvature. Another factor leading to inhomogeneity of the tension is application to the membrane surface of distributed external forces directed tangentially to the membrane plane. A specific example of such forces are the forces arising from viscous friction developing in the course of the cell movement between the membrane bilayer and the proteins anchoring the membrane to the cytoskeletal cortex [14].
Membrane tension generation in cells
The characteristic tensions in plasma membranes are in the range of 0.01–0.04mN/m (see e.g., [2] and refs therein) but for some cells can reach much larger values of 0.15–0.3mN/m [15–18].
One can think of three major origins of forces acting on cell membranes and generating membrane tension: (i) osmotically controlled difference in hydrostatic pressure between the cytosol and the outside medium (see e.g. [19]); (ii) membrane interaction with cytoskeletal components such as sub-membrane acto-myosin cortex [17] and acto-myosin network driving cell motion along external substrates [20,21]; and (iii) forces resulting from cell adhesion to and spreading on external substrates [2] and forces caused by cell-cell adhesion [22]. In specific instances, tension is often produced by interplay between these primary factors.
The membrane tension produced by the forces listed above can be modulated by intracellular structures and processes coupled to the changes in the effective area of the plasma membrane through the exchange of the lipid material between the membrane under question and an effective membrane reservoir. Specifically, a balance between endocytosis consuming the membrane area through budding and abscission of endocytic vesicles and exocytosis replenishing the area through vesicle fusion can modulate the tension [2,4]. Another mechanism relates to an effective reservoir of membrane area stored in caveolae [23]. Reversible flattening of caveolae into the plasma membrane regulates the in-plane membrane area and, hence, the membrane tension.
The tension generation by acto-myosin machinery and modulation by interplay between endo- and exocytosis was clearly demonstrated for cells spreading on extra-cellular substrates [2]. For moving cells (fish keratocytes) the tension was shown to result from counter-action between, on one hand, the pushing forces produced by actin filaments polymerizing against the membrane at the lamellipodial leading edge, and, on the other, the membrane-substrate adhesion at the cell rear. The resulting tension was maximal at the cell front and decreased continuously towards the cell rear because of an effective viscous friction between the membrane and the cytoskeleton [14,15].
In both examples above, the effect of polymerizing actin was counteracted by the contractile activity of myosin II, which pulls the polymerizing actin bundles towards the cell interior, hence, decreasing the pushing force they exert on the membrane and, consequently, reducing the tension. The same must be true for the myosin effect on the tension generated by the cortical acto-myosin layer coupled to the cytosolic face of the plasma membrane. The myosin-driven contraction of the cortex layer is counteracted by the stresses within the membrane bilayer leading to the negative (compressing) contribution to the bilayer tension. This negative contribution can be achieved, directly, through the bilayer in-plane compression or, effectively, through the bilayer local bending between the spots of the cortex anchoring to the bilayer surface. The tension reduction by myosin II activity has been demonstrated experimentally in several studies on different cell types [2,15,24]. Observations of the opposite relationship between the myosin II activity and the membrane tension [25] may be due to raising of the intracellular hydrostatic pressure through a tendency of the cell to reduce its volume driven by the acto-myosin cortex contraction [19], or reflect indirect myosin effects, such as tension control by myosin II dependent endocytosis [26].
Tension in membrane fusion
Mechanisms of membrane fusion
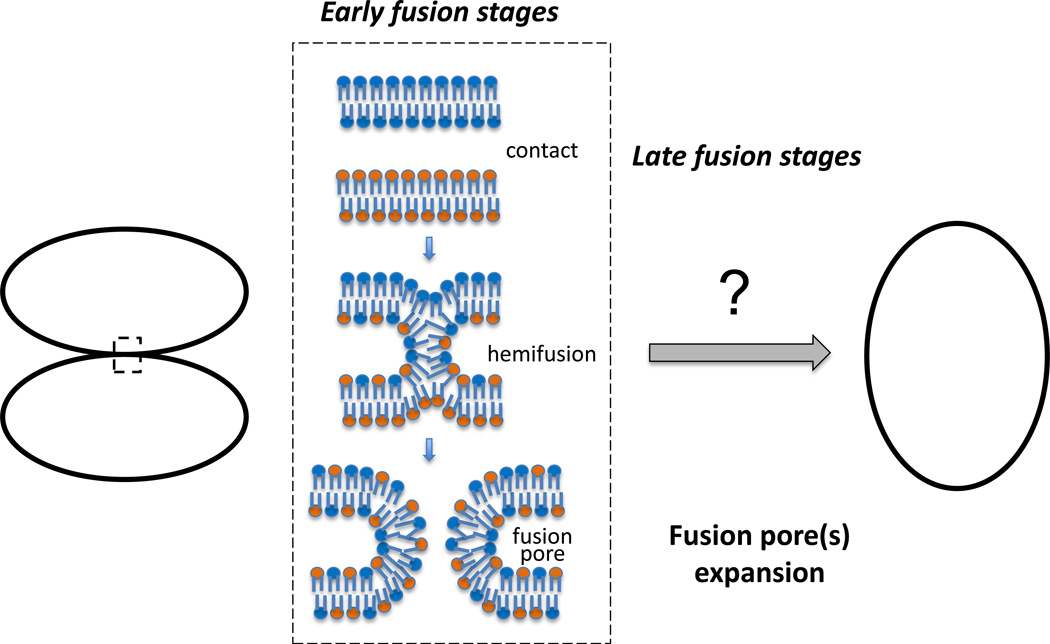
Membrane fusion, merger of two membrane bilayers into one, is ubiquitous in cell biology. Fusion is a key stage in intracellular trafficking of membranes and proteins, including exocytosis. Enveloped viruses utilize fusion to enter cells. Cells fuse in fertilization, muscle and bone formation and maintenance. As fusion between protein-free bilayers, diverse biological fusion processes including well-characterized examples of intracellular, viral and cell-to-cell fusions, apparently start with a local merger of contacting leaflets of the membranes (referred to as hemifusion stalk) followed by opening of a nascent fusion pore (Fig. 2). In this pathway, fusion pore edge is lined by a bent lipid monolayer containing or not containing transmembrane protein domains (TMDs). While this fusion-through-hemifusion pathway seems to be widely accepted for most fusion processes [27], it is still under debate in the case of SNARE-dependent intracellular membrane fusion where an alternative pathway starting from opening of an entirely proteinaceous channel-like fusion pore lined by SNARE TMDs is also considered [28], but see [27,29].
Fig. 2.
Pathway of membrane fusion from early stages (contact–hemifusion–fusion pore opening) to late stages, in which expansion of nascent fusion pore(s) of a few nanometers in diameter to a much larger diameter comparable with fusing vesicle or cell sizes completes unification of two membrane enclosed volumes.
Well-characterized examples of intracellular, viral and cell-to-cell fusions as well as fusion between protein-free bilayers have been dissected into the early and late stages (Fig. 2) driven, at least in some fusion processes, by distinct factors [30–33]. The early stages of fusion are finished by formation of a nanometer-sized fusion pore(s). The essence of the late stages is expansion of the fusion pore to radii comparable with sizes of fusing cells and vesicles. This yields, in the case of cell-to-cell fusion, multinucleated syncytia and, in the case of exocytotic fusion, a complete flattening of the vesicle membrane in the plasma membrane.
Experimental work on diverse fusion processes and theoretical studies demonstrate that fusion pore opening and, especially, its expansion at the late fusion stages are the most energy-demanding fusion stages [31,34]. For instance, in fusion mediated by viral fusogenic proteins (“fusogens”) such as influenza hemagglutinin and in SNARE-dependent fusion, lowering the number of functional viral and intracellular fusion proteins decreased the size of observed fusion pores and shifted the fusion phenotype from fusion pore to hemifusion [31,34–36].
The similarity of fusion pathways and similar dependences of the distinct stages of different fusion processes on the lipid composition of fusing membranes suggested conserved mechanisms of lipid rearrangements in both stages of the fusion reaction. Local membrane restructuring at the early fusion stage is limited by a few nanometer scale. Theoretical analysis based on the description of the membrane as a continuous elastic film and, most recently, molecular simulations have substantiated the physical mechanism, in which the energies of formation of hemifusion stalk and nascent fusion pore are determined by curvature stresses accumulated in the lipid bilayers of the membranes before fusion and released in the course of the early fusion stage [37,38]. It has been suggested that accumulation of the local curvature stresses is driven by specialized fusion proteins (such as SNAREs and their partners, or viral fusion proteins) assembled in relatively small complexes around the fusion sites.
Fusion pore expansion constituting the late stage of fusion process leads to membrane rearrangements, whose scales largely exceed those of the fusion protein complexes and vary between tens of nanometers for the vesicle fusion and tens of microns for cell-cell fusion. Such large scale membrane restructuring must be driven by global factors, persisting within large membrane areas or the entire membranes. The most natural candidate for playing a role of such a large-scale fusion factor is the lateral tension (see e.g. [39]).
Tension drives fusion pore expansion
The role of tension as the driving force of the fusion pore expansion was unambiguously demonstrated for fusion in model systems based on protein-free bilayers. In case of black lipid membranes, fusion pores were driven by a huge surface tension (~1–3 mN/m) generated by the bilayer contact with lipid reservoir [40]. Fusion pore expansion can be also driven by membrane tension generated by osmotic pressure gradient across the membrane [41,42]. In the case of fusion of very small vesicles with sizes comparable with the bilayer thickness (such as 20nm diameter vesicles often used in molecular simulations), fusion completion can be driven by the vesicle unbending, which releases a very significant bending elastic energy equivalent to the lateral tension. This mechanism can be relevant for specific examples of protein-mediated fusion of biological membranes. However, estimations show that that for vesicles with radii exceeding several tens of nanometers, the released bending energy covers only a relatively small part of the fusion pore energy so that the involvement of tension becomes essential. Therefore, recent studies have focused on the hypothesis that fusion pore expansion in biological fusion is powered by the tension in the nearly flat plasma membranes [25,37].
In cell-to-cell fusion initiated by influenza hemagglutinin [43], plasma membrane tension generated by applying a positive hydrostatic pressure to cell interior promoted expansion of the fusion pores. In a recent study on exocytosis in human neuroendocrine cells [25], two regulators of the dynamic properties of actin cytoskeleton, small GTPase Cdc42 and myosin II ATPase, were found to control the expansion of small fusion pores by maintaining tension in plasma membrane. Lowering the tension by blocking activities of either of these proteins lowered the percentage of the exocytotic fusion events that resulted in the full collapse of the vesicle into the plasma membrane rather than in kiss-and-run events with non-expanding and transient fusion pore.
Hypothesis that lateral tension drives fusion explains the data implicating several tension-generating and/or tension-controlling protein machineries in different fusion processes. Actin and actin-regulating proteins are major players in exocytosis [44]. Both myoblast fusion in muscle development and regeneration and macrophage fusion in osteoclast formation [45,46] have been reported to depend on formation of actin-rich podosome-like structures by which one of the fusing cells invades another. Lowering the activity of actin-crosslinking protein myosin II inhibits fusion pore expansion in exocytosis [25,47] and in cell-to-cell fusion [48]. Fusion was shown to depend on proteins, which, potentially, can regulate tension through endocytosis, such as dynamin, clathrin, epsin and BAR-domain proteins. Dynamin was shown to be involved in expansion of fusion pores in exocytosis [49], and in cell-to-cell fusion [46] and, specifically, the late stages of this process [32,50]. Cell-to-cell fusion has been reported to depend on clathrin [46] and F-BAR domain protein GRAF1 [51]. Overexpression in cells of F-BAR domains GRAF1 and FCHo2, and of ENTH domain of epsin, promoted late stages of cell fusion initiated by viral fusogens [33].
Feasibility of fusion pore expansion by membrane tension
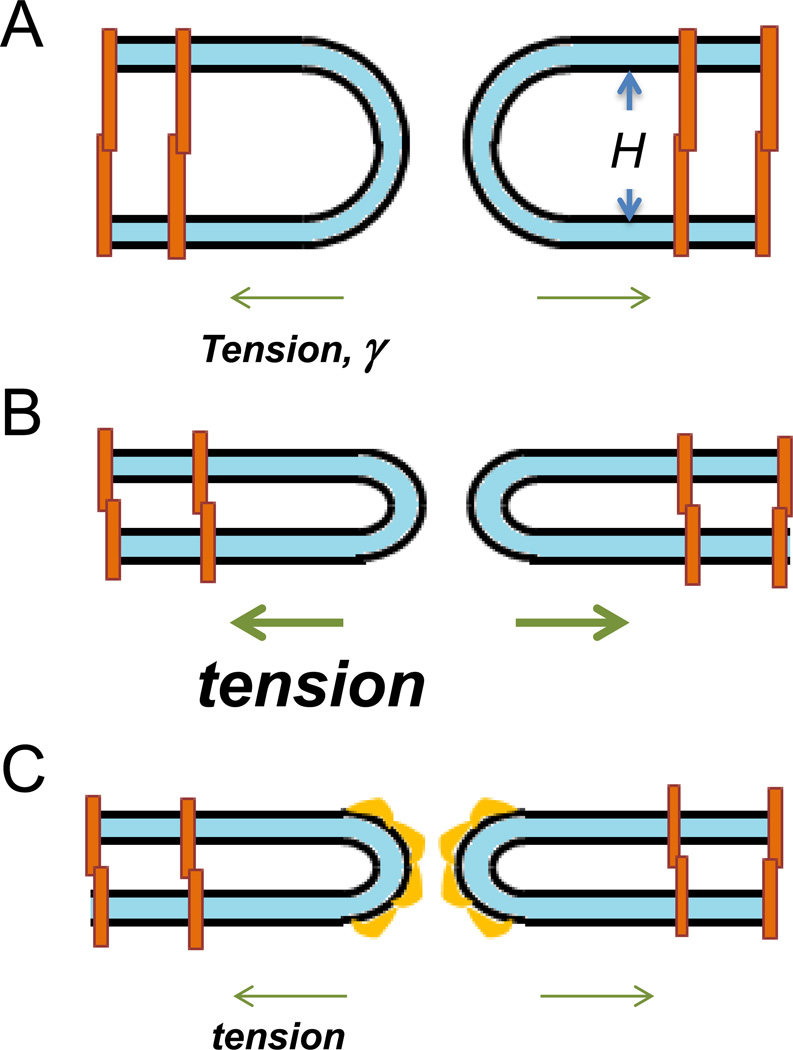
While, qualitatively, the existing experimental data support the role of tension as a major factor expanding the fusion pore, the viability of this mechanism has to be verified by quantitative estimations. There are two potential factors counteracting the fusion pore expansion by tension. The first is the line tension of the pore edge, β, whose essence is the bending energy of the membrane at the pore rim related to unit length of the pore perimeter. The second is the protein-mediated mutual adhesion of the fusing membranes along the area of the inter-membrane contact. In our estimate below we will focus on the line tension because, at least in a specific case of cell-cell fusion initiated by viral fusogens, fusion pore expansion to cell-size radii proceeds by lateral displacement of cell-cell adhesion zone to the periphery of the fusion site [30]. Thus, fusion pore expansion does not necessarily break protein complexes responsible for the cell-cell adhesion and may just move these complexes within a contact plane. We, therefore, estimate the interplay between the membrane lateral tension, γ, and the pore line tension, β. It is known from the theory of membrane rupture that the activation energy of pore expansion, Fp, is related to the lateral and line tensions, . The pore line tension can be expressed, approximately, through the membrane bending modulus, κ, and the distance between the mid-planes of the fusing membranes, H, as . As a result, the activation energy is given by . Note that an increase in the distance between the membranes H lowers the line tension β and the activation energy Fp. The typical value of the membrane bending rigidity is κ = 20kBT [52] (where kBT = 4 10−21Joule is a product of the Boltzmann constant and the absolute temperature). The activation energy that would allow pore expansion to occur within a biologically relevant time scale was estimated to be about [53]. Based on these numbers and the above relationship for Fp, we estimate that, assuming the lateral tension to have a typical reference value of γ = 0.03mN/m ([2] and references therein), the inter-membrane distance has to be around H = 140 nm, which greatly exceeds the typical inter-cellular distances of few tens of nanometers or less. This brings us to a conclusion that the membrane tension in fusing cells has to be larger by an order of magnitude, i.e. have values similar to those measured for moving keratocytes [15]. Indeed, assuming γ = 0.3mN/m, we obtain the required inter-membrane distance to constitute H ≈ 45 nm, which is feasible for cell-cell contacts (Fig. 3A). However, since pre-fusion contacts between the membranes can be much tighter, we suggest that fusion pore expansion is driven by increased membrane tension at the time of fusion (Fig. 3B). Alternatively, fusion pore expansion can be facilitated by a lowering of the pore line tension due to accumulation of membrane bending proteins at the pore edge (Fig. 3C) and [30]).
Fig. 3. Fusion pore expansion is controlled by membrane tension, distance between the membranes and line tension of the pore edge.
A. Membrane tension of 0.3mN/m is sufficient to drive fusion pore expansion for membranes (shown as light blue films) separated by ≥45nm. Proteins that mediate adhesion are shown as orange shapes. B. To drive fusion pore expansion in a tighter contact zone, the membranes have to be subjected to a higher tension. C. In the tight contact zone, accumulation of intracellular membrane-bending proteins at the rim of the pore would lower its line tension and, thus, the membrane tension required to drive the pore expansion.
It has to be noted that, in general, tension might also affect early fusion stages. However, the membrane area changes accompanying generation of a characteristic hemifusion stalk with height of 3nm are small constituting about 100 nm2. The corresponding energy of tension becomes comparable to the stalk bending energy of few tens of kBT only if the tension values are close to 1mN/m. Similar tensions are required to drive expansion of hemifusion diaphragm [54]. As noted above, the typical cell membrane tensions are at least 10 times lower. Hence, in most cases, the effects of membrane tension on the early fusion intermediates can be neglected.
Even very large membrane tensions generated by application of hydrostatic pressure inhibited rather than promoted the early stages of opening of fusion pores in hemagglutinin mediated fusion, possibly, by suppressing the small-scale membrane deformations, which bring the membranes into immediate local contact and prime them for fusion [43]. This finding suggests that any membrane tension-driven promotion of formation of early fusion intermediates is overshadowed by other effects of membrane tension.
Concluding remarks
Tension is a most plausible candidate for driving expansion of the fusion pores at the late stages of membrane fusion processes. However we still do not know why some fusion processes result in fusion pore expansion that fully unify two membrane-enclosed volumes (for instance, in formation of multinucleated cells) while other fusion processes are aborted before completion (for instance, in the kiss-and-run form of exocytosis and, apparently, in generation of cell-cell connecting nanotubes). Elucidation of the tension-fusion link will require a combination of further theoretical analysis, plasma membrane tension measurements and fusion assays. Moreover, since tension may also affect pre-fusion and early fusion stages, evaluation of the role of tension in fusion pore expansion will require fusion assays that specifically characterize late fusion stages [25,32]. We expect better understanding of the role of tension in membrane shaping and remodeling to bring new ways of controlling these processes in healthy cells and in pathophysiology.
HIGHLIGHTS.
Tension in cell membrane is produced by actin-membrane interactions, osmotic and adhesion forces.
As other membrane reshaping processes, membrane fusion depends on lateral tension.
In fusion pore expansion, membrane tension overcomes the line tension of the pore edge.
Acknowledgments
M.M.K. is supported by the Israel Science Foundation (ISF), and holds the Joseph Klafter Chair in Biophysics. The research of L.V.C. is supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Keren K. Membrane tension leads the way. Proc Natl Acad Sci U S A. 2011;108:14379–14380. doi: 10.1073/pnas.1111671108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gauthier NC, Masters TA, Sheetz MP. Mechanical feedback between membrane tension and dynamics. Trends Cell Biol. 2012;22:527–535. doi: 10.1016/j.tcb.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 3.Diz-Munoz A, Fletcher DA, Weiner OD. Use the force: membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 2013;23:47–53. doi: 10.1016/j.tcb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boulant S, Kural C, Zeeh JC, Ubelmann F, Kirchhausen T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat Cell Biol. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Weinberg J, Drubin DG. Clathrin-mediated endocytosis in budding yeast. Trends Cell Biol. 2012;22:1–13. doi: 10.1016/j.tcb.2011.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nicolson GL. Cell Membrane Fluid-Mosaic Structure and Cancer Metastasis. Cancer Res. 2015 doi: 10.1158/0008-5472.CAN-14-3216. [DOI] [PubMed] [Google Scholar]
- 7.Adamson AW. Physical Chemistry of Surfaces. New York: Woley; 1990. [Google Scholar]
- 8.Murphy CL. Thermodynamics of low tension and highly curved interfaces. University of Minnesota; 1966. [Google Scholar]
- 9.Kozlov MM. Some aspects of membrane elasticity. In: Poon WCK, Andelman D, editors. Soft condensed matter physics in molecular and cell biology. CRC press; Taylor & Francis group; 2006. pp. 79–93. Scottish Graduate Series. [Google Scholar]
- 10.Gibbs JW. The scientific papers. New York: Dover; 1961. [Google Scholar]
- 11.Evans E, Skalak R. Mechanics and Thermodynamics of Biomembranes. Florida: CRC Boca Raton; 1980. [Google Scholar]
- 12.Baumgart T, Hess ST, Webb WW. Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature. 2003;425:821–824. doi: 10.1038/nature02013. [DOI] [PubMed] [Google Scholar]
- 13.Kozlov MM, Markin VS. Interface Mechanics - the Shape of Membrane Cylinder. Journal De Physique Ii. 1991;1:805–820. [Google Scholar]
- 14.Schweitzer Y, Lieber AD, Keren K, Kozlov MM. Theoretical Analysis of Membrane Tension in Moving Cells. Biophysical Journal. 2014;106:84–92. doi: 10.1016/j.bpj.2013.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lieber AD, Yehudai-Resheff S, Barnhart EL, Theriot JA, Keren K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Current biology: CB. 2013;23:1409–1417. doi: 10.1016/j.cub.2013.05.063. [DOI] [PubMed] [Google Scholar]
- 16.Pietuch A, Bruckner BR, Janshoff A. Membrane tension homeostasis of epithelial cells through surface area regulation in response to osmotic stress. Biochimica et biophysica acta. 2013;1833:712–722. doi: 10.1016/j.bbamcr.2012.11.006. [DOI] [PubMed] [Google Scholar]
- 17.Braunger JA, Bruckner BR, Nehls S, Pietuch A, Gerke V, Mey I, Janshoff A, Steinem C. Phosphatidylinositol 4,5-bisphosphate alters the number of attachment sites between ezrin and actin filaments: a colloidal probe study. The Journal of biological chemistry. 2014;289:9833–9843. doi: 10.1074/jbc.M113.530659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu Y, Belkina NV, Park C, Nambiar R, Loughhead SM, Patino-Lopez G, Ben-Aissa K, Hao JJ, Kruhlak MJ, Qi H, et al. Constitutively active ezrin increases membrane tension, slows migration, and impedes endothelial transmigration of lymphocytes in vivo in mice. Blood. 2012;119:445–453. doi: 10.1182/blood-2011-07-368860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tinevez JY, Schulze U, Salbreux G, Roensch J, Joanny JF, Paluch E. Role of cortical tension in bleb growth. Proc Natl Acad Sci U S A. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophys J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 22.Maitre JL, Heisenberg CP. The role of adhesion energy in controlling cell-cell contacts. Current opinion in cell biology. 2011;23:508–514. doi: 10.1016/j.ceb.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nassoy P, Lamaze C. Stressing caveolae new role in cell mechanics. Trends in cell biology. 2012;22:381–389. doi: 10.1016/j.tcb.2012.04.007. [DOI] [PubMed] [Google Scholar]
- 24.Houk AR, Jilkine A, Mejean CO, Boltyanskiy R, Dufresne ER, Angenent SB, Altschuler SJ, Wu LF, Weiner OD. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bretou M, Jouannot O, Fanget I, Pierobon P, Larochette N, Gestraud P, Guillon M, Emiliani V, Gasman S, Desnos C, et al. Cdc42 controls the dilation of the exocytotic fusion pore by regulating membrane tension. Molecular biology of the cell. 2014;25:3195–3209. doi: 10.1091/mbc.E14-07-1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chandrasekar I, Goeckeler ZM, Turney SG, Wang P, Wysolmerski RB, Adelstein RS, Bridgman PC. Nonmuscle myosin II is a critical regulator of clathrin-mediated endocytosis. Traffic. 2014;15:418–432. doi: 10.1111/tra.12152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chernomordik LV, Kozlov MM. Membrane hemifusion: crossing a chasm in two leaps. Cell. 2005;123:375–382. doi: 10.1016/j.cell.2005.10.015. [DOI] [PubMed] [Google Scholar]
- 28.Chang C-W, Jackson Meyer B. Synaptobrevin Transmembrane Domain Influences Exocytosis by Perturbing Vesicle Membrane Curvature. Biophysical Journal. 2015;109:76–84. doi: 10.1016/j.bpj.2015.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pieren M, Desfougères Y, Michaillat L, Schmidt A, Mayer A. Vacuolar SNARE Protein Transmembrane Domains Serve as Nonspecific Membrane Anchors with Unequal Roles in Lipid Mixing. Journal of Biological Chemistry. 2015;290:12821–12832. doi: 10.1074/jbc.M115.647776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen A, Leikina E, Melikov K, Podbilewicz B, Kozlov MM, Chernomordik LV. Fusion-pore expansion during syncytium formation is restricted by an actin network. J Cell Sci. 2008;121:3619–3628. doi: 10.1242/jcs.032169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chernomordik LV, Kozlov MM. Protein-lipid interplay in fusion and fission of biological membranes. Annu Rev Biochem. 2003;72:175–207. doi: 10.1146/annurev.biochem.72.121801.161504. [DOI] [PubMed] [Google Scholar]
- 32.Leikina E, Melikov K, Sanyal S, Verma SK, Eun B, Gebert C, Pfeifer K, Lizunov VA, Kozlov MM, Chernomordik LV. Extracellular annexins and dynamin are important for sequential steps in myoblast fusion. J Cell Biol. 2013;200:109–123. doi: 10.1083/jcb.201207012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Richard JP, Leikina E, Langen R, Henne WM, Popova M, Balla T, McMahon HT, Kozlov MM, Chernomordik LV. Intracellular curvature-generating proteins in cell-to-cell fusion. Biochem J. 2011;440:185–193. doi: 10.1042/BJ20111243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cohen FS, Melikyan GB. The energetics of membrane fusion from binding, through hemifusion, pore formation, and pore enlargement. J Membr Biol. 2004;199:1–14. doi: 10.1007/s00232-004-0669-8. [DOI] [PubMed] [Google Scholar]
- 35.Lu X, Zhang F, McNew JA, Shin YK. Membrane fusion induced by neuronal SNAREs transits through hemifusion. J Biol Chem. 2005;280:30538–30541. doi: 10.1074/jbc.M506862200. [DOI] [PubMed] [Google Scholar]
- 36.Risselada HJ, Kutzner C, Grubmuller H. Caught in the act: visualization of SNARE-mediated fusion events in molecular detail. Chembiochem : a European journal of chemical biology. 2011;12:1049–1055. doi: 10.1002/cbic.201100020. [DOI] [PubMed] [Google Scholar]
- 37.Chernomordik LV, Kozlov MM. Mechanics of membrane fusion. Nat Struct Mol Biol. 2008;15:675–683. doi: 10.1038/nsmb.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McMahon HT, Kozlov MM, Martens S. Membrane curvature in synaptic vesicle fusion and beyond. Cell. 2010;140:601–605. doi: 10.1016/j.cell.2010.02.017. [DOI] [PubMed] [Google Scholar]
- 39.Chizmadzhev YA, Kuzmin PI, Kumenko DA, Zimmerberg J, Cohen FS. Dynamics of fusion pores connecting membranes of different tensions. Biophys J. 2000;78:2241–2256. doi: 10.1016/S0006-3495(00)76771-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chernomordik LV, Melikyan GB, Chizmadzhev YA. Biomembrane fusion: a new concept derived from model studies using two interacting planar lipid bilayers. Biochimica et biophysica acta. 1987;906:309–352. doi: 10.1016/0304-4157(87)90016-5. [DOI] [PubMed] [Google Scholar]
- 41.Chanturiya A, Chernomordik LV, Zimmerberg J. Flickering fusion pores comparable with initial exocytotic pores occur in protein-free phospholipid bilayers. Proc Natl Acad Sci U S A. 1997;94:14423–14428. doi: 10.1073/pnas.94.26.14423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zimmerberg J. Molecular mechanisms of membrane fusion: steps during phospholipid and exocytotic membrane fusion. Biosci Rep. 1987;7:251–268. doi: 10.1007/BF01121447. [DOI] [PubMed] [Google Scholar]
- 43.Markosyan RM, Melikyan GB, Cohen FS. Tension of membranes expressing the hemagglutinin of influenza virus inhibits fusion. Biophys J. 1999;77:943–952. doi: 10.1016/S0006-3495(99)76945-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Porat-Shliom N, Milberg O, Masedunskas A, Weigert R. Multiple roles for the actin cytoskeleton during regulated exocytosis. Cellular and molecular life sciences : CMLS. 2013;70:2099–2121. doi: 10.1007/s00018-012-1156-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shilagardi K, Li S, Luo F, Marikar F, Duan R, Jin P, Kim JH, Murnen K, Chen EH. Actin-propelled invasive membrane protrusions promote fusogenic protein engagement during cell-cell fusion. Science. 2013;340:359–363. doi: 10.1126/science.1234781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shin NY, Choi H, Neff L, Wu Y, Saito H, Ferguson SM, De Camilli P, Baron R. Dynamin and endocytosis are required for the fusion of osteoclasts and myoblasts. J Cell Biol. 2014;207:73–89. doi: 10.1083/jcb.201401137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Neco P, Fernandez-Peruchena C, Navas S, Gutierrez LM, de Toledo GA, Ales E. Myosin II contributes to fusion pore expansion during exocytosis. The Journal of biological chemistry. 2008;283:10949–10957. doi: 10.1074/jbc.M709058200. [DOI] [PubMed] [Google Scholar]
- 48.Kim JH, Ren Y, Ng WP, Li S, Son S, Kee YS, Zhang S, Zhang G, Fletcher DA, Robinson DN, et al. Mechanical tension drives cell membrane fusion. Developmental cell. 2015;32:561–573. doi: 10.1016/j.devcel.2015.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Anantharam A, Bittner MA, Aikman RL, Stuenkel EL, Schmid SL, Axelrod D, Holz RW. A new role for the dynamin GTPase in the regulation of fusion pore expansion. Mol Biol Cell. 2011;22:1907–1918. doi: 10.1091/mbc.E11-02-0101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Verma SK, Leikina E, Melikov K, Chernomordik LV. Late stages of the synchronized macrophage fusion in osteoclast formation depend on dynamin. Biochem J. 2014;464:293–300. doi: 10.1042/BJ20141233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Doherty JT, Lenhart KC, Cameron MV, Mack CP, Conlon FL, Taylor JM. Skeletal muscle differentiation and fusion are regulated by the BAR-containing Rho-GTPase-activating protein (Rho-GAP), GRAF1. The Journal of biological chemistry. 2011;286:25903–25921. doi: 10.1074/jbc.M111.243030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Niggemann G, Kummrow M, Helfrich W. The bending rigidity of phosphatidylcholine bilayers. Dependence on experimental methods, sample cell sealing and temperature. J. Phys. II. 1995;5:413–425. [Google Scholar]
- 53.Abidor IG, Arakelyan VB, Chernomordik LV, Chizmadzhev YA, Pastushenko VF, Tarasevich MR. Electrical breakdown of BLM: Main experimental facts and their qualitative discussion. Bioelectrochem. Bioenerg. 1979;6:37–52. [Google Scholar]
- 54.Warner JM, O'Shaughnessy B. The hemifused state on the pathway to membrane fusion. Physical review letters. 2012;108:178101. doi: 10.1103/PhysRevLett.108.178101. [DOI] [PubMed] [Google Scholar]