0–0 Energies Using Hybrid Schemes: Benchmarks of TD-DFT, CIS(D), ADC(2), CC2, and BSE/GW formalisms for 80 Real-Life Compounds

Abstract

The 0–0 energies of 80 medium and large molecules have been computed with a large panel of theoretical formalisms. We have used an approach computationally tractable for large molecules, that is, the structural and vibrational parameters are obtained with TD-DFT, the solvent effects are accounted for with the PCM model, whereas the total and transition energies have been determined with TD-DFT and with five wave function approaches accounting for contributions from double excitations, namely, CIS(D), ADC(2), CC2, SCS-CC2, and SOS-CC2, as well as Green’s function based BSE/GW approach. Atomic basis sets including diffuse functions have been systematically applied, and several variations of the PCM have been evaluated. Using solvent corrections obtained with corrected linear-response approach, we found that three schemes, namely, ADC(2), CC2, and BSE/GW allow one to reach a mean absolute deviation smaller than 0.15 eV compared to the measurements, the two former yielding slightly better correlation with experiments than the latter. CIS(D), SCS-CC2, and SOS-CC2 provide significantly larger deviations, though the latter approach delivers highly consistent transition energies. In addition, we show that (i) ADC(2) and CC2 values are extremely close to each other but for systems absorbing at low energies; (ii) the linear-response PCM scheme tends to overestimate solvation effects; and that (iii) the average impact of nonequilibrium correction on 0–0 energies is negligible.

1. Introduction

Theoretical chemistry now provides a panel of powerful tools to investigate the properties of electronically excited-states (ES). While most studies are still performed in the vertical approximation, that is rely on a frozen ground-state (GS) structure, an increasingly large body of works is exploring the ES potential energy surface.¹ The determination of the optimal ES structures gives access to theoretical fluorescence energies, whereas the calculation of ES vibrations allows one to compute both band shapes and 0–0 energies.² These energies correspond to the difference between ES and GS energies calculated at their respective geometrical minima and are corrected for the difference of zero-point vibrational energies (ZPVE) between the two states. 0–0 energies are of interest because they allow direct and well-grounded comparisons between theoretical and experimental values, the latter being taken as the absorption-fluorescence crossing points (AFCP). This contrasts with vertical transition energies. However, the calculation of the ES ZPVE, needed to compute 0–0 energies, is often computationally prohibitive, and only a limited set of theories can be used in practice to obtain 0–0 energies. Among the available theories, time-dependent density functional theory (TD-DFT),³ and more specifically, the adiabatic approximation to TD-DFT,⁴ are certainly the most popular thanks to the availability of both analytical ES first (gradients) and second (Hessian) derivatives.⁵⁻⁸ If adiabatic TD-DFT is probably the most efficient approach in terms of its accuracy/speed ratio, it suffers from a significant dependency on the selected exchange-correlation functional.⁹ Three other wave function theories can also be routinely used for ES, though with an increased computational burden compared to that of TD-DFT: (i) the configuration interaction singles method with a perturbative correction for double excitations, CIS(D);^10,11 (ii) the second-order algebraic diagrammatic construction, ADC(2);¹²⁻¹⁶ and (iii) the simplest equation-of-motion coupled cluster approach, CC2.^17,18 In most works, these theories as well as their spin component scaled (SCS) or spin opposite scaled (SOS) variants are nevertheless used in the vertical approach as computing ADC(2) and CC2 gradients remains a computationally demanding task, despite efficient implementations with the resolution of identity (RI) technique.¹⁸ Finally, the Bethe-Salpeter equation (BSE) formalism,¹⁹⁻²⁴ a specific formulation of Green’s function many-body perturbation theory initially developed for extended solids, has recently gained much popularity for gas phase organic molecules.²⁵⁻³⁹ Recent all-electron implementations adopting standard quantum chemistry Gaussian-bases could further allow one to compare the BSE formalism with higher-level wave function approaches on a large set of molecules,^36,37,39 showing an accuracy similar to the best TD-DFT calculations for standard Frenkel excitations, without the usual TD-DFT limitations associated with charge-transfer (CT) excitations^29,31 or cyanine-like systems.³⁶ Further, the BSE formalism is parameter free and, in its present adiabatic implementation, offers a scaling comparable to that of TD-DFT within Casida’s formulation.⁴

A clear limitation of the BSE formalism, however, is that analytic forces in the excited states are not available, making the determination of relaxed structure and vibrational modes in these states extremely challenging except for very small systems.⁴⁰ In a recent study, structural parameters, vibrational properties, and solvation effects were determined within TD-DFT, while vertical excitation energies in the gas phase at the DFT/TD-DFT geometries were calculated within the BSE formalism.⁴¹ This is similar to the combination of TD-DFT and high-level wave function approaches that were also used.⁴²⁻⁴⁵ Such a protocol allows one to reach physically sound 0–0 energies at a reasonable computational cost and is thoroughly benchmarked here. There have been several previous benchmark studies of theoretical ES methods in the framework of 0–0 energy calculations, and these works relied on diverse molecular sets.^{42−44,46−51} We summarize here the methodologies, set of molecules, and main conclusions of these earlier works. In a first category, one finds investigations devoted to rather compact molecules for which accurate gas-phase experimental values are available.^44,46,48,49 This choice grants two obvious advantages. On the one hand, there is no error originating from an incomplete environmental model, and on the other hand, a large number of approaches, including correlated wave function schemes, can be used as the investigated molecules are small. The main disadvantage of this choice is that most “real-life” structures cannot be modeled, as gas-phase experiments are often not available for large compounds. The first extended benchmarks in this category were performed by Furche and co-workers in 2011 and 2012.^46,48 They collected 109 transition energies presenting various spin multiplicities in mostly small molecules (the largest compound considered is porphyrin) and tested several exchange-correlation functionals (LSDA, PBE, BP86, TPSS, TPSSh, B3LYP, and PBE0) in the TD-DFT framework. In these works, the geometries and the ZPVE corrections were systematically obtained at the B3LYP level, whereas the def2-TZVP basis set was applied after tests. For a small but representative subset of 15 molecules, both ADC(2) and CC2 were also tested. For this subset, if only single-reference cases are considered, ADC(2) and CC2 were found to outperform TD-DFT, with mean absolute deviations smaller than 0.2 eV for the two wave function approaches. Fang, Oruganti, and Durbeej took a subset of 96 singlet and triplet states from Furche’s original set and assessed a large panel of exchange-correlation functionals (BP86, B3LYP, PBE0, M06-2X, M06-HF, CAM-B3LYP, and ωB97X-D) as well as CC2.⁴⁹ They optimized and determined the ZPVE corrections for all molecules in a consistent manner (CC2 energies on CC2 geometries, M06-2X energies on M06-2X geometries, etc.) but relied on a rather small basis set, namely, cc-pVDZ. They reported a mean absolute error (MAE) of 0.19 eV with CC2 and 0.24 eV with B3LYP. Winter and co-workers used a benchmark set of 66 singlet-states in medium-sized molecules (the largest cases being tetraphenylporphine but most molecules are significantly smaller), for which experimental gas-phase 0–0 energies are available.⁴⁴ They evaluated B3LYP, ADC(2), and CC2 as well SOS-CC2 and SCS-CC2. Like Durbeej and co-workers, they obtained their theoretical estimates by applying a method-consistent protocol, but they relied on much larger atomic basis sets, namely, TZVPP for structural and vibrational parameters and aug-cc-pVTZ for total energies, which certainly implied a huge computational effort. They obtained small MAEs: 0.19 eV for B3LYP in the 0.05–0.08 eV range for the wave function approaches. The removal of diffuse orbitals or the use of ZPVE corrections computed with B3LYP only increased slightly these errors. In a second category, one finds works focusing on real-life structures in solution, and the absorption–fluorescence crossing points were selected as experimental references.^{42,43,47,50,51} Such selection has two advantages: it gives access to much more experimental data, and more importantly, “real-life” structures of actual practical interest can be included in the set. However, such a choice also implies limitations: first, only molecules fluorescing can be considered, and second, one estimates not only the validity of the electronic structure theory but also the adequacy of the environmental model used to reproduce solvation. In 2009 and 2010, Goerigk and Grimme performed benchmarks for 5⁴² and then 12⁴³ large solvated dyes using a wide range of TD-DFT (BLYP, B3LYP, PBE-38, BMK, CAM-B3LYP, B2PLYP, and B2GPPLYP) and wave function approaches (CIS, CIS(D), CC2 as well as various spin-scaled variants of the two latter theories) and an extended atomic basis set, namely, def2-TZVPP. They transformed the experimental AFCP energies into “vertical experimental” values by applying a series of successive theoretical corrections, in order to allow the use of vertical calculations in the effective benchmark step. More precisely, they first performed nonequilibrium linear-response (LR) polarizable continuum model (PCM) calculations⁵² with the PBE0 functional to remove solvent effects. Next, they computed the ZPVE corrections as well as the difference between the adiabatic and vertical absorption energies at the PBE/TZVP level to deduce their reference vertical energies. With this approach, the smallest MAE were obtained with CC2 (0.17 eV) and B2GPPLYP (0.16 eV), a double-hybrid functional including an explicit CIS(D)-like term. In three works,^47,50,51 we used a set of 40 “real-life” molecules and performed functional-consistent benchmarks with 12 exchange correlation functionals including optimally tuned range-separated hybrids (B3LYP, APF-D, PBE0, PBE0-1/3, M06, BMK, M06-2X, CAM-B3LYP, ωB97X-D, LC-PBE, LC-PBE*, and LC-PBE0*). The basis sets used for structural/vibrational and energetic parameters were 6-31+G(d) and 6-311++G(2df,2p), respectively, whereas the solvent effects were accounted for with a refined variation of the PCM approach, namely, the corrected linear-response (cLR) approach. The smallest MAE was obtained with the optimally tuned LC-PBE* (0.20 eV), whereas the highest correlation between theoretical and experimental estimates was attained with M06-2X.

Here, we considered a set of 80 molecules and performed all structural and vibrational calculations with DFT and TD-DFT, for the GS and the ES, respectively. The transition energies (absorption, emission, and adiabatic energies) are determined with CIS(D), ADC(2), CC2, SCS-CC2, SOS-CC2, and BSE/GW in addition to TD-DFT. The solvent effects have been accounted for using several variations of the PCM approach. Though similarities between our approach and some of the previously performed benchmarks are clear, the present work brings added value. Indeed, (i) this is the first work to provide BSE/GW 0–0 energies for a large set of diverse dyes; (ii) this is the largest set of real-life molecules treated to date, allowing one to obtain a better statistical analysis, especially for chemically insightful subsets; (iii) the set was designed to include a large number of very recent experiments (the majority of references are from measurements performed during the 2009–2015 period) to be significant of actual research in the field; (iv) the selected protocol could be applied to large molecules as the time-limiting step (determination of the ZPVE of the ES) is performed at the TD-DFT level; (v) the impact of several solvation approaches is accounted for with widely available methods; and (vi) the wave function adiabatic energies are obtained considering both the GS and ES geometries so that the geometrical relaxation is not a sole TD-DFT contribution. The present study can therefore be viewed as complementary to the one of Winter et al. performed for medium-sized gas-phase cases.⁴⁴

2. Methodology

2.1. Benchmark Set

The molecules included in our benchmark set are shown in Schemes 1, 2, 3, and 4. The experimental AFCP energies obtained for this set are collected in Table 1.⁵³⁻¹¹² This set of molecules is mostly an extension of previous sets,^43,47 with a specific focus on recently proposed molecules. Attention was paid to include compounds representative of several categories (hydrocarbons, push–pull structures, cyanine-like dyes, etc.) as well as to consider the most important families of fluorophores (coumarins, naphthalimides, bimanes, BODIPYs, etc.) and both organic and inorganic compounds. As any benchmark set, it implies biases. We can indeed pinpoint two major limitations: (i) as we use the AFCP energies as reference, only molecules for which both absorption and emission have been measured are considered; and (ii) as stated above, we focus on compounds synthesized and characterized recently.

Scheme 1. Representation of the Molecules under Investigation.

Scheme 2. Representation of the Molecules under Investigation.

Scheme 3. Representation of the Molecules under Investigation.

Scheme 4. Representation of the Molecules under Investigation.

Table 1. Experimental Values Used as Reference in This Study (in eV)^a.

molecule	solvent	0–0	ref	molecule	solvent	0–0	ref
I	cyclohexane	4.56	(60)	XLI	ethanol	4.13	(60)
II	methanol	2.48	(80)	XLII	ethanol	3.78	(60)
III	water	3.46	(56)	XLIII	n-hexane	3.55	(60)
IV	hexane	3.50	(61)	XLIV	toluene	2.18	(68)
V	ethanol	2.98	(54)	XLV	cyclohexane	3.30	(60)
VI	dioxane	3.53	(71)	XLVI	cyclohexane	2.63	(78)
VII	benzene	2.92	(81)	XLVII	chloroform	2.23	(92)
VIII	cyclohexane	1.89	(89)	XLVIII	tetrahydrofuran	3.12	(99)
IX	ethanol	3.10	(53)	XLIX	cyclohexane	3.61	(73)
X	benzene	2.85	(53)	L	cyclohexane	3.26	(60)
XI	dichloromethane	1.95	(60)	LI	ethanol	1.74	(60)
XII	2-methyl-butane	3.18	(79)	LII	dichloromethane	2.33	(106)
XIII	cyclohexane	2.76	(77)	LIII	dichloromethane	2.53	(106)
XIV	cyclohexane	3.11	(70)	LIV	chloroform	2.15	(90)
XV	dichloromethane	2.85	(76)	LV	chloroform	2.03	(90)
XVI	toluene	2.30	(87)	LVI	methanol	3.28	(108)
XVII	ethanol	2.53	(60)	LVII	dichloromethane	2.88	(91)
XVIII	dichloromethane	1.95	(84)	LVIII	tetrahydrofuran	2.99	(95)
XIX	ethanol	2.18	(53)	LIX	tetrahydrofuran	2.33	(95)
XX	benzene	2.29	(53)	LX	tetrahydrofuran	3.08	(97)
XXI	chloroform	3.29	(63)	LXI	ethanol	2.63	(109)
XXII	dichloromethane	3.13	(105)	LXII	ethanol	3.00	(109)
XXIII	acetonitrile	2.99	(85)	LXIII	hexane	3.33	(102)
XXIV	2-methyl-butane	2.98	(62)	LXIV	benzene	2.16	(60)
XXV	chloroform	1.71	(75)	LXV	dichloromethane	2.53	(103)
XXVI	ethanol	2.02	(55)	LXVI	dichloromethane	2.38	(83)
XXVII	chloroform	3.15	(64)	LXVII	tetrahydrofuran	2.82	(93)
XXVIII	dimethylformamide	2.33	(86)	LXVIII	acetonitrile	3.32	(96)
XXIX	dichloromethane	2.24	(88)	LXIX	dichloromethane	2.85	(91)
XXX	ethanol	2.65	(66)	LXX	tetrahydrofuran	2.51	(100)
XXXI	dioxane	2.12	(72)	LXXI	tetrahydrofuran	3.44	(100)
XXXII	dichloromethane	3.25	(69)	LXXII	toluene	3.19	(111)
XXXIII	tetrahydrofuran	3.57	(101)	LXXIII	acetontrile	3.10	(98)
XXXIV	acetontrile	2.76	(82)	LXXIV	methanol	3.31	(94)
XXXV	carbontetrachloride	2.28	(59)	LXXV	methanol	2.61	(94)
XXXVI	hexane	2.72	(74)	LXXVI	tetrahydrofuran	2.75	(104)
XXXVII	dimethyl sulfoxide	3.08	(60)	LXXVII	dimethyl sulfoxide	2.00	(58)
XXXVIII	toluene	2.64	(67)	LXXVIII	chloroform	2.60	(107)
XXXIX	dimethylformamide	2.76	(65)	LXXIX	ethanol	1.84	(110)
XL	toluene	1.83	(57)	LXXX	dichloromethane	2.67	(112)

^aMolecules are depicted in Schemes 1–4. The 0–0 energies are the crossing point between the absorption and fluorescence curves (see Introduction).

2.2. Solvent Effects

As we model large compounds, the solvent effects have to be accounted for, and we have done so using the PCM model.⁵² For excited-state energies, four PCM variations, differing by the approach used to determine the polarization of the excited-state cavity exist: the linear-response (LR),^113,114 the corrected linear-response (cLR),¹¹⁵ the vertical excitation model (VEM),¹¹⁶ and the state-specific (SS) schemes.¹¹⁷ The three latter use one-particle density to determine the ES polarization and are therefore more accurate than the LR approach that relies on transition densities. Among the three advanced models, we have selected the cLR approach that has the dual advantage of being available in the Gaussian09 code¹¹⁸ and being the least computationally intensive.

In addition, one could distinguish two limiting modes of interactions between the solute and the solvent for ES, that is, the equilibrium (eq) and the nonequilibrium (neq) modes. The former considers a solvent fully relaxed after the change of state of the solute and is adapted for ES geometry optimization and calculation of ES frequencies. The latter considers that only the electrons of the solvent have time to adapt to the new state of the solute and is adequate for the calculation of transition energies. Though 0–0 energies are formally equilbrium properties (from minima to minima), a comparison with the experimental AFCP implies to account for nonequilibrium effects (see the next section).

2.3. Protocol

Our computational protocol has been detailed in previous works,^41,45,47 and we only summarize it here. In gas phase, the adiabatic energies are defined as

1

where E^ES and E^GS are the excited and ground-state energies, respectively, whereas R^ES and R^GS are the ES and GS optimal structures, respectively. An alternative exact definition is⁴⁷

2

where ΔE^vert–a and ΔE^vert–f are the vertical absorption and fluorescence energies, that is the difference between the E^ES and E^GS determined on R^GS (for absorption) and R^ES (for fluorescence), respectively; and ΔE^reorg–GS and ΔE^reorg–ES are, respectively, the ground-state and excited-state energy reorganization energies, that is, the difference of the energy computed for R^ES and R^GS considering a given state. The gas-phase 0–0 energies are obtained as follows:

3

where the ZPVE correction reads

4

In this study, R^GS, R^ES, and the associated E^ZPVE are computed with DFT/TD-DFT, whereas E^GS and E^ES are determined with various approaches. While the results of eq 3 can be compared to experimental gas-phase values, further corrections are needed to account for solvent effects. With TD-DFT, we have mainly applied the cLR-PCM approach (see above) and the AFCP energies have been obtained as follows:⁴⁷

5

6

The last term in eq 6 provides corrections for nonequilibrium effects.

7

8

For the wave function schemes [CIS(D), ADC(2), CC2, SCS-CC2, and SOS-CC2], the calculations have been made in gas-phase, so that solvent corrected values have been determined as

9

10

With BSE/GW, one has access to transition energies only, so that E^adia cannot be determined directly. Therefore, an alternative approach to eq 1 was used to determine the adiabatic energies:⁴¹

11

which follows eq 2. The BSE/GW AFCP energies are then obtained as

12

2.4. Computational Details

All DFT and TD-DFT calculations have been performed with the Gaussian09.D01 code.¹¹⁸ We have selected the M06-2X¹¹⁹ functional, a choice justified by previous benchmarks showing that it is one of the most accurate and consistent functionals for ES.^9,47,120,121 Following the extensive basis set assessment in ref (47), we have selected the 6-31+G(d) basis set to determine both the geometrical (R^GS and R^ES) and vibrational (ΔE^ZPVE) parameters. Those calculations have been performed in gas-phase. This choice is justified by the fact that (i) the solvent effects are particularly strong for transition energies but usually much smaller for the structures of conjugated structures; (ii) comparisons among gas, LR. and cLR structures demonstrated that the more accurate cLR geometries are closer to their gas phase counterpart than LR that overshoots the impact of solvation;¹²² (iii) the gas, LR, and cLR ΔE^ZPVE are generally very close to each other;¹²³ and (iv) there is, to the very best of our knowledge, no cLR analytical gradients available, which makes the determination of cLR R^ES beyond computational reach. Comparisons between the results obtained on condensed-phase and gas-phase structures for the 20 first compounds (Scheme 1) can also be found in Section 3.3. All geometry optimizations, both for GS and ES, have been performed using a TIGHT convergence threshold (1 × 10^–5 on residual rms forces). Both the total and transition (TD-)DFT energies (E^GS, E^ES, ΔE^vert–a, ΔE^vert–f, etc.) have been determined with a much larger basis set, namely, 6-311++G(2df,2p). Gaussian09 uses as defaults 6d and 5d basis sets for 6-31+G(d) and 6-311++G(2df,2p), and we have followed these defaults. For DFT and TD-DFT, the heavy metallic atoms have been modeled with the LanL2DZ basis set and pseudopotential.^124,125 As M06-2X is sensitive to the quality of the integration grid,¹²⁶ the so-called ultrafine DFT integration grid containing 99 radial and 590 angular points was systematically applied. For modeling solvent effects, we have used both the LR and cLR PCM-M06-2X/6-311++G(2df,2p) levels. For both GS and ES calculations, Gaussian09 defaults were applied to build the cavity (vDW cavities based on UFF radii scaled by 1.1). Comparisons with the results obtained with the SMD model that relies on smaller radii¹²⁷ are also available in section 3.3. Previous works have also addressed the relationships between the PCM parameters and the ES properties for specific compounds.^128,129

The CIS(D), ADC(2), CC2, SCS-CC2, and SOS-CC2 calculations have been performed in gas-phase with the Turbomole program,¹³⁰ systematically using the RI scheme.^17,18 Default parameters were applied and all of these wave function calculations used the aug-cc-pVTZ basis set (and the corresponding pseudopotentials for the heavy elements, e.g., osmium) to be very close to basis set convergence. Note that we used the SCS and SOS parameters as implemented in Turbomole. For a discussion about alternative spin scaling definitions, we redirect the reader to ref (43). The impact of using a smaller atomic basis set with CIS(D), ADC(2), and CC2 is beyond our scope here as such considerations can be found elsewhere.¹³¹

The GW and BSE calculations have been performed with the FIESTA package,^29,132,133 a Gaussian-basis implementation of the GW and Bethe-Salpeter formalisms using the (Coulomb-fitting) RI approach. Dynamical correlations have been computed within an exact contour deformation technique, avoiding any plasmon-pole approximation. For the GW calculations, the DFT starting eigenstates were obtained with the NWChem package¹³⁴ using the M06-2X functional and the aug-cc-pVTZ atomic basis set. It is important to stress that the BSE approach used here follows a self-consistent GW approach which implies that the selected starting exchange-correlation functional does only marginally influence the final BSE results. In more detail, the calculated G and W operators are built self-consistently by reinjecting the calculated quasiparticle eigenvalues, so that after a few cycles (ca. 3–5), only a small dependency on the final eigenstates, due to the frozen eigenfunctions, pertains. Therefore, in the following, BSE/GW stands more precisely for BSE/evGW@M06-2X, where the labeling evGW indicates partial self-consistency on the eigenvalues at the GW level. The BSE calculations have been performed beyond the Tamm-Dancoff approximation, mixing excitations and de-excitations, and within the standard adiabatic approach, namely, considering only static screening. All unoccupied (virtual) states are included in the sum-over-states required to build the electronic susceptibility and GW self-energy. We redirect the reader to our most recent work for more details and tests about this approach.³⁷

3. Results and Discussion

In the discussion below, we focus mainly on a statistical analysis of the different effects and do not consider a molecule-per-molecule comparison. Indeed, it is our goal to provide an overview of the generic performances of the different approaches without discussing the numerous individual data collected in the course of this study. A complete list of raw data can be found in the Supporting Information (SI) in Tables S-I to S-IV for absorption, Tables S-V to S-VIII for emission, Tables S-IX to S-XII for adiabatic energies, and Tables S-XIV and S-XV for 0–0 energies.

3.1. BSE/GW Scheme

We recall that BSE/GW is a two step process starting with a GW calculation aiming at correcting input Kohn–Sham electronic energy levels and continuing with a BSE calculation adding the electron–hole interaction to yield optical energy excitations. Specifically, the quality of the GW energy levels (in particular the HOMO–LUMO gap) strongly affects the BSE excitation energies.

As stated above, relying on a previous standard benchmark of “theoretical” vertical excitation energies,³⁷ we adopt a partially self-consistent evGW scheme where the GW quasiparticle energies are updated self-consistently, namely, reinjected in the construction of G and W, while keeping the DFT wave functions frozen. This approach has been shown to yield much more accurate BSE/GW optical excitations energies for small and medium-sized organic molecules than the conventional BSE calculations based on nonself-consistent G₀W₀ calculations. The improvement is typically larger than an eV when starting with semilocal functionals, but remains as large as 0.5 eV when starting with a hybrid functional such as PBE0.¹³⁵ Rather than optimizing the starting DFT functional,^39,136 we prefer self-consistency which allows one to bypass this optimization task. Since the self-consistency is partial, the effect of freezing the starting Kohn–Sham eigenfunctions induces a small residual dependence on the starting functional. We test this effect on a subset of 10 compounds, selected to include representatives of the main families of states (cyanine, charge-transfer, etc.). We list in Table 2 the BSE/GW vertical absorption energies computed starting with two hybrid exchange-correlation functionals, namely, M06-2X and PBE0,^135,137 and compare them to their TD-DFT counterparts. For all tested compounds, the BSE/GW energies obtained starting with the PBE0 eigenstates are smaller than their M06-2X counterparts. However, the average effect, −0.071 eV, remains relatively small. Only for one compact molecule (XLI) is the impact of not updating the eigenvectors larger than 0.1 eV. This is consistent with our recent work where Thiel’s set of molecules was treated.³⁷ We underline that the BSE/G₀W₀ approach, in which the DFT eigenvalues are also frozen, yields a much more severe dependency on the initial exchange-correlation functional.³⁹ For comparison, the TD-PBE0 values are also, as expected,¹³⁸ smaller than their TD-M06-2X counterparts, but the average effect of changing the functional is about four times larger with TD-DFT (−0.266 eV) than that with the partially self-consistent BSE/GW approach.

Table 2. Comparisons between the BSE/evGW ΔE^vert–a [aug-cc-pVTZ] Obtained Starting from M06-2X and PBE0 Kohn–Sham Eigenstates for a Subset of Compounds^a.

molecule	BSE/evGW@M06-2X	BSE/evGW@PBE0	TD-M06-2X	TD-PBE0
I	5.066	5.023	5.263	5.003
VIII	2.247	2.181	2.511	2.297
XI	2.226	2.189	2.495	2.449
XXII	3.552	3.467	3.737	3.483
XXIV	3.539	3.506	3.738	3.304
XXXI	2.477	2.419	2.682	2.408
XXXIV	2.931	2.847	3.191	2.930
XLI	4.425	4.288	4.496	4.217
LXII	2.972	2.877	3.154	2.894
LXXIII	3.869	3.795	3.937	3.555

^aOn the right, the corresponding TD-DFT values [6-311++G(2df,2p)] are listed. All values are in eV and have been computed in gas-phase.

As applications of BSE/GW with a Gaussian-based implementation remain scarce, a small comment on basis set effects might be useful. Indeed, while we applied the extended aug-cc-pVTZ atomic basis set in the following, we have also performed calculations with the aug-cc-pVDZ atomic basis set for a subset of compounds.¹³⁹ For this representative panel, the average absolute deviation between the two basis sets is as small as 0.017 eV (see Figure S-1 for a graphical representation). This hints that BSE/GW is probably not particularly sensitive to the size of the basis set for the compounds treated herein and confirms that aug-cc-pVTZ is certainly sufficient for our purposes.

As a conclusion to this section, it can be emphasized that the BSE/GW scheme in the present Coulomb-fitting (RI) and adiabatic formulation offers an O(N⁴) scaling. In particular, the BSE formalism is similar to Casida’s formulation of TD-DFT but with a different kernel relying on the nonlocal screened Coulomb potential W. This should be kept in mind when comparing the following the BSE approach to, e.g., CC2 techniques.

3.2. Gas-Phase Results

We start by a comparison of the gas-phase 0–0 energies obtained with the different approaches through eq 3. We recall that in this equation, the total and transition energies are obtained with various theoretical approaches, whereas the geometries are systematically obtained with (TD-)DFT. Table 3 provides Pearson’s correlation matrix for all investigated methods. From that Table, it is quite obvious that the overall correlation between all tested theories is high (the smallest R being 0.948), especially within the subgroup of wave function schemes. For instance, the ADC(2) and CC2 estimates are extremely consistent with one another (R = 0.996). This is illustrated in Figure 1, where it also appears that ADC(2) and CC2 values are nearly equal for molecules presenting ΔE^0–0 larger than 3.0 eV, whereas stronger deviations are found for compounds absorbing light at smaller energies for which ADC(2) tends to yield smaller transition energies. In our set, the ADC(2) ΔE^0–0 exceeds its CC2 counterpart only in 11 out of 80 cases. Compared to ADC(2), the average CC2 correction is limited to +0.061 eV (0.066 eV absolute difference), an effect that one could probably rate as small in regard to the significantly larger computational effort required for obtaining CC2 transition energies. These trends are consistent with the investigations of Winter and co-workers,⁴⁴ and Harbach and co-workers¹⁴⁰ who both found high similarities between ADC and CC results, despite the smaller computational requirements of the former [both have scalings, but the prefactor of CC2 is significantly less favorable than the one of ADC(2)]. Contrasting with ADC(2), both TD-M06-2X and CIS(D) tend to yield larger values than CC2, with average differences as large as 0.187 and 0.220 eV, respectively. Interestingly, the BSE/GW values are equally spread around the CC2 values, with an average difference as trifling as −0.010 eV. While, the absolute average difference between CC2 and BSE/GW results is significant (0.123 eV), the pattern of differences shown in Figure 2 roughly follows a normal distribution law, and their are only two cases (LXIV and LXVI) for which the absolute difference between the two methods exceeds 0.4 eV. The interested reader might find in the SI comparisons among CC2 and BSE/GW ΔE^vert–a(gas), ΔE^vert–f(gas), and ΔE^adia(gas) energies (Figures S-2, S-3, and S-4). Eventually, using spin scaling variants of CC2 almost systematically shifts the computed values to higher energies with only 4 (3) cases in which SCS-CC2 (SOS-CC2) delivers 0–0 energies smaller than CC2. The average increase with respect to CC2 is significantly larger with SOS (0.251 eV) than with SCS (0.169 eV).

Table 3. Pearson’s Correlation (R) Matrix for the Gas-Phase 0–0 Energies Considering the Full 80 Molecule Set.

method	TD-M06-2X	CIS(D)	ADC(2)	CC2	SCS-CC2	SOS-CC2	BSE/GW
TD-M06-2X	1.000
CIS(D)	0.948	1.000
ADC(2)	0.951	0.986	1.000
CC2	0.960	0.977	0.996	1.000
SCS-CC2	0.966	0.983	0.991	0.990	1.000
SOS-CC2	0.961	0.979	0.982	0.979	0.998	1.000
BSE/GW	0.990	0.959	0.958	0.962	0.975	0.974	1.000

Figure 1.

Comparison between ADC(2) and CC2 ΔE^0–0(gas) obtained for the full set of molecules and given in eV. The central diagonal line indicates a perfect match.

Figure 2.

Histogram showing the dispersion of BSE/GW 0–0 energies in gas-phase compared to their CC2 counterparts for the full set of compounds.

Though comparisons of gas-phase theoretical values and solvated experimental data cannot be viewed as appealing, they are often used in practice, especially for wave function approaches for which calculations accounting for condensed phase effects remain an exception rather than a rule.^141−149 For this reason, we provide in Table 4 the results of such statistical analysis obtained on the basis of eq 3. All mean signed error (MSE) are positive indicating a tendency to overshoot the experimental energies, an outcome that can be partly ascribed to the lack of solvent effects in the calculation: ES tend to be more polarized than GS, and hence, bathochromic shifts are often observed when going from gas to condensed phases (see also below). Among all tested approaches, only ADC(2), CC2, and BSE/GW yield a MAE smaller than 0.2 eV, the other models providing significantly larger deviations, some exceeding 0.3 eV. On the basis of these crude gas phase comparisons, it also appears that TD-DFT is not much less accurate than the wave function schemes, i.e., it yields larger average deviations than CC2 but outperforms both CIS(D) and SOS-CC2. Nevertheless, the wave function methods clearly improve the consistency with the experimental reference data with an R² of at least 0.9 [but again for CIS(D)], a success that neither TD-M06-2X nor BSE/GW could deliver. This general outcome of improved consistency but not necessarily accuracy when going from TD-DFT to “second-order” wave function approaches is well in the line of the conclusions obtained previously for Thiel’s set of small molecules.^37,138,150 Given the results listed in Table 4, one could probably recommend ADC(2) to correct TD-DFT 0–0 energies computed in gas phase as it delivers a valuable compromise among computational cost, accuracy, and consistency.

Table 4. Results of a Statistical Analysis Performed by Accounting for Solvent Effects with Various Models^a.

method	solvent	MSE	MAE	SD	Max(+)	Max(−)	R2
TD-M06-2X	gas	0.264	0.279	0.214	0.142	–0.783	0.859
	LR,eq	0.064	0.168	0.193	0.324	–0.465	0.886
	cLR,eq	0.220	0.235	0.182	0.143	–0.755	0.898
	cLR,neq	0.221	0.236	0.183	0.143	–0.758	0.897
	cLR,eq (SMD)	0.209	0.225	0.177	0.143	–0.728	0.904
CIS(D)	gas	0.293	0.312	0.231	0.579	–0.864	0.886
	LR,eq	0.094	0.176	0.196	0.380	–0.545	0.926
	cLR,eq	0.249	0.263	0.195	0.467	–0.669	0.919
	cLR,eq (SMD)	0.239	0.254	0.195	0.446	–0.669	0.921
ADC(2)	gas	0.010	0.153	0.195	0.449	–0.424	0.907
	LR,eq	–0.189	0.215	0.168	0.534	–0.302	0.937
	cLR,eq	–0.034	0.141	0.177	0.564	–0.405	0.923
	cLR,eq (SMD)	–0.044	0.146	0.180	0.618	–0.414	0.922
CC2	gas	0.072	0.148	0.179	0.281	–0.474	0.907
	LR,eq	–0.128	0.163	0.147	0.489	–0.288	0.940
	cLR,eq	0.028	0.131	0.165	0.468	–0.412	0.921
	cLR,eq (SMD)	0.018	0.133	0.167	0.522	–0.412	0.920
SCS-CC2	gas	0.243	0.247	0.159	0.064	–0.708	0.927
	LR,eq	0.044	0.110	0.133	0.254	–0.384	0.952
	cLR,eq	0.199	0.204	0.128	0.126	–0.559	0.952
	cLR,eq (SMD)	0.189	0.196	0.128	0.180	–0.481	0.953
SOS-CC2	gas	0.326	0.326	0.161	–0.048	–0.854	0.926
	LR,eq	0.129	0.158	0.148	0.198	–0.683	0.940
	cLR,eq	0.282	0.282	0.125	–0.041	–0.705	0.955
	cLR,eq (SMD)	0.271	0.272	0.124	0.013	–0.627	0.955
BSE/GW	gas	0.062	0.182	0.220	0.400	–0.538	0.858
	LR,eq	–0.137	0.187	0.178	0.548	–0.216	0.906
	cLR,eq	0.018	0.147	0.177	0.401	–0.452	0.905
	cLR,eq (SMD)	0.008	0.141	0.171	0.401	–0.425	0.911

^aMSE, MAE, and SD are, respectively, the mean signed error, mean absolute error, and standard deviation with respect to experimental values and are given in eV. Max(+) and Max(−) are the largest positive and negative deviations (eV). R² is the determination coefficient obtained by comparing experimental and theoretical data. Note that the MSE are computed as theory-experiment. For TD-M06-2X, only the results obtained with the largest atomic basis set are displayed. The default PCM model is applied except for when noted as SMD.

Let us now discuss gas-phase Stokes shifts (Δ^SS), obtained as the differences between ΔE^vert–a and ΔE^vert–f. For the set of compounds treated here, Δ^SS ranges from ca. 0.05 to ca. 1.10 eV. We remind the reader that in this work all structures have been optimized with (TD-)DFT so that the differences in Δ^SS computed with different methods reflect the description of the electronic part and not directly the structural variations. As illustrated in Figure 3 by the comparison of CC2 and TD-DFT Δ^SS, all methods provide rather similar Δ^SS, though CC2 delivers slightly smaller values compared to those of the other approaches. Indeed, the TD-M06-2X, CIS(D), ADC(2), and BSE/GW Δ^SS are larger than their CC2 counterparts by an average of +0.050, +0.071, +0.028, and +0.086 eV, respectively.

Figure 3.

Comparison between TD-M06-2X and CC2 Stokes shifts obtained for the full set of molecules and given in eV. The central diagonal line indicates a perfect match.

With TD-M06-2X, we have also briefly investigated the impact of basis set corrections, by comparing the 6-31+G(d) and 6-311++G(2df,2p) ΔE^0–0(gas). As expected, using the larger atomic basis set generally induces a decrease of the transition energies, but both the average effect (−0.013 eV) and the largest deviation (−0.077 eV for LXVII) remain small. When comparing experimental and theoretical values, using the 6-31+G(d) values would only induce a very slight increase of both the MSE (−0.277 eV instead of −0.264 eV) and the MAE (0.286 eV instead of 0.279 eV, see Table 4). In short, at least for TD-DFT, 6-31+G(d) provides results close to convergence, and it is probably not necessary for the production run to choose a larger basis set when modeling low-lying excited states.

3.3. Impact of Solvent Corrections

Let us first discuss the influence of the selected solvent model. In a first stage, considering gas-phase geometries, we have performed cLR-TD-M06-2X/6-311++G(2df,2p) calculations of the key properties (vertical absorption, vertical emission, and 0–0 energies) using both the default Gaussian09 PCM parameters (simply referred to as “PCM” in the following) and the SMD parameters for building the solute cavity (see section 2.4). Figure 4 compares the 0–0 energies obtained with these two models, and the good correlation is obvious. The average difference between the two models is only −0.010 eV (the SMD models tending to provide slightly smaller transition energies), whereas the absolute difference is as small as 0.017 eV. The two largest negative and positive variations are obtained for V (−0.078 eV) and LVI (+0.077 eV). Comparisons between SMD and PCM ΔE^vert–a(cLR, neq) and ΔE^vert–f(cLR, neq) can be found in Figures S-5 and S-6. As stated previously, we have chosen to perform our geometry optimizations in gas-phase for several reasons (see section 2.4). For the first 15 compounds, we have evaluated the ΔE^adia(cLR, eq) determined on gas, PCM, and SMD geometries. The raw results are given in Table S-XVII, and it can be seen that the impact of selecting condensed phase geometries is small. Indeed, the average absolute differences of adiabatic energies is 0.002 eV for PCM structures and 0.007 eV and SMD structures, taking the gas phase geometries as reference. We therefore continue our work with the default PCM parameter and gas-phase geometries except when explicitly noted.

Figure 4.

Comparison between TD-M06-2X 0–0 energies determined with the cLR model in its equilibrium limit with two types of cavity parameters: default (Gaussian09) PCM and SMD. All values are in eV. The central line indicates a perfect match between the two models.

Figure 5 gives the impact on the ΔE^0–0 of the solvent corrections at the LR and cLR levels for all compounds. Note that the data reported in that Figure have been obtained for the 0–0 energies determined in the equilibrium limit. From the bottom panel of Figure 5 that reports the difference between the refined cLR approach and gas phase results, one notices that, as expected, inclusion of solvation tends to decrease the transition energies for most compounds. Indeed, for the full set, the average solvent corrections attains −0.044 eV, with strong variations depending on the compound and solvent considered. XVI is the only dye for which theory predicts a large (>0.1 eV) negative solvatochromism. This specific behavior can be easily understood by noticing that this molecule belongs to the betaine family, a group of zwitterionic dyes,¹⁵¹ in which the dipole moment of the ES tends to be (much) smaller than its GS counterpart, an effect reproduced by PCM-TD-DFT calculations.¹⁵² For XVI, negative solvatochromism is indeed observed experimentally, and a full theoretical rationalization of this outcome is already available.^87,153 The three compounds undergoing the largest positive solvatochromism are LVI, LIX, and LXV, three very strong CT dyes. To our knowledge, no detailed experimental investigations of solvatochromic effects (e.g., from apolar to strongly polar solvents) have been made for these three derivatives. Turning now to the top and central panels of Figure 5, it clearly turns out that the sign of the LR and subsequent cLR corrections are opposite. They actually present the same sign only in 3 out of 80 cases: XII for which the cLR correction is negligible, LIX that undergoes a very strong CT and LXVIII for which the LR correction is trifling. It is also evident from Figure 5 that the LR scheme tends to overestimate the impact of the solvent on the transition energies. Indeed, the mean absolute LR-gas correction for the ΔE^0–0 attains 0.217 eV, whereas its cLR-gas counterpart is only 0.056 eV. As a consequence, using the LR-PCM model to determine transition energies in condensed phase would artificially favor methods overshooting the experimental 0–0 energies (see the next section). These general conclusions are consistent with previous works,^{47,115,117,122,154} and we continue in the following by considering the cLR results only.

Figure 5.

Impact of solvent effects on the 0–0 energies (eq limit) for all compounds.

Let us now turn toward the importance of nonequilibrium corrections evaluated at the cLR level as defined in eqs 7 and 8. As the difference between the (eq) and (neq) results are directly related to the contrast between the static and optical dielectric constants of the medium, it is obvious that the (neq) effects are much larger in polar than in apolar solvents. For the 0–0 energies, the difference between (neq) and (eq) is given in eqs 5 and 7. Including or not the ΔΔE^neq–eq correcting term has a very limited statistical impact on the computed 0–0 energies. This is clear from Table 4: the MSE and MAE vary by 0.001 eV only for the TD-M06-2X results. Indeed, the neq–eq differences for the absorption (positive) and fluorescence (negative) tend to counterbalance each other when assessing AFCP energies. Consequently, the ΔΔE^neq–eq term remains quite small. This correction term ranges from −0.033 eV (XXXIX) to 0.024 eV (LXXIII), with an absolute average value of 0.003 eV. When discussing the statistical effect on 0–0 energies for the full set, this term can be neglected, so we consider cLR,eq values, that are more straightforward to compute, in the following. We underline that the impact of neq effects on the vertical absorption and emission can be more significant. Indeed, while the average differences between ΔE^vert–a(cLR, neq) and ΔE^vert–a(cLR, eq) [ΔE^vert–f(cLR, neq) and ΔE^vert–f(cLR, eq) ] attains 0.016 eV [−0.011 eV] for the full set, if one considers the 25 molecules in strongly polar medium only,¹⁵⁵ this average difference amounts to 0.033 eV [−0.019 eV].

3.4. Solvent Phase Results: Comparison with Experiments

A comparison between experimental 0–0 energies and the results obtained with various levels of theories using both LR and cLR approaches for solvent effects can be found in Table 4. The condensed phase data in that Table were obtained through eqs 9 and 12 for the wave function approaches and BSE/GW, respectively. For the cLR case, Figures 6 and 7, respectively, provide correlation and error distribution diagrams for all methods. From Figure 6, it is clear that TD-M06-2X delivers quite accurate trends but has a tendency to overshoot the experimental transition energies, the MAE being 0.235 eV. This is qualitatively and quantitatively well in the line of our previous benchmark investigation.⁴⁷ Certainly, using exchange-correlation functionals with a smaller amount of exact-exchange, e.g., applying B3LYP, PBE0, or M06, would provide smaller transition energies that would be in better agreement with the experiment. However, such functional choice tends also to yield more extreme errors,⁴⁷ e.g., the energies of CT states become significantly underestimated,^156,157 and the corresponding ES geometries can even be qualitatively incorrect.^158−160 Using CID(D) does not provide any significant improvement (MAE of 0.263 eV) compared to TD-DFT, except for a distribution of the errors slightly closer to normality (see Figure 7) and a slightly improved R². Of course, for both TD-M06-2X and CIS(D), applying the simplest LR-PCM approximation that overestimates the solvatochromic effects delivers smaller MAE (0.168 and 0.176 eV, respectively), but this is due to an error-compensation mechanism that cannot be considered as very satisfying. The two spin-scaled CC2 approaches, SCS-CC2 and SOS-CC2, also significantly overshoot the experimental values (MAE of 0.204 and 0.282 eV, respectively), but they deliver much tighter error distributions (Figure 7). In particular, SOS-CC2 allows one to reach a correlation with experimental value that is very large (R = 0.955), though, again, at the cost of a systematic and significant overestimation of the experimental 0–0 energies. This contrasts with the work of Winter and co-workers,⁴⁴ where SCS-CC2 and SOS-CC2 were found to slightly outperform CC2 in terms of MAE. We also note from Table 4 that applying SMD cavity parameters yields a slight decrease (ca. −0.010 eV) of both MSE and MAE at these four levels of theory (TD-M06-2X, CIS(D), SOS-CC2, and SCS-CC2). These small changes are in line of the variations discussed in the previous section.

Figure 6.

Correlation plots between the computed ΔE^0–0(cLR, eq) and the experimental AFCP energies for all tested methods. All values are in eV. The central line indicates a perfect theory–experiment match. These graphs correspond to the default PCM parameters.

Figure 7.

Histogram showing the error patterns for all tested methods, using the same data as that in Figure 6. Note that the different methods have different Y scales.

The three most satisfying approaches to correct the cLR-PCM TD-DFT 0–0 energies are ADC(2), CC2, and BSE/GW that deliver MAE of 0.141, 0.131, and 0.145 eV, respectively, with again only small variations when the SMD model is applied. Comparing ADC(2) and CC2, one notices very similar error distributions and correlation with experimental values (R = 0.923 and 0.921, respectively). Although ADC(2) slightly underrates the experimental values (MSE = −0.034 eV) while CC2 gives the opposite trend (MSE = +0.028 eV), the differences between the two approaches remain small, and one should probably select the former for 0–0 calculations as its computational cost is more favorable. These trends are consistent with the gas phase results discussed above. BSE/GW yields a slightly poorer correlation with experiment (R = 0.905) than ADC(2) and CC2, but is almost as accurate as CC2, though it is a 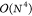theory. At this stage, it is important to remind the reader that the BSE/GW values reported here are obtained on a partially self-consistent scheme based on M06-2X eigenstates. Though we do not expect drastic changes with a fully self-consistent approach nor with other, e.g., B3LYP or PBE0, starting eigenstates (see section 3.1 and ref (37)), the statistical data reported here are indeed related to a specific BSE/GW protocol. With BSE/GW, the two largest absolute deviations are obtained for XIX (Δ = 0.452 eV) and XLVI (Δ = 0.401 eV). The first is a charged acridine dye solvated in ethanol, so that the error can probably be partly ascribed to the lack of explicit solute–solvent hydrogen bonds in the model. The second, is tetracene for which we have checked that the GW values are indeed accurate,¹⁶¹ so that inaccurate energy levels do not explain the outcome. With ADC(2), only three absolute deviations exceed 0.4 eV: LIX (Δ = 0.564 eV), a strong pull–push dye for which the solvent corrections are large (see above), the phthalocyanine XL (Δ = 0.405 eV), and the subporphyrin LXIV (Δ = 0.403 eV). As protic solvents (e.g., methanol, ethanol, and water) tend to act as hydrogen bond donors with the solute, and as continuum models are not completely adequate for describing such specific solute–solvent interactions, we have also performed statistics for the three most satisfying approaches removing the protic solvents from the panel. The MAE of ADC(2), CC2, and BSE/GW now become 0.141 eV, 0.120, and 0.135 eV at the cLR-PCM,eq level. These values are completely similar to the one listed in Table 4, hinting that the incomplete modeling of intermolecular hydrogen bonds are probably not the main key explaining the remaining errors.

3.5. Simplified Protocols

The computation of ΔE^ZPVE remains the computational bottleneck of 0–0 calculations, at least at the TD-DFT level. Indeed, one needs to obtain second derivatives of the ES potential energy surface. It might be tempting to discard this term all together, but its magnitude is not negligible. Indeed, for the systems treated here, the vibrational correction ranges from −0.027 eV (LVII) to −0.150 eV (LVIII), with an average value of −0.089 eV. These maximum and mean values are well in line with previous works.^{43,44,47,162−164} As the distribution of ΔE^ZPVE is quite tight (see Figure S-7), it might therefore be more adequate to use this average value to correct all data, rather than neglect this term completely. This saves a CPU-demanding step and eq 13 becomes

13

and this is reinserted into the subsequent equations of section 2.3. For TD-M06-2X, ADC(2), CC2, and BSE/GW, the results of such a protocol can be found in Table 5. As can be seen, the statistical parameter (MAE, SD, and R²) slightly deteriorates when performing such crude approximations, but the effects are always smaller than 0.010 eV (MAE and SD) and 0.005 (R²) indicating that it might be used in most cases without generating dramatic changes.

Table 5. Results of a Statistical Analysis Performed by Using Simplified Protocols^a.

method	protocol	MSE	MAE	SD	Max(+)	Max(−)	R2
TD-M06-2X	standard	0.220	0.235	0.182	0.143	–0.755	0.898
	eq 13	0.220	0.235	0.185	0.144	–0.778	0.894
ADC(2)	standard	–0.034	0.141	0.177	0.564	–0.405	0.923
	eq 13	–0.033	0.147	0.182	0.591	–0.417	0.922
	eq 14	0.062	0.148	0.183	0.446	–0.473	0.921
	eq 14 + eq 13	0.062	0.150	0.185	0.473	–0.481	0.923
CC2	standard	0.028	0.131	0.165	0.468	–0.412	0.921
	eq 13	0.028	0.138	0.171	0.495	–0.407	0.918
	eq 14	0.128	0.167	0.168	0.354	–0.500	0.921
	eq 14 + eq 13	0.128	0.169	0.170	0.381	–0.507	0.921
BSE/GW	standard	0.018	0.147	0.177	0.401	–0.452	0.905
	eq 13	0.018	0.148	0.178	0.402	–0.475	0.905
	eq 14	0.047	0.137	0.164	0.316	–0.440	0.918
	eq 14 + eq 13	0.047	0.140	0.165	0.317	–0.463	0.918

^aOnly the cLR,eq values obtained with the default PCM parameters are reported. See the footnote in Table 4 and the text for more details.

Another CPU-saving approach, allowing one to divide the effort of the wave function part by a factor of 2, is to compute the 0–0 energies with TD-DFT and correct them by using only the difference between the vertical absorption energies determined with TD-DFT and the wave function scheme. With this protocol that saves the calculation of the emission energies with the wave function method, one now uses

14

instead of eq 9 or eq 12. In other words, relaxation effects are only accounted for at the TD-DFT level. As can be seen in Table 5, this approximation also yields an increase of the error, that is quite significant for CC2 (MAE of 0.167 eV instead of 0.131 eV) but smaller for ADC(2). The MSE significantly increases with ADC(2) and CC2 but is only slightly affected for BSE/GW. We related this smaller sensitivity of the latter approach to the fact the default BSE/GW protocol already relies on TD-DFT to determine the reorganization energies (see eq 11) so that the impact of applying eq 14 is indeed smaller than that for ADC(2) and CC2. In short, though we would not recommend using simplified protocols when technically possible, combining eqs 13 and 14 would allow much faster estimations of the 0–0 energies for only a slight increase of the average deviations.

3.6. Importance of the Chemical Nature

Let us now turn toward an analysis for specific families of dyes. First, we have considered two series of compounds presenting excited-states known to be challenging for “conventional” TD-DFT, namely, the cyanine¹⁶⁵ and charge-transfer^156,157 states. The former corresponds to molecules with a charge delocalized on an odd number of (carbon) atoms, and this group includes squaraines, BODIPYs, charged acridinic dyes, etc. They all share several common theoretical signatures that have been detailed in a recent account,¹⁶⁵ one of which is that TD-DFT tends to overestimate the transition energies significantly. We have set up a series of 9 compounds belonging to the cyanine class.¹⁶⁶ The results of a statistical analysis for this subset are displayed in Table 6. As expected, TD-DFT overshoots the transition energies significantly,^{165,167−169} whereas all other approaches provide much more satisfying results with MAE smaller than 0.2 eV, except for SCS-CC2 and SOS-CC2. For cyanines, the most accurate method appears to be ADC(2) with a MAE of 0.123 eV only. For practical purposes, we also stress that for cyanine derivatives the cLR correction tends to be particularly large, the LR model being insufficient to capture solvation effects.^154,170 The exact definition of CT states remains a matter of intense discussion.¹⁷¹ For this reason, we have selected a subset of 10 dyes only,¹⁷² where the dipolar (not quadrupolar) CT character is crystal clear. For these states, it is known that TD-DFT using standard hybrids leads to too small transition energies^156,157,173 a problem that can be cured with range-separated hybrids,^173−177 in which an increasing amount of exact exchange is applied when the interelectronic distance increases.^178−182 Here, we used M06-2X that encompasses a constant but quite large share of exact exchange (54%) which explains why TD-M06-2X values are not especially inaccurate for CT cases (see Table 6). Consistently with the large change of dipole moment between the ground and excited-states, CT dyes tend to be rather sensitive to solvation effects.^7,117 For this subset, the smallest MAE values are obtained with CC2 (0.175 eV) and BSE/GW (0.171 eV), whereas ADC(2) yields slightly less accurate results (0.200 eV). We found contrasting reports regarding the accuracy of ADC(2) for CT states can be found: Aquino and co-workers found that ADC(2) provides reliable CT states in π-stacked complexes,¹⁸³ whereas Plasser and Dreuw reported an unexpected ADC(2) failure for a specific CT state in an iridium complex.¹⁸⁴

Table 6. Statistical Analysis for the Subgroups of Compounds^a.

method	solvent	MSE	MAE	SD	Max(+)	Max(−)
TD-M06-2X	full set	0.220	0.235	0.182	0.143	–0.755
	cyanine-like	0.449	0.449	0.147	–0.259	–0.755
	dipolar charge-transfer	0.244	0.244	0.175	0.000	–0.493
	hydrocarbons	–0.034	0.071	0.071	0.143	–0.082
	thiophene dyes	0.165	0.169	0.117	0.036	–0.344
	keto dyes	0.308	0.308	0.118	–0.085	–0.493
CIS(D)	full set	0.249	0.263	0.195	0.467	–0.669
	cyanine-like	0.175	0.175	0.128	–0.017	–0.362
	dipolar charge-transfer	0.304	0.304	0.197	–0.010	–0.639
	hydrocarbons	0.182	0.194	0.137	0.060	–0.420
	thiophene dyes	0.225	0.227	0.171	0.022	–0.513
	keto dyes	0.257	0.259	0.185	0.022	–0.520
ADC(2)	full set	–0.034	0.141	0.177	0.564	–0.405
	cyanine-like	–0.020	0.123	0.150	0.280	–0.189
	dipolar charge-transfer	–0.125	0.200	0.217	0.564	–0.195
	hydrocarbons	–0.067	0.110	0.119	0.284	–0.148
	thiophene dyes	–0.060	0.140	0.147	0.238	–0.274
	keto dyes	–0.002	0.134	0.162	0.312	–0.274
CC2	full set	0.028	0.131	0.165	0.468	–0.412
	cyanine-like	0.158	0.188	0.151	0.068	–0.384
	dipolar charge-transfer	–0.071	0.175	0.198	0.468	–0.232
	hydrocarbons	–0.044	0.095	0.110	0.240	–0.165
	thiophene dyes	0.006	0.101	0.127	0.220	–0.292
	keto dyes	0.080	0.116	0.118	0.176	–0.292
SCS-CC2	full set	0.199	0.204	0.128	0.126	–0.559
	cyanine-like	0.224	0.224	0.093	–0.098	–0.432
	dipolar charge-transfer	0.158	0.183	0.159	0.126	–0.392
	hydrocarbons	0.134	0.135	0.089	0.005	–0.290
	thiophene dyes	0.189	0.189	0.107	–0.038	–0.470
	keto dyes	0.263	0.263	0.116	–0.080	–0.558
SOS-CC2	full set	0.282	0.282	0.125	–0.041	–0.705
	cyanine-like	0.265	0.265	0.078	–0.156	–0.450
	dipolar charge-transfer	0.265	0.265	0.142	–0.041	–0.481
	hydrocarbons	0.222	0.222	0.091	–0.073	–0.379
	thiophene dyes	0.278	0.278	0.104	–0.158	–0.558
	keto dyes	0.356	0.356	0.123	–0.204	–0.705
BSE/GW	full set	0.018	0.147	0.177	0.401	–0.452
	cyanine-like	0.176	0.182	0.129	0.026	–0.452
	dipolar charge-transfer	0.085	0.171	0.170	0.241	–0.284
	hydrocarbons	–0.230	0.230	0.097	0.401	0.083
	thiophene dyes	–0.004	0.082	0.107	0.216	–0.219
	keto dyes	0.106	0.137	0.126	0.133	–0.311

^aOnly the cLR,eq results are showed. See the footnote in Table 4 and the text for more details.

One can of course sort dyes by chemical families rather than by the nature of their excited state. We have considered three easily definable groups, namely, pure hydrocarbons, in which the balance between the bright and excited states is not straightforwardly obtainable,¹⁸⁵ thiophene dyes that contain at least one thiophene ring (that is known to be challenging for TD-DFT^186,187), and keto derivatives, presenting at least one C=O function, that constitute one of the most important group in dye chemistry,^188,189 and have been extensively modeled with TD-DFT.¹⁹⁰ These subsets, easily defined from Schemes 1–4, contain 10,¹⁹¹ 16,¹⁹² and 24¹⁹³ members, respectively. The results of a statistical analysis can again be found in Table 6. Surprisingly, it is TD-M06-2X that emerges as the most accurate method for hydrocarbons with a tiny MAE of 0.071 eV. This success is probably due to the consideration of low-lying bright states only.¹⁸⁵ ADC(2) and CC2 are also successful for hydrocarbons (MAE of 0.110 and 0.095 eV, respectively), whereas BSE/GW is much less satisfying for this group (MAE of 0.230 eV). On the contrary, for thiophene-containing compounds, BSE/GW has the clear edge (MAE of 0.082 eV) though both ADC(2) and CC2 again provide average errors below 0.150 eV. Eventually for keto dyes, the TD-M06-2X error is quite large, whereas ADC(2), CC2 and BSE/GW all deliver accurate estimates (MAE of 0.134, 0.116, and 0.137 eV, respectively). From this analysis, it appears that the accuracy of TD-DFT is quite sensitive to the chosen subgroup, whereas those of other approaches is much less, especially ADC(2) that systematically provides MAE below 0.15 eV except for CT systems.

4. Conclusions and Outlook

We have thoroughly investigated the 0–0 energies of 80 real-life compounds using TD-DFT to determine geometries and vibrational signatures and a wide panel of first-principle approaches [CIS(D), ADC(2), CC2, SCS-CC2, SOS-CC2, and BSE/GW] to compute transition energies. Three approximations for solvation effects (LR-PCM and cLR-PCM) have been assessed. It appeared that accounting for solvation tends to bring the theoretical estimates closer to experiment but that the LR-PCM scheme significantly overestimates solvatochromism (by a factor of ca. 3–4) so that cLR-PCM or other approaches accounting for the ES density have to be used. In contrast, the nonequilibrium solvation corrections are almost negligible for 0–0 energies. Using cLR-PCM, CC2, ADC(2), and BSE/GW, that, respectively, present , 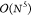and 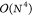formal scalings, provide the most accurate data (MAE of 0.131, 0.141, and 0.147 eV, respectively), the two former yielding slightly better determination coefficients (R² = 0.921 and 0.923) with experiment than the latter (R² = 0.905). For the sake of comparison, the TD-M06-2X MAE and R² are 0.235 eV and 0.898, respectively, but it should be recalled that TD-DFT remains significantly less demanding than all other schemes tested here. We also found that using SMD parameters induces relatively small variations (ca. 0.010 eV) of the computed deviations. In short, one could therefore clearly recommend both ADC(2) and BSE/GW to correct TD-DFT 0–0 energies: they provide, for an acceptable computational effort, significant improvements of the accuracy compared to TD-DFT. As the mean absolute differences with respect to experiment obtained with ADC(2) and BSE/GW are rather small, it is not straightforward to determine if the remaining errors originate in the TD-DFT geometries and harmonic frequencies, in the inherent limitations of ADC(2) and BSE/GW, or in the selection of a continuum solvation model. To partly answer this question, we can refer to the work of Winter and co-workers performed on smaller molecules in gas-phase.⁴⁴ They found that using TD-B3LYP ZPVE instead of ADC(2)’s induces a rather small increase of the MAE (+0.02 eV), indicating that the TD-DFT ZPVE correction term is probably not the main source of errors. In contrast, the MAE reported in Winter’s study for ADC(2) corrected with the TD-DFT’s vibrational term is 0.10 eV,⁴⁴ significantly smaller than the one found here (0.14 eV), and this difference can probably be mainly ascribed to the limitations of continuum models that are used here. Several more specific conclusions have been drawn from the present study: (i) ADC(2) and CC2 yield very similar estimates except for dyes absorbing at small energies; (ii) CIS(D) does not bring significant improvements compared to TD-M06-2X except for cyanine ES; (iii) both SCS-CC2 and SOS-CC2 improve the consistency of the CC2 estimates (larger R²) but tend to overestimate the experimental energies significantly; (iv) Stokes shifts are rather similar for all approaches though CC2 tends to provide slightly smaller values; (v) the ΔE^ZPVE presents a quite tight distribution so that correcting all data with the average value (−0.089 eV) does not deteriorate significantly the average deviations; and (vi) ADC(2) errors are rather independent of the chemical nature of the compound considered, whereas BSE/GW appears particularly accurate for charge-transfer excitations and thiophene-containing structures, with an unexpected relative lack of accuracy for the pure hydrocarbon family.

In short, ADC(2), CC2, and BSE/GW emerged as the most suitable approaches to determine 0–0 energies on the basis of structural and vibrational properties calculated with TD-DFT. Compared to experimental values, these three approaches significantly improve the accuracy of the theoretical estimate and, in part, their correlation with measurements. The next step in the field is probably to obtain analytical forms for the ES gradients at the BSE/GW level.^40,194 This would allow one to compare ADC(2), CC2, and BSE/GW 0–0 energies determined on the corresponding ES structures. Additionally, the accurate calculation of 0–0 energies is only a first step in the simulation of optical spectra, and obtaining band shapes is also highly interesting for performing direct theory–experiment comparisons. For TD-DFT, benchmarks of band topologies performed for significant sets of both organic and inorganic compounds are already available,^50,195−198 but such work remains to be carried out for ADC(2), CC2, and BSE/GW.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b00619.

• Raw values of (transition) energies (ΔE^vert–a, ΔE^vert–f, E^adia, ΔE^ZPVE, and ΔE^0–0); comparison of two basis sets at the BSE/GW level; SMR results; comparisons between CC2 and BSE/GW transition energies; representation of ΔE^ZPVE; Cartesian coordinates for the ground and excited states of all compounds (PDF)

D.J. acknowledges the European Research Council (ERC) and the Région des Pays de la Loire for financial support in the framework of a Starting Grant (Marches -278845) and the LumoMat project, respectively. X.B. acknowledges partial support from the French National Research Agency under contract ANR-12-BS04 “PANELS”.

The authors declare no competing financial interest.