Infant learning: Historical, conceptual, and methodological challenges

Abstract

Acquiring knowledge about the underlying structures of the environment presents a number of challenges for a naive learner. These challenges include the absence of reinforcement to guide learning, the presence of numerous information sources from which only a select few are relevant, and the uncertainty about when an underlying structure may have undergone a change. A crucial implication of these challenges is that the naive learner must make implicit decisions about when to generalize to novel inputs and when to restrict generalization because there are multiple underlying structures. An historical perspective on these challenges is presented and some potential solutions are proposed.

Planning for a Presidential Address poses a significant dilemma – should the focus be on (a) your personal scientific history, (b) key controversies in the field, (c) a tribute to highly talented graduate students and postdocs, (d) a life-long goal of proposing a grand theory, or (e) giving up in desperation and simply delivering your regular colloquium? In the end, this address is a little bit of “all of the above”. I begin with some history on the general topic of learning theory and development (see Stevenson, 1970), and then pose a series of questions – why is learning a hard problem, what enables learning to be tractable given these problems, and are the mechanisms of learning across development continuous, incremental, and progressive? Along the way I highlight a number of methodological challenges that face infancy researchers, and I come to some tentative conclusions about how the field might move forward to address the key questions that will surely continue to vex the next generation of researchers.

A brief history of learning during development

One of the key events in my personal scientific history was the tremendous appreciation for the history of psychology engendered by one of my professors – Robert Wozniak – at the University of Minnesota’s Institute of Child Development. In several courses and countless conversations, Rob highlighted the importance of consulting the history of any discipline before stumbling, unannounced, into a sub-field where others before you have given considerable thought (and often conducted key experiments) to address a particular question. Fortunately for me, my first lab experience as an undergraduate at Michigan State University was with Hiram Fitzgerald, whose own research on infant learning was steeped in the traditions of classical conditioning (Fitzgerald & Brackbill, 1976) that were in turn engendered in him by his mentor Yvonne Brackbill and the major figures in the field before her. The study of learning in infants had a major resurgence of interest in the 1960’s not only in the tradition of classical conditioning, but also in the operant conditioning paradigms adapted to study infants by Lewis Lipsitt (1964) and Hanus Papousek (1959). Two decades later these same principles were used to condition head-turning behavior (Kuhl, 1985). The beauty of these paradigms was their emphasis on unambiguous events: a single context, clear instances of conditioned and unconditioned stimuli, well-defined responses, and the use of primary reinforcers.

Unfortunately, these early examples of classical and operant paradigms exposed a number of problems for any realistic theory of learning in infants. Problem #1 was the fact that most of the natural environment of infants is devoid of primary reinforcers. This of course was one of the key points noted by Edward Tolman (1932) and demonstrated decades later by Harry Harlow (1959). That is, the so-called secondary reinforcers (e.g., curiosity, contact-comfort) were incorrectly characterized as derived from primary reinforcers rather than having primary status on their own. Problem #2 was the fact that the natural environment is filled with high levels of ambiguity – that is, given the myriad of events that co-occur, it is unclear whether a stimulus is causally related to another stimulus (or to a reward) or whether these co-occurrences are merely coincidences that lead to suspicious attributions of causal relations. How does the naïve (infant) learner resolve this ambiguity without the benefit of top-down knowledge that is only available to a mature learner?

The road to addressing these two problems was paved by a second wave of methodological advances in the study of infant learning in the 1970’s and 1980’s, and then a third wave of interest in what has become known as statistical learning in the 1990’s and 2000’s. A key methodological advance was the development and elaboration of the habituation paradigm by Robert Fantz (1964), Frances Horowitz (1974), Robert McCall and Jerome Kagan (1967), and Marc Bornstein (1985). They showed that repeated exposure to a stimulus led to a decline in a criterion response (e.g., looking time), which could then be re-activated by a change in that stimulus. Although this simple habituation paradigm provided an excellent measure of discrimination, it was the addition of a “family” of stimuli during the so-called multiple-habituation phase that allowed the paradigm to address questions of category learning. In the hands of Leslie Cohen and Mark Strauss (1979) and Joseph Fagan (1976), the multiple-habituation paradigm allowed investigators to ask how infants grouped stimuli into categories without the involvement of any conditioned response or primary reinforcer – infants looked for the sake of looking and learned for the sake of learning.

Paradigms that followed in the tradition of operant conditioning, using motor responses other than looking time such as sucking or foot-kicking, showed that infants as young as one day after birth were excellent learners. Siqueland and DeLucia (1969) demonstrated that infants suck to turn on a stimulus, Rovee-Collier, Sullivan, Enright, Lucas, and Fagan (1980) demonstrated that infants kick to wiggle a stimulus, despite the absence of any other reinforcer. And DeCasper and Fifer (1980) showed that newborns suck differently (by starting or delaying a burst of sucks) to one class of auditory stimuli over another. All of these methodological advances in the 1970’s and 1980’s forced the conclusion that classical learning theory must be broadened beyond the limited notion of primary reinforcement to include constructs such as familiarity/novelty, curiosity, control/mastery, efficacy, contingency, and other “hidden causes” as part of the larger family of reinforcers that affect infant learning.

The third wave of interest in infant learning had its beginnings in the work of Barbara Younger and Leslie Cohen in the mid-1980’s. Using the multiple-habituation paradigm that they helped to develop, their question centered on how infants allocate attention to the many visual features that define a class of objects. This question tackles Problem #2 raised earlier – given a complex environment containing many stimulus features, how do infants implicitly decide to attend to just the “right” features that define a class of objects? Younger and Cohen (1983, 1986) reasoned that if a subset of features co-vary across a series of images, then infants should automatically attend to those correlated features, even in the presence of all the other uncorrelated (extraneous) features. Their results confirmed this hypothesis, at least in 10-month-olds (but not 7-month-olds). That is, infants “generalized their habituation to a novel test stimulus that maintained the correlation they had seen, whereas they dishabituated to a stimulus containing equally familiar features but that failed to preserve the correlation” (pp. 864–865). In other words, with no reinforcement to guide their attention, and when confronted with a highly complex, multi-dimensional visual stimulus, infants automatically attended to features that co-occurred in a family of images and generalized their attention to novel images that contained these same feature correlations.

If we fast-forward a decade to a different modality (audition) and a different question (word-segmentation) in the study by Saffran, Aslin, and Newport (1996), we see this same implicit learning mechanism at work. Saffran et al. asked whether infants who are exposed to a multi-dimensional stream of speech elements in the auditory/temporal domain, analogous to Younger and Cohen’s (1983) multiple images in the visual/spatial domain, are able to “parse” that stream into word-like chunks. In a series of experiments (Saffran et al., 1996, 1999; Aslin, Saffran & Newport, 1998), they showed that 8-month-olds can indeed segment these streams of speech (or auditory tones) into their statistically coherent chunks. Moreover, in a series of experiments with adults (Fiser & Aslin, 2002) and infants (Kirkham, Slemmer & Johnson, 2002; Marcovitch & Lewkowicz, 2009), it was shown that this process of extracting temporally-ordered chunks operates in the visual modality as well. And reminiscent of Younger and Cohen (1983, 1986), Fiser and Aslin (2001, 2002, 2005) showed that this same process of extracting feature correlations applies to visual/spatial patterns, although instantiated across 16 to 144 different images rather than the 4 images used by Younger and Cohen.

This brief historical review of infant learning, spanning more than five decades, leads us back to the two problems that any theory of learning must address. Problem #1 – that reinforcement in the natural environment is either not present at all or only rarely – appears to be “solved” by an implicit mechanism of statistical learning. That is, there is a powerful “engine” that operates over any corpus of structured input to extract, without any extrinsic reward, those statistical correlations that are present and, as we will discuss later, generalize to novel exemplars under some circumstances. Problem #2 – that there is ambiguity in the input as to what “counts” as a relevant feature to be analyzed by this powerful statistical-learning mechanism – has not yet been addressed. A corollary to this problem of what to count is how many features can be counted given limited information-processing capacities in young infants? Laboratory studies, particularly in early work on statistical learning, presented infants with a rather simple set of features devoid of ambiguity so that the “proof of concept” of such a learning mechanism could be demonstrated. But these early demonstrations immediately raised a number of important questions: (a) do naïve learners keep track of statistics across time, across space, and for all possible spatial-temporal correlations, (b) if infants can keep track of statistics among “obvious” elements such as syllables or simple shapes, what about elements at lower (e.g., speech formants, visual pixels) or higher (e.g., grammatical categories, visual scenes) levels, and (c) do infants keep track of everything so that they don’t miss anything that could potentially be important to a naïve learner? We turn now to these constraints on learning, which must operate in infants to enable a robust and rapid mechanism to be tractable given the limits on information processing in early development.

Constraints on statistical learning

Two classic hallmarks of infant development are a limited span of attention and an inability to process rapidly presented information (Richards, 2008). Yet findings from statistical learning, particularly in the auditory modality, revealed that infants could not only keep track of rapidly presented events (i.e., 4 syllables/sec), but that they could compute a variety of statistics over these events (e.g., frequencies of occurrence, transitional probabilities). Recent evidence on a key aspect of information processing – short-term memory (STM) – appears to reconcile this seeming contradiction. Although several studies had shown that working memory (WM) in infants was highly limited (e.g., holding only one item in WM during a brief occlusion event in 6-month-olds -- see Ross-Sheehy, Oakes & Luck, 2003; Kaldy & Leslie, 2005), WM is a difficult task because it requires continuous updating. In contrast, STM has no competing task or updating requirement while information is being retained. The classic demonstration of the high capacity of STM was by Sperling (1960) using a partial-report paradigm. The logic of the paradigm was that if all items in a visual array were available in STM, but only a few could be reported verbally before STM decayed, then if a subset of the items were highlighted after the presentation of the array, subjects should have no difficulty reporting on any subset. That is precisely what Sperling found, even for large arrays of items, as long as the subset to be reported was relatively small (e.g., 3–5 items).

A recent study by Blaser and Kaldy (2010) reported a similar pattern of results in 6-month-old infants. They presented infants with an array of up to 10 items varying in shape and color for a brief 1 sec duration and then highlighted two of the items by removing them from the array for ½ sec. When these removed items reappeared, one of them had changed. The dependent measure was whether infants looked at the changed item. As in Sperling (1960), if all of the items in the array were encoded into STM, then regardless of which subset was highlighted, infants should detect the changed item and look longer at it. However, if infants cannot encode all of the items in the array, there will be a set-size limit beyond which the novelty preference for the changed item will fail to exceed chance. This pattern of results was precisely what Blaser and Kaldy found – at set-sizes of 2, 4, and 6 infants looked longer at the changed item, but at set sizes of 8 and 10 they did not. These results suggest that 6-month-olds have a STM capacity of at least 6 items in a briefly presented array. Along with prior results on WM, these results also confirm that infants have more limited information processing capacities than adults, although their capacities are still rather impressive given the absence of task instructions, motivation, and training.

What then mitigates Problem #2 – the inability to keep track of all possible statistics? Over the past two decades, a variety of constraints have been proposed and verified experimentally to account for the naïve learner’s ability to overcome the computational explosion problem (i.e., attempting to keep track of everything). These constraints include the following. Attentional biases – infants appear to “naturally” attend to object shape and to the whole object rather than its parts (Smith, 2003), to syllables rather than phonemes (Bertoncini & Mehler, 1981), to a variety of Gestalt principles (Bhatt & Quinn, 2011) such as proximity, synchrony, and stream segregation (within an octave), and to limit inferences to a single possibility (i.e., mutual exclusivity in object names; Markman, Wasow & Hansen, 2003). Social cues – infants appear to be guided in their attention by the gaze, manual exploration, and pointing gestures of their caregivers (Baldwin, 1993). Environmental simplification – infants benefit from a variety of ways in which caregivers de-clutter or enhance stimuli in their proximal environment (Kuhl et al., 1997). Cross-situational statistical learning – infants can determine by a simplified “process of elimination” that names and objects are linked even when these linkages are inferred rather than overt (Smith & Yu, 2008). Repetition – infants are confronted with a remarkable level of event repetition, both by how their caregivers act and by how they themselves repeat preferred events under their control. One startling statistic computed by Haith (1980) is that the average 2-month-old has sampled its visual environment with over 250,000 fixations (looking times between saccades) since birth.

Despite the logical advantage of the foregoing constraints – which surely must assist in dealing with Problem #2 – it is nevertheless the case that laboratory demonstrations of statistical learning are highly simplified compared to what an infant is actually confronted with in the natural environment. Thus, we should be concerned that such demonstrations are little more than proof-of-concept that under ideal conditions a statistical learning mechanism can solve certain tasks. But does this mechanism “scale up” to more natural and complex learning tasks? There are two answers to this question, at least for studies of statistical learning in the language domain. First, a variety of corpus analyses (Swingley, 2005; Frank, Goldwater, Griffiths & Tenenbaum, 2010) have shown that, to a first approximation, the same types of statistical information manipulated in the lab are present in real language input to infants. Yet in real corpora, these statistical cues are less reliable, and thus one worries that no one cue alone is sufficient. It is important to note, for historical purposes, that initial claims about statistical learning made precisely this point: “Although experience with speech in the real world is unlikely to be as concentrated as it was in these studies, infants in more natural settings presumably benefit from other types of cues correlated with statistical information (p. 1928).” (Saffran et al., 1996). Laboratory studies that eliminate all potentially useful cues except one serve the purpose of showing that the sole cue present in the input is sufficient for learning. But such studies cannot confirm that in the natural environment, where many cues are correlated, any given cue plays a necessary role in learning.

The second answer to the “scale up” question is to conduct laboratory experiments in which two or more cues are presented in combination to see which one “wins” or how each cue is “weighted” in the statistical learning process. Early work that followed this strategy suggested that statistical cues “trump” prosodic cues (Thiessen & Saffran, 2003), at least at the level of lexical prosody (i.e., whether 2-syllable words have a strong-weak or a weak-strong stress pattern). The reason that lexical prosody might take a back seat to statistics is that prosody is language-specific whereas syllable statistics, at least in most languages, are not. Yet there are other levels of prosody that are language-general and so could reasonably serve as universal constraints on which statistics are computed.

One such language-general prosodic constraint is the fact that words never span an intonational phrase – the natural slowing and short pause that typically occurs at boundaries between major grammatical categories (e.g., noun- vs. verb-phrase). Take for example the sentence “The beautiful baby smiled at her mother” which consists of two intonational phrases, with a boundary between “baby” and “smiled”. It is possible to create strong statistical cues between syllables that fall within an intonational phrase, as would be present in any natural language, or between syllables that span an intonational phase boundary, which almost never occurs in natural languages. This design was implemented in Shukla, White, and Aslin (2011) using nonsense syllables as in Saffran et al. (1996), but organized into short sentences rather than continuous streams. A family of such sentences was presented to 6-month-olds as they watched a video display depicting three salient objects. One of the objects consistently underwent motion across trials while the other two objects never moved, thereby drawing infants’ attention to the single moving object. The key feature of the design, implemented across two groups of infants, was that there were syllables with strong statistical links (i.e., words) and syllables with weak statistical links (i.e., part-words), but in only one of the two conditions were the strongly linked syllables within an intonational phrase. Thus, if infants attended only to syllable statistics, regardless of their positioning with respect to intonational phrases, both groups would extract these word-candidates and map them onto the single object in the video display that was moving. However, if infants were constrained to extract syllable statistics when they fell within an intonational phrase, then only infants in the group where the ends of words were aligned with the ends of intonational phrases would map these syllable statistics to the moving object. That is precisely the outcome reported by Shukla et al.

The main reason for describing the Shukla et al. (2011) study is that it illustrates how the statistical learning mechanism of young infants is constrained in a principled way to reduce the computation complexity faced by a naïve learner in the language domain. Intonational phrases are universal characteristics of natural languages that presumably do not themselves have to be learned because they are based on low-level durational and pitch cues. But the Shukla et al. study also illustrates a second important point about the implications of designing laboratory experiments to test infants. As noted earlier, it is natural for experimentalists to eliminate all but one source of information to determine whether it alone is sufficient for learning; that was the goal of the Saffran et al. (1996) study that focused on syllable statistics while eliminating prosodic and repetition cues that are present in natural language input. Subsequent work by Graf Estes, Evans, Alibali, and Saffran (2007) showed that when the input was structured in an incremental manner – streams of nonsense syllables organized into statistically coherent works, followed by the opportunity to map those words onto objects in a referential context – 17-month-olds readily solved this task. Shukla et al.’s results showed that these statistical segmentation and word-mapping tasks can be accomplished at the same time, and moreover in much younger infants (6-month-olds). This suggests that when designing single-cue laboratory experiments, we may be underestimating the learning capabilities of infants because they have already formed expectations about how multiple sources of information are correlated in natural language input. The counter-intuitive implication of this finding is that making an experimental design too simple may make the task for the infant more complex, thereby leading researchers to underestimate the infant’s actual learning capacity.

To summarize this section on the second problem facing the naïve learner – there must be constraints to enable learning to be tractable – the solution seems clear-cut. The computational complexity and interpretive ambiguity about which statistics are the “right” ones to keep track of is solved by a few innate constraints on what to attend to and a learning mechanism that feeds off of these innate constraints to become further constrained by what has been learned so far during development. In the terminology of Bayes theorem, what a learner acquires (called the posterior probabilities) is a combination of what was given by the innate biases (called the priors) and what has already been observed from masses of data (called the likelihoods), filtered through the lens of the innate biases. This is essentially an incremental bootstrapping model of learning, in which a hierarchy of information is built up from two mechanisms – a powerful and robust statistical learning “engine” that is rendered tractable by a few innate biases, coupled with an enormous amount of raw data that once filtered by these innate biases is forever “blocked” from further computations that would divert the learner along an unfruitful path. But this view of the development of learning rests on an assumption of the infant as a rationale allocator of attention to those sources of information that are the most “fruitful”. How does the infant “know” that some information is worthy of their attention and other information is not? The next section tackles this question by reviewing recent work on the fundamental properties of how we interpret looking-time data from infants.

The novelty-familiarity conundrum

The use of looking times as a measure of learning, and a whole host of other underlying perceptual and cognitive processes, has been exploited for the past 50 years of research on infants (see Aslin, 2007). The canonical view of looking times is that they are reactions to stimulation, pulling the infant’s gaze hither and yon based on a combination of exogenous (i.e., stimulus salience) and endogenous (i.e., memory) factors. According to this view, the expected pattern during exposure to a single stimulus or a family of stimuli during the habituation phase should be a decline in looking time as memory builds a “template” of the familiar stimuli. And when a new stimulus is presented during the post-habituation test phase, looking time should rebound to reflect a discrepancy with the template. While this “novelty” response during the test phase is the typical outcome, it is not universal – under some circumstances the post-habituation looking times are longer to the familiar stimulus. For example, although almost all of the findings on infant statistical learning report novelty preferences (i.e., longer looking to the less frequent or less predictable stimuli), there are exceptions (Fiser & Aslin, 2002; Pelucchi, Hay & Saffran, 2009). In fact, in looking-time measures of infant’s preferences for their native language, when there is no immediately preceding habituation phase (but only the long-term exposure prior to visiting the lab for testing), infants typically listen longer to highly familiar stimuli rather than to novel stimuli (Jusczyk & Aslin, 1995).

The foregoing results across literally hundreds of experiments raise the possibility that there is at least one additional variable that is unaccounted for by the canonical reactive view of looking times. Kidd, Piantadosi, and Aslin (2012) hypothesized that if infants also take an active role in sampling their visual environment, then looking times should vary by how much information infants are able to extract on a moment-by-moment basis. To be clear, this does not deny the importance of stimulus salience and memory for repeated events as factors that influence infant looking times. Rather, Kidd et al. asked whether this third factor – the ability to estimate the information content of stimulus events – also plays a role in infant looking times.

The logic of the design employed by Kidd et al. (2012) was to create a quantitatively well-defined family of stimulus events whose salience was randomized (to wash out that effect). Each stimulus event varied in its predictability or surprisal given all previous events in a given sequence. Thus, the goal was to determine, at each stimulus event, whether the infant would continue to look at the display or to terminate fixation and end the trial. Notice that this is quite different from previous studies that ask how long infants will maintain their looking. Kidd et al. asked whether on each stimulus event infants will or will not make an implicit binary decision to stay or go. To achieve this, they created very brief (2 sec) events from an inventory of three possibilities on each trial that varied in information complexity from simple (e.g., AAAAAAA) to complex (e.g., ABACCBBBACAA). The hypothesis was that if infants are active samplers, they will terminate their fixation whenever the sequence of events is either too simple or too complex. The former occurs because there is no further information to be gained by continuing to look at highly expected events, and the latter occurs because the events make no sense (or cannot be predicted).

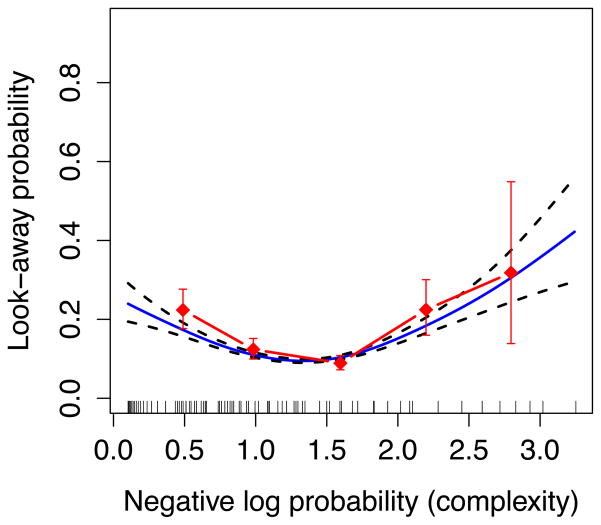
The results of Kidd et al. (2012) confirmed the hypothesis that infants are more likely to terminate their looking to events that are either overly simple or overly complex, given the sequence of events leading up to that terminating event, and less likely to terminate their looking to events of intermediate complexity. This generates a U-shaped function of the likelihood of ending a trial as a function of the information content of the events in the sequence (see Figure 1). Crucially, the U-shaped function was not the result of a variety of other variables that could have plausibly led to this outcome. A special form of regression (Survival Analysis) accounted for factors such as the number of repeated events (e.g., AAA vs. ABC), number of unseen events (e.g., ABA without C), the first instance of an event (e.g., C after ABA), and the overall tendency to look less to events as the sequence continued. Thus, the tendency to maintain fixation to events of intermediate complexity – which Kidd et al. called the Goldilocks effect – appears to be based on an implicit sense that some patterns of information are more or less informative than others and therefore worthy of further sustained attention.

Figure 1.

A number of follow-up experiments confirmed the general nature of the Goldilocks effect. The sequences of events did not have to consist of three possible objects in the display, but could consist of a single object whose presence vs. absence created variations in surprisal. The events did not have to be visual, but could be sequences of auditory stimuli (Kidd, Piantadosi & Aslin, revision under review). And crucially, the U-shape function, which was based on group data, was not an artifact of averaging some infants who had decreasing probabilities of terminating a trial as complexity increased with some infants who showed the opposite pattern. A more detailed analysis if each infant’s data confirmed that 39 of 41 infants showed U-shaped functions, thereby verifying the ubiquity and robustness of this active process of allocating attention to sequential events (Piantadosi, Kidd & Aslin, in press). In on-going work, these same visual events were presented to macaque monkeys in a non-reinforced visual attention task, and a similar U-shaped function was obtained (Kidd, Blanchard, Aslin & Hayden, in prep). Thus, it appears that the general principles by which naïve learners allocate their attention is not unique to human infants or to paradigms used with human infants.

It is important to be clear about how this work on the Goldilocks effect relates to prior work showing U-shaped functions, and to point out several unanswered questions that must be addressed in the future. First, many other researchers have observed U-shaped functions and have proposed a variety of explanations for this occurrence (see special issue of Journal of Cognition and Development, 5, 1–157). Yerkes and Dodson (1908) noted that the efficacy of learning in rats varies with level of arousal, such that low and high arousal predicted poorer learning than a medium level of arousal. Berlyne (1960) proposed that curiosity modulates the likelihood of learning, with low and high curiosity leading to poorer learning outcomes than a medium level of curiosity. Kinney and Kagan (1976) proposed that infants have a tendency to attend maximally to stimuli of moderate complexity (or discrepancy with respect to a family of stimuli) compared to overly simply or overly complex stimuli. The key difference between these past observations is that the proposed mediating mechanism (arousal, curiosity, discrepancy) was not defined quantitatively and was not assessed independently of the measure of attention itself. That is, stimuli were chosen based on intuitions about how they related to the mediating mechanism, and when a U-shaped function was obtained, the mediating mechanism was interpreted as verified. In contrast, Kidd et al. (2012) quantitatively defined information complexity before presenting the stimulus sequences and eliminated the effects of a variety of other potential mediators of the obtained U-shaped function.

The results of Kidd et al. (2012) raise a variety of unanswered questions. First, what enables infants (and monkeys) to implicitly notice that they are failing to “understand” the complex events, and why are they choosing to terminate fixation? One possibility is that learners are evaluating the choice between “making progress” in understanding a sequence of events and failing to see any benefit in attempting to learn something that is more complex compared to reallocating attention to something that is not yet known by may be simpler to learn. That is, attention is selective and can be allocated to multiple sources of information. Learners may have, by prior experience, learned that if a sequence of events is not “mastered” within some period of time, they are likely to find other sources that can be more effectively “mined” for information and are more readily accessible. However, a limitation of the Kidd et al. work is that allocation of attention was not linked to the efficacy of learning. It is possible that the “sweet spot” of the Goldilocks function is where information is best learned, but it is also possible that learning occurs best on the rising portion of the function where information is slightly more complex. There are hints in a recent study by Swan and Kirkham (in press) that learning is in fact facilitated when an intermediate level of predictability is present.

A third limitation of the Goldilocks results is that so far they only apply to sequential events and only to stimuli that are not “special” in some way. The choice of sequential events was driven by the goal of quantitatively characterizing the information complexity of the stimuli (i.e., entropy or surprisal is a well-defined mathematical property). It remains to be seen if similar quantitative metrics of information complexity can be applied to static stimuli. Kidd et al. (2012, in prep) avoided special classes of stimuli such as faces or the mother’s voice precisely because such stimuli are thought to be treated differently, either by innate biases or by past experience, than arbitrarily novel stimuli. Clearly, the valence of certain classes of stimuli must be taken into account to extend the Goldilocks findings to events that are common in the natural environment. And finally, there are potential interactions between spontaneous allocation of attention and the “reward” that could follow – perhaps in the form of a “sense of mastery” or reduced “prediction error” if learning is achieved.

In summary, the Goldilocks work is not merely a methodological sidebar to studies of attention, but also a catalyst for thinking more deeply about what factors control looking times and how these factors influence the interpretation of studies of infant learning. So far we have focused on studies of statistical learning that were limited to asking whether infants can compute and remember items/events to which they were exposed in an immediately preceding familiarization phase. We now turn to the more interesting case of how infants generalize from familiar to novel items/events. After all, knowledge based solely on what we have already experienced is overly restrictive and inefficient – a “smart” learner must be able to make inferences about previously unexperienced items/events to attain the generative capacity of a mature learner.

Non-stationarity and the rules of generalization

The preceding summary of the Goldilocks results highlighted the fact that learners discover structure in the input to which they are exposed by sampling that input with selective attentional mechanisms. Because any natural corpus of input, whether language or vision, will contain variability, a “smart” learner should resist the temptation to gather small samples because they can be misleading – instead learners should integrate over a representative corpus. But this creates a dilemma and a trade-off. The dilemma is that a learner cannot ignore variation within a corpus because the underlying structure to be learned may undergo a change or there may be more than one structure present in a large sample of the input. The trade-off is between small samples that enable rapid learning but risk inferring multiple structures when a single structure (with variability) is present, and larger samples that enable more reliable estimates of the possible presence of multiple structures but slow down the rate of learning of these structures. These concerns define Problem #3 for the naïve learner – is the environment stationary, consisting of a single structure to be learned, or is the environment non-stationary, with two or more structures that must be discovered and retained in memory as separate representations?

Dealing with the non-stationarity problem is not trivial and failing to solve it has significant ramifications for the accuracy of subsequent learning. If a naïve learner has a stationarity bias, then whenever the environment has more nuanced structural components, learning will be sub-optimal. Moreover, if a poor “fit” of a model of the environment is tolerated, then the criterion for subsequent learning may be overly “lax” and prevent further learning. In contrast, if a naïve learner has a non-stationarity bias, then variability due to sampling rather than to the presence of multiple structures will lead to “over-fitting” this natural variability and prevent the model of the environment from generalizing to novel instances of what is actually a uniform structure (i.e., the learner will acquire too much detail).

Although the natural environment is clearly non-stationary, there is a surprising paucity of research on this topic. In fact, the design of almost all statistical learning studies ensures that whichever subset of the corpus is sampled, the statistics are the same. In one of the first studies of non-stationarity, Gebhart, Aslin, and Newport (2009) presented adults with a 10-min stream of nonsense syllables (as in Saffran et al., 1996) and, without informing the subjects, altered the structure half way through the exposure phase. In a post-test that contrasted words and part-words from each of the two structures, Gebhart et al. found that adults learned the syllable statistics of the first structure but not the second (i.e., what was called a statistical garden path). Thus, in the absence of any cues that signal a change of structure, adults have a primacy bias and appear to treat the second structure as a noisy version of the first. However, Gebhart et al. also showed that when there is a clear cue for a change in structure (e.g., by pausing between structures and informing the subjects that there is a new structure), adults learn both structures equally well. Importantly, Gebhart et al. also showed that a cue for a change in structure is not required – when subjects heard an extended version of the second structure, they learned its syllable statistics and yet maintained their learning of the first structure’s syllable statistics. This overall pattern of results suggests that once a structure is learned, it takes extensive evidence that a second structure is present (rather than a noisy version of the first structure) or a strong cue for a change of structure to overcome an initial stationarity bias.

Another interesting finding from Gebhart et al. (2009) was that all cues for a change in structure are not equally effective. When the first structure was spoken in a male voice and the second structure in a female voice, there was no benefit to learning the syllable statistics in the second structure. This is perhaps not surprising given that talker/voice differences in natural languages do not signal a different structure, unless the two talkers are speaking different languages. This bilingual example was examined by Weiss, Gerfen, and Mitchell (2009) using a paradigm similar to Gebhart et al., but with the two structures repeatedly alternating every 2 min. Under these circumstances, there was no evidence of learning either of the two syllable statistics, presumably because the 2 min exposure was insufficient to “tag” the fact that there were two structures. However, when each structure was spoken by a different talker/voice, this tagging was obvious and now subjects learned both syllable statistics. Thus, as in Gebhart et al., when there is a strong cue that indicates the presence of two different contexts, learners are quite adept at keeping track of two separate sets of statistics that describe the two underlying structures.

This notion of context is crucial not only for the efficacy and efficiency of learning, but also for the propensity to generalize. Consider a situation in which a naïve learner is attempting to understand a corpus of environmental input. Even if the learner has a stationarity bias, there are a variety of contextual cues that are very obvious (e.g., time of the day as indicated by sunlight vs. darkness or when a given parent is present vs. a preschool teacher). How does the learner decide which of these contextual cues is relevant – leading to the inference that there is a new structure to be learned – and which contextual cues should be ignored because they are uncorrelated with a change in structure? As noted by Qian, Jaeger, and Aslin (2012), this distinction between cue-sensitivity and cue-relevance is what was earlier referred to as Problem #3 – the presence of contextual ambiguity. That is, learners must be open to the possibility that a cue serves as a contextual signal for a change of structure, but not overly willing to assume that every cue that is discriminable signals such a contextual cue.

Problem #3 has a further implication for what a learner should do after they have partitioned (or not) the environmental input into separate structural representations. If a learner has a stationarity bias and treats multiple structures as being generated by a single representation, then they will incorrectly generalize across those multiple structures. This over-generalization is a common property of early language productions for certain grammatical morphemes (e.g., the –ed ending on verbs). In contrast, if a learner has a non-stationarity bias and falsely infers multiple structures when they are not present in the input, then they will incorrectly restrict generalization. This under-generalization is seen in 5-month-old infants who, after exposure to multiple views of a single person’s face, fail to generalize to a novel view of that same person’s face (Fagan, 1976). This propensity to generalize was also noted in Younger and Cohen (1983) – 7-month-olds appeared to base their learning of multi-feature objects by memorizing exemplars, whereas 10-month-olds extracted the commonalities among the set of objects and generalized to new exemplars that shared these commonalities.

Proposals about the rules of generalization have been a central topic of discussion among learning theorists since the time of Pavlov (1927) and Skinner (1938). A more modern treatment of generalization in the context of statistical learning comes from the work of Marcus, Vijayan, Bandi Rao, and Vishton (1999). In a variant of the syllables-of-speech design of Saffran et al. (1996), Marcus et al. presented 9-month-olds with 3-syllable strings separated by pauses rather than with continuous streams devoid of pauses. These 3-syllable strings were composed from a set of 8 consonant-vowel syllables into one of three different patterns defined by the repetition of one of the syllables, thereby forming AAB, ABA, or ABB “rules”. After exposure to multiple repetitions of the 16 3-syllable strings, infants heard two types of test trials, both of which were composed of entirely new CV syllables. One type of test trial conformed to the familiar “rule” and the other did not. Infants showed a novelty preference – they listened longer to the unfamiliar rule. These results led Marcus et al. to propose that there are two different learning mechanisms: (a) statistical learning that is limited to extracting “surface” patterns embedded in the input to which the infant is exposed, and (b) rule learning that goes beyond the exposure materials to generate “abstract” patterns.

Although this proposed dichotomy between statistical learning and rule learning seems compelling, there are reasons to suggest an alternative hypothesis. Gerken (2006) conducted a follow-up experiment to Marcus et al. (1999) in which separate groups of infants were familiarized to slightly different families of 3-syllable strings. As shown in Table 1, both groups of infants heard a subset of the 16 strings used in Marcus et al. However, one group heard 4 strings that each ended in a different syllable, and the other group heard 4 strings that ended in the same syllable. Importantly, the 4 strings presented to both groups had an AAB pattern. But for the group whose 4 strings ended in the same syllable, an alternative to the AAB “rule” is a rule that is more restrictive – the first two syllables are the same, followed by the syllable /di/. For this group of infants, when presented with test strings that conformed to the AAB rule but not the “ends in /di/” rule, they did not generalize (i.e., they showed a novelty response). In contrast, for the group of infants presented with the set of AAB strings that ended in 4 different syllables, they formed a broader generalization that accommodated novel syllables even in the final-syllable position. This latter group performed as the infants in the Marcus et al. study by forming a “abstract” rule (i.e., AAB), whereas the former group exhibited a more restrictive rule even though AAB was a plausible inference from the strings presented during familiarization.

Table 1.

Design of the Gerken (2006) study showing how two subsets of the 3-syllable strings used in the Marcus et al. (1999) study can influence the “rule” extracted from these strings.

Strings from Marcus et al.	AAB strings from Gerken	Ends-in-/di/ strings from Gerken
le le di	le le di	le le di
le le je
le le li
le le we
wi wi di		wi wi di
wi wi je	wi wi je
wi wi li
wi wi we
ji ji di		ji ji di
ji ji je
ji ji li	ji ji li
ji ji we
de de di		de de di
de de je
de de li
de de we	de de we

The Gerken (2006) study provides an important counterpoint to the hypothesis that statistical learning and rule learning are two separate mechanisms. As argued by Aslin and Newport (2012), the degree of generalization is a function of the patterning of the input to which the learner is exposed. Even canonical statistical learning studies that only test exemplars drawn from the specific stimulus materials to which the learner is exposed can be viewed as an inference problem (see Goldwater, Griffiths & Johnson, 2009). For example, the words and part-words used as test items in Saffran et al. (1996) were drawn from the continuous stream of syllables presented during the familiarization phase. Thus, neither of these test items were exact replicas of what had been presented for “learning”. Yet, infants readily showed reliable differences in “recognition” of these test items. Thus, the proper way to conceptualize any learning task is to ask what are the most plausible inferences that the learner could make based on the patterning of the input.

Reeder, Newport & Aslin (2013) provided extensive evidence that adults will either generalize freely or restrict generalization depending on the patterning of the context in which nonsense words are presented across a family of utterances. Their task consisted of listening to several hundred utterances of variable word-lengths and then being tested on (a) a subset of these familiar utterances, (b) a set of novel utterances that conformed to the underlying grammar, and (c) a set of novel utterances that violated the underlying grammar. Crucially, the number of grammatical categories and which nonsense words were assigned to these categories was unknown to the subjects. In each of 8 separate experiments, the patterning of the nonsense words that surrounded a critical target category differed – in some experiments all possible surrounding contexts were presented in the familiarization utterances, in others some of the surrounding contexts were consistently absent, and in yet others only a single context was present. Thus, as in Gerken (2006), the surrounding contexts varied from providing consistent evidence for generalization to inconsistent evidence for generalization, and finally little or no evidence for generalization (i.e., strong evidence for restricting generalization). Moreover, in two follow-up experiments that more closely mimicked the variability in word frequency (Schuler, Reeder, Newport & Aslin, under review) and the presence of sub-categories (Reeder, Newport & Aslin, under review) that add a further level of context, adults readily generalized or restricted generalization depending on these same principles of patterning in the surrounding contexts. Thus, distributional cues are sufficient to induce learning and modulate generalization.

In summary, the dilemma of Problem #3 – how does a naïve learner deal with the possibility that the environment is non-stationary? – appears to be “solved” by a strong a prior bias to assume stationarity (i.e., a uniform structure) unless there is an obvious contextual cue that signals a structural change, or unless there are consistent gaps in the input for a given context. In the absence of strong contextual cues, a naïve learner runs the risk of over-generalization rather than restricting generalization to the separate structures that are actually present but under-specified in the learner’s representations. Of course, it is not clear what is meant by an “obvious” contextual cue. As noted earlier, there are many highly salient cues that do not signal a relevant change in underlying structure, and there are changes in structure that are not signaled by any contextual cue.

Interestingly, this aspect of Problem #3 – contextual ambiguity – appears to be treated in fundamentally different ways in the motor and cognitive domains. In the domain of motor development, the consequences of failing to learn the underlying structure (e.g., how to control posture, balance, and limb movement for locomotion) is catastrophic, generalization from one regime to the next (e.g., crawling to cruising to walking) is restricted, and the change of context is obvious (e.g., eye-height above the floor). In contrast, in the domain of cognitive development, the consequences of failing to learn the underlying structure (i.e., to not “understand” something) is minimal, generalization is ubiquitous, and a change of context is typically not obvious. Moreover, motor development requires extensive practice, and making inductive “leaps” can be quite risky (e.g., a small step down for an experienced crawler is much less dangerous than that same small step down for a naïve walker). In contrast, cognitive development typically does not rely on practice except by making predictions, and making inductive “leaps” is essential to deal with the computational explosion of information (i.e., Problem #2). The foregoing dichotomy between motor and cognitive development is certainly overstated, but it raises the possibility that there is a continuum of differences among domains of development along the three dimensions of: (a) consequences of failure to learn a structure, (b) propensity to generalize, and (c) relevance of contextual cues.

Meta-questions in development

The foregoing sections lead us to consider some of the broader implications of the three major problems facing naïve learners – absence of reinforcement, informational overload, and contextual ambiguity. Presumably, those of us who study development in infants are interested in the mechanisms and process of developmental change. There are three fundamental ways of conceiving of this change: (a) continuous -- without interruption or sudden change, (b) incremental -- adding/building from previous states, and (c) progressive -- improvement without regression.

The classic view of developmental change is a discontinuous process (e.g., stage-like). Although it is undeniable that the rate of change is variable, the underlying mechanism could nevertheless be uniform. It is seductive to conclude that whenever a discontinuity is observed in some aspect of development, that a new mechanism has emerged. Yet we know that discontinuities can result from a continuous process with an underlying non-linearity (e.g., a thermostat triggers binary actions – on vs. off – despite a linear temperature sensitivity). Moreover, learning itself can change the interpretation of the same input (e.g., the sticky mittens paradigm alters how pre-reaching infants interact with objects; cf. Needham, Barrett & Peterman, 2002).

Development is also traditionally viewed as incremental, in the sense of a serial process of learning a hierarchy of nested structures (much like the building-blocks of a house). This view is undoubtedly too simple, as all biological systems acquire specializations (e.g., organs) that are qualitatively different from their underlying components. Moreover, development is better characterized as a parallel process of incremental additions with feedback interactions that alter subsequent additions. McMurray (2007) provides a nice example of this parallel nature of development in the domain of the vocabulary spurt in child language. The notion of “mental organs” or modules simply reflects the fact that highly efficient sub-mechanisms, or domain-specific expertise, frees up cognitive resources to access more or different types of information from the same corpus of input. This in turn allows the mature learner to “dig deeper” and extract more complex aspects of information that were initially inaccessible to the naïve learner. An interesting methodological point that falls out of this perspective is that the habituation paradigm presumes “processing is complete” once the criterion of habituation has been met. But it seems quite likely that revisiting the same stimuli in a subsequent habituation phase would trigger “further processing” of information that was “missed” by the infant in the initial habituation phase.

Finally, development is commonly viewed as progressive, in the sense of consistently adding more knowledge or becoming more sophisticated. However, regressions are common in development (Bever, 1982), presumably because of competition among sub-systems (e.g., the phenomenon of “perceptual narrowing” in speech and face perception: Pascalis, deHaan & Nelson, 2002; Pons, Lewkowicz, Soto-Faraco, & Sebastián-Gallés, 2009). For researchers to understand whether development is progressive or regressive requires confidence that the same measurement tool in a given domain of development is actually assessing the same underlying competence across age, or when a uniform tool is unavailable, that different measurement tools suited for different age ranges are assessing the same underlying competence. These are not trivial interpretive issues. Moreover, the emergence of some other developmental system (e.g., locomotion) may not only serve to restrict generalization because of an obvious change of context, but also fundamentally change the objects/events to which infants attend (c.f., Bertenthal, Campos & Kermoian, 1994).

In summary, the question of whether development is continuous, incremental, and progressive – particularly in the domain of statistical learning – requires more than just noticing (based on distributional statistics) that two events are different (e.g., words and part-words). It is also necessary to know the implications (for a given task) of those events. It is seductive to assume that, by showing a looking-time preference at an early age, the developmental domain under investigation is “mature” because those preferences are consistent with the mature state. But looking times are not necessarily equivalent to having attained a rich and robust understanding of a corpus of input (i.e., having developed a mature representation of the underlying structures). It is quite possible that non-verbal measures of “capacity X” in infancy are analogous to developmental seeds that will grow into mature knowledge systems, but it also quite possible that these early capacities are replaced by a fundamentally different system that did not require these precursors (see Keen, 2005 for thoughtful discussions on this point).

Concluding remarks

At the end of a presidential address to nearly 1,000 attendees at our biennial conference, it is instructive to return to some historical perspectives on development, both personal and professional. In 1949, the year of my birth, Donald Hebb published his now classic book entitled “The Organization of Behavior”. As a first year graduate student, I purchased a paperback copy for $3.95. There are many kernels of wisdom in this book, but my favorite is the following:

“It is of course a truism that learning is often influenced by earlier learning. Innumerable experiments have shown such a ‘transfer of training’. Learning A may be speeded up, hindered, or qualitatively changed by having learned B before…. If the learning we know and can study, in the mature animal, is heavily loaded with transfer effects, what are the properties of the original learning from which those effects came? How can it be possible even to consider making a theory of learning in general from the data of maturity only? There must be a serious risk that what seems to be learning is really half transfer.” (pp. 109–110)

The present article is my attempt to update Hebb’s insights into a slightly more modern, but fundamentally similar, form based on the past 65 years of research since the book was published, recognizing that the field of infancy research was virtually non-existent in 1949.

I would also like to pay homage to my mentor, Philip Salapatek, by offering the following quote from Kessen, Haith, and Salapatek’s chapter in Carmichael’s Manual of Child Psychology (1970), which was the “bible” in the growing field of infancy research when I entered graduate school:

“Whether one sees the newborn child as neurologically insufficient (Flechsig, 1920), cognitively confused (James, 1890), narcissistic (Freud, 1905), solipsistic (Piaget, 1927), or merely ugly (Hall, 1891), the distance between the new child and the walking, talking, socially discriminating, and perceptive person whom we see hardly 500 days later is awesome.” (p. 287)

I can think of no better term than “awesome” to describe the excitement and vibrancy of our field.