Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Aug 6;5:12137. doi: 10.1038/srep12137

Inherent structure length in metallic glasses: simplicity behind complexity

Yuan Wu 1, Hui Wang 1, Yongqiang Cheng 2, Xiongjun Liu 1, Xidong Hui 1, Taigang Nieh 3, Yandong Wang 1, Zhaoping Lu 1,a
PMCID: PMC4642538  PMID: 26245801

Abstract

One of the central themes in materials science is the structure-property relationship. In conventional crystalline metals, their mechanical behaviour is often dictated by well-defined structural defects such as dislocations, impurities, and twins. However, the structure-property relationship in amorphous alloys is far from being understood, due to great difficulties in characterizing and describing the disordered atomic-level structure. Herein, we report a universal, yet simple, correlation between the macroscopic mechanical properties (i.e., yield strength and shear modulus) and a unique characteristic structural length in metallic glasses (MGs). Our analysis indicates that this characteristic length can incorporate effects of both the inter-atomic distance and valence electron density in MGs, and result in the observed universal correlation. The current findings shed lights on the basic understanding of mechanical properties of MGs from their disordered atomic structures.

Modulus and strength of metallic materials are key properties for their engineering applications1,2, and the knowledge of structural information is prerequisite for understanding the deformation behaviour3,4. In crystalline materials with long-range periodic atomic packing, the relationship between their structure and mechanical properties has been theoretically developed and relatively understood5,6,7,8. However, in glassy materials, especially metallic glasses (MGs), such a structure-property correlation is still missing due to the difficulties in decoding the atomic packing in these disordered solids. Several efforts have been attempted to reveal a scaling behaviour between the glass transition temperature and strength9,10,11,12,13, and the strength has also been found to be proportional to the elastic modulus, corresponding to a nearly-constant yield strain11,12,13. However, a direct correlation between the characteristic length in the “structure” and these mechanical properties of MGs has not yet been established.

For amorphous solids, the total structure factor, S (q), and the resolved pair distribution function (PDF), g(r), are particularly useful in characterizing the non-crystalline structure (q is the wave vector in reciprocal space and r is the nearest neighbour distance between two atoms). From these statistical data, the atomic distribution within a given volume can be well described14,15,16,17,18. In principle, S (q) and g (r) was related by Fourier transformation19, and the first peak position of S (q) plots, usually denoted as q1, specifies the wavelength (λ = 2π/q1) of g (r) at the medium-range length scale or above20,21. Particularly, q1 was found to be a key structural quantity to reflect critical characteristics in atomic network of amorphous matters, such as intermolecular bonding in amorphous ice, interconnected layers of some borates, and the weak chain in chalcogenide glasses22,23,24. It was found that different metallic glasses may have different q1 values and thereby different mechanical properties. For example, Zr-based BMGs generally have a smaller q1 and lower yield strength, as compared with Fe-based BMGs (a typical example is shown in Fig. 1). To find out whether there exists a relationship between q1 and mechanical properties of MGs, most of available data in literature regarding the q1 values and elastic properties of MGs was complied in Table 125–92. By analyzing the structural length and mechanical properties of these MG alloy systems, we discovered a universal relationship between the elastic properties (i.e., the yield strength and moduli) and the wavelength λ (i.e., 2π/q1).

Figure 1.

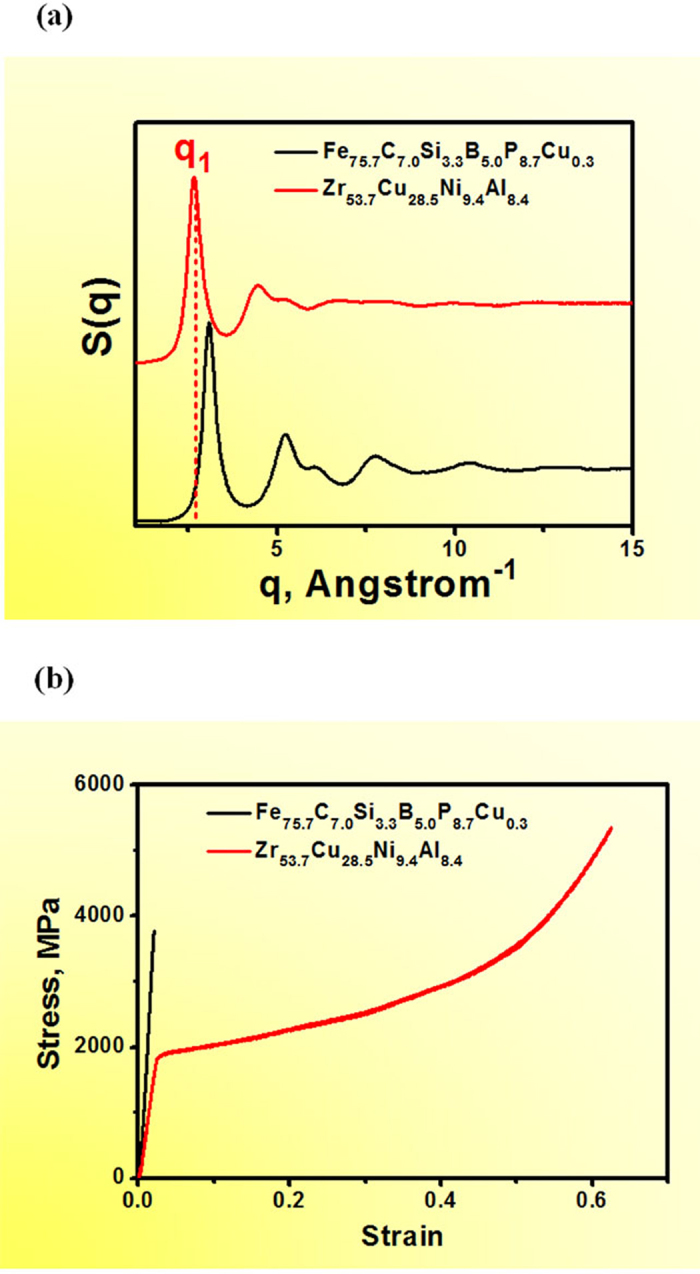
Figure 1

Open in a new tab

S(q) curves (a) and compressive stress-strain curves (b) of two representative Fe- and Zr-based BMGs, showing distinct structural characteristics and deformation behavior.

Table 1.

Alloy q1,Å−1 r1, Å σy,GPa B,GPa G,GPa E,GPa Refs.
Al89La6Ni5 2.541 2.612 1.033       25, 26, 27
Au49Ag5.5Pd2.3Cu26.9Si16.3 2.836 2.816 1.12 132.3 26.5 74.4 28,29
Ca65Mg15Zn20 2.174 3.5 0.364 22.6 10.1 22.4 30,31
Ca60Mg15Cu25 2.239 3.11 0.252       32,33
Cu65Zr35 2.822 2.75 2.019       34,35
Cu64Zr36 2.838   1.944 104.3 34 92 34, 35, 36, 37, 38
Cu61.4Zr38.6 2.801 2.76 1.87       34,35
Cu56Zr44 2.763 2.79 1.82       34,35,39
Cu50Zr50 2.719 2.94 1.772 101.2 31.3 85 34,40, 41, 42
Cu46Zr54 2.674   1.5926 128.5 30 83.5 34,43,44
Cu40Zr60 2.656 2.91 1.333       45,46
Cu33.3Zr66.7 2.564   1.17       46‡
Cu48Zr48Al4 2.71   1.65 113.7 32.4 88.7 47, 48, 49‡
Cu47.5Zr47.5Al5 2.72   1.742 113.7 33 87 47, 48, 49‡
Cu47Zr47Al6 2.72   1.834 113.8 33.8 92.4 47,48,50‡
Cu46Zr46Al8 2.73 2.94 1.926 116.4 34.3 93.7 50,51‡
Cu47Ti33Zr11Ni8Si1 2.875 2.75 2   38.3 100 52,53
Cu47Ti33Zr11Ni8Fe1 2.86   2.008   39 102 53,54
Co43Fe20Ta5.5B31.5 3.186 2.53 5.147 209 102.7 268 55, 56, 57, 58‡
Fe76.0C7.0Si3.3B5.0P8.7 3.025 2.605 3   63.2 165 59‡
Fe75.7C7.0Si3.3B5.0P8.7Cu0.3 3.025 2.615 3.5   70.58 184.2 59‡
[(Fe0.5Co0.5)0.75B0.2Si0.05]96Nb4 3.156   4.21   80.46 210 60,61
Fe40Ni40P14B6 2.922   2.23       62,63
Fe66Nb4B30 3.082   4       64,65
Mg65Cu25Gd10 2.519   0.83 46.3 19.3 50.6 13,66
Mg65Cu25Tb10 2.52   0.76 44.7 19.6 51.3 13,67,68
Mg61Cu28Gd11 2.526   1.075       69,70
Ni60Nb37Sn3 2.944   2.8   58.6 198.6 71
Ni60Nb35Sn5 2.962   2.5 267 54.1 183.2 71
Ni60Sn6(Nb0.8Ta0.2)34 2.93   3.5 189 59.41 161.3 72,73
Ni60Sn6(Nb0.6Ta0.4)34 2.917   3.58 197.6 60.1 163.7 72,73
Ni60Pd20P20 2.99 2.57 2.0       74
Ni60Pd20P17B3 2.99 2.57 2.022 181 38 106 75,76
Pd80Si20 2.727 2.79 1.3 182.6 33.4 94.5 77,78
Pd40Ni40P20 2.886 2.65 1.65 184.9 38.6 108 79
Pd40Cu30Ni10P20 2.9 2.75 1.72 146 34.5 92 80, 81, 82
Ti40Zr25Ni3Cu12Be20 2.72   1.8 109.6 35.5 96.2 13‡
Zr57Ti5Cu20Ni8Al10 2.602 3.11 1.65 99.2 30.1 82 13,83
Zr55Cu35Al10 2.649 2.91 1.74       84
Zr41Ti14Cu12.5Ni10Be22.5 2.84 2.87 1.86 114.7 37.4 101.3 13,85
Zr53.7Cu28.5Ni9.4Al8.4 2.675 2.99 1.85     85 ‡
Zr52.5Ti5Cu17.9Ni14.6Al10 2.658 2.96 1.86 114.1 32.3 88.6 13,45
Zr64.13Cu15.75Ni10.12Al10 2.58   1.721 106.63 28.46 78.41 13,86
Zr62Al8Ni13Cu17 2.585   1.46       87
Zr46Cu37.6Ag8.4Al8 2.76 2.83 1.716 115.5 33.8 92.4 88‡
Zr53.8Cu31.6Ag7Al7.6 2.71   1.518 106 29.9 82 88
Zr48Cu36Al8Ag8 2.66 2.93 1.85   44 115 89‡
La62Al14(Cu5/6Ag1/6)14(Ni1/2Co1/2))10 2.2 3.66 0.65 41 13 35 13,90,91
Y55Al25Co20 2.23   1.203       13,45,92
La55Al25Co20 2.32   0.989 39.34 15.42 40.9 13,45,92
Pr55Al25Co20 2.35   1.007 43.48 17.35 45.9 13,45,92
Nd55Al25Co20 2.33   0.996       13,45,92
Gd55Al25Co20 2.36   0.734       13,45,92
Tb55Al25Co20 2.35   0.834 50.19 22.85 59.53 13,45,92
Dy55Al25Co20 2.42   0.717 52.22 23.52 61.36 13,45,92
Ho55Al25Co20 2.39   0.869 58.81 25.42 66.64 13,45,92
Er55Al25Co20 2.36   1.117 60.7 27.08 70.72 13,45,92
Open in a new tab

Summary of the structural information and mechanical properties of BMGs, including first diffraction peak on the S(q) and G(r) curves, yield strength, and elastic moduli. The experimental procedure can be found in refs 35,59,90.

‡data from the present work.

Figure 2a indicates a strong dependence of the yield strength on the specific length scale λ within the experimental error of measurements, and the fitted scaling relationship is:

Figure 2.

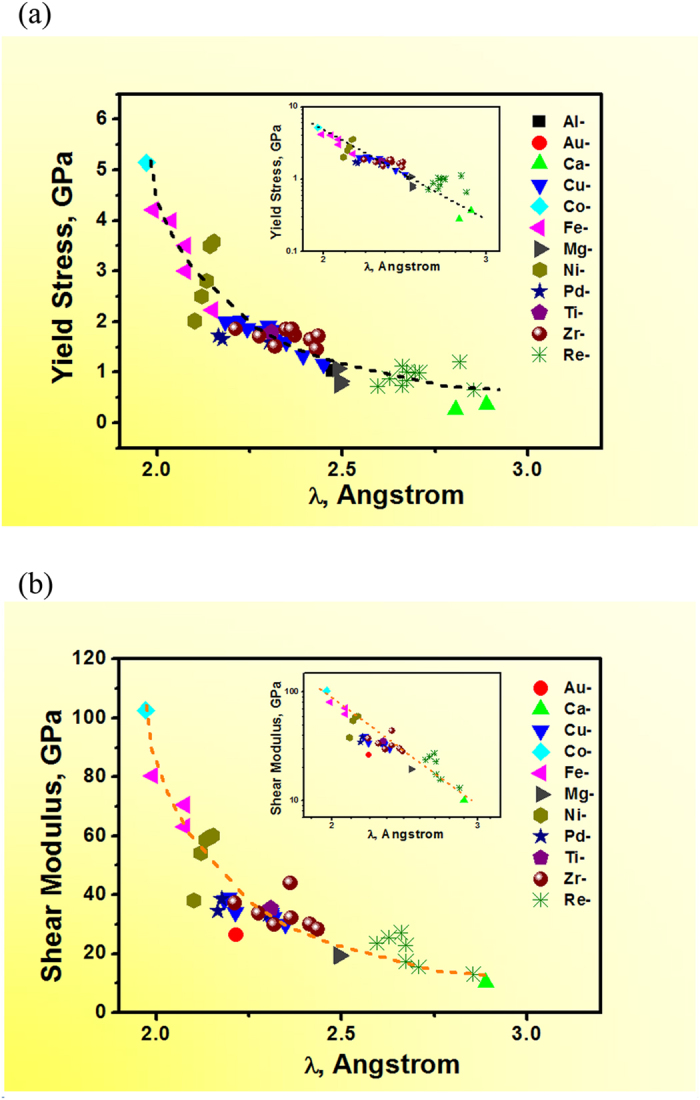
Figure 2

Open in a new tab

Correlation between yield strength (a), shear modulus (b), and the characteristic wavelength, λ for different BMGs;A universal relationship can be observed. The inset shows the corresponding log-log plot.

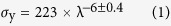graphic file with name srep12137-m1.jpg

Where σy is the yield strength (in unit of GPa) and λ is the wavelength (in unit of Å). Note that the above relationship is generally applicable to different types of MGs, independent of their chemical compositions. With increasing λ, the yield strength of MGs rapidly decreases. For example, Co- and Fe-based MGs containing metalloid constituents have relatively small λ, but high yield strength, whereas Ca- and RE- (rare earth) based MGs exhibit large λ but low yield strength.

Elastic constant, especially the shear modulus, has been shown to be the dominant parameter controlling atomic shear and, consequently, the yielding of metallic glasses10,11,12,13. Using the current data, an intriguing correlation between the shear modulus, G, and the specific length scale λ is also established as shown in Fig. 2b:

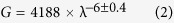graphic file with name srep12137-m2.jpg

where G is the shear modulus (in GPa). Similar to the yield strength, the shear modulus is also strongly dependent upon the specific length scale, i.e., the wavelength λ, with a similar power index. This observation further suggests that yield strength and shear modulus of MGs, in fact, may have the same atomic structural origins11,12,13. Combine Eqs. (1 and 2), we have the shear strain limit of MGs, 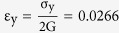Inline graphic, which is in excellent agreement with the value of 0.0267 obtained by Johnson and Samwer11, further validates the above correlations. Noted that systematic errors associated with the experimental measurements of the yield strength and the diffraction patterns collected from different groups might have contributed to the data scattering shown in Fig. 2.

As shown above, the elastic properties (elastic moduli and yield strength) can be directly assessed by the simple parameter λ, in despite of the complex chemistry. In structural materials, the forces that affect elastic stiffness are predominantly electrodynamic, that is, a combination of electrostatics and dynamic exchange forces associated with various quasi-particles, including phonons, photons, electrons, and protons93,94. For metallic materials, the force usually comes from electrostatic interactions resulted from the distribution of electron charge, and the elastic modulus is determined primarily by atomic spacing and valence electron density93,94. It is, therefore, pertinent to establish a correlation between the λ value and the atomic spacing and valence charge in BMGs.

It is necessary to point out that the physical meaning of q1 or λ (2π/q1) has been extensively studied in amorphous matters, for example, inorganic glasses bonded by directionally covalent bonding. In such materials, it was proposed that 2π/q1 could be interpreted as spatial repeat distance of structural unit15. For MGs, which exhibit long-range disordered packing with atoms bonded by nondirectional metallic bonding, the physical significance of q1 has also been discussed in recent years12,14,19. As mentioned before, q1 identifies the wavelength (λ = 2π/q1) of the correlation function g(r) above the first nearest neighbour (i.e., the portion at the high r region of the PDF curves). In terms of atomic packing, this wavelength actually quantifies the distance between the two adjacent atomic neighbors and therefore represents the average inter-atomic distance in MGs14,95.

Based on the spherical-periodic theory, q1 (i.e., 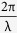Inline graphic) is essentially the Fermi-sphere diameter 2kF for MGs, and λ is the Friedel wavelength96,97,98. The spherical Friedel oscillations in the effective pair potential due to the electronic interaction are similar to those in the structural PDF curves, namely, the electronic wave vector 2kF equals to the structural wave vector q1 (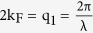Inline graphic)97,98,99. In other words, when the Fermi surfaces of the electrons coincide with the quasi-Brillouin boundaries, a pseudo gap is expected occur in the energy bands for MGs and a corresponding minimal of density of states at the Fermi level, which makes MGs in a relative stable state98,100. Therefore, q1 (or λ) can be treated as an indicator of the electronic interaction in MGs. As a matter of fact, the universal binding-energy relation with interatomic separation has been found in a wide range of crystalline materials101,102, which was believed to be resulted from the scaling between electron density parameter and interatomic distances101,102. However, a universal relation between elastic modulus which is the second derivative of binding energy and interatomic distances was not observed due to crystallographic lattice anisotropy. In MGs, as discussed earlier, q1 (or λ) can represent relative electron density, indicating the proposed universal binding-energy relation also holds well. Due to the atomic isotropic disordering structure of MGs, the universal correlation between the elastic modulus and interatomic distance can also be derived.

It should be noted that there is no distinct relationship between the yield strength and the nearest neighbour distance (r1), as shown in Fig. 3a. The data points are much more scattered, as compared with those in Fig. 2a. For example, even at the same r1 value of ~2.6 angstrom, a large scattering in the yield strength from 1 to 5 GPa was observed. From the atomic packing point of view, r1 represents the first nearest neighbour which can be more easily affected by local atomic environment. Although λ is at the scale of 2-3 angstrom, nevertheless, it actually specifies the wavelength (λ=2π/q1) of g(r) at the large r range (as shown in Fig. 3b)20,21 and reflects the average atomic distance of MGs. Therefore, it can be seen that the average packing characteristic is more determinative to the global elastic properties, rather than the nearest neighbour distance or the localized atomic packing features which may be more contributable to the plastic deformation behavior.

Figure 3. Dependence of the yield strength of MGs on the nearest neighbour distance [r1 on g(r)].

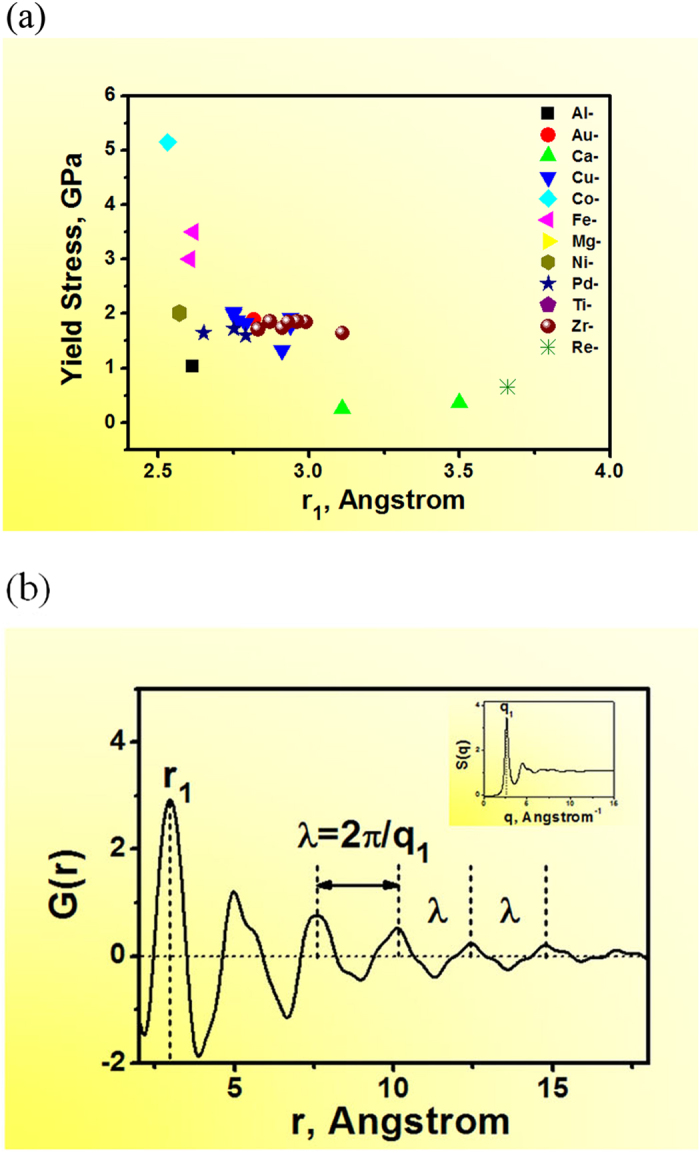
Figure 3

Open in a new tab

(a); no distinct correlation can be observed. Schematic illustration of the meaning of r1 and λ on a typical g(r) curve of Zr-based MG (b), and inset is its corresponding S(q) curve.

It has been long recognized that theoretical strength and modulus of a material depend on their bonding nature, and specifically the bulk modulus is the second derivative of the binding energy with respect to the interatomic distance1,3,4. For instance, molecular crystals are bonded by dipole-dipole forces (similar to that in solid inert gases) and their bulk moduli scale with inter-particle distances raised to the -3 power94. For metallic materials whose atomic bonding is mainly from electrostatic interactions, on the other hand, both valence charge and atomic spacing can contribute to the strength and modulus, and the Keyes parameter K=e2/r4 (e-electron charge, r-atomic distance) is the key scaling parameter94. Limited metallic materials with the same electronic structure show the atomic spacing to be the only decisive parameter for elastic modulus, for example, alkali metals, some ionic crystals, and oxide crystals. In these crystals, the bulk modulus was observed to scale with interatomic spacing raised to the -4 power94. However, when the d-shell electrons become effective in atomic bonding (e.g., in transition metals) or the bonding is more coherent (such as in compounds containing metalloids), the scaling can be complex94. In contrast to these crystals, MGs can be envisioned as materials which are randomly densely-packed with isotropic elastic properties, and the elastic constants can be related to each other through equations: 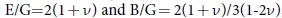Inline graphic, where E, B, 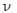Inline graphic are Young’s modulus, bulk modulus, and Poisson’s ratio, respectively. Consequently, elastic constants of any MG can be derived as a function of λ using the universal correlation (Eq. 2) combined with the isotropic relationship. In other words, λ can be treated as an inherent length parameter conveniently incorporating the influence of both the average atomic distance and effective valence electron charge. It is like the “structure fingerprint” providing the information of elastic properties of MGs.

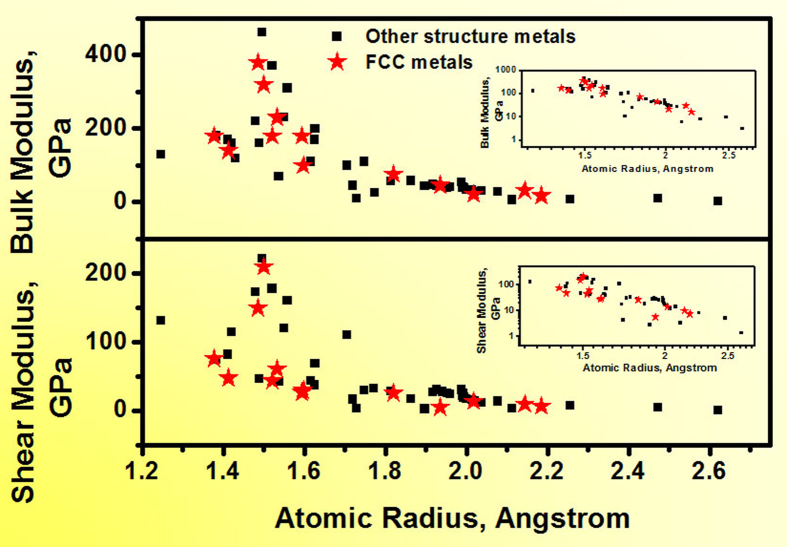
We want to particularly point out that the universal correlation in MGs (Eqs. 1 and 2) is, in fact, even simpler than that in the elemental metals. Figure 4 is the dependence of shear modulus and bulk modulus on the atomic radii for elemental metals [the original data were taken from refs 103,104]. In contrast to Fig. 2, a more scattered scaling relationship is observed even in metals with the same crystalline structure (for example, in FCC- Cu, Ni, Al, Ag, Au, and Pt, indicated by the asterisks). It is noted that the universal scaling relationship in MGs (Eqs. 1 and 2) is based on the fact that λ actually represents the effect of both atomic spacing and valence electron density. In addition, the correlation between the electronic vector 2kF and the structural vector q1, namely, 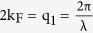Inline graphic must be valid. This latter correlation is, however, not necessarily true in crystalline metals due to their lattice anisotropy at the atomic level. The atomic bonding directionality as well as interatomic distance in various directions leads to the various slip systems for deformation. A non-spherical Brillouin zone subsequently affects the yield strength and elastic modulus for crystalline metals. Metallic glasses, on the other hand, can be taken as metallic materials having isotropic electron cloud. Furthermore, their atomic structures are lack of long-range periodicity and virtually isotropic (i.e., a better spherical symmetry) even down to the atomic level, leading to the universal scaling relationship observed in Fig. 2. It should be noted that λ is obtained from the statistic structural information of MGs, and there are still many uncertainties and challenges in decoding localized/atomic structure of MGs105,106. Prolific motifs about structure-properties relationship still merit in-depth investigation107. For example, atomic density fluctuation and structural heterogeneity frozen in during rapid quenching is expected to result in the fluctuation of inter-atomic distance and valence electron density around the average value108,109,110, also contributes to the error bar of the universal relationship in Eqs. 1 and 2.

Figure 4. Dependence of the shear and bulk modulus on the atomic radius of most elemental metals.

Figure 4

Open in a new tab

The stars represent the crystalline metals with the FCC structure.

In summary, there exists in metallic glasses a unique characteristic length λ (or q1) that exhibits a universal, yet simple, correlation with the mechanical properties such as the modulus and yield strength. The universal relationship appears to be resulted from the fact that metallic glasses are essentially structurally/chemically isotropic as compared to crystalline metals which have certain structural and electronic directionality. Our result demonstrates that, in nature, “more complex” amorphous alloys actually can have a simpler mechanical behavior.

Additional Information

How to cite this article: Wu, Y. et al. Inherent structure length in metallic glasses: simplicity behind complexity. Sci. Rep. 5, 12137; doi: 10.1038/srep12137 (2015).

Acknowledgments

This research was supported in part by National Natural Science Foundation of China (Nos. 51371003, 51422101, 51271212), International Science & Technology Cooperation Program of China, 111 Project (B07003) and Program for Changjiang Scholars and Innovative Research Team in University. Y.W. and X.J.L. acknowledge the financial support from “the Fundamental Research Funds for the Central Universities”. Y.Q.C was supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy. Fruitful discussion with Profs. E. Ma at Johns Hopkins University, U. Ramamurty at Indian Institute of Science and Y.M. Wang at Dalian University of Technology are gratefully acknowledged.

Footnotes

Author Contributions Y.W. and Z.P. Lu designed the experiments and collected the data. All the authors, Y.W., H.W., Y.Q.C., X.J.L., X.D.H., T.G.N., Y.D.W. and Z.P.L. analyzed the data, Y.W., Y.Q.C. and Z.P.L. wrote the paper.

References

  1. Courtney T. H. Mechanical Behavior of Materials (McGraw-Hill, 2000). [Google Scholar]
  2. Ashby M. F. & Greer A. L. Metallic glasses as structural materials. Scripta Mater 54, 321–326 (2006). [Google Scholar]
  3. Cahn R. W. Physical Metallurgy (North-Holland, 1970). [Google Scholar]
  4. Feng D. Metal Physics (Science Press, Beijing, 1999). [Google Scholar]
  5. Friedel J. Dislocations. (Pergamon Press, New York, 1964). [Google Scholar]
  6. Chen M. W. et al. Deformation twinning in nanocrystalline aluminum. Science 300, 1275–1277 (2003). [DOI] [PubMed] [Google Scholar]
  7. Ma E. et al. Strain hardening and large tensile elongation in ultrahigh-strength nano-twinned copper. Appl. Phys. Lett. 85, 4932 (2004). [Google Scholar]
  8. Lu K., Lu L. & Suresh S. Strengthening materials by engineering coherent internal boundaries at the nanoscale. Science 324, 349 (2009). [DOI] [PubMed] [Google Scholar]
  9. Yang B., Liu C. T. & Nieh T. G. Unified equation for the strength of bulk metallic glasses. Appl. Phys. Lett. 88, 221911 (2006). [Google Scholar]
  10. Guan P. F., Chen M. W. & Egami T. Stress-Temperature Scaling for Steady-State Flow in Metallic glasses. Phys. Rev. Lett. 104, 205701 (2010). [DOI] [PubMed] [Google Scholar]
  11. Johnson W. L. & Samwer K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys. Rev. Lett. 95, 195501 (2005). [DOI] [PubMed] [Google Scholar]
  12. Cheng Y. Q., Sheng H. W. & Ma E. Relationship between structure, dynamics, and mechanical properties in metallic glass-forming alloys. Phys. Rev. B 78, 014207 (2008). [Google Scholar]
  13. Wang W. H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 57, 487–656 (2012). [Google Scholar]
  14. Ma D., Stoica A. D. & Wang X. L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nat. Mater. 8, 30–34 (2009). [DOI] [PubMed] [Google Scholar]
  15. Elliott S. R. Medium-range Structural Order in Covalent Amorphous Solids. Nature 345, 445–452 (1991). [Google Scholar]
  16. Gottlicher J. & Pentinghaus H. J. Compositional influence on shape and position of the first sharp diffraction peak (FSDP) in silicate and germinate glasses. Ber. Bunsenges. Phys. Chem. 100, 1563–1568 (1996). [Google Scholar]
  17. Rouxel T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 90, 3019–3039 (2007). [Google Scholar]
  18. Haussler P. Interrelations between atomic and electronic structures-Liquid and amorphous metals as model systems. Phys. Rep. 222, 65–143 (1992). [Google Scholar]
  19. Egami T.& Billinge S. J. L. Underneath the bragg peaks—structural analysis of complex materials. (Pergamon) (2003). [Google Scholar]
  20. Du J. C. & Corrales L. R. Compositional dependence of the first sharp diffraction peaks in alkali silicate glasses: A molecular dynamics study. J. Non-Cryst. Sol. 352, 3255–3269 (2006). [Google Scholar]
  21. Massalski T. B. & Mizutani U. Electronic structure of Hume-rothery phases. Prog. Mater. Sci. 22, 151–262 (1978). [Google Scholar]
  22. Hessinger J., White B. E. & Pohl R. O. Elastic properties of amorphous and crystalline ice films. Planet. Space Sci. 44, 937–944 (1996). [Google Scholar]
  23. Varshneya A. K. Fundamentals of inorganic glasses. (Academic Press Inc., Boston, 1994). [Google Scholar]
  24. Bridge B., Patel N. D. & Waters D. N. On the elastic constants and structure of the pure inorganic oxide glasses. Phys. Stat. Sol. (a) 77, 655–668 (1983). [Google Scholar]
  25. Sheng H. W. et al. Atomic packing in multicomponent aluminum-based metallic glasses. Acta Mater. 56, 6264–6272 (2008). [Google Scholar]
  26. Li G. Q. et al. Local structure variations in Al89La6Ni5 metallic glass. Acta Mater. 57, 804–811 (2009). [Google Scholar]
  27. Guo M. L. et al. Thermal Stability and Mechanical Properties of Spray-Formed and Melt-Spun Al89La6Ni5 Metallic glass Matrix Composites, Materials Transactions JIM 48, 1717–1721 (2007). [Google Scholar]
  28. Wang X. D. et al. Atomic-level structural modifications induced by severe plastic shear deformation in bulk metallic glasses Scripta Mater. 64, 81–84 (2011). [Google Scholar]
  29. Wang L., Lu Z. P. & Nieh T. G. Onset of yielding and shear band nucleation in an Au-based bulk metallic glass. Scripta Mater. 65, 759–762 (2011). [Google Scholar]
  30. Senkov O. N. & Scott J. M. Glass forming ability and thermal stability of ternal Ca-Mg-Zn bulk metallic glasses. J. Non-crystalline Solids 351, 3087–3094 (2005). [Google Scholar]
  31. Wang G. Y., Liaw P. K., Senkov O. N. & Miracle D. B. The duality of fracture behavior in a Ca-based bulk metallic glass. Metallurgical and materials transactions A 42, 1499–1503 (2011). [Google Scholar]
  32. Barney E. R. et al. A neutron and X-ray diffraction study of Ca-Mg-Cu metallic glasses. Intermetallics 19, 860–870 (2011). [Google Scholar]
  33. Senkov O. N., Scott J. M. & Miracle D. B. Composition range and glass forming ability of ternary Ca-Mg-Cu bulk metallic glasses. J. Alloys Compnds. 424, 394–399 (2006). [Google Scholar]
  34. Calvayrac Y. et al. On the stability and structure of Cu-Zr based glasses. Phi. Mag. B 48, 323–332 (1983). [Google Scholar]
  35. Liu X. J. et al. Metallic liquids and glasses: atomic order and global packing. Phys. Rev. Lett. 105, 155501 (2010). [DOI] [PubMed] [Google Scholar]
  36. Kwon O. J. et al. Thermal and mechanical behaviors of Cu-Zr amorphous alloys. Mater. Sci. Eng. A 449, 169–171 (2007). [Google Scholar]
  37. Mattern N. et al. Short-range order of Cu-Zr metallic glasses. J. Alloys Compnds. 485, 163–169 (2009). [Google Scholar]
  38. Ott R. T. et al. Strain dependence of peak widths of reciprocal- and real-space distribution functions of metallic glasses from in situ x-ray scattering and molecular dynamics simulations. Phys. Rev. B 80, 064101 (2009). [Google Scholar]
  39. Park K. W. et al. Atomic packing density and tis influence on the properties of Cu-Zr amorphous alloys. Scripta Mater. 57, 805–808 (2007). [Google Scholar]
  40. Eckert J. et al. High strength ductile Cu-base metallic glass. Intermetallics 14, 876–881 (2006). [Google Scholar]
  41. Baser T. A., Das J., Eckert J. & Baricco M. Glass formation and mechanical properties of (Cu50Zr50)100-xAlx(x=0,4,5,7) bulk metallic glasses. J. Alloys and Compnds. 483, 146–149 (2009). [Google Scholar]
  42. Mattern N. et al. Structural evolution of Cu-Zr metallic glasses under tension. Acta Mater. 57, 4133–4139 (2009). [Google Scholar]
  43. Kwon O. J. et al. Thermal and mechanical behaviors of Cu-Zr amorphous alloys. Mater. Sci. Eng. A 449, 169–171 (2007). [Google Scholar]
  44. Xu D. H., Duan G. & Johnson W. L. Unusual glass-forming ability of bulk amorphous alloys based on ordinary metal copper. Phys. Rev. Lett. 92, 245504 (2004). [DOI] [PubMed] [Google Scholar]
  45. Ma D., Stoica A. D. & Wang X. L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nat. Mater. 8, 30–34 (2009). [DOI] [PubMed] [Google Scholar]
  46. Lu B. F., Li J. F. L., Kong T. & Zhou Y. H. Correlation between mechanical behavior and glass forming ability of Zr-Cu metallic glasses. Intermetallics 19, 1032–1035 (2011). [Google Scholar]
  47. Eckert J. et al. High strength ductile Cu-base metallic glass. Intermetallics 14, 876–881 (2006). [Google Scholar]
  48. Das J. et al. “Work-hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 94, 205501 (2005). [DOI] [PubMed] [Google Scholar]
  49. Baser T. A., Das J., Eckert J. & Baricco M. Glass formation and mechanical properties of (Cu50Zr50)100-xAlx(x=0,4,5,7) bulk metallic glasses. J. Alloys and Compnds. 483, 146–149 (2009). [Google Scholar]
  50. Yu P., Bai H. Y., Tang M. B. & Wang W. H. Excellent glass-forming ability in simple Cu50Zr50-based alloys. J. Non-Crystalline Solids 351, 1328–1332 (2005). [Google Scholar]
  51. Wang X. D. et al. Atomic structure and glass forming ability of Cu46Zr46Al8 bulk metallic glass. J. Appl. Phys. 104, 093519 (2008). [Google Scholar]
  52. Bednarcik J. et al. Microstructural changes induced by thermal treatment in Cu47Ti33Zr11Ni8Si1 metallic glass. Mater. Sci. Eng. A 498, 335–340 (2008). [Google Scholar]
  53. Calin M. et al. Glass formation and crystallization of Cu47Ti33Zr11Ni8×1(X=Fe, Si, Sn, Pb) alloys. Mater. Sci. Eng. A 392, 169–178 (2005). [Google Scholar]
  54. Calin M., Eckert J. & Schultz L. Improved mechanical behavior of Cu-Ti-based bulk metallic glass by in situ formation of nanoscale precipitates. Scripta Mater. 48, 653–658 (2003). [Google Scholar]
  55. Kaban I. et al. Topological and chemical ordering in Co43Fe20Ta5.5B31.5 metallic glass. Phys. Rev. B 79, 212201 (2009). [Google Scholar]
  56. Inoue A. et al. Cobalt-based bulk glassy alloy with ultrahigh strength and soft magnetic properties. Nature Mater. 2, 661–663 (2003). [DOI] [PubMed] [Google Scholar]
  57. Hostert C. et al. Ab initio molecular dynamics model for density, elastic properties and short range order of Co-Fe-Ta-B metallic glass thin films. J. Phys.: Condens. Matter 23, 475401 (2011). [DOI] [PubMed] [Google Scholar]
  58. Wang W. H. Correlations between elastic moduli and properties in bulk metallic glasses. J. Appl. Phys. 99, 093506 (2006). [Google Scholar]
  59. Li H. X. et al. Correlation of nano-clustering and glass formation in alloys with a high solvent content. Scientific Report 3, 1983 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Stoica M. et al. Thermal stability and magnetic properties of FeCoBSiNb bulk metallic glasses. J. alloys Compnds. 504, S123–S128 (2010). [Google Scholar]
  61. Shen B. L., Inoue A. & Chang C. T. Superehigh strength and good soft-magnetic properties of (Fe,Co)-B-Si-Nb bulk glassy alloys with high glass-forming ability. Appl. Phys. Lett. 85, 4911 (2004). [Google Scholar]
  62. Petkov V. Energy-dispersive X-ray diffraction analysis of the structure of disordered materials. J. Non-Crystalline Solids 192, 65–68 (1995). [Google Scholar]
  63. Yao K. F. & Zhang C. Q. Fe-based bulk metallic glass with high plasticity. Appl. Phys. Lett. 90, 061901 (2007). [Google Scholar]
  64. Stoica M. et al. Crystallization kinetics and magnetic properties of Fe66Nb4B30 bulk metallic glass. J. Alloys Compnds. 483, 632–637 (2009). [Google Scholar]
  65. Stoica M., Hajlaoui K., Lemoulec A. & Yavari A. R. New ternary Fe-based bulk metallic glass with high boron content. Phil. Mag. Lett. 86, 267–275 (2006). [Google Scholar]
  66. Park E. S. et al. Correlation between plasticity and fragility in Mg-based bulk metallic glasses with modulated heterogeneity. J. Appl. Phys. 104, 023520 (2008). [Google Scholar]
  67. Zhang Q. R. et al. Effect of substitution of Ni for Cu on glass-forming ability and mechanical properties of Mg-Cu-Tb metallic glass alloys. The Chinese Journal of Nonferrous Metals 17, 303–307 (2007). [Google Scholar]
  68. Xi X. K., Zhao D. Q., Pan M. X. & Wang W. H. Highly processable Mg65Cu25Tb10 bulk metallic glass. J. Non-Crystalline Solids 344, 189–192 (2004). [Google Scholar]
  69. Wang X. D. et al. Atomic packing in Mg61Cu28Gd11 bulk metallic glass. Appl. Phys. Lett. 98, 031901 (2011). [Google Scholar]
  70. Zheng Q. et al. Critical size and strength of the best bulk metallic glass former in the Mg-Cu-Gd ternary system. Scripta Mater. 56, 161–164 (2007). [Google Scholar]
  71. Yim H. C. et al. Structure and mechanical properties of bulk glass-forming Ni-Nb-Sn alloys. Scripta Mater. 54, 187–190 (2006). [Google Scholar]
  72. Schuh C. A. & Nieh T. G. A survey of instrumented indentation studies on metallic glasses. J. Mater. Res. 19, 46–57 (2004). [Google Scholar]
  73. Yim H. C., Tokarz M., Bilello J. C. & Johnson W. L. Structure and properties of Ni60(Nb100-xTax)34Sn6 bulk metallic glass alloys. J. Non-crystalline Solids 352, 747–755 (2006). [Google Scholar]
  74. Zeng Y. Q., Inoue A., Nishiyama N. & Chen M. W. Ni-rich Ni-Pd-P bulk metallic glasses with significantly improved glass-forming ability and mechanical propertis by Si addition. Intermetallics 18, 1790–1793 (2010). [Google Scholar]
  75. Kawashima A. et al. Mechanical properties of a Ni60Pd20P17B3 bulk glassy alloy at cryogenic temperatures. Mater. Sci. Eng. A 498, 475–481 (2008). [Google Scholar]
  76. Matsuura M. et al.Local atomic structure of Ni60Pd20P20 and Ni60Pd20P17B3 bulk metallic glasses and the origin of glass forming ability. J. Alloys Compnds. 496 135–139 (2010). [Google Scholar]
  77. Petkov V. Energy-dispersive X-ray diffraction analysis of the structure of disordered materials. J. Non-Crystalline Solids 192, 65–68 (1995). [Google Scholar]
  78. Yao K. F., Ruan F., Yang Y. Q. & Chen N. Superductile bulk metallic glass. Appl. Phys. Lett. 88, 122106 (2006). [Google Scholar]
  79. Chen N. et al. Influence of minor Si addition on the glass-forming ability and mechanical properties of Pd40Ni40P20 alloy. Acta Mater. 57, 2775–2780 (2009). [Google Scholar]
  80. Mattern N. et al. Structural behavior and glass transition of bulk metallic glasses. J. Non-Crystalline Solids 345, 758–761 (2004). [Google Scholar]
  81. Hirata A., Hirotsu Y., Kuboya S. & Nieh T. G. Local structural fluctuation in Pd-Ni-P bulk metallic glasses examined using nanobeam electron diffraction. J. Alloys Compnds. 483, 64–69 (2009). [Google Scholar]
  82. Haruyama O., Sugiyama K. Sakurai M. & Waseda Y. A local structure change of bulk Pd40Ni40P20 glass during full relaxation. J. Non-Crystalline Solids 353, 3053–3056 (2007). [Google Scholar]
  83. Hufnagel T. C., Ei-Deiry P. & Vinci R. P. Development of shear band structure during deformation of a Zr57Ti5Cu20Ni8Al10 bulk metallic glass. Scripta Mater. 43, 1071–1075 (2000). [Google Scholar]
  84. Fan C. et al. Pair distribution function study and mechanical behavior of as-cast and structurally relaxed Zr-based bulk metallic glasses. Appl. Phys. Lett. 89, 231920 (2006). [Google Scholar]
  85. Hui X. et al. Atomic structure of Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass alloy. Acta Mater. 57, 376–391 (2009). [Google Scholar]
  86. Liu Y. H. et al. Super plastic bulk metallic glasses at room temperature. Science 315, 1385–1388 (2007). [DOI] [PubMed] [Google Scholar]
  87. Wang X. D. et al. Tensile behavior of bulk metallic glasses by in situ x-ray diffraction. Appl. Phys. Lett. 91, 081913 (2007). [Google Scholar]
  88. Wang X. et al. A plastic Zr-Cu-Ag-Al bulk metallic glass. Acta Mater. 59, 1037–104 (2011). [Google Scholar]
  89. Zhang Q. S., Zhang W. & Inoue A. New Cu-Zr-based bulk metallic glasses with large diameters of up to 1.5cm, Scripta Mater. 55, 711–713 (2006). [Google Scholar]
  90. Bednarcik J. et al. Thermal expansion of La-based BMG studied by in situ high-energy X-ray diffraction. J. Alloys Compnds. 504S, S155–S158 (2010). [Google Scholar]
  91. Jiang Q. K. et al. La-based bulk metallic glasses with critical diameter up to 30 mm. Acta Mater. 55, 4409 (2007). [Google Scholar]
  92. Li S. et al. Formation and properties of RE55Al25Co20(RE=Y, Ce, La, Pr, Nd, Gd, Tb, Dy, Ho and Er) bulk metallic glasses. J. Non-Crystalline Solids 354, 1080–1088 (2008). [Google Scholar]
  93. Gilman J. J. Electronic basis of the strength of materials. (Cambridge University Press 2003). [Google Scholar]
  94. Gilman J. J. Micromechanics of Flow in Solids. (McGraw-Hill 1969). [Google Scholar]
  95. Hirata A. et al. Direct observation of local atomic order in a metallic glass. Nature Mater. 10, 28–33 (2011). [DOI] [PubMed] [Google Scholar]
  96. Mizutani U. Electronic structure of metallic glasses. Prog. Mater. Sci. 28, 97–228 (1983). [Google Scholar]
  97. Hafner J. & von Heimendahl L. Microscopic calculations of the stability of metallic glasses. Phys. Rev. Lett. 42, 386–389 (1979). [Google Scholar]
  98. Nagel S. R. & Tauc J. Nearly-free-electron approach to the theory of metallic glass alloys. Phys. Rev. Lett. 35, 380–383 (1975). [Google Scholar]
  99. Han G. et al. The e/a values of ideal metallic glasses in relation to cluster formulae. Acta Mater. 59, 5917–5923 (2000). [Google Scholar]
  100. Yu H. B., Wang W. H. & Bai H. Y. An electronic structure perspective on glass-forming ability in metallic glasses. Appl. Phys. Lett. 96, 081902 (2010). [Google Scholar]
  101. Rose J. H., Ferrante J. & Smith J. R. Universal binding energy curves for metals and bimetallic interfaces. Phys. Rev. Lett. 47, 675 (1981). [Google Scholar]
  102. Banerjea A. & Smith J. R. Origins of the universal binding-energy relation. Phys. Rev. B 37, 6632 (1988). [DOI] [PubMed] [Google Scholar]
  103. King H. W. & Pettifor D. G. in Physical Metallurgy , 3rd ed. Edited by Cahn R. W. & Hassen P. (North-Holland, Amsterdam 1983). [Google Scholar]
  104. Ashcroft N. W. & Mermin N. D. Solid state physics. (Harcourt, inc. 1976). [Google Scholar]
  105. Lee C. Y., Stachurski Z. H. & Welberry T. R. The geometry, topology and structure of amorphous solids. Acta Mater. 58, 615–625 (2010). [Google Scholar]
  106. Wu Z. W., Li M. Z., Wang W. H. & Liu K. X. Hidden topological order and its correlation with glass-forming ability in metallic glasses. Nat. Comm. 6, 6035 (2014). [DOI] [PubMed] [Google Scholar]
  107. Cheng Y. Q. & Ma E. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci. 56, 379–473 (2011). [Google Scholar]
  108. Liu Y. H. et al. Characterization of Nanoscale Mechanical Heterogeneity in a Metallic Glass by Dynamic Force Microscopy. Phys. Rev. Lett. 106, 125504 (2011). [DOI] [PubMed] [Google Scholar]
  109. Wisitsorasak A. & Wolynes P. G. On the strength of glasses. PNAS 1009, 16068 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  110. Wagner H. et al. Local elastic properties of a metallic glass. Nat. Mater. 10, 439–442 (2011). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES