Proper Use of Allele-Specific Expression Improves Statistical Power for cis-eQTL Mapping with RNA-Seq Data

Abstract

Studies of expression quantitative trait loci (eQTLs) offer insight into the molecular mechanisms of loci that were found to be associated with complex diseases and the mechanisms can be classified into cis- and trans-acting regulation. At present, high-throughput RNA sequencing (RNA-seq) is rapidly replacing expression microarrays to assess gene expression abundance. Unlike microarrays that only measure the total expression of each gene, RNA-seq also provides information on allele-specific expression (ASE), which can be used to distinguish cis-eQTLs from trans-eQTLs and, more importantly, enhance cis-eQTL mapping. However, assessing the cis-effect of a candidate eQTL on a gene requires knowledge of the haplotypes connecting the candidate eQTL and the gene, which cannot be inferred with certainty. The existing two-stage approach that first phases the candidate eQTL against the gene and then treats the inferred phase as observed in the association analysis tends to attenuate the estimated cis-effect and reduce the power for detecting a cis-eQTL. In this article, we provide a maximum-likelihood framework for cis-eQTL mapping with RNA-seq data. Our approach integrates the inference of haplotypes and the association analysis into a single stage, and is thus unbiased and statistically powerful. We also develop a pipeline for performing a comprehensive scan of all local eQTLs for all genes in the genome by controlling for false discovery rate, and implement the methods in a computationally efficient software program. The advantages of the proposed methods over the existing ones are demonstrated through realistic simulation studies and an application to empirical breast cancer data from The Cancer Genome Atlas project.

1. INTRODUCTION

Expression quantitative trait loci (eQTLs) mapping searches across the genome for variants that regulate expression levels of messenger RNAs. Studies of eQTLs can not only discover the genetic basis underlying the variation in gene expression but also decipher molecular mechanisms of loci that were found to be associated with complex diseases by genome-wide association studies (GWAS) (Cookson et al. 2009). At present, high-throughput RNA sequencing (RNA-seq) is rapidly replacing expression microarrays to assess gene expression abundance. To date, The Cancer Genome Atlas (TCGA) project has collected RNA-seq data on >5,000 samples over 17 cancers. These data hold the potential to characterize the functional roles of GWAS hits (Welter et al. 2014), which can later be translated into clinical benefits such as cancer treatments. However, traditional methods for eQTL mapping were developed for microarray expression data (Kendziorski and Wang 2006) and may no longer be appropriate for RNA-seq data.

Compared with microarrays that only measure the total expression of each gene, one important feature of RNA-seq is its ability to measure allele-specific expression (ASE). In a diploid individual, each chromosome consists of a paternal copy and a maternal copy, and each gene comprises a paternal allele and a maternal allele. The expression of each allele of a gene is referred to as its ASE, which has been used to distinguish between cis- and trans-eQTLs. By definition, a cis-eQTL is located on the same chromosome as the target gene (e.g., transcriptional factor binding site of the gene) and the DNA variation on the paternal (or maternal) chromosome only influences the transcription process of the paternal (or maternal) gene allele. By contrast, a trans-eQTL can be located anywhere in the genome and influences the transcription of the target gene by modifying the abundance or activity of a protein that regulates the gene; this regulation does not discriminate between the two alleles. Therefore, a cis-regulation typically leads to differential ASE between the two alleles of an individual whereas a trans-regulation generally results in the same amount of expression change. Such a pattern of ASE can be used to distinguish cis-eQTLs from trans-eQTLs. More importantly, the difference in ASE offers another layer of information on top of the total gene expression to enhance cis-eQTL mapping.

With RNA-seq data, the ASE can be measured by sequence reads that are unambiguously mapped to each of the two gene alleles. For an individual, the usable reads must overlap with at least one exonic single nucleotide polymorphism (SNP) at which the individual carries a heterozygous genotype. In Figure 1(a), we illustrate the quantification of ASE for a hypothetical gene with two exons and two exonic SNPs. In individual (i), four and two reads harbor alleles A and T, respectively, at the first exonic SNP, and four and two reads harbor alleles A and G, respectively, at the second exonic SNP. Thus, the ASE is estimated to be eight and four for gene alleles containing the haplotypes A-A and T-G, respectively. In individual (ii), only the eight reads overlapping with the first SNP can be counted into the ASE measure. In individual (iii), no read can be counted into ASE.

Figure 1.

A hypothetical example of cis-eQTL mapping, adapted from Sun (2012). (a) RNA-seq measurements of a hypothetic gene with two exons for three diploid individuals. Because individuals (i) and (ii) have at least one exonic SNPs showing a heterozygous genotype, they have non-zero ASE measurements. In addition, only individual (i) has a heterozygous genotype at the candidate eQTL, so association analysis using ASE is only possible within individual (i). (b) The ASE measurements for individual (i). (c) The TReC for the three individuals.

Using the ASE, cis-eQTL mapping assesses whether one allele of a (biallelic) SNP is associated with a higher or lower ASE than the other allele. We use Figure 1(a-b) to illustrate this process. In individual (i), after the haplotypes are inferred as C-A-A and T-T-G and the ASE is quantified as above, alleles C and T of the candidate cis-eQTL are linked with the ASE measurements of eight and four, respectively (Figure 1[a]). Because allele C is associated with a higher ASE than allele T, this SNP is likely a cis-eQTL (Figure 1[b]). Note that only individuals heterozygous at the candidate eQTL provide information for cis-eQTL mapping. The ASE measured as above is only comparable within individuals, with one ASE measurement serving as the control for the other, but not comparable across individuals.

Evidently, the phase information is essential to link the ASE with the alleles of the candidate cis-eQTL. Many algorithms (Stephens et al. 2001; Browning and Browning 2009; Li et al. 2010; Delaneau et al. 2012) have been developed to infer the haplotype phase from the genotypes of unrelated individuals. It is often reasonable to assume that the inferred phase is accurate within the gene body, because genes are relatively short (Flicek et al. 2011), and RNA-seq reads that span over two or more SNPs provide direct information on the phase. However, the phasing accuracy tends to deteriorate when the haplotypes extend to the candidate eQTL, which is often located in an inter-genic region and can be a few hundred kilobases (kb) away from the gene. Incorrectly linking the SNP alleles with the ASE will greatly compromise the power of cis-eQTL mapping.

Besides the ASE, the total gene expression, which is measured by the total read count (TReC) (i.e., the total number of reads mapped to the gene), also provides information for cis-eQTL mapping. As shown in Figure 1(c), the individual with genotype CC has the highest TReC followed by the individual with CT and then TT, and such a pattern is consistent with the aforementioned observation that allele C is associated with a higher ASE than allele T. Note that the quantification of TReC is not confined to reads that overlap with SNPs showing heterozygous genotypes. Thus, the TReC is generally much greater than the sum of the two ASE measurements and can be compared across individuals.

Traditional methods for eQTL mapping, which were originally developed for microarray expression data, have been applied to the RNA-seq TReC data after normalization (Pickrell et al. 2010). These methods do not exploit the ASE information, ignore the digital nature of the read count data, and cannot distinguish between cis- and trans-eQTLs. To incorporate both the ASE and TReC data available from RNA-seq for cis-eQTL mapping, Sun (2012) proposed a two-stage approach that first phases the candidate eQTL against the target gene and then treats the inferred phase as observed in assessing the cis-effect. This approach, pertaining to single imputation in the missing data literature, has two limitations. First, the phasing process disregards the gene expression, which is potentially informative about the missing phase, especially for a true cis-eQTL. Second, the downstream association analysis ignores the uncertainties in the inferred phase. Consequently, the two-stage approach tends to attenuate the estimated cis-effect and reduce the power for detecting a cis-eQTL. A further challenge, which has not been addressed in previous work, remains to develop computationally efficient methods to evaluate the significance of eQTL findings when multiple, correlated SNPs are tested for each gene.

In this article, we propose a maximum-likelihood approach for cis-eQTL mapping that incorporates both the ASE and TReC data. Unlike Sun (2012), our approach integrates the phasing of the candidate eQTL and the association analysis into a single stage. Thus, our maximum-likelihood estimators (MLEs) for cis-effects are unbiased and statistically efficient in the sense that the corresponding test of association is the most powerful among all valid tests based on the same data and same assumptions. Within the maximum-likelihood framework, we develop a five-step pipeline (Figure 2) for performing the comprehensive analysis of all local eQTLs for all genes in the genome. Here, we restrict the candidate eQTLs to the local SNPs because cis-eQTLs are mostly local and the gene body contains little information about the phase of a SNP if the SNP is too distant. The five steps of our pipeline are (1) testing every candidate eQTL for association with the expression of a gene (referred to as a gene-SNP pair) and focusing on the SNP with the minimum p-value (referred to as the minimum-p SNP) for each gene, (2) assessing the significance of each minimum-p SNP, (3) detecting eQTLs among genome-wide minimum-p SNPs by controlling for false discovery rate (FDR), (4) distinguishing between cis- and trans-acting regulations at detected eQTLs, and (5) estimating the effect sizes at detected eQTLs. We implement the proposed methods, including an ultra-fast permutation process for step (2), in a computationally efficient program. We show in realistic simulation studies that the proposed approach is more powerful than the two-stage approach and the use of the TReC data alone. We further demonstrate the usefulness of the new methodology and software program in an application to the breast cancer data from TCGA.

Figure 2.

A five-step pipeline for performing a genome-wide analysis of cis-eQTLs. TReCASE, TReC and ASE are models that are used in parallel in certain steps.

2. METHODS

2.1 ASE Model

Suppose that each SNP is biallelic with allele values 0 and 1. Thus, each haplotype is a unique sequence of 0s and 1s on one copy of a chromosome. We denote the $\tilde{K}$ possible haplotypes at the $\tilde{M}$ exonic SNPs within a gene by ${\tilde{h}}_1,\dots ,{\tilde{h}}_{\tilde{K}}$, and denote the ordered diplotype consisting of haplotypes ${\tilde{h}}_m$ and ${\tilde{h}}_n$ by $\tilde{H}=({\tilde{h}}_m,{\tilde{h}}_n)$, where m, n = 1, …, $\tilde{K}$. For the reasons mentioned earlier, we assume that $\tilde{H}=({\tilde{h}}_m,{\tilde{h}}_n)$ is known. For a candidate eQTL, let G be the genotype, which is the number of allele 1, and let G₁ be the phase, which is the number of allele 1 on the same chromosomal copy as ${\tilde{h}}_m$. The candidate eQTL can be outside or inside the gene body. We focus on the former case, under which G₁ is unknown for individuals who are heterozygous at the candidate eQTL; the latter case is trivial as G₁ would be known. We use $\tilde{H}$ to infer G₁ by exploiting the linkage disequilibrium (LD) between the exonic SNPs and the candidate eQTL. To this end, we consider the joint distribution of the M = $\tilde{M}$ + 1 SNPs. Let H = (h_k , h_l) be the ordered diplotype at the M SNPs, where k, l = 1, …, K indexing the K possible haplotypes. Write π_k = Pr(h = h_k ) and π = (π₁, …, π_K)^′, where ν^′ denotes the transpose of the vector ν. Under Hardy-Weinberg equilibrium (HWE), the frequency of H = (h_k, h_l) is π_kπ_l, denoted by P_π{H = (h_k, h_l)}. Both H and G₁ are unknown. Once H is inferred as (h_k, h_l), G₁ is simply the value of h_k in the position of the candidate eQTL.

The ASE data are represented by the number of allele-specific reads mapped to ${\tilde{h}}_m$ and the sum of the two allele-specific read counts, denoted by R₁ and R, respectively. Note that R₁ pertains to the same chromosomal copy as G₁. Because R₁ is not comparable across individuals, we model the conditional probability of R₁ = r₁ given R = r by a beta-binomial distribution with a success rate p_k,l and a dispersion parameter ψ,

$$P_{{\beta }_{\text{A}},\psi }(r_1\mid r,(h_k,h_l))=\left(\begin{array}{c}\hfill r\hfill \\ \hfill r_1\hfill \end{array}\right)\frac{{\prod }_{j=0}^{r_1-1}(p_{k,l}+j\psi ){\prod }_{j=0}^{r-r_1-1}(1-p_{k,l}+j\psi )}{{\prod }_{j=1}^{r-1}(1+j\psi )},$$

where

$$p_{k,l}=\{\begin{array}{cc}\text{exp}\left({\beta }_{\text{A}}\right)∕\{1+\text{exp}\left({\beta }_{\text{A}}\right)\}\hfill & ifG=1and{G}_1=1\hfill \\ 1∕\{1+\text{exp}\left({\beta }_{\text{A}}\right)\}\hfill & ifG=1and{G}_1=0\hfill \\ 0.5\hfill & ifG=0or2\hfill \end{array}\phantom{\}}$$ (1)

with β_A characterizing the effect of G₁ on R₁. The beta-binomial distribution is an extension of the binomial distribution Bin(r, p_k,l) to allow for over-dispersion. When there is no allele-specific read, i.e., r = 0, we set P_βA,ψ(r₁|r, (h_k, h_l)) = 1. Note that the covariates (e.g., intercept term, demographical or environmental factors) are ignored, because the comparison is between R₁ and R − R₁ within an individual so that any covariate effect is canceled out.

Because H (or equivalently, G₁) may be missing, the likelihood based on the observed data (R_1i, R_i, G_i, ${\tilde{H}}_i$) (i = 1, …, N) involves a summation:

$$L_{\text{A}}({\beta }_{\text{A}},\psi ,\pi )=\prod _{i=1}^N\sum _{H_i~(G_i,{\tilde{H}}_i)}{P}_{{\beta }_{\text{A}},\psi }(R_{1i}\mid R_i,H_i)P_{\pi }\left(H_i\right),$$ (2)

where H_i ~ (G_i, ${\tilde{H}}_i$) denotes the set of H_is that are compatible with G_i and ${\tilde{H}}_i$. If G_i = 1, such a set consists of two elements, {(1, ${\tilde{h}}_m$), (0, ${\tilde{h}}_n$)} and {(0, ${\tilde{h}}_m$), (1, ${\tilde{h}}_n$)}. If G_i = 0 or 2, then H_i is uniquely determined. As noted earlier, only individuals with G_i = 1 and R_i > 0 provide information about the effect size β_A. However, all individuals with R_i > 0 are used for estimating the over-dispersion parameter ψ, and all, including those with R_i = 0, are used for estimating the haplotype frequencies in π. We refer to (2) as the ASE model. The two-stage approach (Sun 2012) can be viewed as a special case of (2) in that the set H_i ~ (G_i, ${\tilde{H}}_i$) only contains the inferred value and P_π(H_i) factors out.

2.2 TReC and TReCASE Models

Denote the TReC of the gene by T. We adopt the TReC model of Sun (2012) for assessing the effect of genotype G on T. We reformulate his TReC model in this section to conform to the notation in this article. Let X be a set of p covariates including the unit component. The probability of T = t given the genotype G = g and the covariates X = x is formulated through a negative-binomial distribution with mean µ_x,g and a dispersion parameter φ:

$$P_{{\beta }_{\text{T}},\gamma ,\varphi }(t\mid \mathit{x},g)=\frac{\Gamma (t+1∕\varphi )}{t!\Gamma (1∕\varphi )}{\left(\frac{1}{1+\varphi {\mu }_{\mathit{x},g}}\right)}^{1∕\varphi }{\left(\frac{\varphi {\mu }_{\mathit{x},g}}{1+\varphi {\mu }_{\mathit{x},g}}\right)}^t,$$

where Γ(.) is the Gamma function. The negative-binomial distribution is a generalization of the Poisson distribution to allow for over-dispersion. The covariate-adjusted effect of G on T, characterized by β_T, is formulated through the regression model

$$\text{log}\left({\mu }_{\mathit{x},g}\right)={\gamma }^{\prime }\mathit{x}+Ƶ(g,{\beta }_{\text{T}}),$$ (3)

where

$$Ƶ(g,{\beta }_{\text{T}})=\{\begin{array}{cc}0\hfill & ifg=0\hfill \\ \text{log}\{1+\text{exp}\left({\beta }_{\text{T}}\right)\}-\text{log}2\hfill & ifg=1\hfill \\ {\beta }_{\text{T}}\hfill & ifg=2.\hfill \end{array}\phantom{\}}$$ (4)

The form of Ƶ(g, β_T) reflects the additive genetic effect. To see this, we first write log(µ_x,0) = γ^′x and log(µ_x,2) = γ^′x+β_T, from which we obtain β_T = log(µ_x,2/µ_x,0). Then, it follows from the additive effect that log(µ_x,1) = log(µ_x,0 +µ_x,2)−log 2 = log(µ_x,0)+log(1+µ_x,2/µ_x,0)−log 2, which satisfies (3) and (4) after replacing µ_x,2/µ_x,0 by exp(β_T). The additive model is the most commonly used in eQTL studies. Indeed, a cis-effect is additive by definition. Finally, the likelihood based on the data (T_i, X_i, G_i) (i = 1, …, N) takes the form

$$L_{\text{T}}({\beta }_{\text{T}},\gamma ,\varphi )=\prod _{i=1}^N{P}_{{\beta }_{\text{T}},\gamma ,\varphi }(T_i\mid {\mathit{X}}_i,G_i).$$ (5)

When an eQTL cis-regulates the gene expression, we have β_A = β_T. To show this, we introduce υ₁ and υ₀ as the mean ASE corresponding to alleles 1 and 0, respectively, of the candidate eQTL at the baseline of X. For individuals with G = 1 and G₁ = 1, we have p_k,l = υ₁/(υ₁ + υ₀) and then β_A = log{p_k,l/(1 − p_k,l)} = log(υ₁/υ₀); for those with G = 1 and G₁ = 0, we have p_k,l = υ₀/(υ₁ + υ₀) and β_A = log{(1 − p_k,l)/p_k,l} = log(υ₁/υ₀). On the other hand, we have β_T = log(µ_x,2/µ_x,0) = log{2υ₁/(2υ₀)}, where the second equation follows from the additivity assumption. Therefore, we obtain β_A = β_T and denote them by a common effect size β. To combine the ASE and TReC data for inference on β, we employ the joint likelihood

$$L_{\text{TA}}(\beta ,\gamma ,\varphi ,\psi ,\pi )=L_{\text{A}}(\beta ,\psi ,\pi )L_{\text{T}}(\beta ,\gamma ,\varphi ).$$ (6)

We refer to (6) as the TReCASE model. Again, the two-stage approach using the combined data is a special case of (6). A trans-eQTL implies that β_T ≠ 0 and β_A = 0. In that case, the TReCASE model is not appropriate because the ASE data provide no information for the association but simply introduce noise. The TReC model alone should be used for trans-eQTL mapping.

2.3 A Measure of Phasing Accuracy

In theory, the ASE and TReCASE models allow the use of all exonic SNPs in the target gene to predict the phase of a candidate eQTL. In practice, there may be a significant number of exonic SNPs, which would form a large pool of haplotypes and cause some haplotype frequencies too small to be estimated. To balance between the predictive power and the numerical stability, we select a small number of exonic SNPs that provide the best prediction. In this article, we set $\tilde{M}$ to four following much of the literature (de Bakker et al. 2005; Nicolae 2006; Lin et al. 2008). To guide the selection of exonic SNPs, we develop a measure, called Rsq, to quantify the amount of information in a given set of exonic SNPs for predicting the phase; see Appendix A for details. Rsq takes values between 0 and 1, with 0 and 1 indicating that the set of exonic SNPs provide none and complete information, respectively. For a candidate eQTL, we evaluate all sets of $\tilde{M}$ exonic SNPs and select the one with the largest value of Rsq.

2.4 Testing A Gene-SNP Pair

The genome-wide scan of gene-SNP pairs involves tens of thousands of genes and hundreds or thousands of local candidate eQTLs for each gene. Without any prior knowledge about the cis or trans mechanism for each of the massive gene-SNP pairs, we apply the TReC and TReCASE models in parallel. The association testing may be performed by the Wald or likelihood-ratio statistic based on the likelihood functions (5) and (6). However, the calculation of these statistics requires solving for the MLEs of all parameters iteratively for each gene-SNP pair, and hence entails a considerable computational burden. By contrast, the score statistics (derived in Appendix B) are computationally more efficient and numerically more stable, as it only requires solving for the nuisance parameters (i.e., ψ, π, γ, and φ). With the TReC model, in particular, the nuisance parameters only need to be solved once for all tests pertaining to one gene. Thus, we employ the score statistic of each model to produce a p-value for each gene-SNP pair. Both tests have correct type I error even when the additivity assumption for the TReC model or the cis-regulation assumption for the TReCASE model does not hold, because under the null hypothesis there does not exist any association between the SNP and the gene expression (either ASE or total expression). Violation of these assumptions only affects the power. When the effect is cis (hence additive), the test based on the TReCASE model is the most powerful among all valid tests that use the same information. When the effect is trans and additive, the test based on the TReC model is the most powerful. Due to LD, several SNPs can be found to be associated with the expression of a gene by each model. To reduce such redundancy, we focus on the minimum-p SNP. Note that the TReC and TReCASE models may yield different minimum-p SNPs for the same gene.

2.5 Assessing the Significance of the Minimum-p SNP

Due to multiple testing, the score-based p-value at the minimum-p SNP is no longer indicative of the significance level. In addition, such p-values are not comparable across genes, as different genes have different numbers of local SNPs. To evaluate the significance of the minimum-p SNPs, we propose a permutation process that is tailored to the score statistics and features ultra-fast computation. We permute the dataset by fixing (T, X, R₁, R), shuffling G and $\tilde{H}$ as a whole among the individuals, and then randomly switching ${\tilde{h}}_m$ and ${\tilde{h}}_n$ in $\tilde{H}=({\tilde{h}}_m,{\tilde{h}}_n)$ of an individual. Because the nuisance parameters have been estimated without reference to the genetic association in the original dataset, they do not need to be re-estimated in the permuted datasets in which the association is altered. Thus, the analysis of the permuted datasets only involves simple re-evaluation of the cross-products between (T, X, R₁, R) and (G, $\tilde{H}$) in the score statistics. This is fundamentally different from the traditional permutation process employed by Sun (2012), which repeats exactly the same (iterative) analysis for the permuted datasets as for the original one. We generate B permuted datasets (e.g., B = 5, 000) and calculate the permutation p-value by taking the proportion of permuted datasets that generate smaller minimum p-values than the observed one.

2.6 Detecting eQTLs Among Genome-Wide Minimum-p SNPs by FDR Control

We adopt the method of Storey and Tibshirani (Storey and Tibshirani 2003) for estimating FDR. Specifically, for any p-value cutoff p_c, the FDR is estimated by p₀p_cN_total/N_eQTL, where N_total is the total number of minimum-p SNPs, N_eQTL is the number of those with permutation p-values ≤ p_c, and p₀ is the expected proportion of minimum-p SNPs having null effects and is calculated as two times the proportion of minimum-p SNPs with permutation p-values ≥ 0.5. We explore over a fine grid of cutoffs and select the one that generates the desired FDR, e.g., 5% or 10%. Then, the minimum-p SNPs whose permutation p-values lower than the final cutoff are declared as eQTLs. When the procedure is applied to the minimum-p SNPs from the TReC and TReCASE models separately with the same FDR, the combined minimum-p SNPs are also controlled for that FDR level.

2.7 Distinguishing Between cis and trans Mechanisms at eQLTs

After an eQTL is identified, the mechanism can be determined by the following cis-trans test. Let β_A = β and β_T = β + α. The hypotheses are written as

$$H_0(cis-\text{eQTL}):\alpha =0vs.H_1(trans-\text{eQTL}):\alpha \ne 0.$$

We employ a score statistic (derived in Appendix B), which is computationally more efficient and numerically more stable than the likelihood-ratio statistic adopted by Sun (2012).

Up to this point, the TReC and TReCASE models work independently and may identify different eQTLs for the same gene. The cis-trans tests at the two eQTLs may yield the same or different conclusions. If both eQTLs are determined to be cis, we only retain the one identified by TReCASE, in consistent with our focus on only one cis-eQTL for a gene. Likewise, if both eQTLs are established to be trans, we only retain the one identified by TReC. If one eQTL is determined to be cis and another trans, we keep both for future validation, as a gene can be subject to different regulations.

2.8 Estimating Effect Sizes of eQTLs

For a detected eQTL, the effect sizes in the ASE, TReC and TReCASE models can be estimated by maximizing the likelihood functions (2), (5) and (6), respectively. Note that, although the ASE model on its own is not used in the steps described in Sections 2.4-2.7, its effect size offers a unique insight into the ASE data alone. Because of missing phases, the maximization of (2) and (6) can be carried out by the expectation-maximization (EM) algorithms described in Appendix B. The maximization of (5) can be achieved by a standard Newton-Raphson algorithm. By the classical likelihood theory, the MLEs of the effect sizes are consistent, asymptotically normal and asymptotically efficient. Their variances can be estimated by the Louis formula (Louis 1982), as provided in Appendix B.

3. SIMULATION STUDIES

We carried out extensive simulation studies to evaluate the performance of the proposed and two-stage methods in realistic settings. To make a fair comparison between the two approaches, we considered a phasing method for the two-stage approach that uses the same amount of information as the proposed approach. Specifically, the method selects the $\tilde{M}$ exonic SNPs that yield the maximum Rsq for a candidate eQTL, and infers the diplotype H_i for the ith individual by the one that corresponds to the largest $P_{\tilde{\pi }}\left(H_i\right)$ among all H ~ (G, ${\tilde{H}}_i$), where $\tilde{\pi }$ is obtained by maximizing (7) in Appendix A. In Supplementary Method S1, we proved that treating the inferred phase as observed in the ASE model yields a valid test of the hypothesis H₀ : β_A = 0, provided that $\tilde{H}$ is independent of R₁ and R. We refer to the proposed maximum-likelihood approach and the two-stage (imputation) approach as MLE and IMP, respectively. As a benchmark, the approach using the true phase is also included and referred to as TRUE. We set the nominal significance level to be 0.05, which is realistic because the commonly used FDR values of 5% and 10% correspond to the p-value cutoff of 0.023 and 0.062 in our analysis of TCGA breast cancer data.

The first study was focused on the effect size estimation and association testing at a cis-eQTL, when the four exonic SNPs are fixed. We generated genotype data for various sets of five SNPs according to the LD patterns observed in the TCGA breast cancer data (Supplementary Table S1). For each SNP set, we chose one SNP to be the cis-eQTL, leaving the other four to be exonic SNPs. The Rsq values of the exonic SNPs for phasing the cis-eQTL range from 0.56 to 0.93, which represent a wide spectrum of phasing accuracy according to the empirical distribution of Rsq values (Figure 6). Given the cis-eQTL, the expression data were generated from the association models, whose nuisance parameters were set at typical values observed in the TCGA data. Specifically, the TReC T was simulated from a negative-binomial distribution with µ_X,G = 900 × exp{0.1X + Ƶ(G, β_T)} and φ = 0.2, where X was a normal random variable with mean zero and variance one. Then, R was obtained as the integer part of 0.034 × T, where 0.034 was the average proportion of TReC that were allele-specific, and R₁ was simulated from a beta-binomial distribution with p_k,l in (1) and ψ = 0.05. We generated 79 subjects (unless otherwise specified) for each dataset, which was the sample size of the TCGA data we analyzed. We applied the TReCASE model with the MLE, IMP and TRUE methods, and summarized the results in Table 1. As expected, MLE is virtually unbiased in all cases, and the standard error estimates accurately reflect the variability of the effect size estimates. The type I error rates of MLE are slightly greater than the nominal significance level of 0.05 due to the small sample size of 79. They are much closer to 0.05 when the sample size was increased to 500 (Supplementary Table S2). As predicted by our theory, IMP yielded proper type I error under the null hypothesis. In the presence of association, however, the estimates of β produced by IMP are seriously biased towards zero, especially when Rsq is low. Consequently, IMP is uniformly less powerful than MLE; the power difference can be seen more clearly in Figure 3. As Rsq approaches 1, both MLE and IMP are nearly as powerful as TRUE. We also applied the ASE model to the same data, whose results show similar patterns (Supplementary Table S3 and Supplementary Figure S1).

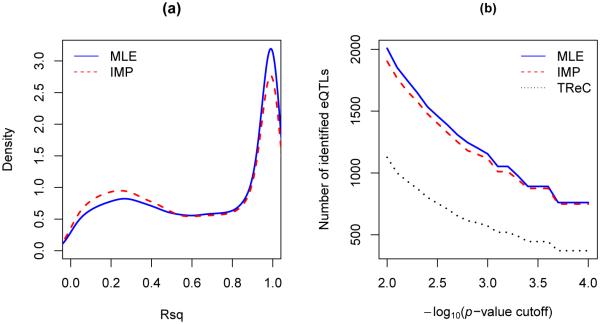
Figure 6.

Results in the analysis of the TCGA data. (a) Distribution of the Rsq values at minimum-p SNPs. (b) Numbers of minimum-p SNPs with permutation p-values passing varying p-value cutoffs at a − log₁₀ scale. MLE and IMP are the maximum-likelihood and two-stage methods, respectively, with the TReASE model. TReC is the TReC model.

Table 1.

Results for the cis-effect of a SNP from the TReCASE model in the first simulation study

				MLE				IMP				TRUE
	Rsq	MAF	β	Bias	SE	SEE	PW	Bias	SE	SEE	PW	Bias	SE	SEE	PW
A1	0.56	0.28	0.0	0.003	0.110	0.106	0.069	0.002	0.089	0.088	0.058	0.001	0.089	0.088	0.054
			0.3	−0.001	0.103	0.101	0.829	−0.095	0.094	0.090	0.618	0.002	0.089	0.088	0.929
A2	0.64	0.39	0.0	0.001	0.092	0.090	0.059	0.001	0.080	0.079	0.053	0.001	0.080	0.079	0.055
			0.3	−0.005	0.088	0.086	0.913	−0.072	0.084	0.080	0.805	0.000	0.080	0.078	0.967
A3	0.78	0.32	0.0	0.000	0.094	0.090	0.062	0.000	0.086	0.084	0.058	−0.001	0.086	0.084	0.059
			0.3	−0.005	0.089	0.086	0.914	−0.038	0.086	0.082	0.880	0.000	0.083	0.081	0.951
A4	0.93	0.21	0.0	0.004	0.100	0.098	0.056	0.004	0.098	0.096	0.054	0.003	0.098	0.096	0.056
			0.3	−0.001	0.100	0.098	0.867	−0.011	0.099	0.097	0.853	0.001	0.098	0.097	0.881

NOTE: MLE, IMP, and TRUE are the maximum-likelihood method, the two-stage method, and the method using the true phase, respectively. A1–A4 denote the four scenarios listed in Supplementary Table S1, with Rsq and MAF indicating the measure of phasing accuracy and the minor allele frequency, respectively, at the candidate eQTL. β is the cis-effect size. Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. PW is the type I error or power for testing zero parameter value at the 0.05 nominal significance level; the tests are based on the Wald statistics. Each entry is based on 10,000 replicates.

Figure 3.

Power of the TReCASE model for testing a cis-eQTL in the first simulation study. The nominal significance level is 0.05. Each power estimate is based on 10,000 replicates.

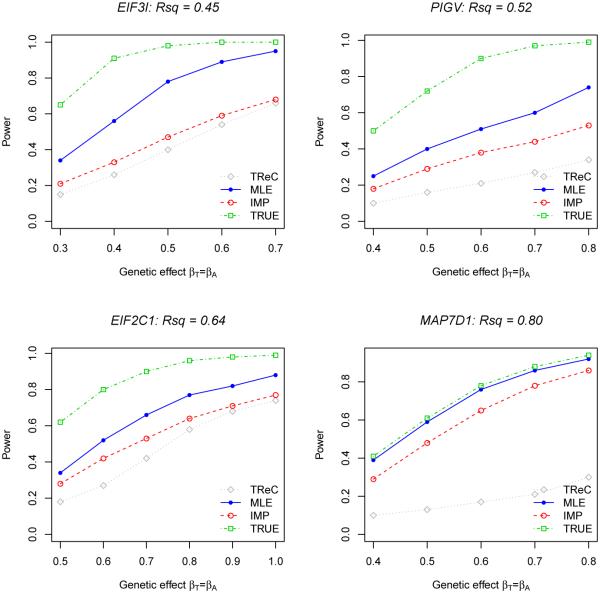
The second simulation study was designed to assess the validity and power of using the minimum-p SNP and the proposed permutation process. Unlike the first study, we generated the genotypes for all the exonic and local SNPs (i.e., within 200 kb of the gene) in various gene regions (Supplementary Table S4) via GWAsimulator (Li and Li 2008), which can mimic the minor allele frequencies (MAF) and LD patterns observed in the TCGA data. We selected a true cis-eQTL for each gene, and simulated the expression data in the same manner as in the first study. To significantly speed up the computation, we pruned out redundant SNPs that were in strong LD with others, so that the remaining SNPs have pairwise Pearson correlation coefficients less than 0.9. Note that the true cis-eQTL may be pruned out as well. We employed the TReC and TReCASE models; for the TReCASE model, we applied the MLE, IMP and TRUE methods. All the SNPs in and flanking a gene were scanned for association with the gene expression, and in the MLE and IMP methods, at most four exonic SNPs were selected for informing the phase of a candidate eQTL. Table 2 summarizes the characteristics of the minimum-p SNPs obtained by various methods. For all genes, the minimum-p SNPs yielded by MLE are in stronger LD with the true cis-eQTLs than those by IMP and by TReC. We used the proposed permutation process to assess the significance of the minimum-p SNPs in all methods. In the absence of any genetic effect, the permutation p-values are distributed uniformly between 0 and 1 (Supplementary Figure S2), confirming the validity of the permutation process even for the small sample size. In the present of cis-effects, MLE is uniformly more powerful than IMP and TReC (Figure 4), and is as powerful as TRUE for gene MAP7D1 whose average value of Rsq at the minimum-p SNPs is as high as 0.80 (Table 2). When Rsq decreases to 0.4 and below, MLE tends to have lower power than TReC (Supplementary Figure S3). This is not surprising because, in such cases, the uncertainties about the phase overweigh the information contained in the ASE data and incorporating the ASE data even hurt the power from using the TReC data alone.

Table 2.

Characteristics of minimum-p SNPs in the second simulation study

	cis-eQTL	TReC		MLE			IMP			TRUE
Gene	MAF	LD	MAP	LD	MAF	Rsq	LD	MAP	Rsq	LD	MAP
EIF3I	0.23	0.72	0.24	0.87	0.25	0.45	0.59	0.27	0.54	0.99	0.23
PIGV	0.15	0.41	0.20	0.61	0.21	0.52	0.44	0.24	0.45	0.88	0.17
EIF2C1	0.10	0.58	0.20	0.64	0.21	0.64	0.53	0.24	0.65	0.83	0.15
MAP7D1	0.11	0.38	0.22	0.71	0.16	0.80	0.65	0.17	0.73	0.78	0.15

NOTE: cis-eQTL is a randomly selected causal SNP for each gene. TReC is the TReC model. MLE, IMP and TRUE are the maximum-likelihood method, the two-stage method, and the method using the true phase, respectively, with the TReCASE model. LD is the average Pearson correlation coefficient between the genotypes of the minimum-p SNP and the cis-eQTL. MAF is the average minor allele frequency. Rsq is the average phasing accuracy. Each entry is based on β_A = β_T = 0.5 and 1,000 replicates.

Figure 4.

Power of the TReCASE model for detecting a cis-eQTL in the second simulation study. Rsq is the average phasing accuracy of the minimum-p SNPs yielded by MLE. The nominal significance level is 0.05. Each power estimate is based on 1,000 replicates.

In the third simulation study, we investigated the MLE and IMP methods in distinguishing between cis- and trans-eQTLs, using the five-SNP settings in the first study. To examine the type I error of the cis-trans test, we considered various cis-effect sizes. As shown in Figure 5, IMP tends to generate inflated type I error (i.e., declaring excessive eQTLs to be trans), especially when Rsq is low and the cis-effect sizes are large. This is because IMP generally yields biased estimates for β_A, thereby creating a difference between β_A and β_T. By contrast, MLE produced reasonable type I error rates in all cases, although a slight inflation can be observed due to the small sample size of 79. We then assessed the power of the cis-trans test by simulating trans-effects, which implies that β_A = 0. As shown in Supplementary Figure S4, IMP has the same power as TRUE, because the phasing does not matter when β_A = 0; note that IMP has accurate control of type I error in this particular case. MLE lost power relative to IMP and TRUE due to its enlarged variance to account for phasing uncertainty, but the power loss is very modest. We also assessed the power of the cis-trans test conditional on β_A ≠ 0, whose alternative hypothesis (β_A ≠ 0 and β_A ≠ β_T), although corresponding to neither cis- nor trans-effect, may exist in reality through other mechanisms. Supplementary Figure S4 displays the power curves when β_A was set to 0.5. Now that the phasing does matter, IMP has a shifted power curve compared to MLE and TRUE; the minimum power is not attained at the null of β_T = β_A = 0.5 but somewhere below 0.5.

Figure 5.

Type I error of the cis-trans test in the third simulation study. The nominal significance level is 0.05. Each estimate of type I error rate is based on 10,000 replicates.

4. APPLICATION TO TCGA DATA

We performed an analysis of local eQTLs (within 200 kb of a gene) for the genome-wide expression in 79 breast cancer (OMIM114480) patients from TCGA, using the RNA-seq data collected from the normal breast tissues only. Although tumor tissues are more relevant to a cancer, studying normal tissues from cancer patients is also important because it provides a baseline for comparison with what happened in tumor tissues. The 79 European females were genotyped at ~1 million SNPs by the Affymetrix 6.0 arrays and imputed against the European population (EUR) in the 1000 Genomes Project (The 1000 Genomes Project Consortium 2012) via MACH (Li et al. 2010), reaching a total of ~36 million SNPs. The TReC and ASE of 19,048 autosomal genes were derived from the RNA-seq data by the R packages asSeq (Sun 2012) and isoform (http://www.bios.unc.edu/~weisun/software/isoform.htm). We note that using the imputation-augmented SNP set greatly increased the number of reads that can be counted into the ASE measurements. Supplementary Method S2 has more details on the processing of the RNA-seq data.

We restricted the candidate eQTLs and the exonic SNPs used for phase prediction to common SNPs with MAF ≥ 5%. By this criterion, the number of candidate eQTLs per gene varied from 7 to 15,536, with a median of 911, and the number of exonic SNPs per gene varied from 1 to 14,314, with a median of 53. As in the second simulation study, we pre-pruned the SNPs, which resulted in median numbers of 373 (ranging from 1 to 6,898) and 21 (ranging from 1 to 6,282) for candidate eQTLs and exonic SNPs, respectively. The TReC model was applied to all the 19,048 genes, including as covariates the log-transformed total read count per sample and three principal components calculated from the standardized TReC data. For numerical stability, we ran the TReCASE model for a candidate eQTL only if at least five samples who are heterozygous at the candidate eQTL had five or more allele-specific reads. Thus, the TReCASE model was applied to 14,414 genes.

First, the genome-wide gene-SNP pairs were scanned and the minimum-p SNPs were obtained. Figure 6(a) displays the Rsq distributions at the minimum-p SNPs by the TReCASE model with the MLE and IMP methods. Compared to MLE, IMP had a tendency to produce minimum-p SNPs with lower Rsq values. Since the ASE data generally stop providing reliable information on the cis-effect when Rsq ≤ 0.4, we filtered out the TReCASE results whose minimum-p SNPs had Rsq ≤ 0.4; such a quality-control (QC) procedure can also relieve the burden of multiple comparisons. As a result, 71.0% and 66.0% of minimum-p SNPs by MLE and IMP, respectively, passing the QC procedure.

Then, permutation p-values for the minimum-p SNPs were calculated. Figure 6(b) shows the numbers of minimum-p SNPs whose permutation p-values pass varying cutoffs. Such a plot can be used to compare the power of different methods for identifying eQTLs. It can be seen that the MLE method was uniformly more powerful than IMP at any cutoff. The relatively small power gain was expected because, for most minimum-p SNPs, the phases were predicted sufficiently well (Figure 6[a]). In particular, 53.3% and 48.0% of minimum-p SNPs by MLE and IMP, respectively, had Rsq ≥ 0.7. Due to the prevalence of eQTLs in the human genome, we do not expect the permutation p-values to follow a uniform distribution; the skewness of the histograms in Supplementary Figure S6 seems reasonable.

Next, we identified a total of 2,486 eQTLs by controlling for an FDR of 5%, and determined their cis or trans mechanisms using the cis-trans test at a nominal significance level of 0.01. Here, we chose a relatively stringent nominal significance level because we wish the test to be less sensitive to the difference between β_A and β_T, which should always exist in real data even for cis-eQTLs. As shown in Table 3, there were 141 genes that were identified with eQTLs by the TReC model but lack of the ASE data; as a result, the TReCASE model did not apply to these genes and the eQTLs were undetermined for the mechanism. There are 23 eQTLs that were identified only by TReC; they are expected to be trans-eQTLs. The reason that 7 of them were determined to be cis is that the cis-trans test may lack power. There are 1,876 eQTLs that were identified only by TReCASE; they are expected to be cis-eQTLs. The reason that 195 of them were determined to be trans is due to the difference between β_T and β_A in the real data. The dominant number of eQTLs that were identified only by TReCASE highlights the importance of exploiting the ASE data for cis-eQTL mapping. Furthermore, there were 410 genes identified with eQTLs by both models. In particular, the two models identified overlapping cis-eQTLs for 179 genes, different cis-eQTLs for 154 genes, and one cis-eQTL and one trans-eQTL for 36 genes. A full list of the 2,486 eQTLs can be found in Supplementary Dataset S1.

Table 3.

Genes identified with eQTLs at an FDR of 5% in the TCGA Data

Test results			Genes
TReC	TReCASE (MLE)	cis-trans	no.
yes	NA	NA	141
yes	no	cis	7
		trans	16
no	yes	cis	1681
		trans	195
yes	yes	cis	179
		trans	29
		cis,cis	154
		cis,trans	36
		trans,trans	12

NOTE: TReC is the TReC model. TReCASE (MLE) is the TReCASE model with the MLE method. Yes and no indicate that the minimum-p SNP is declared as significant and nonsignificant, respectively, by FDR control. NA is not applicable. cis-trans is the cis-trans test. If two different eQTLs within a gene are identified by TReC and TReCASE, their mechanisms are separated by a comma and unordered.

At last, we compared the 2,486 eQTLs with the 134 SNPs found to be associated with breast cancer (referred to as trait-associated SNPs [TASs]) and downloaded from the NHLBI GWAS Catalog (Welter et al. 2014). One eQTL, rs4784227 with alleles C and T, was a TAS. The SNP was reported by Long et al. (2010) to have a highly significant association with breast cancer risk, with an odds ratio of 1.19 per T allele in European Americans. Our analysis identified the SNP to be a cis-eQTL for gene TOX3, with the effect of allele T consistently estimated to be −0.77 by either the ASE, TReC or TReCASE model. Since it has been established that TOX3 functions as a tumor suppressor in breast cancer cells (Cowper-Sal et al. 2012), our eQTL analysis suggested a putative functional role of rs4784227 on breast cancer risk, which has been confirmed in vivo in a breast cancer cell line (Cowper-Sal et al. 2012). Specifically, rs4784227 is located at a binding motif of the transcription factor FOXA1 and allele T of rs4784227 increases the binding affinity of FOXA1, which in turn represses the expression of TOX3. This cis-eQTL would also be identified using the TReCASE model with IMP, but not using the TReC model alone. In total, 6 eQTLs are in the vicinity (i.e., within 10 kb) of breast cancer TASs (Supplementary Tables S5-S6), whereas only 3 are expected by chance, showing evidence of eQTL enrichment among TASs. Like rs4784227, these eQTLs also hold the potential to elucidate the functional roles of the nearby TASs.

5. DISCUSSION

In summary, we developed a powerful and timely tool for cis-eQTL mapping with RNA-seq data. We showed that the proposed approach is more powerful than the existing two-stage approach and the use of total gene expression alone. All the proposed methods are implemented in the R package XXX, which is publicly available at our website. With the empirical data from the TCGA, we demonstrated the ability of our approach to discover cis-eQTLs and to elucidate the functional roles of nearby TASs, and the computational efficiency (e.g., only one day on 50 IBM HS22 machines to analyze the TCGA data) of our software to perform a genome-wide analysis. As functional genomics is rapidly progressing towards unraveling the cis-regulatory control of gene expression and many large-scale RNA-seq studies are underway, our analytical tool may play a key part in the coming years.

Our work significantly improves over the one by Sun (2012). First, we do not phase the candidate eQTL as a priori. Our maximum-likelihood methods phase the candidate eQTL and assess the cis-effect in an iterative fashion, and thus can remove the bias in the estimated effect size and boost the power in detecting a cis-eQTL. Second, we base our methods on score statistics and devise a permutation process that is tailored to the score statistics, thereby reducing the computation time to a mere ~5% of the time required the traditional permutation process. Third, for each SNP-gene pair, Sun (2012) adopted a strategy of first deciding on the cis or trans mechanism by the cis-trans test and then choosing the TReC or TReCASE model based on the test result. This strategy would incur a great computation cost because the computationally intensive cis-trans test has to be applied for every possible SNP-gene pair. In addition, it is unnatural to distinguish between the cis and trans mechanisms before any association is detected.

For the two-stage approach, we have used a small number of exonic SNPs to predict the phase of the candidate eQTL, so that the two-stage approach is compared with our maximum-likelihood approach on equal footing. An alternative is to use a hidden-Markov model (HMM) (Stephens et al. 2001; Browning and Browning 2009; Li et al. 2010; Delaneau et al. 2012), which exploits the LD information over a larger region, and thus may yield more accurate prediction of phase in certain situations. The conclusions regarding the relative merits of the maximum-likelihood approach versus the two-stage approach are expected to hold when an HMM is used.

We have assumed independence between the covariates X and the diplotype H, so that the probability Pr(X|H) factored out from the likelihood (2). This assumption is reasonable if the covariates include demographic variables, such as age and gender, and environmental exposures. If it is believed that X and H are correlated, then we can extend the methodology by adopting a generalized odds-ratio function for Pr(X|H) (Hu et al. 2010). Likelihoods (2) and (6) will then involve the (potentially infinite-dimensional) distribution function of X, which will greatly increase the theoretical and numerical complexity. In addition, assessing the significance of the minimum-p SNP should then rely on the parametric bootstrap, instead of permutation.

We have focused on the minimum-p SNP for each gene. It is possible that other SNPs act independently on the gene expression, but to a lesser extent. To detect such SNPs, we can include the minimum-p SNP as a covariate and search for additional eQTLs conditional on the most significant one. Although it is straightforward to do so with the TReC model, it is less transparent with the ASE model. Not only the regression model (1) should include the minimum-p SNP as a covariate, but also the likelihood (2) should account for the phasing uncertainties of both SNPs.

APPENDIX A: Rsq Measure of Phasing Accuracy

The development of Rsq follows the rational of Li et al. (2010) in developing a measure of accuracy for imputed SNP genotypes. First, for a candidate eQTL and $\tilde{M}$ exonic SNPs, we estimate the corresponding π by maximizing the likelihood that uses the genotype data only:

$$\tilde{L}\left(\pi \right)=\prod _{i=1}^N\sum _{H_i~(G_i,{\tilde{H}}_i)}{P}_{\pi }\left(H_i\right).$$ (7)

Due to the missing H_i, the expectation-maximization (EM) algorithm is the method of choice for the maximization. In the E-step, we evaluate

$${\omega }_{ikl}=\frac{I\left\{(h_k,h_l)~(G_i,{\tilde{H}}_i)\right\}{P}_{\pi }(h_k,h_l)}{{\Sigma }_{(h_{k^{\ast }},h_{l^{\ast }})~(G_i,{\tilde{H}}_i)}{P}_{\pi }(h_{k^{\ast }},h_{l^{\ast }})},$$

and in the M-step, we update π_k by $N^{-1}{\Sigma }_{i=1}^N{\Sigma }_{i=1}^K{\omega }_{ikl}$, where I(.) is the indicator function, i = 1, …, N, and k, l, k^∗, l^∗ = 1, …, K. Denote the maximum likelihood estimator (MLE) of π by $\tilde{\pi }$. Then, for an individual with G = 1 and $\tilde{H}=({\tilde{h}}_m,{\tilde{h}}_n)$, we can estimate G₁ by the expected number of allele 1 on the same chromosome as ${\tilde{h}}_m$, i.e., ${\tilde{G}}_1={\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}∕\{{\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}+{\tilde{\pi }}_{0,m}{\tilde{\pi }}_{1,n}\}$ where the subscript (1, m) represents the haplotype consisting of allele 1 at the candidate eQTL and ${\tilde{h}}_m$ at the exonic SNPs. Although ${\tilde{G}}_1$ is not a form of phasing due to the continuous nature, it is an unbiased estimator of G₁. To quantify the phasing accuracy, a natural measure would be the Pearson correlation coefficient r² between ${\tilde{G}}_1$ and the underlying G₁. Since G₁ is unknown, we estimate r² by the ratio of the sample variance of ${\tilde{G}}_1$ with what would be expected if G₁ was observed (Li et al. 2010), and refer to the estimated r² as the Rsq measure. Specifically, $\text{Rsq}=\text{Var}({\tilde{G}}_1\mid G=1)∕\text{Var}(G_1\mid G=1)$. Write $P_1={\Sigma }_{m,n=1}^{\tilde{K}}{\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}+{\tilde{\pi }}_{0,m}{\tilde{\pi }}_{1,n}$. By simple algebra, we show that $\text{E}({\tilde{G}}_1\mid G=1)={\Sigma }_{m,n=1}^{\tilde{K}}{\tilde{G}}_1{P}_{\tilde{\pi }}({\tilde{h}}_m,{\tilde{h}}_n\mid G=1)=P_1^{-1}{\Sigma }_{m,n=1}^{\tilde{K}}{\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}=0.5$, and $\text{E}({\tilde{G}}_1^2\mid G=1)=P_1^{-1}{\Sigma }_{m,n=1}^{\tilde{K}}{({\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}+{\tilde{\pi }}_{0,m}{\tilde{\pi }}_{1,n})}^{-2}{\left({\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}\right)}^2$. By the symmetry of the two haplotypes, E(G₁|G = 1) = 0.5, E(${\tilde{G}}_1^2$|G = 1) = 0.5, and thus Var(G₁|G = 1) = 0.25. In summary, we develop a measure of phasing accuracy to be

$$\text{Rsq}=-1+4P_1^{-1}\sum _{m,n=1}^{\tilde{K}}{({\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}+{\tilde{\pi }}_{0,m}{\tilde{\pi }}_{1,n})}^{-1}{\left({\tilde{\pi }}_{1,m}{\tilde{\pi }}_{0,n}\right)}^2.$$

We note that the calculation of Rsq, though involving an iterative process to solve for $\tilde{\pi }$, is computationally fast and scalable to the genome-wide scan.

APPENDIX B: Maximum Likelihood Inference

B.1 Inference for ASE model

We obtain the MLEs of β_A, ψ, and π based on the likelihood (2) via the following EM algorithm. The complete-data log-likelihood is

$$l_{\text{A}}({\beta }_{\text{A}},\psi ,\pi )=\sum _{i=1}^N\sum _{k,l=1}^{K}I\{H_i=(h_k,h_l)\}\text{log}\left[P_{{\beta }_{\text{A}},\psi }(R_{1i}\mid R_i,h_k,h_l)P_{\pi }(h_k,h_l)\right].$$

In the E-step, we evaluate E[I{H_i = (h_k, h_l)}|R_1i, R_i, G_i, ${\tilde{H}}_i$], which can be shown to be

$${\omega }_{ikl}=\frac{I\left\{(h_k,h_l)~(G_i,{\tilde{H}}_i)\right\}{P}_{{\beta }_{\text{A}},\psi }(R_{1i}\mid R_i,h_k,h_l)P_{\pi }(h_k,h_l)}{{\Sigma }_{(h_{k^{\ast }},h_{l^{\ast }})~(G_i,{\tilde{H}}_i)}{P}_{{\beta }_{\text{A}},\psi }(R_{1i}\mid R_i,h_{k^{\ast }},h_{l^{\ast }})P_{\pi }(h_{k^{\ast }},h_{l^{\ast }})}.$$ (8)

In the M-step, we maximize l_A(β_A, ψ, π) with I{H_i = (h_k, h_l)} replaced by ω_ikl. Specifically, we update π_k, k = 1, …, K, by

$${\pi }_k^{\text{new}}=N^{-1}\sum _{i=1}^N\sum _{l=1}^K{\omega }_{ikl},$$ (9)

and update β_A and ψ by a one-step Newton-Raphson iteration. Starting with β_A = 0, ψ = 0 and π = $\tilde{\pi }$, where $\tilde{\pi }$ is the MLE based on the likelihood (S1), we iterate between the E-step and M-step until the change in the observed-data log-likelihood is negligible. Denote the MLEs of β_A, ψ, and π by ${\widehat{\beta }}_{\text{A}},\widehat{\psi }$, and $\widehat{\pi }$.

We can estimate the standard errors of ${\widehat{\beta }}_{\text{A}},\widehat{\psi }$, and $\widehat{\pi }$ by the Louis formula (Louis 1982). Write C_k,l,j = p_k,l + jψ, D_k,l,j = 1 − p_k,l + jψ, and I_k,l = I(h_k = h_l), where p_k,l was defined in expression (1). For i = 1, …, N and k, l = 1, …, K, calculate the vector

$${\stackrel{.}{l}}_{ikl}=\left(\begin{array}{c}\hfill \left({\Sigma }_{j=0}^{R_{1i}-1}{C}_{k,l,j}^{-1}-{\Sigma }_{j=0}^{R_i-R_{1i}-1}{D}_{k,l,j}^{-1}\right)\partial p_{k,l}∕\partial {\beta }_{\text{A}}\hfill \\ \hfill {\Sigma }_{j=0}^{R_{1i}-1}j{C}_{k,l,j}^{-1}-{\Sigma }_{j=0}^{R_i-R_{1i}-1}j{D}_{k,l,j}^{-1}-{\Sigma }_{j=0}^{R_{1i}-1}j{(1+j\psi )}^{-1}\hfill \\ \hfill (I_{k,1}+I_{l,1})∕{\pi }_1-(I_{k,K}+I_{l,K})∕{\pi }_K\hfill \\ \hfill ⋮\hfill \\ \hfill (I_{k,K-1}+I_{l,K-1})∕{\pi }_{K-1}-(I_{k,K}+I_{l,K})∕{\pi }_K\hfill \end{array}\right).$$

Calculate the block diagonal matrix $\ddot{\mathit{l}}$_ikl with two blocks. The first block is a 2×2 matrix with two diagonal elements,

$$\left(-\sum _{j=0}^{R_{1i}-1}{C}_{k,l,j}^{-2}-\sum _{j=0}^{R_i-R_{1i}-1}{D}_{k,l,j}^{-2}\right){(\partial p_{k,l}∕\partial {\beta }_{\text{A}})}^2+\left(\sum _{j=0}^{R_{1i}-1}{C}_{k,l,j}^{-1}-\sum _{j=0}^{R_i-R_{1i}-1}{D}_{k,l,j}^{-1}\right)({\partial }^2{p}_{k,l}∕\partial {\beta }_{\text{A}}^2)$$

and

$$-\sum _{j=0}^{R_{1i}-1}{j}^2{C}_{k,l,j}^{-2}-\sum _{j=0}^{R_i-R_{1i}-1}{j}^2{D}_{k,l,j}^{-2}+\sum _{j=1}^{R_i-1}{j}^2{(1+j\psi )}^{-2},$$

and an off-diagonal element

$$\left(-\sum _{j=0}^{R_{1i}-1}{j}^2{C}_{k,l,j}^{-2}+\sum _{j=0}^{R_i-R_{1i}-1}{j}^2{D}_{k,l,j}^{-2}\right)(\partial p_{k,l}∕\partial {\beta }_{\text{A}}).$$

The second block is a (K − 1) × (K − 1) matrix

$$\text{diag}\{-(I_{k,1}+I_{l,1})∕{\pi }_1^2,\cdots ,-(I_{k,K-1}+I_{l,K-1})∕{\pi }_{K-1}^2\}-(I_{k,K}+I_{l,K})∕{\pi }_K^2{\mathit{E}}_{(K-1)\times (K-1)},$$

where E_{(K−1)×(K−1)} is a (K − 1) × (K − 1) matrix with all elements being 1. For subjects with R_i = 0, the elements in $\ddot{\mathit{l}}$_ikl and $\ddot{\mathit{l}}$_ikl associated with the derivative with respect to β_A or ψ are zero. The covariance matrix for ${({\widehat{\beta }}_{\text{A}},\widehat{\psi },{\widehat{\pi }}_1,\dots ,{\widehat{\pi }}_{K-1})}^{\prime }$ is given by ${\Sigma }_{\text{A}}={\mathit{I}}_{\text{A}}^{-1}$, where

$$I_{\text{A}}=-\sum _{ikl}{\omega }_{ikl}{\ddot{l}}_{ikl}-\sum _i\left[\sum _{kl}{\omega }_{ikl}{\stackrel{.}{l}}_{ikl}{\stackrel{.}{l}}_{ikl}^{\prime }-\left\{\sum _{kl}{\omega }_{ikl}{\stackrel{.}{l}}_{ikl}\right\}{\left\{\sum _{kl}{\omega }_{ikl}{\stackrel{.}{l}}_{ikl}\right\}}^{\prime }\right],$$

and ν^′ denotes the transpose of the vector ν. Note that ω_ikl, $\ddot{\mathit{l}}$_ikl and $\ddot{\mathit{l}}$_ikl should be evaluated at the MLEs. The standard errors for ${\widehat{\beta }}_{\text{A}},\widehat{\psi }$, and ${\widehat{\pi }}_1,\dots ,{\widehat{\pi }}_{K-1}$ are the square-roots of the diagonal elements in Σ_A. The standard error for ${\widehat{\pi }}_K=1-{\Sigma }_{k=1}^{K-1}{\widehat{\pi }}_k$ is the square root of (1, …, 1)B(1, …, 1)^′, where B is the last (K − 1) × (K − 1) sub-matrix of Σ_A.

To calculate the score statistic for testing H₀ : β_A = 0, we first produce the restricted MLE of the nuisance parameter $\delta ={(\psi ,{\pi }_1,\dots ,{\pi }_{K-1})}^{\prime }$, denoted by $\tilde{\delta }={(\tilde{\psi },\tilde{\pi },\dots ,{\tilde{\pi }}_{K-1})}^{\prime }$. The $\tilde{\pi },\dots ,{\tilde{\pi }}_{K-1}$ turn out to be the MLEs based on the likelihood (7), and $\tilde{\psi }$ maximizes ${\Sigma }_{i=1}^N\text{log}\left\{P_{{\beta }_{\text{A}}=0,\psi }(R_{1i}\mid R_i)\right\}$. Then, the score and information functions for (β_A, δ^′)^′, which take the forms ${\mathit{U}}_A={\Sigma }_{ikl}{\omega }_{ikl}{\stackrel{.}{l}}_{ikl}$ and I_A, respectively, are evaluated at (0, ${\tilde{\delta }}^{\prime }$)^′. Based on the partition

$${\mathit{U}}_{\text{A}}=\left(\begin{array}{c}\hfill U_{\text{A},\beta }\hfill \\ \hfill {\mathit{U}}_{\text{A},\delta }\hfill \end{array}\right)\text{and}{\mathit{I}}_{\text{A}}=\left(\begin{array}{cc}\hfill I_{\text{A},\beta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\beta \delta }\hfill \\ \hfill {\mathit{I}}_{\text{A},\delta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\delta \delta }\hfill \end{array}\right),$$

where β represents β_A, the score statistic n^−1/2U_A,β is asymptotically zero-mean normal with a variance that can be consistently estimated by n^{−1 {}I_A,ββ − I_A,βδ${\mathit{I}}_{A,\delta \delta }^{-1}$I_A,δβ}.

B.2 Inference for TReC model

The MLEs of β_T, γ, and φ, denoted by ${\widehat{\beta }}_{\text{T}},\widehat{\gamma }$, and $\widehat{\varphi }$, based on the likelihood (5) can be obtained via the Newton-Raphson algorithm with the first and negative second derivative of l_T(β_T, γ, φ) = log{L_T(β_T, γ, φ)}, denoted by U_T and I_T. The covariance matrix for ${({\widehat{\beta }}_{\text{T}},\widehat{\gamma },\widehat{\varphi })}^{\prime }$ is given by ${\mathit{I}}_{\text{T}}^{-1}$, which is evaluated at the MLEs.

To calculate the score statistic for testing H₀ : β_T = 0, we first produce the restricted MLEs of the nuisance parameter ξ = (γ, φ)^′, denoted by $\tilde{\xi }={(\tilde{\gamma },\tilde{\varphi })}^{\prime }$. Then, the score and information functions for (β_T, ξ^′)^′, which take the forms U_T and I_T, respectively, are evaluated at (0, ${\tilde{\xi }}^{\prime }$)^′. Based on the partition

$${\mathit{U}}_{\text{T}}=\left(\begin{array}{c}\hfill U_{\text{T},\beta }\hfill \\ \hfill {\mathit{U}}_{\text{T},\xi }\hfill \end{array}\right)\text{and}{\mathit{I}}_{\text{T}}=\left(\begin{array}{cc}\hfill I_{\text{T},\beta \beta }\hfill & \hfill {\mathit{I}}_{\text{T},\beta \xi }\hfill \\ \hfill {\mathit{I}}_{\text{T},\xi \beta }\hfill & \hfill {\mathit{I}}_{\text{T},\xi \xi }\hfill \end{array}\right),$$

where β represents β_T, the score statistic n^−1/2U_T,β is asymptotically zero-mean normal with a variance that can be consistently estimated by n^{−1 {}I_T,ββ − I_T,βξ${\mathit{I}}_{A,\xi \xi }^{-1}$I_T,ξβ}.

B.3 Inference for TReCASE model

Let β = β_A = β_T. The MLEs of β, δ, and ξ based on the likelihood (6) can be obtained via a similar EM algorithm as for the ASE model. The complete-data log-likelihood is l_TA(β, δ, ξ) = l_A(β, δ) + l_T(β, ξ). In the E-step, we evaluate the ω_ikl in (8). In the M-step, we update π_k, k = 1, …, K, by the ${\pi }_k^{\text{new}}$ in (9) and update β, ψ, and ξ by a one-step Newton-Raphson iteration. Denote the MLEs of β, δ, and ξ by $\widehat{\beta },\widehat{\delta }$, and $\widehat{\xi }$. According to their definitions, $\widehat{\delta }\ne {(\widehat{\psi },{\widehat{\pi }}_1,\dots ,{\widehat{\pi }}_{K-1})}^{\prime }$ and $\widehat{\xi }\ne {(\widehat{\gamma },\widehat{\varphi })}^{\prime }$, as they are MLEs for different models. The covariance matrix for ${(\widehat{\beta },{\widehat{\delta }}^{\prime },{\widehat{\xi }}^{\prime })}^{\prime }$ is given by ${\Sigma }_{\text{TA}}={\mathit{I}}_{\text{TA}}^{-1}$, where

$${\mathit{I}}_{\text{TA}}=\left(\begin{array}{ccc}\hfill I_{\text{A},\beta \beta }+I_{\text{T},\beta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\beta \delta }\hfill & \hfill {\mathit{I}}_{\text{T},\beta \xi }\hfill \\ \hfill {\mathit{I}}_{\text{A},\delta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\delta \delta }\hfill & \hfill 0\hfill \\ \hfill {\mathit{I}}_{\text{T},\xi \beta }\hfill & \hfill 0\hfill & \hfill {\mathit{I}}_{\text{T},\xi \xi }\hfill \end{array}\right).$$

To calculate the score statistic for testing H₀ : β = 0, we first obtain the restricted MLEs for the nuisance parameter τ = (δ^′, ξ^′)^′ to be $\tilde{\tau }={({\tilde{\delta }}^{\prime },\tilde{\xi })}^{\prime }$, where $\tilde{\delta }$ and $\tilde{\xi }$ are restricted MLEs from the ASE and TReC models, respectively. Then, the score and information functions for (β, τ^′)^′, which take the forms U_TA = (U_A,β + U_T,β, U^′_Aδ, U^′_T,ξ)^′ and I_TA, respectively, are evaluated at (0, ${\tilde{\tau }}^{\prime }$)^′. The score statistic and the variance estimator can be constructed in the same fashion as for the ASE model.

B.4 Cis-trans test

Let β_A = β and β_T = β + α. To calculate the score statistic for testing H₀ : α = 0, we first obtain the restricted MLEs for the nuisance parameter τ^∗ = (β, τ^′)^′ to be $\tilde{\tau }\ast ={(\widehat{\beta },\widehat{\delta },{\widehat{\xi }}^{\prime })}^{\prime }$ where $\widehat{\beta },\widehat{\delta }$ and $\widehat{\xi }$ are the MLEs of β, δ, and ξ, respectively, from the TReCASE model. The score and information functions for (α,(τ^∗)^′)^′ take the forms

$${\mathit{U}}_{cis}=\left(\begin{array}{c}\hfill U_{\text{T},\beta }\hfill \\ \hfill U_{\text{A},\beta }+U_{\text{T},\beta }\hfill \\ \hfill U_{\text{A},\delta }\hfill \\ \hfill U_{\text{T},\xi }\hfill \end{array}\right)\text{and}{\mathit{I}}_{cis}=\left(\begin{array}{cccc}\hfill I_{\text{T},\beta ,\beta }\hfill & \hfill I_{\text{T},\beta \beta }\hfill & \hfill 0\hfill & \hfill {\mathit{I}}_{\text{T},\beta \xi }\hfill \\ \hfill I_{\text{T},\beta ,\beta }\hfill & \hfill I_{\text{A},\beta \beta }+I_{\text{T},\beta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\beta \delta }\hfill & \hfill {\mathit{I}}_{\text{T},\beta \xi }\hfill \\ \hfill 0\hfill & \hfill {\mathit{I}}_{\text{A},\delta \beta }\hfill & \hfill {\mathit{I}}_{\text{A},\delta \delta }\hfill & \hfill 0\hfill \\ \hfill {\mathit{I}}_{\text{T},\xi \beta }\hfill & \hfill {\mathit{I}}_{\text{T},\xi \beta }\hfill & \hfill 0\hfill & \hfill {\mathit{I}}_{\text{T},\xi \xi }\hfill \end{array}\right)$$

respectively, which are evaluated at (0, ($\tilde{\tau }$^∗)^′)^′. The score statistic and the variance estimator can be constructed in the same fashion as for the ASE model.