Biological Data Analysis as an Information Theory Problem: Multivariable Dependence Measures and the Shadows Algorithm

Abstract

Information theory is valuable in multiple-variable analysis for being model-free and nonparametric, and for the modest sensitivity to undersampling. We previously introduced a general approach to finding multiple dependencies that provides accurate measures of levels of dependency for subsets of variables in a data set, which is significantly nonzero only if the subset of variables is collectively dependent. This is useful, however, only if we can avoid a combinatorial explosion of calculations for increasing numbers of variables.

 The proposed dependence measure for a subset of variables, τ, differential interaction information, Δ(τ), has the property that for subsets of τ some of the factors of Δ(τ) are significantly nonzero, when the full dependence includes more variables. We use this property to suppress the combinatorial explosion by following the “shadows” of multivariable dependency on smaller subsets. Rather than calculating the marginal entropies of all subsets at each degree level, we need to consider only calculations for subsets of variables with appropriate “shadows.” The number of calculations for n variables at a degree level of d grows therefore, at a much smaller rate than the binomial coefficient (n, d), but depends on the parameters of the “shadows” calculation. This approach, avoiding a combinatorial explosion, enables the use of our multivariable measures on very large data sets. We demonstrate this method on simulated data sets, and characterize the effects of noise and sample numbers. In addition, we analyze a data set of a few thousand mutant yeast strains interacting with a few thousand chemical compounds.

1. Introduction

Biological data, since it is derived from complex systems in which there are many diverse interactions, is characteristically replete with multiple dependencies. Thus, effective analysis of biological data requires the discovery or detection of multivariable dependencies of diverse kinds. We have recently introduced an information theory-based set of dependency measures that has the distinct advantage of separating the detection of the dependence from defining the nature of the dependence (Galas et al., 2014). These measures have the advantage of being model-free and having modest sensitivity to undersampling, but like all multivariable measures, face the prospect of being impractical because of the inherent combinatorial explosion of variable combinations. This difficulty is particularly problematic in biological data sets with a large number of variables.

Calculating marginal entropies of multiple variables in large data sets is a central step in calculating information theory-based measures. These calculations are afflicted with the problem of a combinatorial explosion as the number of variables and the degrees of dependence grows with the dimensionality of the problem. Specifically, for our measures the combinatorial explosion results from the need to calculate marginal entropies for all subsets of variables of the size of the degree of candidate dependences of interest. For a set of data in n variables looking for dependence among d variables, the number of marginal entropies to be calculated, N is given by:

The general measure of dependence among variables that we have defined has the useful property that it is nonzero only if the variables considered are collectively dependent (Galas et al., 2014). This measure for a subset of variables, τ, 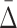(τ), which we call “symmetric delta,” while maximal for the full set of variables that are collectively interdependent, has the property that for variable subsets of τ it can have values that are notably nonzero. We call these lower degree measures “shadows” of Δ. They enable us to follow the trail of shadows for larger and larger sets of variables in a hill climbing-like algorithm to find the maximal dependence set, τ.

In general, information theory measures have several advantages as measures of multiple variable dependence. They are inherently model-free and non-parametric in nature, and they exhibit only modest sensitivity to undersampling (McGill, 1954; Jakulin and Bratko, 2004; Bell, 2003).

Thus, for the discovery of unknown dependencies among large data sets, including many biological data sets, this approach can be a powerful one. This attractive feature can be useful, however, only if we can calculate the necessary quantities in an efficient and reasonable fashion. It has long been recognized that information theory measures, and many others, are impractical if we must calculate measures for all possible subsets of dependent variables as the calculations grow exponentially with the number of variables. This drawback has been decisive in discouraging the general use of information theory measures when there are unknown forms and degrees of dependency in large data sets. Our hill-climbing, shadow-following algorithm is able to overcome this barrier.

This article is structured as follows: We begin with a background section in which the symmetric delta measure is briefly defined and reviewed. A general argument for and description of the delta-shadows algorithm is presented, and a number of data sets are then considered. The simulated data allows us to estimate the quantitative effects of the shadowing and to characterize the effects of noise and sample number on the shadow following. In the next section a large chemi-genomic data set from yeast experiments (Lee et al., 2014) allows us to deal with real biological data in which we discover hidden dependencies.

2. Background

2.1. Measures of dependence—Δ and its properties

The analysis of any complex system would be severely crippled if we restricted ourselves to considering only pairs of variables or functions. Therefore, we need measures for arbitrary numbers of multiple variables considered together. The concept of “interaction information” (McGill, 1954; Jakulin and Bratko, 2004; Sakhanenko and Galas, 2011), proposed long ago, is essentially a multivariable generalization of mutual information (Bell, 2003). For two variables the interaction information is equal to the mutual information and to the Kullback–Leibler divergence of the joint-to-single probability densities of these two variables. Interaction information (essentially the same as coinformation as defined by Bell, 2003) expresses a measure of the information shared by all random variables from a given set (Galas et al., 2010, 2014; Klamt et al., 2009; Sakhanenko and Galas, 2011; Ignac et al., 2012; Ignac et al., 2014). For more than two variables it has properties quite distinct from mutual information, however, including potentially negative values.

We consider interaction information for three-variable dependency, a generalization of mutual information. The three-variable interaction information, I(X₁, X₂, Y), can be thought of as being based on two predictor variables, X₁ and X₂, and a target variable, Y (there is nothing special about the choice of the target variable since I is symmetric under permutation of variables). This symmetry is a powerful property. The three-variable interaction information can be written as the difference between the two-variable interaction information, with and without knowledge of the third variable:

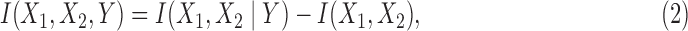where I(X₁, X₂) is the mutual information, and I(X₁, X₂∣Y) is conditional mutual information given Y. When expressed entirely in terms of marginal entropies we have

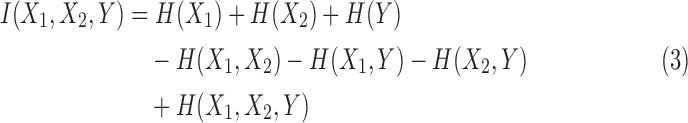H(X_i) is entropy of a random variable X_i, and 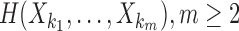, is a joint entropy on a set of m random variables. The symmetry under the variable permutation we mentioned above is apparent from Equation 3.

Consider the interaction information for multiple variables for a set of n variables, 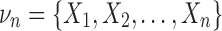. We can write the interaction information in terms of sums of marginal entropies according to the inclusion-exclusion formula, which is the sum of the joint entropies of ν_n. We have,

Given Equation 4, we define the “differential interaction information,” Δ, as the difference between values of successive interaction informations arising from adding variables:

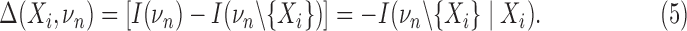The last equality comes from the recursive relation for the interaction information, Equation 2. The differential interaction information is simply that change in interaction information that occurs when we add another variable to the set of n−1 variables. We can then write this differential using the marginal entropies. If {τ_i} are all the subsets of ν_n that contain X_i (note: this is not all subsets) then

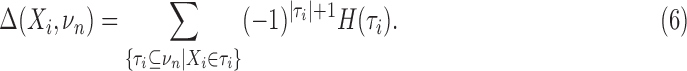Then Δ's for degrees (the number of variables) three and four (denoting the corresponding variables in the subscripts) are

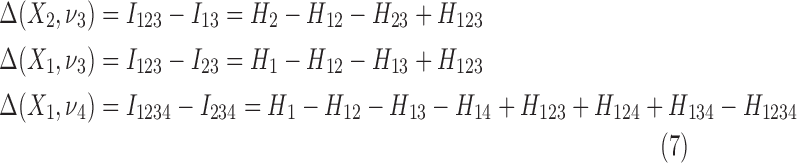The number of terms grows as the power of the number of variables minus one. For the case when the variables are all independent, all elements of Δ(X_i, ν_j) in Equation 5 are zero. These expressions are zero for all numbers of variables, as the joint marginal entropies become additive single entropies and all terms cancel.

The differential interaction information in Equation 5 is based on specifying the target variable, the variable we added to the set of n−1 variables. The differential is the change that results from this addition and is therefore asymmetric in that variable designation (and thus not invariant under permutation.) See Equation 7 for an example of using different target variables. Since our purpose is to detect fully cooperative dependence among the variable set, we want any single measure to be symmetric. A more general measure then can be created by a simple construct that restores symmetry. If we multiply Δ's with all possible choices of the target variable the resulting measure will be symmetric and will provide a general measure that is functional and straightforward. To be specific, we define the symmetric measure as

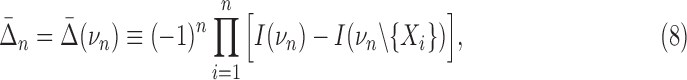where the product is over the choice, i, of a target variable relative to ν_n, n>2, a simple permutation. The difference terms in the bracket in Equation 8 are between the interaction information for the full set ν_n (first term) minus the interaction information for the same set minus a single element. For three variables this expression is (simplifying the notation again)

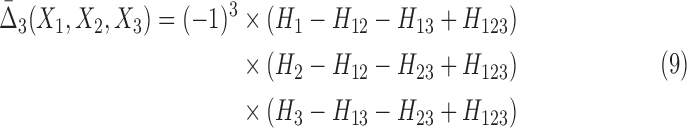This measure has the extremely useful property that it is always small or vanishes unless all variables in the set are interdependent. This can be used to allow us to discover and represent exact variable dependencies as shown in the following section.

3. Measuring Multivariable Dependencies

3.1. Use 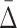to find dependencies of specific size

A measure 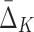of degree K (by degree we mean the cardinality of the variable subset) is designed to capture dependencies of size K and only K (Galas et al., 2014). To illustrate this we compute 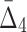on a set of 20 random variables containing one 4-variable dependency.

Example 1: Consider a set of 20 variables, 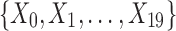and 5000 samples of these variables. The domain of each variable is 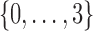. Each variable is uniformly distributed. Moreover, all the variables are i.i.d. except variables X₁₁, X₁₂, X₁₇, X₁₉ that form a 4-dimensional dependency.

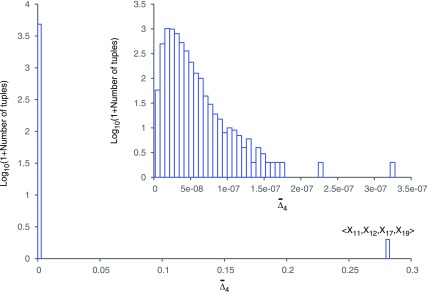
The 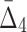easily captures the dependence in Example 1. Figure 1 shows a histogram of all 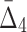values computed on all possible four-variable tuples. This exhaustive analysis shows that 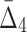is more than five orders of magnitude higher for the tuple 〈X₁₁, X₁₂, X₁₇, X₁₉〉, which is the only functional dependency in the set, than for any other tuple.

FIG. 1.

Histogram of 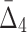values computed on all possible four-variable tuples in Example 1. The rightmost bar corresponds to the only tuple shown in the label with a large 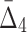value. The inset zooms in on the same histogram.

3.2. 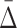 shadows at lower degrees

Given significant values of 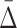at a specific degree (the cardinality of the variable subset), we wish to determine what the 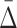values are for the smaller subsets of these variables. These subsets will represent lower degrees of dependence—shadows of the dependence with a higher degree. Consider first the specific case of a three-variable dependence, which is indicated by a significant 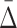for the corresponding three-variable subset τ, and its effect on 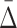of degree two. Can we see a “shadow” of the three-variable dependence in the two-variable regime? We assume that 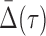is nonzero and ask what we can say about 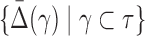, where all γ are the pair subsets.

If we use the very strict definition of collective dependence for three variables defined in table 1 of (Galas et al., 2014), the pairwise mutual information for all pairs γ is zero. Variables X_i, X_j, and X_k form a collective dependence iff

Table 1.

Informative Tuples Selected by the Shadow Algorithm When Applied to Example 1 (See Box 3 and Box 7 with K=3 and K=4)

Pair	MI	Triplet		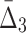Quadruplet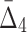
〈X17, X19〉	0.10945	〈X12, X17, X19〉	−0.07303	〈X11, X12, X17, X19〉	0.91699
〈X12, X19〉	0.07967	〈X11, X12, X19〉	−0.05766	〈X1, X11, X17, X19〉	0.283e-6
〈X11, X19〉	0.03758	〈X11, X17, X19〉	−0.03558	〈X4, X11, X17, X19〉	0.257e-6
〈X1, X4〉	0.00357	〈X1, X12, X19〉	−0.397e-5	〈X4, X11, X12, X19〉	0.248e-6
		〈X1, X17, X19〉	−0.362e-5	〈X4, X12, X17, X19〉	0.239e-6
		〈X4, X17, X19〉	−0.319e-5

In red are tuples that are either informative shadows (components of the dependency) or the dependency itself.

This definition directly implies that the respective pairwise entropies are the sums of the single variable entropies, and thus, their values of mutual information are always zero. However, careful consideration of possible dependences, and calculations from simulated data that has one variable entirely dependent on others, shows that the mutual information between pairs of variables is often not zero. Note that the strict definition in Equation 10 applies only to a narrow, and highly restrictive, set of specific functions, as illustrated in the Supplementary Material (available online at www.liebertonline.com/cmb) where we consider in detail the implications of uniformly vanishing shadows. In general, X_i and X_j have some residual dependence, as suggested by the values of pairwise 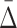's with X_k in this example.

We now come back to our earlier Example 1, where the data set contains only one dependency, which connects four variables. In the section above we showed that by traversing the set of all possible four-variable tuples using 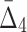, we are able to identify the dependency. Let us now consider the effect of this four-variable dependency on MI and 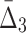, the measures with lower degree. If we use MI and 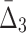to scan the sets of all pairs and triplets correspondingly, we see that they contain considerably less information than 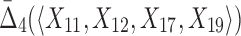(see Fig. 2). 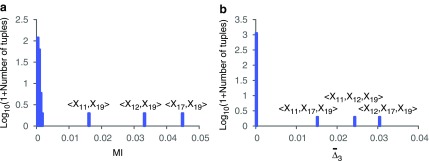This is expected because 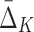is designed to be maximal when there is a K-dimensional dependency. On the other hand, there are pairs (and triplets) that are significantly above the average level of information of all pairs (and triplets). For example, there are three pairs, 〈X₁₁, X₁₉〉, 〈X₁₂, X₁₉〉, and 〈X₁₇, X₁₉〉, that have significantly higher MI than the rest of the pairs (see Fig. 2a). Similarly, there are three triplets, 〈X₁₁, X₁₂, X₁₉〉, 〈X₁₁, X₁₇, X₁₉〉, and 〈X₁₂, X₁₇, X₁₉〉, that have significantly larger 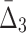than all other triplets (see Fig. 2b).

FIG. 2.

Histogram of (a) MI values and (b) 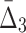values computed on all possible pairs and triplets in Example 1.

The existence of three significant pairs and three significant triplets might suggest that there are several two-way and three-way dependencies. Notice, however, that they consist only of the variables from the set {X₁₁, X₁₂, X₁₇, X₁₉} that form the only functional dependency in the data set of Example 1. Note also that only those pairs and triplets that contain variable X₁₉ are significant. This is consistent with the fact that the four-variable dependency in this simulated data was generated with X₁₉ as a function of three arguments, X₁₁, X₁₂, and X₁₇. These significant pairs and triplets that appear in Figure 2 are called “shadows” to emphasize that they correspond to partial information about the four-variable dependency in the set.

3.3 Using 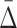shadows to address the problem of combinatorial explosion

As we have shown, 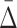is good for measuring a dependency of a specific degree. This measure allows us to estimate a relative strength of a dependency by comparing its 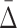value to the distribution of 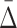values of randomly selected tuples. As a result we conclude that the 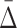measure is suitable for searching for multivariable dependencies in a set of variables. The problem of combinatorial explosion arises, however, when we attempt to search for higher degrees of dependencies. We illustrate the specific problem using Example 1.

In Example 1 we have only 20 variables to consider, as a result we have to traverse only through 190 possible pairs to find pairwise dependencies. To look for higher level dependencies, we have to increase the search space to 1140 triplets (in case of three-variable dependency search), to 4845 quadruplets (in case of four-variable dependency search), and to 15504 tuples (in case of five-variable dependency search). In general, as the degree of the dependencies increases, the search space grows as a binomial coefficient 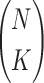, where N is a number of variables and K is the degree of the dependency we are after.

With modern computing power, traversing a high-dimensional search space for a relatively small number of variables (N=10–100) is feasible. However, in real world examples the number of variables is orders of magnitude higher (N=1,000–100,000), making a direct exhaustive traversal of a search space practically infeasible and completely exhaustive of computing resources. For example, when N=20,000, which is typical for gene expression data sets, the two-dimensional search space has about 2×10⁸ pairs, and the three-dimensional search space has about 1.3×10¹² triplets. Then the four-dimensional and five-dimensional search spaces increase to about 6.7×10¹⁵ and 2.7×10¹⁹ tuples, and methods based on exhaustive search will not work: the progression from 10⁴, 10⁸, 10¹², and 10¹⁵ to 10¹⁹ is explosive. We need a more efficient way of searching for high-dimensional dependencies. And for that reason we use “shadows” to address the combinatorial explosion problem.

Recall that by “shadows” we call the tuples with 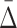values that are significantly above the background level on one hand, and that are combined exclusively from variables of a higher degree dependency on the other hand. Since high-degree dependencies produce some shadows even at the pairwise level (the level of MI), we can avoid the combinatorial explosion when traversing the high-dimensional search space by detecting the low degree shadows first and then using them to limit ourselves to a set of informative variables and thus reduce the search space. In the next section we describe an algorithm employing these shadows.

4. Shadow Algorithm

We want an algorithm for implicating multivariable dependencies of different degrees using 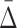. The naïve approach would be to exhaustively search sets of all possible K-tuples for every degree K starting from two, which will fail when the number of random variables is large enough, as in the case of typical biological data sets. We have shown that high-degree dependencies (K=3 and up) are reflected in lower degree dependencies called shadows. For example, a four-variable dependence in Example 1 is seen in the two- and three-dimensional search space as a set of pairwise and ternary shadows. These shadow dependencies are encountered early in the search process, since they have low degree, and can provide hints about high degree dependencies that caused them.

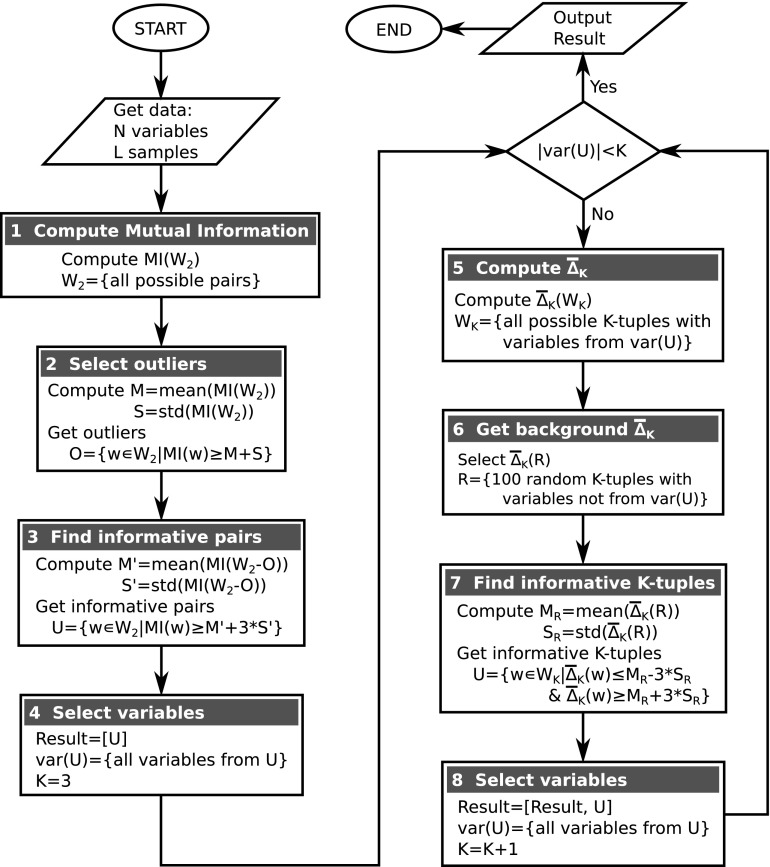
Using this fact we can devise an algorithm for seeking dependencies without the combinatorial explosion. The flow chart in Figure 3 illustrates an algorithm that employs shadows to search for high-degree dependencies. In general terms, the algorithm inductively searches for dependencies of degree K by traversing only through those K-tuples that are constructed from variables involved in shadows of degree (K−1). At the start, the algorithm traverses through all possible pairs and constructs a set of two-variable shadows then limits the variable set based on that information.

FIG. 3.

Flow chart depicting the shadow algorithm.

Given an input data set, which can be viewed as a table with L rows and N columns representing N random variables and L samples, the algorithm starts by searching for all two-variable dependencies and shadows. Although variations are possible here, we compute MI for all possible pairs and then select the significant pairs (this is reasonable even for 20,000 variables). To select the significant pairs, the algorithm first identifies a set of obvious outliers O (Box 2 in Fig. 3) and then evaluates the significance of pairs based on statistics of the set without outliers O (Box 3 in Fig. 3). At this stage the algorithm produces a set U of significant pairs and a set var(U) of variables involved in these pairs by applying a threshold to the shadows to be included.

The algorithm then moves to searching for three-variable dependencies and shadows. This step is similar to the search for pairwise dependencies except that the algorithm restricts the search space and computes 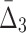only for triplets that are composed from the variables involved in the pairwise shadows [var(U) in Box 4]. To evaluate the significance of 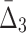for these pairs, the algorithm selects a set R of 100 random triplets whose variables are not from var(U) (Box 6) and computes the statistics of the set 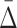(R) (Box 7). At this iteration the algorithm produces a set of significant triplets U and updates the set var(U) to only those variables that are present in U. The algorithm then proceeds to the next iteration by incrementing the size of dependencies under surveillance and repeating the process above.

Note that the termination of the algorithm is certain, since the total number of variables is finite (N) and the degree of dependencies being searched for is incremented at each iteration of the algorithm. The algorithm would definitely stop when the dimension reaches N. Moreover, after each iteration, the set of variables is restricted, forcing the algorithm to stop much sooner.

4.1. Shadows in Example 1 (simulated data, one four-dim dependency)

Let us now demonstrate this approach by applying the shadow algorithm to Example 1. Recall that there is one dependency connecting variables X₁₁, X₁₂, X₁₇, and X₁₉. At the first stage (Boxes 1–4 in Fig. 3) the algorithm computes MI for all 190 pairs. The significance threshold results in four significant pairs (see Table 1), which contain six variables. At the first iteration of the loop (Boxes 5–8, K=3) the algorithm computes 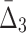for only 20 triplets (and 100 random triplets to determine significance), which is strikingly different from a naïve case, exhaustively computing 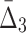for all possible 1,140 triplets. Based on the 100 random triplets, the algorithm detects six significant triplets, and as a result the number of variables stays the same, six. At the second iteration (K=4), the algorithm computes 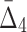for 15 tuples (and 100 random tuples) as opposed to traversing the entire set of 4845 tuples. There are five significant tuples containing the same set of six variables. At the third iteration (K=5), the algorithm computes 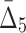for six tuples (and 100 random tuples) as opposed to analyzing the entire set of 15504 tuples. None of these six tuples are significant and the algorithm stops, resulting in the identification of a four-variable dependence.

Note that, although it picked up two noninformative variables (X₁ and X₄) and several tuples associated with them, the algorithm selected all four dependent variables and followed the shadows to the four-variable dependency while keeping the search much smaller than the full set of tuples.

4.2. Shadows in Example 2 (simulated data, two dependencies: four-dim and three-dim)

We now apply the shadow algorithm to a somewhat more complex case, Example 2, with two overlapping dependencies of different degree.

Example 2: Consider a set of 20 variables, 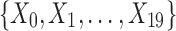, and 5000 samples of these variables. The domain of each variable is {0, 1, 2, 3}. Each variable is uniformly distributed. Moreover, all the variables are i.i.d. except variables X₉, X₁₁, X₁₂, X₁₇, X₁₈, and X₁₉ that form two specified dependencies, 〈X₉, X₁₇, X₁₈〉 and 〈X₁₁, X₁₂, X₁₇, X₁₉〉. In contrast to Example 1, Example 2 has two dependencies that have one variable in common.

The application of the shadow algorithm to Example 2 is not as straightforward as for Example 1. Table 2 shows the informative tuples for each stage of the algorithm up to K=5.

Table 2.

Informative Tuples Selected by the Shadow Algorithm When Applied to Example 2

Tuple	Measure (MI or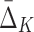)	Tuple	Measure ()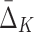
Set U of informative pairs in Box 3		Set U of informative pairs in Box 7, K=4
〈X9, X17〉	0.49258	〈X11, X12, X17, X19〉	0.84814
〈X9, X18〉	0.26382	〈X9, X11, X12, X19〉	0.01012
〈X17, X19〉	0.13630	〈X9, X12, X18, X19〉	0.00566
〈X12, X19〉	0.07933	〈X9, X11, X18, X19〉	0.00277
〈X9, X19〉	0.04204	〈X9, X11, X17, X19〉	0.437e-5
〈X11, X19〉	0.03002	〈X9, X12, X17, X19〉	0.210e-5
Set U of informative triplets in Box 7, K=3		〈X12, X17, X18, X19〉	0.029e-5
〈X9, X17, X18〉	−3.26088	〈X9, X11, X17, X18〉	−0.101e-6
〈X12, X17, X19〉	−0.07257	〈X9, X17, X18, X19〉	−0.00003
〈X11, X12, X19〉	−0.06230	Set U of informative tuples in Box 7, K=5
〈X11, X17, X19〉	−0.04037	〈X9, X11, X12, X18, X19〉	−0.04639
〈X9, X18, X19〉	−0.00309	〈X9, X11, X12, X17, X19〉	−0.00015
〈X9, X11, X19〉	−0.00031	〈X9, X11, X17, X18, X19〉	0.00002
〈X9, X12, X19〉	−0.00017	〈X9, X12, X17, X18, X19〉	0.00005
〈X9, X17, X19〉	−0.00013
〈X9, X11, X17〉	−1.378e-5
〈X9, X11, X18〉	−0.804e-5
〈X9, X12, X18〉	−0.489e-5

In red are tuples that are either informative shadows (components of the dependency) or the dependency itself.

Since two dependencies overlap (have a common variable), this introduces more peripheral tuples into the set U. For example, at the pairwise level, the algorithm adds 〈X₉, X₁₉〉 into the set U, because this pair has high MI. Since variables X₉ and X₁₉ are indirectly connected through variable X₁₇, it is more likely that they are somewhat correlated, which results in higher MI. We observe the same behavior for other iterations of the algorithm.

Note that both three-variable and four-variable dependencies are captured by the algorithm—they correspond to the tuples with largest absolute value of 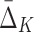. Note also that four-variable tuples from the set U that contain all three variables from the three-variable dependency have negative 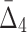values. While all other tuples, including the four-variable dependency, have positive 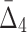values.

4.3. Factors in the detection of dependencies

In this section we examine the effect of various factors on the detection of variable dependency, including number of variables, number of samples, and noise levels.

4.3.1. Number of variables

As the degree grows, the number of different entropies required for computing the differential interaction information measure (Δ) also grows. From Equation 6, the number of entropy terms computed on subsets of M variables required for computation of Δ_K is equal to a binomial coefficient 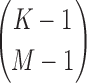, M=1,…,K. The number of entropy terms of the same size (computed on the subsets of variables of the same size) for measures to each degree are simply binomial coefficients (see Supplementary Material, Table S1).

The search space for the dependencies grows quickly with the increase of their degree. Table 3 shows the size of the full exhaustive search for each degree up to six variables for Examples 1 and 2. The size of the search space is given in terms of the number of measures we must compute in order to find the dependencies in the data, as well as in terms of the number of entropies computed during the search. We compared the size of the exhaustive search with the size of the search performed by the shadow algorithm on Examples 1 and 2. In Examples 1 and 2, the shadow algorithm avoids the combinatorial explosion of the search space, as shown in Table 3.

Table 3.

Number of Measures (MI and 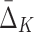) and the Corresponding Number of Entropy Terms Computed During the Exhaustive Full Search as Compared to the Shadow Algorithm, When Applied to Examples 1 and 2

Degree	No. of measures	No. of entropy terms	No. of measures	No. of entropy terms
	Full search (Example 1 and 2)		Shadow algorithm (Example 1 and 2)
2 (MI)	190	570	190	570
3 (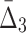)	1,140	13,680	20	240
4 (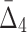)	4,845	155,040	15	360
5 (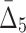)	15,504	1,240,320	6	288
6 (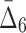)	38,760	3,720,960	0	0

4.3.2. Number of samples

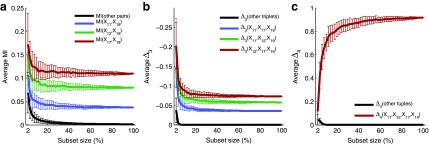
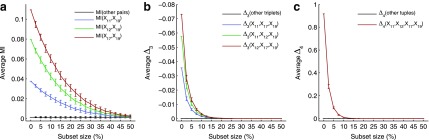
In this section we investigate how the sample size affects the strength of detected dependencies and shadows. In particular we are interested to see how MI and 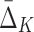are affected by the change in the amount of data. Consider example 1. Figure 2 shows that there are three pairs whose MI is considerably higher than the MI of all other pairs. Figure 4a tracks MI of these three pairs computed on subsets of the original data set of 5000 samples, starting from 100 data points (2%) and gradually increasing it to the full set. Similarly, there are three triplets that have significantly larger 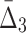than all other triplets, as seen in Figure 2. Figure 4b tracks values of 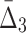for these three triplets across different sample sizes. Finally, there is one four-variable tuple that corresponds to the only dependency in the set (see Fig. 1). Figure 4c shows how the change in the sample size affects the value of 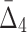for this dependency.

FIG. 4.

Effect of data set size on information measured by (a) mutual information, (b) 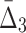, and (c) 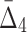. The points of the curves are computed by applying the corresponding measures to a set of selected tuples (see legend). Instead of using the entire set of 5000 samples from Example 1, the measurement is computed on a randomly selected subset. The process of randomly selecting a subset of samples is repeated 100 times for each subset size and the average and standard deviation are plotted. The x-axis shows the subset size for corresponding values of the measures and ranges from 100 to 5,000 with an increment of 100 samples. Additionally, each black curve is an average across all tuples that were not selected (the background), and the error bars are maximal standard deviation across these tuples.

Each point in Figure 4 depicts an average and standard deviation of a measure, MI, 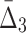, or 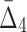, over 100 subsets of a specific size, drawn randomly from the original data set of 5000 samples. For all these measures, standard deviation is high for small subsets and steadily decreases as the size of subsets increases. This is expected since small subsets do not fully sample the underlying functional dependency of Example 1, so the amount of information fluctuates considerably between small subsets of data. On the other hand, the amount of information does not change much between large subsets, since they nearly completely sample the dependency.

For all the measures, MI, 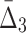, and 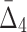, an average value fluctuates at first and then stabilizes as the subset size increases. For MI (Fig. 4a) the average value decreases for small subsets and stabilizes for subsets that are 20% of the original set or larger. Note that, in contrast to MI, values of 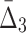are negative. As a result, 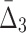behavior is opposite of MI—it increases for small subsets and stabilizes for subsets that are 20% or larger. Contrary to MI and 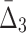, the average value of 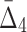increases throughout the increase of the subset size. The average 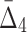value grows logarithmically—for smaller subsets the increase of 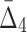is larger, but it gets smaller for larger subsets. The behavior of 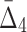, shown in Figure 4c, is different from MI and 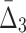behaviors, shown in Figure 4a and b, because we compute 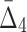for four variables that constitute a four-variable dependency, as opposed to computing MI and 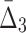for two or three variables that constitute only a limited part of this four-variable dependency.

4.3.3. Effect of noise

In this section we study how noise in the data affects the information measured by MI, 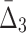, and 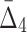. We use data from Example 1 and add variable amounts of noise to it. The 20-by-5000 input data matrix is essentially treated as a 100,000-long vector. Adding the fraction m of noise, then, corresponds to randomly choosing m×1000 elements of that vector and changing these elements to different randomly chosen values. This is repeated 100 times, and we compute an average information measure for a noise level m. Figure 5 shows the effect of different levels of noise on the information content of the data, as measured by MI, 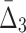, and 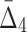. We immediately see a relationship that has the effect that as more noise is added the amount of information decreases, and then converges to the informational level of the background.

FIG. 5.

Effect of noise on (a) mutual information, (b) 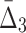, and (c) 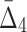. The points of the curves are computed by applying the measures to a set of selected tuples of Example 1 (see legend). The first point of each curve corresponds to a measurement value computed on the data without noise. All other points are the values of corresponding measures computed on data with noise averaged across 100 repeats, and the error bars represent standard deviation. The x-axis shows the amount of noise for corresponding values of the measures and ranges from 0 to 50% with 2.5% incremental increases. Additionally, the black curve is an average across all tuples that were not selected (the background) and the error bars are maximal standard deviation across these tuples.

Note that on average the values of higher-degree information measures (e.g., 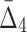) degrade faster with noise than those of lower-degree. Moreover, the error bars (standard deviations) become smaller with more noise. This decrease is stronger for higher degrees, K, of information measures, from MI to 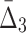, and to 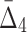. This behavior can be attributed to the way the noise is introduced into the data: When a random element selected for the introduction of noise, the likelihood that it is related to a selected pair of variables (out of 20 variables) is smaller than the likelihood that it will be related to a selected tuple of four variables. As a result, increasing noise degrades higher-degree measures faster: 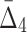values degrade much faster than MI values.

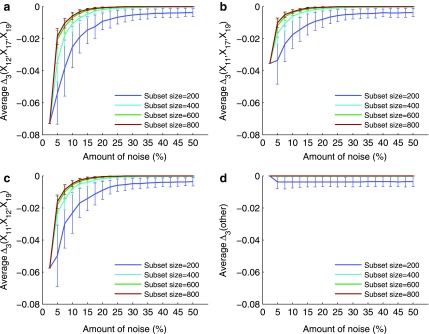
One of the main questions of interest is whether we are able to detect the shadows, and thus the dependencies from the background given uncertainty (in this case, noise added to the data). In order to answer this question we compute the difference between the information content of a selected tuple and the average information content of the background. This difference is measured in terms of the number of standard deviations of the information of the tuple computed across 100 random repeats. Performing this analysis for MI, 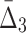, and 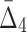for every noise level yields the results shown in Supplementary Figure S1. The selected tuples in these figures are those from Figures 1 and 2 of Example 1, which are either the dependency or its shadows.

Supplementary Figure S1 illustrates our ability to detect the shadow tuples. The horizontal line, set at the level of two standard deviations, separates the information values that we can detect from the values that are statistically indistinguishable from the background. On the one hand, this figure shows that the information measures with low K (such as MI) rise much further above the background when the noise level is relatively low than the measures with higher K (such as 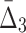). This shows that it is relatively easy to detect pairwise shadows when the level of noise is low. On the other hand, all measures, MI, 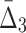, and 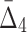, drop to the level of two standard deviations when the level of noise is about 35%. In section 4.3.4, we will see that this is specifically a property of a large sample set (5,000 samples). The threshold of detectability is different for measures with different K when the sample size is smaller.

Another way of analyzing the detectability of a shadow tuple is to use ANOVA (a one-way analysis of variance). ANOVA tests whether the population means of data taken from two different groups are equal. The two groups in this case are the values of an information measure of a shadow tuple and the values of the information measure of the background tuples for a specific degree K of the measure and a specific level of noise. Supplementary Figure S2 shows the results of the ANOVA test applied to values of MI, 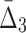, and .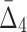

Using ANOVA testing we can distinguish MI values of the shadow pairs from the values of the background pairs for all noise levels up to 50% (see Supplementary Fig. S2a). We see a similar result for 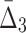values: The P-value starts to increase when the noise level rises above 40% (see Supplementary Fig. S2b). The detectability of the four-variable dependency measured with 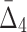continuously decreases when the noise level rises and, when the level of noise reaches 50%, it becomes impossible to distinguish the dependency from the background using the ANOVA test (Supplementary Fig. S2c). Although surprising at first, the fact that noise, especially at lower levels, does not have a very significant effect on our ability to detect the shadow tuples in Example 1 can be explained by the large size of our sample set (5,000). This is further confirmed in section 4.3.4, showing the analysis of noise effects on the detectability of shadows calculated from small sample subsets.

4.3.4. Effects of sample size vs. noise levels

We now study how the information measured by MI, 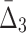, and 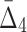is affected by the size of the data set and the amount of noise simultaneously, which allows us to evaluate the relative importance of these parameters.

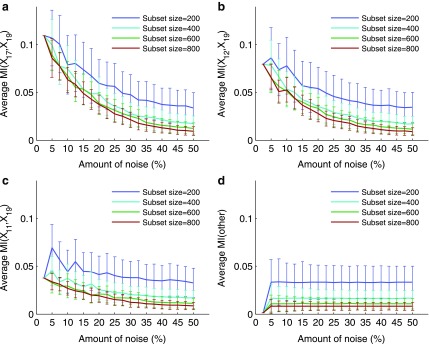
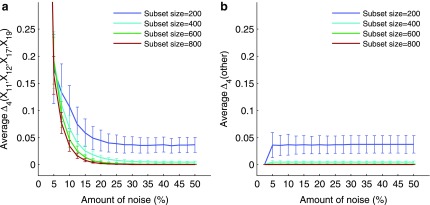
Figure 6 shows that the overall value of MI decreases as the amount of noise increases. Note also that for the three selected pairs the error bars become slightly smaller with the increase of noise. This is consistent with the idea that the amount of information decreases, becoming increasingly similar to the amount of information of random, noninformative pairs, and therefore becomes less sensitive to permutation. At the same time the error bars are larger for smaller subsets, since even a small amount of noise can distort more information in a smaller set than in a larger set. Note that MI computed on small sets is sensitive to noise (seen as a fluctuating curve), but it becomes more robust as the data size increases (the curve becomes smoother). Note also that although the MI values for selected pairs are larger for smaller sets, the MI values for background pairs (pairs chosen randomly) are also larger.

FIG. 6.

The effect of noise and the input data size on mutual information between two variables. Plots (a–c) illustrate the analysis of mutual information (MI) for three selected pairs, 〈X₁₇, X₁₉〉, 〈X₁₂, X₁₉〉, and 〈X₁₁, X₁₉〉. The first point of each plot shows an MI value computed on the entire set of 5,000 samples with no noise. Every other point shows MI computed on small randomly selected subsets with noise. For each size and noise level, a subset was selected 10 times, and for each subset we added noise and computed MI 100 times. The plots show the average and standard deviation of MI for subset sizes and 19 noise levels (from 5% to 50%). Plot (d) illustrates the same analysis for all other pairs. Each point in (d) is computed similarly to (a–c) and averaged across all pairs, and each error bar is a maximum standard deviation across all pairs.

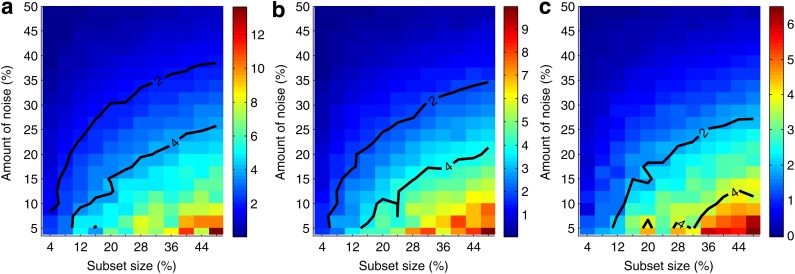
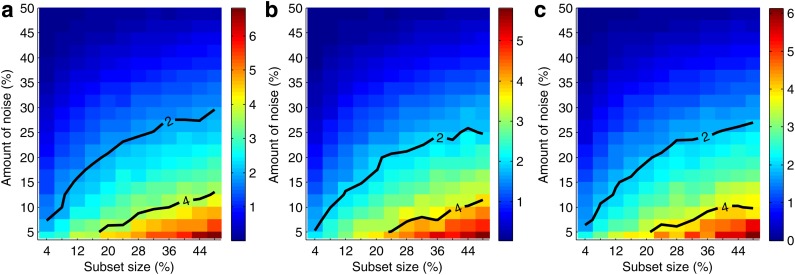
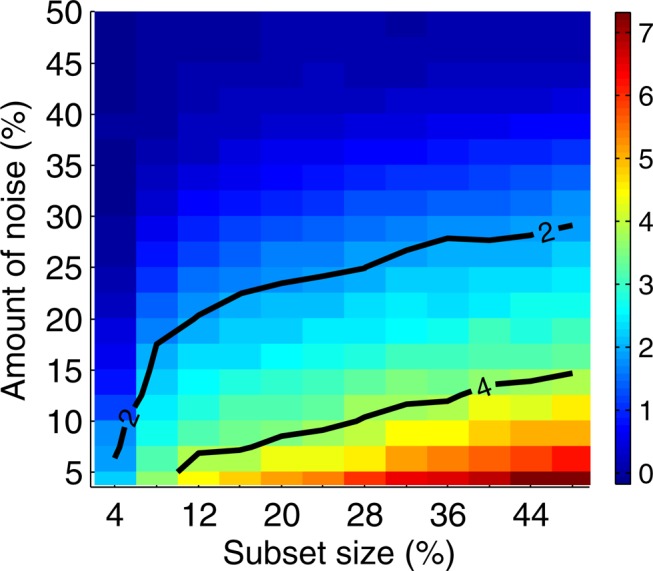
Figure 7 and Supplementary Figure S3 illustrate our ability to distinguish the informative pairs from the background. We see that the power to distinguish the informative pairs decreases with more noise. This power is lower for smaller subsets, and it takes a smaller amount of noise to make it difficult to distinguish the informative pairs from the rest. We can tolerate a lot more noise when distinguishing the informative pairs on larger subsets. For example, for pair 〈X₁₇, X₁₉〉, if we have 200 samples, then we can tolerate less than 8% of noise before losing power to distinguish this pair from the background. With 400 samples, however, we can tolerate up to 17.5% noise. And for 600 samples, this threshold goes up to 22.5%, and for 800 to 27.5% of noise.

FIG. 7.

Information gain over background as a function of data size and amount of noise. Given a set of 5,000 samples and a subset size X, we randomly choose 10 subsets with size X. Then for each subset, we randomly seed noise up to a specified level and compute MI for all the pairs. We then repeat random noise assignment 100 times and do that for each subset. Finally we take an average for every pair. We also average MI for all noninformative pairs (other than 〈X₁₇, X₁₉〉, 〈X₁₂, X₁₉〉, and 〈X₁₁, X₁₉〉) into one value we call background MI. Three plots of the figure show heat maps for the three informative pairs, (a) 〈X₁₇, X₁₉〉, (b) 〈X₁₂, X₁₉〉, and (c) 〈X₁₁, X₁₉〉. Each point of the heat map corresponds to a difference between the average MI of the pair and the background MI for a given subset size and noise level. The difference is scaled by the size of the standard deviation of the MI of the pair, so the color bar corresponds to the number of standard deviations the average MI of the pair is from the average background MI. Two contours are shown for the difference equal to two and four standard deviations.

We now look at the three-dimensional dependencies and analyze the effect of noise and sample size on the information measured using 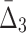. The behavior of 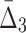, which is illustrated in Figure 8, is similar to that of mutual information. The ability to distinguish a three-variable dependency from the background is illustrated in Figure 9 and Supplementary Figure S4.

FIG. 8.

The effect of noise and amount of data on 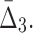Plots (a–c) illustrate the analysis of 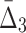for three selected tuples, 〈X₁₂, X₁₇, X₁₉〉, 〈X₁₁, X₁₇, X₁₉〉, and 〈X₁₁, X₁₂, X₁₉〉. Plot (d) illustrates the same analysis for all other tuples. All the points of these plots are calculated similarly to those in Figure 6.

FIG. 9.

Information gain over background as a function of data size and amount of noise. Three plots of the figure show heat maps for the three informative tuples, (a) 〈X₁₂, X₁₇, X₁₉〉, (b) 〈X₁₁, X₁₇, X₁₉〉, (c) 〈X₁₁, X₁₂, X₁₉〉. These heat maps are computed similarly to those in Figure 7.

We also looked at the information measured by 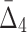and how it changes with different levels of noise and sizes of data (see Fig. 10). The detectability of the four variable dependency is illustrated in Figure 11 and Supplementary Figure S5.

FIG. 10.

The effect of noise and amount of data on 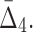Plot (a) illustrates the analysis of 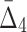for the tuple 〈X₁₁, X₁₂, X₁₇, X₁₉〉. Plot (b) illustrates the same analysis for all other tuples. All the points of these plots are calculated similarly to those in Figures 6 and 8.

FIG. 11.

Information gain over background as a function of data size and amount of noise. The figure shows a heat map for the informative tuple 〈X₁₁, X₁₂, X₁₇, X₁₉〉. This heat map is computed similarly to those in Figures 7 and 9.

Comparing the information gain over background as a function of data set size and amount of noise for several tuples across various information measures (MI, 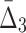, 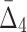) reveals that the information gain is smoother for measures of a higher degree as can be seen in Figures 7, 9, and 11, as well as Supplementary Figures S3, S4, and S5 of the Supplementary Material. As expected, a weaker dependency requires more data in order for the information gain to be substantial enough for the dependency to be detectable from the background. Moreover, weaker dependencies allow a smaller amount of noise to be present in the data, as compared to stronger dependencies, before becoming undetectable.

Dependencies with higher degree, scored by the higher degree measures, are more robust to the decrease of the size of data; with no noise, higher degree dependencies require less data to be detectable than dependencies with a lower degree. This is somewhat paradoxical. On the other hand, higher degree dependencies are more sensitive to the increase of noise: for a given amount of data, increasing the amount of noise makes dependencies with a higher degree become undetectable sooner than dependencies with a lower degree.

Overall this means that there are different regimes exhibited by data sets of various size and quality. The balance between data set size and noise levels ultimately dictates what can be detected and points to the importance of our being able to estimate the noise content of data sets before we can determine what can be detected with what size data set.

5. Application to Yeast Hiphop Data

We chose a large biological data set to test the application of the shadow algorithm. These yeast data were generated using a large set of strains with genetic loss-of-function mutations for which the cellular growth response to small-molecule, chemical compounds were measured. The data were generated on both heterozygous strains and homozygous, diploid strains. These are called haploinsufficiency profiling (HIP), and homozygous profiling (HOP) in this chemo-genomic platform (Lee et al., 2014). The HIP data set covers 1,095 strains that are heterozygous for deletions of the essential genes in the yeast genome, and the HOP data set covers 4810 strains that are homozygous for deletions of nonessential genes in the yeast genome. The growth or fitness defects of each of these strains were scored for 3,356 chemicals. Thus, the entire data set consists of 5,905 strains (representing essential and nonessential genes) measured across 3,356 chemical screens. We examined dependencies among genes, and all the strains are considered as variables, and all the chemical screens are considered as instances of a response of these variables.

In order to apply our information theory-based method, we bin the real valued fitness defect scores of each strain s into four integer values using the following intervals:

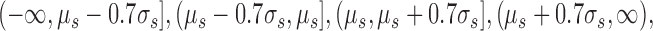where μ_s and σ_s are the mean and standard deviation of fitness defect scores for strain s. These intervals were selected to have a relatively even balance of binned scores.

The shadow algorithm is applied as shown in Figure 12 and Table 4. At the first step of the algorithm we compute mutual information (MI) for every pair of 5,905 strains (see Fig. 12a). The algorithm then selects a small number of outlier pairs that are (i) significant and (ii) contain a reasonable number of variables (a small enough number of variables for the set of all possible triplets of these variables to be computable). Using 20 standard deviations above the mean as a cut-off identifies a set of 11,771 outlier pairs that satisfies both of the above conditions: They are significant and contain only 1,051 variables, resulting in a computationally manageable set of triplets (“only” 193M triplets). If we chose a less stringent cut-off of 10 standard deviations above the mean, we would have selected 125,384 outlier pairs containing 2,647 variables, which would have resulted in a computationally infeasible set of 3 billion triplets.

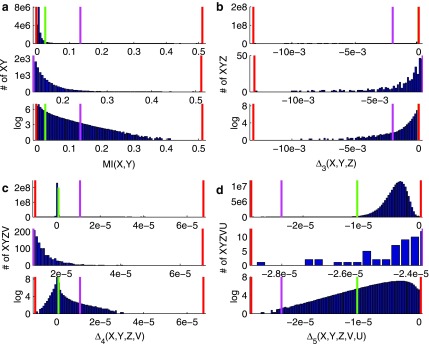
FIG. 12.

Histograms of dependency measures computed for various sets of tuples. Panel (a) shows distribution of mutual information values computed on all possible pairs of the entire set of genes (5,905 genes). Similarly, panel (b) shows 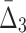values computed on all possible triplets of the set of genes involved in pairs with high MI (1051 genes involved in pairs that are above 20 standard deviations threshold). Selecting 279 variables from high 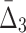triplets (above 1,000 st. dev.) and computing 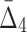on all possible quads results in a distribution shown in panel (c). Finally, computing on all possible 5-variable tuples of 118 variables involved in high 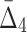quads (above 55 st. dev.) results in a distribution shown in panel (d). Each panel is composed of three subpanels showing the original distribution, its magnified tail, and the distribution in the log-scale (from top down). The red vertical lines show the minimal and maximal values of each distribution, the green lines show three st. dev. from the mean, and the pink lines show the thresholds used for selecting the informative tuples at each step.

Table 4.

Parameters of the Shadow Algorithm Applied to HIPHOP Data

Step no.	No. of input variables	Degree of measure	No. of corresponding tuples	Cut-off	No. of tuples passed cut-off	Num. of variables passed cut-off
1	5905	2 (MI)	17,431,560	20 std	11771	1051
2	1051	3 (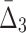)	192,937,325	1000 std	383	279
3	279	4 (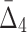)	247,073,751	55 std	987	118
4	118	5 (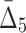)	174,963,438	10.3 std	53	74

Columns 2 and 7 show the number of input and output variables at each step, column 4 shows the number of tuples traversed during each step, and columns 5 and 6 show the cut-off values and the corresponding outlier tuples.

At the second step of the algorithm we compute 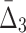for every possible triplet of 1,051 variables selected at the first step (see Fig. 12b and Table 4, row 2). This time we use a cut-off of 1,000 standard deviations in order to reduce a set of outlier triplets to a reasonable number: 383 triplets containing 279 variables. Note the unusually large cut-off value—an indicator of high significance of the selected outlier triplets and a sign that lots more of candidate three-variable dependencies are left out by the algorithm, which is inevitable when we are trying to tackle the problem of combinatorial explosion. The shadow algorithm proceeds to the following steps in a similar fashion, selecting outlier tuples with increasing degree (987 and 53 tuples based on computation of 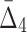and 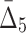correspondingly) and gradually decreasing the number of variables to 118 and then to 74 (see Table 4 and Fig. 12c and d). Note that these outlier tuples selected at each step of the algorithm are candidate multivariable dependencies. Note also that with each step of the algorithm the significance of the corresponding set of dependencies is dropping, which can be seen by the cut-off values (1,000 to 55 to 10.3, see Table 4) and by the shape of the distribution of measures (the distribution of 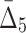values in Fig. 12d looks lognormal, suggesting that there are not many five-variable dependencies in the set). For these reasons we stopped the shadow algorithm at the forth step and focused our attention on two, three, and four-variable dependencies.

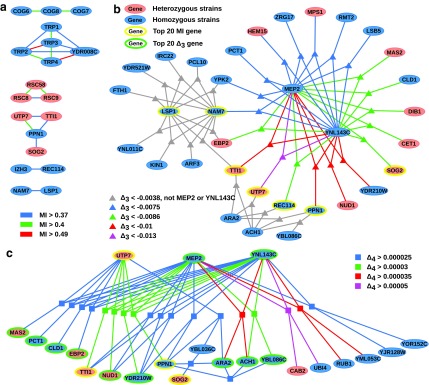
To illustrate the kind of biological information captured by our method, we considered the top 20 two-, three-, and four-way dependencies. First we looked closer at the top 20 pairs of genes with the highest mutual information. Figure 13a shows a dependency network comprised of these 20 pairs. There are four clusters of genes. The largest cluster is composed of five genes, four of which (TRP1-4) are from the same pathway (phenylalanine, tyrosine, and tryptophan biosynthesis), and the fifth one (YDR008C) overlaps with TRP1. The second cluster connects three genes (COG6-8) from Golgi transport complex (Whyte and Munro, 2001). The third cluster connects three genes (RSC8, RSC9, RSC58) from the RSC chromatin remodeling complex (Cairns et al., 1996).

FIG. 13.

Dependency networks constructed using tuples with the highest information content. Panel (a) shows the dependency networks of specific homozygous and heterozygous strains where each edge represents the existence of high MI between two genes and the color shows the magnitude of MI. Similarly, panels (b) and (c) show the networks where hyper edges connect three and four genes (respectively) representing the existence of high 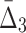and 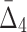among these genes. A three-way hyper edge is shown with a triangle and four-way hyper edge with a square. Bold nodes indicate genes that appeared in networks based on dependencies with lower dimension.

These three clusters are constructed based only on their mutual information without making any model assumptions. In this example, high MI in two genes indicates that these genes respond to a significantly large number of chemicals with a consistent behavior (similar to correlation). Therefore, it is expected that genes within clusters of high MI will share something in common: similar function, same pathway, same cellular component, etc. This is precisely the case for the three clusters above. The fourth cluster, however, is more interesting as it spans four genes—UTP7, TTI1, PPN1, and SOG2—that do not have an apparently common function. The investigation of the biological meaning of this dependence will be considered elsewhere.

Looking at the triplets of genes with the highest values of 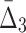reveals that all 20 top triplets (and 85 out of the top 100) contain the same two genes, MEP2 and YNL143C. Figure 13b shows the top 20 triplets spanning 22 genes, 6 of which are from the top 20 pairs. It is important to note that these top 20 three-way dependencies cannot be identified at the pairwise level of the analysis. One might expect to see two or three strong pairwise dependencies between genes of a high- 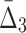triplet. However (MEP2, YNL143C) is the only detectable pair within each triplet from the set of top 20 three-way dependencies. All other pairs within each of these triplets have low MI and cannot be detected at the pairwise level.

Figure 13c shows 20 four-variable dependencies that have the highest value of 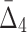. Similar to the three-variable case, MEP2 and YNL142C are three main hubs participating in all but two dependencies. UTP7 is another prominent hub that is involved in nine dependencies (eight of which also involve MEP2 and YNL142C). Note that several of these four-way dependencies, and in particular the dependency with the highest 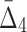, cannot be detected using only two-way and three-way dependency analysis. A tuple with high 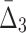(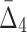) value indicates that the growth values of corresponding genes consistently follow some function across a subset of chemical screens. The number of these chemical screens must be big enough for the value of measure 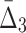(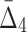) to be detectable (statistically distinguishable from the background). The larger the subset of chemical screens consistent with the underlying function, the greater the value of the measure. Consequently, the gene triplets and quads with the highest 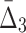and 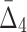values are good candidates for further in-depth analysis and experimental validation.

There are a couple of important questions that still have to be answered. One is a question of significance. What is the best way to estimate our confidence that a gene tuple is functionally dependent? And can we find an optimal confidence cut-off? The question of significance is closely related to the second question: finding the underlying function that is the source of the dependence. Since the method calculates a measure of dependence and does not predict or make any assumptions about the underlying nature of the dependence, it can only provide information about whether or not a dependency exists. The next step would be to model the underlying function and to identify which chemical screens are consistent with the function shedding more light on the biological process behind the function.

The question of finding the optimal confidence cut-off for detection of significant multivariate dependencies is also related to challenges with computational complexity of the dependency detection. Table 5 shows how the cut-off at each step of the shadow algorithm reduces the size of the search space. For example, when looking for the three-variable dependencies, the search space is reduced from 34 billion triplets that would have taken us 953 hours on our computer to 193 million that took only 5 hours. Table 5 also shows the rate of computation for each measure per 10,000 tuples. The rate is increasing for measures with higher degree and almost four-fold higher for 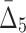compared to MI, which is expected since the number of entropy terms grows quickly with increasing degree (see section 4.3.1 for more details).

Table 5.

The Size of the Search Space and Running Time of the Shadow Algorithm

Step no.	Degree	No. of all possible tuples	No. of tuples	Time (hours)	Rate (sec per 10K)
1	2 (MI)	1.743e+07	17,431,560	0.5	0.9634
2	3 (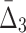)	3.430e+10	192,937,325	5	0.9330
3	4 (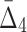)	5.061e+13	247,073,751	11	1.6028
4	5 (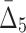)	5.973e+16	174,963,438	18	3.7036

Column 3 shows the size of the entire search space at each step of the algorithm, whereas column 4 shows the size of the actual search space. Column 5 shows the time it took to complete the actual search space, and column 6 shows the rate of computing per 10,000 measures.

6. Discussion and Conclusions

The approach we have previously introduced has been developed further in this article, and an algorithm is described that resolves the combinatorial explosion problem inherent to these kinds of analyses. This resolution is essential to the practical use of the method on large biological data sets. The general approach to multiple dependency measures provides an accurate measure of the level of dependency for a given subset of variables in a data set, and the value of these measures is significantly nonzero only if the subset of variables has an essential, collective dependency. This attractive feature is useful, of course, only if we can calculate all the necessary quantities and find a way around the combinatorial explosion as the variables and the potential degrees of dependence increase. The computational complexity increases as a multiple of the binomial coefficient of the number of variables. We have found that the “symmetric deltas,” 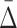(τ), for a given subset of variables, τ, have the property that for variable subsets of τ the symmetric delta can have values that are significantly nonzero, even though the highest degree dependence includes the full subset, τ. We use this property to reduce the dimensionally driven combinatorial explosion by following the “shadows” that the multivariable dependency casts onto smaller subsets and calculating only with those, thereby reducing the number of variables considered at each level. Think of the shadow concept by considering the relationship between, for example, a hypergraph edge among three variables and the set of three pairwise edges between these. Not all of these pairwise edges can be zero.

Instead of having to calculate the marginal entropies of all subsets at each degree level, we need to consider only subsets of the variables that exhibit an appropriate “shadow.” Thus, the number of calculations for n variables at a degree level of d grows, not as the binomial coefficient 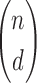, but at a much smaller rate that depends on the significance threshold and other chosen parameters of the “shadow” calculation as illustrated in our example (Table 5). This approach enables the widespread use of our multivariable measures on large data sets. The effects of noise and sample numbers on the method are also examined systematically and enable us to define the practical limits of statistical power and conclude overall that the method is both general and highly effective on complex data sets.

We demonstrated this method on simulated data sets, and also analyzed the yeast HIPHOP data set. This biological data involves a large number of mutant strains (a few thousand) interacting with a large number of chemical compounds (a few thousand). The number of variables dictates that the problem of multivariable dependence cannot be approached to find higher degree dependencies without encountering a significant combinatorial explosion. Our method successfully avoids the explosion and uncovers a complex set of dependencies up to the degree of four variables. Note that for this data set there are more than 10¹⁴ possible dependencies at that degree. The question of significance here is an important one. What is the best way to estimate our confidence that a gene tuple is functionally dependent? The permutation test was used to address the complex of factors affecting significance.

The method calculates a measure of dependence and does not predict or make any assumptions about the underlying nature of the dependence, so it provides information only about whether or not a dependency exists. Modeling the underlying functional dependence using the specific data, or additional information from outside this data set are required to identify the nature of the variable dependencies and the biological process behind the function. The introduction of this algorithm, based on the shadows of lower degree dependencies, should provide a powerful method for using the proposed information theory measures for high variable number data sets and enable the detection of high degree dependencies.

Acknowledgments

We are grateful to Aimee Dudley for suggesting the HIPHOP data set, for stimulating discussions, and for comments on the manuscript, and to John Mulligan for comments and suggestions. This work was supported in part by NSF IIS-1340619, by the Luxembourg Centre for Systems Biolomedicine, and the Pacific Northwest Diabetes Research Institute.

Author Disclosure Statement

No competing financial interests exist.