Analysis and Interpretation of Superresolution Single-Particle Trajectories

Abstract

A large number (tens of thousands) of single molecular trajectories on a cell membrane can now be collected by superresolution methods. The data contains information about the diffusive motion of molecule, proteins, or receptors and here we review methods for its recovery by statistical analysis of the data. The information includes the forces, organization of the membrane, the diffusion tensor, the long-time behavior of the trajectories, and more. To recover the long-time behavior and statistics of long trajectories, a stochastic model of their nonequilibrium motion is required. Modeling and data analysis serve extracting novel biophysical features at an unprecedented spatiotemporal resolution. The review presents data analysis, modeling, and stochastic simulations applied in particular on surface receptors evolving in neuronal cells.

Main Text

Single-particle trajectories (SPT) acquired from digital images can be short or long. The goal of statistical analysis of the data is to extract local physical properties of the particles and their environment, such as velocity or processivity, diffusion coefficient (or tensor), confinement, or local density of obstacles reflecting the presence of biological objects of different sizes. SPT objects vary from the cell micrometer scale to the recently achieved nanometer scale of molecular motion; however, the acquired data are very different in the two extreme cases of micro- to nanometer of the spatial scale. At the cellular level, the motion of swimming algae, biflagellate cells, spermatozoa, and many other active swimmers, is mostly ballistic (driven by a deterministic velocity) (1). The motion of cells is usually analyzed by sequencing the trajectories in epochs of diffusion or of deterministic velocity. Recent studies of cell motion in confined microfluidic chambers, made of a pillar lattice (2, 3), indicates that cell motion can result from their interaction with the local environment. Tracking algorithms allow connecting the dots of acquired points to generate trajectories (4, 5).

Motion of molecules is usually driven by diffusion, a process like the spread of ink in water that involves no fluidic motion. Diffusion, such as Brownian motion, was first explained by Einstein (6) as the manifestation of random thermal collisions of the Brownian particle with those of the surrounding fluid, be it gas or liquid. Einstein claimed that the phenomenon of diffusion (Brownian motion) is a confirmation of kinetic theory (7, 8). Brownian motion in a field of force was described by Langevin in his celebrated equation (9, 10). Obviously, methods of detecting and tracking single diffusing particles are much more complicated than those for tracking cellular size particles. Because diffusion may involve forces other than thermal collisions, a physical model of the tracked molecular motion is needed to provide a framework for the analysis of the acquired trajectories.

Large numbers (tens of thousands) of short receptor trajectories can now be collected by superresolution methods (11, 12), at tens-of-nanometers precision for motion occurring on a cell membrane. What can be extracted from such data? Do trajectories exactly represent the underlying physical process that produces them? Acquired data are actually spatially and temporally coarse-grained by the sampling apparatus so that many obstacles on the membrane surface are washed out. Thus the sampled molecular process cannot be modeled by the overdamped Langevin equation, which describes diffusion on the microscopic level. Therefore, to recover long-time behavior, physical quantities, and statistics of entire trajectories of the sampled diffusion process, a stochastic model of the acquired data is required and data analysis is needed to calibrate the model. We describe here coarse-grained models that are based on the local biophysical properties underlying receptor motion (13). For studying long trajectories, other statistical approaches have been developed in the context of anomalous diffusion (14, 15, 16). We review here recent models that we have developed and a statistical approach to the study of local biophysical properties underlying receptor motion on a membrane surface that can be revealed from the large number of short trajectories. These methods are used to interpret data, recover physical laws, and organize the membrane, therefore bridging the gap between molecular processes and their role in cell physiology. The analysis and methodology reviewed here follow in the tradition of Brownian motion theory and simulations and ignores electric forces and charges. Calculation of fluctuating electric forces from the fluctuating densities of charge may have significant effects, and constructing a theoretical framework is certainly a challenging task for future research.

Description of random short single particle trajectories from live cell imaging

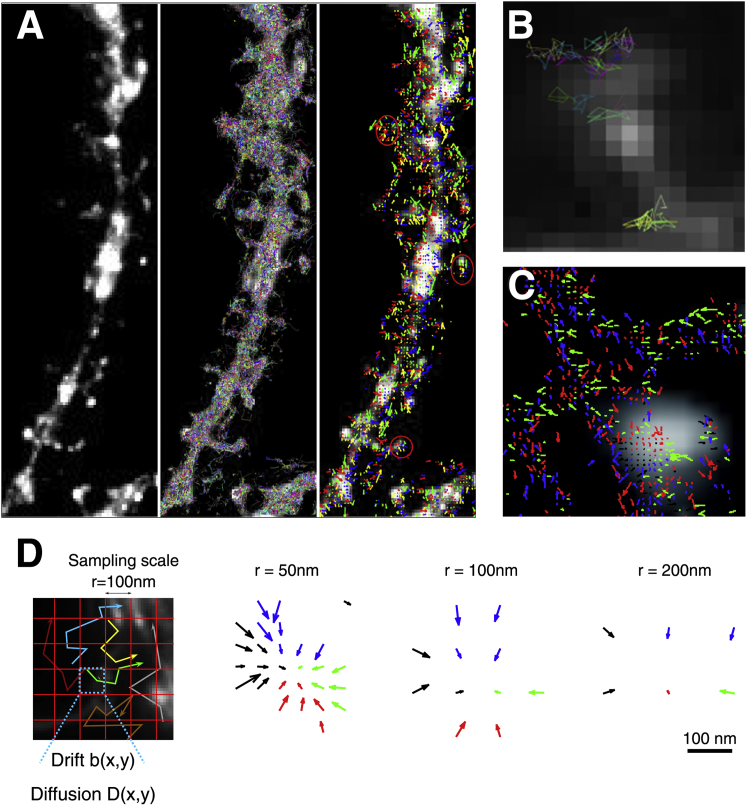
The trajectories in Fig. 1 are the projections on the focal plane of random trajectories of particles moving on a cell membrane. Although we present here trajectories acquired on neuronal cells, the situation is generic to any cell and trafficking molecule. The points of the trajectories are acquired at given time intervals, usually ∼10–50 ms apart (17). The trajectory fragments shown in Fig. 1 B are rectilinear interpolations of the projections of these points. The data contain information about the deterministic and random forces that drive the particles on the membrane. The extraction of this information from the data is not a trivial problem and it requires some insight into the physical model of the motion and into the effect of sampling on this model.

Figure 1.

Description of large superresolution data and their analysis from Hoze et al. (13). (A) Confocal image of a neuron, superresolution trajectories, and the computed vector field. (B) Magnification of coarse-grained trajectory where tracked consecutive points are connected by a straight line. (C) Magnification of the vector field. (D) Discretization of the image into pixels of size r, where each vector is computed at three scales r = 50, 100, 150 nm, showing that converging arrows are persistent across a scaling analysis. To see this figure in color, go online.

The information contained in the data can potentially elucidate the membrane organization, the way in which organization sustains the physiology of neuronal transmission, and the plasticity, and even how molecular structure determines cellular function. The information is essential even for just comparing moments and distributions between different experimental conditions.

Moreover, some features of the particle motion get lost or distorted in the process of acquiring the data. First, the spatio-temporal resolution of the data coarse-grains the motion into one that possibly has no potential, no fluctuation-dissipation principle (10), and no simple relation between the density and the energy, whatever it may mean in this context, as explained below. Second, assume the stationary density p(x) of points is calculated from the data. The diffusion coefficient D(x) (or tensor) of the coarse-grained trajectories may be x dependent, due to local obstacles. Then the density no longer has the classical exponential Boltzmann form (18), thus breaking the connection between the density and the energy profile. Third, the projection of the random motion (even when it exists), from a surface to the focal plane, introduces apparent forces to the projected motion that are due to local surface curvatures that distort the energy landscape (19).

The physics of diffusion on a membrane and its coarse-grained image

The microscopic physical model of receptor motion in a homogenous membrane is the overdamped limit of the Saffman-Delbrück-Langevin model (20, 21). The model assumes that the diffusion of a receptor embedded in a membrane surface is generated by a diffusion coefficient D and a field of force F(X), according to the overdamped Langevin equation

$$\dot{\mathit{X}}\left(t\right)=\frac{\mathit{F}\left(\mathit{X}\left(t\right)\right)}{\gamma }+\sqrt{2D}\dot{\mathit{w}}\left(t\right),$$ (1)

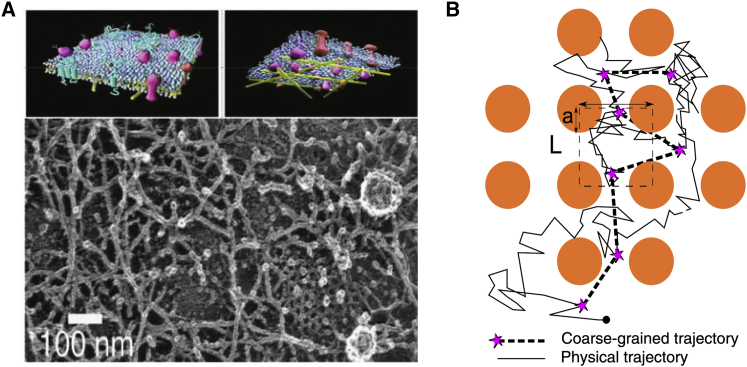
where $\dot{\mathit{w}}\left(t\right)$ is a vector of independent standard δ-correlated Gaussian white noises and γ is the dynamical viscosity (10). The source of the driving noise $\dot{\mathit{w}}\left(t\right)$ is the thermal agitation of the ambient water and membrane molecules (see also the Appendix for a summary of classical notions about stochastic process). The microscopic model in Eq. 1, however, cannot be used directly to model the superresolution data, because the trajectory fragments are not collected on the microscopic timescale of the thermal motion on a homogeneous membrane, but instead on a coarser timescale of the recording apparatus. Thus, short events that are due to the crowding organization of a variety of obstacles on the membrane are not resolved in the data (Fig. 2). Therefore, to be more realistic, the model in Eq. 1 has to be coarse-grained on a coarser spatiotemporal scale into an effective stochastic equation, as seen in Holcman and Hoze (22) and Hoze et al. (13))

$$\dot{\mathit{X}}\left(t\right)=\mathit{b}\left(\mathit{X}\left(t\right)\right)+\sqrt{2}{\mathit{B}}_e\left(\mathit{X}\left(t\right)\right)\dot{\mathit{w}}\left(t\right),$$ (2)

with the empirical drift field b(X) and diffusion matrix B_e(X), where ${\mathit{D}}_e\left(\mathit{X}\right)=\left(1/2\right){\mathit{B}}_e\left(\mathit{X}\right){\mathit{B}}_e^T\left(\mathit{X}\right)$ (T is the transposition) is the effective diffusion tensor. The observed effective diffusion tensor needs not be isotropic and can be state-dependent, whereas the friction coefficient γ in Eq. 1 remains constant and the microscopic diffusion coefficient (or tensor) D may remain isotropic. Obviously, the impenetrable obstacles that slow down the effective diffusion affect neither the microscopic physical properties of the diffusing particle nor those of the membrane. Note that the effective field b(X) may have no potential even if F(X) does (see Schuss (10)). Similarly, Einstein’s fluctuation-dissipation principle may not hold for the coarse-grained equation (Eq. 2) recovered from the recorded short trajectories.

Figure 2.

Schematic representation of a physical versus coarse-grained trajectory. (A) Organization of a neuronal membrane containing microdomains made of overlapping filaments and obstacles, permission from A. Kusumi). (B) In this scheme, a physical trajectory is generated by the overdamped Langevin equation (Eq. 1) while the coarse-grained trajectory is sampled at fixed time interval Δt (indicated by purple stars). The obstacles are not directly visible. To see this figure in color, go online.

Construction of the coarse-grained model from trajectories

The coarse-grained model from Eq. 2 is recovered from the conditional moments of the trajectory increment ΔX(t) = X(t + Δt) − X(t) (10, 18, 23, 24),

$$\begin{array}{c}\mathit{b}\left(\mathit{x}\right)=\underset{\Delta t\to 0}{\text{lim}}\frac{\mathbb{E}\left[\Delta \mathit{X}\left(t\right)|\mathit{X}\left(t\right)=\mathit{x}\right]}{\Delta t},\\ {\mathit{D}}_e\left(\mathit{x}\right)=\underset{\Delta t\to 0}{\text{lim}}\frac{\mathbb{E}\left[\Delta \mathit{X}{\left(t\right)}^T\Delta \mathit{X}\left(t\right)|\mathit{X}\left(t\right)=\mathit{x}\right]}{2\Delta t}.\end{array}$$ (3)

Here, the notation $\mathbb{E}$[·|X(t) = x] means averaging over all trajectories that are at point x at time t. Indeed, the coefficients of Eq. 1 can be statistically estimated at each point X = (X¹, X²) of the membrane (or rather in the focal plane) from an infinitely large sample of its trajectories in the neighborhood of the point X at time t. In practice, the expectations in Eq. 3 are estimated by finite sample averages and Δt is the time resolution of the recording of the trajectories, as described in Hoze et al. (13). The expressions in Eq. 3 are approximated in Hoze et al. (13) at the time step Δt = 0.050 s (of the sampled data), where 200 points falling in any bin is usually enough for the estimation.

To compute the empirical drift and diffusion coefficients, we first partition the data into square bins B(xk,r) of side r (Fig. 1 D). Starting with a sample of N_t projected trajectories $\left\{x^i\left(t_j\right),i=\mathrm{1,2},\dots N_t,j=\mathrm{1,2},\dots ,N_s\right\}$, where t_j values are the sampling times, the generalization of the expressions in Eq. 3 for the drift b(x) = (b_x(x),b_y(x)) is

$$\begin{array}{l}{b}_x\left({\mathit{x}}_k\right)\approx \frac{1}{N_k}\stackrel{N_t}{\sum _{j=1}}\stackrel{N_s-1}{\sum _{i=0,{\tilde{\mathit{x}}}_{\mathit{i}}^{\mathit{j}}\in B\left({\mathit{x}}_k,r\right)}}\left(\frac{{\tilde{x}}_{i+1}^j-{\tilde{x}}_i^j}{\Delta t}\right),\\ b_y\left({\mathit{x}}_k\right)\approx \frac{1}{N_k}\stackrel{N_t}{\sum _{j=1}}\stackrel{N_s-1}{\sum _{i=0,{\tilde{\mathit{x}}}_i^j\in B\left({\mathit{x}}_k,r\right)}}\left(\frac{{\tilde{y}}_{i+1}^j-{\tilde{y}}_i^j}{\Delta t}\right),\end{array}$$ (4)

where N_k is the number of points in bin B(x_k,r). An illustration of applying the empirical estimator from Eq. 4 to compute the drift from trajectories is shown in Fig. 1, A–C, where the vector field is computed on each bin. The arrows are colored depending on their direction. The image is discretized into bins of size r. In Fig. 1 D, the vector field shows converging arrows, computed at three scales r = 50, 100, 200 nm, showing that these converging arrows is persistent across scales. Similarly, the components of the effective diffusion tensor D_e(x_k) are approximated by the empirical sums

$$\begin{array}{c}{D}_{xx}\left({\mathit{x}}_k\right)\approx \frac{1}{N_k}\stackrel{N_t}{\sum _{j=1}}\stackrel{N_s-1}{\sum _{i=0,{\mathit{x}}_i\in B\left({\mathit{x}}_k,r\right)}}\frac{{\left(x_{i+1}-x_i\right)}^2}{2\Delta t},\\ D_{yy}\left({\mathit{x}}_k\right)\approx \frac{1}{N_k}\stackrel{N_t}{\sum _{j=1}}\stackrel{N_s-1}{\sum _{i=0,{\mathit{x}}_i\in B\left({\mathit{x}}_k,r\right)}}\frac{{\left(y_{i+1}-y_i\right)}^2}{2\Delta t},\\ D_{xy}\left({\mathit{x}}_k\right)\approx \frac{1}{N_k}\stackrel{N_t}{\sum _{j=1}}\stackrel{N_s-1}{\sum _{i=0,X_i\in B\left({\mathit{x}}_k,r\right)}}\frac{\left(y_{i+1}-y_i\right)\left(x_{i+1}-x_i\right)}{2\Delta t}.\end{array}$$ (5)

By definition, the moment estimation from Eqs. 4 and 5 requires small fragments of trajectories passing through each point of the membrane surface, which is precisely the massive data generated by the sptPALM technique (11, 12) on biological samples. The empirical estimator defined by Eq. 3 has been used over the past 60 years in signal processing (25) and recently applied in several cell biology contexts (26), where it is shown to be optimal.

Equations 4 and 5 do not assume any a priori distribution of the data or a priori knowledge of transition probability. This is in contrast with recent Bayesian methods (27, 28) based on parametric estimators, where the model in Eq. 1 was used and the probability density function of the trajectories is assumed to be Gaussian on every short time interval, with the infinitesimal moments indicated in Eq. 1. Consequently, these moments are determined by the maximum likelihood method applied to the Gaussian density. As explained above, there is no such thing as a Gaussian distribution in a bounded domain or on a closed surface. For example, there exists no Gaussian density on a sphere or a cylinder or even a one-dimensional closed segment (see Appendix). In particular, the probability density function of Eq. 1 cannot be Gaussian when any boundary behavior of the trajectories X(t) of Eq. 1 is prescribed. For example, if the boundary is impermeable to trajectories, there is a finite probability that trajectories reach a point y from a point x in a domain by reflection in the boundary. These facts eliminate the possibility of maximum likelihood estimation of the field. Actually, there is no need for it, because the method used in Hoze et al. (13) gives the correct estimates for the diffusion model, as described in Metzler et al. (15). The difference between the maximum likelihood and the diffusion estimates become pronounced near boundaries or on narrow necks of a surface. The estimates presented in Masson et al. (27) seem overly optimistic as far as the relation between the theoretical and the sampled trajectories is concerned. Finally, it is not clear how to estimate the accumulation of local errors due to the Gaussian approximation, especially for the computation of local energy. The analysis of Hoze et al. (13) is based on the assumption that the molecular motion is a diffusion process, whose local drift and diffusion coefficients are estimated from local conditional moments of the many available trajectory fragments. The estimates in Hoze et al. (13) are the standard nonparametric empirical estimates of the drift and diffusion coefficients known for decades (10, 18, 25, 29).

Finally, recovering a physical process from many short projected trajectories involves computing the first and second moments (drift and diffusion tensor D(x)) for trajectories moving on a surface from the projected ones. For example, the relation between the diffusion coefficient D_s on a curve, parameterized by y = f(x) and the projected one D(x) on a line, is

$$D_s\left(x\right)=\frac{D\left(x\right)}{1+f^{\prime 2}\left(x\right)}.$$ (6)

Expressions for two-dimensional surfaces are derived in Holcman et al. (19). Recovering the diffusion tensor D(x) requires solving a nonlinear second-order partial differential equations. The curvature creates an artificial drift component, described by

$$a_{\text{geometric}}\left(x\right)=-\frac{D\left(x\right)f^{\prime }\left(x\right)f^{\prime }\left(x\right)}{{\left[1+f^{\prime 2}\left(x\right)\right]}^2},$$ (7)

where f′ and f″ are the first and second derivatives, respectively, with respect to the x variable. The dynamics of a projected trajectory contains an additional drift due to the projection. In general, projected trajectories contain both a geometrical drift induced by the projection, and a physical drift. Both drifts are mixed in empirical estimations, but can be teased apart by a procedure, which is computationally costly (19). Once the physical diffusion tensor is recovered from data, a model of crowding is necessary to express the microscopic diffusion coefficient D in terms of the density and organization of obstacles. The nonlinear relation between the effective diffusion tensor and the density of round obstacles organized in a square lattice was found analytically and numerically in Hoze et al. (30). The theory predicts that the surface of dendritic spine should be occupied by 70% of obstacles, while it is only 50% for dendrites.

The potential wells and their energy

The organization of the neuronal membrane was recently probed at a nanometer resolution using many superresolution trajectories (11), yet interpreting high density regions was unclear until the Langevin model was used. The local biophysical properties underlying receptor motion based on coarse-graining revealed that the converging arrows shown in Fig. 1 A can result from attracting potential wells of large sizes (13) describing long-range interactions (see Fig. 3). These wells were first predicted theoretically in Schuss and Holcman (31) and Taflia and Holcman (32) (see also Saxton (33) for corrals). Indeed, potential wells were postulated to be due to an effective field accounting for local traps (32) or a flat well located at the postsynaptic density of synapses (31). However, physical relations among the local molecular residue that can generate chemical interactions, and the size, depth, and energy of the potential well, remain unclear (34). Fig. 3 shows that regions of high density of points colocalize with the potential wells, of the size of hundreds of nanometers.

Figure 3.

Analysis of receptor (GluR2) trajectories. (A) Distribution density function of GluR2, based on the analysis of sptPALM trajectories. Four boxed areas show regions of high density. (B) Magnification of the boxed areas in (A). (Red ellipses) Range of the potential wells. (C) Potential well patterns, characterized by a converging field of forces to an attractor. (D) The overlay of the highest receptor densities (red) with the hippocampal confocal neuronal image reveals that these potential wells (green) do not colocalize with the synaptic marker homer (from Hoze et al. (13)). To see this figure in color, go online.

The drift field b(x) in Eq. 2 represents a force that acts on the diffusing particle, regardless of the existence or nonexistence of a potential well (35). In the case where D(x) is locally constant and the coarse-grained drift field b(x) is a gradient of a potential locally b(x) = −∇U(x), the density of particle represents locally the Boltzmann density e^−U(x)/D. The force field can form potential wells, generically approximated locally as a paraboloid with an analytical representation $U\left(\mathit{x}\right)=A\left({\left(x/a\right)}^2+{\left(y/b\right)}^2\right)+O{\left(x,y\right)}^2$ (where A, a, and b are three parameters to be determined) valid on a small elliptic domains. Four examples of parabolic potential wells located on a dendritic surface are shown in Fig. 3, A–C (13).

Potential wells are local anisotropic structures with a basin of attraction approximated as an ellipse, the size of which is a few hundreds of nanometers. These potential wells cannot be created directly by local molecular interactions (which can extend to only a few nanometers), although mutation or deletion of receptor residue can affect the statistics of both the number and energy of a well. A molecular origin of the well would be inconsistent with the hundreds-of-nanometers size of the effective potential well that has been reported so far (13, 27). At this stage, the relations among the local molecular energy and the size and depth of potential wells remain unclear, and future research should clarify their identity (13, 34).

Counterexample, extension of the SPT analysis, and novel organized features

Are areas of large density necessarily due to long-range interactions and potential wells? It was found that inhomogeneous distribution of molecules could be due to random concentration fluctuations or to the topology of the membrane, unevenly sampled under total internal reflection fluorescence microscopy; this could indicate the presence of unexpected interactions modifying the protein distribution. However, in agreement with the organization of this protein (12), no potential wells could be extracted that are responsible for the regions of high density of vesicular stomatitis virus glycoprotein (VSVG) (Fig. 4 I, A–C). This result confirms that VSVG is primarily freely diffusing and shows that the distribution of heterogeneities is not generated by any molecular long-range interaction. This example shows that local interaction or local aggregation can create regions of high density in the absence of any long-range interactions.

Figure 4.

Analysis of superresolution trajectories. We start with VSVG proteins. (I, A) Four samples of sptPALM trajectories (n = 30,000) of VSVG proteins. I. (I, B) Density map of the VSVG proteins containing high density areas. (I, C) Diffusion coefficient maps. Low diffusion regions are colocalized with high protein density (red squares). (I, D) Field of forces in the four squares. No potential wells can be detected, showing that proteins do not interact at potential wells. Scale bars 200 nm. Analysis of influenza virus. (I, E) Samples of influenza virus trajectories. (I, F) Examples of one directed (a), one confined (b), and two recurrent (c and d) virus trajectories. (I, G) Potential wells from the confined steps of influenza trajectories, confirming the strong presence of wells. II. A potential well on the dendritic shaft prevents receptors from entering into a dendritic spine. Trajectories were acquired during 1 min every 15 min. (II, A) Confocal image of the dendrite from a cultured hippocampal neuron. (II, B) Magnification of the region (outlined by the red square) in (II, A). (II, C) Receptor trajectories between the dendritic shaft and a single spine. (II, D) Density of points obtained from trajectories of (II, C). (II, E) As long as the potential well at the base of the spine (red circle) persists, no AMPAR trajectories can enter into the spine. After 45 min, the potential disappears and a large number of trajectories can be found inside the spine head, maintained by a potential well. (II, F) Characteristics over time of the potential well at the base (and in the head) of the dendritic spine. Scale bars (II, C–E) 1 μm. To see this figure in color, go online.

The statistical method presented above (Construction of the Coarse-Grained Model from Trajectories) that relies on a large amount of short trajectories can also be used to extract information from long recurrent trajectories, where time averaging is equivalent to space averaging (ergodicity assumption). For example, from viral trajectories that present recurrent motion in a confined microdomain, it is possible to extract potential wells of sizes 200 nm (Fig. 4 I, E–G). Finally, once it becomes clear that potential wells carry physical information, their presence indicate a molecular or subcellular organization involved in controlling trafficking, flux, or number of particles (molecules, receptors, etc.). The physical notion of a potential well is more than a statistical entity; it represents a mixture of physical forces induced by a subcellular and molecular organization at tens to hundreds of nanometers, and thus can be used to interpret trafficking. For example, the appearance or disappearance of wells is certainly a means to regulate trafficking, as shown in Fig. 4 II; as long as a potential well is presented at the base of a dendritic spine, no trajectories can penetrate into the spine head; but after it disappeared, a large number of trajectories can be detected in the spine head, suggesting that wells can regulate the flux of receptors in dendritic spines (13, 22) and thus regulate synaptic transmission and perhaps plasticity. This relation between physical object and membrane trafficking is a first step toward anchoring cellular trafficking in physical concepts. Undoubtedly additional regulatory mechanisms associated to potential wells will be unraveled in the near future.

Effects of measurements noise

The inclusion of Gaussian instrumental noise in the model of the measurements has been investigated in Vestergaard et al. (26). In this case, the model of the acquired data is

$$\dot{\mathit{Y}}=\dot{\mathit{X}}+\sigma \dot{\mathit{\xi }},$$ (8)

where ξ(t) is modeled as standard Brownian motion, independent of w(t); and σ is a small parameter that represents the assumption that the measurements noise is small relative to all other parameters in the model. In this case, the model from Eq. 2 of the acquired data is replaced with

$$\dot{\mathit{Y}}=\mathit{b}\left(\mathit{Y}\right)+\sqrt{2}{\mathit{B}}_e\left(\mathit{Y}\right)\dot{\mathit{w}}+\sigma c\left(\mathit{Y}\right)\mathit{\xi }+O\left({\sigma }^2{\mathit{\xi }}^2\right),$$ (9)

where c(Y) depends on b(Y) and B_e(Y), or instead replaced with the discrete version of Eq. 9. Due to the independence of the noises, the expectations in the corresponding version of Hoze and Holcman (unpublished data) give the same drift and diffusion tensor with a correction of ∼σ² (unpublished data) induced by a varying drift. In particular, the extracted attractors of the drift fields and their stability change insignificantly with the amplitude σ. In particular, this analysis shows that wells cannot be due to tracking artifacts or fixed spots. Finally, the drift varies significantly at potential wells and any Gaussian approximation should include a term with the Laplacian of the potential well ΔV. The motion blur due to the open camera shutter during acquisition can also be included in the analysis, as recently discussed in Berglund (36) and Vestergaard et al. (26).

Numerical simulations in empirical domains

Once the coefficients b(x) and D_e(x) are reconstructed by the method given in Construction of the Coarse-Grained Model from Trajectories, any number of trajectories from Eq. 2 can be simulated at any time resolution for arbitrarily long times in a routine manner, using numerical procedures described in Holcman and Hoze (22) (Fig. 5 A). The long trajectories can reveal the biological timescale of molecular trafficking events. For example, the distribution of the time a receptor resides in a dendritic spine can be recovered from long trajectories, but not from short ones. Similarly, the transition time from the dendrite to the head of the spine can be determined by such simulations (Fig. 5). Using coarse-grained stochastic simulations, it was found that the residence time of a receptor in a dendritic spine was ∼3 min when the motion was pure diffusion and ∼4 min, 30 s when an inward drift was applied.

Figure 5.

Stochastic numerical simulations in empirical domains (22). (A) Scheme of an algorithm that converts a large number of single-particle trajectories into drift and diffusion tensors (B). (C) A low-pass filter is used to remove isolated pixels of simulations. (D) Example of a vector field and a stochastic trajectory generated in the image of a dendritic spine. (E) Example of a trajectory generated with and without a drift. Poissonian statistics are collected and the exit rate is the reciprocal of the residence time of a receptor in a spine. To see this figure in color, go online.

The computation of the mean first passage time to any boundary that requires either solving a boundary value problem (10) or running Brownian simulations can be solved by generating as many trajectories as needed in an empirical domain obtained from the microscopy image of the cell, with appropriate conditions at the boundary. Finally, it should be borne in mind that simulations in the projection plane involve various difficulties due to incomplete coverage of the surface by projected points. A new approach to this problem is proposed in Holcman and Hoze (22).

Simulations can serve other different purposes, but there are several pitfalls that should be avoided when performing stochastic simulations in empirical domains: the Fokker-Planck equation that describes the probability density function cannot be approximated by master equations, especially when the drift vector and diffusion tensor are not known in the entire domain, which is usually the case. Ignoring boundary behavior of trajectories distorts the Markovian simulation scheme, which requires a nontrivial reflection procedure at the boundary. The only way to extract a Fokker-Planck equation from data is to estimate the coefficients from the data, as described above. Simulations of long trajectories of the assumed diffusion process can be run once the coefficients have been estimated in the entire domain and their boundary behavior has been determined. If the coefficients cannot be recovered, filtering procedures are needed to eliminate unresolved pixels. A smoothing procedure is also necessary to avoid the effect of a discontinuous diffusion tensor introduced during the discretization procedure for the estimation step. We recall that simulated trajectories characteristics cannot be compared to experimental ones, because theoretically, as explained above, all diffusion processes may have the same trajectories, but with different probabilities. Simulated trajectories do not match empirical trajectories. What can be matched are the various statistics of the trajectories, although it is not enough to match moments; statistics, such as first passage times (which may be rare events), cannot be extracted from short simulations and certainly not from short fragments of trajectories.

Conclusions

There seem to be four general lessons to be learned from this review, as follows:

• 1)In order to gain insight into the molecular motion on a membrane from superresolution single-particle trajectories, an adequate physical model is needed. The simplest one attributes the motion of receptors on the membrane to diffusion. Thus, a relevant model is the Saffman-Delbrück version of Langevin’s equation (20, 21) for the motion of transmembrane molecules. Such a model assumes a field of force and a diffusion coefficient in a homogenous membrane. The physical origin of the force field should be found. It is important to note that the single particle trajectories of superresolution data are acquired with finite resolution, so the data necessarily undergo spatio-temporal coarse-graining on an inhomogeneous membrane, which may contain a variety of obstacles at various spatial scales. Thus a physical model of the coarse-grained trajectories does not necessarily satisfy the conditions of Langevin’s equation. For example, the fluctuation-dissipation principle does not necessarily hold for the coarse-grained trajectories, or for the drift field (which may not be a gradient of a potential; see ring structures extracted in Holcman and Hoze (35)).
• 2)Langevin’s overdamped equation is based on the assumption that the acquired trajectories are those of a diffusion process, which is not obviously true. To use a diffusion model, the data have to satisfy certain criteria. Specifically, their first and second infinitesimal moments have to be O(1) for Δt → 0, while a moment of order >2 (e.g., of order 2 + δ for some δ > 0) has to be o(1) as Δt → 0. When these conditions are satisfied, the two moments can be statistically estimated from the data, and they completely determine the diffusion process (36).
• 3)Once the diffusion model has been determined, it is possible to generate numerical simulations of long trajectories and thus acquire statistics that are not contained in the short recorded trajectories. Stochastic simulations of trajectories from Eq. 2 can be generated by Euler’s, or any other scheme (37). These trajectories can be used to calculate unidirectional fluxes, residence times, escape rates from any domain of interest, and so on (see also Holcman and Hoze (35) for a partial implementation).
• 4)There is a gaping chasm between physical scenarios and cell biology (38) that remains open. Certainly, new physics underlying the recorded motion can emerge from a diffusion model and its simulations, and should be expected to shed some light on physical properties of the membrane, on the dynamics of the cytoskeleton, and possibly on the biochemical properties of interacting molecular partners.

Editor: Brian Salzberg.

Appendix: Dictionary of Diffusion Theory

Basic notions

The basic notions of random processes begin with the standard definition of a random (stochastic) process X(t) in the space ${\mathbb{R}}^{\mathit{d}}$ (or in any other state space S). Loosely speaking, it is a collection of random variables X(t) ∈ S ordered by time. This means that for each t and every event A in S, the specific event {X(t) ∈ A} occurs with a given probability, Pr{A}. If the probability Pr{A} has a density function p(x,t), then we write p(x,t) = Pr{X(t) = x} and

$$\text{Pr}\left\{A\right\}=\text{Pr}\left\{\mathit{X}\left(t\right)\in A\right\}=\underset{A}{\int }p\left(\mathit{x},t\right)d\mathit{x}.$$ (10)

If the values of X(t) are confined to a subset Ω ⊂ ${\mathbb{R}}^3$, the process is said to be defined in Ω. For example, the Brownian motion with diffusion coefficient D in ${\mathbb{R}}^3$, whose trajectories start out at the origin, has the probability density function

$$\begin{array}{l}\text{Pr}\left\{\mathit{X}\left(t\right)=\mathit{x}\right\}=\frac{\text{exp}\left\{-|\mathit{x}{|}^2/2Dt\right\}}{{\left(2\pi Dt\right)}^{3/2}},\\ \text{for}\mathit{x}\in {\mathbb{R}}^3,t>0,\end{array}$$ (11)

thus, Brownian motion is a Gaussian process.

A stochastic process X(t) is said to be given if all its multidimensional joint probabilities Pr{X(t₁) ∈ A₁, X(t₂) ∈ A₂,…,X(t_n) ∈ A_n} for all t₁ < t₂ < ··· < t_n and A₁,A₂,…,A_n ⊂ S and all n, are known. The transition probability density function p(y,t|x,s) of a stochastic process X(t) in Ω is the conditional density

$$\begin{array}{l}p\left(\mathit{y},t|\mathit{x},s\right)=\text{Pr}\left\{\mathit{X}\left(t\right)=\mathit{y}|\mathit{X}\left(s\right)=\mathit{x}\right\},\\ \text{for}\mathit{x},\mathit{y}\in \Omega ,t>s.\end{array}$$ (12)

The transition probability density function of pure Brownian motion is

$$\begin{array}{l}\text{Pr}\left\{\mathit{X}\left(t\right)=\mathit{y}|\mathit{X}\left(s\right)=\mathit{x}\right\}=\frac{\text{exp}\left\{-\frac{|\mathit{y}-\mathit{x}{|}^2}{2D\left(t-s\right)}\right\},}{{\left(2\pi D\left(t-s\right)\right)}^{3/2}}\\ \text{for}\mathit{y},\mathit{x}\in {\mathbb{R}}^3,t>s.\end{array}$$ (13)

For example, the density of the multidimensional joint probability Pr{X(t₁) ∈ A₁, X(t₂) ∈ A₂,…,X(t_n) ∈ A_n} for Brownian motion is given by

$$\text{Pr}\left\{\mathit{X}\left(t_1\right)={\mathit{x}}_1,\mathit{X}\left(t_2\right)={\mathit{x}}_2,\dots ,\mathit{X}\left(t_n\right)={\mathit{x}}_n\right\}=$$ (14)

$$p\left({\mathit{x}}_n,t_n|{\mathit{x}}_{n-1},t_{n-1}\right)p\left({\mathit{x}}_{n-1},t_{n-1}|{\mathit{x}}_{n-2},t_{n-2}\right)\cdots p\left({\mathit{x}}_2,t_2|{\mathit{x}}_1,t_1\right).$$ (15)

It should be borne in mind that by definition, a Gaussian random variable or random process is defined only in full space and not in a finite domain or on a closed surface. Thus, a recorded trajectory fragment of motion on a neuronal membrane cannot be taken from a Gaussian process. For example, Brownian motion with reflecting boundaries in an interval of length L has the transition density

$$p\left(y,t|x\right)=\sum _{n\in Z}\frac{1}{\sqrt{4\pi Dt}}\left(e^{-{\left(x-y-nL\right)}^2/4Dt}+e^{-{\left(x+y+nL\right)}^2/4Dt}\right),$$ (16)

which is not Gaussian.

Markov and diffusion processes

A continuous-time Markov process X(t) is a stochastic process such that

$$\text{Pr}\left\{\mathit{X}\left(t_n\right)\in A_n|\mathit{X}\left(t_{n-1}\right)\in A_{n-1},\mathit{X}\left(t_{n-2}\right)\in A_{n-2},\dots ,\mathit{X}\left(t_1\right)\in A_1\right\}=\text{Pr}\left\{\mathit{X}\left(t_n\right)\in A_n|\mathit{X}\left(t_{n-1}\right)\in A_{n-1}\right\},$$ (17)

for all t₁ < t₂ < ··· t_n and A₁,A₂,…,A_n ∈ S. That is, the process forgets its past. Obviously, a Markov process is completely determined by its transition probability density function.

A diffusion process X(t) in the entire space ${\mathbb{R}}^3$ is defined mathematically as a Markov process such that the first and second infinitesimal moments of the increment ΔX(t) = X(t + Δt) – X(t), defined as

$$\begin{array}{c}\mathit{b}\left(\mathit{x},t\right)=\underset{\Delta t\to 0}{\text{lim}}\frac{\mathbb{E}\left[\Delta \mathit{X}\left(t\right)|\mathit{X}\left(t\right)=\mathit{x}\right]}{\Delta t},\\ \mathit{D}\left(\mathit{x},t\right)=\underset{\Delta t\to 0}{\text{lim}}\frac{\mathbb{E}\left[\Delta \mathit{X}{\left(t\right)}^T\Delta \mathit{X}\left(t\right)|\mathit{X}\left(t\right)=\mathit{x}\right]}{2\Delta t},\end{array}$$ (18)

are finite and a higher moment vanishes. That is, there is δ > 0 such that

$$\underset{\Delta t\to 0}{\text{lim}}\frac{\mathbb{E}\left[|\Delta \mathit{X}\left(t\right){|}^{2+\delta }|\mathit{X}\left(t\right)=\mathit{x}\right]}{\Delta t}=0.$$ (19)

The vector field b(x,t) in ${\mathbb{R}}^3$ is called the infinitesimal drift and D(x,t) is called the diffusion tensor. There is always a matrix B(x,t), called the diffusion matrix, such that $\mathit{D}\left(\mathit{x},t\right)=\left(1/2\right)\mathit{B}\left(\mathit{x},t\right){\mathit{B}}^T\left(\mathit{x},t\right)$.

Stochastic differential equations

Given a sufficiently regular drift field b(x,t) and diffusion matrix B(x,t), there is a diffusion process whose drift field and diffusion tensors in Eq. 18 are the given ones. The diffusion process is constructed as a limit of the Euler numerical scheme

$$\begin{array}{c}{\mathit{X}}_{\Delta }\left(t+\Delta t\right)={\mathit{X}}_{\Delta }\left(t\right)+\mathit{b}\left({\mathit{X}}_{\Delta }\left(t\right),t\right)\Delta t+\mathit{B}\left({\mathit{X}}_{\Delta }\left(t\right),t\right)\mathit{n}\left(t\right)\sqrt{\Delta t},\\ \mathit{X}\left(0\right)={\mathit{X}}_0,\end{array}$$ (20)

where for each t the vectors n(t) = (n₁(t), n₂(t), n₃(t))^T are standard independent normal (Gaussian) variables $\mathcal{N}$(0,1). It can be shown that X_Δ(t) converges (in some sense) to a diffusion process X(t), whose infinitesimal drift and diffusion are the given ones (10). The limit process is defined as the solution of the stochastic differential equation

$$\dot{\mathit{X}}\left(t\right)=\mathit{b}\left(\mathit{X}\left(t\right),t\right)+\mathit{B}\left(\mathit{X}\left(t\right),t\right)\dot{\mathit{w}}\left(t\right).$$ (21)

The limiting process is

$$\mathit{w}\left(t\right)=\underset{\Delta t_j\to 0}{\text{lim}}\sum _j\mathit{n}\left(t_j\right)\sqrt{\Delta t_j},$$ (22)

where $t={\sum }_j\Delta t_j$ is called the Wiener process, or Brownian motion; and $\dot{\mathit{w}}\left(t\right)$ is called Gaussian δ-correlated white noise (10).

Trajectories of a diffusion process

It can be shown a posteriori that the stochastic process X(t) defined by Hoze and Holcman (unpublished data) is a diffusion process, and thus, the drift and diffusion coefficients determine the trajectories, and the trajectories determine the coefficients uniquely by Metzler et al. (15). The possible trajectories of a diffusion process are transformations of Brownian trajectories and thus are all possible continuous functions. Different diffusions assign to them different probabilities, so there is no direct way to recognize a diffusion process by looking at its trajectories; the recognition comes through Metzler et al. (15).

If the process X(t) is confined to a finite domain Ω ⊂ ${\mathbb{R}}^3$ with specified boundary behavior, the trajectories of X(t) in Ω are different than those in ${\mathbb{R}}^3$, because they may be absorbed; totally, or partially, reflected in the boundary; stay in the boundary for a random time; and so on. Thus, a diffusion process confined to a finite domain cannot be Gaussian; even a confined Brownian motion is not Gaussian. A diffusion process on a finite surface, such as diffusion on a sphere, is defined by local projections on the tangent plane at each point. The diffusion process in the tangent plane is projected back onto the surface (39). Obviously, such a diffusion process cannot be Gaussian. In all cases, however, Metzler et al. (15) determines the coefficients in Ω. In the stationary case, once the drift field and diffusion matrix have been determined at each point of the domain Ω, arbitrary long trajectories of the process can be simulated by solving Eq. 21 with the Euler scheme from Eq. 20.