Predictive Spatiotemporal Manipulation of Signaling Perturbations Using Optogenetics

Abstract

Recently developed optogenetic methods promise to revolutionize cell biology by allowing signaling perturbations to be controlled in space and time with light. However, a quantitative analysis of the relationship between a custom-defined illumination pattern and the resulting signaling perturbation is lacking. Here, we characterize the biophysical processes governing the localized recruitment of the Cryptochrome CRY2 to its membrane-anchored CIBN partner. We develop a quantitative framework and present simple procedures that enable predictive manipulation of protein distributions on the plasma membrane with a spatial resolution of 5 μm. We show that protein gradients of desired levels can be established in a few tens of seconds and then steadily maintained. These protein gradients can be entirely relocalized in a few minutes. We apply our approach to the control of the Cdc42 Rho GTPase activity. By inducing strong localized signaling perturbation, we are able to monitor the initiation of cell polarity and migration with a remarkable reproducibility despite cell-to-cell variability.

Introduction

Over the last couple of years, the development of optogenetics actuators for cell biology has dramatically increased. The toolbox of light-gated molecular systems is continuously expanding, with photosensitive proteins covering almost all the spectrum from UV to far red (reviewed in Pathak et al. (1)). It is now possible to control many intracellular processes (reviewed in Tischer and Weiner (2)), such as receptor transduction (3), protein degradation (4), protein localization (5), or protein sequestration (6) with an optogenetic approach. This success can be attributed to the fact that optogenetic tools are genetically encoded, triggered by light such that they can be easily modulated in time and space, have fast kinetics and excellent reactivity, and that most of them are reversible.

One of the most striking benefits of optogenetics is the ability to perform transient and spatially confined signaling perturbations (7). Indeed, most of the usual genetic and pharmacologic approaches induce only permanent and global perturbations on protein signaling. But, in their natural context, almost all signaling proteins in the cell display rich spatiotemporal patterns of activity as observed with fluorescent reporters and biosensors (8, 9). One important question is to know whether the spatiotemporal features of optogenetically controlled activity patterns can match those of endogenous signaling activities. In fact, a proper characterization of the spatial and temporal resolutions that can be achieved with contemporary optogenetic tools is still lacking. Here we address this problem by developing a quantitative biophysical approach enabling a predictive manipulation of protein distribution at the subcellular scale.

Among the optogenetic molecular systems proposed recently to control cell polarity and migration (10, 11, 12, 13) or intracellular signaling through protein localization (14, 15, 16), the CRY2/CIBN dimerizer system (17) appears especially promising (18) and versatile (6). Importantly, it presents a low dark activity but a strong and robust binding upon light activation without the need for a cofactor (19). In a 2012 study on lipid signaling, Idevall-Hagren et al. (15) demonstrated that local CRY2 protein recruitment to the plasma membrane was achievable. Yet, a comprehensive framework for the quantitative control in space and time of protein recruitment to the membrane is still lacking.

Here we present a predictive subcellular control of protein distribution on the plasma membrane. By studying the biophysical parameters governing the molecular processes of the CRY2/CIBN optogenetic system for plasma membrane targeting, we report a simple, easy to set up, reproducible, and versatile method to control signaling activities at a subcellular scale and with a temporal control of a few tens of seconds. Importantly we provide a set of rules allowing an inexperienced user to apply spatially restricted signaling perturbations within the cell. Eventually, we demonstrate the efficiency of the CRY2/CIBN system to activate endogenous signaling pathways by inducing cell migration through local and sustained subcellular activations of cdc42.

Materials and Methods

Cloning

The Intersectin DH PH domain linker (ITSN(DHPH)-Linker) gene was amplified from ITSN(DHPH)-Linker-YFP-PIF (gift from O. Weiner, University of California, San Francisco) and cloned into CRY2PHR-mCherry (gift from C. Tucker (University of Colorado, Denver), hereafter called “CRY2”) using Nhe1 and Xho1 enzyme sites that resulted in ITSN(DHPH)-Linker-CRY2PHR-mCherry. All plasmids contain the generic CMV promoter (backbone pmCherryN1 from Clontech Laboratories, Mountain View, CA).

Cell culture and transfection

NIH 3T3 fibroblasts and HeLa cells were cultured at 37°C in 5% CO₂ in DMEM (Dulbecco’s modified Eagle’s medium) supplemented with 10% fetal calf serum. Transfections were performed using X-tremeGENE 9 (Roche Applied Science, Penzburg, Bavaria, Germany) according to the manufacturer’s instructions using an equal amount of cDNA for the two dimerizer CIBN and CRY2 (1 μg/mL).

Live cell imaging

Twenty-five-mm glass coverslips were prepared both with and without round patterns of fibronectin bovine protein (Life Technologies, Carlsbad, CA) as described in Azioune et al. (20). For imaging, cells were dissociated using Accutase (Life Technologies) and incubated on those coverslips for at least 45 min. Experiments were performed at 37°C in 5% CO₂ in a heating chamber (Pecon, Meyer Instruments, Houston, TX) placed on an inverted microscope model No. IX71 equipped with a 60× objective with NA 1.45 (Olympus, Melville, NY). The microscope was controlled with the software Metamorph (Molecular Devices, Eugene, OR). Differential interference contrast (DIC) imaging was performed with a far red filter in the illumination path to avoid CRY2 activation. Total internal reflection fluorescence (TIRF) images were acquired using an azimuthal TIRF module (ilas²; Roper Scientific, Tucson, AZ) and laser power and exposure time were chosen to prevent photobleaching.

Fluorescence quantification and cell segmentation

We analyzed movies with custom-built routines in MATLAB (The MathWorks, Natick, MA). We removed background from raw images, and extracted kymographs and mean fluorescence in a region of interest (ROI) over time. The segmentation of cell borders (for example) was performed on fluorescence images using a threshold based on the average level of the noise (MATLAB function “Graythresh”). The membrane ruffling activity (see Fig. 6 d) was determined using DIC images on which we applied a detection of pixel intensity changes (using MATLAB function edges).

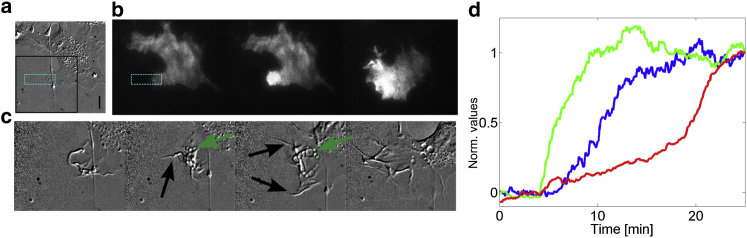
Figure 6.

Local activation of Cdc42 in fibroblast cell generates membrane activity and cell barycenter displacement. (a–c) DIC images (a and c) and TIRF images (b) of a fibroblast illuminated locally by a rectangular ROI (1 pulse every 20 s, blue region). (a) The cell is represented before the activation routine. Scale bar = 10 μm. (b) TIRF images before, at 1 min, and 50 min after activation. (c) Zoom-in of the black area of (a) for 8, 17, 30, and 50 min after the beginning of the activation routine. (Black arrows) Presence of filopodia; (green arrows) localization of vesicles. (d) Quantification of pmCRY2 recruitment in the activation area (green), of membrane activity (blue) and of cell barycenter displacement (red) over time normalized between 0 and 1. To see this figure in color, go online.

Normalization

All recruitment curves obtained from TIRF images were normalized to the fold increase of fluorescence (relative changes): after background subtraction, the value of fluorescence for each time point was divided by the initial fluorescence (averaged over the first frames without activation). The curves in Fig. 6 d were normalized between 0 and 1 to compare the kinetics. The curves in Figs. 2, e and f, and 3, a–c, were normalized between 0 and 1, where 1 stands for the maximal recruitment. The exponential gradients of Fig. 4 e were normalized using the same procedure as in Gregor et al. (21) to align the distributions of CRY2 coming from different cells without introducing a spatial bias in the averaging procedure.

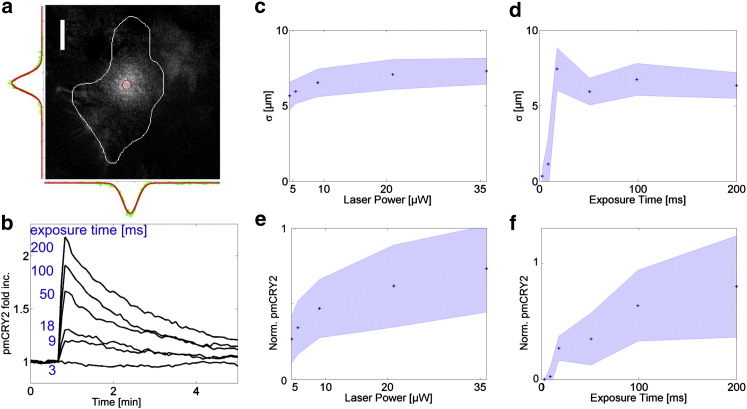
Figure 2.

CRY2 recruitment as a function of illumination characteristics. (a) Differential TIRF image of pmCRY2 3s after the illumination with a local pulse of blue light. (White line) Contour of the cell. (Side curves) pmCRY2 intensity (green) and Gaussian fit (red) along a line across the activation area (red circle). Scale bar = 10 μm. (b) Quantification of the mean intensity in the activation area (red circle, a) divided by its mean value before activation as a function of time for activating pulses of different duration in a single cell. The exposure times were chosen equal to 3, 9, 18, 50, 100, and 200 ms. Images are taken every 5 s. The temporal decay (∼80 s) is governed by lateral diffusion because the diffusion time is smaller than the complex dissociation (185 s) for such point activations. (c–f) Mean values (blue dots) and standard deviation (blue-shaded regions) of pmCRY initial Gaussian distribution after a single pulse of activation. The average width σ (c and d), and total integrated amount (e and f) calculated from the integral of the Gaussian 2πσ_xσ_yA are plotted as a function of laser power (c and e) and exposure time (d and f). In (d) and (f) the laser power is fixed at 5.5 μW and the pulse durations are 3, 9, 18, 50, 100, and 200 ms (N = 15 cells). In (c) and (e) the exposure is fixed at 50 ms and the laser power is set to 4.5, 5.5, 9, 21, and 36 μW (N = 25 cells). To see this figure in color, go online.

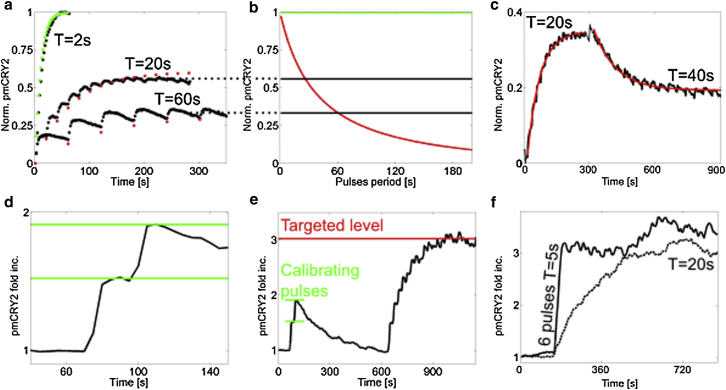
Figure 3.

Level control of pmCRY2 using pulse frequency. (a) Experimental TIRF intensity of pmCRY2 (black) as a function of time in the same cell for different activation frequencies (one pulse of 50 ms and 21 μW every 2, 20, and 60 s). The intensity is normalized by the final level of the curve with the period of 2 s. The parameters f and C₀ were obtained from the fitted theoretical values of M_n (green dots) to the experimental curve of period 2 s. These parameters were used to predict the theoretical values of M_n for periods of 20 and 60 s (red dots). (b) Theoretical dependency of the pmCRY2 steady-state value (red) on the period of the activating pulses for f and C₀ extracted in (a). (Black lines) Final level of pmCRY2 for the experimental curves (shown in black) in (a), which correspond theoretically to periods of 26 and 61 s. (c) Experimental values of pmCRY2 over time for a single cell (black). After 5 min, the initial stimulations done every 20 s have been modified to one pulse every 40 s. The experimental curve was fitted with exponentially relaxing functions (red). The normalization is done with regards to the maximal steady value as in (a and b). (d and e) pmCRY2 over time after 2 pulses of blue light spaced out by 25 s and then regular periodic pulses (a period of 25 s after 10 min). (d) Initial 150 s of this experiment (one image every 5 s) with the two calibrating response levels used to extract the parameters f and C₀ (green lines). (e) pmCRY2 over time (black) for the total duration of the experiment with the targeted level (computed using f and C₀ from (d), red line). (f) pmCRY2 over time for a local activation with a constant frequency either with (black) or without (dashed black) a first round of activation at high frequency (six pulses with periodicity of 5 s). In both cases, the steady state is maintained with one pulse every 20 s (50 ms at 9 μW power). To see this figure in color, go online.

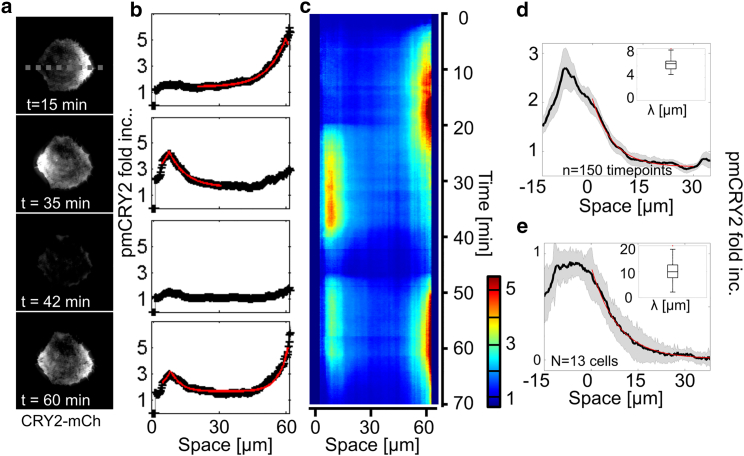
Figure 4.

pmCRY2 spatial distribution for a punctual activation. (a–c) CRY2-mCherry TIRF signals of a cell being successively activated in different points (a) and its corresponding kymograph (c) showing the quantified pmCRY2 profile along a horizontal line as exemplified for t = 15, 35, 42, and 60 min (b). First activations between time t = 2 min and t = 20 min in the right of the cell (one pulse every 25s). Second activation routine between t = 20 min and t = 35 min on the left of the cell. Third set of activations between t = 46 and 60 min on both sides. The decaying spatial distributions at steady state (black) were fitted with exponentially decreasing functions (red). The cell is initially plated on a 50-μm-diameter round pattern of fibronectin. (d) Quantification of the variability of the exponential gradient over time. An exponential gradient was established on one side of a round cell and maintained for >30 min (Movie S4). (Black line) Average gradient over 30 min; (gray shadow) 1 standard deviation. (Inset) Boxplot of the decay lengths measured for each time point (n = 150), λ_exp = 6.3 ± 1 μm. (e) Quantification of the variability of the exponential gradient for different cells. For each of the 13 cells, we used the time-averaged distribution of pmCRY2 to compute the average and SD of the pmCRY2 exponential gradient (see Materials and Methods for the normalization procedure). (Inset) Boxplot of the decay lengths measured for each cell, λ_exp = 10.5 ± 5 μm. To see this figure in color, go online.

Fluorescence recovery after photobleaching experiments and photoactivation

For fluorescence recovery after photobleaching (FRAP) experiments on CIBN-GFP-CAAX, we used a 50-mW 405-nm laser at full power controlled by a FRAP head (Roper Scientific) to photobleach a round area with a diameter of 3 μm during 1 s. To photoactivate CRY2, we used the same FRAP head, but we used a 488-nm laser at low laser power (5–10%). The FRAP data were analyzed considering a purely diffusive process in two dimensions, which leads to the recovery (22)

$$C_{\text{tot}}\left(t\right)=\int Cdxdy=\text{exp}\left(-\frac{2{\tau }_D}{t}\right)\left[I_0\left(\frac{2{\tau }_D}{t}\right)+I_1\left(\frac{2{\tau }_D}{t}\right)\right],$$

where C is the amount of plasma membrane CIBN at positions x, y and time t, τ_D = a²/4D is the diffusion time (a being the radius of the bleached area), and I₀ and I₁ are the modified Bessel functions of the first kind. Experimentally, C_tot(t) was obtained by integrating the fluorescence intensity over the whole ROI used for photobleaching. We determined the value of the diffusion coefficient D by fitting the experimental recovery curve to the theoretical expectation (Fig. S1, a–c, in the Supporting Material).

To measure the dissociation kinetics of the CRY2/CIBN dimer, we assumed a first-order dissociation process such that

$$M_{\text{tot}}\left(t\right)\propto \text{exp}\left(-k_{\text{off}}t\right),$$

where M_tot(t) is the total amount of plasma membrane CRY2, and k_off is the dissociation rate. By fitting the experimental data with an exponentially decaying function (Fig. S1, d–f) we obtained the dissociation time as τ_off = 1/k_off.

Results

Local recruitment of CRY2-mCherry at the basal plasma membrane

The plasma membrane CRY2/CIBN optogenetic system is composed of two proteins that are expressed by the cell: CIBN-GFP-CAAX (CIBN) localized at the cell membrane with a CAAX anchor and CRY2PHR-mCherry (CRY2), which is initially cytoplasmic (17). Under blue illumination (<525 nm), CRY2 changes conformation and gains the ability to bind to CIBN. In cells expressing these two proteins, the formation of the dimer leads to a relocalization of CRY2 from the cytoplasm to the cell membrane. In our experiments, we used a 488-nm focalized scanning laser beam at low power (4–20 μW) to shine light in a selected ROI. We quantified the amount of CRY2 at the basal plasma membrane (pmCRY2) by imaging the cell in TIRF mode, thereby imaging CRY2 proteins only when they become recruited.

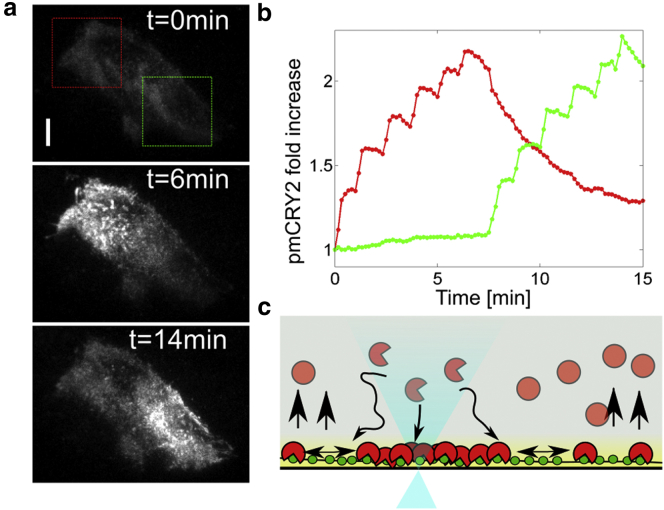
By periodically shining blue light in a restricted area of a cell (6 pulses of 100 ms spaced out by 80 s in the indicated red box followed by six pulses in the indicated green box, Fig. 1, a and b, and Movie S1 in the Supporting Material), we recruited CRY2 locally at the plasma membrane, in the region of activation. After a pulse, the cytoplasmic volume partly depleted of CRY2 is refilled in a few seconds with fresh nonactivated CRY2. This replenishment allows the recruitment of more CRY2 as observed by the increasing amount of pmCRY2 each time a pulse of light is applied (Fig. 1 b). The evolution of pmCRY2 between each light pulse and after the total illumination sequence is controlled by the lateral diffusion and natural dissociation of the light activated CRY2/CIBN dimer. On the one hand, the lateral diffusion of the dimer at the plasma membrane tends to homogenize the pmCRY2 concentration over the whole cell membrane. This is revealed by the slight but continuous increase of fluorescence in the green region while recruitment is done in the red region (Fig. 1 b, from 0 to 7 min). In addition, the complex dissociation decreases the amount of pmCRY2, as observed in the red region when no light is shone (Fig. 1 b, from 7 to 15 min). Therefore, the binding, diffusion, and dissociation processes (summarized in Fig. 1 c) are the key parameters controlling the level and the spatial distribution of pmCRY2. In the following sections, we quantify the biophysical characteristics of these processes to set up a predictive framework of pmCRY2 dynamics.

Figure 1.

Physical processes responsible for local recruitment of pmCRY2. (a) CRY2-mCherry TIRF images before illumination (top) and after six local activations in the indicated red box (middle) and after six activations in the indicated green box (bottom). (b) Quantification of the relative increase of signal in the red and green region over time. (c) Scheme of the biophysical processes involved in CRY2-mCherry localization at the plasma membrane. Inactive cytoplasmic CRY2 (solid red circles) changes conformation upon illumination into an active state (open red circle) that diffuses to the membrane and binds CIBN (solid green circles). (Yellow region) Evanescent TIRF field. (Black arrows) Diffusion-limited membrane recruitment, lateral diffusion, and dimer dissociation altogether representing the cycle of CRY2 in a steady and localized stimulation (blue cone of light). To see this figure in color, go online.

CRY2 membrane distribution following a single pulse of light

To map the relationship between the illumination properties and pmCRY2 initial distribution, we first characterized the elementary response to a single localized pulse of light. Right after a pulse, the maximal pmCRY2 recruitment is observed after a characteristic time of τ_on = 2.2 s ± 0.4 s (N = 10) (Fig. S1, g–i). This time is very fast in comparison to all other characteristic times of this system and is similar to the characteristic time for the replenishment of the activated volume by a cytoplasmic protein diffusing with a diffusion coefficient of ∼10 μm²/s. For a 3-μm diameter pulse of blue light of 100-ms duration, the pmCRY2 initial distribution is well fitted by a Gaussian function (Fig. 2 a) with a standard deviation of 6 ± 1 μm. The use of a focused laser together with the large numerical aperture of the objective leads to the activation of CRY2 in a relatively wide conical volume. Assuming an angle of divergence of ∼45°, the maximal lateral extension of the cone of light will be of the order of the height L of the cell, estimated to be L ∼ 3–5 μm. Once activated, CRY2 proteins diffuse through the cytoplasm before reaching the plasma membrane and binding to CIBN. The distribution of the distance traveled laterally, before the binding event, is known (23), and it follows an exponential function of characteristic length $\sim L/\sqrt{3}$. The overall Gaussian shape of pmCRY2 then results from the convolution of the cone of activation with the spatial profile set by the three-dimensional diffusion of light-activated CRY2 and capture at the plasma membrane.

We defined the total amount of pmCRY2 being recruited in a single pulse as the integral of the initial Gaussian distribution, namely M_sp = 2πσ_xσ_yA, where σ_x, σ_y are the widths along the two major axes and A is the amplitude of the Gaussian distribution. By increasing the exposure time (T_exp) of the blue pulse from 3 to 200 ms (the laser power P being fixed to 5.5 μW; see Movie S2), we could increase A in a progressive manner (Fig. 2 b). We also varied independently P from 4.5 to 36 μW with T_exp = 50 ms and systematically assessed the dependence of M_sp on these two parameters. M_sp increases as a function of P and T_exp up to a plateau, which is reached when all CRY2 proteins in the illuminated volume are activated (Fig. 2, e and f). By further increasing T_exp on a timescale comparable to τ_on, the quantity M_sp would start to increase slowly over the plateau because a diffusive flux of inactivated CRY2 would appear in the illuminated volume. This diffusive regime is not easily quantifiable and we restricted our analysis to short pulses.

Importantly, we did not observe any dependency of σ as increasing amounts of pmCRY2 were recruited (Fig. 2, c and d). This means that the membrane anchor CIBN is not limiting and that large local concentrations of pmCRY2 can be achieved. This is coherent with our observation that, in our configuration of transient transfections, the small CIBN-GFP protein (∼50 kDa) was always expressed by the cell in a larger amount than the CRY2-mCherry protein (∼100 kDa).

Altogether, the amount of pmCRY2 recruited in a single pulse, M_sp, behaves as expected for a first-order Michaelis-Menten law,

$$M_{sp}\propto C\frac{P{T}_{\text{exp}}}{{\left[P{T}_{\text{exp}}\right]}_{1/2}+P{T}_{\text{exp}}},$$ (1)

where ${\left[P{T}_{\text{exp}}\right]}_{1/2}$ is the value of the product PT_exp needed to achieve half of the maximal recruitment (for instance ${\left[P{T}_{\text{exp}}\right]}_{1/2}$ is reached for P = 9 μW and T_exp = 50 ms), and C is the cytoplasmic concentration of CRY2 (we checked that M_sp was proportional to C for given values of P and T_exp; data not shown).

CRY2/CIBN lateral diffusion and dissociation

The initial pmCRY2 distribution obtained after a pulse of light is subsequently smoothed out by the lateral diffusion of CIBN-GFP. Using FRAP experiments, we characterized the diffusion of either the CIBN-GFP protein alone or in complex with CRY2-mCherry (Fig. S1, a–c). We measured a similar diffusion coefficient of 0.1 μm²/s ± 0.03 μm²/s in both cases (Fig. S1 c), which is in good agreement with the diffusion coefficient expected for a phospholipid or a protein anchored in the membrane (24). This value sets the characteristic time for diffusion, which is 100 min to diffuse over the whole length (∼50 μm) of the basal plasma membrane and 20 s for a small activation region of ∼3 μm size.

The total amount of pmCRY2 decreases over time due to the dissociation of the CRY2/CIBN dimer. We experimentally characterized this process by quantifying the pmCRY2 decay over time after inducing a recruitment on the whole cell (Fig. S1, d and e). We observed a single exponential decay of pmCRY2 signal, indicative of a one-step dissociation process. The characteristic dissociation time τ = 1/k_off is 185 ± 40 s, which means that 63% of the pmCRY2 disappears in 3 min and 95% in 9 min, in agreement with prior reports (17).

Quantitative control of pmCRY2 level with frequency modulation

Because the CRY2/CIBN complex dissociates, we can expect that steady levels of pmCRY2 can be maintained over time through continuous illumination with blue light. The actual steady-state value would be determined by the intensity of activating light as it was done previously for the PhyB/PIF6 system (14). In this study, a determined level of recruitment was targeted by finely tuning the intensity of light using a computer-assisted feedback loop (25). Here, we explored a different, and possibly simpler, strategy to perform a direct control of pmCRY2 steady-state levels. Rather than continuously illuminating the cell with blue light, we recruited CRY2 in successive batches using periodic pulses. Indeed, the amount of pmCRY2 recruited with a single pulse can be characterized, allowing us to then predictively target a selected steady-state value by only modulating the frequency of light pulses. From a practical standpoint, this periodic approach fits naturally with standard routines commonly used to acquire time-lapse movies with multiple wavelengths. In the following section, we develop the modeling framework describing pmCRY2 dynamics under periodic stimulations.

We call M_n and M_n^∗ the number of CRY2 proteins bound to plasma membrane before and after the nth activation pulse. C_n represents the number of CRY2 proteins in the cytoplasm. We assume the following hypotheses: 1) the total number of CRY2 proteins, C₀ = M_n + C_n, is conserved over time; 2) the quantity of protein recruited after a pulse is proportional to the number of cytoplasmic CRY2 through a factor f (smaller than 1): M_n^∗ = M_n + f × C_n; and 3) pmCRY2 is released with a rate k_off = 1/τ such that M_n+1 = M_n^∗exp(−Δt/τ), where Δt is the time interval between two light pulses. Hence, the number of pmCRY2 proteins at time n+1 is

$$M_{n+1}=\left[M_n\left(1-f\right)+f{C}_0\right]e^{-\frac{\Delta t}{\tau }},$$ (2)

which yields the solution

$$M_n=\frac{1-{\left(1-f\right)}^n{e}^{-n\frac{\Delta t}{\tau }}}{1-\left(1-f\right)e^{-\frac{\Delta t}{\tau }}}f{C}_0{e}^{-\frac{\Delta t}{\tau }}.$$ (3)

For many applications, we are just interested in the final steady amount of recruited protein, which corresponds to the limit M_n+1 = M_n = M_∞. In this limit, Eq. 3 reduces to

$$M_{\infty }=\frac{f{C}_0}{e^{\frac{\Delta t}{\tau }}-\left(1-f\right)}.$$ (4)

We first checked our ability to modify the pmCRY2 steady-state level by tuning Δt on a single cell. By activating the same cell with three different periods (2, 20, and 60 s) while letting it rest to its basal level between each round of activation, we induced three pmCRY2 steady-state levels (Fig. 3 a). To validate our theoretical expressions for M_∞ and M_n, we extracted the values of f and C₀ from the curve corresponding to Δt = 2 s. The value of C₀ was obtained from the steady-state level of pmCRY2 reached for Δt = 2 s, which was then normalized to 1. We assumed that for this stimulation condition all the cytoplasmic CRY2 was bound to the plasma membrane since Δt << τ. The value of f was then determined from the step increase of pmCRY2 after the first pulse, which is equal to fC₀ (f = 0.2). As seen in Fig. 3 a, for the two other conditions (Δt = 20 s and Δt = 60 s), the agreement between the expected theoretical values of M_n and experiment is excellent. The full dependency of the steady-state level as a function of Δt is plotted in red in Fig. 3 b. This curve can be used to predict the interval duration between light pulses that should be used to achieve a desired steady-state value of pmCRY2, expressed as a fraction of the maximal value (constant illumination). Note that the steady-state level of pmCRY2 can be modified in real time by changing the periodicity of the pulses (Fig. 3 c).

Although the predictive approach described above does work, the determination of the two central parameters C₀ and f requires us first to induce a full recruitment of pmCRY2. Those two parameters can be alternatively obtained by simply shining two calibrating pulses of blue light. These two pulses need to be spaced by a time larger than the characteristic time needed to equilibrate concentration in the cytosol by diffusion (τ_on ∼ 3 s) but shorter than the characteristic time of the lateral diffusion at the cell membrane and of the complex disassociation (∼180 s). Once the two successive levels of pmCRY2 M₁^∗ and M₂^∗ are known, we can express the values of f and C₀ as

$$f=1-\left(M_2^{\ast }/M_1^{\ast }-1\right)e^{\frac{\Delta t}{\tau }},$$

$$C_0=M_1^{\ast }/f.$$

We measured the two levels M₁^∗ and M₂^∗ for a representative cell activated with two pulses spaced by 25 s (Fig. 3 d). From those two values, we determined the parameters f and C₀ and used them to predict the steady state that would be achieved with a period Δt = 25 s (Fig. 3 e). Using this predictive approach, the targeted level is reached with a relative error of 30% (N = 5), which is mainly due to the uncertainties in the determination of M₁^∗ and M₂^∗. Compared to the first method based on a first full recruitment of pmCRY2, the two-pulses method is less accurate, but only requires a relatively small recruitment—which could be beneficial when dealing with signaling perturbations.

Shortening the time to reach the steady state

As predicted by our model (Eq. 3) and observed by fitting the data (Fig. 3 c), the steady-state levels are reached exponentially with time with a characteristic time τ. However, one can shorten this time by first doing a high-frequency activation to directly target this steady value. We have to determine from Eqs. 3 and 4 the number of activating pulses needed to reach a fraction x of the steady state M_n = xM_∞ (under the condition that Δt > τ_on):

$$n=\frac{\text{ln}\left(1-x\right)}{\text{ln}\left(1-f\right)-\Delta t/\tau }.$$

Taking a numerical example, we can see that seven pulses are needed to reach 90% (x = 0.9) of the steady value corresponding to an interval between pulses of Δt = 20 s and a fraction of the total CRY2 recruited in one pulse of f = 0.2. In addition, we calculated the number of fast pulses of period Δt_f << Δt needed to reach the fraction x of the steady state corresponding to the period Δt as

$$n_f=\frac{\text{ln}\left(1-x_f\right)}{\text{ln}\left(1-f\right)-\Delta t_f/\tau },$$

where $x_f=(e^{\Delta t_f/\tau }-\left(1-f\right))/(e^{\Delta t/\tau }-\left(1-f\right))$ is the fraction of the fast frequency steady state equaling the slow frequency steady state. Coming back to our numerical example, only four pulses of period Δt_f = 5 s are needed to reach the steady value corresponding to the period Δt = 20 s. In this case, the steady state is reached in ∼20 s instead of the ∼140 s we would need with a constant frequency of pulses. Using this approach, we can induce and maintain the steady-state level predicted for Δt = 20 s with a fast off/on control (Fig. 3 f).

Spatial distribution of pmCRY2

We now consider the subcellular distribution of pmCRY2 following a spatially localized activation. The processes of binding to the plasma membrane, lateral diffusion, and dissociation can be combined in the following diffusion-reaction equation satisfied by the number of recruited pmCRY2 as a function of time and position on the membrane,

$$\frac{\partial M\left(x,y,t\right)}{\partial t}=D{\Delta }_{2d}M\left(x,y,t\right)-k_{\text{off}}M\left(x,y,t\right)+S\left(x,y,t\right),$$ (5)

where Δ_2d is the Laplacian operator in two dimensions and S(x,y,t) is the source term, which is directly related to the characteristics of the activating blue light: laser power, exposure time, frequency of pulses, and spatial extension of the illuminated area.

Equation 5 is found in many other biological contexts. Indeed, a localized source with diffusion and degradation is a general physical process known to generate molecular gradients as illustrated by the morphogen gradients that pattern tissues during embryogenesis (26). This equation introduces a typical length scale $\lambda =\sqrt{D/k_{\text{off}}}$, which is the key parameter dictating the spatial distribution of pmCRY2. This characteristic length scale sets the lower limit of the size over which CRY2 can be recruited. In our case, considering the value of D and k_off previously determined, we obtain λ = 4.5 μm. This value explains why we can achieve local recruitment in a HeLa cell (Fig. 1 a), which is ∼10 times larger.

To underline the role of λ, cells were initially plated on 50-μm-diameter round pattern of fibronectin to obtain calibrated cellular shapes. We performed experiments with periodic stimulations in a circular region with diameter 3 μm and chose a period of pulses (25 s) smaller than the dissociation time. We could establish and maintain a subcellular gradient of pmCRY2 (Fig. 4, a–e, and Movies S3 and S4) quantified by the fluorescence profile at steady state along a line going through two extremities of the cell. As expected from the solution of Eq. 5 for a one-dimensional infinite space with a point source, the distribution of pmCRY2 at steady state (M^∗_ss) is well fitted with an exponentially decaying function,

$$M_{ss}^{\ast }\left(x|x_0\right)\propto {\text{e}}^{-\frac{\left|x-x_0\right|}{{\lambda }_{\text{exp}}}},$$

where x₀ is the position of the point source and λ_exp the experimental decay length of the exponential function. We measured a characteristic length λ_exp = 10.5 ± 5 μm (Fig. 4 e). This value is approximately twice larger than the theoretical expectation λ = 4.5 μm because the source term in our experiments is not perfectly punctual. Indeed, the activations are performed in a disk and CRY2 proteins diffuse laterally in the cytoplasm before binding to CIBN.

Thanks to the dynamic property of the steady state, the exponential gradient of pmCRY2 could be entirely reversed by moving the activating spot of light within a timescale 3τ ∼ 9 min, which is limited by the dissociation kinetics (Fig. 4, a–c). Note that the amplitudes of the left and right exponential gradients differ because the local geometry of the cell contributes to the amount of pmCRY2 recruited in one batch (the parameter f). Thus, to perform a local recruitment with a precisely targeted level, the calibration pulses need to be done in the same region. Overall, the temporal variability of the exponential gradient (15% variations in λ_exp, Fig. 4 d and Movie S4) is much lower than the intercellular variability (45% variations in λ_exp, Fig. 4 e).

The knowledge of pmCRY2 profiles at steady state for a punctual illumination can be used to compute the relation between any light pattern and pmCRY2 spatial distribution. The distribution of pmCRY2 at steady state (M_ss) is the convolution of the illumination distribution S(x₀) and the propagator M^∗_ss:

$$M_{ss}\left(x\right)=\int d{x}_0{M}_{ss}^{\ast }\left(x|x_0\right)S\left(x_0\right).$$ (6)

In Fig. S2, a and b, we illustrated theoretically this convolution by replacing the integral by a sum of exponentially decaying curves with a weight depending on the illumination characteristics. For example, if the activation is done uniformly in a rectangular region, the source term in one dimension will be a rectangle function and the corresponding steady-state concentration will be a plateau with exponentially decaying tails on the sides of the activated region (Fig. S2 a). A linear pattern of light will lead to a linear pmCRY2 profile in the central region surrounded by exponentially decaying tails on its border (Fig. S2 b).

Experimentally, the source term is not pointlike because of CRY2 cytoplasmic diffusion. As shown in Fig. 2 a, a single pulse leads to a Gaussian distribution of pmCRY2, which depends on cell height. The steady-state solution of the diffusion-reaction equation can also be solved with a Gaussian source term (27), but the solution is more complex. However, the effect of this extended source is minor for large regions of activation. By shining light in a square region, we observe a plateau of pmCRY2 in the illuminated region surrounded by decaying tails of characteristic length λ_exp (Fig. S2, c and d).

Altogether, using Eq. 6 we can achieve any desired spatial profile of pmCRY2 provided that its local sharpness is not greater than the 10-μm exponential decaying function. Importantly, if we are not entirely depleting the cytoplasm from CRY2, changing the frequency of pulses affects only the overall amount of recruitment. One can thus control the level of pmCRY2 independently of its spatial profile, and the predictive control of pmCRY2 levels with the frequency of pulses presented above still applies for spatially heterogeneous illuminations.

Subcellular control of Cdc42 activity

The presented optogenetic approach allows the manipulation of protein distribution with a spatial resolution of a few microns and a temporal resolution of a few minutes. This makes it a good candidate to perturb Rho GTPase signaling, which presents spatiotemporal patterns of activities with similar characteristics (8, 9). As a matter of fact, the endogenous mechanisms giving rise to patterns of Rho GTPase activation most probably rely on diffusion-reaction processes similar to the ones described above (28, 29).

We demonstrate here our approach to the Rho GTPase Cdc42 with a similar strategy to that developed initially with the PhyB/PIF6 optogenetic system (14). The strategy is based on the local recruitment to the plasma membrane of the Intersectin (ITSN) guanine exchange factor (GEF) catalytic domain (DHPH domain). The catalytic domain of ITSN is specific to Cdc42 and triggers the transition from its inactive GDP-loaded state to its active GTP-loaded state. By itself, the catalytic domain does not localize to the plasma membrane and is expected to remain inactive in the cytosol. We fused this domain to CRY2-mCherry so that light could be used to rescue its membrane localization and induce Cdc42 signaling. When the fusion was expressed in cells and in the absence of activating light, we did not notice any phenotypical change due to a constitutive activation of Cdc42 in the dark. However, under blue light illumination, ITSN-DHPH-CRY2-mCherry (optoGEF-Cdc42) was recruited at the plasma membrane and led to the activation of the endogenous pool of Cdc42.

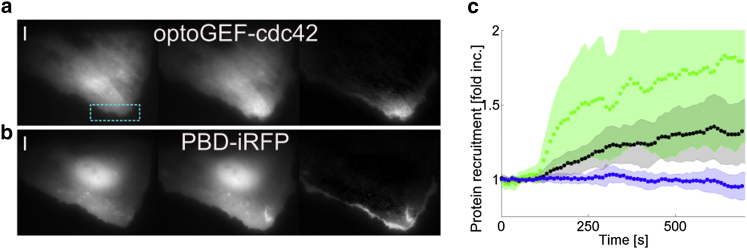
Following a sustained activation in a subcellular region, the recruitment of optoGEF-Cdc42 (Fig. 5 a) showed characteristics similar to the pmCRY2 distributions presented above with a constant value inside the region of activation and an exponential tail of decay length λ_exp = 9 ± 1.5 μm (Fig. S3). This subcellular recruitment induced Cdc42 activity, as observed by the localization of the effector Pak1 Binding Domain fused to the infraRed Fluorescent Protein (PBD-iRFP). Remarkably, the optoGEF-Cdc42 and PBD-iRFP signals are enriched at the same place (Fig. 5, a and b), and we did not observe a significant spatial extension of the signaling activity despite the catalytic nature of our optogenetic actuator OptoGEF Cdc42. As noted previously for Rac1 (30), this suggests that either Cdc42 proteins have a reduced mobility when activated or that activated Cdc42 proteins are rapidly deactivated before they move away from the region of activation. In terms of kinetics, optoGEF-Cdc42 and PBD-iRFP recruitments are similar with almost no delay (Fig. 5 c). Thus, the relationship between optoGEF-Cdc42 distribution and Cdc42 activation can be assumed immediate and linear.

Figure 5.

Local recruitment of optoGEF-Cdc42 activates Cdc42. (a and b) TIRF images of OptoGEF-Cdc42 (a) and PBD-iRFP (b) before activation (left), 6 min after activation (middle), and differential images (right). (Blue rectangle) Activations. (c) Average time courses (dots) and standard deviation (shaded regions) over N = 10 cells of OptoGEF-Cdc42 (green) and PBD-iRFP (black) in the activated region (one image every 10 s, one activation every frame starting at time 100 s). PBD quantification in another region of the cell is represented as a control (blue). To see this figure in color, go online.

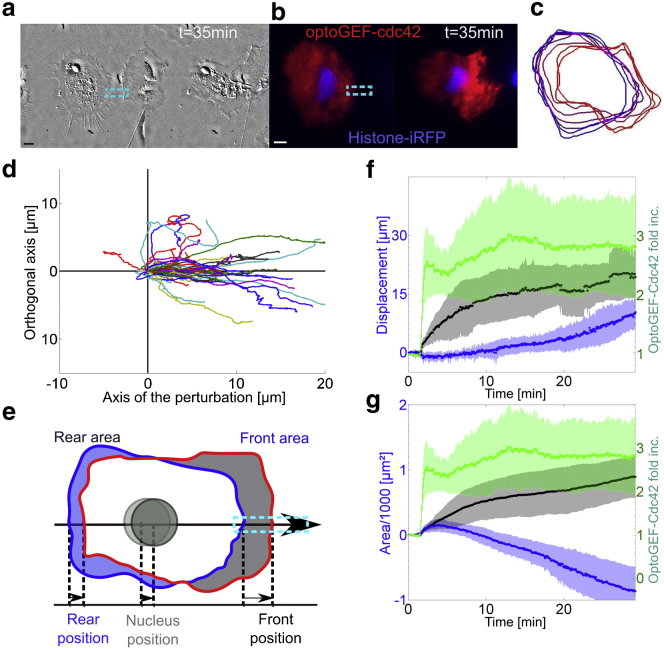
At the morphological level, by applying and maintaining a subcellular gradient of optoGEF-Cdc42 (Fig. 6, a–d and Movie S5) we provoked a direct and major effect on the cell phenotype. A couple of minutes after recruitment (Fig. 6 b), we observed a large increase in membrane activity, the formation of filopodia, membrane extrusions, and macropinocytotic vesicles (Fig. 6, c and d). These events came along with alternating phases of membrane protrusion and retraction, with a timing of few minutes. In addition to these local morphological effects, our optogenetic perturbation also affected the global phenotype of the cell. After a period of 10 min, the cell barycenter started to move (Fig. 6 d). The optoGEF-Cdc42 pattern is extending as the cell gets into the activation region and the cell retracts at its opposite side. From an initially unpolarized state, the cell adopted a clear front-to-rear polarized migrating phenotype. Such optogenetic initiation of migration was extremely robust; even blebbing cells or cells engaged in cell-to-cell contact could be triggered into a migratory state (Movies S6 and S7).

We then performed sharp off-on local Cdc42 optogenetic activation on a large number of HeLa cells (Fig. 7, a and b and Movies S8 and S9) to quantify the time course of polarity formation and migration initiation. By segmenting the cell contour over time (Fig. 7 c), we extracted the time course of the cell barycenter displacement (Fig. 7 d) and cell front/rear displacements and areas along the migration axis (summarize in Fig. 7 e). Following the optogenetic activation, the front of the cell started to move in <2 min while the rear of the cell started to retract after a delay of ∼10 min (Fig. 7 f). These dynamics are consistent with what has been observed recently using a light-activated Rac1-GPCR system to induce immune cell migration (13). In all cases, the displacement of the nucleus was following the rear of the cell (data not shown), suggesting that a net movement of the cell was achieved only when the back of the cell started to retract. The time course of the front and rear areas (Fig. 7 g) showed that both increased initially. This unexpected small extension of the rear area could be either due to an unmeasurable leakage of the optogenetic activation or to a global cellular response to the local strong increase of Cdc42 activity.

Figure 7.

Quantitative measurement of HeLa cell movement in response to optoGEF-Cdc42 gradient. (a and b) Local activation of Cdc42 in a HeLa cell expressing OptoGEF-Cdc42 and H2B-iRFP. DIC images (a) and fluorescent images (b) showing mCherry (red) and iRFP (blue) at two time points, before (left) and 28 min after activation (right). (Dashed-blue rectangles) Area of blue illumination. (c) Outline of the cell for increasing time points (from blue to red) over 30 min. The outer border of the cell was segmented from TIRF mCherry images every 4 min. (d) Quantification of the displacement of the cell barycenter for 30 min moves along and perpendicularly to the main axis of the cell for N = 36 cells. The main axis is defined by a line passing through the cell barycenter at t = 0 min and the position of the recruitment. (e–g) Quantification of cell movement induced by local Cdc42 activation for N = 5 cells. (e) Scheme of the different elements being quantified: cell front, rear, and nucleus displacement along the migration axis and the evolution of the areas of the front and the rear. (f and g) Quantification of OptoGEF-Cdc42 in the photoactivated region (green) and of the barycenter displacement (f) and area (g) of the front (black) and the rear (blue) of the cell. The photoactivation was done with six pulses of 50 ms every 5 s, followed by pulses of 50 ms every 25 s. (Shaded areas) Mean ± SD (dots). To see this figure in color, go online.

Discussion

The use of optogenetic molecular systems to perform intracellular signaling perturbations is rapidly increasing. The main advantage of using light compared to other approaches such as chemically induced dimerization methods (31) is the ability to apply spatially restricted perturbations. Yet, the conditions required to achieve a given subcellular spatial resolution depend on precise knowledge of the biophysical processes involved during the optogenetic activation. Using the CRY2/CIBN light-inducible dimerization system for manipulating protein distribution on the plasma membrane, we provided an in-depth characterization of these processes. We showed that the two intrinsic parameters controlling the dynamics of membrane-bound dimers are the lateral diffusion coefficient D of the dimer and its lifetime τ.

The recruitment of CRY2 to the plasma membrane occurs in a few seconds, enabling fast perturbations. For most of the intracellular signaling pathways, this timing is one order-of-magnitude faster than the cellular response, and the perturbation can be assumed instantaneous. However, the lifetime of the complex limits the shutdown of induced perturbations and 10 min are needed to go back to the resting state. Thus, one inconvenience of the CRY2/CIBN system is that it precludes the temporal dissection of intracellular signal processing at frequencies >1/600 = 0.0025 Hz, as recently done for the Ras/ERK pathway using the PhyB/PIF6 system (32). Yet, in many cases, one is interested in dissecting the temporal order of events after a signal is imposed. In this situation, the only requirement is to be able to impose a fast off/on perturbation and to maintain it over time. We showed an example of such an approach for dissecting the initiation of cell migration with a localized cdc42 perturbation, as discussed further below.

We achieved a control in the level of membrane-recruited CRY2 through the modulation of the frequency of activating light pulses. The advantage of this method compared to continuous illumination is that it allows a predictive control of the steady-state level and it limits the exposure of cell to light. Ideally, activating pulses should be short and strong enough to activate all CRY2 present in the illuminated volume of the cytoplasm without entering into the three-dimensional diffusive replenishment regime. Thus each batch of activated CRY2 will be maximal and more reproducible. Typically, the pulses are 100-ms long with a light intensity comparable to the one used for imaging.

The steady-state level of CRY2 recruitment reached for a maintained pulsatile activation depends only on two parameters: the initial cytoplasmic concentration of CRY2 and the fraction of this concentration, which is depleted in one pulse. We showed that these two parameters could be measured before the establishment of a targeted level by applying two successive light pulses. Yet, this calibration needs to be done before each specific activation in a cell, which can be problematic for high-throughput approaches. To overcome this limitation, further quantitative analyses should be performed on stable cell lines expressing a titrated amount of each optogenetic partner (using lentiviral infection and FACS sorting as done in Toettcher et al. (32), for example) and making use of adhesive micropatterns to normalize cell shapes (20).

However, not all experiments require a specified steady value. The relatively slow dissociation of the CRY2/CIBN dimer allows sparse stimulations. As a general guideline, one pulse every 5 s will give a high steady-state value and one pulse every 100 s is close to the lowest limit. In between, the steady state depends exponentially on the frequency of pulses (Fig. 3 b). This general rule applies independently of the actual experimental details such as cell height, volume of illumination, etc. Yet, to perform a fast off/on recruitment and to maintain it steadily, it is necessary to quantify the recruitment parameters beforehand. For more complex time courses of CRY2 recruitment, we refer to the recent publication (33) on the optogenetic control of gene transcription, which relies on the same principle of frequency modulation.

One should note that all quantifications were based on relative fold increases from an initial background value and not on absolute concentrations. The quantification was done on TIRF images and we found that the background value was mainly due to the leaking signal from the initial cytoplasmic CRY2. Thus, both the background value and the absolute amount of recruitment scale with the level of CRY2 expression. Even though for signaling only the absolute concentration of activated proteins matters, the relative fold increase still provides an easy way to characterize perturbation intensities and to compare different optogenetic systems. In this regard, we remarked that we could achieve much higher levels of recruitment using the CRY2/CIBN system than with the PhyB/PIF6 (14) or TULIPS (16) systems. This observation can be explained by the cytosolic photosensitive protein being always in deficit with respect to the number of binding sites on the membrane. Through the successive recruitment of cytoplasmic batches, the local concentration of membrane dimers can be increased to high levels.

For local recruitment, we showed that the distribution of CRY2 on the plasma membrane was restricted by the length scale $\lambda =\sqrt{D\tau }$ ∼5 μm. The elementary steady-state response for a pointlike illumination is an exponential distribution with a decay length of λ. When the illumination is done in extended regions, the steady-state distribution is the convolution of the exponential distribution with the illumination pattern. This means that sharp spatial borders cannot be achieved and that the distribution of CRY2 on the membrane will always present exponential tails at the edge of the illuminated region. This inherent limitation of the CRY2/CIBN dimerizer could be optimized in the future by decreasing the lifetime of the complex or by immobilizing the membrane anchor. Note that this limitation is not specific to this case, but can be extended to all other optogenetic systems that are passively reversible. More generally, the reaction-diffusion processes we described in this work are common to all optogenetic systems. For example, the PA-Rac diffuses with a coefficient D = 0.55 μm²/s and reverses to a dark state in 43 s (10). This means that the length scale associated with this system is $\lambda =\sqrt{D\tau }$ ∼5 μm, similar to the CRY2/CIBN system. Recently, there has been an increased interest in the control of clustering and oligomerization processes with optogenetics (6, 34). In these cases, the clusters induced by light are probably larger than the typical size of the intracellular meshwork of actin (35, 36) (∼100 nm) and will remain almost immobile (D ∼ 0), thus enabling sharp local activations (λ ∼ 0). The actively reversible systems, such as the PhyB/PIF6 (14) and Dronpa (37) systems, are not subjected to an inherent spatial limitation as the reversion is inducible with light and thus sharp local activation can be achieved (38).

In our experimental conditions, the membrane-anchored CIBN was systematically expressed in large excess compared to the cytosolic CRY2. On the contrary, in our hands the PhyB/PIF6 and TULIPS systems tend to be in the opposite situation with a large excess of the cytoplasmic component. The imbalance of concentrations toward the membrane anchor has practical implications, as follows. First, because the membrane anchor is not limiting, the spatial distribution of membrane-bound CRY2 does not depend on the amount of recruited CRY2. Indeed, we have never observed any spatial spreading of the pmCRY2 signal exceeding our predicted value. If CIBN proteins were limiting, we would expect to see an extension of the pmCRY2 signal because the local saturation of CIBN sites would require activated CRY2 to bind further away. Thus, the level can be controlled independently of the spatial distribution and vice versa. Second, when CRY2 proteins are recruited locally, the distribution of the whole cellular amount of CRY2 is redistributed. Indeed, at steady state most of the CRY2 proteins will be depleted from the cytoplasm and will be bound on the plasma membrane. For local stimulations, CRY2 is depleted away from the region of activation and gets concentrated there. This overall manipulation of protein distribution enables the imaging of CRY2 relocalization in epifluorescence. Moreover, it allows the imaging of GFP signals if the acquisition is done once in a while to interfere minimally with the local stimulation.

Altogether, thanks to its low background and excellent reactivity (19), the CRY2/CIBN optogenetic system allows the manipulation of protein distribution on the plasma membrane over a wide dynamic range, using a simple procedure for its spatiotemporal control. This makes it a tool of choice for signaling perturbations. We assessed its potential by designing a fusion of CRY2 with the catalytic domain of Intersectin, a specific GEF for the Rho GTPase Cdc42. A similar strategy was previously developed with the PhyB-PIF6 dimerization system (14). In this study, Levskaya et al. (14) reported Cdc42 activation through the recruitment of the Cdc42 GTP binding domain of WASP (WASP-GBD). In another study, using the Dronpa system to gate the activity of ITSN on the plasma membrane, Zhou et al. (37) demonstrated local and global formation of filopodia. Using a light-gated, constitutively active form of Cdc42, Wu et al. (10) reported filopodia and membrane ruffle formation. Our optoGEF-Cdc42 construct had a strong potency in locally activating the endogenous pool of Cdc42 as well as forming filopodia, membrane ruffles, and macropinocytotic vesicles. Compared to the previous optogenetic activation of Cdc42, our perturbative approach was strong enough to induce cell migration. In this regard, an increasing number of optogenetic strategies have been proposed to control cell migration, including photoactivable Rac, optogenetic trapping (6), GPCR control (13), or light activation of growth factor receptors (3). In comparison to these methods, our optogenetic tool has the advantage of activating only the endogenous pool of the Rho GTPase (no overexpression) in a direct fashion (no intermediates). Importantly, we showed that the pattern of activated Cdc42 was matching the pattern of recruited optoGEF-Cdc42. Thus, the imaging of CRY2 recruitment provides a faithful measure of the imposed signaling perturbation. This information is of prime interest when performing quantitative analyses of input-output relationships along the Cdc42 signaling pathway.

Cell polarity and migration are highly complex processes that involve the spatiotemporal regulation of many signaling pathways, effectors, and the cell cytoskeleton. Migrating cells are characterized by a front and a back that are tightly coordinated to ensure net movement. There are many modalities of cell migration, depending on environmental cues or cellular specificities (39). Thus, there is no consensus on a universal mechanism by which cells polarize and migrate; many functional modules (9) and mechanical processes can cooperate or act individually in specific contexts to polarize cells (40). Rho GTPases are frequently involved in cell polarity and migration but the numerous feedbacks arising from signaling cross talks and cytoskeleton dynamics render difficult the identification of their role in the initiation and maintenance of a polarized state. The use of optogenetics to induce signaling perturbation offers a unique tool to overcome this complexity. We showed here that, by applying and maintaining a spatially restricted Cdc42 activity, we were able to sequence in time the events leading to cell polarization and migration in a reproducible fashion. The induction of a fast and strong perturbation shifts the functioning point of the intracellular signaling system on a timescale shorter than the ones on which feedbacks operate. Hence, such perturbations reveal the causality in signal transduction by temporarily holding down the feedbacks that are responsible for the high degree of correlation among all elements of the intracellular circuitry.

Conclusions

In this work, we presented a quantitative framework allowing the predictive manipulation of protein gradients with the CRY2/CIBN optogenetic dimerizer system. We provided a comprehensive description of the CRY2 plasma membrane recruitment and we measured the relevant biophysical parameters. Cell shape and geometry have a large impact on CRY2 membrane distribution and the implementation of a spatiotemporal feedback system would provide a significantly higher degree of control. A closed loop system requires the segmentation of the cell contour, the quantification of pmCRY2 distribution, and the application of a computed correction with the illumination. With regard to this last task, our quantitative framework will be of use to build the feedback model required to converge toward a targeted distribution of the optogenetic actuator.

We applied the CRY2/CIBN optogenetic system to dissect the initiation of cell migration following Cdc42 activation on a coarse scale by only monitoring the cellular morphology. Future works should include a more exhaustive analysis of the dynamics of selected intracellular components. In particular, we observed that even if we induced very large local concentrations of optoGEF-Cdc42, we did not saturate the endogenous pool of Cdc42. The dynamics of our reporter of Cdc42 activity, PBD-iRFP, appeared linear in space and time. It would be interesting to assess systematically if this relation holds for all perturbations and for downstream components. The front and back antagonistic functions require a nonlinear integration at some level of the transduction machinery, and optogenetics could help to pinpoint the mechanisms underlying this task.

Author Contributions

L.V. performed the experiments; L.V. and M.C. analyzed the data; F.E. and F.d.P performed preliminary experiments; A.R. performed experiments for the revision of the work; X.M. participated in the discussion of the results; L.V., F.E., M.D., and M.C. designed the research; and L.V., M.D., and M.C. wrote the article.

Editor: Klaus Hahn.

Supporting Material

Movie S1. Maintenance of a Spatially Restricted Distribution of pmCRY2

TIRF mCherry images of a HeLa cell transfected with CRY2-mCherry and CIBN-GFP and locally activated with 2 × 6 pulses of blue light. The area of activation is localized in the red, then in the green region. Scale bar = 10 μm. (Movie is related to Fig. 1.)

Movie S2. pmCRY2 Distribution after Single Pulses of Localized Light with Increasing Exposure Times

TIRF mCherry images of a HeLa cell transfected with CRY2-mCherry and CIBN-GFP. The area of activation (circle of 12 pixels diameter) is represented each time the activating light is shined. Scale bar = 10 μm. (Movie is related to Fig. 2.)

Movie S3. Remote Control of a pmCRY2 Exponential Gradients

TIRF mCherry images of a HeLa cell transfected with CRY2-mCherry and CIBN-GFP and plated on a round pattern of fibronectin. The area of activation is represented each time a blue light is shined. The area of activation is first on the right side of the cell, then on the left side of it, and finally at both sides. Scale bar = 10 μm. (Movie is related to Fig. 4.)

Movie S4. Maintained pmCRY2 Exponential Gradient

(First panel) TIRF mCherry images of a HeLa cell transfected with CRY2-mCherry and CIBN-GFP and plated on a round pattern of fibronectin. The area of activation is represented each time a blue light is shined. Scale bar = 10 μm. (Second panel) Kymograph corresponding to the quantification of the gradient along the horizontal axis. The actual time is represented by the moving line. (Third panel) Instantaneous pmCRY2 gradient (black curve) fitted by an exponentially decaying function (red curve). (Movie is related to Fig. 4.)

Movie S5. Local Recruitment of OptoGEF-Cdc42 in an NIH 3T3 Fibroblast

Fibroblast cells transfected with OptoGEF-Cdc42 and CIBN-GFP. The area of activation is represented each time a blue light is shined. (Left) DIC images. (Right) TIRF mCherry images. Scale bar = 10 μm. (Movie is related to Fig. 6.)

Movie S6. Separation of Two Cells in Contact by Local Recruitment of OptoGEF-Cdc42 in a HeLa Cell

DIC image of a HeLa cell transiently transfected with OptoGEF-Cdc42 and CIBN-GFP. The area of activation is represented each time a blue light is shined. Scale bar = 10 μm.

Movie S7. Induction of Spreading and Migration in an Initially Blebbing HeLa Cell by Local Recruitment of OptoGEF-Cdc42

DIC image of a HeLa cell transiently transfected with OptoGEF-Cdc42and CIBN-GFP. The area of activation is represented each time a blue light is shined. Scale bar = 10 μm.

Movie S8. Local Recruitment of OptoGEF-Cdc42 in a HeLa Cell

HeLa cells transfected with OptoGEF-Cdc42, CIBN-GFP, and Histone 2B-iRFP. The area of activation is represented each time a blue light is shined. (Left) DIC images. (Right) TIRF mCherry images (red) and bright-field iRFP signal (blue). Scale bar = 10 μm. (Movie is related to Fig. 7, a–c.)

Movie S9. Local Recruitment of OptoGEF-Cdc42 in Four HeLa Cells

HeLa cells transfected with OptoGEF-Cdc42-mCherry, CIBN-GFP, and H2B-iRFP for two of them. The area of activation is represented each time a blue light is shined. (Top) DIC images. (Bottom) TIRF mCherry images (red); bright-field iRFP (blue). Scale bar = 10 μm. (Movie is related to Fig. 7, f and g.)