Abstract
In this work, a chemomechanical model describing the growth dynamics of cell-matrix adhesion structures (i.e., focal adhesions (FAs)) is developed. We show that there are three regimes for FA evolution depending on their size. Specifically, nascent adhesions with initial lengths below a critical value that are yet to engage in actin fibers will dissolve, whereas bigger ones will grow into mature FAs with a steady state size. In adhesions where growth surpasses the steady state size, disassembly will occur until their sizes are reduced to the equilibrium state. This finding arises from the fact that polymerization of adhesion proteins is force-dependent. Under actomyosin contraction, individual integrin bonds within small FAs (i.e., nascent adhesions or focal complexes) must transmit higher loads while the phenomenon of stress concentration occurs at the edge of large adhesion patches. As such, an effective stiffness of the FA-extracellular matrix complex that is either too small or too large will be relatively low, resulting in a limited actomyosin pulling force developed at the edge that is insufficient to prevent disassembly. Furthermore, it is found that a stiffer extracellular matrix and/or nucleus, as well as a stronger chemomechanical feedback, will induce larger adhesions along with a higher level of contraction force. Interestingly, switching the extracellular side from an elastic half-space, corresponding to some widely used in vitro gel substrates, to a one-dimensional fiber (as in the case of cells anchoring to a fibrous scaffold in vivo) does not qualitative change these conclusions. Our model predictions are in good agreement with a variety of experimental observations obtained in this study as well as those reported in the literature. Furthermore, this new model, to our knowledge, provides a framework with which to understand how both intracellular and extracellular perturbations lead to changes in adhesion structure number and size.
Introduction
To perform functions such as proliferation (1), differentiation (2), and locomotion (3), living cells establish stable attachments to the extracellular matrix (ECM) via the formation of specialized receptor-mediated contact foci. Among all adhesion structures perhaps the best-known are focal adhesions (FAs), with a molecular structure composed of a diverse population of structural and signaling proteins. Roughly speaking, individual integrin receptors, responsible for forming molecular bonds between ECM ligands and intracellular adhesion proteins, are laterally reinforced by a layer/complex of proteins including vinculin, paxillin, and talin (4), collectively known as the adhesome or adhesion patch. This layer of proteins is then connected to the cytoskeleton/nucleus of the cell via stress fibers, composed of actin filaments and myosin motors. In addition to physically linking the cytoskeleton to the ECM, FAs also serve as signaling hubs for cells to receive information from their microenvironment and hence are believed to play key roles in processes such as development (5, 6), tumorigenesis (7, 8), and wound healing (9).
Interestingly, besides biochemical factors, accumulating evidence has demonstrated that formation and function of FAs is tightly regulated by mechanical cues (10, 11, 12, 13, 14, 15, 16). For example, it has been shown that forces generated by actomyosin contraction are essential for the stabilization of FAs (10). Furthermore, FAs display directional growth parallel to an externally applied load (11). Numerous observations also indicate that cells form larger (and more) FAs on stiffer substrates as well as develop higher intracellular traction forces (12, 13, 14, 15, 16). Various attempts have been made to theoretically explain the force-induced growth of FAs via thermodynamic arguments (17) or by examining the anisotropic stress/strain field generated in the adhesion plaque (18, 19). The lifetime/stability of adhesion structures (i.e., clusters) has also been analyzed by considering the nonuniform load distribution among molecular bonds as well as their force-modulated association/dissociation kinetics (20, 21, 22). Recently, the question of how ECM rigidity affects integrin dynamics in cells has been examined by several studies that suggest that a compliant substrate will generally impair integrin clustering (23, 24) and lead to oscillatory traction forces along with a slow retrograde flow of F-actin (25, 26).
Despite these aforementioned efforts, several important issues remain unsettled. First, in most existing models, the size of the adhesion plaque is often taken as a constant (18, 19, 20, 21, 22) or is not included in the formulation (25, 26). Likewise, ECM rigidity is often not taken into consideration in some models (17). In reality, it is conceivable that small adhesion patches can be nucleated and, depending on factors like its initial size and the stimuli received, a nascent structure (i.e., focal complex) can either grow into a mature adhesion (i.e., FA) or totally dissolve (27, 28). Significant efforts have been made to model the formation and evolution of FAs. For instance, by describing various processes involved in FA assembly via rate equations, a theoretical model (29) has been developed that captures several experimental findings. However, determining different rate parameters from experiments remains challenging. Recently, a stochastic model was also proposed by considering the force-dependent integrin binding/unbinding that drives FA growth/decay (30). This description successfully predicts sizes of FAs that were comparable to experimental observations. One assumption in this model is that the force acting on each integrin was assumed to be the same and along the normal direction. However, recent observations have indicated that the force distribution within a FA is nonuniform (12) and that the majority of force is actually applied tangentially to FAs (31). Given that the size of FAs is believed to significantly affect processes like cell migration (32) and actin recruitment/polymerization (33), this issue should be of great fundamental and practical interest. In addition, the question of whether (and how) cells will anchor themselves differently on a flat surface, like synthetic gel substrates with low porosity, or in a fibrous in-vivo-like scaffold has attracted increasing attention experimentally (34, 35). However, it seems that very few modeling efforts have been spent to address this important issue. Finally, recent observations also suggested that the physical properties of cell nucleus (12, 13) can influence the size of adhesion plaques (i.e., FAs) and intracellular tension levels, but, to the best of our knowledge, no theoretical explanation has been provided.
To address these concepts, we developed a chemomechanical model to describe the growth dynamics of adhesion plaques where important features such as the actomyosin feedback and nucleus deformability have all been taken into account. In particular, we show that pulling forces large enough to induce further assembly of adhesion proteins can only be developed at the edge of a plaque when its size is within an intermediate range, reflecting the fact that integrin bonds within small/nascent focal complexes must transmit higher loads while the phenomenon of stress concentration will take place at the edge of large adhesion patches (i.e., stabilizing as FAs). In addition, the model predicts that both nuclear and ECM rigidities tightly regulate the equilibrium length of fully developed FAs, with a stiffer surrounding environment or nucleus leading to larger adhesion plaques coupled with a higher intracellular traction force. Interestingly, switching the extracellular side from an elastic half-space (i.e., as many in vitro substrate/gels) to a one-dimensional fiber (simulating in vivo mesenchymal fibrous microenvironments) does not lead to qualitative changes to these conclusions. Connections between our model predictions and various experimental observations will also be discussed.
Materials and Methods
Model formulation: mechanical response of the system
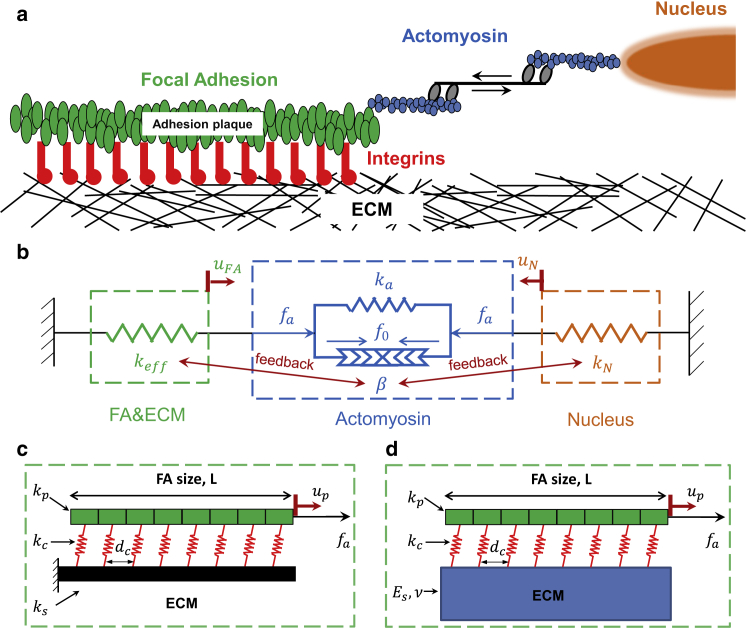
In light of the fact that a focal adhesion (consisting of individual integrins that bind to the ECM and to an intracellular layer/complex of reinforcing actin binding proteins) is connected to the cell nucleus via the actomyosin stress fiber (Fig. 1 a), a structural model as shown in Fig. 1 b is adopted here to describe the response of this ECM/FA (including adaptor adhesome proteins)-actomyosin-nucleus assembly. For simplicity, the FA-ECM complex is treated as a spring (green box in Fig. 1 b) with effective stiffness depending on the FA size and mechanical properties of the ECM, as will be illustrated later. In addition, a contractile element in parallel with a linear spring (blue box in Fig. 1 b) is used to represent myosin motors in the elastic actin stress fibers. Finally, the cell nucleus is modeled as another spring to reflect its deformability.
Figure 1.
(a) Schematic representation of the cell-to-ECM adhesions. (b) Structural model of the ECM/FA-Actomyosin-Nucleus assembly. Two types of ECM are considered in this study: a one-dimensional elastic fiber (c) and a continuous elastic medium (d), in which dc indicates integrin spacing and adhesion plaque is assumed to consist of the units of plaque protein complex (green block) and integrin (red spring). To see this figure in color, go online.
At this point, it is necessary to differentiate two types of extracellular environments that a cell can sense (on its ventral side). For the case of cells anchoring themselves in a scaffold composed of fibers, such as collagen fibrils with diameters on the order of hundreds of nanometers (36, 37) that are comparable to the size of FAs, it is reasonable to treat the ECM as an elastic fiber (Fig. 1 c), given that the entire adhesion structure (i.e., three-dimensional matrix adhesion) will likely be formed on a single fiber (38). On the other hand, for many synthetic substrates (such as PDMS and PAA) with low porosity, the anchoring distance between ECM proteins coated on the surface to induce formation of cell-ECM adhesion is generally small. In this case, the cell may not see the ventral side as an individual fiber, but rather as a continuous medium (Fig. 1 d). We proceed by considering both of these cases in this study.
If the adhesion plaque is treated as an elastic fiber of length, L, connected to the ECM via a series of equally spaced springs representing the integrin bonds formed, then the force generated in the substrate (γs) and the plaque (γp) can be expressed as γs = ksdcdus/dx and γp = kpdcdup/dx, respectively, where ks and us (or kp and up) are, respectively, the stiffness and displacement of the ECM (or the adhesion plaque), and dc is the spacing between integrins. Equilibrium requires that γs and γp must be related to the integrin clutch force γc through
| (1) |
Because each integrin bond is modeled as a spring, γc takes the simple form
| (2) |
where kc is the effective spring constant of the clutch. Note that possible sliding-induced friction between the adhesion plaque and the ECM has been neglected here for simplicity. It was widely reported that integrin binding can occur within seconds (12, 25, 26), which is much faster than the assembly of proteins in the FA (taking minutes to complete (39)). Therefore, in this study, it is assumed that assembly of the adhesion plaque is the rate-limiting step and that new integrin bonds will be rapidly formed as the adhesion plaque grows. On the other hand, once formed, the integrin-ECM bonds are treated as permanent unless disassembly of plaque proteins takes place at the corresponding site for the given time frame. With the help of Eq. 2, Eq. 1 can finally be simplified to
| (3) |
We proceed by assuming that the ECM is fixed at one end and free at the other, i.e., us(0) = 0 and dus/dx|x=L = 0 (refer to Fig. 1 c), while the plaque is pulled by the actomyosin force fa on the side proximal and remains traction-free at the other, i.e., kpdcdup/dx|x=L = fa and dup/dx|x=0 = 0 (refer to the Supporting Material for a detailed discussion on the boundary conditions). To make sure that there is room for integrins to bind, the ECM fiber beneath the FA is assumed to be of the same size as the FA. Solutions of Eq. 3, satisfying all the imposed boundary conditions, can be obtained as
| (4) |
where Lc is a characteristic length defined by
| (5) |
4Lc gives a length-scale far below which force is more or less evenly shared by the integrins within the plaque, while beyond this length the load will only be transmitted to integrin bonds within a distance ∼2Lc from the adhesion edge.
Given that the pulling force fa is acting at the end of the adhesion plaque, the effective stiffness of the FA/ECM complex can be defined as
| (6) |
with uFA being the displacement of the plaque at x = L, that is,
| (7) |
If, on the other hand, the ECM is treated as a continuous medium (Fig. 1 d), then the Green’s function for an elastic half-plane (40) can be used to relate the integrin clutch force to the substrate displacement (refer to the Supporting Material). The governing equations in this case become
| (8) |
where Es and ν, respectively, are the elastic modulus and Poisson’s ratio (taken to be 0.5 because most biological materials are known to be incompressible) of the ECM. Because closed-form solutions for the elastic fields cannot be derived in this case, numerical techniques are employed to obtain the relationship between fa (i.e., the pulling force acting on FA) and uFA (i.e., the substrate displacement at the location where the force is applied). This allows us to estimate the apparent stiffness of the FA, keff, defined in Eq. 6. Specifically, in this study, numerical simulations were carried out using the finite-element package COMSOL (COMSOL, Burlington, MA) where an elastic fiber (representing the adhesion plaque) was pulled at one end on a large elastic substrate, with springs connecting them (refer to the Supporting Material for details).
Finally, to determine the magnitude of fa, recall that the actomyosin network is represented by a contractile element in parallel with a linear spring (Fig. 1 b). Using mechanical force balance shown in Fig. 1 b, we have
| (9) |
where ka represents the stiffness of stress fiber, f0 stands for the base level contractile force generated by myosin motors, and β stands for the chemomechanical feedback effect. Base-level contractile force is defined as the total force generated by motors associated with one FA without activation of force-dependent stress fiber/myosin motor recruitment. For simplicity, the FA is assumed to be static on the ECM, and therefore the myosin motors are in a stall state (sliding velocity is zero) and f0 represents the stall force. Stresses on FAs activate signaling pathways that initiate active myosin motors and stress fiber recruitment (41, 42). Recruited myosin motors and stress fibers will in return further enhance the forces acting on FAs, thus forming a chemomechanical feedback system. The feedback parameter β is introduced to capture the essential effect in the system, which is to increase the contractile force over the baseline value. For simplicity, this parameter is taken as a constant (0.8) in the allowable range of 0 to1. Because the nucleus is simplified as a spring (with a spring constant kN), its displacement under actomyosin contraction is
| (10) |
Combining Eqs. 6, 9, and 10, the pulling force generated by actomyosin can be obtained as
| (11) |
Note that the pulling force increases with increasing feedback parameter and with increasing nuclear stiffness and the effective stiffness of the adhesion plaque, which in turn depends on its length and the stiffness of the ECM.
Model formulation: growth dynamics of the adhesion plaque
With the elastic fields within the FA at hand, we can now consider its growth via recruitment of additional adhesion proteins (e.g., vinculin, talin, paxillin) into the plaque. To simplify the analysis, we proceed by assuming that protein recruitment/disassembly can only take place at the ends of the plaque as suggested in other models (18) and progresses in a quasi-equilibrium manner. In addition, we express the chemical potential difference of a segment of protein (with length dc) assembled into the plaque and in the cytosol as
| (12) |
where Δμ0 is the chemical potential change in the absence of mechanical load (the factor 2 comes from the fact that the plaque can grow at either end), and ΔEre is the mechanical contribution (17), which takes the form
| (13) |
consistent with experimental observations (43) that tensile force promotes FA assembly and stabilization. Following the classical theory of linear kinetic relation, the plaque recruitment flux J (i.e., the FA growth rate) can be related to Δμ as
| (14) |
where D is a constant describing the kinetics of protein assembly. In steady state, the plaque will possess a constant size and hence J = 0.
The values of parameters adopted in this study along with their sources are listed in Table 1 (44, 45, 46, 47, 48, 49, 50). In addition, the physical meanings of all of the other variables in our model are also gathered in Table 2.
Table 1.
List of parameters used in the model
| Model Parameter | Description | Typical Value | Source |
|---|---|---|---|
| Es | substrate modulus | ∼1∼50 kPa | typical modulus of hydrogels used as ECM (34, 39) |
| ks | substrate stiffness | ∼1–100 pN/nm | estimated collagen fiber stiffness from experiment (36, 37, 44) |
| kc | integrin stiffness | 5 pN/nm | estimated from Fisher et al. (45), of the order of pN/nm |
| kp | plaque stiffness | 1 pN/nm | estimated from Fisher et al. (45), of the order of pN/nm |
| dc | integrin spacing | ∼100 nm | Cavalcanti-Adam et al. (46), 108 nm |
| f0 | actin pulling force without feedback | ∼100 pN | Mogilner and Oster (47), 0–200 pN |
| ka | actin stiffness | ∼50 pN/nm | Kojima et al. (48), 43.7–65.3 pN/nm |
| β | feedback coefficient | 0–1 | free parameter |
| kN | nuclear stiffness | 10–50 pN/nm | estimated from experiment, of the order of pN/nm (49, 50) |
| Δμ0 | energy barrier for protein recruitment without mechanical load | 10–250 kBT | Nicolas et al. (18) |
Table 2.
Variables and their physical meaning
| Model Variables | Physical Meaning |
|---|---|
| γs | force in the substrate (ECM) |
| γp | force in the FA plaque |
| Lc | characteristic length for force transmission |
| keff | effective stiffness of the FA-ECM complex |
| up | FA plaque displacement |
| us | substrate (ECM) displacement |
| uFA | FA displacement at the proximal end |
| uN | nuclear displacement |
| fa | contractile force generated by actin |
| Δμ | chemical potential difference of adding one protein complex segment to the FA plaque |
| J | FA plaque recruitment flux |
Results and Discussion
The stiffness a cell senses increases first and then decreases as the FA grows in size
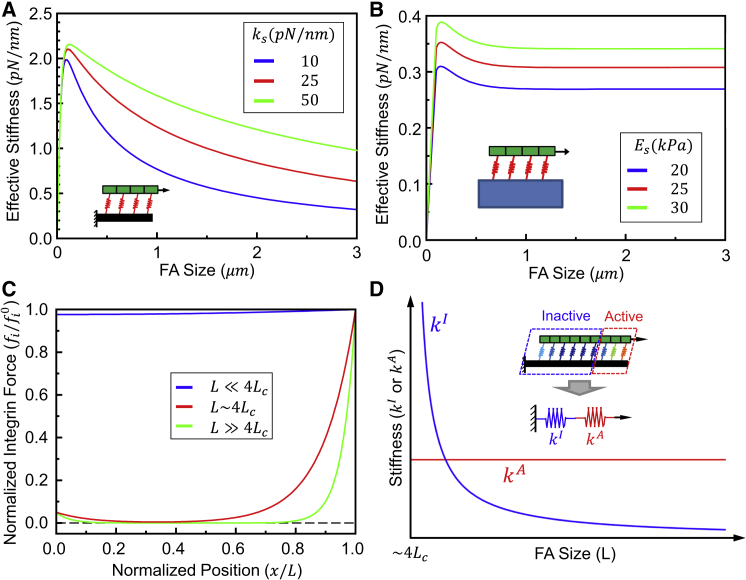
A quantity of key interest is the effective stiffness (keff) of FA-ECM complex, which physically represents the apparent mechanical stiffness of the extracellular environment that a cell senses. This parameter is plotted in Figs. 2 A and 3 both as a function of FA size and ECM rigidity, with the extracellular portion of the adhesion treated as either an elastic fiber or a continuous half-space. Interestingly, in both cases, keff reaches a maximum at a certain intermediate FA size. The major difference between the two descriptions is that this quantity will undergo monotonic decrease as the size of the FA further increases if ECM is modeled as a one-dimensional fiber. Conversely, when the ECM is treated as a continuous medium, keff will eventually reach a saturation value as the FA becomes very large (Fig. 2 B). We must point out that the overall trends of our predictions will not change if contractile force is taken to be distributed uniformly over the adhesion, instead of only acting at the right edge (refer to the Supporting Material).
Figure 2.
The effective stiffness of a focal adhesion as a function of its size and ECM stiffness, which in (A) is treated as an elastic fiber and in (B) is modeled as an elastic medium. (C) Normalized integrin force distribution (fi0 = fi(x = L)) for FAs of different sizes. For small FAs, integrin force distributes almost uniformly. The force-free region begins to show up when FA size is comparable to 4Lc; the leading edge carries the majority of integrin force and the size of this highly loaded region is a constant if FA size is much larger than 4Lc. A large FA (>>4Lc) can be divided into two parts based on the integrin force; the effective stiffnesses of the two parts are shown, respectively, in (D). Note that the horizontal axis in (D) is starting from L ∼ 4Lc. To see this figure in color, go online.
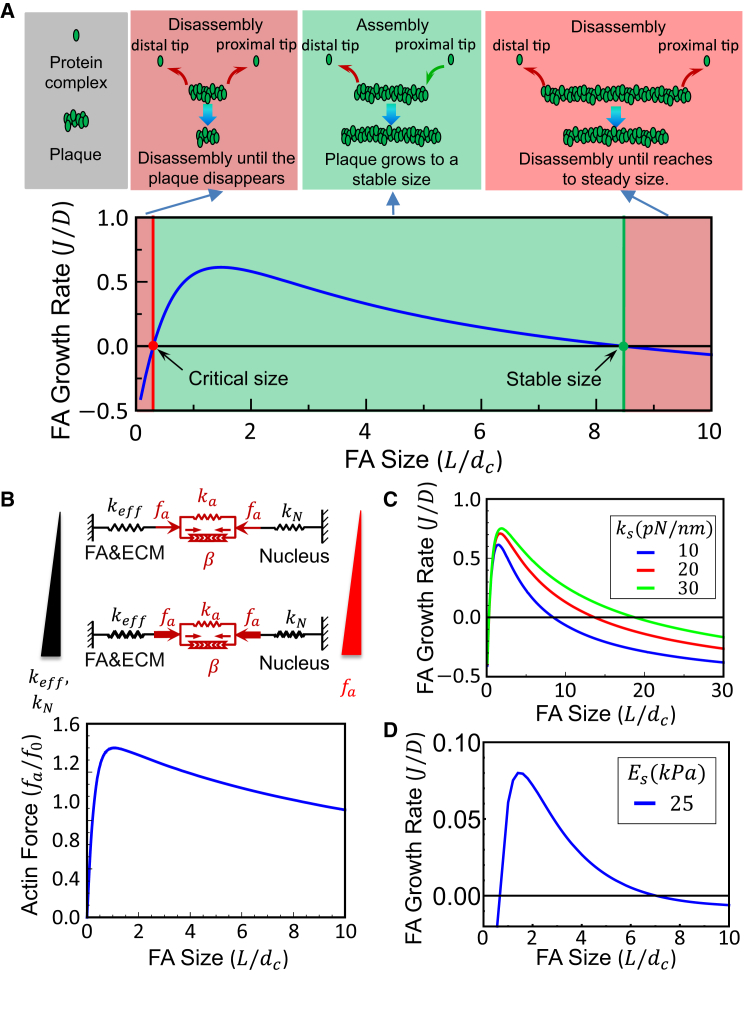
Figure 3.
(A) Generic shape of the plaque recruitment flux (J) as a function of FA size, from which two quantities of central interest, i.e., the critical size for nascent adhesions develop into mature ones, and the stable size for a fully developed FA, can be identified. The value J is positive only when the plaque size is between these two values. (B) Higher actomyosin pulling force is induced by a stiffer ECM/FA complex and/or a more rigid nucleus (top); for a given surrounding environment and nuclear property, the actin force will always reach its maximum at an intermediate FA size (bottom). Influence of the size of FA on its growth rate on fibrous (C) and continuous ECM (D) show that larger FAs will be formed on stiffer substrates. To see this figure in color, go online.
To better understand this key observation, the force distribution among integrin bonds with ECM treated as an elastic fiber was examined. As shown in Fig. 2 C, integrins carry the load uniformly for small FAs (L = 4Lc), while a force-free region emerges at the center when the FA size reaches ∼4Lc. For very large FAs (L >> 4Lc), only a region at the leading edge carries the majority of the applied force and the size of this region remains the same regardless of actual FA length. This is an inherent aspect of a shear lag loading scenario, where load penetration into an object is limited by the critical shear lag length. As such, for a given force acting on a small FA (L = 4Lc), larger FAs result in more integrins to evenly share the load and thus a smaller overall displacement, leading to the monotonic increase of keff with regard to the FA size. In contrast, a larger FA (L >> 4Lc) can be divided into an inactive and an active part, based on the integrin loading pattern, which is equivalent to two springs in series. The active part refers to the region that carries the majority of the load at the leading edge and the inactive part is the rest of the FA. Because the size of the active part is insensitive to FA length, the effective stiffness kA of this portion is therefore a constant, as shown by the red line in Fig. 2 D. For the inactive part, only the ECM fiber (connecting the active part with the boundary) is under loading and thus for this region kI ∼ EA/LI, where E is the fiber modulus, A is the cross-section area, and LI is the length of the inactive portion. Because LI increases as FAs becomes larger, the effective stiffness kI is a monotonic decreasing function of FA size as shown by the blue line in Fig. 2 D. The effective stiffness of the whole FA for a large FA (L >> 4Lc) thus scales with keff ∼ kIkA/(kI + kA) = kA – (kA)2/ (kI + kA). Consider the fact that kA is a constant and kI decreases as FAs become larger for large FAs (L >> 4Lc); the overall effective stiffness will therefore decrease with increasing FA size under this limit. As such, dc is an increasing function of FA size for small adhesion (L = 4Lc) but a decreasing function of FA size for large adhesion (L >> 4Lc), and thus reaches its maximum when FAs reach an intermediate size (L ∼ 4Lc). When treating the ECM as a continuum elastic medium the findings are similar, except that a saturation value for dc will be reached when the FA becomes very large (refer to the Supporting Material for details).
For large FAs, keff scales with 1/L (from Eqs. 6 and 7). Therefore, keff can only reach zero when the FA is infinitely large, which clearly is physiologically impossible. Furthermore, for FAs with a length of ∼10 μm, approximately twofold larger than that measured in our experiments, keff remains nonvanishing. To summarize, keff defined here will assume reasonable values when the FA size is within the physiologically relevant range.
FA plaque recruitment is divided into three regimes by two important sizes: nucleation size and stable size
The generic shape of the plaque recruitment flux J, as a function of FA size, is given in Fig. 3 A. An immediate observation from this prediction is that the value of J is positive only when Lnu < L < Lst, where Lst stands for the stable size of the plaque while Lnu can be understood as the critical size a nascent plaque must overcome to initiate elongation (i.e., minimum nucleation size). The plaque dynamics can be divided into three regimes as depicted in Fig. 3 A. Newly nucleated FAs with sizes smaller than Lnu will dissemble and eventually disappear (i.e., as described for unstable nascent focal complexes (51)). In comparison, a small FA will increase in size toward a stable length once it passes this critical value. Larger FAs (L > Lst), on the other hand, are predicted to shrink until they reach the stable size. Fig. 3 C shows how the rigidity of the ECM (a one-dimensional fiber) influences the growth rate of FAs. Our model suggests that the stable structure/plaque size increases monotonically as the external environment becomes stiffer, in agreement with recent experimental observations (13), while the critical size decreases, indicating more adhesions would form on a stiffer environment. In addition, Fig. 3 C also shows that the adhesion plaque can grow faster (i.e., has a larger J) on a stiffer ECM for large FAs, in agreement with recent experimental findings (13). Note that, due to random factors like variations in the surface topology and chemistry of the ECM, the sizes of FAs in reality will not be uniform but are expected to be distributed around the stable value predicted here.
This nonmonotonic growth rate and FA size relation can be understood by examining the intracellular tension levels predicted by the model under each configuration. As illustrated in Eq. 11, larger contractile forces will develop when cells sense a stiffer environment, with this stiffness input originating from either a more rigid nucleus or a stiffer FA/ECM complex (Fig. 3 B, top). Consequently, our model predicts that there exists an optimum size for FA to induce maximum intracellular traction force (Fig. 3 B, bottom), corresponding to the peak value of keff shown in Fig. 2, A and B. Given that fa is the driving force for plaque growth (refer to Eqs. 12–14), this explains why the recruitment flux J will be large for FAs with intermediate sizes as well as why this quantity increases with higher ECM or nuclear rigidity (Fig. 3, A, C, and D).
It is worth pointing out that a similar growth rate and size relationship for FAs (as illustrated in Fig. 3 A), as well as the conclusion that more and larger adhesions will be induced by stiffer substrates, has also been predicted by a model from Walcott et al. (30). However, unlike this study, that model treated the ECM as an array of uncoupled springs, capable of binding to integrins, and actin force was applied in the vertical direction and uniformly distributed throughout the FAs. In light of recent evidence showing that forces on FAs are almost purely tangential (31) and nonuniformly distributed (12), it appears that these assumptions are reasonable for small FAs where each integrin carries more or less the same load. As such, both this model and that of Walcott et al. (30) predict similar ECM stiffness-independent FA growth for small adhesions. However, as FAs become larger, our model shows that the tangentially applied actin force, together with a realistic treatment of the ECM (one-dimensional fiber or continuous elastic medium), will lead to load distribution in the adhesion plaque that is highly nonuniform. The size of the region for force concentration at the proximal tip of FAs depends on ECM stiffness (refer to Eq. 5), which ultimately influences the FA effective stiffness for large FAs, a feature that is not captured by the model proposed by Walcott et al. (30). From this perspective, our model may serve as a more refined and comprehensive alternative for evaluating FA growth dynamics across a range of length scales.
Cells attached to stiffer cell-derived fibrous ECM substrates build elongated adhesion structures
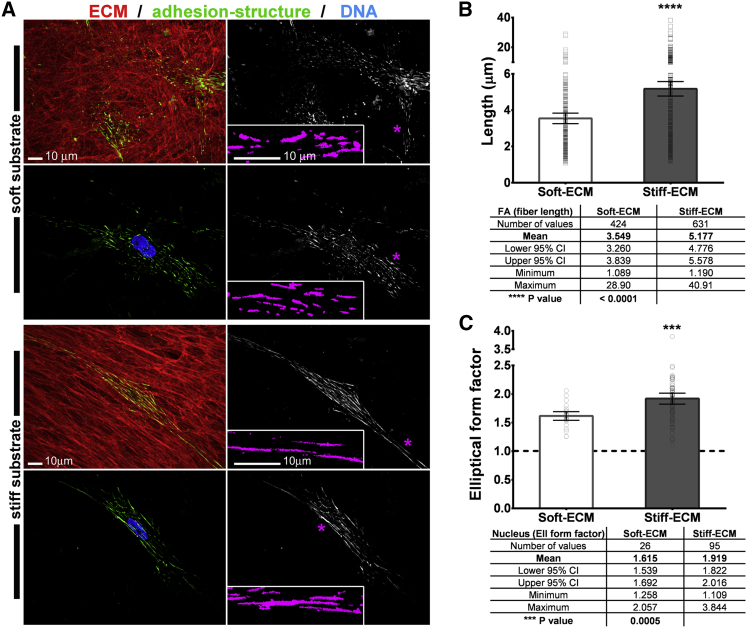
To validate the predicted increase in adhesion structure size, we utilized well-characterized, in vivo, mimetic-cell-derived fibrous ECMs (38, 52). In this system, the physiologic difference between the cells producing the ECM results in a fibrous ECM of different stiffness (53). Isogenic human fibroblasts were used to produce the relatively soft and stiff ECMs and cells that had produced the soft ECMs were cultured overnight on both fibrous substrates. As predicted, results revealed formation of larger (45.87%, P < 0.0001) adhesion structures formed by cells cultured in to the relatively stiffer ECMs compared to the length of the structures formed by the same cells cultured within the softer ECM (Fig. 4, A and B). Specifically, the stable FA size predicted by our model will decrease from 5.25 to 3.5 μm when the ECM rigidities changes from 7.5 to 5 kPa (see the Supporting Material for details), which is in good agreement with our observations here (i.e., these two values were measured to be ∼5.1 and 3.5 μm, respectively). Moreover, nuclei shape/deformability was observed in response to stiffening of the ECM (2–5 kPa in soft versus 5–15 kPa in stiff ECM, which simulate many normal versus tumoral microenvironments in vivo (53). Cells showed increased elliptical (18.82%, P = 0.0005) nuclear shape within a stiffer ECM (Fig. 4, A and C). As the model suggests that more adhesions will form on stiffer ECMs (as verified by data shown in Fig. 4 B), we expect that the force exerted on the nuclei will be larger on stiffer ECMs, leading to a more pronounced shape change of the nuclei; this is consistent with the experiment findings and shown in Fig. 4 C.
Figure 4.
Cells form larger adhesion structures on stiffer fibrous ECM matrices. Primary human fibroblasts cultured within soft (A, top two panels), or stiff (A, bottom two panels) fibrous ECMs (red) display increased length of integrin-labeled adhesion structures (green on left and corresponding monochromatic on right panels). (Blue) Elongated nucleus. (Insets) Magnifications of digitally recognized adhesion structures (purple) corresponding to the areas marked (asterisks). Fiber length measurements of adhesion structures (i.e., FAs) revealed a larger mean for cells cultured on stiff ECM (B). Analysis of the elliptical (Ell) form factor is shown in (C). To see this figure in color, go online.
Cells with stiffer nuclei have a lower barrier for FA formation and assemble larger FAs
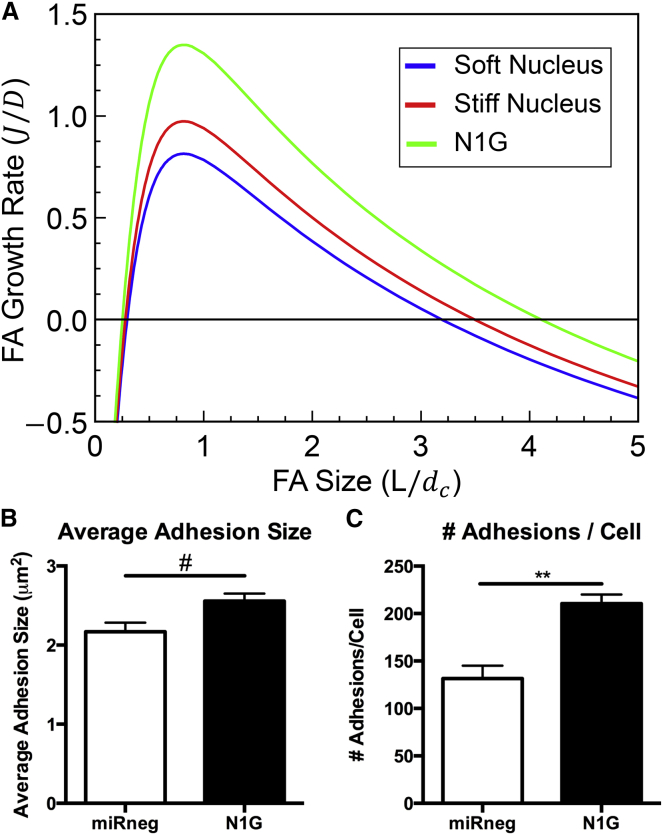
Our model also predicts a dependence of FA size on nuclear stiffness. As has been illustrated by several publications, some FAs are linked to basilar stress fibers, while others connect with the nucleus (54). Those that interact with the nucleus (a stiff but deformable object in the cell) are likely influenced by the structural and mechanical properties of this organelle. As shown in Fig. 5 A, cells that have a stiffer nucleus would be predicted to have a smaller critical FA recruitment size, meaning that the energetic barrier to FA formation would be lower. Similarly, the model predicts that a stiffer nucleus would also lead to a larger stable FA size. It is known that the nucleus is physically connected to stress fibers via the linker-of-nucleoskeleton-and-cytoskeleton complex. One specific linker-of-nucleoskeleton-and-cytoskeleton complex component that is known to regulate force transfer to the nucleus is nesprin 1 giant (N1G) (55). To simulate the effect of decreased nuclear connectivity to the cytoskeleton (as would occur with N1G knockdown), the nucleus was removed from the model altogether (Fig. 5 A, N1G). Under these circumstances, the model predicts an increase in stable FA size and decrease in nucleation size.
Figure 5.
Nuclear stiffness influences maximum FA growth rate and stable size (A). Adhesion average size (B) and adhesions per cell (C) both increase for N1G knockdown cells. Decoupling the actin pulling force and the deformable nucleus results in an increase in both average adhesion size and number of FAs per cell. Mean ± SE, # p < 0.05, ∗∗p < 0.01, n = 7–10 cells/group. To see this figure in color, go online.
To confirm these model-predicted results experimentally, and to determine the influence of the nucleus on FA size, nuclear connectivity to the cytoskeleton was eliminated via knockdown of N1G. Consistent with the model prediction, knockdown of N1G resulted in a significant increase in both the average size (Fig. 5 B) and average number (Fig. 5 C) of FAs in each cell. Essentially, knockdown of N1G in this context is comparable to replacing the deformable nucleus in our model with a rigid body.
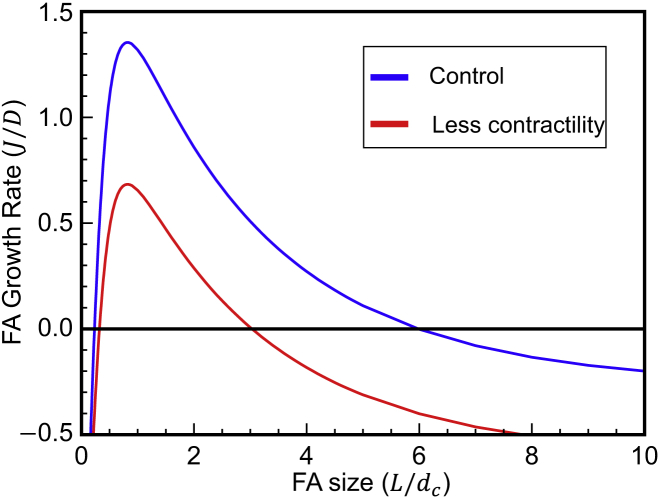
Increased contractility leads to a small drop in the FA nucleation barrier and a significant increase in stable FA size
It is well documented that cell contractility is essential for the formation of FAs, independent of ECM stiffness. Our model predicts that for cells with a lower actin pulling force (i.e., weaker contractility), the nucleation barrier for FAs will be larger while their steady-state size will become smaller (Fig. 6). Our previous experimental observations (53) show that FA sizes for Cav1 knockout mouse embryonic fibroblasts (contractility-reduced cells) are significantly smaller than wild-type fibroblasts, which is consistent with our model predictions.
Figure 6.
Increased contractility results in larger stable FAs and a smaller FA nucleation barrier. To see this figure in color, go online.
Conclusions
In this study, we developed a chemomechanical model to predict the growth of adhesion plaques, a process strongly influenced by the assembly of adhesion proteins as well as the stress buildup in the plaque itself (induced by actomyosin contractions). Main findings obtained here are summarized as follows:
-
1)
FA recruitment is divided to three regimes by two quantities of key interest, i.e., the stable size and the critical size. Nascent FAs smaller than a critical size dissolve, while bigger ones grow to a mature state whose size is limited by the stable size. Meanwhile, FAs that are too large disassemble until their sizes reduce to the stable size. Using realistic parameter values, these two sizes (length along FA long axis) were predicted to be ∼0.02 and ∼2 μm, respectively, for NIH 3T3 fibroblasts cultured on a PAA gel substrate with shear modulus of 16 kPa, in agreement with experiments (39).
-
2)
We quantitatively demonstrated how the aforementioned stable and nucleation sizes are influenced by the incorporation dynamics of adhesion proteins as well as the deformability of the substrate, the nucleus, and the plaque itself. In particular, we found that a stiffer substrate will lead to bigger plaques. In addition, with increasing substrate rigidity, more adhesions are predicted to form as a result of the diminishing nucleation size. These predictions are consistent with our experimental results (as shown in Fig. 4, A–C) and other existing results in literature (12, 14). As for nucleus stiffness, similar effects were found, where a stiffer nucleus led to a larger FA stable size and a smaller critical size. Again, this conclusion is verified by our experiments as shown in Fig. 5.
-
3)
Interestingly, the model also predicts that the growth of the plaque is significantly influenced by contractility (see the Supporting Material). Specifically, high levels of contractility will lead to bigger plaques, which is in agreement with previous observations (53). Additionally, more adhesions are expected with increasing contractility, due to the decreasing nucleation size. These predictions compare favorably with the findings that low contractility leads to decreased vinculin recruitment (56).
To make these predictions/findings transparent, the influence of key parameters on the formation of FAs is gathered in Table 3.
Table 3.
Influence of key parameters on the characteristics of FAs
| FA Characteristics | Key Parameters |
|---|---|
| Lnu, FA critical size | ks, ECM stiffness (−); kN, nucleus stiffness (−); f0, contractility (−) |
| Lst, FA stable size | ks, ECM stiffness (+); kN, nucleus stiffness (+); f0, contractility (+) |
| Number of FAs | ks, ECM stiffness (+); kN, nucleus stiffness (+); f0, contractility (+) |
The plus (+) sign means the corresponding characteristic is increasing with the increase of the parameter, and vice versa for the minus (−) sign.
We believe that this model can also be used to study phenomena such as cell locomotion (57) and stretch-induced cell reorientation (58, 59), where forces generated inside the cell and the turnover of FAs are known to play pivotal roles; indeed efforts along these lines, as of this writing, are underway.
Author Contributions
V.B.S. conceived the model; X.C., Y.L. and V.B.S. formulated the mathematical framework; X.C. carried out the computations; T.P.D., J.F.-B., E.C., and R.L.M. designed the experiments; T.P.D. and J.F.-B. conducted the experiments; and X.C., Y.L., T.P.D., J.F.-B., E.C., R.L.M., and V.B.S. wrote the article.
Acknowledgments
Research reported in this publication was supported by the National Institutes of Health with funds from the National Institute of Biomedical Imaging and Bioengineering under award Nos. R01EB017753 (to V.B.S.) and R01EB002425 (to R.L.M.); the National Cancer Institute under award Nos. U01CA202177, U54CA193417 (to V.B.S.), and R01CA113451 (to E.C.); and the U.S. National Science Foundation under grant No. CMMI-1312392 (to V.B.S.). Additional support was provided by a University Research Foundation Award from the University of Pennsylvania (to V.B.S. and R.L.M.) and an appropriation from the state of Pennsylvania to the Fox Chase Cancer Center (P30-CA006927).
Editor: Sean Sun.
Footnotes
Supporting Materials and Methods and seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00936-4.
Supporting Citations
Refs. (60, 61) appear in the Supporting Material.
Supporting Material
References
- 1.Nelson C.M., Jean R.P., Chen C.S. Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. USA. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 3.Janmey P.A., Winer J.P., Wen Q. The hard life of soft cells. Cell Motil. Cytoskeleton. 2009;66:597–605. doi: 10.1002/cm.20382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kanchanawong P., Shtengel G., Waterman C.M. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gorfinkiel N., Blanchard G.B., Martinez Arias A. Mechanical control of global cell behaviour during dorsal closure in Drosophila. Development. 2009;136:1889–1898. doi: 10.1242/dev.030866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mammoto T., Ingber D.E. Mechanical control of tissue and organ development. Development. 2010;137:1407–1420. doi: 10.1242/dev.024166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kumar S., Weaver V.M. Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Paszek M.J., Zahir N., Weaver V.M. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 9.Fenteany G., Janmey P.A., Stossel T.P. Signaling pathways and cell mechanics involved in wound closure by epithelial cell sheets. Curr. Biol. 2000;10:831–838. doi: 10.1016/s0960-9822(00)00579-0. [DOI] [PubMed] [Google Scholar]
- 10.Oakes P.W., Beckham Y., Gardel M.L. Tension is required but not sufficient for focal adhesion maturation without a stress fiber template. J. Cell Biol. 2012;196:363–374. doi: 10.1083/jcb.201107042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Riveline D., Zamir E., Bershadsky A.D. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 2001;153:1175–1186. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Plotnikov S.V., Pasapera A.M., Waterman C.M. Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell. 2012;151:1513–1527. doi: 10.1016/j.cell.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Trichet L., Le Digabel J., Ladoux B. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc. Natl. Acad. Sci. USA. 2012;109:6933–6938. doi: 10.1073/pnas.1117810109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Peyton S.R., Putnam A.J. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. J. Cell. Physiol. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- 15.Guo W.H., Frey M.T., Wang Y.L. Substrate rigidity regulates the formation and maintenance of tissues. Biophys. J. 2006;90:2213–2220. doi: 10.1529/biophysj.105.070144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lele T.P., Pendse J., Ingber D.E. Mechanical forces alter zyxin unbinding kinetics within focal adhesions of living cells. J. Cell. Physiol. 2006;207:187–194. doi: 10.1002/jcp.20550. [DOI] [PubMed] [Google Scholar]
- 17.Shemesh T., Geiger B., Kozlov M.M. Focal adhesions as mechanosensors: a physical mechanism. Proc. Natl. Acad. Sci. USA. 2005;102:12383–12388. doi: 10.1073/pnas.0500254102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nicolas A., Safran S.A. Limitation of cell adhesion by the elasticity of the extracellular matrix. Biophys. J. 2006;91:61–73. doi: 10.1529/biophysj.105.077115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lin Y., Freund L.B. Optimum size of a molecular bond cluster in adhesion. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:021909. doi: 10.1103/PhysRevE.78.021909. [DOI] [PubMed] [Google Scholar]
- 21.Qian J., Wang J., Gao H. Lifetime and strength of periodic bond clusters between elastic media under inclined loading. Biophys. J. 2009;97:2438–2445. doi: 10.1016/j.bpj.2009.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhang W., Lin Y., Gao H. Tuning molecular adhesion via material anisotropy. Adv. Funct. Mater. 2013;23:4729–4738. [Google Scholar]
- 23.Nicolas A., Besser A., Safran S.A. Dynamics of cellular focal adhesions on deformable substrates: consequences for cell force microscopy. Biophys. J. 2008;95:527–539. doi: 10.1529/biophysj.107.127399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Paszek M.J., Boettiger D., Hammer D.A. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLOS Comput. Biol. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 26.Bangasser B.L., Rosenfeld S.S., Odde D.J. Determinants of maximal force transmission in a motor-clutch model of cell traction in a compliant microenvironment. Biophys. J. 2013;105:581–592. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zamir E., Katz B.Z., Kam Z. Molecular diversity of cell-matrix adhesions. J. Cell Sci. 1999;112:1655–1669. doi: 10.1242/jcs.112.11.1655. [DOI] [PubMed] [Google Scholar]
- 28.Dugina V., Fontao L., Gabbiani G. Focal adhesion features during myofibroblastic differentiation are controlled by intracellular and extracellular factors. J. Cell Sci. 2001;114:3285–3296. doi: 10.1242/jcs.114.18.3285. [DOI] [PubMed] [Google Scholar]
- 29.Choi C.K., Vicente-Manzanares M., Horwitz A.R. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Walcott S., Kim D.-H., Sun S.X. Nucleation and decay initiation are the stiffness-sensitive phases of focal adhesion maturation. Biophys. J. 2011;101:2919–2928. doi: 10.1016/j.bpj.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Legant W.R., Choi C.K., Chen C.S. Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions. Proc. Natl. Acad. Sci. USA. 2013;110:881–886. doi: 10.1073/pnas.1207997110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kim D.-H., Wirtz D. Focal adhesion size uniquely predicts cell migration. FASEB J. 2013;27:1351–1361. doi: 10.1096/fj.12-220160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Goffin J.M., Pittet P., Hinz B. Focal adhesion size controls tension-dependent recruitment of α-smooth muscle actin to stress fibers. J. Cell Biol. 2006;172:259–268. doi: 10.1083/jcb.200506179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Trappmann B., Gautrot J.E., Huck W.T. Extracellular-matrix tethering regulates stem-cell fate. Nat. Mater. 2012;11:642–649. doi: 10.1038/nmat3339. [DOI] [PubMed] [Google Scholar]
- 35.Wen J.H., Vincent L.G., Engler A.J. Interplay of matrix stiffness and protein tethering in stem cell differentiation. Nat. Mater. 2014;13:979–987. doi: 10.1038/nmat4051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Matthews J.A., Wnek G.E., Bowlin G.L. Electrospinning of collagen nanofibers. Biomacromolecules. 2002;3:232–238. doi: 10.1021/bm015533u. [DOI] [PubMed] [Google Scholar]
- 37.Keene D.R., Sakai L.Y., Burgeson R.E. Type III collagen can be present on banded collagen fibrils regardless of fibril diameter. J. Cell Biol. 1987;105:2393–2402. doi: 10.1083/jcb.105.5.2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cukierman E., Pankov R., Yamada K.M. Taking cell-matrix adhesions to the third dimension. Science. 2001;294:1708–1712. doi: 10.1126/science.1064829. [DOI] [PubMed] [Google Scholar]
- 39.Stricker J., Aratyn-Schaus Y., Gardel M.L. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys. J. 2011;100:2883–2893. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Johnson K.L. Cambridge University Press; New York: 1985. Contact Mechanics. [Google Scholar]
- 41.Zemel A., Rehfeldt F., Safran S.A. Optimal matrix rigidity for stress fiber polarization in stem cells. Nat. Phys. 2010;6:468–473. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Besser A., Schwarz U.S. Coupling biochemistry and mechanics in cell adhesion: a model for inhomogeneous stress fiber contraction. New J. Phys. 2007;9:425. [Google Scholar]
- 43.Grashoff C., Hoffman B.D., Schwartz M.A. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gentleman E., Lay A.N., Dee K.C. Mechanical characterization of collagen fibers and scaffolds for tissue engineering. Biomaterials. 2003;24:3805–3813. doi: 10.1016/s0142-9612(03)00206-0. [DOI] [PubMed] [Google Scholar]
- 45.Fisher T.E., Oberhauser A.F., Fernandez J.M. The study of protein mechanics with the atomic force microscope. Trends Biochem. Sci. 1999;24:379–384. doi: 10.1016/s0968-0004(99)01453-x. [DOI] [PubMed] [Google Scholar]
- 46.Cavalcanti-Adam E.A., Micoulet A., Spatz J.P. Lateral spacing of integrin ligands influences cell spreading and focal adhesion assembly. Eur. J. Cell Biol. 2006;85:219–224. doi: 10.1016/j.ejcb.2005.09.011. [DOI] [PubMed] [Google Scholar]
- 47.Mogilner A., Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophys. J. 2003;84:1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kojima H., Ishijima A., Yanagida T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 1994;91:12962–12966. doi: 10.1073/pnas.91.26.12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Caille N., Thoumine O., Meister J.-J. Contribution of the nucleus to the mechanical properties of endothelial cells. J. Biomech. 2002;35:177–187. doi: 10.1016/s0021-9290(01)00201-9. [DOI] [PubMed] [Google Scholar]
- 50.Mathur A.B., Reichert W.M., Truskey G.A. Flow and high affinity binding affect the elastic modulus of the nucleus, cell body and the stress fibers of endothelial cells. Ann. Biomed. Eng. 2007;35:1120–1130. doi: 10.1007/s10439-007-9288-8. [DOI] [PubMed] [Google Scholar]
- 51.Cukierman E., Pankov R., Yamada K.M. Cell interactions with three-dimensional matrices. Curr. Opin. Cell Biol. 2002;14:633–639. doi: 10.1016/s0955-0674(02)00364-2. [DOI] [PubMed] [Google Scholar]
- 52.Castelló-Cros R., Cukierman E. Stromagenesis during tumorigenesis: characterization of tumor-associated fibroblasts and stroma-derived 3D matrices. Methods Mol. Biol. 2009;522:275–305. doi: 10.1007/978-1-59745-413-1_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Goetz J.G., Minguet S., Del Pozo M.A. Biomechanical remodeling of the microenvironment by stromal caveolin-1 favors tumor invasion and metastasis. Cell. 2011;146:148–163. doi: 10.1016/j.cell.2011.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chancellor T.J., Lee J., Lele T. Actomyosin tension exerted on the nucleus through nesprin-1 connections influences endothelial cell adhesion, migration, and cyclic strain-induced reorientation. Biophys. J. 2010;99:115–123. doi: 10.1016/j.bpj.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lombardi M.L., Jaalouk D.E., Lammerding J. The interaction between nesprins and sun proteins at the nuclear envelope is critical for force transmission between the nucleus and cytoskeleton. J. Biol. Chem. 2011;286:26743–26753. doi: 10.1074/jbc.M111.233700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Dumbauld D.W., Shin H., García A.J. Contractility modulates cell adhesion strengthening through focal adhesion kinase and assembly of vinculin-containing focal adhesions. J. Cell. Physiol. 2010;223:746–756. doi: 10.1002/jcp.22084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pelham R.J., Jr., Wang Yl. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Qian J., Liu H., Gao H. A mechanochemical model of cell reorientation on substrates under cyclic stretch. PLoS One. 2013;8:e65864. doi: 10.1371/journal.pone.0065864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ao M., Brewer B.M., Li D. Stretching fibroblasts remodels fibronectin and alters cancer cell migration. Sci. Rep. 2015;5:8334. doi: 10.1038/srep08334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Doyle A.D., Kutys M.L., Yamada K.M. Micro-environmental control of cell migration—myosin IIA is required for efficient migration in fibrillar environments through control of cell adhesion dynamics. J. Cell Sci. 2012;125:2244–2256. doi: 10.1242/jcs.098806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Beacham D.A., Amatangelo M.D., Cukierman E. Preparation of extracellular matrices produced by cultured and primary fibroblasts. Curr. Protoc. Cell Biol. 2007;Chapter 10 doi: 10.1002/0471143030.cb1009s33. Unit 10.9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.