Lack of Dependence of the Sizes of the Mesoscopic Protein Clusters on Electrostatics

Abstract

Protein-rich clusters of steady submicron size and narrow size distribution exist in protein solutions in apparent violation of the classical laws of phase equilibrium. Even though they contain a minor fraction of the total protein, evidence suggests that they may serve as essential precursors for the nucleation of ordered solids such as crystals, sickle-cell hemoglobin polymers, and amyloid fibrils. The cluster formation mechanism remains elusive. We use the highly basic protein lysozyme at nearly neutral and lower pH as a model and explore the response of the cluster population to the electrostatic forces, which govern numerous biophysical phenomena, including crystallization and fibrillization. We tune the strength of intermolecular electrostatic forces by varying the solution ionic strength I and pH and find that despite the weaker repulsion at higher I and pH, the cluster size remains constant. Cluster responses to the presence of urea and ethanol demonstrate that cluster formation is controlled by hydrophobic interactions between the peptide backbones, exposed to the solvent after partial protein unfolding that may lead to transient protein oligomers. These findings reveal that the mechanism of the mesoscopic clusters is fundamentally different from those underlying the two main classes of ordered protein solid phases, crystals and amyloid fibrils, and partial unfolding of the protein chain may play a significant role.

Introduction

Protein solutions exhibit at least three distinct classes of compact aggregates that are often referred to as “clusters”. Small clusters containing 2–10 molecules have been observed in solutions of lysozyme, insulin, and a monoclonal human antibody (1, 2, 3, 4) and are likely present in solutions of other proteins under conditions conducive of mild intermolecular repulsion. These aggregates hold a significant fraction of the total soluble protein, and their average size strongly increases with the protein concentration (2, 3, 4). Importantly, these clusters do not represent permanent structures (5) and are often viewed as dynamic formations with intermediate-range order and a lifetime of ∼25 ns (2, 6).

Clusters of the second class contain ∼1000 protein molecules (7, 8, 9). They only exist at conditions at which short-range attraction and long-range repulsion are delicately balanced: near the isoelectric point of the respective proteins and in the presence of a finely tuned concentration of a crowding agent (7), or in the vicinity of charge inversion induced by bound multivalent cations (8, 9). Similarly to the small clusters, they hold a significant fraction of the total soluble protein and the cluster sizes increase with the protein concentration (6, 10). Interestingly, while the small clusters strongly increase the solution viscosity (4, 11), the formation of the larger clusters reduces viscosity (7). In view of their effects on the solution's rheology, clusters of these two classes are scrutinized with the goal of increasing the fluidity of concentrated solutions of proteins with medical applications, e.g., monoclonal antibodies (low viscosity is deemed essential for enhanced production, purification, and delivery of these drugs (4, 7)).

Clusters of the third class have been called “mesoscopic” and demonstrated in solutions of numerous proteins at various pH values ionicities, temperatures, and compositions (12, 13, 14, 15, 16). They are distinct in several ways from the former two. Their diameters vary from ∼100 nm for the relatively small lysozyme (14) to several hundred nanometers for larger proteins (15, 17). These clusters are likely liquid (the liquid state of clusters has been evidenced in solutions of lysozyme (18), glucose isomerase (18), lumazine synthase (12), three human hemoglobin variants (19), and several other proteins (17)), and are stable for extended periods (14). Assuming that the protein concentration in the clusters is ∼500 mg mL⁻¹, similar to that in the dense protein liquid existing at similar conditions, each of them contains 10⁵–10⁶ protein molecules (13, 15, 17, 19). This number is orders-of-magnitude greater than for clusters of classes I and II. The free energy cost of high protein concentration in the clusters was evaluated for lysozyme and hemoglobin as ∼10 k_BT (k_B, Boltzmann constant; T, temperature) by integrating the concentration dependence of the osmotic compressibility (determined by static light scattering) of homogeneous solutions with concentrations similar to that in the clusters (13, 20). The Boltzmann relation predicts that owing to this free energy excess, the mesoscopic clusters would hold only 10⁻⁵–10⁻³ of the total soluble protein. This prediction is borne out by experiment, demonstrating that the clusters are in approximate equilibrium with the solution (14, 20); an early study had claimed that the clusters are nonequilibrium formations (13). Experimental determinations of the fraction of the solution volume occupied by the cluster population yield values in the range 10⁻⁷–10⁻³ (13, 14, 15, 17, 19). The low fraction of protein held in the mesoscopic clusters is in stark contrast with the clusters of the other two classes. In further contrast, the sizes of the mesoscopic clusters do not depend on the protein concentration in the host solution (14, 15, 21).

Because of their low population volume, the mesoscopic clusters do not affect the bulk solution properties. They are of interest because they may hold the key to understanding and control of ordered protein aggregation: evidence suggests that in many cases the clusters present essential sites for the nucleation of ordered solids of both folded proteins, such as crystals (17, 18, 22, 23) and sickle-cell hemoglobin polymers (24), and partially misfolded chains that form amyloid fibrils (25, 26, 27). Furthermore, the mesoscopic clusters may relate to the non-membrane-bound compartments (nucleoli, centrosomes, Cajal bodies, etc.) found to consist of dense protein/RNA liquid in several organisms (28, 29, 30, 31).

The mechanisms of formation of the clusters of classes I and II appear to be well understood in the context of colloid clustering theories (32, 33, 34). These clusters represent a balance among short-range attractions (due to depletion agents (7, 10), ion bridges (8), or shape complementarity (4)), which cause condensation, and long-range screened Coulomb repulsion, which constrains the size of the condensate domains (4, 7, 8, 10, 35). In this approach, the larger size of the class II clusters appears as the result of the nearly neutral charge of the protein molecules at the conditions of their synthesis. Furthermore, for clusters of both classes I and II, tuning the strength of Coulomb repulsion through the solution ionicity becomes an essential tool to control the average cluster size, degree of clustering, and the associated bulk solution properties (4, 7, 8, 10).

There is significantly less clarity on the nature and mechanisms of the mesoscopic clusters. Their small population volume and stable mesoscopic size challenge our understanding of phase ordering. Although the clusters are likely liquid (12, 17, 19), their region of existence in the protein solution phase diagram is away from the conditions of liquid-liquid coexistence (12, 13, 19). These clusters are much larger than what the colloid scenario for clusters of classes I and II predicts (36). An entirely distinct approach proposes that the mesoscopic clusters consist of a concentrated mixture of transient protein oligomers and monomers (13). The clusters result from interplay of monomer influx, oligomer formation, and subsequent oligomer outflow and decay. Similar reaction-diffusion schemes are derived within the hydrodynamic description by connecting the rate of approach to equilibrium and the degree of deviation from equilibrium (37). By solving two coupled reaction-diffusion equations, in which both diffusivities and reaction constants are explicitly present, the cluster size R₂ emerges as a function of the oligomer diffusivity D_oligomer and decay rate constant k_oligomer (13):

$$R_2={\left(D_{\text{oligomer}}/k_{\text{oligomer}}\right)}^{1/2}.$$ (1)

While the oligomer mechanism appears to fit the available data on the mesoscopic clusters better than the colloid theory, the applicability of either mechanism to the latter cluster class has never been systematically tested. In light of the important role that Coulomb forces play for the clusters of classes I and II, here we probe their effects on the properties of the mesoscopic clusters as a test of the colloid clustering scenario.

From a fundamental perspective, Coulomb forces determine protein three-dimensional structure (38, 39), substrate binding (40, 41), enzyme activation (42, 43), signal transduction (44), etc. Importantly, Coulomb forces govern two major classes of protein aggregation: amyloid fibrillation (45, 46, 47) and crystallization (48, 49). Hence, understanding of their role in cluster formation will highlight the similarities and differences between the formation mechanisms of the mesoscopic clusters and those two major classes of protein aggregates. Furthermore, as electrostatic forces can bind protein oligomers (50), Coulomb interactions could contribute to the oligomer scenario. Thus, quantifying the effect of Coulomb forces on the mesoscopic clusters is crucial for establishing how the clusters form. In turn, these insights may suggest strategies to control cluster populations and, in view of the clusters’ role in nucleation, the formation of ordered protein solids. Finally, the mesoscopic clusters are sometimes misidentified as clusters of class II (7, 8, 9). Thus, establishing the mechanism of formation of the mesoscopic clusters and the respective role of the Coulomb forces will allow clear distinctions between these three cluster classes and elucidate complex clustering behaviors in protein solutions.

Materials and Methods

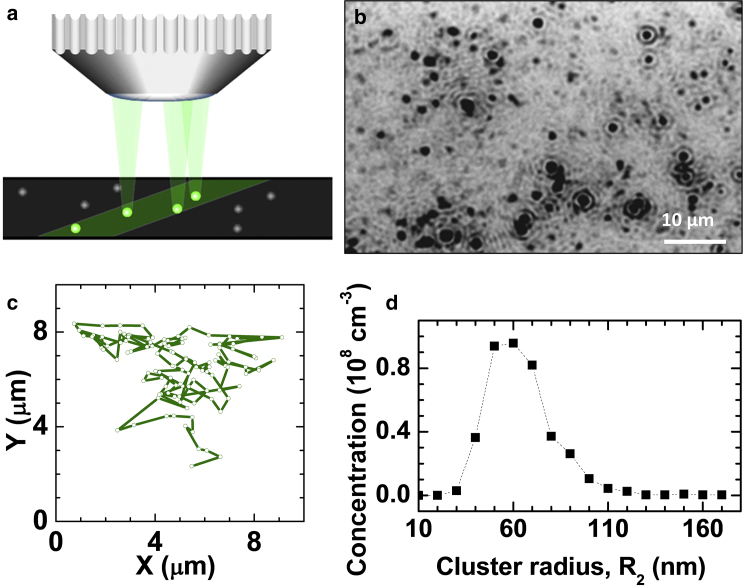
To quantify the characteristics of the cluster populations, we employ dynamic light scattering (DLS) and Brownian microscopy (BM) (19, 51). The application of DLS to characterization of the cluster populations is discussed in detail in Pan et al. (19) and Li et al. (51). BM, illustrated later in Fig. 1, a–c, is a relatively new method that serves to detect and monitor the motions of protein-rich clusters as in Fig. 1 b; see the Supporting Material for details. Fig. 1 d displays an example of a cluster size distribution, determined by BM. Both DLS and BM rely on light scattered at wavevectors of order μm⁻¹ and probe length scales in the range 10⁻³–10 μm. The Rayleigh law, according to which the scattered intensity scales as the sixth power of the scatterers’ sizes, makes these two techniques particularly well suited to study the mesoscopic clusters, which are 50–100× larger than the monomers, but are present at very low concentration.

Figure 1.

Cluster characterization by Brownian microscopy. (a) Schematic of the BM setup. A green laser illuminates a thin solution layer. The light scattered by particles in the solution is collected by a microscope lens. (b) A representative BM image shown as a negative. The observed volume is ∼120 × 80 × 5 μm³. The clusters are seen as black spots. (c) A typical cluster trajectory determined from a sequence of images. The cluster diffusivities and sizes are evaluated from such trajectories. (d) Distribution of cluster sizes, determined from trajectories such as the one in (c). Only clusters registered for longer than 1 s are considered. To see this figure in color, go online.

Small-angle x-ray and neutron scattering (SAXS and SANS, respectively) have been employed to characterize clusters of classes I and II (1, 2, 4, 6, 8, 9). These methods record intensity scattered at wavevectors of order Å⁻¹ and probe length scales of the order of nanometers. They identify clusters owing to local ordering at the probed length scales within the clusters and only detect clusters that occupy a significant fraction of solution volume. This requirement also applies to nuclear spin echo, a method employed to probe the dynamic properties of small clusters (2, 6). Thus, these three methods would be of limited utility in investigations of the mesoscopic clusters.

Results and Discussion

Model system

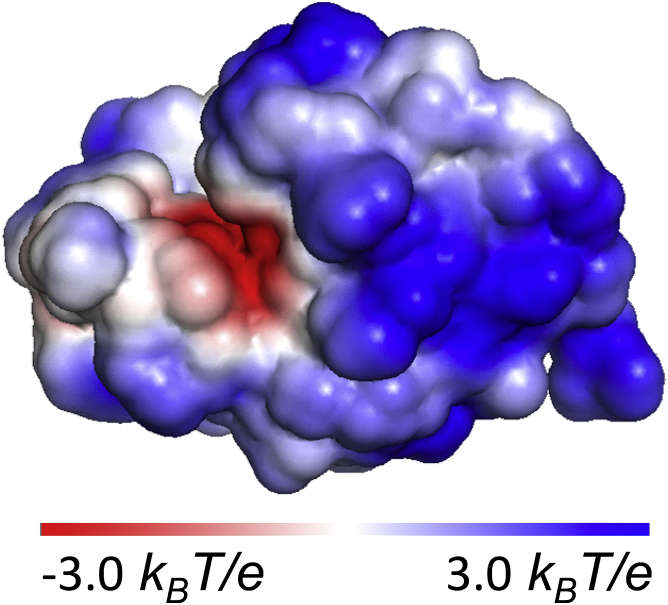
Our model protein, lysozyme, has an isoelectric point at pH = 11.35 (52), which is one of the highest documented for any protein (53). As a result, even at the highest pH = 7.8 probed here, protonation of basic and acidic surface amino-acid groups leads to a significant +8 net charge on the lysozyme monomer (54); 17 positive and nine negative groups were identified at this pH in Chan et al. (50). At the lowest pH = 3.8 tested here, the net charge increases to +15 (54). This high net positive charge, illustrated in Fig. 2, amplifies the significance of the Coulomb forces for aggregation behaviors of lysozyme, and makes this protein a suitable model system for this work.

Figure 2.

The distribution of electrostatic potential at the solvent-accessible surface of a lysozyme molecule at pH = 7.8; k_B, Boltzmann constant; T, temperature; and e, elementary charge. The Protein Data Bank (PBD) structure file PDB: 2VB1 was used. The protonation state of each acid or basic residue was evaluated at the chosen pH with PROPKA 3.0 (propka.org). The electrostatic map was computed online with the Adaptive Poisson-Boltzmann Solver and drawn using the software PyMOL (www.pymol.org). To see this figure in color, go online.

Characterization of the intermolecular Coulomb forces

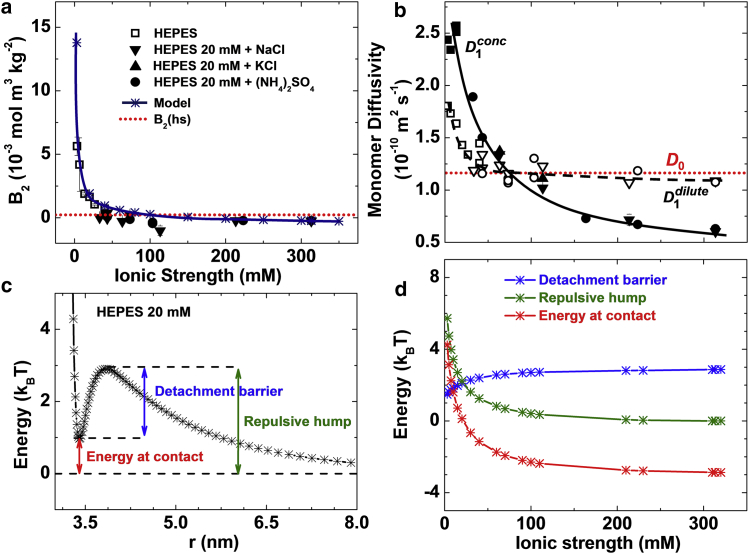
We tune the strength of the Coulomb interactions between lysozyme molecules in two ways: by varying the solution ionic strength I, which directly controls the Debye screening (55), and the solution pH, which determines the protein’s charge. We characterize the intermolecular interactions in terms of three parameters: the second osmotic virial coefficient, B₂, an azimuthally and spatially averaged characteristic of the pairwise interaction potential (56) that is obtained from the slopes of Debye plots, determined by static light scattering, and presented in Fig. S1 in the Supporting Material; the diffusivity of protein monomers in dilute solutions, D₁^dilute; and the diffusivity in concentrated solutions, D₁^conc. The values D₁^dilute and D₁^conc were determined from the faster shoulder in the autocorrelation function of the intensity of light scattered off the solution, seen in Fig. S2. The viscosities of all solvents used in this study were practically independent of the salt concentration and identity. Hence, D₁^dilute and D₁^conc trends in Fig. 3 b indicate the response of the protein dynamics to variations in intermolecular interactions. Note that while B₂ and D₁^dilute account for the interactions at long intermolecular separations, D₁^conc is weighted toward short separations.

Figure 3.

Characterization of the intermolecular interactions in solution at pH = 7.8. (a) The dependence of the second osmotic virial coefficient B₂ on the ionic strength I, varied through the concentration of HEPES buffer or by adding KCl, NaCl, or (NH₄)₂SO₄. The values of B₂ computed using the model represented in Fig. S3 are also shown. B₂(hs) = 4 V_MN_AM_w⁻² = 2.35 × 10⁻⁴ mol m³ kg⁻² for hard spheres (V_M = 2.0 × 10⁻²⁶ m³, molecular volume; N_A, Avogadro’s number; M_w = 14.5 kg mol⁻¹, lysozyme molecular weight) is shown for comparison. (b) The dependence of monomer diffusivity in dilute (D₁^dilute, measured at 9 mg mL⁻¹, open symbols) and concentrated (D₁^conc, measured at 100 mg mL⁻¹, solid symbols) solutions on the ionic strength, varied by the addition of the same electrolytes as in (a). The Stokes-Einstein diffusivity (or self-diffusivity) D₀ = 1.20 × 10⁻¹⁰ m² s⁻¹ of a sphere of radius 1.7 nm in a solution with viscosity 1.06 mPa s is shown. Solid and dashed lines are guides for the eye. (c) Potential of mean force (PMF) between a pair of molecules as a function of the distance between their centers of mass calculated using a numerical model illustrated in Fig. S3 at ionic strength I = 13.3 mM. (d) The dependences of the energy at contact, repulsive hump, and detachment barrier, defined in (c) on the ionic strength. To see this figure in color, go online.

The dependences of B₂, D₁^dilute, and D₁^conc on the ionic strength I are displayed in Fig. 3, a and b. We have varied I from 3 to 333 mM by increasing the concentration of HEPES buffer or adding NaCl, KCl, or (NH₄)₂SO₄. The data sets corresponding to the four salts follow the same trend, implying that the intermolecular interactions depend on the solution electrostatics but not on the salt identity. The decreasing values B₂, D₁^dilute, and D₁^conc at increasing I are consistent with the expectation that the Debye screening due to free ions significantly weakens the Coulomb repulsion. At I > 100 mM, B₂ becomes lower than its value for hard spheres B₂(hs), while D₁^dilute drops below the value of lysozyme’s self-diffusivity D₀. Both observations indicate a switch to weak intermolecular attraction and imply that electrostatic repulsion is largely screened by the ions in the solution. The diffusivity D₁^conc exhibits a stronger dependence on I than D₁^dilute, indicating that Coulomb repulsion is more sensitive to electrolyte concentration at short than at long separations.

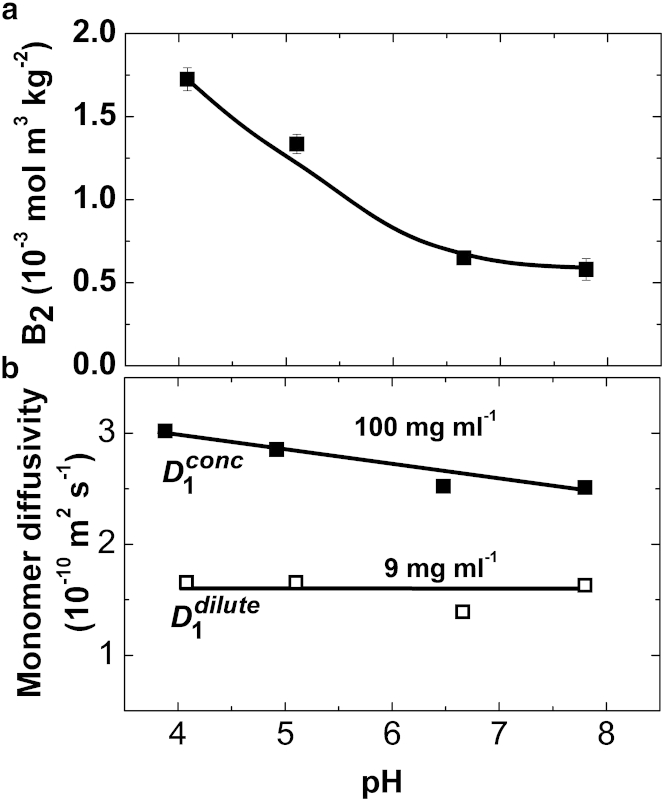
The dependences of B₂, D₁^dilute, and D₁^conc on pH, displayed in Fig. 4, a and b, reveal that the values of the three parameters decrease as pH increases. This is expected: because higher pH values are closer to the isoelectric point, the protein net molecular charge should decrease, leading to weaker electrostatic repulsion. The decrease in D₁^conc in Fig. 4 b is stronger than in D₁^dilute, again implying that Coulomb repulsion is more sensitive to the protein’s charge at short than at long separations.

Figure 4.

pH effects on the intermolecular interactions. (a) Dependence of the second osmotic virial coefficient B₂ on the solution pH. (b) Dependencies of the monomer diffusivities in dilute and concentrated solutions, D₁^dilute and D₁^conc, respectively.

While the effects of pH on B₂, D₁^dilute, and D₁^conc link directly to the decrease of the molecule’s charge at higher pH, the correlation between B₂ and I displayed in Fig. 3 a requires additional discussion. We employ a computational model following Chan et al. (50). We represent every protein molecule as a sphere with discrete charges as illustrated in Fig. S3. We consider interactions of pairs of molecules. Besides the Coulomb forces, we include an adjustable short-range contribution to the overall interaction that accounts for van der Waals attraction and steric repulsion; we assume that neither of the latter forces depends on I. Because of the molecules’ net positive charge, the majority of pair configurations are repulsive; still, there are several attractive configurations, such as the one depicted in Fig. S3 b, in which a negative Asp⁸⁷ faces a positive Arg⁴⁵ while a neutral His¹⁵ faces a positive Arg⁶⁸.

We sample all possible orientations of a pair of molecules using appropriate Boltzmann weights (50). The resulting angular-averaged potential of mean force (PMF) at I = 13.3 mM and pH = 7.8 is shown in Fig. 3 c. Three characteristics of this PMF relevant to the discussion of aggregation include the energy at contact, association barrier, i.e., repulsive hump, and detachment barrier; their dependences on I are displayed in Fig. 3 d.

The values of B₂ computed using these pairwise potentials are shown in Fig. 3 a. The predictions of the model agree well with the experimental data at high ionic strengths, and slightly underestimate the attraction at I < 120 mM. The latter discrepancy is likely due to solvent-structuring interactions that are not included in the model. The good overall agreement of the model with the B₂ data indicates that the Coulomb interactions adequately account for the observed response of the pairwise intermolecular interactions to increasing ionic strength.

The effects of the Coulomb forces on the cluster population

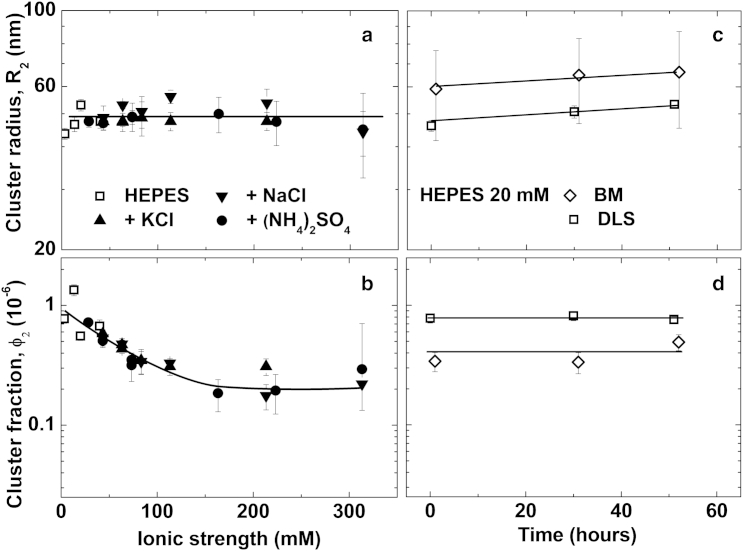
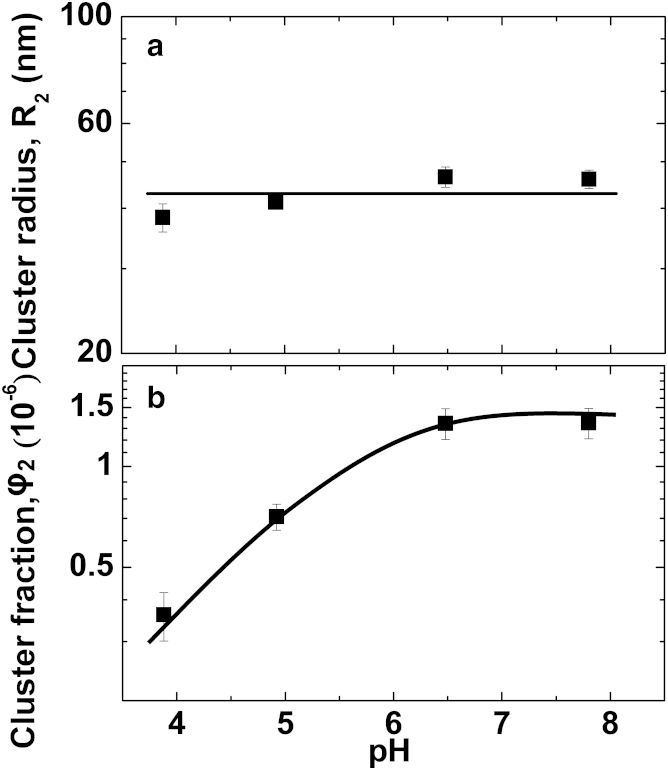
The responses of the average cluster radius R₂ and the volume fraction occupied by the clusters φ₂ to changes in the solution ionic strength I are displayed in Fig. 5, a and b. R₂ is independent of I, within the experimental error, while φ₂ decreases approximately fourfold as I increases from 3 to ∼100 mM and saturates at higher I values. Fig. 5, c and d, reveals that the values of R₂ and φ₂ are relatively steady in time (the slow R₂ growth likely reflects an Ostwald-like ripening of the clusters (14)). The effects of pH on R₂ and φ₂ are displayed in Fig. 6, a and b, respectively. Similarly to the trend in Fig. 5 a, the cluster radius R₂ depends weakly on solution pH; several repetitions of this experiment revealed no pH dependence. The cluster volume fraction φ₂ increases by ∼4× as pH increases from 3.8 to 7.8.

Figure 5.

Populations of protein-rich clusters in 100 mg mL⁻¹ lysozyme solutions in HEPES buffer at pH = 7.8 characterized by DLS and BM. (a) Dependence of the average cluster radius R₂ on ionic strength. Solution ionic strength was varied through the concentration of four electrolytes, as indicated in the graph. (b) Cluster volume fraction φ₂, determined from the same DLS autocorrelation functions as R₂, as a function of the solution ionic strength. (c and d) The evolutions of cluster size R₂ in (c) and volume fraction φ₂ in (d), determined by DLS and BM. The results of the two methods are similar, within their errors; the inherent error of the φ₂ determination may be up to 50% (16).

Figure 6.

pH effects on the cluster characteristics, the cluster radius R₂ in (a), and the cluster volume fraction φ₂ in (b).

The apparent increase in the cluster volume fraction φ₂ at higher pH is expected: the protein charge should decrease with pH, thus reducing protein-protein repulsion; this reduction should be stronger when the molecules are closer, i.e., at higher concentrations. The decreasing trends of D₁^high and D₁^low with increasing pH in Fig. 3 b are consistent with these expectations. However, Figs. 5 and 6 also reveal at least three anomalous cluster behaviors. First, the behaviors of R₂ and φ₂ as functions of I are decoupled; this observation is in contrast with conventional phase transformations—such as solidification or liquefaction—in which the domain size of the incipient phase increases concurrently with its overall volume. Second is the anomaly of the cluster size, which is independent of the solution’s ionic strength or pH despite the decreasing intermolecular repulsion at higher values of the two parameters, evidenced by Figs. 3, a and b, and 4, a and b. Third, there is the puzzling behavior is the decreasing cluster volume fraction φ₂ at high ionic strength I in Fig. 5 b. This contradicts the expectation that weaker repulsion in concentrated solutions, revealed by the D₁^high trend in Fig. 3 b, should lead to cluster stabilization and, hence, to a higher cluster volume fraction, similarly to the observations at higher pH in Fig. 6 b. Note that the three anomalous behaviors contradict general rules of phase transformations and solution thermodynamics irrespective of a specific model of cluster formation.

The decoupled behaviors of R₂ and φ₂ at increasing I indicate that R₂ and φ₂ are controlled by distinct mechanisms. This observation agrees with the oligomer mechanism of cluster formation by which R₂ is determined by the kinetics of decay of the oligomers accumulated in the clusters (13), while φ₂ reflects the high free energy cost of bringing together positively charged molecules (13, 14). The second feature, the lack of correlation between the cluster size R₂ and the solution ionic strength and pH, indicates that cluster formation is not governed by Coulomb interactions. Thus, neither the colloid scenario of Coulomb-regulated cluster formation (32, 36), discussed above, nor a mechanism relying on electrostatically bound oligomer, could underlie the mesoscopic clusters in lysozyme solutions. The third peculiarity of the above data is discussed in the next subsection.

Another example of Coulomb-independent behavior is presented by proteins of the γ-crystalline family (16). These crystallines form clusters that are clearly mesoscopic: each cluster contains a large number of monomers; the total cluster population occupies low volume. Similarly to the lysozyme clusters, the clusters of γ-crystalline retain a size of ∼100 nm as pH is varied from 6.8 to 10 and the NaCl concentration, from 150 to 350 mM (16). (The cluster disaggregation at pH and NaCl concentration values outside these ranges (16) may be due to a protein-specific mechanism that is beyond the assumptions of the clustering models discussed here.)

With many other studied proteins, clusters are observed at ionic strengths higher than 100 mM (12, 13, 14, 16, 17, 24), at which the Debye length is shorter than the molecular size and, hence, the lifetimes of electrostatically bound oligomers would be insignificant. Hence, Coulomb-regulated colloid clustering and Coulomb-mediated oligomerization can be dismissed as formation mechanisms of the mesoscopic clusters in solutions of these proteins.

Water-structuring interactions and partial protein unfolding

The anomalous decrease of φ₂ at high I in Fig. 5 b is akin to salting-in, i.e., the increase of solubility of proteins and colloids at increasing ionicity. This decrease contradicts the trend of decreasing molecular repulsion at high ionic strength, revealed by Fig. 3, a and b, for protein concentrations up to 100 mg mL⁻¹, and suggests that forces other than Coulomb are at play. These hypothetical forces must then destabilize the dense liquid held in the clusters, in which the protein concentration is ∼500 mg mL⁻¹ (13) and the intermolecular separation is shorter than 1 nm (13). Possible candidates are water-structuring forces that operate at similarly short separations (55). They are classified either as hydration, due to water structuring at polar surface patches and augmented by the presence of ions and other kosmotropes (55, 57), or hydrophobic, due to water layering along nonpolar surface patches (55). Thus, increasing concentrations of kosmotropic ions could induce the buildup of hydration layers and hydration repulsion at short intermolecular separations that destabilize the cluster phase.

To test the role of hydration and hydrophobic forces in cluster formation, we added urea and ethanol to the probed solutions. Urea is known to destabilize the native structure of most proteins; addition of 8 M urea in aqueous solutions causes full protein unfolding (58, 59, 60). The contemporary consensus appears to be that urea is a universal denaturant because it interacts favorably with the peptide backbone (61). The amino-acid side chains assist the action of urea by additional preferential interaction with it and by diluting the effective concentration of the backbone amides (62, 63, 64). The interactions of urea with the backbone and side chains involve intercalation and destruction of the water structures (chaotropic action) (65). Ethanol forms homogeneous solutions with water at concentrations <2.8 M (66). Similarly to urea, ethanol is a chaotropic agent; however, it accumulates in the vicinity of nonpolar amino-acid residues and disrupts adjacent water structures. It strips off as many as 16 bound water molecules from the lysozyme surface (67) and may form hydrogen bonds to its hydroxyl groups (68). In important contrast to urea, ethanol does not interact with the peptide backbone and, hence, it induces protein unfolding only at high concentrations: a recent study demonstrated that ethanol does not affect the conformations of lysozyme α-helixes and β-sheets at concentrations as high as 2.5 M (68).

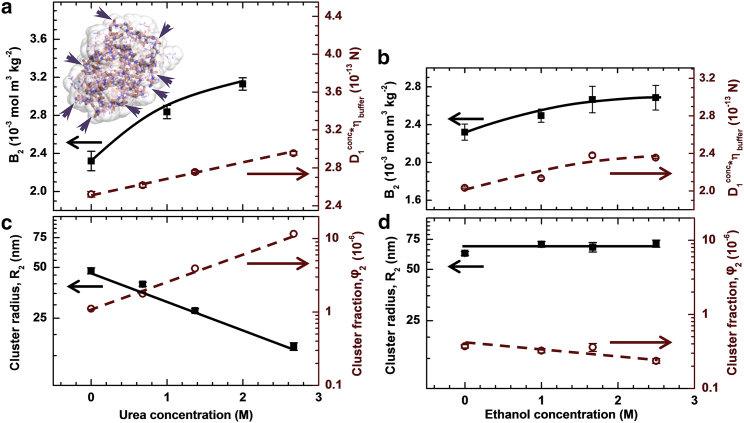
We have characterized the effects of urea and ethanol at concentrations up to ∼2.5 M on the protein interactions in terms of the second osmotic virial coefficient B₂ (determined from plots in Fig. S6) and the product of monomer diffusivity and buffer viscosity D₁^concη_buffer (in contrast to the salts used to modify protein interactions in Figs. 3, 4, and 5, urea and ethanol significantly affect the buffer viscosity at the applied concentrations). The results in Fig. 7, a and b, reveal that the addition of urea or ethanol perceptibly enhances intermolecular repulsion, likely by weakening the hydrophobic attraction. The ethanol effects are consistent with disruption of the water structures, likely around the nonpolar surface amino-acid residues. In addition, urea likely acts also on the peptide backbone exposed to the solvent (backbone segments accessible to urea in the native confirmation are illustrated in the inset in Fig. 7 a; the solvent exposure of additional backbone segments due to partial protein unfolding is supported by evidence below). Thus, stronger urea-induced repulsion is consistent with weakening of the water structures around these backbone segments.

Figure 7.

The role of hydrophobic interactions and partial unfolding in cluster formation. All data are for 100 mg mL⁻¹ lysozyme solutions in 20 mM HEPES at pH = 7.8, in which the ionic strength I = 13.3 mM. (a and b) Variation of the second virial coefficient B₂ (left ordinate, solid symbols) and of the product of monomer diffusion coefficient D₁^conc in 100 mg mL⁻¹ solutions and the buffer viscosity η_buffer (right ordinate, open symbols) as functions of the concentration of urea and (a) and ethanol in (b). (Inset in a) The native structure of lysozyme and its solvent-accessible surface. (Arrows) Locations at which the peptide backbone is exposed to the solvent. (c and d) The response of the cluster radius R₂ (left ordinate, solid symbols) and volume fraction φ₂ (right ordinate, open symbols) to increasing concentrations of urea and (c) and ethanol in (d). To see this figure in color, go online.

While the ethanol-induced increase in B₂ (∼15%) is comparable to that of D₁^concη_buffer, the increase in B₂ with adding urea (∼40%) is stronger than that of D₁^concη_buffer (∼20%). As discussed above, D₁^concη_buffer is weighted toward short intermolecular separations. Hence, this discrepancy indicates that urea boosts repulsion more efficiently at long distances. Because the mismatch is not observed with ethanol, we assign it to urea-enhanced partial protein unfolding. It exposes to the solvent nonpolar side chains that in the native structure are tucked inside. The resulting hydrophobic attraction acts at the short range, at which it mitigates the repulsion caused by urea coating the protein backbone.

The data in Fig. 7 c demonstrate that the addition of urea reduces the cluster radius R₂ approximately threefold, while increasing the cluster population volume fraction φ₂ by an order of magnitude. The addition of ethanol does not affect R₂ and weakly lowers φ₂ (Fig. 7 d). The decoupled behaviors of R₂ and φ₂ in the presence of urea exclude protein denaturation and aggregation induced by this additive as the cause of the observed trends. We carried out two additional tests of the possibility of denaturation. First, we determined R₂ and φ₂ in a protein solution containing 1.25 M urea, prepared by mixing a solution with 2.5 M urea with an equal volume of a protein solution of the same concentration and no urea. The measured R₂ and φ₂ (Fig. S7) were practically identical to those in directly prepared 1.25 M urea, indicating that cluster formation and its constituent processes are reversible. Second, we monitored the evolution of the cluster population over 24 h. We found (Fig. S8) that R₂ and φ₂ did not change from the values established within 30 min after the addition of urea (Fig. 7 c). In combination with the conclusion of cluster reversibility, the latter observation implies that the cluster population is in equilibrium with the solution, similar to its behavior in the absence of urea (13).

The R₂ and φ₂ responses to urea are anomalous from a classical viewpoint: a significant increase in the cluster-phase volume is accompanied by a decrease in its characteristic dimension. On the other hand, they are compatible with the oligomer mechanism of cluster formation, according to which R₂ and φ₂ are independently regulated. Furthermore, comparing the variations of R₂ due to the addition of urea and ethanol indicates that oligomers bound by backbone-to-backbone contacts are crucial for cluster formation. The accumulation of urea around the peptide backbone would accelerate the decay of such oligomers and increase the corresponding rate constant k_oligomer and lead, according to Eq. 1, to smaller clusters. Because ethanol does not interact with the backbone, it does not affect R₂. The responses of φ₂ to urea and ethanol highlight the role of partial protein unfolding in oligomer stabilization and cluster formation. Enhanced protein unfolding by urea (tentatively indicated by the discrepancy in the B₂ and D₁^concη_buffer trends in Fig. 7 a) exposes hidden nonpolar amino-acid residues. Because the attractive hydrophobic interactions between the residues are short-ranged, this stabilizes the cluster phase more than in the dilute solution and hence increases φ₂.

Looking back at the effects of electrolytes, we note that one of the used salts, (NH₄)₂SO₄, combines electrostatic with kosmotropic and chaotropic actions due to its two ions, i.e., SO₄^2- stabilizes the water shells around proteins and the native protein conformation, while NH₄⁺ destabilizes water structures and tends to denature proteins (69). It appears that at the highest concentration used here, 100 mM (higher concentrations lead to fast crystallization), the chaotropic action is not exhibited; the protein conformation is stable; and the action of (NH₄)₂SO₄ is fully accounted for by its contribution to the ionic strength I.

The responses of R₂ and φ₂ to the presence of urea and ethanol in Fig. 7 are not dramatic, implying that the cluster formation mechanism has not been modified by these two additives. These responses identify partial protein unfolding as the likely cause behind the existence of mesoscopic clusters in lysozyme solutions with widely ranging compositions. Note that only a small fraction, 10⁻⁶–10⁻⁴, of the total soluble protein partially unfolds and is held in the clusters. The unfolding exposes to the solvent the peptide backbone and nonpolar amino-acid residues, hidden in the native conformation, enables hydrophobic bonds between backbone segments, and stabilizes the cluster phase through hydrophobic attraction between the exposed nonpolar amino-acid residues. We have demonstrated that the constituent steps in this scenario are reversible, which indicates that it is fully compatible with the oligomer mechanism of cluster formation (13), wherein backbone-to-backbone contacts support transient oligomers.

Conclusions

These results demonstrate that the Coulomb forces that govern aggregation in biological systems and many other phenomena in nature do not affect the size of the mesoscopic clusters in lysozyme solutions. In addition to their large size, high amount of protein contained in each cluster, small fraction of total protein held in the clusters, and concentration independence of the size, the insensitivity of the cluster size to Coulomb forces distinguishes the mesoscopic clusters sharply from the two other classes of clusters observed in protein solutions. The mesoscopic clusters exhibits other behaviors that are in contrast with established laws of phase equilibrium: decoupled responses of cluster phase volume and cluster size to variations of the ionic strength, pH, and additive concentration; and decreased cluster phase volume upon stronger intermolecular attraction. These responses demonstrate that the mesoscopic clusters represent, to our knowledge, a novel class of protein condensate that forms by a fundamentally different mechanism from protein crystals and amyloid fibrils, and from the two other known types of protein clusters. Our observations indicate that the clusters form by a unique mechanism, i.e., by the accumulation of transient protein oligomers that are linked by hydrophobic bonds between the peptide backbones exposed to the solvent after partial protein unfolding. Because the mesoscopic clusters have been suggested in many cases as crucial precursors to the formation of the two main classes of protein aggregates, crystals and amyloid fibrils, our findings indicate that fine-tuning of the intra- and intermolecular water-structuring interactions may be an essential tool to control the cluster population and in this way enhance or suppress protein crystallization and fibrillization.

Author Contributions

M.A.V. performed the experiments, H.Y.C. designed the numerical model and carried out the model computations, V.L. designed the numerical model and edited the text, and P.G.V. conceived the study, designed the experiments and wrote the article with contributions from M.A.V. and V.L. All authors discussed the results and commented on the article.

Editor: Rohit Pappu.