Are all biases missing data problems?

Abstract

Estimating causal effects is a frequent goal of epidemiologic studies. Traditionally, there have been three established systematic threats to consistent estimation of causal effects. These three threats are bias due to confounders, selection, and measurement error. Confounding, selection, and measurement bias have typically been characterized as distinct types of biases. However, each of these biases can also be characterized as missing data problems that can be addressed with missing data solutions. Here we describe how the aforementioned systematic threats arise from missing data as well as review methods and their related assumptions for reducing each bias type. We also link the assumptions made by the reviewed methods to the missing completely at random (MCAR) and missing at random (MAR) assumptions made in the missing data framework that allow for valid inferences to be made based on the observed, incomplete data.

Introduction

A common objective in epidemiologic studies is to estimate the causal effect of an exposure on the occurrence of a specific outcome. Historically, there have been three recognized systematic threats to consistent estimation of causal effects. These three threats are bias due to confounders, selection, and measurement error [1]. Confounding, selection, and measurement bias have typically been characterized as distinct types of biases. However, these biases can also be characterized as missing data problems that arise when incomplete information must be used to estimate quantities of interest (e.g., causal effect) that would be obtained from the complete information if it were available [2, 3].

In studies conducted to estimate causal effects, information is incomplete on the individual-level potential outcomes (also known as the counterfactual outcomes). The individual-level potential outcome is the outcome that would have been observed for a given individual under an intervention to set the exposure for that individual to a specific level [1, 4]. At best researchers can observe the potential outcome for a given individual under their observed exposure while the individual-level potential outcome for their unobserved exposure level(s) is missing. Missing individual-level potential outcomes often shift the focus to estimating aggregate rather than individual causal effects [5]. Estimating aggregate causal effects typically requires calculating the mean or another relevant function (e.g., median) of the individual-level potential outcome distribution.

In epidemiologic studies confounding bias typically occurs when incomplete observed data are used to estimate relevant functions of the individual-level potential outcomes and in turn aggregate causal effects. Selection and measurement error can lead to additional missing individual-level potential outcomes, which can hinder accurate estimation of relevant functions and in turn result in bias. As with any missing data problem, however, these biases can be addressed by accurately completing the missing individual-level potential outcomes before estimating the relevant function [5–15]. Alternatively, the relevant function can often be directly estimated from the observed data without completing the missing individual-level potential outcomes [4]. Accurate estimation of the relevant function will result in the aggregate associational effects that are commonly calculated using the observed data equaling the aggregate causal effects of interest that would have been obtained if the individual-level potential outcomes were known/available [4].

Therefore, the objective of this paper is to first describe how confounding, selection, and measurement bias arise from missing data on individual-level potential outcomes. Second, we will review methods that reduce bias stemming from missing individual-level potential outcomes while emphasizing techniques that directly estimate the relevant function of the potential outcome distribution without completing the missing individual-level potential outcomes given their greater use in the epidemiologic literature. Third, we will detail the assumptions that must be met for each of the described methods to reduce the relevant bias type. To further characterize the aforementioned biases as missing data problems, we will link the assumptions made by the reviewed methods to the missing completely at random (MCAR) and missing at random (MAR) assumptions that are made in the missing data framework and allow for valid inferences to be made based on the observed, incomplete data [2]. A summary of our review is included in Table 1. To aid in our description, we first define general notation and provide basic definitions that we will build upon in subsequent sections of the paper.

Table 1.

Source of and methods to reduce bias due to missing data on the individual-level potential outcomes

Bias type and source	Method	Applications of less commonly used methods published in the literature in the last 3 years
Confounding - missing individual-level potential outcomes for unobserved exposure levels	Randomization [1, 4], stratification [1, 4], restriction [1, 4], matching [1, 4], standardization [1, 4], standard regression adjustment [1, 4], propensity scores [24–26], inverse probability weighting [27, 28], instrumental variables [29–32], g-estimation [10–12], g-computation formula [35, 36], bayesian approaches [5, 7], and doubly robust estimators [39, 40]	Davies et al. [33] use an instrumental variable approach to estimate the effect of COX-2 selective nonsteroidal antiinflammtory drugs on the incidence of upper gastrointestinal complications and myocardial infarction.
		Swanson et al. [34] offer guidelines for how to report instrumental variable analyses using the Davies et al. [33] paper as an example.
		Naimi et al. [8] use g-estimation to estimate the cumulative effect of occupational asbestos exposure on time to lung cancer mortality with annotated SAS code provided in an earlier commentary [9].
		Keil et al. [37] provide a simple introduction to the parametric g-formula with annotated SAS code for implementing the method and demonstrate its use when examining the effect of a hypothetical treatment to prevent graft-versus-host disease on mortality among bone marrow transplant patients.
		Neugebauer et al. [41] use doubly robust targeted minimum loss-based estimation with super learning to address confounding bias while examining the effect of various glucose-lowering strategies on albuminuria among adults with Type-2 diabetes and provide annotated R code for implementation.
Selection - missing individual-level potential outcomes among persons not selected	Standard regression adjustment [4, 15, 51], inverse probability weighting [4, 15, 51], redistribute-to-the-right algorithm [14], standardization [61], g-computation formula [35], multiple imputation [13], principal stratification [57], doubly robust estimators [41, 54], and instrumental variables [62–64]	Gottesman et al. [52] use inverse probability weighting as well as imputation to address potential selection bias due to death and loss to follow up when examining the effect of education on cognitive change.
		Neugebauer et al. [41] use doubly robust targeted minimum loss-based estimation with super learning to address selection bias while examining the effect of various glucose-lowering strategies on albuminuria among adults with Type-2 diabetes and provide annotated R code for implementation.
		Shardell et al. [54] use doubly robust augmented inverse probability weighted estimation to address selection bias due to death and lost to follow up when examining the effect of Vitamin D use on physical functioning among older adults.
		McGovern et al. [64] use an instrumental variable approach to correct for selection bias when estimating the prevalence of HIV among men in Ghana and Zambia.
Measurement - missing individual-level potential outcomes when exposure, outcome, or covariates are measured with error	Bias analysis [1, 50, 73–75], regression calibration [76, 77], modified maximum likelihood [78–80], multiple imputation [77, 81], and propensity score calibration [82–84]	See Funk and Landi [75] for recent published applications

General notation and basic definitions

Let capital letters denote random variables while lower case letters and numbers represent particular values of the random variables. Now suppose in a hypothetical cohort study, A(the exposure) represents a binary indicator of aspirin use at the start of the study (1: yes; 0: no) and Y(the outcome) is an individual-level indicator of dying subsequent to the start of the study (1: yes; 0: no). Further, Y^a denotes the individual-level potential outcome for Y under an intervention to set aspirin use to level a and L is a binary indicator of male gender (1: yes; 0: no).

Next we specify the consistency condition for all subjects that Y^A = Y. This condition states that the observed individual-level outcome among study participants is the individual-level potential outcome that would have been observed under an intervention to set the exposure to the observed exposure level if the exposure was measured without error [16–19]. For instance, study participants who used aspirin at study entry and died during follow up would have still died if they were assigned to use aspirin at the start of the study. The consistency condition is required to make appropriate causal inference based on the observed data.

Typically in epidemiologic studies the aggregate causal effect of interest is the average causal effect [4]. The causal risk ratio (RR) will be the average causal effect that will be the focus of this paper, acknowledging that the issues discussed in subsequent sections often equally apply to other measures (e.g., causal rate ratio). In the context of the hypothetical cohort study, the causal RR is a function of the mean of Y^a, E[Y^a], and compares aspirin users to non-aspirin users via the following quantity: E[Y^a=1]/ E[Y^a=0] = P(Y^a=1 = 1)/P(Y^a=0 = 1). The numerator of the causal RR is the risk of subsequent death had all individuals in the study population used aspirin at study entry, while the denominator is the risk of subsequent death had no individuals in the study population used aspirin at study entry.

When there is a non-zero probability of observing each exposure level (i.e., positivity) and the exposure groups are equivalent/exchangeable on all factors related to Y (i.e., individual-level potential outcomes are MCAR [2]), the mean of Y conditional on A, E[Y | A], can validly be used to calculate the aforementioned E[Y^a] and in turn accurately estimate the causal RR via the associational RR, E[Y | A = 1]/E[Y | A = 0] = P(Y = 1 | A = 1)/P(Y = 1 | A = 0). The associational RR is obtained by comparing disjoint subsets of the study population with different exposure levels. Specifically, the risk of death among individuals who used aspirin at study entry is compared to the risk of death among individuals who did not use aspirin at study entry. Bias occurs when the average associational and causal effects are unequal due to a lack of positivity or lack of exchangeability [4]. The lack of positivity or exchangeability in this context has also been referred to as non-ignorability of the treatment assignment mechanism [4, 20].

Bias due to missing individual-level potential outcome data

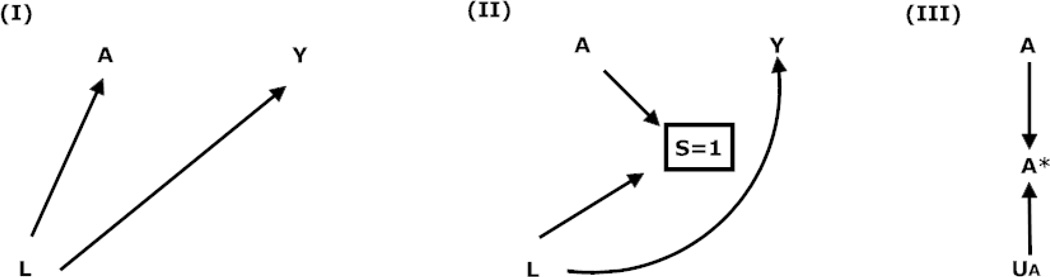
If all potential outcomes were known at the individual level then the presence of factors that have been traditionally referred to as confounders, the presence of selection, or the presence of measurement error would pose no threat to identifying causal effects (i.e., no bias). Therefore, the following sections describe how confounding, selection, and measurement bias arise from missing individual-level potential outcomes. Table 2 depicts which individual-level potential outcomes are missing for each bias type. Further, the Figure represents each bias type as a causal diagram. Unless otherwise specified, when discussing one type of bias we assume the absence of other bias types.

Table 2.

Missing individual-level potential outcomes by bias type given the consistency condition

Bias type	S	A	A*	Y	Ya=0	Ya=1
Confounding - missing individual-level potential outcomes for unobserved exposure levels	1	1	1	1	?	1
	1	0	0	0	0	?
Selection - missing individual-level potential outcomes among persons not selected	0	?	?	?	?	?
	0	?	?	?	?	?
Measurement - missing individual-level potential outcomes when exposure, outcome, or covariates are measured with error	1	1	0	1	?	1
	1	0	1	0	0	?

S (binary indicator of selection); A (binary exposure); A^* (measured version of A); Y (outcome);

Y^a (potential outcome for Y; note for simplicity the superscripted s has been suppressed)

Figure.

Causal diagram depicting confounding, selection, and measurement bias in the absence of a true causal effect between an exposure (A) and outcome (Y)

Boxes represent restriction due to selection

Confounding bias

Confounding bias occurs because potential outcomes for a given person under study are not seen for unobserved exposure levels. For instance, as shown in Table 2, whether an aspirin user (A = 1) who died (Y = 1) would have lived had they not used aspirin is not observed (Y^a=0 = ?). Similarly, whether a non-aspirin user (A = 0) who lived (Y = 0) would have died had they used aspirin is not observed (Y^a=1 = ?). Missing individual-level potential outcomes often shifts the focus from estimating individual to aggregate causal effects (e.g., causal RR) in epidemiologic studies given the greater ease in accurately estimating aggregate rather than individual causal effects [4, 5].

Validly estimating the causal RR requires accurately estimating E[Y^a]. When positivity and exchangeability hold, the mean of the observed outcomes conditional on A, E[Y | A], can be used to accurately estimate E[Y^a]. For instance, the mean outcome among persons observed to take aspirin, E[Y | A = 1], can be used to estimate the mean potential outcome of the persons observed to not take aspirin had they taken aspirin, E[Y^a=1 | A = 0], and in turn the mean potential outcome had all participants in our hypothetical cohort study taken aspirin, E[Y^a=1]. Unfortunately, estimation of E[Y^a] is not always accurate due to lack of positivity or exchangeability.

Exchangeability violations can occur when factors such as L in Diagram (I) of the Figure that are associated with the exposure and outcome exist (e.g., males are more likely than females to take aspirin and die). Such factors have traditionally been referred to as confounders [1, 4]. The existence of potential confounders may result in E[Y | A] ≠ E[Y^a=A] since any observed outcome may be due to the effect of the exposure, the related confounder, or both. The lack of exchangeability on confounders across exposure levels can result in bias; meaning the average associational and causal effect measures are unequal (e.g., P(Y = 1 | A = 1)/P(Y = 1 | A = 0) ≠ P(Y^a=1 = 1)/P(Y^a=0 = 1)). This bias is depicted in Diagram (I) of the Figure by the open non-causal path from A to Y via L.

Selection bias

Now consider that the population from the hypothetical cohort study was selected from a source population that represents a target population that we would like to make inferences about. Therefore, let S be a binary indicator of selection into the study population from the source population (1:selected; 0:not selected) and Y^a,s denote the potential outcome for Y under an intervention to set aspirin use to a and selection to s. The causal RR with selection will now be represented as P(Y^a=1,s=1 = 1)/P(Y^a=0,s=1 = 1). This causal RR compares the same individuals had everyone in the source population been selected and aspirin use been assigned versus not assigned. In contrast, the associational RR with selection, P(Y = 1 | A = 1, S = 1)/P(Y = 1 | A = 0, S = 1), compares disjoint subsets of the observed study population by their observed aspirin use.

Although not captured by the definition of S in the hypothetical cohort study, selection could also occur when going from the study population to the analytic sample and from the analytic sample at study entry to a given risk set subsequent to study entry [15]. As shown in Table 2, selection can result in missing exposure, observed outcome, and individual-level potential outcome values for persons who were not selected into a given study population, analytic sample, or risk set (A = ?, Y = ?, Y^a=1 = ?, Y^a=0 = ?) [3].

When estimating the causal RR, an analysis that disregards the aforementioned selection results in the mean of the observed outcomes among the selected persons (e.g., P(Y = 1 | A, S = 1)) being used to estimate the mean potential outcome of the not selected persons (e.g., P(Y^a = 1 | A, S = 0)). This estimation is inaccurate when the probability of being selected is not greater than zero (i.e., non-positivity) or the mean potential outcomes among persons who were selected (e.g., P(Y^a = 1 | A, S = 1)) are not exchangeable with the missing mean potential outcomes among those who were not selected (e.g., P(Y^a = 1 | A, S = 0)).Here, exchangeability is defined as equivalence between those who were and were not selected on factors related to the outcome and in turn their potential outcomes conditional on the exposure [21]. Exchangeability occurs when the potential outcomes among those who were not selected are MCAR or MAR conditional on the exposure [2]. Positivity plus exchangeability is equivalent to ignorability of the selection mechanism [4, 20].

The lack of exchangeability between those who were and were not selected can occur if factors such as L in Diagram (II) of the Figure that are associated with selection and the outcome exist such that those who were selected (e.g., mostly men) are more or less likely to develop the outcome (e.g., die) than those who were not selected. The lack of exchangeability between those who were and were not selected may result in a lack of exchangeability across different exposure levels and in turn bias (e.g., P(Y = 1 | A = 1, S = 1)/P(Y = 1 | A = 0, S = 1) ≠ P(Y^a=1,s=1 = 1)/P(Y^{a=0, s=1} = 1)) [21, 22]. This bias in Diagram (II) of the Figure is represented by the open non-causal path from A to Y via L and S.

Measurement bias

Now consider that in the hypothetical cohort the exposure, outcome, or confounders/covariates may have been measured with error. Measurement error is a type of missing data because the true value for the exposure, outcome, or confounder/covariate is not known. Therefore, let A^* be the measured version of A via self-report, U_A be the measurement error for A, Y^* be the measured version of Y obtained from medical record abstraction, U_Y be the measurement error for Y, L^* be the measured version of L obtained from medical record abstraction, and U_L be the measurement error for L. The associational effect with measurement error is now represented as P(Y^* = 1 | A^* = 1, S = 1)/P(Y* = 1 | A* = 0, S = 1) and compares disjoint subsets of the observed study population by their reported rather than actual/true aspirin use.

In the presence of U_Y the individual-level potential outcomes that correspond to the observed exposure levels are missing since the observed outcomes are missing. Even when the outcome is measured perfectly (no U_Y) like in Table 2, if the exposure is measured with error (A ≠ A^*), the individual-level potential outcomes that correspond to the observed exposure levels are still missing (Y^a=A* = ?) due to the incorrect labeling of persons who are actually exposed as unexposed and vice versa [3].

Therefore, like in the case of Diagram (III) in the Figure where confounding and selection bias do not exist, errors in measurement of the exposure (U_A) and/or outcome (U_Y) can result in bias (e.g., P(Y^* = 1 | A^* = 1, S =1)/P(Y^* = 1 | A^* = 0, S = 1) ≠ P(Y^a=1,s=1 = 1)/P(Y^a=0,s=1 = 1)) that would not exist had study participants been compared based on their true outcome level and aspirin use (e.g., P(Y = 1 | A = 1, S = 1)/P(Y = 1 | A = 0, S = 1) = P(Y^a=1,s=1 = 1)/P(Y^a=0,s=1 = 1)). Even when the exposure and outcome are measured perfectly, confounder/covariate measurement error (L ≠ L^*) is problematic when confounding or selection bias exist. Specifically, errors in the measurement of factors that contribute to the confounding or selection bias hinders the accurate estimation of E[Y^a] based on information about the aforementioned factors using methods outlined in the next section [23].

Methods and assumptions necessary to reduce bias due to missing individual-level potential outcomes

Confounding bias

Approaches that have been more frequently used in the epidemiologic literature to address confounding bias due to missing individual-level potential outcomes include randomization, standardization, restriction, matching, stratification, standard regression adjustment, propensity scores, and inverse probability weighting (IPW) [1, 4, 24–28]. In the case of the binary time-fixed indicator of aspirin use, randomization, stratification, restriction, matching, standardization, standard regression adjustment, and propensity scores would use the mean observed outcome among the non-aspirin users to estimate the mean potential outcome among aspirin users and in turn the entire study population had they not used aspirin. Likewise, the mean observed outcome among the aspirin users would be used to estimate the mean potential outcome of non-aspirin users and in turn the entire study population had they used aspirin.

Randomization helps ensure that the estimate is accurate by assigning the exposure randomly such that the distribution of measured and unmeasured confounders is expected to be equivalent across different levels of the exposure. Standardization and matching (e.g., individual, frequency, propensity score) reduce differences in the confounder distribution across different exposure groups. Stratification, restriction, and standard regression adjustment ensures the estimation is accurate by only performing the estimation within strata of measured potential confounders where greater balance on potential confounders is expected. Propensity score subclassification analogously performs the estimation within strata of scores that are a function of the potential confounders where again greater balance on potential confounders is expected.

The greater balance on the confounder distribution across different exposure levels expected to be achieved by each of the above described methods blocks the open non-causal pathway from A to Y via L in Diagram (I) of the Figure by effectively either removing the arrow from L to A or by conditioning on L. This blocking in turn reduces the occurrence of differences in the outcome across exposure levels that occur for reasons beyond the exposure that hinder accurate estimation. Despite the aforementioned expectation, balance is only achieved when necessary assumptions and conditions are met.

IPW procedures can be used to re-weight the observed data to generate a pseudo-population with the corresponding outcomes that would have been observed had everyone in the study population been exposed and unexposed (e.g., used aspirin and did not use aspirin). This re-weighting is usually done as a function of the measured potential confounders and similar to randomization removes the arrow from L to A. The re-weighted data therefore yields a pseudo-population where the aforementioned measured potential confounders are not associated with the exposure and the estimation of E[Y^a] is therefore accurate when necessary assumptions and conditions are met. Stabilized versions of the aforementioned weights can be estimated that preserve the original sample size of the study population and enhance the precision of estimates. When a measured time-varying confounder that is affected by prior exposure exists, IPW procedures may be less biased, but more imprecise, than more traditional approaches including standard regression adjustment [27, 28].

Less commonly used methods in the epidemiologic literature that address confounding bias when necessary assumptions and conditions are met include instrumental variable approaches [29–34], g-estimation [8–12], the g-computation formula [35–37], and Bayesian techniques [5, 7]. Despite their potential to circumvent bias due to measured and unmeasured potential confounders, instrumental variable approaches have been less frequently employed in observational epidemiologic studies in part due to the limited number of suitable instruments in this setting [31, 32]. Although g-estimation and the g-computation formula may also be less biased than traditional approaches in the setting of a measured time-varying confounder that is affected by prior exposure, these g-methods are also infrequently used by epidemiologists along with Bayesian techniques [5, 7] likely due to their greater complexity compared to other methods. However, more recent applications of these g-methods and Bayesian approaches that provide code should facilitate greater consideration of these valuable techniques [5, 8, 9, 37, 38].

Another set of complex and therefore also less utilized methods include doubly robust estimators. Doubly robust estimators represent more flexible strategies for confounder control, which in certain settings can yield more valid and precise effect estimates compared to the aforementioned techniques [39, 40]. Thus, despite their greater complexity, doubly robust estimators should be more readily considered for use by applied researchers as well especially because code is now also widely available to implement these methods [41].

Each of the previously described methods requires the consistency condition and assumes exchangeability (potential outcomes are MCAR or MAR conditional on measured potential confounders), positivity, and correct model specification (when semi-parametric and fully parametric techniques are employed) [4, 42]. Here positivity requires a non-zero probability of each instrument/exposure level marginally or within every observed combination of potential confounders. The exclusion restriction, which requires the instrument to only affect the outcome through the exposure, is also necessary for the instrumental variable approach.

Some methods are more sensitive to assumption violations and may be less efficient than others. Therefore, when selecting which method(s) to use to estimate a given causal effect, careful consideration should be given to which method(s) is most feasible and appropriate in a given research setting. The results from multiple methods can also be compared. Further, sensitivity analysis techniques [43–50] should be readily employed concurrently with the selected technique(s) to assess the robustness of inferences in the presence of potential assumption violations.

Selection bias

The two approaches that have been most commonly used in the epidemiologic literature to address selection bias due to missing individual-level potential outcomes include standard regression adjustment and IPW [4, 15, 51, 52]. Standard regression adjustment ensures that the estimation of a relevant function of the individual-level potential outcomes (e.g., P(Y^a = 1 | A, S = 0)) is accurate by only performing the estimation within strata of measured covariates that are associated with selection and the outcome of interest such as L in Diagram (II) of the Figure. Differences in the distribution of covariates like L between selected and not selected persons is the source of differences in the relevant function between selected and not selected persons and in turn the selection bias. Thus estimating the relevant function within strata of L should be accurate and reduce selection bias when necessary assumptions and conditions are met. Further, estimating the relevant function within strata of L is equivalent to conditioning on L in Diagram (II) of the Figure and blocking the open non-causal pathway from A to Y via S and L.

IPW can be used in a broader number of selection bias scenarios than standard regression adjustment to facilitate the accurate estimation of relevant functions and in turn reduce selection bias [15]. Specifically, IPW procedures re-weight the observed data to generate a pseudo-population that includes the missing individual-level potential outcomes of those individuals who were not selected. This re-weighting is performed as a function of the measured covariates that are associated with selection and the outcome of interest (e.g., L). The re-weighted data therefore yields a pseudo-population where the covariates used to estimate the weights are no longer associated with selection (e.g., the arrow from L to S in Diagram (II) of the Figure is removed) and the resulting estimated relevant function of the individual-level potential outcomes is accurate when necessary assumptions and conditions are met.

Stabilized versions of the aforementioned selection weights can be estimated that preserve the number of observed outcomes and enhance the precision of estimates. When competing risks are a source of the potential selection bias (e.g., dying before the outcome occurs or is assessed), IPW [53, 54] as well as other methods [55–58] have been used to address the potential selection bias. However, there remains considerable debate regarding whether estimating relevant functions of the individual-level potential outcomes using methods such as IPW is appropriate when the potential outcome is undefined, like in the case where the competing risk is death [59, 60].

Standard regression adjustment, IPW, as well as other techniques including more flexible doubly robust estimators [13, 14, 35, 41, 54–57, 61] for reducing selection bias require the consistency condition and assume exchangeability, positivity, and correct model specification (when semi-parametric and fully parametric techniques are employed) [4, 21, 42]. Here exchangeability requires no unmeasured covariates that contribute to the selection bias (i.e., potential outcomes are MAR conditional on exposure and measured covariates) while positivity requires a non-zero probability of being selected within every exposure level and observed combination of the exposure and the covariates that contribute to the selection bias. Given that unmeasured covariates likely exist, more recently employed instrumental variable approaches [62–64] to address selection bias related to measured and unmeasured covariates are appealing. However, suitable instruments that satisfy the exclusion restriction (instrument only associated with the outcome through selection) are likely limited. Therefore, after selecting the technique(s) most appropriate for the particular research setting, sensitivity analysis procedures [50, 65–72] should be employed concurrently with the selected technique(s) to assess the robustness of inferences in the presence of potential assumption violations.

Measurement bias

Bias analysis techniques [1, 50, 73–75] can be used to obtain more accurate estimates of relevant functions of the individual-level potential outcomes when measurement error is present and necessary assumptions and conditions are met. Specifically, simple bias analysis [1, 50] uses validity measures (e.g., sensitivity and specificity or positive predictive value and negative predictive value) obtained from validation data, expert opinions, or the published literature to correctly classify participants by their misclassified exposure, outcome, or covariate. When the validity measures are accurate this reclassification aids in the valid estimation of the functions of the individual-level potential outcomes of interest by effectively removing the arrows from U_A to A^* and U_Y to Y^* in Diagram (III) of the Figure or from U_L to L^* (not shown).

Recently Funk and Landi [75] provided a nice review of the aforementioned simple bias analysis as well as other methods for addressing measurement bias. Other discussed methods include probabilistic bias analysis [1, 50], Bayesian bias analysis [1, 73, 74], regression calibration [76, 77], modified maximum likelihood [78–80], multiple imputation [77, 81], and propensity score calibration [82–84] which all also require that appropriate assumptions are met. The review also articulates the research settings when each of these approaches is most appropriate.

Conclusions

In epidemiologic studies, the three main threats to obtaining consistent estimates of causal effects can be characterized as missing data problems that can be addressed using a myriad of methods so that associational effects equal the desired causal effects of interest. Each of these methods makes assumptions. Many of these assumptions cannot be tested empirically. Therefore, the application of these methods should be based on the research setting and combined with sensitivity analyses to examine how robust inferences are to potential violations in relevant assumptions.