The Impact of the Texas Top 10 Percent Law on College Enrollment: A Regression Discontinuity Approach

Abstract

We use regression discontinuity methods on a representative survey of Texas high school seniors to discern the impact on flagship-enrollment behavior of the Texas top 10 percent law, which guarantees admission to any Texas public university to students who graduate in the top decile of their class. By comparing students at and immediately below the cut-point for automatic admission, we find that the top 10 percent law affects flagship enrollment of Hispanic students eligible for the admission guarantee, as well as rank-eligible graduates from high schools where minority students predominate and from high schools with the state average share of economically disadvantaged students. Our findings are robust to various model specifications and different bandwidth choices using local linear estimation.

Introduction

Following the 5th Circuit Court’s 1996¹ judicial ban on the use of race and ethnicity in college admissions decisions, minority representation at the University of Texas at Austin (UT) and Texas A&M University (TAMU) declined appreciably (Chapa & Lazaro, 1998; Card & Krueger, 2005; Horn & Flores, 2003). In response, the Texas legislature passed H.B. 588, popularly known as the top 10 percent law, which guarantees college admission to students who graduate in the top decile of their high school class. Furthermore, Rank-eligible graduates are allowed to select their postsecondary institution. Because the top 10 percent law was motivated partly by a desire to restore minority representation at the public flagships, higher education administrators, researchers, and legislators have tracked minority student enrollment trends (Walker & Lavergne, 2001; Montejano, 2001; Kain, O'Brien, & Jargowsky, 2005; Chapa & Lazaro, 1998).

Evaluations of the change in admission regime fall into two general classes—those based on institutional administrative data before and after the top 10 percent law was enacted (Montejano, 2001; Long & Tienda, 2008; Card & Krueger, 2005; Alfonso & Calcagno, 2007) and those based on longitudinal survey data (Tienda & Niu, 2006a; 2006b). Enrollment trends depend on applications as well as the probability of admission; therefore several researchers have also considered how changes in admission regimes influence all three outcomes. Using institutional administrative data, Koffman and Tienda (2008) claim that graduates from affluent schools are the major beneficiaries of the admission guarantee because they are significantly more likely to apply to one of the public flagships compared with their cohorts who graduated from high schools that served students of low to moderate socioeconomic status. Harris and Tienda (2010) also find that black and Hispanic application rates to UT and TAMU fell after affirmative action was judicially banned in Texas, but rebounded after the top 10 percent law went into effect, albeit not to levels that existed under affirmative action. Alfonso and Calcagno (2007) show that demographic trends were partly responsible for the observed shifts in the representation of minority applicants and enrollees. Long and Tienda (2008) exploit the natural experiment in Texas college admissions by using administrative data to examine changes in admission and enrollment probabilities at Texas public institutions and conclude that the percent plan is an ineffective proxy for race-sensitive criteria in college admissions.

Similar results obtain in other states, such as Washington, where Brown and Hirschman (2006) document lower minority enrollment after voters passed Initiative 200, which prohibited consideration of race in college admissions. Their analyses also trace the minority enrollment decline to a drop in applications. But in California, Lomibao and associates (2004) claim that the lower representation of minority students following the public referendum banning affirmative action resulted not from the lower number of applications from minority student applicants, which actually rose steadily, but rather from their lower odds of admission.

Studies based on administrative records cannot consider the range of alternatives that students considered in their college decision-making, however. Using survey data, Niu, Tienda, and Cortes (2006) examined both how institutional characteristics influence students’ college preferences and enrollment behavior under the top 10 percent law, showing that distance, cost, and availability of financial aid are important determinants of matriculation decisions. Further, Niu and Tienda (2008a) find that the type of high school attended is more salient than class rank in delimiting students’ choice sets and ultimately their enrollment outcomes. These papers based on survey data share two limitations. First, because class rank is self-reported—either unknown or estimated by a significant number of students—claims about its influence on post-secondary outcomes are approximate. A more significant drawback is the lack of a comparison group whose admission was not governed by the top 10 percent law, which limits the authors’ ability to draw causal inferences.

Accordingly, this paper addresses both limitations first by using transcript-verified class rank information and second by applying a regression discontinuity technique to estimate the impact of the Texas top 10 percent law on enrollment decisions at one of the two public flagships: University of Texas at Austin (UT) or Texas A& M University (TAMU). The quasi-experimental design that fully exploits the richness of the survey data improves upon analyses that use either approach alone. Specifically, we examine college going behavior of Texas students approaching top 10 percent high school class rank status and estimate the discontinuity in flagship enrollment at the cutoff point.

The second section discusses the provisions of the top 10 percent law, its underlying assumptions, and their testable implications. In the third section we describe the data and our application of the regression discontinuity technique and present graphic displays and Probit estimates of the impact of the top 10 percent law on flagship enrollment. We find evidence of discontinuity in flagship enrollment for Hispanic students and graduates from predominately minority high schools. We also find discontinuity in flagship enrollment for graduates from high schools with the state average share of economically disadvantaged students. Combined with evidence that the share of enrollees admitted automatically to UT and TAMU has risen significantly since 1998 (Tienda & Sullivan, 2009), our results are in line with the law’s goal of restoring ethno-racial diversity and broadening access to Texas’s public flagships to students from underrepresented high schools (see also Long, Saenz, & Tienda, in press). Furthermore, our findings of discontinuity are robust to various model specifications and different bandwidth choices using local linear estimation, as reported in the fifth section. The concluding section summarizes the findings and discusses them in light of growing discontent with the top 10 percent law, which has become as controversial as the affirmative action regime it replaced.

Policy Context

Passed in 1997 and in force by 1998, the top 10 percent law qualifies all graduates ranked in the top decile of their senior class for automatic admission to any Texas public college or university. To be admitted, however, applicants must submit a completed application, including standardized test scores, although these are disregarded for rank-eligible students. The uniform admission law also specified 18 factors that universities may consider in admitting students who do not graduate in the top 10 percent of their high school class, including socioeconomic status, second language ability, and indications that the student overcame adversity (see Long & Tienda, 2008).

Although the top 10 percent law was triggered by the judicial ban on affirmative action, the architects of H.B.588 had a broader vision, namely to create a fair, race-neutral college admission policy. Recognizing that a handful of affluent, largely suburban high schools sent large numbers of students to UT and TAMU while hundreds of others sent none, the legislation’s key sponsor (the late Irma Rangel) sought to broaden college access both by ensuring that (1) “the very best students of each school in the state” could pursue postsecondary education (Montejano, 2001) and (2) that the public flagships better represent the geographic, socioeconomic, and ethno-racial make-up of the state (Giovanola, 2005; Olivas, 2007). Given the pervasive economic and racial segregation of Texas public schools (Reardon, 2003; Tienda & Niu, 2006b), broadening access to the most selective public institutions was made possible by determining eligibility for the admission guarantee on a school-specific basis. That is, rather than compete with students across the state to qualify for automatic admission, seniors compete with their own classmates in striving for a class rank at or above the top decile of their cohort.

Furthermore, unlike California, which stipulates uniform criteria for calculating class rank, Texas high schools have considerable autonomy in how they derive class rank distributions, such as whether to give greater weight to more rigorous classes. The law also did not stipulate a required academic curriculum to qualify for the admission guarantee. In response to criticisms that students were “gaming the system” by avoiding rigorous courses in order to boost their class rank, in 2001 the Texas legislature passed an amendment requiring prospective beneficiaries to complete the recommended or advanced curriculum (Tienda & Sullivan, 2009).²

Supporters of the Texas top 10 percent regime herald it as a merit-based alternative to affirmative action, emphasizing that the law broadened access to the public flagships by applying a uniform merit criterion across all high schools. Class rank serves as the sole forcing function to identify the highest achievers in each high school, regardless of curriculum, academic rigor, and resources. Although the admission guarantee does not guarantee enrollment, opponents offer two major criticisms to argue that the law should be rescinded. First, although technically race-neutral, the percent plan disguises the use of race in admissions because of pervasive school segregation. Second, the use of a single metric to gauge merit allegedly gives undue advantages to rank-eligible graduates from underperforming schools relative to seniors from the most competitive schools ranked below the admission guarantee.

The shift from a race-conscious admission regime to a percentage plan with a known admission guarantee has several testable implications about whether the law altered the likelihood of minority student enrollment at one of the public flagships. First, given the rapid growth and diversification of Texas’s college-age population, it is unclear whether gains in minority college enrollment after the top 10 percent law was implemented were attributable to the new admission regime or to changing population composition (Alfonso & Calcagno, 2007). Our application of regression discontinuity methods considers how the impact of the top 10 percent law differs for Hispanic, black, Asian, and white students. Second, because the success of the uniform admission regime in restoring campus diversity was partly achieved by qualifying for automatic admission minority students who attend segregated schools (Tienda & Niu, 2006b), we assess whether the impact of the law on flagship enrollment rates differs according to the ethno-racial composition of high schools.

Finally, recognizing that vigorous outreach and scholarship programs were a necessary adjunct to successfully recruit high achieving students from low income families, administrators at UT-Austin and TAMU campuses targeted scholarships for high schools with low college-going traditions and high shares of economically disadvantaged students (Walker & Lavergne, 2001; Domina, 2007). Designated Longhorn (UT) and Century (TAMU) high schools, a subset of rank-eligible graduates from these campuses are offered tuition scholarships to attend the respective institution. Therefore, we evaluate whether the impact of the law on enrollment at the flagship campuses differ for students from Longhorn and Century high schools.

Data and Methods

The empirical analyses are based on the senior cohort of the Texas Higher Education Opportunity Project (THEOP) survey data, a representative, longitudinal study of Texas public high school students who were first surveyed during spring of 2002 using a paper and pencil in-class survey instrument (N=13,803).³ For cost reasons, the longitudinal sample is based on a random subsample of the baseline respondents (N=5,836), who were re-interviewed by phone one year following high school graduation. To guarantee the maximum possible precision for blacks and Asians, all baseline respondents from these groups were included in the longitudinal sample; proportionate samples of Hispanics and non-Hispanic whites were randomly drawn for the sample balance. The response rate for the wave-2 interviews was 70 percent, and sample weights for the follow-up interviews were recalibrated to the original population.⁴

In addition to basic demographic, socioeconomic, and standard tracking information, the baseline survey obtained self-reported information about grades, decile class rank, and future plans. The first follow-up survey (wave 2) recorded whether respondents actually enrolled in college one year after high school graduation, and if so, where. For students who participated in the second interview, actual class rank, standardized test scores, and high school GPA were subjected to a transcript verification procedure, which was conducted by high school administrators or staff. About 86 percent of records were so verified; moreover, the transcript-based class rank is precisely measured, which is necessary for application of regression discontinuity techniques.⁵

The Outcome Variable

We examine the impact of the top 10 percent law on whether respondents attended one of the two public flagships, either the University of Texas at Austin (UT) and Texas A&M University (TAMU), where affirmative action was most used before the judicial ban (THECB, 1998), and where minority representation fell when consideration of race and ethnicity in college decisions was outlawed (Chapa & Lazaro, 1998).

Demographic Subgroups and High School Strata

Because the top 10 percent law was designed to broaden access to selective public institutions for students from underrepresented high school and demographic groups, we estimate identical specifications separately for white, black, Hispanic, and Asian students. Furthermore, we use administrative data from the Texas Education Agency (TEA) to characterize Texas high schools based on their ethno-racial composition and socioeconomic heterogeneity. High schools were sorted into five strata based on the ethno-racial composition using the percent white as a baseline referent: (1) predominantly (more than 80 percent) white; (2) majority (60 to 80 percent) white; (3) integrated (40 to 60 percent white); (4) majority minority (20 to 40 percent white); and (5) predominately minority (less than 20 percent white).

To evaluate whether and to what extent the top 10 percent law facilitated enrollment of students from economically disadvantaged high schools, we developed a 5-category typology that stratifies high schools according to their economic status and their college-going traditions.⁶ Using an indicator of the percent of students ever economically disadvantaged, high schools were first sorted into quartiles, where schools in the lowest quartile poor were designated affluent; those in the highest quartile poor were labeled resource poor; and the remainder classified as average. Affluent schools were further divided into feeder high schools, which had very strong traditions of sending students to the two public flagships, and the resource-poor schools were sorted into those that were designated for Longhorn or Century scholarships (Tienda & Niu, 2006a).

The five mutually exclusive economic strata include:

• affluent high schools: low shares of economically disadvantaged students;

• feeder high schools: affluent schools with strong traditions of sending students to UT and TAMU;

• poor high schools: high shares of economically disadvantaged students;

• Longhorn/Century schools: poor high schools with low college-going traditions that were targeted for outreach and scholarship programs by UT and TAMU;

• typical high schools: average shares of economically disadvantaged students.

Although the high school segregation and economic indicators overlap somewhat, they represent substantively different constructs. For example, typical high schools include predominately minority, integrated, and majority white high schools. None of the predominately minority schools are classified as affluent or feeder high schools, but they include typical, poor, and Longhorn/Century high schools. Between 69 and 74 percent of students from affluent and feeder high schools are white, but only between one-quarter and one-fifth of students from schools with large shares of economically disadvantaged students are white. At schools ranked in the second and third quartiles based on their share of economically disadvantaged students, about half of students are white, one-third Hispanic, 9 percent African American and 3 percent Asian, which corresponds with the ethno-racial make-up of Texas graduates circa 2002 (Tienda & Sullivan, 2009). (Appendix 1 provides further details.) We expect to find an impact of the top 10 percent law on flagship enrollment among top performing underrepresented minority students as well as graduates from minority high schools and from resource-poor high schools.

The Regression Discontinuity Approach

To estimate the impact of the Texas top 10 percent law on flagship enrollment, we simulate experimental conditions through the use of regression discontinuity (RD) methods. In their original paper, Thistlethwaite and Campbell (1960) studied two groups of near-winner students—one that was awarded Certificates of Merit and another that merely received letters of commendation based on qualifying scores—to estimate the effect of the Certificate of Merit on a student’s other scholarship receipt and career plans. In this RD design, a single treatment divides subjects into the treated and untreated groups, namely receipt of the merit certificate. Therefore, a distinct discontinuity at the cutoff point provides evidence of the treatment effect. A key assumption is other characteristics correlated with the probability of being treated trend smoothly through the cutoff point.

In education research, the RD design has recently been applied to estimate the effect of financial aid on college enrollment (Van der Klaauw, 2002; Kane, 2003); the effect of remedial education on student achievement (Jacob & Lefgren, 2004; Moss & Yeaton, 2006; Martorell & McFarlin, 2008); and the impacts of failing the high school exit exam on eventually obtaining a diploma, attending college, and wages (Martorell, 2004). The RD approach is well suited for our analytical objectives because the top 10 percent law stipulates the exact cutoff point needed to implement the RD framework. Our application of the RD design estimates the impact of the top 10 percent law as follows:

$$y=\alpha g(\mathit{\text{rank}})+\gamma T+\beta Z+\epsilon ,\text{where}T=1\mathrm{i}\mathrm{f}\mathit{\text{rank}}\le 10$$ (1)

In this specification, y indicates whether a student enrolled (0/1) in one of the public flagships; g(rank) is a continuous function of actual high school percentile class rank; T is the top 10 percent status indicator function; Z is a vector of individual characteristics affecting college enrollment outcomes; and ε is an error term. Students who rank below the 10 percent rank cut-point are placed in the control group (T = 0), and students ranked at or above the 10 percent cut-point (percentile rank equal to the top decile) are placed in the treatment group (T = 1).

In a sharp regression-discontinuity design, where all top decile students are placed in the control group, assignment coincides with treatment status, thus γ gives the intent-to-treat (ITT) effect. Because ITT represents the average effect of making the program available to its targeted group, γ estimates the difference that policymakers would observe from implementing the program given certain levels of non-participation (Heckman, LaLonde, & Smith, 1999). Besides its policy relevance, ITT represents a complex combination of the treatment effects for participants and non-participants.⁷

Assuming the error term ε in equation (1) is distributed normally, it can be estimated with a probit specification;

$$\mathit{\text{Prob}}(y=1)=\Phi (\alpha g(\mathit{\text{rank}})+\gamma T+\beta Z),$$ (2)

then prob(y = 1|T = 1) - prob(y = 1|T = 0) gives the estimated marginal intent-to-treat (ITT) effect of the 10 percent law on students’ college enrollment. Because the estimated impact only applies to those near the cut-point, the impact of the law on students far away from the threshold may be quite different.

Flagship enrollment is assumed to be a continuous function of high school percentile class rank, g(rank), but the estimates will be biased or inefficient if g is misspecified. Over-specified models are unbiased, albeit inefficient, but under-specified models generally are both biased and inefficient. Therefore, when the functional form is misspecified, over-specification is preferred and under-specification should be avoided (Trochim, 1984). We estimate models separately with 2nd order and with 4th order polynomial terms on class rank and report both sets of results to demonstrate that estimates are not sensitive to model specification.

Following Imbens and Lemieux’s (2008) guidance on implementing the regression discontinuity technique, we also estimate local linear regressions with the simple rectangular kernel and further verify the robustness of the results to different bandwidth choices⁸. That is, we estimate models with linear terms on class rank using only observations within small bandwidths around the cut-point. Starting with a bandwidth of 10 percentage points on either side of the cut-point, we shrink the interval to 4 percentage points around the cut-point and show that results are not sensitive to the bandwidth choices. We also re-estimate the models with 2nd and with 4th order polynomial terms on class rank using only observations within a small bandwidth on either side of the cutoff point to test further the robustness of the findings.

Statistical Controls

The baseline probit models are estimated with and without Z—the vector of controls that are known to influence college enrollment: family SES variables (parental education and home ownership), respondent’s college disposition (grade level when respondent first considered college), and standardized test information (test score and a dummy indexing if the test was not taken).⁹ With rare exceptions, inclusion of family SES and college disposition variables does not substantively change estimates of the impact of the top 10 percent law on flagship enrollment. This result confirms an assumption needed for application of regression discontinuity technique, namely that observed student characteristics other than class rank trend smoothly through the cutoff-point.

Results

Descriptive statistics for top decile students and those ranked at or below the 10th percentile verify whether the basic assumption of regression-discontinuity design holds in our sample, namely whether in the absence of the treatment, students near the cutoff point in the class rank distribution are similar. The first two columns in Table 1 compare sample means for students ranked in the top 10 percent and those ranked below (11 to 100 percent). Flagship enrollment means are significantly different between those above and below the cut-point when students from the full class rank distribution are considered, and with a few exceptions, so also are the student characteristics known to influence college enrollment.

Table 1.

Sample Means by Top 10 Percent Status and Class Rank Bandwidths

	Full Range		±8 Percent		±4 Percent		±2 Percent
	Top 10 percent	11– 100 percent	3–10 percent	11– 18 percent	7–10 percent	11– 14 percent	9–10 percent	11–12 percent
Outcome Variable
Flagship Enrollment	0.33	0.04***	0.31	0.16***	0.32	0.19***	0.30	0.19*
Control Variables
Race/Ethnicity
White	0.45	0.37	0.44	0.48	0.45	0.51	0.50	0.49
Black	0.11	0.19***	0.13	0.10	0.12	0.10	0.09	0.09
Hispanic	0.28	0.38***	0.29	0.32	0.29	0.29	0.27	0.33
Asian	0.15	0.05***	0.13	0.70***	0.12	0.07†	0.12	0.09
Other/Missing	0.01	0.02	0.01	0.02	0.02	0.02	0.01	0.01
Parental Education
Less Than High School	0.11	0.16***	0.11	0.17**	0.11	0.16†	0.10	0.16†
High School	0.17	0.21**	0.18	0.19	0.19	0.18	0.19	0.19
Some College	0.25	0.23	0.25	0.21	0.24	0.18	0.20	0.21
College and Higher	0.38	0.21***	0.35	0.31	0.33	0.35	0.36	0.33
Don't Know/Missing	0.09	0.19***	0.11	0.12	0.12	0.13	0.15	0.11
Home Ownership
Own	0.82	0.70***	0.80	0.76	0.80	0.74†	0.78	0.76
Rent	0.11	0.15**	0.12	0.14	0.02	0.02	0.12	0.14
Don’t Know/Missing	0.07	0.15***	0.08	0.10	0.09	0.13	0.09	0.09
First Thought About College Going
Always	0.78	0.54***	0.75	0.72	0.73	0.75	0.74	0.75
Middle High School	0.10	0.12	0.12	0.09	0.14	0.09	0.13	0.09
High School	0.07	0.19***	0.07	0.13	0.07	0.10	0.07	0.11
Don’t Know/Missing	0.05	0.15***	0.06	0.06	0.07	0.06	0.07	0.06
Test Information
Test Not Taken	0.04	0.40***	0.05	0.13***	0.06	0.14***	0.06	0.12†
Test Scores	1134	900***	1097	1022***	1080	1041**	1085	1037*
N	725	4214	545	520	287	272	143	140

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

At narrower intervals around the cut-point—3 to 10 percent versus 11 to 18 percent and 7 to 10 percent versus 11 to 14 percent—significant differences in flagship enrollment persist for students ranked above and below the 10 percent rank; however, most of the differences in the covariates are statistically insignificant. Exceptions include Asian origin, having parents with less than high school education, whether a college entrance exam was taken, and test scores. When the class rank interval is further narrowed to a 2 percent point range on either side of the cut-point—9 to 10 percent vs. 11 to 12 percent—differences in flagship enrollment remain statistically significant (p ≤ 0.02). At this bandwidth, Asian origin students ranked above and below the cut-point are not statistically different, but students’ whose parents lack high school and those who did not take a standardized test differ marginally by eligibility for automatic admission. Mean test scores of students above and below the cut-point do differ significantly for this bandwidth.

Among the student characteristics used to predict flagship enrollment, the only one reflecting a behavioral choice is whether to take a standardized test. Although standardized test results are not considered for students eligible for the admission guarantee, scores must be reported for applications to be complete. Compared with lower-ranked students, top decile graduates, especially black and Hispanic students as well as those from predominately minority and resource-poor high schools should have strong incentives to take one or more entrance exams. By the same token, lower-ranked students may be discouraged from taking the test, especially those ranked well below the second decile. Therefore, it is conceivable that the top 10 percent law influences test-taking behavior.

Dickson (2006) uses test taking as a proxy for college enrollment when she examines the consequences of ending affirmative action in Texas. She finds that the percent of minority students applying to college increased significantly when the percent plan was accompanied by changes in financial aid, but changes in test-taking behavior appears to be inconsequential for flagship enrollment. Below we show that estimates of discontinuity in flagship enrollment at the cutoff point are not affected by adding test-taking variables along with other covariates. We attribute this result to the fact very few students around the cutoff point did not take a test. As a sensitivity test we repeat the analyses of flagship enrollment including only test takers and produce virtually identical estimates of discontinuity (point estimates differ at the second decimal place, but significance levels remain unchanged).¹⁰

We also examine differences in flagship enrollment and relevant covariates separately for Hispanics and graduates from predominately minority high schools and schools where the average share of economically disadvantaged students typifies the statewide average. As we demonstrate below, the top 10 percent law affected flagship enrollment for these three subgroups. Appendix Tables 2a through 2c reveal that for these three groups, flagship enrollment differences between students above or below the 10 percent cut-point are sizable and statistically significant even as the interval width around the cutoff point is narrowed. Furthermore, with a few exceptions, differences in characteristics of students ranked above and below the cut-point also vanish as the class rank interval narrows. Particularly for graduates from typical high schools, only test scores differentiate students by top 10 percent status.

Figure 1 presents the distribution of high school seniors by actual percentile class rank. Although the eligibility rule is known and students near the cutoff point may work harder to improve their class rank or try to game the system by taking less challenging courses, it is difficult for individual students or teachers to intentionally alter their position at the cutoff point. Furthermore, both UT and TAMU require high schools to report students’ precise numerical class rank and the senior class size in order to calculate class rank percentile. The sample class rank distribution is upwardly skewed, but the cumulative class rank distribution is smooth throughout and no significant clumping appears around the 10^th percentile rank.¹¹

Figure 1. Distribution of High school Seniors by Actual Class Rank Percentile.

Source: THEOP Wave 1 & 2 Senior Surveys.

The subsequent analyses estimate the intent-to-treat effect of the top 10 percent law on students’ flagship enrollment first for the pooled sample, and subsequently for three group-specific comparisons: (1) race and ethnic groups; (2) high school ethno-racial composition strata; and (3) high school socioeconomic composition. Following visual displays of the impact of the top 10 percent law on enrollment at UT or TAMU, we report probit regression discontinuity estimates of the main intent-to-treat (ITT) effect of the top 10 percent law on flagship enrollment. All tables report marginal effects calculated at the sample means for students at the cut-point, which we empirically validate in a final empirical analysis.

Visual Representation

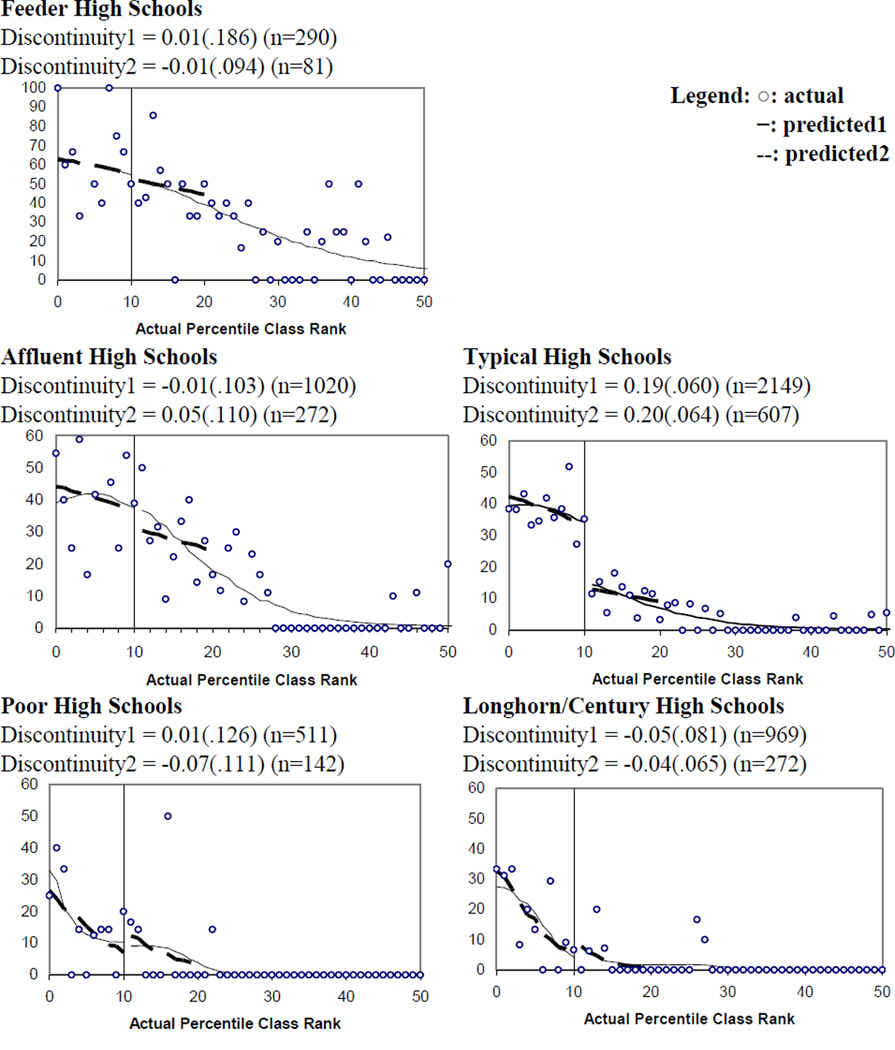
Figures 2 through 4 provide visual evidence of discernible discontinuity in the relationship between class rank and flagship enrollment at the 10 percent cut-point. In each of the graphs, the open circles represent the average flagship enrollment rate for students with a particular class rank. Superimposed smooth lines depict the predicted enrollment probability from a baseline probit specification with 4th order polynomials in class rank estimated over the entire class rank range; the superimposed dotted lines represent the predicted enrollment probability from a baseline probit specification with a linear term in class rank estimated over the top 20 percent of the class rank distribution. Overall, the predicted enrollment probabilities track the local averages reasonably well, and a discontinuity is visually discernible where the probit models yield statistically significant point estimates. The two superimposed lines mostly overlap, which indicates that the estimates are not sensitive either to model specifications or to the bandwidth used in estimation. Because the flagship enrollment rates are close to zero among students at or below the 50th percentile class rank, for parsimony we exclude them from the graphic presentation. In addition, group-specific enrollment rates at UT and TAMU are generally below 60 percent, therefore most graphs are presented within this range.

Figure 2. Probability of Flagship Enrollment by Actual Percentile Class Rank and Students' Race/Ethnicity.

Source: THEOP Wave 1 & 2 Senior Surveys.

Notes: The predicted probabilities are from baseline probit regressions.

Predicted 1: Predicted values from baseline probit regressions with 4th order polynomial in class rank estimated over the full range of class rank.

Predicted 2: Predicted values from baseline probit regressions with linear term in class rank estimated over the top 20 percent of class rank.

Four substantive findings emerge from the visual display and underlying empirical estimates. First, the top 10 percent law does not appear to affect the likelihood of enrollment at the public flagships when the analysis is conducted over all seniors. Although the top graph in Figure 2 shows a disjuncture in flagship enrollment at the cutoff point, the six-point gap is imprecisely estimated.

Second, and as intended by Rangel and her supporters, the top 10 percent law appears to impact flagship enrollment for Hispanics, but not other groups. Specifically, the graph depicting white students’ enrollment at TAMU or UT shows no discontinuity at the cutoff point, and probit estimates of 1 or 2 percentage points are not statistically significant. By contrast, the graph for Hispanics suggests a rather large discontinuity at the cut-point for enrollment at UT or TAMU; probit estimates yield a disjuncture of 12 to 14 percentage points. The estimated discontinuity for black students is very small and statistically insignificant.¹² For Asian students both the estimated marginal effects and associated standard errors are large.

Third, flagship enrollment decisions of students from predominantly white high schools are unaffected by the top 10 percent law, but this is not so for graduates from predominantly minority high schools. In Figure 3, the graphs for graduates from predominately white high schools and those from integrated high schools show an inconsistent enrollment pattern by class rank. Among these students the magnitude of estimated discontinuity is sensitive both to model specifications and the bandwidth used for estimation, but also fails to attain statistical significance. The graphs also show no visible disjuncture at the cut-point for students from either majority white or majority minority high schools, as confirmed by the statistically insignificant probit estimates. For graduates from predominately minority high schools, by contrast, a discontinuity at the cutoff point is clearly discernible and the sizable probit estimates are statistically significant. Specifically, at the class rank cutoff point, seniors from high schools with 80 percent or more minority students are about 14 percentage points more likely to enroll at UT or TAMU than their classmates ranked immediately below the cutoff point.¹³

Figure 3. Probability of Flagship Enrollment by Actual Percentile Class Rank and High School Racial/Ethnic Composition.

Source: THEOP Wave 1 & 2 Senior Surveys.

Notes: The predicted probabilities are from baseline probit regressions.

Predicted 1: Predicted values from baseline probit regressions with 4th order polynomial in class rank estimated over the full range of class rank.

Predicted 2: Predicted values from baseline probit regressions with linear term in class rank estimated over the top 20 percent of class rank.

Fourth, the top 10 percent law also boosts flagship enrollment among students who graduate from high schools with average shares of economically disadvantaged students. Because the Longhorn/Century scholarship programs were designed by UT and TAMU to recruit rank-eligible students from resource poor schools with low college-going traditions, the lack of a discontinuity in flagship enrollment was surprising. This finding does not mean that the targeted outreach efforts and targeted scholarship programs are inconsequential, however. Other studies find that the scholarship programs do increase minority enrollment at the public flagships (Domina, 2007; Niu et al., 2006). Rather, our failure to identify a significant impact partly reflects the limited number of scholarships available at each of the Longhorn and Century high schools. We verified this hunch by examining the class rank distribution among graduates for Longhorn and Century schools who enroll at one of flagships and find that nearly three-fourths of these students ranked in the top 7th percentile or better of their graduating class.¹⁴

The right-middle graph in Figure 4 shows a large disjuncture at the cutoff point for flagship enrollment among graduates from typical high schools. Moreover, the probit estimates indicate a relatively large and statistically significant discontinuity in flagship enrollment—on the order of 19 to 20 percentage points. The remaining graphs in Figure 4 lack a clear disjunction at the cutoff point, which correspond to a small and statistically insignificant discontinuity estimates in the probit models.

Figure 4. Probability of Flagship Enrollment by Actual Percentile Class Rank and High School Economic Strata.

Source: THEOP Wave 1 & 2 Senior Surveys.

Notes: The predicted probabilities are from baseline probit regressions.

Predicted 1: Predicted values from baseline probit regressions with 4th order polynomial in class rank estimated over the full range of class rank.

Predicted 2: Predicted values from baseline probit regressions with linear term in class rank estimated over the top 20 percent of class rank.

The Boosting Effect of the Law on Flagship Enrollment

Thus far we established evidence of discontinuity at the 10 percent class rank cut-point for three subgroups: Hispanic students, those from predominately minority high schools, and those from high schools with average shares of economically disadvantaged students. For students near the cut-point, however, the apparent disjunction could result from either or both of the following mechanisms: (1) The top 10 percent law boosts the flagship enrollment probability for those ranked immediately above the cutoff point; and (2) the top 10 percent law dampens the flagship enrollment probability for those ranked immediately below the cutoff point. Our survey data does not permit us to ascertain their relative weights and whether both mechanisms operate, but findings from other studies based on administrative data suggest that the observed discontinuity largely reflects the boosting effect of the top 10 percent law on flagship enrollment among rank-eligible students.

Our findings of a discontinuity in flagship enrollment among top decile graduates from predominately minority schools are consistent with Tienda and Niu’s (2006b) results showing that most black and Hispanic students who qualify for the admission guarantee attend predominately minority schools. Because each school has discretion to determine the class rank distribution (for example, whether to weight honors and AP courses more heavily), the law has no capacity to influence which students actually qualify for the admission guarantee. Niu and Tienda (2008b) examine administrative data from students enrolled at UT-Austin between 1990 and 2003 and also find support consistent with a claim about the boosting effects of the law. They show that during the first four years the law was in force, growing saturation of UT with students qualified for automatic admission came at the expense of graduates ranked at or below the third decile of their high school class. Freshmen ranked in the second decile of their high school classes maintained their cohort share until 2002, but thereafter their cohort share fell because the university rescinded a temporary increase in the freshman class size between 2000 and 2003 (Tienda & Sullivan, 2009). This interpretation of the discontinuity estimates for Hispanic students also aligns with evidence that Hispanic enrollment rebounded at both flagships after 1998, albeit unevenly (Harris & Tienda, 2010).¹⁵

Given the stated intent of the law, we expected to find that the law boosts flagship enrollment among Hispanics and those from predominately minority high schools. Therefore, we were surprised to find strong evidence that the law benefits graduates from typical high schools—those classified in the second and third quartiles based on low income students. That nearly half of Texas public high school seniors attend such typical schools attests to the profound impact of the top 10 percent law in broadening access to the public flagships (Montejano, 2001; Long et al., in press). For example, 795 different Texas high schools were represented in the UT 1996 admission cohort, compared with 943 high schools in the 2004 admitted pool, roughly a 19 percent increase. Not all admitted students actually matriculate, thus the number of schools represented among enrolled students was lower—616 in 1996 versus 815 in 2004. The higher number of high schools represented at the flagship campuses indicates some success of the top 10 percent law in broadening access to students from high schools with low sending rates to UT and TAMU.

Robustness Checks and Marginal Effects

We implement several procedures to check the robustness of our findings. First, we estimate two probit specifications using all observations over the entire class rank distribution: one with a 2nd order class rank polynomial and another with a 4th order class rank polynomial. Second, we obtain local linear estimators by estimating probit models with a linear specification in class rank using only observations in small intervals around the cutoff points. Third, we add control variables to the baseline models and compare the estimates obtained for the top 10 percent status indicator. With few exceptions, the marginal effect estimates differ only slightly based on statistical specifications, bandwidth choices, and addition of control variables, which attests to the robustness of our key findings. We detail each procedure in turn.

Table 2, which presents marginal effects derived from probit models with 2nd and 4th order class rank polynomials over the full class rank distribution, confirms that our baseline results are not sensitive to model specification. For the baseline models, the marginal effect estimates differ only by a few percentage points, but significance levels persist. Similar results obtain when control variables are added to the baseline specifications. Estimates that are small in magnitude fail to reach statistical significance and those that are significant tend to be large in magnitude. Specifically, the flagship enrollment discontinuity reaches a magnitude of at least 10 percentage points for Hispanics, for students from predominately minority high schools, and those from typical high schools.

Table 2.

Regression Discontinuity Estimates of the Impact of the Top 10 Percent Law on Flagship Enrollment: Texas Public High School Seniors in 2002

Marginal Effects, S.E. in parenthesis
	Model Specifications
	2nd Order Polynomial		4th Order Polynomial
Controls Included	NO	YES	NO	YES
All (n=4939)	0.04 (.033)	0.03 (.034)	0.06 (.041)	0.09 (.042)
By Race/Ethnicty
White (n=1899)	−0.03 (.052)	−0.05 (.054)	0.01 (.064)	0.04 (.066)
Black (n=860)	0.07 (.085)	0.08 (.105)	0.02 (.114)	0.04 (.139)
Hispanic (n=1804)	0.12 (.052) *	0.10 (.051)†	0.12 (.059)*	0.11 (.061)†
Asian (n=292)	0.20 (.140)	0.27 (.157)	0.08 (.174)	0.09 (.197)
By High School Racial/Ethnic Composition
Predominately White (n=543)	−0.17 (.135)	−0.14 (.139)	−0.18 (.159)	−0.15 (.169)
Majority White (n=1161)	−0.03 (.069)	−0.05 (.074)	−0.02 (.085)	0.00 (.095)
Integrated (n=1044)	0.09 (.081)	0.11 (.085)	0.05 (.105)	0.08 (.118)
Majority Minority (n=353)	0.07 (.095)	0.00 (.007)	0.06 (.089)	0.00 (.003)
Predominately Minority (n=1838)	0.13 (.048) **	0.11 (.043)**	0.14 (.058)*	0.16 (.058)**
By High School Economic Strata
Feeder (n=290)	−0.06 (.142)	−0.10 (.147)	0.01 (.186)	0.08 (.204)
Affluent (n=1020)	−0.08 (.083)	−0.10 (.087)	−0.01 (.103)	−0.02 (.109)
Typical (n=2149)	0.14 (.050) **	0.13 (.047)**	0.19 (.060)**	0.21 (.059)***
Poor (n=511)	−0.08 (.107)	−0.07 (.112)	0.01 (.126)	0.05 (.130)
Longhorn/Century (n=969)	−0.01 (.060)	0.01 (.057)	−0.05 (.081)	−0.05 (.108)

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Notes: Each cell represents the estimated discontinuity in the outcome, defined as the marginal effect of being in the top decile. Equations are estimated with a probit specification, and marginal effects are calculated at the means for students at the cutoff point:

• Flagship Enrollment = α0+ α1*rank+ α2*rank2+ γ*·Top10%+ βZ+ ε;
• Flagship Enrollment = α0+ α1*rank+ α2*rank2+ α3*rank3+ α4*rank4+ γ*Top10%+ βZ+ ε;

where Z is a control vector that includes family SES variables (parent education and home ownership), student’s college disposition (grade level when student first considered college) and standadized test (test scores and test not taken dummy).

Asian students are an exception to this generalization because point estimates are sensitive to model specifications. Specifically, the model with 2nd order polynomials renders a much larger marginal effect estimate compared to that with 4th order polynomials, but neither is statistically significant. Below we show that estimates for Asians are also sensitive to bandwidth choices. Graduates from predominately white high schools are a second exception: The estimated marginal effects are large (and negative), but never distinguishable from zero. Below we show that the magnitude of the estimates for students from predominately white high schools is much smaller when estimated over small intervals around the cutoff point.

Second, our results are not sensitive to the class rank bandwidth used in estimation. To obtain local linear estimators, we estimated probit models with a linear class rank term over small intervals around the cut-point—starting from 10 percentage points at either side then shrinking to 4 percentage points at either side. For parsimony, Table 3 only presents marginal effects obtained using observations located at 10, 8, 6, and 4 percentage points on either side of the cut-point. With few exceptions, these estimates are fairly similar to the baseline specifications both in magnitude and statistical significance. Exceptions occur for instances of small case numbers such as Asians, students from majority minority high schools, and students from poor high schools . Although the marginal effect for graduates from integrated high schools is fairly large, the point estimate does not attain statistical significance. Therefore, the main story persists: We find a large and statistically significant discontinuity at the cut-point in flagship enrollment for Hispanic students, those from predominately minority high schools, and those from typical high schools. Compared with estimates obtained from the full range of the class rank distribution and high order polynomials, the estimated discontinuities are similar (although the statistical significance level is lower).¹⁶

Table 3.

Regression Discontinuity Estimates of the Impact of the Top 10 Percent Law on Flagship Enrollment: Texas Public High School Seniors in 2002

Marginal Effects, S.E. in parenthesis
	Class Rank Bandwidths
	±10 percent		N	±8 percent		N
Control Included	NO	YES		NO	YES
All	0.07 (.044)	0.10 (.044)*	1,374	0.10 (.050)*	0.11 (.051)*	1,065
By Student Race/Ethnicty
White	0.02 (.069)	0.05 (.071)	630	0.04 (.078)	0.06 (.081)	493
Black	0.01 (.130)	0.00 (.167)	149	0.05 (.140)	0.02 (.167)	122
Hispanic	0.14 (.061)*	0.12 (.056)*	423	0.19 (.066)**	0.17 (.064)*	323
Asian	0.24 (.155)	0.37 (.168)*	152	0.25 (.184)	0.31 (.215)	109
By High School Racial/Ethnic Composition
Predominately White	−0.06 (.172)	0.01 (.184)	133	−0.05 (.197)	0.05 (.218)	105
Majority White	−0.01 (.094)	0.01 (.105)	328	0.00 (.106)	0.00 (.117)	263
Integrated	0.14 (.096)	0.21 (.101)*	301	0.15 (.110)	0.22 (.119)†	231
Majority Minority	0.02 (.085)	0.00 (.003)	103	0.09 (.095)	0.00 (.000)	82
Predominately Minority	0.14 (.061) *	0.16 (.058)**	509	0.19 (.071)*	0.19 (.069)**	384
By High School Economic Strata
Feeder	0.02 (.202)	0.09 (.234)	81	0.05 (.231)	0.07 (.284)	65
Affluent	0.05 (.110)	0.02 (.123)	272	0.05 (.126)	−0.02 (.144)	211
Typical	0.20 (.064) **	0.22 (.060)***	607	0.22 (.073)**	0.22 (.069)**	467
Poor	−0.07 (.111)	0.01 (.091)	142	0.04 (.113)	0.21 (.182)	107
Longhorn/Century	−0.04 (.065)	−0.01 (.084)	272	−0.02 (.073)	0.01 (.089)	215
	Class Rank Bandwidths
	±6 percent		N	±4 percent		N
Control Included	NO	YES		NO	YES
All	0.10 (.059)†	0.10 (.060)	818	0.08 (.073)	0.04 (.076)	559
By Student Race/Ethnicty
White	0.05 (.090)	0.04 (.095)	386	0.08 (.111)	0.07 (.120)	268
Black	0.01 (.175)	−0.10 (.227)	96	−0.05 (.232)	−0.11 (.280)	63
Hispanic	0.22 (.076)**	0.19 (.074)*	240	0.15 (.093)	0.14 (.091)	163
Asian	0.05 (.233)	0.17 (.275)	81	−0.06 (.282)	−0.05 (.344)	55
By High School Racial/Ethnic Composition
Predominately White	−0.05 (.224)	0.03 (.254)	80	0.00 (.170)	0.17 (.319)	54
Majority White	0.01 (.123)	0.03 (.136)	210	0.02 (.153)	−0.01 (.185)	147
Integrated	0.10 (.135)	0.13 (.156)	175	0.18 (.158)	0.16 (.198)	124
Majority Minority	0.08 (.130)	0.00 (.000)	59	−0.04 (.226)	0.00 (.000)	43
Predominately Minority	0.21 (.083)*	0.20 (.083)*	294	0.10 (.106)	0.11 (.116)	191
By High School Economic Strata
Feeder	0.03 (.267)	0.10 (.335)	55	0.12 (.309)	0.05 (71.4)	41
Affluent	0.00 (.148)	0.00 (.167)	159	−0.10 (.181)	−0.12 (.211)	111
Typical	0.19 (.087)*	0.20 (.083)*	364	0.19 (.105)†	0.21 (.115)†	249
Poor	0.13 (.132)	0.19 (.197)	79	−0.04 (.182)	0.11 (.262)	50
Longhorn/Century	−0.02 (.090)	−0.02 (.101)	161	−0.05 (.131)	−0.16 (.242)	108

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Notes: See notes to Table 2 for further details. Results reported here are from linear specifications.

These statistical results are highly consistent with the graphic analyses described above in that large, visually discernible flagship enrollment disjunctures are consistently corroborated by statistically significant discontinuities based on alternative model specifications and variable class rank bandwidths used in estimation. This is the case for Hispanic students, those from predominately minority high schools, and those from typical high schools.

Particularly for graduates from typical high schools, the visual analysis clearly shows a large disjuncture at the cutoff point with little noisiness, and the statistical modeling renders a stable and significant marginal effect ranging between 19 and 22 percentage points, depending on the model specification and bandwidth choice. This sizable marginal effect is obtained with a 4th order polynomial specification over entire class rank distribution; with a linear or 2nd order polynomial specification over small intervals around class rank cutoff point ranging from 10 to 4 percent at either side; and also with a 4th order polynomial specification estimated using observations ranging from 10 to 6 percent at either side of the cut-point. Graphs for Hispanic students and graduates from predominately minority high schools reveal a large disjuncture at the cutoff point with some noisiness; for these groups the statistical modeling also generates statistically significant point estimates, with magnitudes that fluctuate by a few percentage points depending on the specification.

For some groups—namely Asian students, those from predominately white high schools, and those from integrated high schools—the graphs indicate an erratic association between flagship enrollment and class rank and the estimated marginal effects are sensitive to model specifications or bandwidth choices, or both. Statistical models occasionally render a fairly large marginal effect, but these never attain significance. Even the apparent disjuncture for the pooled sample of seniors fails to attain statistical significance under alternative model specifications and bandwidth choices. In rare instances the magnitude of the discontinuity increases, but never reaches statistical significance at conventional levels.

The consistency between graphic analysis and statistic modeling is expected. Imbens and Lemieux (2008) stress the importance of graphic analysis to identify a discontinuity at the cutoff point, and point out: “The formal statistical analyses . . . are essentially just sophisticated versions of this, and if the basic plot does not show any evidence of discontinuity, there is relatively little chance that the more sophisticated analyses will lead to robust and credible estimates with statistically and substantially significant magnitudes” (p.622). Our results are entirely consistent with their claim.

Our third procedure for checking robustness involves adding a set of covariates to the baseline models. With rare exceptions, the inclusion of race/ethnicity, family SES, college disposition, and test-taking does not substantively change the estimated marginal effects, which change by only a few (mostly just 1 or 2) percentage points relative to the baseline models, and the significance levels are sustained in most instances. The inclusion of covariates increases either the magnitude or the statistical significance of the estimate for two subgroups—Asian students and those from integrated high schools—but this occurrence is infrequent.

The similarity of the estimates with and without covariates suggests that the top 10 percent status indicator does not capture discontinuity in background characteristics at the cut-point. As shown in Table 1 and Appendix Tables 2a through 2c, differences in most covariates disappear for comparisons of students within small intervals around the 10 percent class rank cut-point. As an additional check, we explicitly test the discontinuity in the covariates by treating each of them as a dependent variable with the same models used to predict flagship enrollment. First we estimate models over the entire class rank distribution with 2nd and 4th order class rank polynomials, as well as local linear regressions. Graphs that plot each of these covariates against the class rank distribution reveal the absence of discontinuity at the cut-point for most covariates, with three notable exceptions presaged by Table 1, namely whether parents have less than high school education, whether students took entrance exams, and their test scores.¹⁷

The first two exceptions represent a small percentage of Texas high school graduates and the test score difference is modest. Furthermore, for the three subgroups where a discontinuity in flagship enrollment obtains at the cut-point, two covariates—test not taken and actual test score—are significant predictors of flagship enrollment, yet the magnitude of the point estimate is quite small. Other significant predictors of flagship enrollment show no discontinuity at the cutoff point.¹⁸ That is, students ranked around the 10 percent cut-point required to qualify for automatic admission are essentially similar in most attributes that influence college-going behavior; hence, the observed differences in flagship enrollment likely represent the impact of top 10 percent law on students immediately around the cutoff point.

Calculation of Marginal Effects

There does not seem to be consensus about which sample means to use in calculations based on a probit specification. For example, Kane (2003) calculates the marginal effects at the sample means for all observations used in the estimation, but Martorell (2004) calculates the marginal effects at the sample means for observations at the cut-point. Like Martorell, we derive marginal effects at the sample means for students at the cut-point to obtain discontinuity estimates for a substantive reason—that is, we focus on the cutoff point established by law.

The marginal effects should not be sensitive to which set of means are used if the cut-point is around the mean, or if the relationship between class rank and each outcome variable is flat. In our case, however, the mean class rank for all observations used in estimation differs from the cut-point established by law. Furthermore, because the relation between class rank and flagship enrollment exhibits a significant slope, marginal effects calculated at the means for all observations used in estimation would differ substantially from the marginal effects calculated at the means for students at the cutoff point. As the bandwidth around the cut-point shrinks, the mean class rank for all observations used in estimation approach the cut-point. In these instances the marginal effects calculated at the means for all observations used in estimation would approach the marginal effects calculated at the means for students at the cutoff point. Our sensitivity analyses confirm this result.

Table 4 presents marginal effects calculated both at means for all observations used in probit estimation and at means for students at the cut-point. For comparison, we also present coefficients from a linear probability model. Reported marginal effects were generated from the specification with 4th order polynomials in class rank. The first set of estimates uses all observations over the full class rank distribution; the second set uses the top two deciles of the class rank distribution; and the final set is derived from observations ranked 8 percentage points above or below the cut-point.

Table 4.

Regression Discontinuity Estimates of the Top 10 Percent Law on Flagship Enrollment: Texas Public High School Seniors in 2002

Linear probability model coefficients (OLS) and marginal effects (ME), S.E. in parenthesis
	Class Rank Bandwidths
	Full Range			±10 percent			±8 percent
	OLS	ME1	ME2	OLS	ME1	ME2	OLS	ME1	ME2
All	0.08***	0.01	0.06	0.11†	0.09	0.10	0.09	0.09	0.10
	(.023)	(.011)	(.041)	(.060)	(.059)	(.063)	(.068)	(.067)	(.070)
By Student Race/Ethnicty
White	0.02	0.00	0.01	0.05	0.04	0.05	0.11	0.10	0.11
	(.041)	(.022)	(.064)	(.091)	(.091)	(.096)	(.103)	(.102)	(.105)
Black	0.04	0.00	0.02	0.03	−0.01	−0.02	−0.06	−0.04	−0.05
	(.051)	(.016)	(.114)	(.179)	(.164)	(.213)	(.207)	(.199)	(.240)
Hispanic	0.13***	0.01*	0.12*	0.21*	0.18*	0.20*	0.17†	0.16†	0.18†
	(.029)	(.024)	(.059)	(.084)	(.088)	(.083)	(.091)	(.092)	(.086)
Asian	0.24*	0.00	0.08	0.20	0.22	0.22	−0.05	−0.06	−0.06
	(.110)	(.001)	(.174)	(.241)	(.227)	(.238)	(.280)	(.286)	(.286)
By High School Racial/Ethnic Composition
Predominately White	−0.12	0.00	−0.18	0.02	0.03	0.02	0.00	0.00	0.00
	(.087)	(.000)	(.159)	(.237)	(.234)	(.225)	(.273)	(.267)	(.265)
Majority White	−0.02	−0.01	−0.02	0.02	0.00	0.00	0.04	0.04	0.04
	(.052)	(.025)	(.085)	(.123)	(.124)	(.132)	(.141)	(.139)	(.146)
Integrated	0.15**	0.00	0.05	0.11	0.09	0.10	0.10	0.08	0.09
	(.052)	(.000)	(.105)	(.133)	(.129)	(.144)	(.152)	(.148)	(.167)
Majority Minority	0.02	0.00	0.06	0.15	0.01	0.04	0.05	-	-
	(.056)	(.000)	(.089)	(.132)	(.071)	(.236)	(.128)	-	-
Predominately Minority	0.15***	0.03*	0.14*	0.19*	0.17*	0.21*	0.15	0.18†	0.18†
	(.032)	(.020)	(.058)	(.090)	(.081)	(.091)	(.101)	(.100)	(.091)
By High School Economic Strata
Feeder	−0.00	0.01	0.01	0.07	0.07	0.07	0.10	0.10	0.10
	(.137)	(.120)	(.186)	(.281)	(.175)	(.265)	(.321)	(.310)	(.309)
Affluent	0.02	−0.00	−0.01	0.03	0.03	0.03	−0.02	−0.02	−0.02
	(.058)	(.019)	(.103)	(.149)	(.147)	(.154)	(.170)	(.168)	(.178)
Typical	0.21***	0.05**	0.19**	0.21*	0.21*	0.22*	0.17†	0.17†	0.18†
	(.033)	(.025)	(.060)	(.090)	(.089)	(.089)	(.101)	(.103)	(.101)
Poor	−0.06	0.00	0.01	0.06	0.08	0.09	0.06	0.04	0.05
	(.053)	(.000)	(.126)	(.151)	(.117)	(.138)	(.163)	(.145)	(.155)
Longhorn/Century	−0.03	0.00	−0.05	−0.02	0.01	0.03	−0.04	0.01	0.04
	(.034)	(.000)	(.081)	(.094)	(.025)	(.113)	(.098)	(.032)	(.096)

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10,

^-can not be properly estimated.

Notes: OLS: Linear probability model coefficient, ME1: marginal effect calculated at the sample means, ME2: marginal effect calculated at the means for students at the cutoff point.

Results are generated from baseline models with 4^th order class rank polynomial.

Results confirm that marginal effects calculated at means for all observations differ greatly from those calculated at means for students at the cutoff point when observations over the full class rank distribution are used in estimation. Yet, the latter are similar to coefficients obtained from linear probability models with much larger standard errors. As the intervals around the cut-point shrink, the differences in two sets of marginal effects vanish and approximate the coefficients estimated from linear probability models. Standard errors for all three sets of estimates based on smaller bandwidths are relatively similar. Therefore, both substantive and empirical considerations support our decision to calculate marginal effects at the means for students at the cut-point to discern statistically significant discontinuities in flagship enrollment.

Conclusions

In crafting House Bill 588, the late Irma Rangel argued that public institutions should serve all Texas residents; by intent she sought to create “a fair, race-neutral admissions structure providing students from all backgrounds and [all] parts of the state an opportunity to continue their educations” (Giovanola, 2005: p.31). Aware that a small number of suburban high schools sent disproportionate numbers of students to the University of Texas at Austin and Texas A&M University, the law’s chief architects sought to better represent the state’s geographic, socioeconomic, and ethnic diversity at all public postsecondary institutions, but the public flagships in particular. Using a regression discontinuity design, we evaluate whether the top 10 percent law influenced decisions of rank-eligible students to enroll at UT or TAMU.

Comparisons of flagship enrollment between students at the cut-point and those immediately below indicate that the top 10 percent law impacts the likelihood of flagship enrollment for Hispanic students and students who graduate from predominantly minority high schools. In addition, the top 10 percent law affects flagship enrollment among students who graduate from typical high schools, many of which have weak traditions of sending students to the flagship campuses (Long et al., in press). These results are robust to alternative specifications and bandwidth choices around the cutoff point. Combined with other studies about changes in enrollment behavior of top 10 percent students based on institutional administrative data (Long & Tienda, 2008; Dickson, 2006; Kain et al., 2005; Harris & Tienda, 2010), our results are also striking in their consistency with the intent of the law, including (1) to restore ethno-racial and socioeconomic diversity at the public flagships and (2) to increase college access to a broader spectrum of the Texas population, which includes representation of high schools that historically sent few or no students to UT and TAMU.

Because administrators at UT and TAMU understood that an admission guarantee was insufficient to raise enrollment of underrepresented groups, and low-income minority students in particular, both institutions targeted rank-eligible graduates from high schools designated to receive Longhorn and Century scholarships. That we did not find discontinuity at the cutoff point in flagship enrollment among students who graduated from these high schools likely reflects the very limited number of scholarships offered at each high school, and their concentration among the highest ranked students within the range eligible for the admission guarantee.

On balance, it appears that the top 10 percent law has achieved its broad goal of broadening access, particularly for Hispanics and graduates of schools where minority students predominate, as well as average high schools with limited prior representation at UT or TAMU. We must emphasize, however, that our application of the RD approach cannot compare the effectiveness of the top 10 percent law and affirmative action as a strategy to diversify college campuses. In fact, other studies have concluded that it is neither an efficient nor effective alternative to recruit black and Hispanic students (Kain et al., 2005, Long & Tienda, 2008; Harris & Tienda, 2010).

This point warrants further consideration in light of potential future revisions to the top 10 percent law.¹⁹ Pressure to modify or rescind the law has been mounting since 2002 in response to the growing saturation of the UT-Austin campus with automatically admitted students, and with greater force since the 2003 Grutter decision. In a widely publicized presidential address, President Powers (2008) outlined several serious but unintended consequences of the law, notably the saturation of the UT-Austin campus with students eligible for automatic admission. Although Texas A&M has also witnessed an increase in the share of who qualify for the guarantee, approximately half of its current enrollees qualified for automatic admission. The saturation of the UT campus results from the law’s permissiveness in guaranteeing rank-eligible students access to a public campus of their choice, which provides no mechanism to allocate rank-eligible applicants among public institutions.

But with growing demand for access to slots at four-year institutions, the cut-point for an admission guarantee might be more stringent, possibly varying over time depending on the size of the applicant pool. Students who fall below the cutoff, which likely would vary from year to year depending on the size and composition of the applicant pool would be admitted using the full range of criteria approved for full file review. This approach seems reasonable on its face in that it reconciles the demography of the state with long-standing inequities in access, but it will be ineffective if not tied to financial aid to ensure that rank-eligible graduates from low income families have the means to enroll.

Appendix 1

Racical/Ethnic Composition by High School Economic Strata (Column Percent)

	Feeder	Affluent	Typical	Poor	Longhorn/ Century
White	69	74	52	11	10
Black	3	9	9	7	18
Hispanic	19	12	33	82	70
Asian	8	3	3	0	2
Other/Missing	1	2	2	0	1
Total	100	100	100	100	100
N	290	1020	2149	511	969

Source: THEOP Wave 1 & 2 Senior Surveys.

Appendix 2

a. Variable Means by Top 10 Percent Status and Class Rank Bandwidth: Hispanic Students
	Full Range		±8 percent		±4 percent		±2 percent
	Top 10 percent	11– 100 percent	3–10 percent	11–18 percent	7–10 percent	11–14 percent	9–10 percent	11– 12 percent
Outcome Variable
Flagship Enrollment	0.23	0.01***	0.20	0.05***	0.24	0.05***	0.23	0.04**
Control Variables
Parental Education
Less Than High School	0.28	0.33	0.27	0.41**	0.24	0.42*	0.23	0.43*
High School	0.18	0.19	0.19	0.22	0.24	0.22	0.18	0.17
Some College	0.22	0.16*	0.21	0.16	0.19	0.14	0.15	0.17
College and Higher	0.18	0.09***	0.18	0.10*	0.15	0.10	0.15	0.13
Don’t Know/Missing	0.13	0.24***	0.15	0.12	0.18	0.13	0.28	0.09*
Home Ownership
Own	0.80	0.68***	0.77	0.72	0.76	0.71	0.62	0.83*
Rent	0.12	0.14	0.13	0.17	0.12	0.18	0.23	0.15
Don’t Know/Missing	0.09	0.17**	0.10	0.10	0.12	0.11	0.15	0.02*
First Thought About College Going
Always	0.69	0.45***	0.67	0.61	0.63	0.67	0.59	0.72
Middle High School	0.12	0.14	0.13	0.13	0.17	0.10	0.18	0.07
High School	0.13	0.24***	0.14	0.25*	0.14	0.22	0.13	0.22
Don’t Know/Missing	0.06	0.17***	0.06	0.01*	0.06	0.01	0.10	0.00*
Test Information
Test Not Taken	0.07	0.53***	0.08	0.24***	0.08	0.25**	0.08	0.24*
Test Scores	1024	837***	1001	919***	990	924**	980	927†
N	206	1598	156	167	84	79	39	46

b. Variable Means by Top 10 Percent Status and Class Rank Bandwidth: Students from Predominately Minority High Schools
	Full Range		±8 percent		±4 percent		±2 percent
	Top 10 percent	11– 100 percent	3–10 percent	11– 18 percent	7–10 percent	11– 14 percent	9–10 percent	11–12 percent
Outcome Variable
Flagship Enrollment	0.31	0.01***	0.27	0.06***	0.30	0.07***	0.23	0.08*
Control Variables
Race/Ethnicity
White	0.07	0.06	0.06	0.09	0.06	0.11	0.09	0.16
Black	0.18	0.24*	0.20	0.20	0.16	0.21	0.17	0.18
Hispanic	0.55	0.64**	0.55	0.62	0.58	0.59	0.60	0.59
Asian	0.19	0.05***	0.17	0.07**	0.18	0.09†	0.13	0.06
Other/Missing	0.01	0.01	0.01	0.02	0.02	0.00	0.02	0.00
Parental Education
Less Than High School	0.21	0.26*	0.21	0.33**	0.23	0.30	0.21	0.31
High School	0.22	0.19	0.23	0.21	0.23	0.22	0.28	0.22
Some College	0.25	0.18**	0.24	0.21	0.19	0.18	0.11	0.22
College and Higher	0.22	0.13***	0.20	0.16	0.19	0.18	0.19	0.16
Don’t Know/Missing	0.12	0.23***	0.13	0.10	0.15	0.11	0.21	0.08†
Home Ownership
Own	0.76	0.60***	0.71	0.63	0.73	0.57*	0.57	0.63
Rent	0.16	0.21†	0.20	0.26	0.19	0.25	0.30	0.27
Don’t Know/Missing	0.08	0.19***	0.10	0.12	0.08	0.17*	0.13	0.10
First Thought About College Going
Always	0.69	0.48***	0.67	0.67	0.63	0.74	0.57	0.78*
Middle High School	0.16	0.14	0.17	0.11	0.22	0.07**	0.25	0.06**
High School	0.10	0.22***	0.10	0.18*	0.10	0.14	0.11	0.12
Don’t Know/Missing	0.05	0.16***	0.05	0.04	0.06	0.06	0.06	0.04
Test Information
Test Not Taken	0.07	0.50***	0.07	0.21***	0.08	0.23**	0.09	0.18
Test Scores	1042	832***	999	922***	988	924**	980	923*
N	278	1560	204	180	104	87	49	47

c. Variable Means by Top 10 Percent Status and Class Rank Bandwidth: Students from Typical High Schools
	Full Range		±8 percent		±4 percent		±2 percent
	Top 10 percent	11– 100 percent	3–10 percent	11– 18 percent	7–10 percent	11–14 percent	9–10 percent	11–12 percent
Outcome Variable
Flagship Enrollment	0.38	0.03***	0.37	0.12***	0.38	0.14**	0.31	0.14*
Control Variables
Race/Ethnicity
White	0.55	0.41***	0.55	0.63†	0.55	0.64	0.67	0.60
Black	0.06	0.20***	0.08	0.08	0.10	0.08	0.04	0.07
Hispanic	0.17	0.31***	0.18	0.19	0.20	0.16	0.21	0.22
Asian	0.20	0.06***	0.17	0.09**	0.14	0.09	0.07	0.09
Other/Missing	0.02	0.02	0.02	0.02	0.02	0.03	0.00	0.02
Parental Education
Less Than High School	0.07	0.13*	0.07	0.09	0.06	0.09	0.06	0.08
High School	0.18	0.24*	0.20	0.23	0.21	0.21	0.22	0.23
Some College	0.23	0.24	0.23	0.25	0.24	0.22	0.16	0.23
College and Higher	0.43	0.22***	0.41	0.32*	0.38	0.37	0.45	0.37
Don’t Know/Missing	0.08	0.18***	0.09	0.12	0.11	0.11	0.10	0.09
Home Ownership
Own	0.84	0.70***	0.82	0.78	0.83	0.76	0.82	0.78
Rent	0.11	0.16*	0.12	0.13	0.11	0.13	0.12	0.12
Don’t Know/Missing	0.05	0.14***	0.06	0.09	0.06	0.11	0.06	0.09
First Thought About College Going
Always	0.81	0.54***	0.79	0.74	0.77	0.75	0.78	0.78
Middle High School	0.09	0.12†	0.09	0.09	0.11	0.09	0.10	0.11
High School	0.05	0.17***	0.05	0.09	0.06	0.07	0.07	0.06
Don’t Know/Missing	0.05	0.17***	0.07	0.08	0.06	0.09	0.04	0.05
Test Information
Test Not Taken	0.04	0.41***	0.05	0.12*	0.07	0.12	0.09	0.08
Test Scores	1160	903***	1115	1044***	1103	1058**	1100	1051*
N	329	1820	245	222	133	116	67	65

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Appendix 3

a. Marginal Effects of Control variables on Flagship Enrollment With & Without Class Rank and Top 10 Percent Status
	All Seniors (n=4939)		Hispanics (n=1804)
Class Rank Variables & Top 10 Percent Status Included	YES	NO	YES	NO
Control Variables
Race/Ethnicity
Black	0.01 (.041)	0.02 (.024)
Hispanic	−0.03 (.032)	0.02 (.019)
Asian	0.15 (.042)***	0.14 (.032)***
Other/Missing	−0.05 (.085)	−0.03 (.044)
Parental Education
Less Than High School	−0.02 (.050)	0.00 (.030)	−0.05 (.053)	−0.01 (.021)
Some College	0.04 (.037)	0.02 (.022)	−0.03 (.057)	−0.01 (.021)
College and Higher	0.07 (.035)*	0.04 (.021)†	0.01 (.066)	0.00 (.025)
Don’t Know/Missing	0.02 (.053)	0.02 (.031)	−0.01 (.082)	0.00 (.031)
Home Ownership
Rent	−0.12 (.036)**	−0.06 (.018)**	−0.12 (.058)†	−0.05 (.018)*
Don’t Know/Missing	0.03 (.048)	0.01 (.028)	0.09 (.098)	0.03 (.039)
First Thought About College Going
Middle High School	−0.05 (.038)	−0.03 (.020)	−0.06 (.056)	−0.03 (.017)†
High School	−0.17 (.037)***	−0.11 (.014)***	−0.08 (.052)	−0.04 (.016)†
Don’t Know/Missing	−0.04 (.046)	−0.04 (.022)†	−0.11 (.072)	−0.05 (.017)†
Test Information
Test Not Taken	−0.16 (.037)***	−0.12 (.012)***	−0.05 (.058)	−0.05 (.013)**
Test Scores	0.0007 (.0001)***	0.0007 (.0001)***	0.0006 (.0002)***	0.0004 (.0001)***

b. Marginal Effects of Control variables on Flagship Enrollment With & Without Class Rank Variables, Top 10 Percent Status
	Students from Predominately Minority High Schools (n=1838)		Students from Typical High Schools (n=2149)
Class Rank Variables & Top 10 Percent Status Included	YES	NO	YES	NO
Control Variables
Race/Ethnicity
Black	−0.04 (.075)	−0.00 (.032)	0.03 (.075)	−0.00 (.036)
Hispanic	−0.09 (.078)	0.00 (.030)	0.02 (.055)	0.02 (.029)
Asian	0.09 (.092)	0.11 (.059)*	0.21 (.060)***	0.18 (.046)***
Other/Missing	-- --	-- --	0.05 (.155)	−0.01 (.067)
Parental Education
Less Than High School	−0.02 (.067)	0.00 (.028)	−0.02 (.091)	−0.00 (.046)
Some College	0.07 (.068)	0.03 (.030)	0.09 (.063)	0.05 (.035)
College and Higher	0.02 (.066)	0.00 (.026)	0.09 (.057)	0.06 (.031)†
Don’t Know/Missing	0.06 (.091)	0.02 (.037)	0.03 (.090)	0.03 (.049)
Home Ownership
Rent	−0.03 (.056)	−0.02 (.021)	−0.14 (.058)*	−0.07 (.024)*
Don’t Know/Missing	0.06 (.088)	0.01 (.034)	−0.01 (.085)	−0.03 (.038)
First Thought About College Going
Middle High School	−0.08 (.054)	−0.03 (.020)	−0.05 (.065)	−0.02 (.030)
High School	−0.17 (.053)*	−0.07 (.014)***	−0.26 (.069)**	−0.12 (.019)***
Don’t Know/Missing	−0.11 (.073)	−0.05 (.021)†	−0.01 (.075)	−0.03 (.031)
Test Information
Test Not Taken	−0.08 (.058)	−0.06 (.014)***	−0.18 (.061)*	−0.11 (.017)***
Test Scores	0.0006 (.0002)***	0.0005 (.0001)***	0.0005 (.0002)***	0.0006 (.0001)***

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Note: Results reported here come from the specification with 4^th order polynomials in class rank.

Source: THEOP Wave 1 & 2 Senior Surveys.

^***p<0.001,

^**p<0.01,

^*p<0.05,

^†p<0.10

Note: Results reported here come from the specification with 4^th order polynomials in class rank.