Joint Estimation of Multiple Precision Matrices with Common Structures

Abstract

Estimation of inverse covariance matrices, known as precision matrices, is important in various areas of statistical analysis. In this article, we consider estimation of multiple precision matrices sharing some common structures. In this setting, estimating each precision matrix separately can be suboptimal as it ignores potential common structures. This article proposes a new approach to parameterize each precision matrix as a sum of common and unique components and estimate multiple precision matrices in a constrained l₁ minimization framework. We establish both estimation and selection consistency of the proposed estimator in the high dimensional setting. The proposed estimator achieves a faster convergence rate for the common structure in certain cases. Our numerical examples demonstrate that our new estimator can perform better than several existing methods in terms of the entropy loss and Frobenius loss. An application to a glioblastoma cancer data set reveals some interesting gene networks across multiple cancer subtypes.

1. Introduction

Estimation of a precision matrix, which is an inverse covariance matrix, has attracted a lot of attention recently. One reason is that the precision matrix plays an important role in various areas of statistical analysis. For example, some classification techniques such as linear discriminant analysis and quadratic discriminant analysis require good estimates of precision matrices. In addition, estimation of a precision matrix is essential to establish conditional dependence relationships in the context of Gaussian graphical models. Another reason is that the high-dimensional nature of many modern statistical applications makes the problem of estimating a precision matrix very challenging. In situations where the dimension p is comparable to or much larger than the sample size n, more feasible and stable techniques are required for accurate estimation of a precision matrix.

To tackle such problems, various penalized maximum likelihood methods have been considered by many researchers in recent years (Yuan and Lin, 2007; Banerjee et al., 2008; Friedman et al., 2008; Rothman et al., 2008; Lam and Fan, 2009; Fan et al., 2009, and many more). These approaches produce a sparse estimator of the precision matrix by maximizing the penalized Gaussian likelihood with sparse penalties such as the l₁ penalty and the smoothly clipped absolute deviation penalty (Fan and Li, 2001). Ravikumar et al. (2011) studied the theoretical properties of the l₁ penalized likelihood estimator for a broad class of population distributions.

Instead of using likelihood approaches, several techniques take advantage of the connection between linear regression and the entries of the precision matrix. See for example Meinshausen and Bühlmann (2006); Peng et al. (2009); Yuan (2010). In particular, these approaches convert the estimation problem of the precision matrix into relevant regression problems and solve them with sparse regression techniques accordingly. One advantage of these approaches is that they can handle a wide range of distributions including the Gaussian case. Cai et al. (2011) recently proposed a very interesting method to directly estimate the precision matrix without the Gaussian distributional assumption. This approach solves a constrained l₁ minimization problem to obtain a sparse estimator of the precision matrix. They showed that the proposed estimator has a faster convergence rate than the l₁ penalized likelihood estimator for some non-Gaussian cases.

All aforementioned approaches focus on estimation of a single precision matrix. The fundamental assumption of these approaches is that all observations follow the same distribution. However, in some real applications, this assumption can be unreasonable. As a motivating example, consider the glioblastoma multiforme (GBM) cancer data set studied by The Cancer Genome Atlas Research Network (The Cancer Genome Atlas Research Network, 2008). It is shown in the literature that the GBM cancer can be classified into four subtypes (Verhaak et al., 2010). In this case, it would be more realistic to assume that the distribution of gene expression levels can vary from one subtype to another, which results in multiple precision matrices to estimate (Lee et al., 2012). A naive way to estimate them is to model each subtype separately. However, in this separate approach, modeling of one subtype completely ignores the information on other subtypes. This can be suboptimal if there exists some common structure across different subtypes.

To improve the estimation in presence of some common structure, several joint estimation methods have been proposed recently in a penalized likelihood framework. See for example Guo et al. (2011); Honorio and Samaras (2012); Danaher et al. (2014). These methods employ various group penalties in the Gaussian likelihood framework to link the estimation of separate precision matrices.

In this article, we propose a new method to jointly estimate multiple precision matrices. Our approach uses a novel representation of each precision matrix as a sum of common and unique matrices. Then we apply sparse constrained optimization on the common and unique components. The proposed method is applicable for a broad class of distributions including both the Gaussian and some non-Gaussian cases. The main strength of our method is that it uses all available information to jointly estimate the common and unique structures, which can be more preferable than separate modelings. The estimation can be improved if the precision matrices are similar to each other. Furthermore, our method is able to discover unique structures of each precision matrix, which enables us to identify differences among multiple precision matrices. The proposed estimator is shown to achieve a faster convergence rate for the common structures in certain cases.

The rest of this article is organized as follows. In Section 2, we introduce our proposed method after reviewing some existing separate approaches. We establish its theoretical properties in Section 3. Section 4 develops computational algorithms to obtain a solution for the proposed method. Simulated examples are presented in Section 5 to demonstrate performance of our estimator and analysis of a glioblastoma cancer data example is provided in Section 6. The proofs of theorems are provided in Appendix.

2. Methodology

In this section, we introduce a new method for estimating multiple precision matrices in an l₁ minimization framework. Consider a heterogeneous data set with G different groups. For the gth group (g = 1, …, G), let $\{x_1^{(\mathrm{g})},\dots ,x_{n_g}^{(\mathrm{g})}\}$ be an independent and identically distributed random sample of size n_g, where $x_k^{(\mathrm{g})}={(x_{ki}^{(\mathrm{g})},\dots ,x_{kp}^{(\mathrm{g})})}^{\mathrm{T}}$ is a p-dimensional random vector with the covariance matrix ${\mathrm{\Sigma }}_0^{(\mathrm{g})}$ and precision matrix ${\mathrm{\Omega }}_0^{(\mathrm{g})}≔{({\mathrm{\Sigma }}_0^{(\mathrm{g})})}^{-1}$. For detailed illustration of our proposed method, we first define some notations similar to Cai et al. (2011). For a matrix X = (x_ij) ∈ ℛ^p×q, we define the elementwise l₁ norm ${\Vert X\Vert }_1={\sum }_{i=1}^p{\sum }_{j=1}^q|x_{ij}|$, the elementwise l_∞ norm |X|_∞ = max_{1≤i≤p,1≤j≤q} |x_ij| and the matrix l₁ norm ${\Vert X\Vert }_{L_1}={\text{max}}_{1\le j\le q}{\sum }_{i=1}^p|x_{ij}|$. For a vector x = (x₁, …, x_p)^T ∈ ℛ^p, |x|₁ and |x|_∞ denote vector l₁ and l_∞ norms respectively. The notation X ≻ 0 indicates that X is positive definite. Let I be a p × p identity matrix. For the gth group, Σ̂^(g) denotes the sample covariance matrix. Write ${\mathrm{\Omega }}_0^{(\mathrm{g})}=({\omega }_{ij,0}^{(\mathrm{g})})$; g = 1, …, G.

Our aim is to estimate the precision matrices, ${\mathrm{\Omega }}_0^{(1)},\dots ,{\mathrm{\Omega }}_0^{(\mathrm{G})}$. The most naive way to achieve this goal is to estimate each precision matrix separately by taking the inverses of the sample covariance matrices. However, in high dimensional cases, the sample covariance matrices are not only unstable for estimating the covariance matrices, but also not invertible. To estimate the precision matrix in high dimensions, various estimators have been introduced in the literature. For example, various l₁ penalized Gaussian likelihood estimators have been studied intensively in the literature (see for example, Yuan and Lin, 2007; Banerjee et al., 2008; Friedman et al., 2008; Rothman et al., 2008). In this framework, the precision matrices can be estimated by solving the following G optimization problems:

$$\underset{{\mathrm{\Omega }}^{(\mathrm{g})}\succ 0}{\text{min}}\text{tr}({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\mathrm{\Omega }}^{(\mathrm{g})})-\text{log}\{\text{det}({\mathrm{\Omega }}^{(\mathrm{g})})\}+{\lambda }_g\sum _{i\ne j}|w_{ij}^{(\mathrm{g})}|,g=1,\dots ,G,$$ (1)

where λ_g is a tuning parameter which controls the degree of the sparsity in the estimated precision matrices. Other sparse penalized Gaussian likelihood estimators have been proposed as well (Lam and Fan, 2009; Fan et al., 2009).

Recently, Cai et al. (2011) proposed an interesting method of constrained l₁ minimization for inverse matrix estimation (CLIME), which can be directly implemented using linear programming. In particular, the CLIME estimator of ${\mathrm{\Omega }}_0^{(\mathrm{g})}$ is the solution of the following optimization problem:

$$\text{min}{\Vert {\mathrm{\Omega }}^{(\mathrm{g})}\Vert }_1\text{subject to}:{|{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\mathrm{\Omega }}^{(\mathrm{g})}-I|}_{\infty }\le {\lambda }_g,$$ (2)

where Σ̂^(g) is the sample covariance matrix and λ_g is a tuning parameter. As the optimization problem in (2) does not require symmetry of the solution, the final CLIME estimator is obtained by symmetrizing the solution of (2). The CLIME estimator does not need the Gaussian distributional assumption. Cai et al. (2011) showed that the convergence rate of the CLIME estimator is faster than that of the l₁ penalized Gaussian likelihood estimator if the underlying true distribution has polynomial-type tails.

To estimate multiple precision matrices, ${\mathrm{\Omega }}_0^{(1)},\dots ,{\mathrm{\Omega }}_0^{(\mathrm{G})}$, we can build G individual models using the optimization problem (1) or (2). However, these separate approaches can be suboptimal when the precision matrices share some common structure. Several recent papers have proposed joint estimations of multiple precision matrices under the Gaussian distributional assumption to improve estimation. In particular, such an estimator is the solution of

$$\underset{\{\mathrm{\Omega }\}}{\text{min}}\sum _{g=1}^G{n}_g[\text{tr}({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\mathrm{\Omega }}^{(\mathrm{g})})-\text{log}\{\text{det}({\mathrm{\Omega }}^{(\mathrm{g})})\}]+P(\{\mathrm{\Omega }\}),$$

where n_g is the sample size of the g-th group, {Ω} = {Ω⁽¹⁾, …, Ω^(G)}, and P({Ω}) is a penalty function that encourages similarity across the G estimated precision matrices. For example, Guo et al. (2011) employs a non-convex penalty called hierarchical group penalty which has the form, $P(\{\mathrm{\Omega }\})=\lambda {\sum }_{i\ne j}{({\sum }_{g=1}^G|{\omega }_{ij}^{(\mathrm{g})}|)}^{1/2}$. Honorio and Samaras (2012) adopts a convex penalty, $P(\{\mathrm{\Omega }\})=\lambda {\sum }_{i\ne j}{|({\omega }_{ij}^{(1)},\dots ,{\omega }_{ij}^{(\mathrm{G})})|}_p(p>1)$ where | · |_p is the vector l_p norm. To separately control the sparsity level and the extent of similarity, Danaher et al. (2014) considered a fused lasso penalty, $P(\{\mathrm{\Omega }\})={\lambda }_1{\sum }_{g=1}^G{\sum }_{i\ne j}|{\omega }_{ij}^{(\mathrm{g})}|+{\lambda }_2{\sum }_{g<g\prime }{\sum }_{ij}|{\omega }_{ij}^{(\mathrm{g})}-{\omega }_{ij}^{(\mathrm{g}\prime )}|$. In some simulation settings, they showed that the joint estimation can perform better than separate l₁ penalized normal likelihood estimation. As pointed by Ravikumar et al. (2011), these penalized Gaussian likelihood estimators are applicable even for some mild non-Gaussian data since maximizing a penalized likelihood can be interpreted as minimizing a penalized log-determinant Bregman divergence. However, these approaches were mainly designed for Gaussian data and can be less efficient when the underlying distribution becomes far from Gaussian. In this paper, we propose a new joint method for estimating multiple precision matrices, which is less dependent on the distributional assumption and applicable for both Gaussian and non-Gaussian cases.

In our joint estimation method, we take the multi-task learning perspective and first define the common structure M₀ and the unique structure $R_0^{(\mathrm{g})}$ as

$$M_0≔\frac{1}{G}\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})},R_0^{(\mathrm{g})}≔{\mathrm{\Omega }}_0^{(\mathrm{g})}-M_0;g=1,\dots ,G.$$

It follows from the definition that ${\sum }_{g=1}^G{R}_0^{(\mathrm{g})}=0$, and consequently our representation is identifiable. The idea of decomposing parameters into common and individual structures was previously considered in the context of supervised multi-tasking learning (Evgeniou and Pontil, 2004). Their aim was to improve prediction performance of supervised multi-tasking learning. Here we focus on better estimation of precision matrices with the common and individual structures. The unique structure is defined to capture different strength of the edges across all classes. In a special case that an element of M₀ is zero, then the corresponding nonzero element in $R_0^{(\mathrm{g})}$ can be interpreted as a unique edge. Thus, the unique structure can address differences in magnitude as well as unique edges. If all precision matrices are very similar, then the unique structures defined above would be close to zero. In this case, it can be natural and advantageous to encourage sparsity among $\{R_0^{(1)},\dots ,R_0^{(\mathrm{G})}\}$ in the estimation. To estimate the precision matrices consistently in high dimensions, it is also necessary to assume some special structure of M₀ as well. In our work, we also assume that M₀ is sparse. To estimate $\{M_0,R_0^{(1)},\dots ,R_0^{(\mathrm{G})}\}$, we propose the following constrained l₁ minimization criterion:

$$\text{min}\{{\Vert M\Vert }_1+\nu \sum _{g=1}^G{\Vert R^{(\mathrm{g})}\Vert }_1\}$$

$$\mathrm{s}.\mathrm{t}{|\frac{1}{G}\sum _{g=1}^G\{{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(M+R^{(\mathrm{g})})-I\}|}_{\infty }\le {\lambda }_1,{|{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(M+R^{(\mathrm{g})})-I|}_{\infty }\le {\lambda }_2,\sum _{g=1}^G{R}^{(\mathrm{g})}=0,$$ (3)

where λ₁ and λ₂ are tuning parameters and ν is a prespecified weight. Note that if λ₁ > λ₂, then the second inequality constraints in (3) imply the first inequality constraint. Therefore, we only consider a pair of (λ₁, λ₂) satisfying λ₁ ≤ λ₂. The first inequality constraint in (3) reflects how close the final estimators are to the inverses of the sample covariance matrices in an average sense. On the other hand, the second inequality constraint controls an individual level of closeness between the estimators and the sample covariance matrices.

For illustration, consider an extreme case where all the precision matrices are the same. In this case, the unique structures may be negligible and the first inequality constraint in (3) approximately reduces to ${|(G^{-1}{\sum }_{g=1}^G{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})M-I|}_{\infty }\le {\lambda }_1$. Therefore, we can pool all the sample covariance matrices to estimate the common structure which is the precision matrix in this case. This would be advantageous than building each model separately. The value of ν in (3) reflects how complex the unique structures of the resulting estimators are. If the resulting estimators are expected to be very similar from each other, then a large value of ν is preferred. In Section 3, ν is set to be G⁻¹ or G^−1/2 for our theoretical results.

Similar to Cai et al. (2011), the solutions in (3) are not symmetric in general. Therefore, the final estimators are obtained after a symmetrization step. Let {M̂, R̂⁽¹⁾, …, R̂^(G)} be the solution of (3). Then we define ${\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}≔\hat{M}+{\hat{R}}^{(\mathrm{g})}$; g = 1, …, G. The final estimator of $\{{\mathrm{\Omega }}_0^{(1)},\dots ,{\mathrm{\Omega }}_0^{(\mathrm{G})}\}$ is obtained by symmetrizing $\{{\hat{\mathrm{\Omega }}}_1^{(1)},\dots ,{\hat{\mathrm{\Omega }}}_1^{(\mathrm{G})}\}$ as follows. Let ${\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}=({\hat{\omega }}_{ij,1}^{(\mathrm{g})})$. Our joint estimator of multiple precision matrices (JEMP), {Ω̂⁽¹⁾, …, Ω̂^(G)}, is defined as symmetric matrices, {${\hat{\mathrm{\Omega }}}^{(\mathrm{g})}=({\hat{\omega }}_{ij}^{(\mathrm{g})})$; g = 1, …, G} with

$${\hat{\omega }}_{ij}^{(\mathrm{g})}={\hat{\omega }}_{ij,1}^{(\mathrm{g})}I\{\sum _{g=1}^G|{\hat{\omega }}_{ij,1}^{(\mathrm{g})}|\le \sum _{g=1}^G|{\hat{\omega }}_{ji,1}^{(\mathrm{g})}|\}+{\hat{\omega }}_{ji,1}^{(\mathrm{g})}I\{\sum _{g=1}^G|{\hat{\omega }}_{ij,1}^{(\mathrm{g})}|>\sum _{g=1}^G|{\hat{\omega }}_{ji,1}^{(\mathrm{g})}|\};g=1,\dots ,G.$$

Note that the solution Ω̂^(g) is not necessarily positive definite. Although there is no guarantee for the solution to be positive definite, it can be positive definite with high probability. In our simulation study, we observed that within a reasonable range of tuning parameters, almost all solutions are positive definite. Furthermore, one can perform projection of the estimator to the space of positive definite matrices to ensure positive definitiveness as discussed in Yuan (2010).

As a remark, although we focus on generalizing CLIME for multiple graph estimation in this paper, our proposed common and unique structure approach can also be applied to the graphical lasso estimator under the Gaussian assumption as pointed out by one reviewer. As a future research direction, it would be interesting to investigate how the common and unique structure framework works in the graphical lasso estimator.

3. Theoretical Properties

In this section, we investigate theoretical properties of our proposed joint estimator JEMP. In particular, we first construct the convergence rate of our estimator in the high dimensional setting. Then we show that the convergence rate can be improved for the common structure of the precision matrices in certain cases. Finally, the model selection consistency is shown with an additional thresholding step.

For theoretical properties, we follow the set-up of Cai et al. (2011) and the results therein are also used for our technical derivations. In this section, for simplicity, we assume that n = n₁ = ⋯ = n_G. We consider the following class of matrices,

$$𝒰≔\{\mathrm{\Omega }:\mathrm{\Omega }\succ 0,{\Vert \mathrm{\Omega }\Vert }_{L_1}\le C_M\},$$

and assume that ${\mathrm{\Omega }}_0^{(\mathrm{g})}\in 𝒰$ for all g = 1, …, G. This assumption requires that the true precision matrices are sparse in terms of the l₁ norm while allowing them to have many small entries. Write $E(x^{(\mathrm{g})})={({\mu }_1^{(\mathrm{g})},\dots ,{\mu }_p^{(\mathrm{g})})}^{\mathrm{T}}$. We also make the following moment condition on x^(g) for our theoretical results.

Condition 1

There exists some 0 < η < 1/4 such that $E[\text{exp}\{t{(x_i^{(\mathrm{g})}-{\mu }_i^{(\mathrm{g})})}^2\}]\le K<\infty$ for all |t| ≤ η and all i, g and G log p/n ≤ η, where K is a bounded constant.

Condition 1 indicates that the components of x^(g) are uniformly sub-Gaussian. This condition is satisfied if x^(g) follows a multivariate Gaussian distribution or has uniformly bounded components.

Theorem 1

Assume Condition 1 holds. Let λ₁ = λ₂ = 3C_MC₀(log p/n)^1/2, where C₀ = 2η⁻²(2 + τ + η⁻¹e²K²)² and τ > 0. Set ν = G⁻¹. Then

$$\underset{ij}{\text{max}}(\frac{1}{G}\sum _{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|)\le 6C_M^2{C}_0{\left(\frac{\text{log}p}{n}\right)}^{1/2},$$

with probability greater than 1 − 4Gp^−τ.

In an average sense, the convergence rate can be viewed the same as that of the CLIME estimator which is of order (log p/n)^1/2. In this theorem, the first inequality constraint in (3) does not play any role in the estimation procedure as we set λ₁ = λ₂. In the next theorem, with properly chosen λ₁, we construct a faster convergence rate for the common part under certain conditions.

Theorem 2

Assume Condition 1 holds. Suppose that there exists C_R > 0 such that ${\Vert R_0^{(\mathrm{g})}\Vert }_{L_1}\le C_R$ for all g = 1, …, G and $({\sum }_{g=1}^G{\Vert R_0^{(\mathrm{g})}\Vert }_{L_1})\le C_R{G}^{1/2}$. Set ν = G^−1/2 and let λ₁ = (C_M + C_R)C₀{log p/(nG)}^1/2 and λ₂ = C_MC₀(log p/n)^1/2. Then

$${|\hat{M}-M_0|}_{\infty }\le C_0(2C_M^2+4C_M{C}_R+C_R^2){\left(\frac{\text{log}p}{nG}\right)}^{1/2},$$

with probability greater than 1 − 2(1 + 3G)p^−τ.

Theorem 2 states that our proposed method can estimate the common part more efficiently with the corresponding convergence rate of order {log p/(nG)}^1/2, which is faster than the order (log p/n)^1/2.

Note that our theorems show consistency of our estimator in terms of the elementwise l_∞ norm. On the other hand, Guo et al. (2011) showed consistency of their estimator under the Frobenious norm. Therefore, our theoretical results are not directly comparable to the theorems in Guo et al. (2011). However, it is worthwhile to note that our Theorem 2 reveals the effect of G on the consistency while the theorems in Guo et al. (2011) do not show explicitly how their estimator can have advantage over separate estimation in terms of consistency.

Besides its estimation consistency, we also prove the model selection consistency of our estimator which means that it reveals the exact set of nonzero components in the true precision matrices with high probability. For this result, a thresholding step is introduced. In particular, a threshold estimator ${\tilde{\mathrm{\Omega }}}^{(\mathrm{g})}=({\tilde{\omega }}_{ij}^{(\mathrm{g})})$ based on {Ω̂⁽¹⁾, …, Ω̂^(G)} is defined as,

$${\tilde{\omega }}_{ij}^{(\mathrm{g})}={\hat{\omega }}_{ij}^{(\mathrm{g})}I\{|{\hat{\omega }}_{ij}^{(\mathrm{g})}|\ge {\delta }_n\},$$

where δ_n ≥ 2C_MGλ₂ and λ₂ is given in Theorem 1. To state the model selection consistency precisely, we define

$${𝒮}_0≔\{(i,j,g):{\omega }_{ij,0}^{(\mathrm{g})}\ne 0\},\widehat{𝒮}≔\{(i,j,g):{\tilde{\omega }}_{ij}^{(\mathrm{g})}\ne 0\}\text{and}{\theta }_{\text{min}}≔\underset{(i,j,g)\in {𝒮}_0}{\text{min}}\sum _{g=1}^G|{\omega }_{ij,0}^{(\mathrm{g})}|.$$

Then the next theorem states the model selection consistency of our estimator.

Theorem 3

Assume Condition 1 holds. If θ_min > 2δ_n, then

$$\mathit{\text{pr}}({𝒮}_0=\widehat{𝒮})\ge 1-4G{p}^{-\tau }.$$

4. Numerical Algorithm

In this section, we describe how to obtain the numerical solutions of the optimization problem (3). In Section 4.1, the optimization problem (3) is decomposed into p individual subproblems and a linear programming approach is used to solve them. In Section 4.2, we describe another algorithm using the alternating directions method of multiplier (ADMM). Section 4.3 explains how the tuning parameters can be selected.

4.1 Decomposition of (3)

Similar to the Lemma 1 in Cai et al. (2011), one can show that the optimization problem (3) can be decomposed into p individual minimization problems. In particular, let e_i be the ith column of I. For 1 ≤ i ≤ p, let $\{{\hat{m}}_i,{\hat{r}}_i^{(1)},\dots ,{\hat{r}}_i^{(\mathrm{G})}\}$ be the solution of the following optimization problem:

$$\text{min}\{{|m|}_1+\nu \sum _{g=1}^G{|r^{(\mathrm{g})}|}_1\}$$

$$\mathrm{s}.\mathrm{t}.{|\frac{1}{G}\sum _{g=1}^G\{{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(m+r^{(\mathrm{g})})-e_i\}|}_{\infty }\le {\lambda }_1,{|{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(m+r^{(\mathrm{g})})-e_i|}_{\infty }\le {\lambda }_2,\sum _{g=1}^G{r}^{(\mathrm{g})}=0,$$ (4)

where m, r⁽¹⁾, …, r^(G) are vectors in ℛ^p. We can show that solving the optimization problem (3) is equivalent to solving the p optimization problems in (4). The optimization problem in (4) can be further reformulated as a linear programming problem and the simplex method is used to solve this problem (Boyd and Vandenberghe, 2004). For our simulation study and the GBM data analysis, we obtain the solution of (3) using the efficient R-package fastclime, which provides a generic fast linear programming solver (Pang et al., 2014).

4.2 An ADMM Algorithm

In this section, we describe an alternating directions method of multipliers (ADMM) algorithm to solve (4) which can be potentially more scalable than the previously explained linear programming approach. We refer the reader to Boyd et al. (2010) for detailed explanation of ADMM algorithms and their convergence properties.

To reformulate (4) into an appropriate ADMM form, define y = (m^T, νr^(1)T, …, νr^(G)T)^T, $z_m={\sum }_{g=1}^G\{{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(m+r^{(\mathrm{g})})-e_i\}/G$, z_g = Σ̂^(g)(m + r^(g)) − e_i, and z = (z₁^T, …, z_G^T, z_m^T)^T. Denote the a × a identity matrix as I_a×a and the a × b zero matrix as O_a×b. Then the problem (4) can be rewritten as

$$\text{min}{|y|}_1\mathrm{s}.\mathrm{t}.{|z_m|}_{\infty }\le {\lambda }_1,{|z_g|}_{\infty }\le {\lambda }_2,Ay-Bz=C,\text{where}$$ (5)

$$A=\left(\begin{array}{ccccc}\hfill {\hat{\mathrm{\Sigma }}}^{(1)}\hfill & \hfill {\nu }^{-1}{\hat{\mathrm{\Sigma }}}^{(1)}\hfill & \hfill O_{p\times p}\hfill & \hfill \dots \hfill & \hfill O_{p\times p}\hfill \\ \hfill {\hat{\mathrm{\Sigma }}}^{(2)}\hfill & \hfill O_{p\times p}\hfill & \hfill {\nu }^{-1}{\hat{\mathrm{\Sigma }}}^{(2)}\hfill & \hfill \dots \hfill & \hfill O_{p\times p}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\hat{\mathrm{\Sigma }}}^{(\mathrm{G})}\hfill & \hfill O_{p\times p}\hfill & \hfill O_{p\times p}\hfill & \hfill \dots \hfill & \hfill {\nu }^{-1}{\hat{\mathrm{\Sigma }}}^{(\mathrm{G})}\hfill \\ \hfill G^{-1}{\sum }_{g=1}^G{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}\hfill & \hfill {(\nu G)}^{-1}{\hat{\mathrm{\Sigma }}}^{(1)}\hfill & \hfill {(\nu G)}^{-1}{\hat{\mathrm{\Sigma }}}^{(2)}\hfill & \hfill \dots \hfill & \hfill {(\nu G)}^{-1}{\hat{\mathrm{\Sigma }}}^{(\mathrm{G})}\hfill \\ \hfill O_{p\times p}\hfill & \hfill I_{p\times p}\hfill & \hfill I_{p\times p}\hfill & \hfill \dots \hfill & \hfill I_{p\times p}\hfill \end{array}\right),$$

$B=\left(\begin{array}{c}\hfill I_{(1+G)p\times (1+G)p}\hfill \\ \hfill O_{p\times (1+G)p}\hfill \end{array}\right)$, and C = (e_i^T, …, e_i^T, O_p×1)^T. The scaled augmented Lagrangian for (5) is given by

$$L(y,z,u)={|y|}_1+\frac{\rho }{2}{\Vert Ay-Bz-C+u\Vert }_2^2,\mathrm{s}.\mathrm{t}.{|z_m|}_{\infty }\le {\lambda }_1,{|z_g|}_{\infty }\le {\lambda }_2,$$

where u is a (2+G)p-dimensional vector of dual variables. With the current solution z^k, u^k, the ADMM algorithm updates solutions sequentially as follows:

1. y^k+1 = argmin_yL(y, z^k, u^k).

2. z^k+1 = argmin_zL(y^k+1, z, u^k), s.t. |z_m|_∞ ≤ λ₁, |z_g|_∞ ≤ λ₂.

3. u^k+1 = u^k + Ay^k+1 − B_z^k+1 − c.

As ${\text{argmin}}_{y}L(y,z^k,u^k)={\text{argmin}}_y\{{|y|}_1+\frac{\rho }{2}{\Vert Ay-B{z}^k-C+u^k\Vert }_2^2\}$, the step (a) can be viewed as an L₁ penalized least squares problem. Therefore, the step (a) can be solved using some existing algorithms for L₁ penalized least squares problems. In addition, one can show that the step (b) has a closed form of solution, z^k+1 = min{max{A′ y^k+1−C′ + (u^k)′, −λ}, λ} where A′ is the submatrix of A consisting of the first (1 + G)p rows, C′ and (u^k)′ are the corresponding subvectors of C and u^k, and λ is a (1 + G)p-dimensional vector of which the first Gp elements are λ₂ and the rest are λ₁. Note that scalability and computational speed of this ADMM algorithm largely depend on the algorithm used for the step (a) as the other steps have the explicit form of solutions.

4.3 Tuning Parameter Selection

To apply our method, we need to choose the tuning parameters, λ₁ and λ₂. In practice, we construct several models with many pairs of λ₁ and λ₂ satisfying λ₁ ≤ λ₂ and evaluate them to determine the optimal pair. To evaluate each estimator, we measure the likelihood loss (LL) used in Cai et al. (2011) and its definition is

$$\mathrm{L}\mathrm{L}=\sum _{g=1}^G\text{tr}({\hat{\mathrm{\Sigma }}}_{\upsilon }^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})})-\text{log}\{\text{det}({\hat{\mathrm{\Omega }}}^{(\mathrm{g})})\},$$

where ${\hat{\mathrm{\Sigma }}}_v^{(\mathrm{g})}$ is the sample covariance matrix of the gth group computed from an independent validation set. As mentioned in Section 2, the likelihood loss can be applicable for both Gaussian and some non-Gaussian data as it corresponds to the log-determinant Bregman divergence between the estimators and empirical precision matrices in the validation set. Among several pairs of tuning values, we select the pair which minimizes LL. If a validation set is not available, a K-fold cross-validation can be combined to this criterion. In particular, we first randomly split the data set into K parts of equal sizes. Denote the data in the kth part by $\{X_{(k)}^{(1)},\dots ,X_{(k)}^{(\mathrm{G})}\}$ which is used as a validation set for the kth estimator. For each k, with a given value of (λ₁, λ₂), we obtain estimators using all observations which do not belong to $\{X_{(k)}^{(1)},\dots ,X_{(k)}^{(\mathrm{G})}\}$ and denote them as $\{{\hat{\mathrm{\Omega }}}_{(k)}^{(\mathrm{G})},\dots ,{\hat{\mathrm{\Omega }}}_{(k)}^{(\mathrm{G})}\}$. Then the likelihood loss (LL) is defined as

$$\mathrm{L}\mathrm{L}=\sum _{k=1}^K\sum _{g=1}^G\text{tr}({\hat{\mathrm{\Sigma }}}_{(k)}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_{(k)}^{(\mathrm{g})})-\text{log}\{\text{det}({\hat{\mathrm{\Omega }}}_{(k)}^{(\mathrm{g})})\},$$

where ${\hat{\mathrm{\Sigma }}}_{(k)}^{(\mathrm{g})}$ is the sample covariance matrix of the gth group using $X_{(k)}^{(\mathrm{g})}$. Once the optimal pair is selected which minimizes LL, the final model is constructed using all data points with the selected pair.

5. Simulated Examples

In this section, we carry out simulation studies to assess the numerical performance of our proposed method. In particular, we compare the numerical performance of five methods: two separate methods and three joint methods. In separate approaches, each precision matrix is estimated separately via the CLIME estimator or the GLASSO estimator. For joint approaches, all precision matrices are estimated together using our JEMP estimator, the fused graphical lasso (FGL) estimator by Danaher et al. (2014), or the estimator by Guo et al. (2011), which we refer to as JOINT estimator hereafter. In our proposed method, ν is set to be G^−1/2. We also tried different values of ν such as G⁻¹, and the results are similar thus omitted. We consider three models as described below: the first two from Guo et al. (2011) and the last from Rothman et al. (2008); Cai et al. (2011). In all models, we set p = 100, G = 3 and ${\mathrm{\Omega }}_0^{(\mathrm{g})}={\mathrm{\Omega }}_c+U^{(\mathrm{g})}$, where Ω_c is common in all groups and U^(g) represents unique structure to the gth group. The common part, Ω_c, is generated as follows:

• Model 1. Ω_c is a tridiagonal precision matrix. In particular, ${\mathrm{\Sigma }}_c≔{\mathrm{\Omega }}_c^{-1}=({\sigma }_{ij})$ is first constructed, where σ_ij = exp(−|d_i − d_j|/2), d₁ < … < d_p, and d_i − d_i−1 ~ Unif(0.5, 1), i = 2, …, p. Then let ${\mathrm{\Omega }}_c={\mathrm{\Sigma }}_c^{-1}$.

• Model 2. Ω_c is a 3 nearest-neighbor network. In particular, p points are randomly picked on a unit square and all pairwise distances among the points are calculated. Then we find 3 nearest neighbors for each point and a pair of symmetric entries in Ω_c corresponding to a pair of neighbors has a value randomly chosen from the interval [−1, −0.5] ∪ [0.5, 1].

• Model 3. Ω_c = Γ + δI, where each off-diagonal entry in Γ is generated independently from 0.5y, with y following the Bernoulli distribution with success probability 0.02. Here, δ is selected so that the condition number of Ω_c is equal to p.

For each U^(g), we randomly pick a pair of symmetric off-diagonal entries and replace them with values randomly chosen from the interval [−1, −0.5]∪[0.5, 1]. We repeat this procedure until ${\sum }_{i<j}I(|u_{ij}^{(\mathrm{g})}|>0)/{\sum }_{i<j}I(|{\omega }_{ij,c}|>0)=\rho$, where Ω_c = (ω_ij,c) and $U^{(\mathrm{g})}=u_{ij}^{(\mathrm{g})}$. Therefore, ρ is the ratio of the number of unique nonzero entries to the number of common nonzero entries. We consider four values of ρ = 0, 0.25, 1 and 4. To make the resulting precision matrices positive-definite, each diagonal element of each matrix ${\mathrm{\Omega }}_0^{(\mathrm{g})}$ is replaced with 1.5 times the sum of the absolute values of the corresponding row. Finally, each matrix ${\mathrm{\Omega }}_0^{(\mathrm{g})}$ is standardized to have unit diagonals. Note that in the case of ρ = 1 or 4, the true precision matrices are quite different from each other. From these cases, we can assess how joint methods work when the precision matrices are not similar. In addition, we also consider Model 4 below to assess how JEMP works when the precision matrices have different structures from each other.

• Model 4. ${\mathrm{\Omega }}_0^{(1)}$ is the tridiagonal precision matrix as in Model 1, ${\mathrm{\Omega }}_0^{(2)}$ is the 3 nearest-neighbor network in Model 2, and ${\mathrm{\Omega }}_0^{(3)}$ is the random network in Model 3.

For each group in each model, we generate a training sample of size n = 100 from either a multivariate normal distribution $N(0,{\mathrm{\Sigma }}_0^{(\mathrm{g})})$ or a multivariate t-distribution with the covariance matrix ${\mathrm{\Sigma }}_0^{(\mathrm{g})}$ and degrees of freedom of 3 or 5. In order to select optimal tuning parameters, an independent validation set of size n = 100 is also generated from the same distribution of the training sample. For each estimator, optimal tuning parameters are selected as described in Section 4. We replicate simulations 50 times for each model.

To compare performance of five different methods, we use the average entropy loss and the average Frobenius loss defined as,

$$\mathrm{E}\mathrm{L}=G^{-1}\sum _{g=1}^G\{\text{tr}({\mathrm{\Sigma }}_0^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})})-\text{log det}({\mathrm{\Sigma }}_0^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})})-p\},$$

$$\mathrm{F}\mathrm{L}=G^{-1}\sum _{g=1}^G{\Vert {\mathrm{\Omega }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Omega }}}^{(\mathrm{g})}\Vert }_F^2,$$

where ‖․‖_F is the Frobenius norm of a matrix.

Table 1 reports the results for Model 1. In terms of estimation accuracy, the three joint estimation methods, JEMP, FGL, and JOINT, outperform the two separate estimation methods while JEMP and FGL show better performance than JOINT. In Gaussian cases, FGL exhibits slightly smaller losses than JEMP. However, JEMP outperforms FGL in terms of entropy loss for some cases when the underlying distribution is t₅. If the true underlying distribution is t₃, then JEMP clearly outperforms FGL in both entropy loss and Frobenius loss for all cases. This indicates that our proposed JEMP can have some advantage in estimation for some non-Gaussian data. Overall, JEMP shows very competitive performance compared with other methods. Tables 2–3 report the results for Models 2 and 3 respectively. Performances of the methods show similar patterns as in Model 1. JEMP and FGL perform best while FGL is slightly better in Gaussian cases and JEMP has the best performance in the t₃ case.

Table 1.

Comparison summaries using Entropy loss (EL) and Frobenius loss (FL) over 50 replications for Model 1.

		ρ = 0		ρ = 0.25
		EL	FL	EL	FL
Normal	CLIME	4.42 (0.02)	8.57 (0.03)	4.35 (0.02)	8.42 (0.03)
	GLASSO	3.70 (0.02)	6.90 (0.03)	3.60 (0.02)	6.73 (0.03)
	JOINT	3.43 (0.02)	6.64 (0.04)	3.41 (0.02)	6.61 (0.03)
	FGL	1.99 (0.02)	3.75 (0.03)	2.09 (0.02)	3.92 (0.03)
	JEMP	2.08 (0.02)	4.06 (0.04)	2.20 (0.02)	4.31 (0.04)
t (DF=5)	CLIME	5.75 (0.17)	10.63 (0.26)	5.81 (0.19)	10.75 (0.33)
	GLASSO	5.60 (0.09)	10.23 (0.16)	5.45 (0.09)	10.00 (0.16)
	JOINT	5.08 (0.11)	9.44 (0.15)	5.01 (0.12)	9.28 (0.19)
	FGL	3.47 (0.07)	6.12 (0.11)	3.46 (0.08)	6.12 (0.11)
	JEMP	3.21 (0.06)	6.14 (0.11)	3.41 (0.10)	6.52 (0.19)
t (DF=3)	CLIME	10.34 (0.83)	18.08 (1.05)	10.15 (0.91)	17.25 (1.06)
	GLASSO	11.87 (0.33)	24.10 (0.95)	11.78 (0.33)	24.21 (0.95)
	JOINT	8.84 (0.58)	15.16 (0.85)	8.95 (0.66)	15.17 (0.92)
	FGL	7.01 (0.24)	12.39 (0.52)	7.40 (0.31)	13.23 (0.66)
	JEMP	6.02 (0.33)	11.56 (0.73)	5.95 (0.30)	11.16 (0.62)
		ρ = 1		ρ = 4
		EL	FL	EL	FL
Normal	CLIME	4.23 (0.02)	8.15 (0.03)	3.67 (0.01)	6.95 (0.03)
	GLASSO	3.37 (0.02)	6.33 (0.03)	2.57 (0.01)	4.96 (0.03)
	JOINT	3.27 (0.01)	6.40 (0.03)	2.51 (0.01)	4.95 (0.02)
	FGL	2.18 (0.01)	4.07 (0.02)	1.82 (0.01)	3.47 (0.02)
	JEMP	2.38 (0.01)	4.77 (0.04)	2.11 (0.01)	4.28 (0.02)
t (DF=5)	CLIME	5.53 (0.16)	10.12 (0.23)	4.83 (0.17)	8.72 (0.25)
	GLASSO	5.11 (0.09)	9.54 (0.17)	4.28 (0.09)	8.35 (0.19)
	JOINT	4.71 (0.10)	8.71 (0.14)	3.87 (0.12))	7.03 (0.16)
	FGL	3.31 (0.07)	5.95 (0.11)	2.54 (0.06)	4.68 (0.10)
	JEMP	3.32 (0.07)	6.40 (0.13)	2.78 (0.07)	5.35 (0.12)
t (DF=3)	CLIME	9.89 (0.86)	17.82 (1.16)	8.93 (0.91)	16.58 (1.28)
	GLASSO	11.32 (0.32)	23.77 (0.99)	10.42 (0.31)	23.70 (1.05)
	JOINT	9.27 (1.68)	14.23 (1.26)	7.14 (0.65)	11.90 (0.72)
	FGL	6.51 (0.25)	11.73 (0.56)	5.95 (0.27)	11.55 (0.67)
	JEMP	5.71 (0.29)	10.99 (0.73)	4.72 (0.24)	9.04 (0.49)

Table 2.

Comparison summaries using Entropy loss (EL) and Frobenius loss (FL) over 50 replications for Model 2.

		ρ = 0		ρ = 0.25
		EL	FL	EL	FL
Normal	CLIME	5.10 (0.02)	9.80 (0.04)	5.05 (0.02)	9.68 (0.04)
	GLASSO	4.50 (0.02)	8.07 (0.03)	4.44 (0.02)	7.98 (0.03)
	JOINT	3.89 (0.02)	7.42 (0.04)	4.13 (0.02)	7.84 (0.04)
	FGL	2.26 (0.02)	4.26 (0.03)	2.70 (0.02)	5.02 (0.03)
	JEMP	2.31 (0.02)	4.44 (0.03)	2.80 (0.02)	5.36 (0.03)
t (DF=5)	CLIME	6.60 (0.17)	12.03 (0.25)	6.62 (0.19)	12.09 (0.32)
	GLASSO	6.78 (0.09)	11.67 (0.15)	6.56 (0.09)	11.37 (0.14)
	JOINT	6.16 (0.10)	11.18 (0.16)	6.12 (0.14)	11.14 (0.23)
	FGL	4.03 (0.07)	6.88 (0.11)	4.28 (0.07)	7.30 (0.10)
	JEMP	3.74 (0.06)	6.98 (0.11)	4.15 (0.09)	7.72 (0.20)
t (DF=3)	CLIME	11.41 (0.87)	19.55 (1.06)	11.16 (0.93)	18.66 (1.09)
	GLASSO	13.16 (0.34)	24.31 (0.88)	12.90 (0.34)	24.29 (0.88)
	JOINT	10.14 (0.56)	16.96 (0.80)	10.24 (0.68)	17.03 (0.94)
	FGL	8.34 (0.28)	13.78 (0.55)	8.55 (0.31)	14.16 (0.59)
	JEMP	7.17 (0.36)	13.31 (0.84)	7.08 (0.31)	12.76 (0.61)
		ρ = 1		ρ = 4
		EL	FL	EL	FL
Normal	CLIME	4.84 (0.02)	9.27 (0.04)	3.77 (0.01)	7.14 (0.03)
	GLASSO	4.07 (0.02)	7.42 (0.03)	2.68 (0.01)	5.09 (0.02)
	JOINT	3.99 (0.01)	7.72 (0.03)	2.63 (0.01)	5.16 (0.02)
	FGL	2.99 (0.01)	5.51 (0.02)	1.98 (0.01)	3.74 (0.01)
	JEMP	3.20 (0.01)	6.34 (0.04)	2.35 (0.01)	4.74 (0.02)
t (DF=5)	CLIME	6.14 (0.16)	11.22 (0.24)	4.95 (0.17)	8.96 (0.25)
	GLASSO	5.85 (0.09)	10.52 (0.16)	4.44 (0.09)	8.56 (0.18)
	JOINT	5.44 (0.10)	10.05 (0.15)	4.02 (0.12)	7.32 (0.16)
	FGL	4.07 (0.07)	7.17 (0.10)	2.68 (0.06)	4.91 (0.10)
	JEMP	4.11 (0.06)	7.87 (0.13)	3.00 (0.07)	5.77 (0.13)
t (DF=3)	CLIME	10.53 (0.88)	18.53 (1.15)	9.10 (0.92)	16.84 (1.29)
	GLASSO	12.11 (0.32)	23.89 (0.93)	10.59 (0.32)	23.77 (1.04)
	JOINT	10.00 (1.67)	15.26 (1.26)	7.27 (0.64)	12.10 (0.72)
	FGL	7.23 (0.25)	12.34 (0.52)	7.27 (0.64)	11.50 (0.64)
	JEMP	6.59 (0.31)	12.19 (0.70)	4.99 (0.26)	9.48 (0.53)

Table 3.

Comparison summaries using Entropy loss (EL) and Frobenius loss (FL) over 50 replications for Model 3.

		ρ = 0		ρ = 0.25
		EL	FL	EL	FL
Normal	CLIME	3.62 (0.02)	6.87 (0.03)	3.92 (0.02)	7.51 (0.04)
	GLASSO	2.60 (0.01)	5.03 (0.03)	3.03 (0.01)	5.78 (0.03)
	JOINT	2.53 (0.01)	4.97 (0.02)	2.99 (0.01)	5.89 (0.03)
	FGL	1.54 (0.01)	2.95 (0.02)	2.21 (0.01)	4.16 (0.02)
	JEMP	1.80 (0.01)	3.61 (0.03)	2.48 (0.01)	4.96 (0.03)
t (DF=5)	CLIME	4.77 (0.17)	8.68 (0.26)	5.23 (0.19)	9.63 (0.33)
	GLASSO	4.32 (0.09)	8.42 (0.20)	4.82 (0.09)	9.11 (0.18)
	JOINT	3.84 (0.12)	7.02 (0.16)	4.43 (0.15)	8.10 (0.21)
	FGL	2.54 (0.06)	4.68 (0.10)	3.11 (0.07)	5.62 (0.10)
	JEMP	2.60 (0.06)	4.99 (0.11)	3.35 (0.10)	6.44 (0.18)
t (DF=3)	CLIME	9.08 (0.84)	16.05 (1.07)	9.40 (0.92)	15.92 (1.06)
	GLASSO	10.64 (0.33)	24.09 (1.06)	11.14 (0.33)	24.26 (1.01)
	JOINT	7.54 (0.57)	13.03 (0.87)	8.35 (0.66)	14.09 (0.89)
	FGL	5.87 (0.26)	11.39 (0.65)	6.72 (0.30)	12.53 (0.70)
	JEMP	5.05 (0.37)	10.10 (0.93)	5.49 (0.30)	10.44 (0.66)
		ρ = 1		ρ = 4
		EL	FL	EL	FL
Normal	CLIME	4.33 (0.02)	8.33 (0.03)	4.03 (0.02)	7.68 (0.03)
	GLASSO	3.52 (0.02)	6.54 (0.03)	3.00 (0.01)	5.67 (0.03)
	JOINT	3.50 (0.01)	6.86 (0.02)	2.94 (0.01)	5.78 (0.02)
	FGL	2.90 (0.01)	5.37 (0.02)	2.28 (0.01)	4.28 (0.01)
	JEMP	3.17 (0.01)	6.40 (0.02)	2.66 (0.01)	5.40 (0.02)
t (DF=5)	CLIME	5.64 (0.16)	10.31 (0.23)	5.20 (0.17)	9.42 (0.26)
	GLASSO	5.31 (0.09)	9.81 (0.17)	4.71 (0.09)	8.93 (0.18)
	JOINT	4.91 (0.11)	9.09 (0.14)	4.29 (0.12)	7.86 (0.17)
	FGL	3.66 (0.06)	6.53 (0.10)	2.98 (0.07)	5.40 (0.10)
	JEMP	3.93 (0.07)	7.56 (0.12)	3.27 (0.07)	6.32 (0.14)
t (DF=3)	CLIME	10.00 (0.87)	17.87 (1.16)	9.36 (0.88)	17.25 (1.26)
	GLASSO	11.60 (0.32)	23.89 (0.97)	10.89 (0.31)	23.79 (0.99)
	JOINT	9.52 (1.68)	14.60 (1.27)	7.57 (0.63)	12.59 (0.71)
	FGL	6.71 (0.24)	11.84 (0.52)	6.36 (0.26)	11.87 (0.61)
	JEMP	5.90 (0.26)	11.02 (0.59)	5.20 (0.26)	9.70 (0.51)

Table 4 summarizes the results for Model 4 in which the true precision matrices have different structures. As in Models 1–3, our method outperforms JOINT, CLIME, and GLASSO for all cases. It shows competitive performance with FGL when the distribution is Gaussian or t₅. However, it outperforms FGL in the case of t₃ distribution. This indicates that our method works as well even when structures of precision matrices are different from each other. Note that the precision matrices in Model 4 share many zero components although their main structures are different. Joint methods can work better here since they encourage many common zeros to be estimated as zeros simultaneously.

Table 4 .

Comparison summaries using Entropy loss (EL) and Frobenius loss (FL) over 50 replications for Model 4.

	Normal		t (DF=5)		t (DF=3)
	EL	FL	EL	FL	EL	FL
CLIME	4.39 (0.02)	8.45 (0.04)	6.06 (0.39)	10.82 (0.43)	10.59 (1.03)	17.35 (1.08)
GLASSO	3.62 (0.02)	6.71 (0.03)	5.57 (0.11)	10.02 (0.14)	11.79 (0.43)	24.06 (1.29)
JOINT	3.68 (0.01)	7.16 (0.03)	5.24 (0.14)	9.56 (0.17)	8.28 (0.37)	13.83 (0.50)
FGL	3.12 (0.01)	5.75 (0.02)	3.85 (0.07)	6.84 (0.11)	7.08 (0.33)	12.26 (0.71)
JEMP	3.50 (0.01)	7.04 (0.02)	4.27 (0.08)	8.17 (0.14)	6.22 (0.29)	11.27 (0.60)

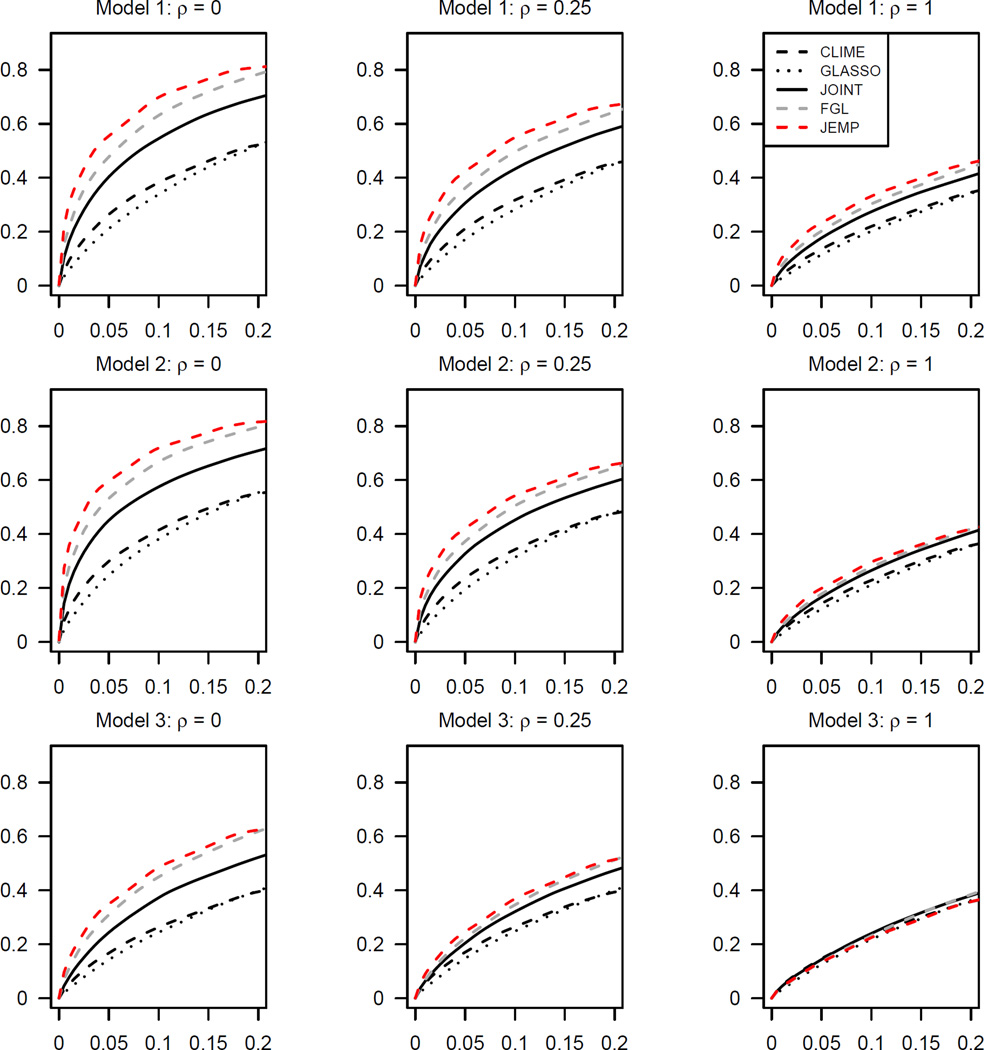
Figures 1–3 show the estimated receiver operating characteristic (ROC) curves averaged over 50 replications. In the Gaussian case of Figure 1, JEMP and FGL show similar performance and outperform the others except the case of ρ = 1 in Model 3. In Figures 2 and 3 of multivariate t-distributions, it can be observed that JEMP has better ROC curves when ρ = 0 for all three models. It also shows better performance than the others when ρ = 0.25 for Models 1–2. When ρ = 1, all ROC curves move closer together. This is because the true precision matrices become much denser in terms of the number of edges and thus all methods have some difficulty in edge selection. Overall, our proposed JEMP estimator delivers competitive performance in terms of both estimation accuracy and selection.

Figure 1.

Receiver operating characteristic curves averaged over 50 replications from Gaussian distributions. In each panel, the horizontal and vertical axes are false positive rate and sensitivity respectively. Here, ρ is the ratio of the number of unique nonzero entries to the number of common nonzero entries.

Figure 3.

Receiver operating characteristic curves averaged over 50 replications from t₃ distributions. In each panel, the horizontal and vertical axes are false positive rate and sensitivity respectively. Here, ρ is the ratio of the number of unique nonzero entries to the number of common nonzero entries.

Figure 2.

Receiver operating characteristic curves averaged over 50 replications from t₅ distributions. In each panel, the horizontal and vertical axes are false positive rate and sensitivity respectively. Here, ρ is the ratio of the number of unique nonzero entries to the number of common nonzero entries.

Note that JEMP and FGL encourage the estimated precision matrices to be similar across all classes. This can be advantageous especially when the true precision matrices have many common values. Therefore, JEMP and FGL can have better performance than JOINT for such problems.

In terms of computational complexity, JEMP can be more intensive than separate estimation methods and JOINT as it involves a pair of tuning parameters (λ₁, λ₂) satisfying λ₁ ≤ λ₂. The computational cost of JEMP can be potentially reduced using the ADMM algorithm discussed in Section 4 with a further improved algorithm for the least squares step.

6. Application on Glioblastoma Cancer Data

In this section, we apply our joint method to a Glioblastoma cancer data set. The data set consists of 17814 gene expression levels of 482 GBM patients. The patients were classified into four subtypes, namely, classical, mesenchymal, neural, and proneural with sample sizes of 127, 145, 85, and 125 respectively (Verhaak et al., 2010). These subtypes are shown to be different biologically, while at the same time, share similarities as well since they all belong to GBM cancer. In this application, we consider the signature genes reported by Verhaak et al. (2010). They established 210 signature genes for each subtype, which results 840 signature genes in total. These signature genes are highly distinctive for four subtypes and reported to have good predictive power for subtype prediction. In our analysis, the goal is to produce graphical presentation of relationships among these signature genes in each subtype based on the estimation of the precision matrices. Among the 840 signature genes, we excluded the genes with no subtype information or the genes with missing values. As a result, total 680 genes were included in our analysis. To produce interpretable graphical models using our JEMP estimator, we set the values of the tuning parameters as λ₁ = 0.30 and λ₂ = 0.40. JEMP estimated 214 edges shared among all subtypes, 9 edges present only in two subtypes, and 1 edge present only in three subtypes.

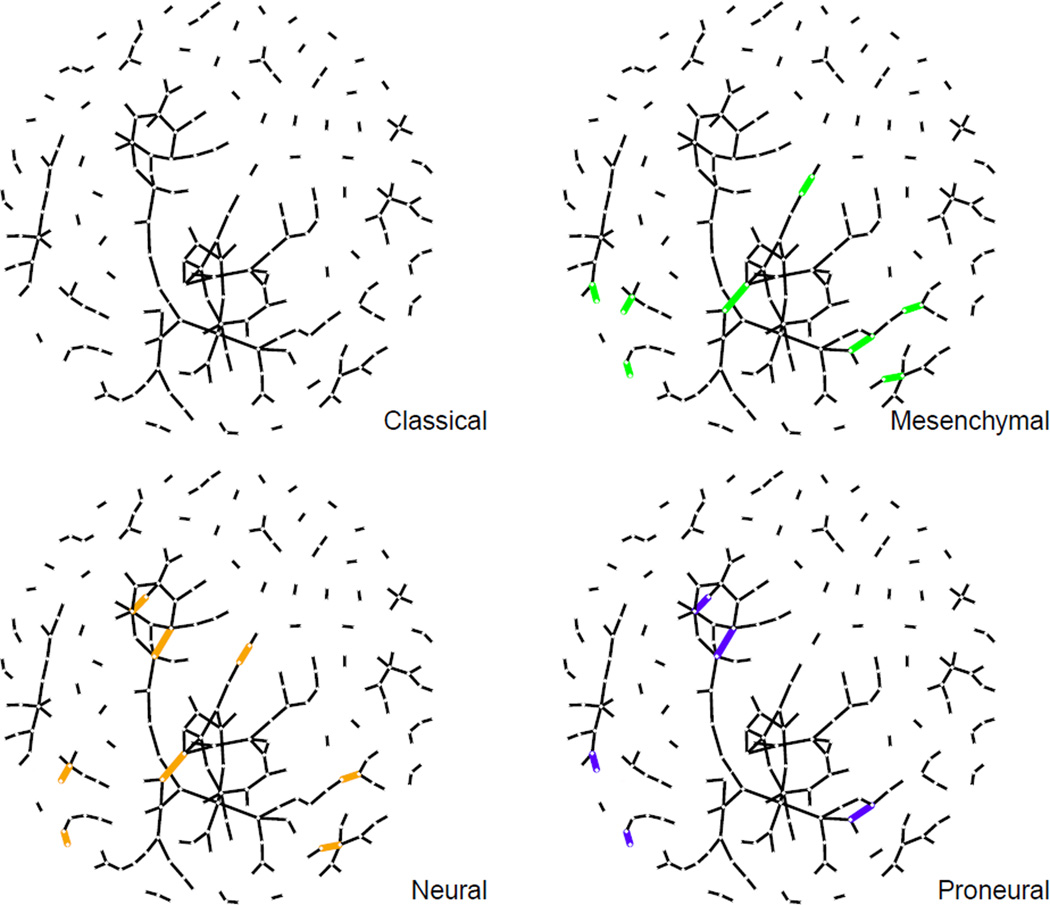
The resulting gene networks are shown in Figure 4. The black lines are the edges shared by all subtypes and the thick grey lines are the unique edges present only in two or three subtypes. It is noticeable that most of edges are black lines, which means that they appear in all subtypes. This indicates that the networks of the signature genes reported by Verhaak et al. (2010) may be very similar across all subtypes as they all belong to GBM cancer.

Figure 4.

Graphical presentation of conditional dependence structures among genes using our estimator of precision matrices. The black lines are the edges shared in all subtypes and the thick grey lines are the unique edges present only in two or three subtypes. The red, green, blue and orange genes are classical, mesenchymal, proneural and neural genes respectively (Verhaak et al., 2010).

All of the small red network’s genes in the upper region belong to the ZNF gene family. This network includes ZNF211, ZNF227, ZNF228, ZNF235, ZNF419, and ZNF671. These are known to be involved in making zinc finger proteins, which are regulatory proteins that are related to many cellular functions. As they are all involved in the same biological process, it may seem reasonable that this network is shared in all GBM subtypes.

The red genes are signature genes for the classical subtype. Likewise, green, blue and orange genes are the mesenchymal, proneural and neural signature genes respectively. Each class of signature genes tends to have more links with the genes in the same class. This is expected because each class of signature genes is more likely to be highly co-expressed.

Each estimated network for each subtype is depicted in Figure 5. The black lines are the edges shared by all subtypes and the colored lines are the edges appearing only in two or three subtypes. One interesting edge is the one between EGFR and MEOX2. It does not appear in the classical subtype while it is shared by all the other subtypes. EGFR is known to be involved in cell proliferation and Verhaak et al. (2010) demonstrated the essential role of this gene in GBM tumor genesis. Furthermore, high rates of EGFR alteration were claimed in the classical subtype. Therefore, studying the relationship between EGFR and MEOX2 can be an interesting direction for future investigation as only the classical subtype lacks this edge.

Figure 5.

Four gene networks corresponding to four subtypes of the GMB cancer. In each network, the black lines are the edges shared in all subtypes. The colored lines are the edge shared only in two or three subtypes.

There are 9 edges appearing only in two subtypes. These include SCG3 and ACSBG1, GRIK5 and BTBD2, NCF4 and CSTA, IFI30 and BATF, HK3 and SLC11A1, ACSBG1 and SCG3, GPM6A and OLIG2, C1orf61 and CKB, and PPFIA2 and GRM1. It would be also interesting to investigate these relationships further as they are unique only in two subtypes. For example, the edge between OLIG2 and GPM6A does not appear in the proneural subtype while it is shared by Neural and Mesenchymal subtypes. High expression of OLIG2 was observed in the proneural subtype (Verhaak et al., 2010), which can down-regulate the tumor suppressor p21. Therefore, it may be helpful to investigate the relationship between OLIG2 and GPM6A for understanding the effect of OLIG2 in the proneural subtype.

Appendix A

Write ${\mathrm{\Sigma }}_0^{(\mathrm{g})}=({\sigma }_{ij,0}^{(\mathrm{g})})$ and ${\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}=({\hat{\sigma }}_{ij}^{(\mathrm{g})})$. Let m_j,0 and $r_{j,0}^{(\mathrm{g})}$ be the jth columns of M₀ and $R_0^{(\mathrm{g})}$ respectively. Define the jth columns of M̂ and R̂^(g) as m̂_j and ${\hat{r}}_j^{(\mathrm{g})}$ respectively. We first state some results established by Cai et al. (2011) in the proof of their Theorem 1.

Lemma 4

Suppose Condition 1 holds. For any fixed g = 1, …, G, with probability greater than 1 − 4p^−τ,

$$\underset{ij}{\text{max}}|{\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})}|\le C_0{\left(\frac{\text{log}p}{n}\right)}^{1/2},$$

where C₀ is given in Theorem 1.

Proof

[Proof of Theorem 1] It follows from Lemma 4 that

$$\underset{ij}{\text{max}}|{\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})}|\le {\lambda }_2/(3C_M)\text{for all}g=1,\dots ,G,$$ (6)

with probability greater than 1 − 4Gp^−τ. All following arguments assume (6) holds. First, we have that

$${|({\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-{\mathrm{\Omega }}_0^{(\mathrm{g})})e_j|}_{\infty }={|{\mathrm{\Omega }}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-I)e_j|}_{\infty }\le {\Vert {\mathrm{\Omega }}_0^{(\mathrm{g})}\Vert }_{L_1}{|({\mathrm{\Sigma }}_0^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-I)e_j|}_{\infty }\le C_M\{{|({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_{\infty }+{|({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-I)e_j|}_{\infty }\}\le C_M{|{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_1{|{\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}|}_{\infty }+C_M{\lambda }_2\le {|{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_1{\lambda }_2/3+C_M{\lambda }_2,$$

for all g = 1, …, G. Second, note that $\{M_0,R_0^{(1)},\dots ,R_0^{(\mathrm{G})}\}$ is a feasible solution of (3) as ${|I-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(M_0+R_0^{(\mathrm{g})})|}_{\infty }={|({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\mathrm{\Omega }}_0^{(\mathrm{g})}|}_{\infty }\le {\Vert {\mathrm{\Omega }}_0^{(\mathrm{g})}\Vert }_{L_1}{|{\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}|}_{\infty }\le C_M{\lambda }_2/(3C_M)<{\lambda }_2$ and λ₁ = λ₂. Therefore, we have that

$$\sum _{g=1}^G{|({\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-{\mathrm{\Omega }}_0^{(\mathrm{g})})e_j|}_{\infty }\le \sum _{g=1}^G{|{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_1{\lambda }_2/3+G{C}_M{\lambda }_2\le G\{{|{\hat{m}}_j|}_1+G^{-1}\sum _{g=1}^G{|{\hat{r}}_j^{(\mathrm{g})}|}_1\}{\lambda }_2/3+G{C}_M{\lambda }_2\le G\{{|m_{j,0}|}_1+G^{-1}\sum _{g=1}^G{|r_{j,0}^{(\mathrm{g})}|}_1\}{\lambda }_2/3+G{C}_M{\lambda }_2\le G3C_M{\lambda }_2/3+G{C}_M{\lambda }_2=2G{C}_M{\lambda }_2=6G{C}_M^2{C}_0{(\text{log}p/n)}^{1/2}.$$

By the inequality

$$\underset{ij}{\text{max}}(\frac{1}{G}\sum _{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|)\le \underset{j}{\text{max}}\frac{1}{G}\sum _{g=1}^G{|({\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-{\mathrm{\Omega }}_0^{(\mathrm{g})})e_j|}_{\infty }\le 6C_M^2{C}_0{\left(\frac{\text{log}p}{n}\right)}^{1/2},$$

the proof is completed.

Lemma 5

With probability greater than 1 − 2(1 + G)p^−τ, the following holds:

$$\underset{ij}{\text{max}}|\sum _{g=1}^G({\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})})|\le C_0{\left(\frac{G\text{log}p}{n}\right)}^{1/2}.$$

Proof

We adopt a similar technique used in Cai et al. (2011) for the proof of their Theorem 1. Without loss of generality, we assume that ${\mu }_i^{(\mathrm{g})}=0$ for all i and g. Let $y_{kij}^{(\mathrm{g})}≔x_{ki}^{(\mathrm{g})}{x}_{kj}^{(\mathrm{g})}-E(x_{ki}^{(\mathrm{g})}{x}_{kj}^{(\mathrm{g})})$. Define ${\overline{x}}_i^{(\mathrm{g})}≔{\sum }_{k=1}^n{x}_{ki}^{(\mathrm{g})}/n$; i = 1, …, p, g = 1, …, G. Then ${\sum }_{g=1}^G({\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})})={\sum }_{g=1}^G({\sum }_{k=1}^n{y}_{kij}^{(\mathrm{g})}/n-{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_j^{(\mathrm{g})})$. Let t ≔ η(log p)^1/2(nG)^−1/2 and C₁ ≔ 2 + τ + η⁻¹K². Using the Markov’s inequality and the inequality |exp(s) − 1 − s| ≤ s² exp{max(s, 0)} for any s ∈ ℛ, we can show that

$$\text{pr}\{\frac{1}{n}\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}\ge {\eta }^{-1}{C}_1{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\}=\text{pr}\{\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}\ge {\eta }^{-1}{C}_1{(nG\text{log}p)}^{1/2}\}\le \text{exp}\{-t{\eta }^{-1}{C}_1{(nG\text{log}p)}^{1/2}\}E\left\{\text{exp}\right(t\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}\left)\right\}=\text{exp}\{-C_1\text{log}p\}\prod _{g=1}^G\prod _{k=1}^{n}E\{\text{exp}(t{y}_{kij}^{(\mathrm{g})})\}=\text{exp}[-C_1\text{log}p+\sum _{g=1}^{G}n\text{log}\{E\left(e^{t{y}_{kij}^{(\mathrm{g})}}\right)\left\}\right]\le \text{exp}[-C_1\text{log}p+\sum _{g=1}^{G}n\{E\left(e^{t{y}_{kij}^{(\mathrm{g})}}\right)-1\left\}\right]=\text{exp}[-C_1\text{log}p+\sum _{g=1}^{G}n\{E(e^{t{y}_{kij}^{(\mathrm{g})}}-t{y}_{kij}^{(\mathrm{g})}-1)\left\}\right]\le \text{exp}\{-C_1\text{log}p+\sum _{g=1}^{G}n{t}^{2}E({y_{kij}^{(\mathrm{g})}}^2{e}^{|t{y}_{kij}^{(\mathrm{g})}|}\left)\right\}\le \text{exp}\{-C_1\text{log}p+\sum _{g=1}^G{(\eta G)}^{-1}{K}^2\text{log}p\}.$$ (7)

The last inequality (7) holds since

$$n{t}^{2}E\left({y_{kij}^{(\mathrm{g})}}^2{e}^{|t{y}_{kij}^{(\mathrm{g})}|}\right)={(\eta G)}^{-1}(\text{log}p)E\left\{{({\eta }^{3/2}|y_{kij}^{(\mathrm{g})}|)}^2{e}^{t|y_{kij}^{(\mathrm{g})}|}\right\}$$

and

$$E\left\{{({\eta }^{3/2}|y_{kij}^{(\mathrm{g})}|)}^2{e}^{t|y_{kij}^{(\mathrm{g})}|}\right\}\le E\left\{e^{{\eta }^{3/2}|y_{kij}^{(\mathrm{g})}|}{e}^{t|y_{kij}^{(\mathrm{g})}|}\right\}\le E\left\{e^{{\eta }^{3/2}|y_{kij}^{(\mathrm{g})}|}{e}^{{\eta }^{3/2}|y_{kij}^{(\mathrm{g})}|}\right\}\le E\left\{e^{\eta |y_{kij}^{(\mathrm{g})}|}\right\}\le E\left\{e^{\eta |x_{ki}^{(\mathrm{g})}{x}_{kj}^{(\mathrm{g})}|+\eta E(|x_{ki}^{(\mathrm{g})}{x}_{kj}^{(\mathrm{g})}|)}\right\}\le {\left\{E\right(e^{\eta |x_{ki}^{(\mathrm{g})}{x}_{kj}^{(\mathrm{g})}|}\left)\right\}}^2\le {\left\{E\right(e^{\eta x_{ki}^{{(\mathrm{g})}^2}/2+\eta x_{kj}^{{(\mathrm{g})}^2}/2}\left)\right\}}^2\le E\left(e^{\eta x_{ki}^{{(\mathrm{g})}^2}}\right)E\left(e^{\eta x_{kj}^{{(\mathrm{g})}^2}}\right)\le K^2.$$

From (7), it follows that

$$\text{pr}\{\frac{1}{n}\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}\ge {\eta }^{-1}{C}_1{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\}\le \text{exp}\{-C_1\text{log}p+{\eta }^{-1}{K}^2\text{log}p\}\le p^{-(\tau +2)}.$$

Therefore, we have

$$\text{pr}\left\{\underset{ij}{\text{max}}\right|\frac{1}{n}\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}|\ge {\eta }^{-1}{C}_1{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\}\le 2p^{-\tau }.$$ (8)

Next, let C₂ = 2 + τ + η⁻¹(eK)². Cai et al. (2011) showed in the proof of their Theorem 1 that

$$\text{pr}(\underset{ij}{\text{max}}|{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_j^{(\mathrm{g})}|\ge {\eta }^{-2}{C}_2^2\text{log}p/n)\le 2p^{-\tau -1}.$$

Using this result, we have that

$$\text{pr}(\underset{ij}{\text{max}}|\sum _{g=1}^G{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_j^{(\mathrm{g})}|\ge {\eta }^{-2}{C}_2^{2}G\text{log}p/n)\le \text{pr}(\sum _{g=1}^G\underset{ij}{\text{max}}|{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_i^{(\mathrm{g})}|\ge {\eta }^{-2}{C}_2^{2}G\text{log}p/n)\le \sum _{g=1}^G\text{pr}(\underset{ij}{\text{max}}|{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_j^{(\mathrm{g})}|\ge {\eta }^{-2}{C}_2^{2}G\text{log}p/n)\le \sum _{g=1}^{G}2p^{-\tau -1}\le 2G{p}^{-\tau }$$ (9)

By (8), (9) and the inequality $C_0>{\eta }^{-1}{C}_1+{\eta }^{-2}{C}_2^2{(G\text{log}p/n)}^{1/2}$, we see that

$$\text{pr}\{\underset{ij}{\text{max}}|\sum _{g=1}^G({\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})})|\ge C_0{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\}\le \text{pr}\left\{\underset{ij}{\text{max}}\right|\frac{1}{n}\sum _{g=1}^G\sum _{k=1}^n{y}_{kij}^{(\mathrm{g})}\left|\ge {\eta }^{-1}{C}_1{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\right\}+\text{pr}(\underset{ij}{\text{max}}|\sum _{g=1}^G{\overline{x}}_i^{(\mathrm{g})}{\overline{x}}_j^{(\mathrm{g})}|\ge {\eta }^{-2}{C}_2^{2}G\text{log}p/n)\le 2(1+G)p^{-\tau }.$$

The proof is completed.

Proof

[Proof of Theorem 2] By Lemma 4 and 5, we see that

$$\underset{ij}{\text{max}}|\sum _{g=1}^G({\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})})|\le C_0{\left(\frac{G\text{log}p}{n}\right)}^{1/2}\text{and}\underset{ij}{\text{max}}|{\hat{\sigma }}_{ij}^{(\mathrm{g})}-{\sigma }_{ij,0}^{(\mathrm{g})}|\le C_0{\left(\frac{\text{log}p}{n}\right)}^{1/2},$$ (10)

for all g = 1, …, G with probability greater than 1−2(1+3G)p^−τ. All following arguments assume (10) holds. Note that $\{M_0,R_0^{(1)},\dots ,R_0^{(\mathrm{G})}\}$ is a feasible solution of (3) as

$${|I-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(M_0+R_0^{(\mathrm{g})})|}_{\infty }={|({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\mathrm{\Omega }}_0^{(\mathrm{g})}|}_{\infty }\le {\Vert {\mathrm{\Omega }}_0^{(\mathrm{g})}\Vert }_{L_1}{|{\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}|}_{\infty }\le C_M{C}_0(\text{log}p/n)1/2={\lambda }_2$$

and

$${|G^{-1}\sum _{g=1}^G\{I-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}(M_0+R_0^{(\mathrm{g})})\}|}_{\infty }\le {|G^{-1}\sum _{g=1}^G({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})M_0|}_{\infty }+{|G^{-1}\sum _{g=1}^G({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})R_0^{(\mathrm{g})}|}_{\infty }\le {\Vert M_0\Vert }_{L_1}{|G^{-1}\sum _{g=1}^G({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})|}_{\infty }+G^{-1}\sum _{g=1}^G{\Vert R_0^{(\mathrm{g})}\Vert }_{L_1}{|{\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}|}_{\infty }\le C_M{C}_0{\{\text{log}p/(nG)\}}^{1/2}+C_R{C}_0{\{\text{log}p/(nG)\}}^{1/2}={\lambda }_1.$$

Now, we find an upper bound of ${|G(\hat{M}-M_0)e_j|}_{\infty }={|{\sum }_{g=1}^G({\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-{\mathrm{\Omega }}_0^{(\mathrm{g})}{e}_j|}_{\infty }$. In particular, we use

$${|\sum _{g=1}^G({\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-{\mathrm{\Omega }}_0^{(\mathrm{g})})e_j|}_{\infty }\le {|\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_{\infty }+{|\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})}({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-I)e_j|}_{\infty }.$$ (11)

First, consider the first term in the right-hand side of (11). We can show that

$${|\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_{\infty }\le {|\sum _{g=1}^G{M}_0({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{m}}_j|}_{\infty }+{|\sum _{g=1}^G{M}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{r}}_j^{(\mathrm{g})}|}_{\infty }+{|\sum _{g=1}^G{R}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{m}}_j|}_{\infty }+{|\sum _{g=1}^G{R}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{r}}_j^{(\mathrm{g})}|}_{\infty }\le {\Vert M_0\Vert }_{L_1}\{{|\sum _{g=1}^G({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})|}_{\infty }{|{\hat{m}}_j|}_1+\sum _{g=1}^G{|{\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}|}_{\infty }{|{\hat{r}}_j^{(\mathrm{g})}|}_1\}+\sum _{g=1}^G{|R_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})|}_{\infty }{|{\hat{m}}_j|}_1+\sum _{g=1}^G{|R_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})})|}_{\infty }{|{\hat{r}}_j^{(\mathrm{g})}|}_1.$$

Using the assumptions ${\Vert R_0^{(\mathrm{g})}\Vert }_{L_1}\le C_R$ and ${\sum }_{g=1}^G{\Vert R_0^{(\mathrm{g})}\Vert }_{L_1}\le G^{1/2}{C}_R$, we have

$${|\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})}({\mathrm{\Sigma }}_0^{(\mathrm{g})}-{\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}){\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}{e}_j|}_{\infty }\le C_M{C}_0{(G\text{log}p/n)}^{1/2}{|{\hat{m}}_j|}_1+C_M{C}_0{(\text{log}p/n)}^{1/2}\sum _{g=1}^G{|{\hat{r}}_j^{(\mathrm{g})}|}_1+C_R{C}_0{(G\text{log}p/n)}^{1/2}{|{\hat{m}}_j|}_1+C_R{C}_0{(\text{log}p/n)}^{1/2}\sum _{g=1}^G{|{\hat{r}}_j^{(\mathrm{g})}|}_1\le C_0(C_M+C_R){(G\text{log}p/n)}^{1/2}({|{\hat{m}}_j|}_1+G^{-1/2}\sum _{g=1}^G{|{\hat{r}}_j^{(\mathrm{g})}|}_1)\le C_0(C_M+C_R){(G\text{log}p/n)}^{1/2}({|m_{j,0}|}_1+G^{-1/2}\sum _{g=1}^G{|r_{j,0}^{(\mathrm{g})}|}_1)\le C_0{(C_M+C_R)}^2{(G\text{log}p/n)}^{1/2}.$$ (12)

For the second term in the right-hand side of (11), note that

$${|\sum _{g=1}^G{\mathrm{\Omega }}_0^{(\mathrm{g})}({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}_1^{(\mathrm{g})}-I)e_j|}_{\infty }\le {|\sum _{g=1}^G{M}_0({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})}-I)e_j|}_{\infty }+{|\sum _{g=1}^G{R}_0^{(\mathrm{g})}({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})}-I)e_j|}_{\infty }\le {\Vert M_0\Vert }_{L_1}{|\sum _{g=1}^G({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})}-I)e_j|}_{\infty }+\sum _{g=1}^G{\Vert R_0^{(\mathrm{g})}\Vert }_{L_1}{|({\hat{\mathrm{\Sigma }}}^{(\mathrm{g})}{\hat{\mathrm{\Omega }}}^{(\mathrm{g})}-I)e_j|}_{\infty }\le C_M{\lambda }_1+G^{1/2}{C}_R{\lambda }_2=C_0{C}_M(C_M+2C_R){(G\text{log}p/n)}^{1/2}.$$ (13)

By (11), (12), (13) and the equality |M̂ − M₀|_∞ = max_j |(M̂ − M₀)e_j |_∞, we have

$${|\hat{M}-M_0|}_{\infty }\le C_0(2C_M^2+4C_M{C}_R+C_R^2){\left(\frac{\text{log}p}{nG}\right)}^{1/2}.$$

The proof is completed.

Proof

[Proof of Theorem 3] By Theorem 1, we see that

$$\underset{ij}{\text{max}}\sum _{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|\le 2G{C}_M{\lambda }_2\le {\delta }_n,$$ (14)

with probability greater than 1 − 4Gp^−τ. We show that S₀ = Ŝ when (14) holds. For any (i, j, g) ∉ S₀, we have $|{\hat{\omega }}_{ij}^{(\mathrm{g})}|=|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|\le {\sum }_{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|\le {\delta }_n$. Therefore, we see ${\tilde{\omega }}_{ij}^{(\mathrm{g})}=0$, which implies Ŝ ⊂ S₀. On the other hand, for any (i, j, g) ∈ S₀, we have $|{\hat{\omega }}_{ij}^{(\mathrm{g})}|\ge |{\omega }_{ij,0}^{(\mathrm{g})}|-|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|\ge |{\omega }_{ij,0}^{(\mathrm{g})}|-{\sum }_{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|>{\delta }_n$. Therefore, we see that ${\tilde{\omega }}_{ij}^{(\mathrm{g})}\ne 0$, which implies S₀ ⊂ Ŝ. In summary, we see that S₀ = Ŝ if (14) holds, which implies that $\mathrm{p}\mathrm{r}(S_0=Ŝ)\ge \mathrm{p}\mathrm{r}({\text{max}}_{ij}{\sum }_{g=1}^G|{\hat{\omega }}_{ij}^{(\mathrm{g})}-{\omega }_{ij,0}^{(\mathrm{g})}|\le {\delta }_n)$.