Regression analysis of sparse asynchronous longitudinal data

Summary

We consider estimation of regression models for sparse asynchronous longitudinal observations, where time-dependent responses and covariates are observed intermittently within subjects. Unlike with synchronous data, where the response and covariates are observed at the same time point, with asynchronous data, the observation times are mismatched. Simple kernel-weighted estimating equations are proposed for generalized linear models with either time invariant or time-dependent coefficients under smoothness assumptions for the covariate processes which are similar to those for synchronous data. For models with either time invariant or time-dependent coefficients, the estimators are consistent and asymptotically normal but converge at slower rates than those achieved with synchronous data. Simulation studies evidence that the methods perform well with realistic sample sizes and may be superior to a naive application of methods for synchronous data based on an ad hoc last value carried forward approach. The practical utility of the methods is illustrated on data from a study on human immunodeficiency virus.

1. Introduction

In many longitudinal studies, measurements are taken at irregularly spaced and sparse time points. The sparsity refers to the availability of only a few observations per subject. In the classical longitudinal set-up, a small number of measurements of response and covariates are synchronized within individuals, meaning that they are observed at the same time points, with the measurement times varying across individuals. However, in many applications, observed covariates and response variables may be mismatched over time within individuals, leading to asynchronous data. This greatly complicates the study of the association between response and covariates, with virtually all available longitudinal regression methods developed for the synchronous setting.

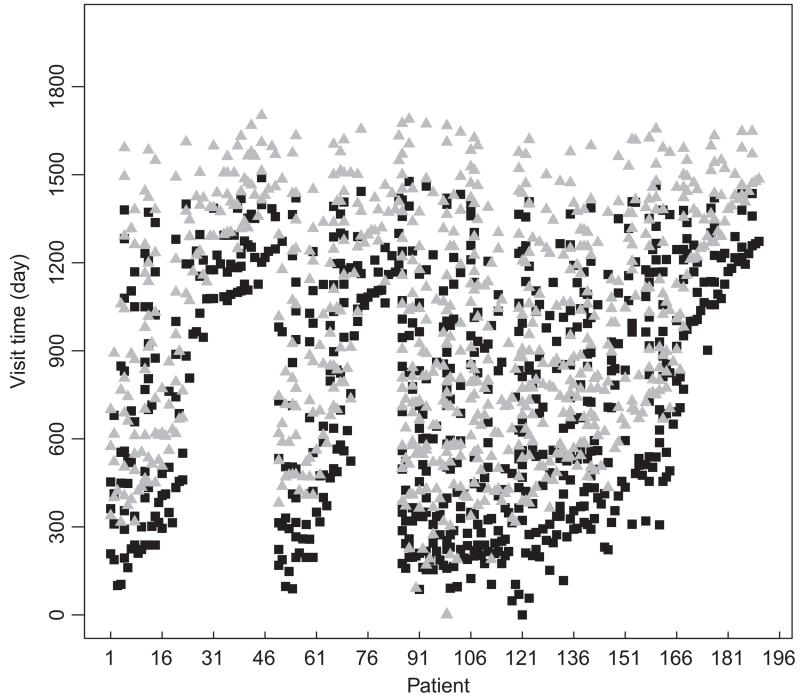
Often no synchronous data may be available and existing methods are not applicable to asynchronous data. In educational studies, it is of interest to associate subjective evaluations of students’ performance and objective test results. However, subjective information is usually collected through interviews or phone calls, which are obtained at different time points. In clinical epidemiology, one may study the links between biomarkers, sampled repeatedly at laboratory visits, with self-reported measures of function and quality of life, captured via outpatient phone interviews. In other clinical settings, the relationship between two biomarkers may be of interest, with laboratory visits scheduled at different times by design to address logistical issues which prevent their simultaneous observation. As an example, in a prospective observational cohort study (Wohl et al., 2005), a total of 191 patients were followed for up to 5 years, with human immunodeficiency virus (HIV) viral load and CD4 cell counts measured repeatedly on these patients. Fig. 1 displays the observation times for the two variables: we see clearly that sparse measurements are taken on each variable for each subject and that the study protocol has specified that the viral load and CD4 cell count are obtained at laboratary visits on different days. Hence, there are no synchronous data within individuals, as would be needed by the existing methods. It is well known in the medical literature that HIV viral load and CD4 cell counts are negatively associated (Hoffman et al., 2010). The ad hoc but commonly adopted last value carried forward approach which employs synchronous data methods does not identify this association in the data analysis in Section 5.

Fig. 1.

. Observation times of CD4 cell counts () and HIV viral load (■) by patient

The goal of this paper is to develop simple, computationally efficient and theoretically justified estimators for longitudinal regression models based on such sparse asynchronous data. A popular regression model for longitudinal data with time varying response and covariates is the generalized linear model

$$E\left\{Y\right(t)\mid X(t\left)\right\}=g\left\{X{\left(t\right)}^{\mathrm{T}}\beta \right\},$$ (1)

where g is a known, strictly increasing and continuously twice-differentiable link function, t is a univariate time index, X(t) is a vector of time varying covariates plus intercept term, Y(t) is a time varying response and β is an unknown time invariant regression parameter. Model (1) characterizes the conditional mean of Y(t) given X(t) while leaving its dependence structure and distributional form completely unspecified. Existing methodology (Diggle et al. (2002) and references therein) for model (1) assumes that X and Y are observed at the same time points within individuals, with the resulting estimators based on this synchronous data being n^1/2 consistent and asymptotically normal. To our knowledge, estimation via generalized estimating equations (Diggle et al., 2002) has not been studied with asynchronous data and it is unclear whether parametric rates of convergence are achievable.

A more flexible model is the generalized varying-coefficient model that allows the unknown regression coefficient β(t) to vary over time in model (1):

$$E\left\{Y\right(t)\mid X(t\left)\right\}=g\left\{X{\left(t\right)}^{\mathrm{T}}\beta \right(t\left)\right\}.$$ (2)

For the identity link function, as recently reviewed by Fan and Zhang (2008), estimation for sparse synchronous longitudinal data may be based on two main approaches: global and local. Local methods, which include local likelihood, may be based on local polynomial smoothing (Wu et al., 1998; Hoover et al., 1998; Fan and Zhang, 2000; Wu and Chiang, 2000). Global approaches employ alternative basic function representations for the data and regression coefficients, such as polynomial spline (Huang et al., 2002, 2004), smoothing spline (Hoover et al., 1998; Chiang et al., 2001; Fan and Zhang, 2000) and functional data analytic approximations (Yao et al., 2005; Zhou et al., 2008; Sentürk and Muller, 2010; Zhou et al., 2008). Interestingly, whereas the optimal non-parametric rates of convergence for estimation of β(t) are the same for the local and global approaches with sparse longitudinal data, the global approaches can incorporate within-subject correlation structure in the estimation procedure, similarly to generalized estimating equations (Diggle et al., 2002). Qu and Li (2006) employed penalized splines with quadratic inference functions. Fan et al. (2007) studied non-parametric estimation of the covariance function. Other related work can be found in Sun et al. (2007) and references therein. Establishing efficiency gains for the global approaches is challenging for the time-dependent parameter estimators, owing to slow rates of convergence.

Hybrids of models (1) and (2) have been widely investigated with synchronous longitudinal data, where some of the regression parameters are time invariant and some are time dependent. The so-called partial linear model is a variant inwhich the intercept termis time varyingwhereas other coefficients are constant. In general, the time-independent parameter may be estimated at the usual parametric rates. An important discovery that was made by Lin and Carroll (2001) is that the commonly used forms of the kernel methods cannot incorporate within-subject correlation to improve efficiency of the time invariant parameter estimator. Wang (2003) proposed an innovative kernel method, which assumes knowledge of the true correlation structure, yielding efficiency gains. The idea was extended by Wang et al. (2005) to achieve the semiparametric efficient bound that was computed in Lin and Carroll (2001) for the time-independent parameter. A counting process approach on the observation time was adopted by Martinussen and Scheike (1999, 2001), Cheng and Wei (2000) and Lin and Ying (2001), which enables n^1/2-consistent estimation of the time-independent parameter without explicit smoothing.

In this paper, we propose estimators for models (1) and (2) with asynchronous longitudinal data. Extending Martinussen and Scheike’s (2010) representation of synchronous data, we formulate the observation process by using a bivariate counting process for the observation times of the covariate and response variables. For subject i=1, … , n,

$$N_i(t,s)=\sum _{j=1}^{L_i}\sum _{k=1}^{M_i}I(T_{\mathit{ij}}⩽t,S_{\mathit{ik}}⩽s)$$

counts the number of observation times up to t on the response and up to s on the covariates, where T_ij , j = 1, … ,L_i, are the observation times for the response and S_ik, k = 1, … ,M_i, are the observation times for the covariates, i.e., with sparse asynchronous longitudinal data, we observe for i=1, … , n

$$\begin{array}{cc}\hfill Y_i\left(T_{\mathit{ij}}\right),& j=1,\dots ,L_i,\hfill \\ \hfill X_i\left(S_{\mathit{ik}}\right),& k=1,\dots ,M_i,\hfill \end{array}$$

where L_i and M_i are finite with probability 1. To use existing methods for synchronous longitudinal data, where L_i=M_i and T_ij=S_ij , j=1, … , L_i, for each observed response, one may carry forward the most recently observed covariate. As evidenced by the numerical studies in Sections 4 and 5, this ad hoc approach may incur substantial bias.

To obtain estimators for models (1) and (2) with asynchronous data, we adapt local kernel weighting techniques to estimating equations that have previously been developed for synchronous data. Our main idea is intuitive: we downweight those observationswhich are distant in time, either from each other or from a known fixed time. This enables the use of all covariate observations for each observed response. These methods require similar smoothness assumptions on the covariate trajectories to those employed with synchronous data. In practice, there may be scenarios where it is necessary to preprocess the covariate X(t) when applying the methodologies of the paper. With a suitable choice of the bandwidth controlling the kernel weighting, the estimators for the time invariant coefficient and time-dependent coefficient are shown to be consistent and asymptotically normal, with simple plug-in variance estimators. The usual cross-validation for bandwidth selection does not work because the data are non-synchronous but we develop a novel data-adaptive bandwidth selection procedure which works well in simulation studies. The choice of the local method versus a global method is based in part on computational and inferential simplicity and, in part, by the fact that it is unclear that efficiency gains are achievable given the slow rates of convergence of the estimators. The optimal rates of convergences for our local estimators for models (1) and (2) with asynchronous data are slower than the corresponding optimal rates which may be achieved with synchronous data. In addition, the estimator for the time-independent model converges more slowly than the parametric rate n^−1/2 for synchronous data. Given this lack of n^−1/2-consistency, the extent to which efficiency gains with synchronous data for time-independent parameter estimation by using global methods carry over to the asynchronous setting is not obvious. These results are detailed in Sections 2 and 3.

The remainder of the paper is organized as follows. In Section 2, we discuss estimation for model (1) with time-independent coefficients by using asynchronous data and provide the corresponding theoretical findings. The results for the time-dependent model (2) are given in Section 3. Section 4 reports simulation studies and Section 5 applies our procedure to data from the HIV study, exhibiting improved performance versus the last value carried forward approach with synchronous data methods. Concluding remarks are given in Section 6. Proofs of results from Sections 2 and 3 are given in Appendix A.

The data that are analysed in the paper and the programs that were used to analyse them can be obtained from http://wileyonlinelibrary.com/journal/rss-datasets

2. Time invariant coefficient

2.1. Estimation

Suppose that we have a random sample of n subjects. For the ith subject, let Y_i(t) be the response variable at time t and let X_i(t) be a p × 1 vector of possibly time-dependent covariates. The response Y_i(t) may be a continuous, categorical or count variable, whereas the covariate X_i(t) may include time-independent covariates, such as an intercept term, in addition to time varying covariates. The main requirement for the validity of the methods presented below is that, if the time varying covariates in X_i(t) are multivariate, then the different covariates are measured at the same time points. Precise conditions on X_i(t) are provided in the theoretical discussion in Section 2.2 and do not differ considerably from those needed for estimation with synchronous data.

We now focus on the regression model (1) that relates Y_i(t) to X_i(t) through a time invariant coefficient. To estimate β, we propose to use kernel weighting in a working independence generalized estimating equation (Diggle et al., 2002) which has previously been developed for synchronous data. The resulting estimating equation is

$$U_n\left(\beta \right)=n^{-1}\sum _{i=1}^n\sum _{j=1}^{L_i}\sum _{k=1}^{M_i}{K}_h(T_{\mathit{ij}}-S_{\mathit{ik}})\times X_i\left(S_{\mathit{ik}}\right)\times \left[Y_i\right(T_{\mathit{ij}})-g\{X_i{\left(S_{\mathit{ik}}\right)}^{\mathrm{T}}\beta \left\}\right].$$ (3)

Using counting process notation, this is equivalent to

$$U_n\left(\beta \right)=n^{-1}\sum _{i=1}^n\int \int K_h(t-s)X_i\left(s\right)\left[Y_i\right(t)-g\{X_i{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\mathrm{d}{N}_i(t,s),$$ (4)

where K_h(t)=K(t/h)/h, K(t) is a symmetric kernel function, which is usually taken to be the Epanechnikov kernel K(t)=0.75(1–t²)₊, and h is the bandwidth.

The kernelweighting accounts for the fact that the covariate and response are mismatched and permits contributions to U_n(β) from all possible pairings of response and covariate observations. It requires that the observation times T_ij and S_ik, i=1, … , n, should be close for some but not all subjects. The theoretical results that are presented below require only that these observation times are close for a very small fraction of the overall sample of n individuals. If the observation times for covariate and response are close to each other, then the kernel weight is close to 1; however, if the observation times are far apart, then the contribution to the estimating equation (3) may be 0. In general, the relative contribution to U_n(β) is determined by the closeness of the covariate and response measurement times. Note that, for a response measured at a particular time T_ij , there may be multiple S_iks at which covariates are measured which contribute to the estimating equation. We solve U_n(β)=0 to obtain an estimate for β, which is denoted by $\widehat{\beta }$. Regarding the computations, once the kernel function K has been chosen and the bandwidth has been fixed, the estimating equation can be solved by using a standard Newton–Raphson implementation for generalized linear models, with good convergence properties.

2.2. Asymptotic properties

We next study the asymptotic properties of $\widehat{\beta }$, including the bias–variance trade-off with respect to the bandwidth selection. We allow the observations of X_i(·) and the observations of Y_i(·) to be arbitrarily correlated. We specify our assumptions on the covariance structure as follows. For s, t ∈ [0, τ], let var{Y(t)|X(t)}=σ{t, X(t)}² and cov{Y(s), Y(t)|X(s) X(t)}=r{s, t, X(s), X(t)}, where τ is the maximum follow-up time. Observe that the conditional variances and correlations of Y are completely unspecified and may depend on X.

We need the following conditions.

Condition 1. N_i(t, s) is independent of (Y_i, X_i) and, moreover, E{dN_i(t, s)} = λ(t, s)dt ds, where λ(t, s) is a twice-continuous differentiable function for any 0 ⩽ t, s ⩽ τ. In addition, Borel measure for $\mathcal{G}=\left\{\lambda \right(t,t)>0,t\in [0,\tau \left]\right\}$ is strictly positive. For t₁ ≠ s₁ and t₂ ≠ s₂, $\mathbb{P}\left\{\mathrm{d}N\right(t_1,t_2)=1\mid N(s_1,s_2)-N(s_1-,s_2-)=1\}=f(t_1,t_2,s_1,s_2)\mathrm{d}{t}_1\mathrm{d}{t}_2$ where f(t₁, t₂, s₁, s₂) is continuous for t₁ ≠ s₁, and t₂ ≠ s₂ and f(t₁±, t₂±, s₁±, s₂±) exists.

Condition 2. If there is a vector γ such that γ^TX(s)=0 for any $s\in \mathcal{G}$ with probability 1, then γ=0.

Condition 3. For any β in a neighbourhood of β₀, the true value of β, E[X(s)g{X(t)^Tβ}] is continuously twice differentiable in (t, s)∈[0, τ]^⊗2 and |g′{X(t)^Tη}|⩽q{||X(t)||} for some q(·) satisfying that E[||X(t)||⁴q{||X(t)||}²] is uniformly bounded in t. Additionally, E{||X(t)||⁴}<∞. Furthermore, E[X(s₁)X(s₂)^Tr{t₁, t₂, X(t₁), X(t₂)}] and E[X(s₁)X(s₂)^T_g {X(t₁)^Tβ₀}g{X(t₂)^T β₀}] are continuously twice differentiable in (s₁, s₂, t₁, t₂)∈[0, τ]^⊗4. Moreover,

$$\int E[\Vert X(s)X{\left(s\right)}^{\mathrm{T}}\Vert \sigma {\{s,X(s\left)\right\}}^2]\lambda (s,s)\mathrm{d}s<\infty ,$$

and

$$\int E[\Vert X(s)X{\left(s\right)}^{\mathrm{T}}\Vert g^{\prime }{\left\{X\right(s)}^{\mathrm{T}}{\beta }_0\}\left]\lambda \right(s,s)\mathrm{d}s<\infty .$$

Condition 4. K(·) is a symmetric density function satisfying ∫ z² K(z)dz < ∞ and ∫ K(z)² dz < ∞. Additionally, nh → ∞.

Condition 5. nh⁵ → 0.

Condition 1 requires that the observation process is independent of both the response and the covariates. We require that λ(s, t) is positive in a neighbourhood of the diagonal where s=t at some time points, but not all time points, and λ(s, t) need not be greater than 0 when s ≠ t. Analogous assumptions have been widely utilized with synchronous data, as in Lin and Ying (2001), Yao et al. (2005) and Martinussen and Scheike (2010). We consider the sparse longitudinal set-up where the number of observations N_i(t, s) has finite expectation but may have infinite support, similarly to Martinussen and Scheike (2010) with synchronous data. This differs from the dense setting that is popular in functional data analysis where L_i and M_i → ∞ as n → ∞ for all i. Condition 2 ensures identifiability of β whereas condition 3 posits smoothness assumptions on the expectation of some functionals of X(s) and gives additional regularity conditions on the observation intensity λ. The latter condition implies that the covariance function of X(t) is twice continuously differentiable. Such a condition is not satisfied by processes having independent increments. For Gaussian processes, the implication is that X(t) has continuous but not necessarily differentiable sample paths with probability 1. In theory, the condition may still allow the actual path of X(s) to be discontinuous, as with categorical covariates which jump according to a point process, where discontinuities may occur with zero measure. In Section 6, we discuss the possibility of relaxing condition 3. Conditions 4 and 5 specify valid kernels and bandwidths.

The following theorem, which is established in Appendix A, states the asymptotic properties of $\widehat{\beta }$.

Theorem 1. Under conditions 1–4, the asymptotic distribution of $\widehat{\beta }$ satisfies

$${\left(\mathit{nh}\right)}^{1∕2}\left\{A\right({\beta }_0\left)\right(\widehat{\beta }-{\beta }_0)+{\mathit{Ch}}^2\}\to N(0,\Sigma ),$$ (5)

where A(β₀) = ∫_s E[X(s)g′{X(s)^Tβ₀}X(s)^T]λ(s, s)ds, β₀ is the true regression coefficient and C is a constant, which can be found in Appendix A. The asymptotic variance

$$\Sigma =\int K{\left(z\right)}^2\mathrm{d}z\int E\left[X\right(s\left)X{\left(s\right)}^{\mathrm{T}}\sigma {\{s,X(s\left)\right\}}^2\right]\lambda (s,s)\mathrm{d}s.$$ (6)

The asymptotic results do not depend on λ(s, t) for s ≠ t as we are dealing with asynchronous data in which the response and covariates are never ‘perfectly’ matched, i.e. there is zero measure associated with identical observation times. The variance depends critically on the joint density of the observation times on the diagonal, which determines how quickly information accumulates from an asynchronous response and covariates across subjects. For the case where synchronous data occur with positive probability, synchronous data methods may be employed with the synchronous portion of the data and will yield improved convergence rates relatively to the methods proposed above for pure asynchronous data.

If the bandwidth is further restricted by condition 5, then the asymptotic bias in condition (5) vanishes and $\widehat{\beta }$ is consistent.

Corollary 1. Under conditions 1–5, $\widehat{\beta }$ is consistent and converges to a mean 0 normal distribution given in theorem 1.

For statistical inference, it is challenging to estimate the variance in equation (6) directly, owing to the time varying quantities σ and λ, which are difficult to estimate well without imposing additional assumptions on the covariate and response processes. In practice, we estimate Σ by

$$\widehat{\Sigma }=\frac{1}{n^2}\sum _{i=1}^n{\left(\int \int K_h(t-s)X_i\left(s\right)\left[Y_i\right(t)-g\{X_i{\left(s\right)}^{\mathrm{T}}\widehat{\beta }\left\}\right]\mathrm{d}{N}_i(t,s)\right)}^{\otimes 2}$$

and estimate the variance of $\widehat{\beta }$ by the sandwich formula

$${\left\{{\phantom{\mid }\frac{\partial U_n\left(\beta \right)}{\partial \beta }\mid }_{\beta =\widehat{\beta }}\right\}}^{-1}\widehat{\Sigma }{\left({\left\{{\phantom{\mid }\frac{\partial U_n\left(\beta \right)}{\partial \beta }\mid }_{\beta =\widehat{\beta }}\right\}}^{-1}\right)}^{\mathrm{T}}.$$

This approach has been adopted by Cheng and Wei (2000) and Lin and Ying (2001) with synchronous data as well.

Corollary 2. Under conditions 1–5, the sandwich formula consistently estimates the variance of $\widehat{\beta }$.

Our method depends on the selection of the bandwidth. Theoretically speaking, condition 4 says that the bandwidth cannot be too small (smaller than O(n⁻¹)); otherwise, the variance will be quite large. However, to eliminate the asymptotic bias, we require a small bandwidth. Theorem 1 indicates that the bias is of order O(n^1/2h^5/2), so we should choose bandwidth h=o(n^−1/5). With this choice of bandwidth, we achieve a rate of convergence o(n^2/5), which is slower than the parametric n^1/2 rate of convergence for synchronous data under model (1).

We propose a data-adaptive bandwidth selection procedure despite the fact that traditional cross-validation methods are not applicable owing to asynchronous measurement times for the covariates and response. On the basis of condition (5), we first regress $\widehat{\beta }\left(h\right)$ on h² in a reasonable range of h to obtain the slope estimate $\widehat{C}$. To obtain the variance, we split the data randomly into two parts and obtain regression coefficient estimates ${\widehat{\beta }}_1\left(h\right)$ and ${\widehat{\beta }}_2\left(h\right)$ based on each half-sample. The variance of $\widehat{\beta }\left(h\right)$ is then estimated by $\widehat{V}\left(h\right)={\left\{{\widehat{\beta }}_1\right(h)-{\widehat{\beta }}_2(h\left)\right\}}^2∕4$. Using both $\widehat{C}$ and ${\widehat{V}}_h$, we thus calculate the mean-squared error as ${\widehat{C}}^2{h}^4+\widehat{V}\left(h\right)$ on the basis of theorem 1. Finally, we select the optimal bandwidth h minimizing this mean-squared error.

Our numerical studies show that small bias may be achieved for bandwidths between n⁻¹ and n^−1/2, with stable variance estimation and confidence interval coverage for bandwidths larger than n^−4/5. Within this range, the bias diminishes as the sample size increases, as predicted by theorem 1. Methods based on asynchronous data are generally less efficient than those based on synchronous data, with the information in synchronous data dominating that in asynchronous data. Numerical studies (which are not reported) demonstrate that, in moderate sample sizes, asynchronous data may yield comparable but reduced efficiency when there are a large number of observation times for the covariate process.

3. Time-dependent coefficients

The observed data are the same as in Section 2. Suppose that we are interested in estimating the coefficient β(t) in model (2) at a fixed time point t. Similarly to synchronous data, in the asynchronous set-up, neither the response Y(t) nor the covariate X(t) is generally observed at time t. However, one may utilize measurements of these variables which are taken close in time to t to estimate β(t). Kernel weighting is employed to downweight measurements of Y(t) and X(t) on the basis of their distance from t. Recall that, in Section 2, a single bandwidth was used to weight on the basis of the distance between the covariate and response measurements. The main difference in this section is that two bandwidths are needed to weight separately on the basis of the distance of the response measurement fromtime t and the distance of the covariate measurement from time t. Fitting model (2) with synchronous data requires only a single bandwidth, since the response and covariate are always measured at the same time points.

The doubly kernel-weighted estimating equation for β(t) is

$$U_n\left\{\beta \right(t\left)\right\}=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{L_i}\sum _{k=1}^{M_i}{K}_{h_1,h_2}(T_{\mathit{ij}}-t,S_{\mathit{ik}}-t)\times X_i\left(S_{\mathit{ik}}\right)\times \left[Y_i\right(T_{\mathit{ij}})-g\{X_i{\left(S_{\mathit{ik}}\right)}^{\mathrm{T}}\beta \left(t\right)\left\}\right],$$ (7)

where K_h1,h2(t, s)=K(t/h₁, s/h₂)/(h₁h₂) and K(t, s) is a bivariate kernel function, say, the product of univariate Epanechnikov kernels K(t, s)=0.5625(1–t²)+(1–s²)₊. We solve equation (7) to obtain an estimate for β(t), which is denoted as $\widehat{\beta }\left(t\right)$. Computationally, the Newton–Raphson iterative method can be utilized after choosing K_h1,h2 and fixing the bandwidths. As this estimating equation leads to separate estimates of β(t) at each time point t, the resulting inferential procedures that are described below are pointwise and not simultaneous. To obtain the trajectory of $\widehat{\beta }\left(t\right)$, one solves equation (7) on a dense grid of time points in (0, τ).

To derive the large sample properties of the estimator, we need the following assumptions.

Condition 1′. N_i(t, s) is independent of (Y_i, X_i) and, moreover, E{dN_i(t, s)}=λ(t, s)dtds, where λ(t, s) is twice continuous differentiable for any 0⩽t, s⩽τ and is strictly positive for t=s. For t₁ ≠ s₁, t₂ ≠ s₂, $\mathbb{P}\left\{\mathrm{d}N\right(t_1,t_2)=1\mid N(s_1,s_2)-N(s_1-,s_2-)=1\}=f(t_1,t_2,s_1,s_2)\mathrm{d}{t}_1\mathrm{d}{t}_2$ where f(t₁, t₂, s₁, s₂) is continuous for t₁ ≠ s₁ and t₂ ≠ s₂ and f(t₁±, t₂±, s₁±, s₂±) exists.

Condition 2′. For any fixed time point t, if there is a vector γ such that γ^T X(t)=0, then γ=0.

Condition 3′. E[X(s₁)g{X(s₂)^T β(s₃)}] is continuously twice differentiable in (s₁, s₂, s₃) ∈ s[0, τ]^⊗3 and |g′{X(t)^Tη}⩽q{||X(t)||} for some q(·) satisfying that E[||X(t)||⁴q{||X(t)||²}] is uniformly bounded in t. Moreover, E[X(t₁)X(s₁)^Tr{s₂, t₂, X(s₂), X(t₂)}] is continuously twice differentiable in (t₁, s₁, t₂, s₂)∈[0, τ]^⊗4 and E[X(t₁)X(s₁)^T g{X(t₂)^T β₀(t)}g{X(s₂)^T β₀(t)}] is continuously twice differentiable in (t₁, s₁, t₂, s₂, t)∈[0, τ]^⊗5.

Condition 4′. The kernel function K(x, y) is a symmetric bivariate density function for x and y. In addition, ∫ |x³y|K(x, y)dxdy < ∞, ∫ |xy³|K(x, y)dxdy < ∞, ∫ x² y² K(x, y) dx dy < ∞ and ∫ K(x, y)²dx dy < ∞. Moreover, nh₁h₂ → ∞.

Condition 5′. ${\left(n{h}_1{h}_2\right)}^{1∕2}(h_1^2+h_2^2)\to 0$.

Conditions 1′–5′ are similar in spirit to conditions 1–5 in Section 2. Condition 1′ strengthens condition 1, requiring that, to estimate β(t) at time t, λ(t, t)>0. Condition 2′ is a modified identifiability assumption for β(t) at time t. Condition 3′ posits the requirements on the covariance function of the covariate process, with the implications similar to those discussed in Section 2. Conditions 4′ and 5′ are provided for the kernel function and the bandwidth.

We establish the asymptotic distribution of $\widehat{\beta }\left(t\right)$ in the following theorem.

Theorem 2. Under conditions 1′–4′, the asymptotic distribution of $\widehat{\beta }\left(t\right)$ for any fixed time point t ∈ (0, τ) based on solving U_n{β(t)} in equation (7) is

$${\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left[B\right\{{\beta }_0\left(t\right),t\left\}\right\{\widehat{\beta }\left(t\right)-{\beta }_0\left(t\right)\}+D_1(t)h_1^2+D_2(t)h_1{h}_2+D_3(t\left)h_2^2\right]\to N\{0,{\Sigma }^{\ast }(t\left)\right\},$$

where B{β₀(t),t}= λ(t,t)E[X(t)g′{X(t)^T β₀(t)} X(t)^T], β₀(t) is the true coefficient function and D₁(t),D₂(t) and D₃(t) are known functions, whose specific forms can be found in Appendix A. The variance function is

$${\Sigma }^{\ast }\left(t\right)=\int \int K{(z_1,z_2)}^2\mathrm{d}{z}_1\mathrm{d}{z}_{2}E\left[X\right(t\left)X{\left(t\right)}^T\sigma {\{t,X(t\left)\right\}}^2\right]\lambda (t,t).$$ (8)

If the bandwidth is further restricted by condition 5′, then the asymptotic bias in equation (8) vanishes and $\widehat{\beta }\left(t\right)$ is consistent for β₀(t), as stated in the following corollary.

Corollary 3. Under conditions 1′–5′ $\widehat{\beta }\left(t\right)$ is consistent and converges to the zero-mean normal distribution given in theorem 2 for any t ∈(0, τ).

For any fixed time point t, the variance estimator for $\widehat{\beta }\left(t\right)$ may be obtained by expanding the estimating equation (7) similarly to the time invariant case.

Corollary 4. Under conditions 1′–5′, for any fixed time point t ∈ (0, τ), the sandwich formula consistently estimates the variance of $\widehat{\beta }\left(t\right)$.

If we let h=h₁=h₂, on the basis of condition 4′, a valid bandwidth is larger than O(n^−1/2). In contrast, theorem 2 indicates that the bias is of order O(n^1/2h³), so we should choose bandwidth h=o(n^−1/6). With this choice of bandwidth, we achieve o(n^1/3) rate of convergence, which is slower than the o(n^2/5) rate of convergence for the synchronous case with time-dependent coefficient (Martinussen and Scheike, 2010). In general, similarly to model (1), asynchronous estimators for model (2) converge more slowly and are less efficient than those based on synchronous data.

Our numerical studies show that bandwidths near n^−1/2 perform well with moderate sample sizes. As with model (1), the automation of bandwidth selection for estimation of β(t) is challenging with asynchronous data because the calculation of error criteria for use in cross-validation is unclear. Our suggested procedure calculates the integrated mean-squared error. This is accomplished through calculating mean-squared errors separately at time points of interest by adapting the approach for time-independent coefficients in Section 2. We then sum them to obtain integrated mean-square errors and choose the bandwidth that minimizes this summation. This procedure performs well in the simulation studies.

4. Numerical studies

In this section we investigate finite sample properties of the estimators that were proposed in Section 2 and Section 3 through Monte Carlo simulation.

4.1. Time invariant coefficient

We first study the performance of the estimator for the time invariant coefficient in model (1).We generate 1000 data sets, each consisting of n = 100, 400, 900 subjects. The number of observation times for the response Y(t) was Poisson distributed with intensity rate 5, and similarly for the number of observation times for the covariate X(t). With these two numbers of measurements, the observation times for the response and covariate are generated from the uniform distribution Unif(0,1) independently. The covariate process is Gaussian, with values at fixed time points being multivariate normal with mean 0, variance 1 and correlation exp(−|t_ij–t_ik|), where t_ij is the jth measurement time and t_ik is the kth measurement time for the response, both on subject i. Whereas realizations of this Gaussian process may not be differentiable on the diagonal, the resulting expectations in conditions 3 and 3′ are bounded and smoothly differentiable, as required for the validity of the asynchronous estimator. At the data-generating stage, to generate the response, we include the response observation times with the covariate observation times when generating the covariates that are needed for simulating responses at the response observation times. The responses were generated from

$$Y\left(t\right)={\beta }_0+X\left(t\right){\beta }_1+\epsilon \left(t\right),$$ (9)

where β₀ is the intercept, β₁ is a time-independent coefficient and ε(t) is Gaussian, with mean 0, variance 1 and cov{ε(s), ε(t)} = 2^−|t–s|. Once the response has been generated, we remove the covariate measurements at the response observation times from the observed covariate values. In this simulation, we set β₀=0.5 and β₁=1.5 and assess the performance of ${\widehat{\beta }}_1$. The results are very similar for other choices of βs. Under a logistic regression model for a binary response, the simulation set-up is similar to that for the continuous response except that the link function is g(x)=exp(x)/{1+exp(x)} and the response variable is generated through Y(t)=I(Unif(0,1)⩽1/[1+exp{−β₀−X(t)β₁}]).

On the basis of our theory, we use different bandwidths in the range of (n^−1/5,n⁻¹ when solving equation (3) to find ${\widehat{\beta }}_1$. The kernel function is the Epanechnikov kernel, which is K(x)=0.75(1 – x²)+. Similar results were obtained by using other kernels. We evaluate the accuracies of the asymptotic approximations by calculating the average bias, the average relative bias and the empirical standard deviation of ${\widehat{\beta }}_1$ across the 1000 data sets. We also calculate a model-based standard error and the corresponding 0.95 confidence interval based on the normal approximation. The automated bandwidth procedure that was described in Section 2 was also employed for estimation.

Table 1 summarizes the main results over 1000 simulations, where ‘auto’ means bandwidths based on the adaptive selection procedure, ‘BD’ represents different bandwidths, ‘Bias’ is the empirical bias, ‘RB’ is Bias divided by the true β₁, ‘SD’ is the sample standard deviation, ‘SE’ is the average of the standard error estimates and ‘CP’ represents the coverage probability of the 95% confidence interval for β₁. We observe that as the sample size increases the bias decreases and is small, that the empirical and model-based standard errors tend to agree reasonably well and that the coverage is close to the nominal 0.95-level. The performance improves with larger sample sizes.

Table 1.

Simulation results with time invariant coefficient for the linear and logistic models

n	BD	Results for linear regression model					Results for logistic regression model
		Bias	RB	SD	SE	CP (%)	Bias	RB	SD	SE	CP (%)
100	n −0.5	−0.056	−0.038	0.119	0.107	88	−0.069	−0.046	0.210	0.204	92
	n −0.6	−0.036	−0.024	0.125	0.111	90	−0.023	−0.015	0.255	0.241	92
	n −0.8	−0.014	−0.009	0.146	0.130	91	0.056	0.037	0.387	0.355	94
	n −0.9	−0.010	−0.007	0.163	0.146	91	0.110	0.073	0.494	0.445	94
	auto	−0.005	−0.003	0.159	0.141	90	0.083	0.055	0.457	0.396	92
400	n −0.5	−0.027	−0.018	0.063	0.061	92	−0.044	−0.030	0.133	0.132	94
	n −0.6	−0.016	−0.011	0.070	0.068	92	−0.013	−0.009	0.174	0.168	94
	n −0.8	−0.004	−0.003	0.101	0.096	92	0.043	0.029	0.308	0.292	94
	n −0.9	−0.004	−0.003	0.130	0.120	92	0.109	0.073	0.457	0.398	94
	auto	−0.002	−0.001	0.117	0.106	92	0.058	0.039	0.360	0.331	94
900	n −0.5	−0.024	−0.016	0.047	0.044	91	−0.029	−0.020	0.092	0.104	96
	n −0.6	−0.011	−0.007	0.053	0.052	94	−0.007	−0.005	0.123	0.139	97
	n −0.8	−0.001	−0.001	0.089	0.084	92	0.035	0.024	0.278	0.269	94
	n −0.9	−0.003	−0.002	0.116	0.112	93	0.090	0.060	0.389	0.386	96
	auto	0.006	0.004	0.096	0.096	95	0.055	0.037	0.361	0.308	92

4.2. Time-dependent coefficient

We next study the properties of the estimator for the time-dependent coefficient in model (2). We consider a wide range of functional forms, including β(t)=0.4t+0.5, β(t)=sin(2πt) and β(t)=t^1/2. The responses were generated from the model

$$Y\left(t\right)=0.5+X\left(t\right)\beta \left(t\right)+\epsilon \left(t\right).$$ (10)

The simulation set-up is identical to that in Section 4.1, except that we increase the Poisson intensity to 10. We employ the same bandwidth for the response and the covariate observation times. In addition to a fixed bandwidth, we also adopt a data-adaptive bandwidth selection procedure as described in Section 3.

The results (Table 2) are similar to those for the time-independent coefficient. For all functional forms of β(t), as the sample size increases, the bias is well controlled, the empirical and model-based standard errors agree reasonably well and the empirical coverage probability is close to the nominal 0.95-level. The performance tends to improve as the sample size increases. The empirical results appear to support the (nh₁h₂)^1/2 rate of convergence in theorem 2, with the empirical standard errors diminishing roughly proportionally to this rate.

Table 2.

Simulation results with time-dependent coefficient for linear regression

Model	t	Results for n = 400					Results for n = 900
		BD	RB	SD	SE	CP (%)	RB	SD	SE	CP (%)
β(t) = 0.4t + 0.5	0.1	n −1/2	−0.011	0.113	0.109	92	0.006	0.101	0.091	92
		auto	−0.004	0.105	0.111	95	−0.047	0.086	0.090	96
	0.3	n −1/2	−0.023	0.126	0.112	95	−0.004	0.095	0.094	94
		auto	0.009	0.114	0.103	96	−0.024	0.084	0.092	95
β(t)=√t	0.1	n −1/2	0.006	0.103	0.108	92	−0.025	0.084	0.094	96
		auto	0.003	0.105	0.111	95	−0.072	0.086	0.090	98
	0.3	n −1/2	−0.013	0.120	0.111	92	−0.005	0.112	0.096	95
		auto	0.011	0.114	0.103	96	−0.025	0.084	0.092	95
β(t)=sin (2πt)	0.1	n −1/2	−0.006	0.107	0.107	95	−0.006	0.114	0.094	91
		auto	−0.024	0.108	0.111	95	−0.024	0.096	0.091	95
	0.3	n −1/2	−0.016	0.115	0.125	92	−0.009	0.092	0.106	98
		auto	−0.012	0.120	0.101	96	−0.021	0.090	0.090	96

Similar results were obtained for a time-dependent logistic regression and have been omitted.

4.3. Comparison with last value carried forward method

In longitudinal studies, a naive approach to analysing asynchronous data is the last value carried forward method. If data at a certain time point are missing, then the observation at the most recent time point in the past is used in an analysis for synchronous data. It is well known that this method is theoretically biased. However, in practice, it is often employed, owing to its conceptual simplicity and ease of implementation. In this subsection, we study its performance in simulation studies under the time-independent coefficient model (1).

The simulation set-up is the same as in Section 4.1. For the last value carried forward procedure, in applying generalized estimating equations for synchronous data (Diggle et al., 2002), for a response observed at time t_ij, the covariate at time t_ij was taken to be the covariate observed at time s=max(x⩽t_ij, x∈{s_i1,…,s_imi}}). This corresponds to the most recent observation time relative to the response. For a response, if no covariate is observed before the response’s observation time, then the observed response is omitted from the analysis.

Table 3 summarizes the results based on linear and logistic link functions when β₁ = 1.5. The results for other choices of β₁ are very similar andwe omit the details. The bias is substantial and does not attenuate as the sample size increases. Because of decreasing variance, as the sample size increases, the coverage probability deteriorates. This is especially true for the logistic regression which has 0 coverage probability when the sample size n = 900.

Table 3.

Summary statistics by using the last value carried forward approach

n	Results for linear regression model					Results for logistic regression model
	Bias	RB	SD	SE	CP (%)	Bias	RB	SD	SE	CP (%)
100	−0.122	−0.081	0.094	0.091	73	−0.199	−0.133	0.113	0.174	78
400	−0.123	−0.082	0.046	0.047	24	−0.206	−0.137	0.054	0.087	33
900	−0.123	−0.082	0.032	0.031	3	−0.208	−0.138	0.032	0.058	0

5. Application to human immunodeficiency virus data

We now illustrate the proposed inferential procedures for models (1) and (2) with a comparison with the last value carried forward approach on data from the HIV study that was described in Section 1. A total of 190 HIV patients were followed from July 1997 to September 2002. Details of the study design, methods and medical implications are given in Wohl et al. (2005). During this study, all patients were scheduled to have their measurements taken during semiannual visits, with HIV viral load and CD4 cell counts obtained separately at different laboratories. Because many patients missed visits and the HIV infection occurred randomly during the study, there are unequal numbers of repeated measurements on viral load and CD4 cell count and there are different measurement times for the two variables. These data are sparse and purely asynchronous.

In our analysis, we took the CD4 cell counts as the covariate and HIV viral load as the response. Both CD4 cell count and HIV viral load are continuous variables with skewed distribution. As is customary, we log-transformed these variables before the analysis. Since the measurement timescale is not in Unif(0, 1), we use the interquantile range to do adjustment. We first fit model (1) with bandwidths h=2(Q₃–Q₁)n^−γ, where Q₃ is the 0.75-quantile and Q₁ is the 0.25-quantile of the pooled sample of measurement times for the covariate and response, n is the number of patients and γ=0.3, 0.5, 0.7. The time-independent coefficient model is

$$\mathrm{HIV}\left(t\right)={\beta }_0+{\beta }_1\mathrm{CD}4\left(t\right)+\epsilon \left(t\right).$$ (11)

Coefficient estimateswere obtained by the estimating equation (3) based on different bandwidths and data-driven bandwidth selection procedure, auto. For comparison, we also use the last value carried forward approach, lvcf, for coefficient estimation. The resulting estimates and standard errors are given in Table 4.

Table 4.

Summary statistics for ${\widehat{\beta }}_1$ based on model (11)

Parameter	Results for the following values of h(n−γ):
	289(n −0.3 )	101(n −0.5 )	35(n −0.7 )	134(auto)	lvcf
${\widehat{\beta }}_1$	−1.182	−1.130	−1.074	−1.178	0.003
$\mathrm{SE}\left({\widehat{\beta }}_1\right)$	0.685	0.832	1.143	0.816	1.806
z-value	−1.727	−1.359	−0.940	−1.444	0.0001

From Table 4, using the estimates from equation (3),we can clearly see the negative relationship between CD4 cell counts and HIV viral load, which has been verified in earlier medical studies. For different choices of bandwidth, the point estimate does not change much, but the variance decreases as the bandwidth increases, as expected. Overall, on the basis of these analyses, there appears to be at least some evidence that CD4 cell count and HIV viral load are associated. In contrast, the last value carried forward approach suggests a very weak positive association, in a direction which is opposite to that observed in previous studies and in the current analysis using estimating equation (3).

To investigate whether the relationship between CD4 cell counts and HIV viral load varies over time, we fit the varying-coefficient model

$$\mathrm{HIV}\left(t\right)={\beta }_0+{\beta }_1\left(t\right)\mathrm{CD}4\left(t\right)+\epsilon \left(t\right).$$ (12)

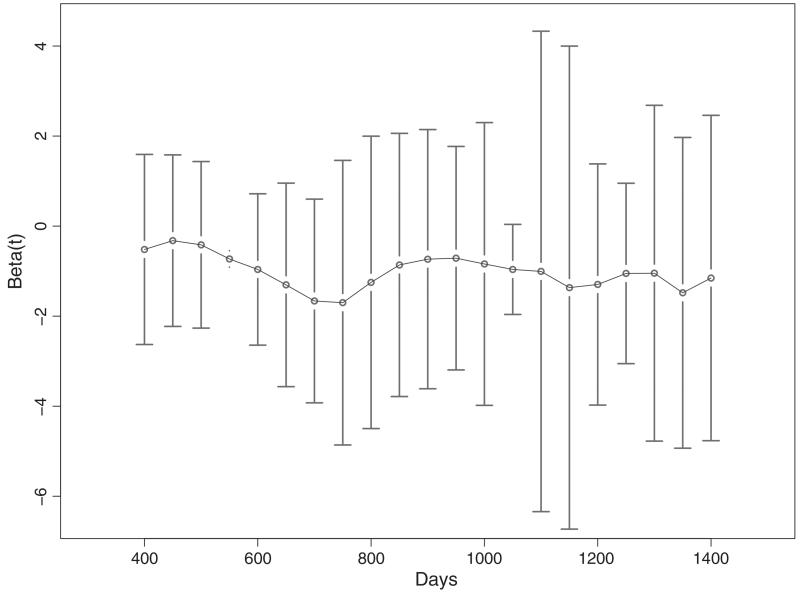
In Fig. 2, we depict the coefficient estimates and 95% confidence intervals based on automatic bandwidth selection. From the plot, we see that the negative association is relatively constant over time and comparable in magnitude with that obtained under model (11). The pointwise intervals cover 0 at all time points. The results seem to support the use of a simpler model based on an assumption of time-independent regression parameters.

Fig. 2.

Trajectory of time varying coefficient estimation with a data-adaptive bandwidth based on model (12): h = 102 days

To check conditions 1 and 1′ on the observation intensity, one may construct plots of the observation times. For condition 1, a histogram (which has been omitted) of the differences between T_ij and the closest S_ik was roughly normal and centred near 0, suggesting that the assumption holds in this data set. For condition 1′, we plotted T_ij versus S_ik (which has been omitted) and found that, for time points between 400 and 1400, there was sufficient information on the diagonal where s=t to permit estimation of β(t).

6. Concluding remarks

In this paper, we proposed kernel-weighted estimating equations for generalized linear models with asynchronous longitudinal data. The methods include estimators for models with either time invariant coefficient β or time-dependent coefficient β(t). The procedureswere developed by extending the univariate counting process framework for the observation process for synchronous data to a bivariate counting process set-up that is appropriate for asynchronous data. The resulting theory demonstrates that the rates of convergence that are achieved with asynchronous data are generally slower than those achieved with synchronous data and that, even under the time-independent model (1), parametric rates of convergence are not achievable.

To borrow information from nearby points, we require the covariance function of X(t) to be twice continuously differentiable for t=s. These assumptions are sufficient for our theoretical arguments and are similar to those required for synchronous data for estimation of β(t), where at least some smoothness of X(t) is needed. One may relax the continuous differentiability assumption such that the covariance function of X(t) is continuously differentiable from either the left-hand or right-hand side. This relaxation allows a more general class of X(t), including processes with independent increments, such as Poisson processes and Brownian motion. The trade-off is that the resulting kernel-weighted estimators will have an asymptotic bias which is of the order h instead of h² as stated in theorem 1, and the resulting convergence rates and optimal bandwidths may differ. The theoretical justification for these results requires non-trivial modifications of the proofs in this paper and are left for further research.

Global approaches like functional data analysis (Yao et al., 2005; Sentürk and Muller, 2010) or basis approximations (Zhou et al., 2008) for synchronized data provide added structure for incorporating correlation between observations in the estimation procedure. The extension to asynchronous data does not appear to have been studied in the literature. Given the slow rates of convergence for the local method, the extent to which global methods will improve efficiency is unclear. Additional assumptions may be required to achieve such gains and may be more restrictive than the minimal set of conditions that are specified in theorems 1 and 2. A deeper investigation of these issues is clearly warranted but is beyond the scope of the current paper.

In this paper, we did not consider the partially time-dependent model, in which some coefficients are time invariant and some coefficients are time dependent. As in earlier work on this model with synchronous data, a two-step procedure may be useful for estimation. This merits further investigation.

The asymptotic theory for $\widehat{\beta }\left(t\right)$ under model (2) in Section 3 is pointwise. The construction of simultaneous confidence intervals and hypothesis tests for the time-dependent coefficients would be useful in applications, like the HIV study. This requires a careful theoretical study of the uniform convergence properties of the estimator like in Zhou and Wu (2010). Future work is planned.

Appendix A

In this appendix, we provide details on the proofs of theorem 1 and theorem 2. Our main tools are empirical processes and central limit theorems.

A.1. Proof of theorem 1

The key idea is to establish the relationship

$$\begin{array}{cc}\hfill \underset{\mid \beta -{\beta }_0\mid <M{\left(\mathit{nh}\right)}^{-1∕2}}{\sup }\mid {\left(\mathit{nh}\right)}^{1∕2}{U}_n\left(\beta \right)-{\left(\mathit{nh}\right)}^{1∕2}& \left[U_n\right({\beta }_0)-E\{U_n\left({\beta }_0\right)\left\}\right]-{\left(\mathit{nh}\right)}^{1∕2}A\left({\beta }_0\right)(\beta -{\beta }_0)\mid \hfill \\ \hfill & ={\mathit{Cn}}^{1∕2}{h}^{5∕2}+o_p\left(n^{1∕2}{h}^{5∕2}\right)+o_p\{1+{\left(\mathit{nh}\right)}^{1∕2}\mid \beta -{\beta }_0\mid \},\hfill \end{array}$$ (13)

where A(β₀) is given in theorem 1 and

$$\begin{array}{cc}\hfill C=& {\int }_z{z}^{2}K\left(z\right)[2^{-1}{\int }_s{\phantom{\mid }\frac{\partial {\lambda }^2(x,s)}{\partial x^2}\mid }_{x=s}\left\{F_{{\beta }_0}\right(s,0)-F_{\beta }(s,0\left)\right\}\mathrm{d}s\phantom{]}\hfill \\ \hfill & +\phantom{[}{\int }_s\left\{{\phantom{\mid }\frac{\partial \lambda (x,s)}{\partial x}\mid }_{x=s}{\phantom{\mid }\frac{\partial F_{{\beta }_0}(s,y)}{\partial y}\mid }_{y=0}+2^{-1}\lambda (s,s){\phantom{\mid }\frac{\partial F_{{\beta }_0}^2(s,y)}{\partial y^2}\mid }_{y=0}\right\}\mathrm{d}s]\mathrm{d}z,\hfill \end{array}$$

where F_β(s, y)=E[X(s) g{X(s + y)^Tβ}]. To obtain result (13), first, using ${\mathcal{P}}_n$ and $\mathcal{P}$ to denote the empirical measure and true probability measure respectively, we obtain

$$\begin{array}{cc}\hfill {\left(\mathit{nh}\right)}^{1∕2}{U}_n\left(\beta \right)=& {\left(\mathit{nh}\right)}^{1∕2}({\mathcal{P}}_n-\mathcal{P})\left(\int \int K_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\mathrm{d}N(t,s)\right)\hfill \\ \hfill & +{\left(\mathit{nh}\right)}^{1∕2}E\left(\int \int K_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\mathrm{d}N(t,s)\right)\hfill \\ \hfill =& \mathrm{I}+\mathrm{II}\hfill \end{array}$$ (14)

For the second term on the right-hand side of equation (14), we have

$$\begin{array}{cc}\hfill & \mathrm{II}={\left(\mathit{nh}\right)}^{1∕2}\int \int K_h(t-s)\left(E\right[X\left(s\right)g\left\{X{\left(t\right)}^{\mathrm{T}}{\beta }_0\right\}]-E[X\left(s\right)g\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}\left]\right)\lambda (t,s)\mathrm{d}t\mathrm{d}s\hfill \\ \hfill & ={\left(\mathit{nh}\right)}^{1∕2}\int \int K\left(z\right)\left(E\right[X\left(s\right)g\left\{X{(s+\mathit{hz})}^{\mathrm{T}}{\beta }_0\right\}]-E[X\left(s\right)g\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}\left]\right)\lambda (s+\mathit{hz},s)\mathrm{d}s\mathrm{d}z.\hfill \end{array}$$

Recall that F_β0(s, hz) = E[X(s) g{X(s + hz)^Tβ₀}]. Using condition 3 and after the Taylor series expansion of F_β0 (s, hz), since ∫ z K(z) dz = 0 and ∫ K(z) dz = 1, we obtain

$$\begin{array}{cc}\hfill \mathrm{II}=& {\left(\mathit{nh}\right)}^{1∕2}{\int }_s\left(E\right[X\left(s\right)g\left\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\right\}]-E[X\left(s\right)g\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}\left]\right)\lambda (s,s)\mathrm{d}s\hfill \\ \hfill & +({\int }_z{z}^{2}K\left(z\right)[2^{-1}{\int }_s{\phantom{\mid }\frac{\partial {\lambda }^2(x,s)}{\partial x^2}\mid }_{x=s}\left\{F_{{\beta }_0}\right(s,0)-F_{\beta }(s,0\left)\right\}\mathrm{d}s\phantom{]}\phantom{)}\hfill \\ \hfill & +\phantom{(}\phantom{[}{\int }_s\left\{{\phantom{\mid }\frac{\partial \lambda (x,s)}{\partial x}\mid }_{x=s}{\phantom{\mid }\frac{\partial F_{{\beta }_0}(s,y)}{\partial y}\mid }_{y=0}+2^{-1}\lambda (s,s){\phantom{\mid }\frac{\partial F_{{\beta }_0}^2(s,y)}{\partial y^2}\mid }_{y=0}\right\}\mathrm{d}s]\mathrm{d}z)n^{1∕2}{h}^{5∕2}+o_p\left(n^{1∕2}{h}^{5∕2}\right).\hfill \end{array}$$ (15)

We then extract the main terms

$$\begin{array}{cc}\hfill \mathrm{II}& =-{\left(\mathit{nh}\right)}^{1∕2}{\int }_{s}E\left[X\right(s\left)g^{\prime }\right\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\left\}X{\left(s\right)}^{\mathrm{T}}\right]\lambda (s,s)\mathrm{d}s(\beta -{\beta }_0)+{\mathit{Cn}}^{1∕2}{h}^{5∕2}+o_p\left(n^{1∕2}{h}^{5∕2}\right)+{\left(\mathit{nh}\right)}^{1∕2}o(\mid \beta -{\beta }_0\mid )\hfill \\ \hfill & \equiv -{\left(\mathit{nh}\right)}^{1∕2}A\left({\beta }_0\right)(\beta -{\beta }_0)+{\mathit{Cn}}^{1∕2}{h}^{5∕2}+o_p\left(n^{1∕2}{h}^{5∕2}\right)+{\left(\mathit{nh}\right)}^{1∕2}o(\mid \beta -{\beta }_0\mid ).\hfill \end{array}$$ (16)

Moreover, if γ^T A(β₀)γ =0, then γ^T X(s)=0 almost surely for $s\in \mathcal{G}$, so γ =0 from condition 2. Thus, A(β₀) is a positive definite matrix, and thus non-singular. For the first term on the right-hand side of equation (14), we consider the class of functions

$$\left\{\int \int h^{1∕2}{K}_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\mathrm{d}N(t,s):\mid \beta -{\beta }_0\mid <\epsilon \right\}$$

for a given constant ε. Note that the functions in this class are Lipschitz continuous in β and the Lipschitz constant is uniformly bounded by

$$M_1=\underset{\mid \beta -{\beta }_0\mid <\epsilon }{\sup }\int \int h^{1∕2}{K}_h(t-s){\Vert X\left(s\right)\Vert }^2\Vert g^{\prime }\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}\Vert \mathrm{d}N(t,s).$$

Since, by condition 3,

$$M_1^2⩽{(\Vert {\beta }_0\Vert +\epsilon )}^2\int \int h{K}_h{(t-s)}^2{\Vert X\left(s\right)\Vert }^{4}q{\{\Vert X(s)\Vert \}}^2\mathrm{d}N(t,s)N(\tau ,\tau ),$$

we have

$$\begin{array}{cc}\hfill E[M_1^2\mid N(\cdot ,\cdot \left)\right]& ⩽{(\Vert {\beta }_0\Vert +\epsilon )}^{2}N(\tau ,\tau )\int \int h{K}_h{(t-s)}^{2}E\left[{\Vert X\left(s\right)\Vert }^{4}q{\{\Vert X(s)\Vert \}}^2\right]\mathrm{d}N(t,s)\hfill \\ \hfill & ⩽M_{2}N(\tau ,\tau )\int \int h{K}_h{(t-s)}^2\mathrm{d}N(t,s)\hfill \end{array}$$

for some constant M₂. Conditionally on N(τ, τ), E{∫ ∫ h K_h(t - s)² dN(t, s)|N(τ, τ)} can be easily verified to be finite. Therefore, $E\left(M_1^2\right)$ is finite. Therefore, this class is a P-Donsker class by the Jain–Marcus theorem (van der Vaart and Wellner, 1996). As the result, we obtain that the first term on the right-hand side of equation (14) for |β–β₀| < M(nh)^−1/2 is equal to

$$\begin{array}{cc}\hfill {\left(\mathit{nh}\right)}^{1∕2}({\mathcal{P}}_n-\mathcal{P})\left(\int \int K_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\mathrm{d}N(t,s)\right)+o_p\left(1\right)& \hfill \\ \hfill ={\left(\mathit{nh}\right)}^{1∕2}\left[U_n\right({\beta }_0)-E\{& U_n\left({\beta }_0\right)\left\}\right]+o_p\left(1\right).\hfill \end{array}$$ (17)

Combining equations (15) and (17) and by condition 4, we obtain result (13).

Consequently,

$${\left(\mathit{nh}\right)}^{1∕2}A\left({\beta }_0\right)(\widehat{\beta }-{\beta }_0)+{\mathit{Cn}}^{1∕2}{h}^{5∕2}+o_p\left(n^{1∕2}{h}^{5∕2}\right)+o_p\{1+{\left(\mathit{nh}\right)}^{1∕2}\mid \widehat{\beta }-{\beta }_0\mid \}={\left(\mathit{nh}\right)}^{1∕2}\left[U_n\right({\beta }_0)-E\{U_n\left({\beta }_0\right)\left\}\right].$$ (18)

In contrast, following a similar argument to that before, we can calculate

$$\Sigma =\mathrm{var}\left(\int \int h^{1∕2}{K}_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\mathrm{d}N(t,s)\right)$$

as follows:

$$\begin{array}{cc}\hfill \Sigma =& hE\left[\phantom{\{}\mathrm{var}\{\int \int k_h(t-s)X\left(s\right)Y\left(t\right)\mathrm{d}N(t,s)\mid X\left(s\right),s\in [0,\tau ];N(t,s),(t,s)\in {[0,\tau ]}^{\otimes 2}\}\right]\hfill \\ \hfill & +h\mathrm{var}\left(\int \int K_h(t-s)X\left(s\right)\left[g\right\{X{\left(t\right)}^{\mathrm{T}}{\beta }_0\}-g\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\mathrm{d}N(t,s)\right)\hfill \\ \hfill =& hE(\phantom{\{}\int \int \int \int K_h(t_1-s_1)K_h(t_2-s_2)X\left(s_1\right)X{\left(s_2\right)}^{\mathrm{T}}\left[r\right\{t_1,t_2,X\left(t_1\right),X\left(t_2\right)\}\phantom{)}\hfill \\ \hfill & \phantom{(}+g\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right\}g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right\}\left]\mathrm{d}N\right(t_1,s_1\left)\mathrm{d}N\right(t_2,s_2))-hE\left({\left[\int \int K_h(t-s)X\left(s\right)g\left\{X{\left(t\right)}^{\mathrm{T}}{\beta }_0\right\}\mathrm{d}N(t,s)\right]}^2\right)\hfill \\ \hfill & +hE(\int \int \int \int K_h(t_1-s_1)K_h(t_2-s_2)X\left(s_1\right)X{\left(s_2\right)}^{\mathrm{T}}\left[g\right\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\}-g\{X{\left(s_1\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\phantom{)}\hfill \\ \hfill & \phantom{(}\times \left[g\right\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\}-g\{X{\left(s_2\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\mathrm{d}N(t_1,s_1)\mathrm{d}N(t_2,s_2))\hfill \\ \hfill & -h{\left\{\int \int K_h(t-s)E\left(X\right(s\left)\right[g\left\{X{\left(t\right)}^{\mathrm{T}}{\beta }_0\right\}-g\left\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\right\}\left]\right)\lambda (t,s)\mathrm{d}t\mathrm{d}s\right\}}^2\hfill \\ \hfill =& {\mathrm{I}}_1-{\mathrm{I}}_2+{\mathrm{I}}_3-{\mathrm{I}}_4.\hfill \end{array}$$

Using conditioning arguments, we obtain

$$\begin{array}{cc}\hfill {\mathrm{I}}_1=& h{\int }_{t_1\ne t_2}{\int }_{s_1\ne s_2}{K}_h(t_1-s_1)K_h(t_2-s_2)E\left(X\right(s_1\left)X{\left(s_2\right)}^{\mathrm{T}}\right[r\{t_1,t_2,X(t_1),X(t_2\left)\right\}\hfill \\ \hfill & +g\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right\}g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right\}\left]\right)f(t_1,t_2,s_1,s_2)\lambda (t_2,s_2)\mathrm{d}{t}_1\mathrm{d}{s}_1\mathrm{d}{t}_2\mathrm{d}{s}_2\hfill \\ \hfill & +h{\int }_{t_1}{\int }_{s_1\ne s_2}{K}_h(t_1-s_1)K_h(t_1-s_2)E\left(X\right(s_1\left)X{\left(s_2\right)}^{\mathrm{T}}\right[{\sigma }^2\{t_1,X(t_1\left)\right\}\hfill \\ \hfill & +g{\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right\}}^2\left]\right)f(t_1,t_1,s_1,s_2)\lambda (t_1,s_2)\mathrm{d}{t}_1\mathrm{d}{s}_1\mathrm{d}{s}_2\hfill \\ \hfill & +h{\int }_{t_1\ne t_2}{\int }_{s_1}{K}_h(t_1-s_1)K_h(t_2-s_1)E\left(X\right(s_1\left)X{\left(s_1\right)}^{\mathrm{T}}\right[r\{t_1,t_2,X(t_1),X(t_2\left)\right\}\hfill \\ \hfill & +g\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right\}g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right\}\left]\right)f(t_1,t_2,s_1,s_1)\lambda (t_2,s_1)\mathrm{d}{t}_1\mathrm{d}{s}_1\mathrm{d}{t}_2\hfill \\ \hfill & +h{\int }_{t_1}{\int }_{s_1}{K}_h{(t_1-s_1)}^{2}E\left(X\right(s_1\left)X{\left(s_1\right)}^{\mathrm{T}}\right[{\sigma }^2\{t_1,X(t_1\left)\right\}+g{\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right\}}^2\left]\right)\lambda (t_1,s_1)\mathrm{d}{t}_1\mathrm{d}{s}_1.\hfill \end{array}$$

After a change of variables and incorporating conditions 3 and 4, the first three terms in term I are all of order O(h) and the last term equals

$$\int K{\left(z\right)}^2\mathrm{d}z\int E\left(X\right(s\left)X{\left(s\right)}^{\mathrm{T}}\right[{\sigma }^2\{s,X(s\left)\right\}+g{\left\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\right\}}^2\left]\right)\lambda (s,s)\mathrm{d}s.$$

So we have

$${\mathrm{I}}_1=\int K{\left(z\right)}^2\mathrm{d}z\int E\left(X\right(s\left)X{\left(s\right)}^{\mathrm{T}}\right[{\sigma }^2\{s,X(s\left)\right\}+g{\left\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\right\}}^2\left]\right)\lambda (s,s)\mathrm{d}s+O\left(h\right).$$ (19)

Similarly, it can be shown that

$${\mathrm{I}}_2=\int K{\left(z\right)}^2\mathrm{d}z\int E\left[X\right(s\left)X{\left(s\right)}^{\mathrm{T}}g{\left\{X{\left(s\right)}^{\mathrm{T}}{\beta }_0\right\}}^2\right]\lambda (s,s)\mathrm{d}s+O\left(h\right)$$ (20)

and I₃ – I₄ =O(h²). Therefore, we have

$$\Sigma =\int K{\left(z\right)}^2\mathrm{d}z\int E\left\{X\right(s\left)X{\left(s\right)}^{\mathrm{T}}\right\}\sigma {\{s,X(s\left)\right\}}^2\lambda (s,s)\mathrm{d}s.$$ (21)

To prove the asymptotic normality, we verify the Lyapunov condition. Define

$${\psi }_i={\left(\mathit{nh}\right)}^{1∕2}{n}^{-1}\int \int K_h(t-s)X_i\left(s\right)\left[Y_i\right(t)-g\{X_i{\left(s\right)}^{\mathrm{T}}{\beta }_0\left\}\right]\mathrm{d}{N}_i(t,s).$$

Similarly to the calculation of Σ,

$$\sum _{i=1}^{n}E\left\{{\mid {\psi }_i-E\left({\psi }_i\right)\mid }^3\right\}=nO\left\{{\left(\mathit{nh}\right)}^{3∕2}{n}^{-3}{h}^{-2}\right\}=O\left\{{\left(\mathit{nh}\right)}^{-1∕2}\right\}.$$

Therefore,

$${\left(\mathit{nh}\right)}^{1∕2}\left[U_n\right({\beta }_0)-E\{U_n\left({\beta }_0\right)\left\}\right]\underset{\mathrm{d}}{\to }N(0,\Sigma ).$$ (22)

Combining with equation (18), we finish the proof of theorem 1.

A.2. Proof of corollary 2

We next show the consistency of the variance estimate. To begin with, we have

$$\frac{\partial U_n\left(\beta \right)}{\partial \beta }=n^{-1}\sum _{i=1}^n\int \int K_n(t-s)X_i\left(s\right)[-g^{\prime }\{X_i{\left(s\right)}^{\mathrm{T}}\beta \left\}{X}_i{\left(s\right)}^{\mathrm{T}}\right]\mathrm{d}{N}_i(t,s).$$ (23)

Using a similar argument to that to obtain equation (17), we show that

$$\left\{\int \int K_n(t-s)X_i\left(s\right)[-g^{\prime }\{X_i{\left(s\right)}^{\mathrm{T}}\beta \left\}{X}_i{\left(s\right)}^{\mathrm{T}}\right]\mathrm{d}{N}_i(t,s):\mid \beta -{\beta }_0\mid <\epsilon \right\}$$

is a P-Glivenko–Cantelli class. Therefore,

$$\underset{\mid \beta -{\beta }_0\mid <\epsilon }{\sup }{\mid \frac{\partial U_n\left(\beta \right)}{\partial \beta }\mid }_{\beta =\widehat{\beta }}-E\{\phantom{\{}{\phantom{\mid }\frac{\partial U_n\left(\beta \right)}{\partial \beta }\mid }_{\beta =\widehat{\beta }}\}\mid \to 0$$

in probability. Since $\widehat{\beta }$ is consistent for β₀, by the continuous mapping theorem, $\partial U_n\left(\beta \right)∕\partial \beta {\mid }_{\beta =\widehat{\beta }}$ converges in probability to −A(β₀). Similarly, let

$$\tilde{\Sigma }\left(\beta \right)=\frac{1}{n^2}\sum _{i=1}^n{\left(\int \int K_h(t-s)X_i\left(s\right)\left[Y_i\right(t)-g\{X_i{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\right)}^{\otimes 2};$$

then ${\sup }_{\mid \beta -{\beta }_0\mid <\epsilon }\mid \tilde{\Sigma }\left(\beta \right)-E\left\{\tilde{\Sigma }\right(\beta \left)\right\}\mid \to 0$ in probability. However,

$$E\left\{\tilde{\Sigma }\right(\beta \left)\right\}=\frac{1}{n}E{\left(\int \int K_h(t-s)X\left(s\right)\left[Y\right(t)-g\{X{\left(s\right)}^{\mathrm{T}}\beta \left\}\right]\right)}^{\otimes 2}.$$

After a change of variables, and by condition 3,

$$\begin{array}{cc}\hfill E\left\{\tilde{\Sigma }\right(\beta \left)\right\}=& \frac{1}{\mathit{nh}}\int \int \left\{K{\left(z\right)}^{2}E\right(X\left(s\right)[\sigma {\{s+\mathit{hz},X(s+\mathit{hz}\left)\right\}}^2+g{\left\{X{(s+\mathit{hz})}^{\mathrm{T}}\beta \right\}}^2\hfill \\ \hfill & -2g\left\{X{(s+\mathit{hz})}^{\mathrm{T}}\beta \right\}g\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}+g{\left\{X{\left(s\right)}^{\mathrm{T}}\beta \right\}}^2\left]X{\left(s\right)}^{\mathrm{T}}\right)\lambda (s,s)+o\left(h\right)\}\mathrm{d}s\mathrm{d}z\hfill \\ \hfill =& \frac{1}{\mathit{nh}}\left\{\int \int K{\left(z\right)}^{2}E\left[X\right(s\left)\sigma {\{s,X(s\left)\right\}}^{2}X{\left(s\right)}^{\mathrm{T}}\right]\lambda (s,s)\mathrm{d}z\mathrm{d}s+o\left(h\right)\right\}.\hfill \end{array}$$

Therefore,

$$\left(\mathit{nh}\right)\widehat{\Sigma }\stackrel{\mathrm{p}}{\to }\Sigma \text{as}\mathit{nh}\to \infty .$$

The consistency of the variance estimate follows.

A.3. Proof of theorem 2

Denote G(s₁, s₂)=E[X(t + s₁)g{X(t + s₂)^Tβ₀(t + s₂)} − X(t + s₁)g{X(t + s₁)^T β(t)}]. We first establish the relationship

$$\begin{array}{cc}\hfill \underset{\mid \beta \left(t\right)-{\beta }_0\left(t\right)\mid <M{\left({\mathit{nh}}_1{h}_2\right)}^{-1∕2}}{\sup }\mid {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}{U}_n\left\{\beta \right(t\left)\right\}-& {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}B\left\{{\beta }_0\right(t),t\}\left\{\beta \right(t)-{\beta }_0(t\left)\right\}\hfill \\ \hfill -{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left(U_n\right\{{\beta }_0\left(t\right)\}-E[U_n\left\{{\beta }_0\right(t\left)\right\}\left]\right)\mid =& {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left\{D_1\right(t)h_1^2+D_2(t)h_1{h}_2+D_3(t\left)h_2^2\right\}\hfill \\ \hfill & +o_p\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\right(h_1^2+h_1{h}_2+h_2^2\left)\right\}\hfill \\ \hfill & +o_p\{1+{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\mid \beta (t)-{\beta }_0(t)\mid \},\hfill \end{array}$$ (24)

where B{β₀(t), t} is defined in theorem 2,

$$\begin{array}{cc}\hfill D_1\left(t\right)=& \int \int K(z_1,z_2)\{{\phantom{\mid }\frac{\partial G(x,y)}{\partial x}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}{\phantom{\mid }\frac{\partial \lambda (x,y)}{\partial x}\mid }_{\begin{array}{c}x=t\hfill \\ y=t\hfill \end{array}}+2^{-1}G(0,0){\phantom{\mid }\frac{\partial {\lambda }^2(x,y)}{\partial x^2}\mid }_{\begin{array}{c}\hfill x=t\hfill \\ \hfill y=t\hfill \end{array}}\phantom{\}}\hfill \\ \hfill & \phantom{\{}+2^{-1}\lambda (t,t){\phantom{\mid }\frac{\partial G^2(x,y)}{\partial x^2}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}\}{z}_1^2\mathrm{d}{z}_1\mathrm{d}{z}_2,\hfill \\ \hfill D_2\left(t\right)=& \int \int K(z_1,z_2)\{{\phantom{\mid }\frac{\partial G(x,y)}{\partial x}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}{\phantom{\mid }\frac{\partial \lambda (x,y)}{\partial y}\mid }_{\begin{array}{c}x=t\hfill \\ y=t\hfill \end{array}}+{\phantom{\mid }\frac{\partial G(x,y)}{\partial y}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}{\phantom{\mid }\frac{\partial \lambda (x,y)}{\partial x}\mid }_{\begin{array}{c}\hfill x=t\hfill \\ \hfill y=t\hfill \end{array}}\phantom{\}}\hfill \\ \hfill & +\phantom{\{}G(0,0){\phantom{\mid }\frac{\partial {\lambda }^2(x,y)}{\partial x\partial y}\mid }_{\begin{array}{c}\hfill x=t\hfill \\ \hfill y=t\hfill \end{array}}+\lambda (t,t){\phantom{\mid }\frac{\partial G^2(x,y)}{\partial x\partial y}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}\}{z}_1{z}_2\mathrm{d}{z}_1\mathrm{d}{z}_2,\hfill \end{array}$$

and

$$D_3\left(t\right)=\int \int K(z_1,z_2)\left\{{\phantom{\mid }\frac{\partial G(x,y)}{\partial y}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}{\phantom{\mid }\frac{\partial \lambda (x,y)}{\partial y}\mid }_{\begin{array}{c}x=t\hfill \\ y=t\hfill \end{array}}+2^{-1}G(0,0){\phantom{\mid }\frac{\partial {\lambda }^2(x,y)}{\partial y^2}\mid }_{\begin{array}{c}\hfill x=t\hfill \\ \hfill y=t\hfill \end{array}}+2^{-1}\lambda (t,t){\phantom{\mid }\frac{\partial G^2(x,y)}{\partial y^2}\mid }_{\begin{array}{c}\hfill x=0\hfill \\ \hfill y=0\hfill \end{array}}\right\}{z}_2^2\mathrm{d}{z}_1\mathrm{d}{z}_2.$$

To obtain equation (24), first, using ${\mathcal{P}}_n$ and $\mathcal{P}$ to denote the empirical measure and true probability measure respectively, we have

$$\begin{array}{cc}\hfill {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}{U}_n\left\{\beta \right(t\left)\right\}=& {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}({\mathcal{P}}_n-\mathcal{P})\left(\int \int K_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)\left[Y\right(t_2)-g\{X{\left(t_1\right)}^{\mathrm{T}}\beta \left(t\right)\left\}\right]\mathrm{d}N(t_1,t_2)\right)\hfill \\ \hfill & +{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}E\left(\int \int K_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)\left[Y\right(t_2)-g\{X{\left(t_1\right)}^{\mathrm{T}}\beta \left(t\right)\left\}\right]\mathrm{d}N(t_1,t_2)\right)\hfill \\ \hfill =& \mathrm{I}+\mathrm{II}.\hfill \end{array}$$ (25)

For the second term on the right-hand side of equation (25), we have

$$\mathrm{II}={\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\int \int K_{h_1,h_2}(t_1-t,t_2-t)E\left(X\right(t_1\left)\right[g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right(t_2\left)\right\}-g\left\{X{\left(t_1\right)}^{\mathrm{T}}\beta \right(t\left)\right\}\left]\right)\lambda (t_1,t_2)\mathrm{d}{t}_1\mathrm{d}{t}_2.$$

Recall that G(s₁, s₂)=E[X(t + s₁) g{X(t + s₂)^Tβ₀(t + s₂/} − X(t + s₁) g{X(t + s₁)^T β(t)}] and we can do a Taylor series expansion of G around (0, 0). Taking into account conditions 3′ and 4′, and after a change of variables, we obtain

$$\begin{array}{cc}\hfill \mathrm{II}=& {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\int \int K(s_1,s_2)E\left(X\right(t\left)\right[g\left\{X{\left(t\right)}^{\mathrm{T}}{\beta }_0\right(t\left)\right\}-g\left\{X{\left(t\right)}^{\mathrm{T}}\beta \right(t\left)\right\}\left]\right)\lambda (t,t)\mathrm{d}{s}_1\mathrm{d}{s}_2\hfill \\ \hfill & +{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left\{D_1\right(t)h_1^2+D_2(t)h_1{h}_2+D_3(t\left)h_2^2\right\}+o_p\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\right(h_1^2+h_1{h}_2+h_2^2\left)\right\}\hfill \\ \hfill \equiv & -{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}B\left\{{\beta }_0\right(t),t\}\left\{\beta \right(t)-{\beta }_0(t\left)\right\}+{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left\{D_1\right(t)h_1^2+D_2(t)h_1{h}_2+D_3(t\left)h_2^2\right\}\hfill \\ \hfill & +o_p\{{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\mid \beta (t)-{\beta }_0(t)\mid \}+o_p\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\right(h_1^2+h_1{h}_2+h_2^2\left)\right\},\hfill \end{array}$$ (26)

where we did another Taylor series expansion of function g{X(t)^T β(t)} at X(t)^T β₀(t) for any fixed t.

For any fixed t, if γ^T B{β₀(t), t}γ=0, then γ^T X(t)=0, so γ=0 from condition 2′. Thus B{β₀(t), t} is a non-singular matrix. For term I, we consider the class of functions

$$\left\{{\left(h_1{h}_2\right)}^{1∕2}\int \int K_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)\left[Y\right(t_2)-g\{X{\left(t_1\right)}^{\mathrm{T}}\beta \left(t\right)\left\}\right]\mathrm{d}N(t_1,t_2):\mid \beta \left(t\right)-{\beta }_0\left(t\right)\mid <\epsilon \right\}$$

for a given constant ε. Similarly to the proof in theorem 1, we can show that this is a P-Donsker class for any fixed time point t by the Jain–Marcus theorem. We therefore obtain that the first term on the right-hand side of equation (25) for |β(t) – β₀(t)| < M(nh₁h₂)^−1/2 is equal to

$$\begin{array}{cc}\hfill {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}({\mathcal{P}}_n-\mathcal{P})\left(\int \int K_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)\left[Y\right(t_2)-g\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\right)& \mathrm{d}N(t_1,t_2)+o_p\left(1\right)\hfill \\ \hfill ={\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left(U_n\right\{{\beta }_0\left(t\right)\}-E[U_n& \left\{{\beta }_0\right(t\left)\right\}\left]\right)+o_p\left(1\right).\hfill \end{array}$$ (27)

Combining equations (25), (26) and (27) and, by condition 4′, we obtain equation (24). Therefore,

$$\begin{array}{cc}\hfill {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}B\left\{{\beta }_0\right(t),t\}\left\{\widehat{\beta }\right(t)-{\beta }_0(t\left)\right\}& +{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left\{D_1\right(t)h_1^2+D_2(t)h_1{h}_2+D_3(t\left)h_2^2\right\}\hfill \\ \hfill & +o_p\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\right(h_1^2+h_1{h}_2+h_2^2\left)\right\}+o_p\{1+{\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\mid \widehat{\beta }(t)-{\beta }_0(t)\mid \}\hfill \\ \hfill =& {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left(U_n\right\{{\beta }_0\left(t\right)\}-E[U_n\left\{{\beta }_0\right(t\left)\right\}\left]\right).\hfill \end{array}$$

Now we show that (nh₁h₂)^1/2 U_n{β₀(t)} follows the central limit theorem. In other words, we wish to derive the distribution of

$$\begin{array}{cc}\hfill {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}& \{n^{-1}\sum _{i=1}^n\int \int K_{h_1,h_2}(t_1-t,t_2-t)X_i\left(t_1\right)\left[Y_i\right(t_2)-g\{X_i{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\mathrm{d}{N}_i(t_1,t_2)\phantom{\}}\hfill \\ \hfill & \phantom{\{}-n^{-1}\sum _{i=1}^{n}E\left(\int \int {\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)X_i\left(t_1\right)\left[Y_i\right(t_2)-g\{X_i{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\mathrm{d}{N}_i(t_1,t_2)\right)\}.\hfill \end{array}$$ (28)

For convenience, we denote the above sum as $n^{1∕2}{n}^{-1}{\Sigma }_{i=1}^n{W}_i\left(t\right)$, where

$$W_i\left(t\right)=\int \int {\left(h_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)X_i\left(t_1\right)\left[Y_i\right(t_2)-g\{X_i{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\mathrm{d}{N}_i(t_1,t_2)-E\left(\int \int {\left(h_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)X_i\left(t_1\right)\left[Y_i\right(t_2)-g\{X_i{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\mathrm{d}{N}_i(t_1,t_2)\right).$$ (29)

Since this is an independent and identically distributed sum, we need to calculate only Σ*(t)=var{W₁(t)}. We have

$$\begin{array}{cc}\hfill \mathrm{var}\left\{W_1\right(t\left)\right\}=& E\left[\mathrm{var}\right\{W_1\left(t\right)\mid X\left(s\right),s\in [0,\tau ];N(t,s),(t,s)\in {[0,\tau ]}^{\otimes 2}\left\}\right]\hfill \\ \hfill & +\mathrm{var}\left[E\right\{W_1\left(t\right)\mid X\left(s\right),s\in [0,\tau ];N(t,s),(t,s)\in {[0,\tau ]}^{\otimes 2}\left\}\right].\hfill \end{array}$$

Similarly to calculation of the order of Σ, we obtain

$$\begin{array}{cc}\hfill E\left[\mathrm{var}\right\{& W_1\left(t\right)\mid X\left(s\right),s\in [0,\tau ];N(t,s),(t,s)\in {[0,\tau ]}^{\otimes 2}\left\}\right]\hfill \\ \hfill =& E\left[\mathrm{var}\left\{\phantom{\mid }\int \int {\left(h_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)Y\left(t_2\right)\mathrm{d}N(t_1,t_2)\mid X\left(s\right),s\in [0,\tau ];N(t,s)\in {[0,\tau ]}^{\otimes 2}\right\}\right]\hfill \\ \hfill =& \int \int \int \int h_1{h}_2{K}_{h_1,h_2}(t_1-t,t_2-t)K_{h_1,h_2}(s_1-t,s_2-t)E\left(X\right(t_1\left)X{\left(s_1\right)}^{\mathrm{T}}\right[r\{s_2,t_2,X(s_2),X(t_2\left)\right\}\hfill \\ \hfill & +g\left\{X{\left(s_2\right)}^{\mathrm{T}}{\beta }_0\right\}g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right\}\left]\right)E\left\{\mathrm{d}N\right(t_1,t_2\left)\mathrm{d}N\right(s_1,s_2\left)\right\}-\int \int \int \int h_1{h}_2{K}_{h_1,h_2}(t_1-t,t_2-t)\hfill \\ \hfill & \times K_{h_1,h_2}(s_1-t,s_2-t)E\left[X\right(t_1\left)X{\left(s_1\right)}^{\mathrm{T}}g\right\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}g\right\{X{\left(s_2\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]E\left\{\mathrm{d}N\right(t_1,t_2\left)\mathrm{d}N\right(s_1,s_2\left)\right\}\hfill \\ \hfill & =\int \int K{(z_1,z_2)}^2\mathrm{d}{z}_1\mathrm{d}{z}_{2}E\left[X\right(t\left)X{\left(t\right)}^{\mathrm{T}}\sigma {\{t,X(t\left)\right\}}^2\right]\lambda (t,t)+O\left\{h_1{h}_2\right(h_1+h_2\left)\right\},\hfill \end{array}$$

by conditions 4′ and 5′ and a change of variables. Similarly to the proof of theorem 1, we have

$$\begin{array}{cc}\hfill \mathrm{var}[E& \left\{W_1\right(t)\mid X(s),s\in [0,\tau ],N_i(t,s),(t,s)\in {[0,\tau ]}^{\otimes 2}\}]\hfill \\ \hfill & =\mathrm{var}\left(\int \int {\left(h_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)X\left(t_1\right)\left[g\right\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\left(t_2\right)\}-g\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]\mathrm{d}N(t_1,t_2)\right)\hfill \\ \hfill & =E\int \int h_1{h}_2{K}_{h_1,h_2}{(t_1-t,t_2-t)}^{2}X\left(t_1\right)X{\left(t_1\right)}^{\mathrm{T}}{\left[g\right\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\left(t_2\right)\}-g\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\left(t\right)\left\}\right]}^2\mathrm{d}N(t_1,t_2)+O\left(h_1{h}_2\right)-{\left\{\int \int {\left(h_1{h}_2\right)}^{1∕2}{K}_{h_1,h_2}(t_1-t,t_2-t)E\left(X\right(t_1\left)\right[g\left\{X{\left(t_2\right)}^{\mathrm{T}}{\beta }_0\right(t_2\left)\right\}-g\left\{X{\left(t_1\right)}^{\mathrm{T}}{\beta }_0\right(t\left)\right\}\left]\right)\times \lambda (t_1,t_2)\mathrm{d}{t}_1\mathrm{d}{t}_2\right\}}^2\hfill \\ \hfill & =O(h_1^2+h_1{h}_2+h_2^2).\hfill \end{array}$$

Therefore, we have

$${\Sigma }^{\ast }\left(t\right)=\int \int K{(z_1,z_2)}^2\mathrm{d}{z}_1\mathrm{d}{z}_{2}E\left[X\right(t\left)X{\left(t\right)}^{\mathrm{T}}\sigma {\{t,X(t\left)\right\}}^2\right]\lambda (t,t).$$ (30)

Similarly, we have

$$\sum _{i=1}^{n}E\left\{{\mid W_i-E\left(W_i\right)\mid }^3\right\}=nO\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{3∕2}{n}^{-3}{n}^{-3}{\left(h_1{h}_2\right)}^{-2}\right\}=O\left\{{\left({\mathit{nh}}_1{h}_2\right)}^{-1∕2}\right\},$$

which verifies that the Lyapunov condition holds.

Thus

$${\left({\mathit{nh}}_1{h}_2\right)}^{1∕2}\left(U_n\right\{{\beta }_0\left(t\right)\}-E[U_n\left\{{\beta }_0\right(t\left)\right\}\left]\right)\underset{\mathrm{d}}{\to }N\{0,{\Sigma }^{\ast }(t\left)\right\}.$$ (31)

Combining with equation (24), the conclusion of theorem 2 holds.

A.4. Proof of corollary 4

The consistency of the variance estimate can similarly be shown as in the proof of corollary 2 and we omit the details.