A longitudinal model for disease progression was developed and applied to multiple sclerosis

Abstract

Objectives

To develop a model of disease progression using multiple sclerosis (MS) as an exemplar.

Study Design and Settings

Two observational cohorts, the University of Wales MS (UoWMS), UK (1976), and British Columbia MS (BCMS) database, Canada (1980), with longitudinal disability data [the Expanded Disability Status Scale (EDSS)] were used; individuals potentially eligible for MS disease-modifying drugs treatments, but who were unexposed, were selected. Multilevel modeling was used to estimate the EDSS trajectory over time in one data set and validated in the other; challenges addressed included the choice and function of time axis, complex observation-level variation, adjustments for MS relapses, and autocorrelation.

Results

The best-fitting model for the UoWMS cohort (404 individuals, and 2,290 EDSS observations) included a nonlinear function of time since onset. Measurement error decreased over time and ad hoc methods reduced autocorrelation and the effect of relapse. Replication within the BCMS cohort (978 individuals and 7,335 EDSS observations) led to a model with similar time (years) coefficients, time [0.22 (95% confidence interval {CI}: 0.19, 0.26), 0.16 (95% CI: 0.10, 0.22)] and log time [−0.13 (95% CI: −0.39, 0.14), −0.15 (95% CI: −0.70, 0.40)] for BCMS and UoWMS, respectively.

Conclusion

It is possible to develop robust models of disability progression for chronic disease. However, explicit validation is important given the complex methodological challenges faced.

What is new?

• •Considering different functions of time to find the best-fitting trajectory of the Expanded Disability Status Scale (EDSS).
• •Accounting for nonconstant measurement error in the multilevel model of EDSS.
• •Adjusting data to avoid including the potential confounding effects of short-term disease fluctuations (i.e., multiple sclerosis relapses) on an individual's background longer-term disability outcomes.
• •Investigating autocorrelation and suitable approaches to minimize this.
• •Replicating and cross-validating the model in an independent cohort.

1. Introduction

Prognostic models for chronic diseases [1] are needed to guide management decisions and counseling of patients and their families. Such models can consider outcomes ranging from treatment response to changes in disability [2], [3], [4] and may model individual disease trajectories. This poses technical challenges because progression may be nonlinear, the outcome measure(s) may not be continuous or normally distributed, and individuals may have been observed a different number of times and at irregular intervals.

One example in which modeling long-term trajectories poses challenges is multiple sclerosis (MS). MS is a chronic inflammatory neurodegenerative disorder, with considerable interindividual variation in the disease course. Most patients present with relapsing-remitting MS (RRMS), in which symptoms appear for a varying amount of time and then disappear (either partially or completely). However, over time individuals with RRMS can progress to secondary progressive MS (SPMS), where the frequency of relapses decreases and the accumulation of disability increases steadily [5].

Disability in individuals with MS is commonly measured using the Expanded Disability Status Scale (EDSS) [6]. EDSS is an ordinal scale, based on a neurologist's examination, ranging from 0 (normal neurologic examination) to 10 (death due to MS) in half unit increments (but there is no score of 0.5). Previous studies of EDSS progression have used survival analysis [7], [8], [9], considering the time to specific milestones, for example, an EDSS score of 6, which is equivalent to needing an aid to walk. This ignores available data both before and after reaching the milestone and therefore fails to differentiate two individuals reaching a milestone at the same time but with different trajectories.

Empirical percentiles derived at yearly intervals and data-smoothing techniques have been used to create disability curves over time at different percentiles [10], [11]. These methods do not model how a given individual changes over time or the relationship between the centiles and patient characteristics.

Markov models have been used to relate progression in MS to age and disease duration as well as other baseline covariates [12], [13]. However, such models assume that further progression essentially depends only on the previous measurement and may be less able to cope with issues such as missing data and the need for imputation.

An alternative approach is using multilevel repeated measure models where observations are clustered within individuals [14]. We have used multilevel models to model disability after stroke [4], [15], and prostate-specific antigen changes in men with localized prostate cancer [16], [17]. Such models could account for both within and between patient variability of the EDSS measurements in MS. These multilevel models are ideal to analyze unbalanced data, that is, where observations are unequally spaced in time and differ in number between individuals. Multilevel models have been used to model the accumulation of disability in MS using a transformation of EDSS [18], assuming a quadratic curve for each individual and ignoring observation-level (within individual) variation over time. Our aim was to develop a generalizable model for the natural history of patients with relapsing-onset MS in two independent data sets who were not treated with any specific disease modifying therapy (DMT) for MS but who would have been eligible for a DMT. This was to facilitate future comparisons with long-term cohorts of DMT-treated patients, such as the UK MS risk sharing scheme [13], [19]. Here, we report how we have approached a variety of analytical challenges and our proposed solutions for the development of our natural history (untreated) model of MS disease progression.

2. Methods

2.1. Study design and settings

We used data from the University of Wales MS (UoWMS) cohort, United Kingdom, and the British Columbia MS (BCMS) database, Canada, to develop and validate the model.

2.1.1. UoWMS cohort

The University Hospital of Wales is the major tertiary referral center for neurology in Wales, United Kingdom, serving a local population of 1.2 million and provides a network of MS clinics across South East Wales. Data were initially collected in a cross-sectional study in 1985 [20] and were updated periodically [21], [22], until 2002 when data were essentially collected prospectively [23]. Sociodemographic and clinical features at disease onset are recorded in a standardized fashion, including degree of recovery and initial interrelapse interval. Approximately 1,000 patient contacts are documented annually, and clinical data, including EDSS scores, are collected routinely at presentation and at each visit. The database, at the time of extraction, had around 2,000 registered MS patients with 1,283 and 809 patients having at least 2 or 4 or more EDSS scores over time, respectively.

2.1.2. BCMS cohort

BCMS database [8], [24], [25], [26], [27], [28], [29], [30], established in 1980, is population based, estimating to capture 80% of the BCMS population. Strengths of the BCMS database include longitudinal follow-up of both DMT-treated and untreated patients, and consistent care provided by the same four core neurologists who have examined over 85% of the patients considered for this study. EDSS scores are recorded after a face-to-face consultation with an MS specialist neurologist. As of 2009, the database contained records for over 5,900 MS patients spanning 28 years (>25,000 cumulative years) of prospective follow-up, from four MS clinics in British Columbia.

2.1.3. Eligibility criteria

We included patients in either cohort (UoWMS and BCMS) if they ever became eligible for DMTs. This eligibility was according to the 2001 Association of British Neurologists (ABN) criteria for interferon beta and glatiramer acetate (IFN-β/GA) use (adapted from online supplementary appendix IV Health Service Circular 2002/2004), defined as: aged ≥18 years, EDSS ≤6.5, and had ≥2 relapses during the previous 2 years. Similar criteria are broadly adopted in other legislative areas as well as the United Kingdom and British Columbia, Canada. All EDSS observations before a patient reaching the ABN eligibility criteria were excluded.

A relapse was defined as worsening neurologic symptoms lasting >24 hours, in the absence of fever or infection. The starting date of each relapse was recorded by an MS specialist neurologist.

As we wished to model the natural history of MS, we truncated the patient profiles once a DMT was initiated. In addition, in the BCMS cohort, the data were truncated to 1995, the last year in which the DMTs were not widely available in British Columbia. This was to avoid “indication bias” whereby a patient's trajectory may influence the decision as to whether they started a DMT [27].

2.2. General multilevel model

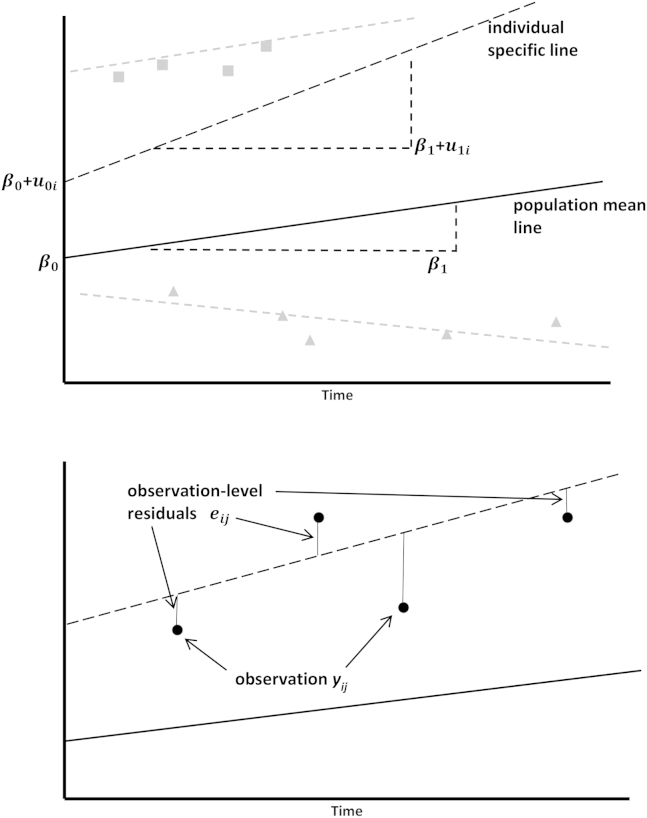
We modeled the EDSS scores of individuals with MS using multilevel models [14]. Our model had two levels: observations (level 1) within individuals (level 2). A simple multilevel repeated measure model is a linear random intercept and random slope model. This type of model estimates a linear population mean along with a specific line for each individual. A graphical representation of the model shown below is given in Fig. 1.

$$y_{ij}={\beta }_0+u_{0i}+\left({\beta }_1+u_{1i}\right)·t_{ij}+e_{ij}\text{,}$$ (1)

where $y_{ij}$ and $t_{ij}$ are the EDSS score and the time variable for the ith individual at the jth time point. Hence, ${\beta }_0+u_{0i}$ is the ith individual's baseline EDSS, whereas ${\beta }_0$ is the mean baseline EDSS, and ${\beta }_1+u_{1i}$ is the ith individual's slope over time, whereas ${\beta }_1$ is the mean slope over time.

Fig. 1.

Graphical representation of the simple multilevel model with linear random intercept and random slope model as shown within Equation (1). Squares are subject 1, circles subject 2, and triangles subjects 3.

The $u_{ki}$ (k = 0, 1) is often referred to as the individual-level random effects and the $e_{ij}$ as the observation-level random effects, whereas the β_k (k = 0, 1) are the fixed effects. Conceptually, the individual-level random-effects measure the deviation of the individual-specific line from the population mean line, and the observation-level random-effects measure the deviation of observations about the individual-specific line.

The $e_{ij}$ is assumed normally distributed with mean zero and variance ${\sigma }^2$, and $u_{0i}\text{and}{u}_{1i}$ are assumed normally distributed with mean zero and an unstructured covariance matrix $D_u$.

Removing u_1i from the equation would give us a linear random intercept model, and removing both u_0i and u_1i would give us a linear fixed effects only model.

2.3. Developing the model

We initially developed our model using the UoWMS data set and then used the BCMS data set for replication. The model was originally developed in UoWMS (the smaller of the two cohorts) because access to the BCMS data set was only possible at the University of British Columbia, Canada. We cross-validated each model using the other data set.

2.3.1. Choice of time axis

We considered modeling EDSS as a function of either the age of an individual or the time since onset of MS at each observation [8], [24]. It is important to center the time axis at a meaningful time point such as the minimum age of the onset (18 years) or zero for the time since onset. Models with different types of time are nonnested but use the same data, so the Akaike information criterion (AIC) was used to compare the models, selecting the model with the lower AIC. In addition, we considered the root mean square error (RMSE) for the difference between the individual-specific predicted EDSS and observed EDSS, and the proportion of these differences that were less than 0.5 or more than or equal to 2 EDSS points.

2.3.2. Choice of function of time

The next model choice was the best-fitting trajectory of EDSS. A simple multilevel model (see Equation 1) allows a random intercept and slope for each individual. Options for more complex models include fractional polynomials to choose the best-fitting curve [4], [31], fitting cubic (or linear) splines, finding a transformation of the outcome or time axis (or both) which have a linear relationship, or smoothing. We used fractional polynomials [4] to find the best-fitting trajectory because these require all data to be positive we added one to time. This procedure, see Web Appendix A at www.jclinepi.com, tests what functions of time best represent the individual trajectories of EDSS over time. Fractional polynomials have the advantage that the model has a simple algebraic form. Linear splines also have a simple form but assume biologically implausible piecewise linear growth [32]. Cubic (or other complex) splines, although more flexible, are more difficult for prediction purposes than fractional polynomials as they require estimation of the curves between each knot point rather than one single global curve. Also, all splines involve the selection of knot points, which would further complicate the multilevel model. Having selected the best-fitting fractional polynomial for each time axis, we then compared these two models using the same criteria as above.

As sensitivity analyses, we repeated the fractional polynomial procedure on a restricted data set, only including observations made within 30 and then 15 years from MS symptom onset to check to what extent outliers were influencing the choice of trajectory.

The model with both the best-fitting time axis and function of that time-axis is referred to hereafter as the “best-fitting” simple model.

2.3.3. Observation-level variation

Observation-level variation is the extent to which EDSS observations on a given individual at any one time are likely to differ and can be considered as a mixture of measurement error and within-person fluctuation, which will change over time, because there is greater interrater and intrarater variability for lower EDSS values [33], [34]. To examine complex measurement error empirically, we plotted the observation-level residuals against time for the best-fitting simple model. Fractional polynomials were then used to obtain the best-fitting function of time for the observation-level variance, in the same way as described in the previous section, see Web Appendix B at www.jclinepi.com. The best-fitting simple model, with the addition of the selected best-fitting observation-level variance function, is referred to as the “complex” model.

2.3.4. Autocorrelation

Autocorrelation occurs when measures on the same individual are correlated more than would be implied by the overall within-individual correlation. We investigated autocorrelation by examining the association in lagged differences between observations and the individual-specific predictions. A large correlation coefficient for these lagged differences can indicate autocorrelation.

As an ad hoc method to reduce autocorrelation, we divided each individual's time axis into quarter year intervals. If there was more than one observation within that interval, a new observation was created by taking the median time and the median EDSS score of all the observations within that interval.

Other possible methods to take into account autocorrelation would be autoregressive-moving average models. We could also have created a more complex model with an autocorrelation parameter that is a function of the time between observations within an individual [35]. Other methods to account for autocorrelation usually require data to be balanced, and more research is necessary to incorporate methods for measuring autocorrelation in unbalanced repeated measure models.

2.3.5. Relapses

Our focus was to model the true accumulation of disability over time and avoid short-term disability secondary to an acute relapse. Consequently, all EDSS observations recorded within 1 month postrelapse were removed from both data sets. However, some patients may continue to improve in physical disability beyond the 1-month postrelapse window [36]. Therefore, we carried out sensitivity analyses using the complex model taking account of autocorrelation, by also removing all observations within 3 and then 6 months after a documented relapse.

2.3.6. Assessing model assumptions and fit

We assessed the normality of the residuals by using QQ plots and the fit of the model by comparing the actual and predicted EDSS values. All analyses were carried out using Stata software (Texas, USA) [37], and all multilevel models were estimated by the runmlwin command [38].

2.3.7. Indication bias

We could bias our results by censoring individual observations after they started treatment because individuals who start treatment might differ to those who never started treatment. We avoided “indication bias” in the BCMS cohort by truncating the data at 1995. However, because of the smaller size of the UoWMS cohort, we instead tested for indication bias by including “starting a DMT” as a covariate within the multilevel model.

2.3.8. Conditional predictions for cross-validation

We carried out external validation using the model from one cohort to predict the data from the other cohort, by predicting future trajectory based on the first observed EDSS score for each individual [4], [39]. We used the BCMS model to predict the UoWMS data and the UoWMS model to predict the BCMS data. The EDSS scores were predicted using the complex model accounting for autocorrelation and relapses.

3. Results

Table 1 shows the characteristics of the MS patients included in the two cohorts, that is, those reaching eligibility for drug treatment. The BCMS data set included more than twice as many individuals as the UoWMS and had a larger number of EDSS observations per person. However, the patient characteristics were similar for sex and proportion ever starting a DMT. For age and disease duration at ABN eligibility and the proportion of patients with SPMS at ABN eligibility, there was some moderate evidence of a difference between data sets (P-values between 0.018 and 0.052) although these differences were small. BCMS patients were on average 2 years younger at the onset than UoWMS patients, although the longer disease duration at ABN eligibility meant that they were only 1.3 years younger on average at ABN eligibility. A higher proportion of the BCMS cohort reached secondary progressive disease during follow-up, possibly due to the longer length of follow-up. There were a slightly greater number of relapses in the 2 years before ABN eligibility and a moderately higher EDSS at baseline in the UoWMS compared with the BCMS cohort. The BCMS cohort had a higher average time between observations.

Table 1.

Patient demographics of all those eligible^a for disease-modifying drug treatment within the two multiple sclerosis cohorts from British Columbia, Canada, and the University of Wales, United Kingdom, with all observations made within 1 month postrelapse removed

Mean (SD; range) or N (%) unless otherwise stated	British Columbia, Canada	University of Wales, United Kingdom	P-value difference
N	978	404
Number of EDSS observations; mean per person(range)	7,335; 7.5 (1–73)	2,290; 5.7 (1–72)
Females	728 (74.4%)	306 (75.7%)	0.611b
Age at the onset, yr	29.1 (8.6; 3.4–61.1)	31.1 (8.7; 13.4–60.0)	<0.001c
Age at eligibility, yr	37.3 (9.3; 18.1–7.0)	38.6 (9.1; 18.8–80.1)	0.018c
Disease duration at eligibility, yr	8.2 (6.9; 0.2–38.9)	7.4 (7.1; 0.5–43.8)	0.052c
SPMS reached by eligibility date	150 (15.3%)	83 (20.5%)	0.019b
Ever reached SPMSd	563 (57.6%)	139 (34.4%)	<0.001b
Relapses in 2 years before eligibility: median(quartiles; range)	2.9 (1.2; 2–9)	3.5 (0.9; 2–9)
EDSS at eligibility: median(quartiles; range)	2 (1,3.5; 0–6.5)	3.5 (2,4.5; 0–6.5)
Year of EDSS at eligibility: range	1980–1995	1976–2011
Year of last EDSS included in the present study: range	1981–1995	1984–2011
Prospective follow-up timed, yr (first eligible EDSS to last DMT-free EDSS)	5.8 (3.8, 0–15)	2.98 (3.9, 0–29.3)	<0.001c
Prospectively followedd, ≥5 years	560 (57.3%)	92 (22.8%)	<0.001b
Prospectively followedd, ≥10 years	159 (16.3%)	16 (4.0%)	<0.001b
Time between observations, yr	0.9 (1.0; 0.0, 11.3)	0.6 (1.2; 0.0, 21.3)	<0.001c
Ever prescribed a DMTe	232 (23.7%)	109 (27.0%)	0.201b

Abbreviations: SD, standard deviation; EDSS, Expanded Disability Status Scale; SPMS, secondary progressive MS; DMT, disease modifying therapy; BCMS, British Columbia MS.

^aUsing the Association of British Neurologists (ABN) criteria.

^bChi-squared test.

^cT-test.

^dFor the BCMS cohort only includes observations made within the dates of the truncated data set, that is, 1980–1995.

^eIncludes DMT exposure up until 2011 in the BCMS cohort, that is, beyond the 1980–1995 window.

3.1. Choice of time axis

For the UoWMS cohort, Table 2 compares the linear fixed effects, linear random intercept, and linear random slope and intercept models with age and time since onset as the time axes. The models with time since onset as the time axis had a substantially lower AIC, a lower RMSE, higher proportions of observations within 0.5 EDSS (apart from the fixed effects only model), and a similar proportion of observations out by two or more EDSS. The random intercept and slope models had better fit by all the criteria than the random intercept and fixed effects only models. When comparing the best-fitting models with degree 2 fractional polynomials for the individual trajectories (i.e., for fixed effects and individual-level random effects) for age vs. time since onset (Supplementary Table 1), the latter consistently had lower AICs, implying that time since onset should be chosen as the time axis.

Table 2.

Akaike information criterion (AIC), root mean square error (RMSE), and percentage of observations within 0.5 EDSS and 2 or more EDSS of all the models fitted using the difference between the observations and individual-level predictions^a

Model	AIC	RMSE individual-level predictions	% (N) within ±0.5 EDSS individual-level predictions	% (N) ≥2 EDSS difference individual-level predictions
Linear fixed effects only (age)	9496.11	1.92	17.6 (404/2,290)	32.3 (739/2,290)
Linear random intercept (age)	6549.66	0.71	61.8 (1,416/2,290)	1.9 (43/2,290)
Linear random slope and intercept (age)	6256.66	0.59	69.7 (1,595/2,290)	0.7 (15/2,290)
Linear fixed effects only (time since onset)	9385.02	1.88	15.6 (357/2,290)	31.9 (731/2,290)
Linear random intercept (time since onset)	6525.80	0.71	62.1 (1,421/2,290)	1.7 (38/2,290)
Linear random slope and intercept (time since onset)	6203.40	0.58	70.7 (1,619/2,290)	0.7 (16/2,290)
$\sqrt{t}$ log t (time since onset)	6063.25	0.55	71.2% (1,630/2,290)	0.5 (11/2,290)
t, log t (time since onset)	6066.72	0.54	72.5 (1,660/2,290)	0.5 (11/2,290)
t, log t (time since onset), adding t to observation-level variance	6013.40	0.55	71.2 (1,630/2,290)	0.5 (11/2,290)
t, log t (time since onset) adding t to observation-level variance with restriction Var(t) = 0	6018.23	0.55	72.1 (1,651/2,290)	0.5 (11/2,290)

Abbreviation: EDSS, Expanded Disability Status Scale.

^aIndividual-level predictions are the fixed effects plus the individual-level residuals.

3.2. Choice of powers of time

There was strong evidence of an improvement in model fit when comparing degree 2 fractional polynomials to degree 1 [P < 0.001, degrees of freedom (d.f.) = 5]. Supplementary Table 2 shows that models including linear and log time, or square root and log time, are consistently the models with the two smallest AICs. The exception was for the data set restricted to 0–15 years since onset; however, the AIC in this case was close to that of the best model (a difference of only 5). Comparing the RMSE of these two models, Table 2, however, shows that the model with linear and log time tends to fit the observed data better. Thus, the final simple model included time since onset and log of time since onset for the individual trajectories (i.e., for the fixed and individual-level random effects).

3.3. Observation-level variation

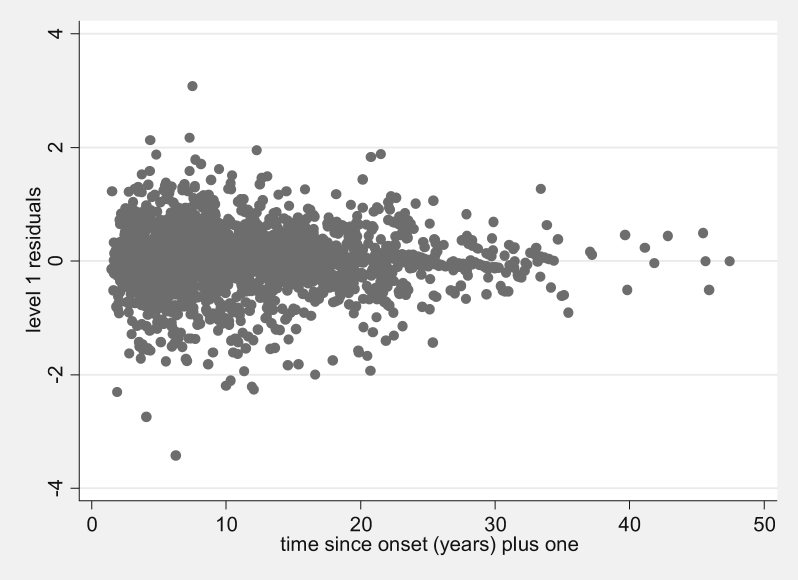
The observation-level residuals from the best-fitting simple model appear to decrease over time (Fig. 2).

Fig. 2.

Observation-level (level 1) residuals plotted over time since onset for the UoWMS best-fitting simple model with linear and log time since onset (n = 2,290).

Fractional polynomials of degree 2 for the observation-level random effects tended not to converge, so we only considered fractional polynomials of degree 1. Adding a linear time term to the observation-level random effects showed a clear improvement in the model fit (P < 0.001, d.f. = 3) compared with the model where observation-level random effects had constant variance. The best-fitting model included the square root of time in the observation-level random effects. The difference between the models with linear time and square root of time as observation-level random effects was small (difference in AIC = 1.1), so the model with linear time in the observation-level random effects was included for ease of interpretation.

We constrained the observation-level time variance term to be equal to zero because its 95% confidence interval (CI) included zero. Hence, we only allowed the covariance term between the constant and observation-level time term to be freely estimated, which amounts to the assumption that observation-level variance decreases linearly over time. This constraint had minimal impact on the model fit (Table 2). Hence, the complex model is of the form

$$y_{ij}={\beta }_0+u_{0i}+e_{1ij}+\left({\beta }_1+u_{1i}+e_{2ij}\right)t_{ij}+\left({\beta }_2+u_{2i}\right)·\log t_{ij}\text{,}\text{where}\left\{e_{lij}\right\}\sim N_2\left(0,D_e\right)\text{,}\left\{u_{li}\right\}\sim N_3\left(0,D_u\right)\text{.}$$ (2)

As described in the methods, we have added one to time since onset, to ensure strict positivity of log time. Unstructured covariance matrices, D_e and D_u, were used for the individual and observation-level random effects with a slight modification to the observation-level variance as discussed above, see Web Appendix C at www.jclinepi.com.

3.4. Autocorrelation

Supplementary Table 3 shows that in our model, we have some autocorrelation, with a correlation coefficient between consecutive observation-level residuals of 0.17 with some evidence that this increases with an individual's number of observations presumably due to a greater chance of having an observation close together. Using quarter year intervals (see methods) reduced the UoWMS data set from 2,290 to 1,876 observations with a maximum number of observations for a single individual being reduced from 72 to 26. Supplementary Table 3 shows that the correlations between lagged residuals were lower in this reduced data set.

3.5. Relapses

There was little difference in the fixed-effect estimates and individual-level random effects between the three models when EDSS scores were removed at 1, 3, or 6 months postrelapse, with all the 95% CIs overlapping (based on Equation (2), see Supplementary Table 4). However, when we consider the observation-level random effects, there is some evidence that the variance of the constant term is lower in the 6 month model compared with the 1 month model. For our final model, we choose the 3 month model, which seemed to have similar variance in the constant term when compared with the 6 month model.

3.6. Assessing model assumptions and fit

The QQ plots from the complex model (Equation (2)) with observations up to 3 months postrelapse removed and accounting for autocorrelation are shown in Supplementary Figure 1 and are close to normal.

Supplementary Figure 2 shows the observed vs. predicted values from the complex model adjusted for autocorrelation and relapses, which are all relatively close to the reference line of perfect predictions. The difference between observed and predicted values has an average of −0.003, a 95% central range (2.5th to 97.5th percentiles) of −1.13 to 0.97 and an RMSE of 0.48. Supplementary Figure 3 shows the observations and fitted patient-specific lines for six randomly chosen individuals with at least three observations.

3.7. Indication bias

When including a binary variable “ever used DMT” as a fixed effect, we found little evidence that those who started treatment have a different intercept (P = 0.88) or different progression (P = 0.83 for interaction with time and P = 0.86 for interaction with log time). This provides some evidence that “indication bias” was not a major issue in the UoWMS cohort.

3.8. Model development with the BCMS data

Developing the model on the BCMS data gave very similar results. Time since MS symptom onset was found to be a better time axis than age. Linear and log time for the individual trajectories gave very good fit to the data, although linear and square root time did give slightly better fit. Adding a linear time term to the observation-level random effects gave a model with better fit, and fractional polynomials of degree 2 showed little improvement.

In contrast to the UoWMS results, the model fitted to the data with all observations 1 month postrelapse removed gave similar results as those with all observations 3 and 6 months postonset of relapse removed (data not shown). Hence, our final BCMS model was based on the model with observations 1 month postrelapse removed.

3.9. Comparison of UoWMS and BCMS models and model validation

The UoWMS model had a higher fixed effect, higher individual-level random effect, and lower observation-level random effect for the constant term than the BCMS model (Table 3).

Table 3.

Parameter estimates, mean (95% CI), of the final UoWMS and BCMS models

Variable	BCMS (n = 6,447)	UoWMS (n = 1,589)
Fixed effects
Intercept	1.05 (0.79, 1.31)	2.63 (2.00, 3.27)
Time since onset	0.22 (0.19, 0.26)	0.16 (0.10, 0.22)
Log time since onset	−0.13 (−0.39, 0.14)	−0.15 (−0.70, 0.40)
Individual-level (level 2) random effects
Var(intercept)	2.80 (1.87, 3.73)	8.67 (5.05, 12.29)
Cov(intercept, time)	0.09 (−0.05, 0.24)	0.09 (−0.23, 0.40)
Var(time)	0.10 (0.08, 0.12)	0.08 (0.05, 0.12)
Cov(intercept, log time)	−2.73 (−3.82, −1.63)	−5.38 (−8.57, −2.19)
Cov(time, log time)	−0.65 (−0.81, −0.48)	−0.60 (−0.92, −0.28)
Var(log time)	6.14 (4.78, 7.49)	7.13 (4.01, 10.27)
Observation-level (level 1) random effects
Var(intercept)	0.76 (0.70, 0.82)	0.40 (0.35, 0.45)
Cov(intercept, time)	−0.004 (−0.005, −0.002)	−0.003 (−0.005, −0.002)
Var(time)	Set equal to zero	Set equal to zero

Abbreviations: CI, confidence interval; UoWMS, the University of Wales MS; BCMS, British Columbia MS.

This indicates that the UoWMS patient population had a higher average EDSS at the presumed onset of disease, greater variation between individuals in EDSS at the onset, and slightly lower variation within individuals in EDSS at the onset (Table 1). The coefficients for the trajectory of EDSS over time and log time, and the other variances and covariances of the individual-level and observation-level random effects are remarkably similar between the two cohorts. The fixed effects would correspond to an average increase over 10 years from the onset of 1.9 EDSS and 1.3 EDSS points within the BCMS and UoWMS models, respectively.

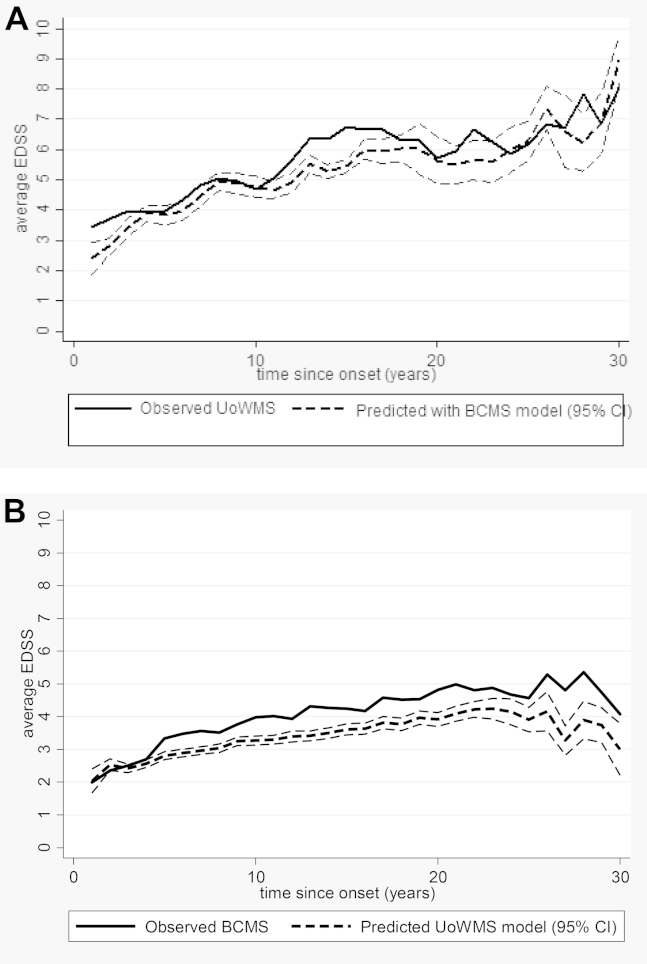
We used the coefficients from the final BCMS model to predict EDSS in the UoWMS data set (with the EDSS scores removed 3 months postrelapse) conditional on the baseline EDSS, rounding the continuous prediction to the nearest true EDSS score. We observed a reasonable model fit with a mean difference between prediction and observed being −0.44 [standard deviation (SD): 1.36] and an RMSE of 1.46; 49.2% of predictions were within 0.5 units of the observed EDSS, whereas 22.5% of predictions were out by 2 or more EDSS units. These conditional predictions from the BCMS model are shown along with the observed EDSS in the UoWMS cohort, averaged within yearly bands, in Fig. 3A and Supplementary Table 5.

Fig. 3.

(A) and (B) The upper graph shows the observed EDSS within the UoWMS cohort and the conditional predictions using the BCMS model. The lower graph shows the observed EDSS within the BCMS cohort and the conditional predictions using the UoWMS model. The plotted data, over a 30-year period, are the annual means at each year since time of the onset where data was grouped into yearly bins that is 0–0.5, 0.5–1.5, and so forth. EDSS, Expanded Disability Status Scale; UoWMS, the University of Wales MS; BCMS, British Columbia MS; CI, confidence interval.

We also used the coefficients from the final UoWMS model to predict EDSS in the BCMS data set conditional on the baseline EDSS. The mean difference between prediction and observed was −0.61 (SD: 1.83), with some evidence of underprediction over time and RMSE of 1.93. Only 35.9% of predictions were within 0.5 units of the observed EDSS, whereas 35.8% of predictions were out by 2 or more EDSS. These conditional predictions from the UoWMS model are shown along with the observed EDSS in the BCMS cohort, averaged within yearly bands, in Fig. 3B and Supplementary Table 6.

4. Discussion

We used two large independent cohorts of MS patients from Canada and the United Kingdom to build a complex multilevel model for EDSS trajectory. Using the same model building strategy resulted in the models for both cohorts having the same time axis, powers of time that were consistent with each other and the same parameterization of observation-level variation. The average levels of disability in the two cohorts were different, but the average patterns of change were similar. This provided evidence that our model is transportable to other populations. When two cohorts are not available, it may be necessary to use other validation techniques such as randomly splitting the data set or using bootstrap or jackknife techniques.

Two key choices made here related to the functional form of the time axis. When both “time since onset” and “age” were considered, the best-fitting time axis was the former. The pattern of EDSS progression was not linear and fractional polynomials allowed us to identify the best-fitting trajectory. This approach has been developed and used for identification of nonlinear relationships in nonrepeated measures regression [40], [41]. However, their use in multilevel models has been less widespread [4], [42], [43]. This may be because of increasing complexity of the models and also because of the additional need to parameterize the individual-level and observation-level random effects.

We found that observation-level variation (comprising measurement error and short term fluctuations in the EDSS) reduced as time progressed [i.e., as disability (EDSS) increased]. Previous work has shown that measurement error is lower for higher EDSS values [33], [34] and that short-term improvements in disability are more likely earlier in the disease course [29]. Identification of complex observation-level variation highlights the importance of model checking when fitting multilevel longitudinal models.

Our ad hoc approach to adjust for the autocorrelation present was successful in reducing it further. A more robust approach might be to adjust the interval for merging multiple observations into one and then estimate the lagged residual correlation for each different interval. However, this would need to be balanced by the effect of concatenating too many observations and reducing any real fluctuations in EDSS due to using averaged data points. There is some evidence [44] that moderate misspecification of the observation-level variation has little impact on the fixed-effects estimates. The moderate amount of autocorrelation present here had little influence on our estimates of average EDSS progression (the fixed-effect estimates were very similar in the models with and without concatenated observations).

Removal of observation (EDSS) scores within 1 month postrelapse appeared adequate for the BCMS cohort, but in the UoWMS cohort, the optimal window was 3 months postrelapse. This is consistent with the general approach to data collection within the BCMS database (EDSS scores were intended to be collected outside the influence of an acute relapse [8]), as well as with previous findings from the BCMS study [29]. Others have also shown that most improvement in physical disability occurs within 2 months postrelapse [36]. This underscores the importance of exploring local effects within cohorts.

We treated the ordinal EDSS score as a continuous measure, which facilitates the interpretation of the model parameters but does not imply that the meaning of a point change in EDSS is equivalent in terms of disability progression across the range of scores. All the models showed good fit to the observed data with normally distributed residuals. Researchers seeking to model repeated measures of ordinal scores should assess the normality of the residuals as a key model check, but our results show that this assumption may be satisfied even if the outcome measure itself is ordinal and/or not normally distributed.

Modeling the trajectory of EDSS against the time since MS symptom onset showed a good fit in both cohorts. Cross-validating our models by predicting the future EDSS trajectory conditional on the first observation in one data set using the model derived on the other data set showed reasonably good fit, with about half of all predicted EDSS scores within 0.5 EDSS of the observed when validating the BCMS model in the UoWMS data. However, the UoWMS model performed less well in the BCMS data, with evidence of underprediction at almost all time points. This is not surprising given the relative sizes of the two data set. The higher within-individual variation within the BCMS data set means that predictions within the BCMS data are likely to show greater variation than predictions made on the UoWMS data. Our ability to examine model fit in two different populations is important in validating any prognostic model. Using a repeated measures model to predict individual trajectories based on one or more observations has been done before [4], [15], [45], but further research needs to examine whether additional covariates can explain why the trajectory of some subjects was not well predicted in our current model. Bayesian methods could also be used, such that the previous model estimates form priors for parameters to be estimated using a small number of observations from an individual [46].

Truncating data once a DMT was started (UoWMS) or to 1995 (BCMS data) resulted in an average follow-up time for individuals of 3 and 5.8 years, respectively. We had limited data with 10 years of follow-up or greater (16% and 4% of individuals, respectively). However, because individuals enter the study at different times since onset, we are able to model this without extrapolation. Examining Fig. 3 shows little evidence that the fit to our data is worse at the upper end of 20–30 years since time of the onset.

Although the models are generally similar for most parameters, it seems there is higher between-individual variation in the UoWMS model and higher within-individual variation in the BCMS model. One reason for this could be an inherent difference between individuals from Canada and Wales or a difference in when and how individuals accessed the health systems in each area. Also, the BCMS cohort was mainly seen by the same four core neurologists, which would reduce any between-rater variation.

The corresponding Markov model that was fitted to the BCMS cohort [13] showed about a 2.2 EDSS increase over a 10-year period since ABN eligibility. Looking at our fixed effects over the same period (approx. 8–18 years since onset) would correspond to a similar average increase of 2.1 and 1.5 EDSS within the BCMS and UoWMS models, respectively. Using the fixed effects, we would expect the average time from the onset to reaching an EDSS of 6 to be 23.1 and 23.4 years using the UoWMS and BCMS models, respectively. Scalfari [7] reported a mean time from the onset of 21.2 years (95% CI: 19.8, 22.6) to reaching EDSS 6, and Tremlett [8], who looked at six studies, reported the median times ranging from 15 to 32 years, consistent with our estimates. Comparing our study to one previous multilevel model for MS [18] is difficult given their transformation of EDSS into weighted change of EDSS. However, they did include a quadratic term whose estimate was positive, which creates a similar shape to a negative log term with rate of change increasing over time.

Our results have implications for the design and analysis of MS intervention trials, leading to more sensitive assessment of treatment effects over time than cross-sectional analyses of EDSS at fixed time points. Average EDSS could be similar in an intervention and control arm after a fixed follow-up period, but if the trajectory was different, the intervention might still be considered an effective treatment in the short and medium terms.

The development of this multilevel model is an important methodological achievement that will enable prediction of the expected long-term disease trajectory in other populations. This is especially necessary for extrapolating the findings from randomized controlled trials (which are often short term, lasting no more than 2–3 years) or for interpreting findings from DMT exposed cohorts of patients with no specific unexposed control cohort. In particular, these models facilitate natural history predictions within the UK MS risk sharing scheme to determine the efficacy of DMTs. It is only by modeling longer term follow-up of such studies that one can advise patients about the potential therapeutic benefits that accrue in the long term.