Abstract
Regression analysis of censored failure observations via the proportional hazards model permits time-varying covariates which are observed at death times. In practice, such longitudinal covariates are typically sparse and only measured at infrequent and irregularly spaced follow-up times. Full likelihood analyses of joint models for longitudinal and survival data impose stringent modelling assumptions which are difficult to verify in practice and which are complicated both inferentially and computationally. In this article, a simple kernel weighted score function is proposed with minimal assumptions. Two scenarios are considered: half kernel estimation in which observation ceases at the time of the event and full kernel estimation for data where observation may continue after the event, as with recurrent events data. It is established that these estimators are consistent and asymptotically normal. However, they converge at rates which are slower than the parametric rates which may be achieved with fully observed covariates, with the full kernel method achieving an optimal convergence rate which is superior to that of the half kernel method. Simulation results demonstrate that the large sample approximations are adequate for practical use and may yield improved performance relative to last value carried forward approach and joint modelling method. The analysis of the data from a cardiac arrest study demonstrates the utility of the proposed methods.
Keywords: Convergence rates, Cox model, Kernel weighted estimation, Sparse longitudinal covariates
1 Introduction
In biomedical and public health research, it is common to observe both longitudinal data, with repeated measurements of a variable at a number of time points, and event history data, in which times to recurrent or terminating events are recorded. In such studies, investigators may be interested in evaluating the effects of longitudinal covariates on the occurrence of events. The usual proportional hazards analysis may not be applicable when the time-dependent covariates are measured intermittently.
These issues may be understood more precisely by representing the event history using counting processes. In the failure time setting, N(t) indicates whether an event has occurred by time t and Z(·) is a p-dimensional covariate process. For single event data, the Cox model specifies the hazard function for N(t) conditionally on the history of Z(r), r ≤ t as
| (1.1) |
where λ0(·) is an unspecified baseline hazard function and β0 is a vector of unknown regression parameters. With recurrent event data, there may be multiple jumps in N(t) and model (1.1) refers to the Andersen and Gill (1982) proportional intensity model. The standard partial likelihood analysis of the model (1.1) requires the full trajectory of the covariates. Similar issues arise with recurrent events when relaxing the intensity assumption (1.1) to the proportional rate model
| (1.2) |
where μ0(·) is an unspecified function and β0 is a vector of unknown regression parameters. The estimation procedures for models (1.1) and (1.2) require knowledge of Z(t) at those event times where a subject is still under observation.
The simplest method for handling incompletely observed longitudinal covariates in the above models is to naïvely impute missing values using the last value carried forward approach. The missing values of Z(r) may be replaced by the most recent observed values of Z(u), u ≤ r. This approach may be generalized to permit additional utilization of lagged covariates, as discussed in Andersen and Liestol (2003). While these ad hoc imputation approaches are conceptually simple and may be implemented using standard software, they lack rigorous theoretical justification and may incur substantial bias. An alternative to these naïve techniques is to jointly model the longitudinal covariates and the event history data (Ibrahim, Chu and Chen (2010)). There has been considerable interest in modelling the dependence between these two processes via shared random effects (Hogan and Laird (1997)). Under such assumptions, the joint distribution of N(·) and Z(·) may be fully specified (Degruttola and Tu (1994), Faucett and Thomas (1996), Henderson, Diggle and Dobson (2000), Xu and Zeger (2001)). To obtain more exible modeling, Yao (2007) adopted a non-parametric functional principal component approach to model the longitudinal process and Cox model for the time-to-event outcome. The modelling assumptions are rather strong and the computation and inference are complicated, requiring full nonparametric maximum likelihood (Dupuy, Grama and Mesbah (2006), Tsiatis, Degruttola and Wulfsohn (1995), Wulfsohn and Tsiatis (1997), Zeng and Cai (2005)) or likelihood motivated procedures, like the conditional score approach in Tsiatis and Davidian (2001). The theoretical justification depends critically on correct model specification, which may involve assumptions which are unverifiable from the observed data. A comprehensive review of the joint modelling approach is given in Tsiatis and Davidian (2004) and Rizopoulos (2012).
In this article, we develop simple, computationally efficient, and theoretically justified estimators for model (1.1) and (1.2) using intermittently collected longitudinal covariates which require minimal assumptions on the joint distribution of N(·) and Z(·). The main idea is to modify the naïve imputation approaches like those in Andersen and Liestol (2003) to obtain theoretically justified estimation procedures which are valid under weak assumptions. A kernel weighting scheme is used to downweight imputed covariate values in the partial likelihood, where those observations which are distant in time from the event time receive less weight. Such kernel weighting approach has been adopted by Cai and Sun (2003) and Tian, Zucker and Wei (2005) for time-dependent coefficient in Cox model. However, there are fundamental differences between our work and the time-varying coefficient methodology. The estimation of time-varying regression parameters assumes that the covariate effect varies with respect to time while we assume that the covariate is a dynamic process with fixed coefficient. The smoothing methods employed by Cai and Sun (2003) and Tian, Zucker and Wei (2005) which localize the partial likelihood in time are not applicable in our setting, where smoothing occurs at the individual level, as opposed to the population level, where the same weights are applied to all individuals. The dependence structure between the longitudinal measurements and the event history process is otherwise unspecified, in contrast to the joint models. With a suitable choice of the bandwidth, the estimators for the regression coefficients are consistent and asymptotically normal, with simple plug-in variance estimators. Interestingly, the optimal rates of convergence for β0 are slower than the usual parametric rate with time-invariant covariates. For recurrent events data, one may include both forward and backward lagged covariates, employing covariate information observed after event times. Our theoretical results demonstrate that using all available covariate information yields an estimator which converges at n2/5, while the estimator which only uses backward lagged covariates converges more slowly than n2/5. These results are detailed in Sections 2–3.
In Section 2, we propose estimation for the Cox model for single event data using half kernel smoothing with backward lagged covariates and present the corresponding theoretical findings. The results for full kernel smoothing including both forward and backward lagged covariates are given in Section 3. We report the results of our simulation studies in Section 4, exhibiting improved performance versus the last value carried forward approach and joint modelling method. The joint modelling approach exhibits efficiency gains when the joint model is correctly specified but may exhibit substantial bias and poor coverage under model misspecification. We then apply our method to data from a cardiac arrest study in Section 5. In this analysis, the joint modelling approach has convergence issues, with the corresponding results being somewhat unreliable. Concluding remarks are given in Section 6. Proofs of the results from Sections 2 and 3 are given in the Appendix provided in a supplementary materials file.
2 Half Kernel Estimation with Backward Lagged Covariates
Let T be the failure time and let C be the corresponding censoring variable. We assume that censoring is coarsened at random such that T and C are conditionally independent given Z(·) (Gill, van der Laan and Robin (1997)). Let {(Ti, Zi(·), Ci), i = 1, …, n} be n independent copies of {(T, Z(·), C)}. The longitudinal covariates are observed at Mi observation times Rik ≤ Xi, k = 1, …, Mi, where Xi = min(Ti, Ci), and Mi is assumed finite with probability one such that the observed covariates are sparse. The p-dimensional covariate process may include both time-independent and time-dependent covariates, under the restriction that the time-dependent covariates are observed at the same time points within individuals. The timing of the measurements Rik, k = 1, …, Mi is assumed exogenous in the sense that the decision to schedule a measurement is made independently of the measurement. The observed data consist of the n independent realizations {Xi, Δi, Zi(Rik), Rik, k = 1, …, Mi}, i = 1, …, n, where Δi equals 1 if Xi = Ti and 0 otherwise.
Following Andersen and Liestol (2003), one may utilize backward lagged covariates in imputing missing covariates in the partial likelihood for estimation of β0 in model (1.1). To ease the presentation, we adopt the counting process notation, where Ni(t) = I(Xi ≤ t, Δi = 1) and Yi(t) = I(Xi ≥ t). If the covariate Zi(t) were fully observed for all t < Xi, then one might construct the following partial likelihood
| (2.3) |
where
The log partial likelihood is:
where τ is a pre-specified time point such that pr(Xi > τ) > 0. Because Zi(u), i = 1, …, n, are not observed continuously, ln(β) is not computable from the observed data. We propose using lagged covariate values with observation times smaller than u, where we downweight covariates at times distant from u in dNi(u) and Yi(u). This approach formalizes the lagging strategy in Andersen and Liestol (2003), with the kernel weighting enabling the use of all available lagged covariates. If the covariate observation times for a subject are all far away from the event time, then this subject may be disregarded in the calculation of partial likelihood but not in the last value carried forward approach, where the most recent observed covariate is used. With irregularly observed longitudinal covariates, as the number of subjects increases, borrowing strength across subjects, the longitudinal measurements times will become dense. To exploit this accumulation of information, one may “smooth” an individual’s contributions to the partial likelihood based on the distance of their observed covariates to the time of interest. The resulting log partial likelihood up to time t is:
| (2.4) |
where Khn(t) = K(t/hn)/hn, hn is the bandwidth and the kernel function K(t) is a symmetric probability density with support [−1, 1], mean 0, and bounded first derivative.
Define β̂n to be maximizer of . This estimator is a root of the score function Un(β) = 0, where
| (2.5) |
a⊗0 = 1, a⊗1 = a, a⊗2 = aaT. For i = 1, …, n,
is a realization of N*(t), the counting process for the covariate observation times. Observe that the smoothing leads to different weights for different individuals inside the integral in Un(β), which differs from smoothing methods for proportional hazards model with time-dependent regression parameters (Cai and Sun (2003); Tian, Zucker and Wei (2005)), where the same weights are applied to all individuals inside the integral. Since (2.4) is concave in β, there exists a unique root of the estimating function (2.5). In addition, E{dN*(t)} = λ*(t)dt, and
, where λ*(t) and λ0(t) are twice continuous differentiable and strictly positive for t ∈ [0, τ], and
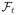 is the filtration, which includes all information in N(s), Y(s) and Z(s) up to time t, as well as the measurement times.
is the filtration, which includes all information in N(s), Y(s) and Z(s) up to time t, as well as the measurement times.
To state our key results, additional notation and regularity conditions are needed. Denote
where s(k)(β, t) is the limit of , k = 0, 1, 2. That is,
Let
and let
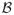 be a compact set of Rp that includes a neighbourhood of β0. Assume that the following conditions hold:
be a compact set of Rp that includes a neighbourhood of β0. Assume that the following conditions hold:
-
(A1)
The covariate process Z(t) is left continuous, has right-hand limit and is contained in a bounded subset with total variation bounded by a constant c < ∞ almost surely. Moreover, is twice continuously differentiable for u, v ∈ [0, τ]⊗2.
-
(A2)
N*(t) is independent of N(t) and Z(t). In addition, and N*(τ) is bounded by a finite constant.
-
(A3)There exists a neighbourhood
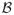 of β0 such that
of β0 such that
(2.6) -
(A4)
v1(β0) is non-singular.
-
(A5)
K(z) is a symmetric density function satisfying ∫ K(z)2dz < ∞, hn → 0, , and nhn → ∞.
Condition (A1) posits a certain level of smoothness on Z(t). It is worth emphasizing that joint modelling strategies (Tsiatis and Davidian (2004)) generally imply at least this level of smoothness, if not stronger. The condition (A2) requires that the covariate observation process is independent of the covariates and the event history process. This is somewhat stronger than the missing at random assumption under which a valid likelihood might be constructed with joint modelling assumptions. Condition (A3) places mild restrictions on the variability of Z(t), which would typically be satisfied in practice, and guarantees that β̂n has finite variance in large samples. Condition (A4) ensures that the variance-covariance matrix is positive definite. Condition (A5) states the restrictions on the kernel bandwidths.
The following theorem, which is established in the Appendix, states the asymptotic properties of β̂n based on solving (2.5) with kernel bandwidth selected to yield consistent estimation:
Theorem 1
Under conditions (A1)–(A5), β̂n is consistent and the asymptotic distribution of β̂n satisfies
| (2.7) |
where
and
For statistical inference, it is challenging to estimate the variance in (2.7) directly, owing to time-varying quantities which depend on unknown values of Z(·) which are not available in the intermittent longitudinal covariate observations. In practice, we employ estimating equation (2.5) to estimate Σ(β0) by and estimate the variance of β̂n by the sandwich formula .
Corollary 1
Under conditions (A1)–(A5), the sandwich formula consistently estimates the variance of β̂n.
Our method depends on an appropriate choice of bandwidth. Theoretically speaking, condition (A5) says that the bandwidth cannot be too small; otherwise, the variance will be quite large. On the other hand, to eliminate the asymptotic bias, one requires a small bandwidth. With hn = o(n−1/3), we achieve an optimal rate of convergence o(n1/3). This result provides insight into the ad hoc procedure of Andersen and Liestol (2003). When tuning the partial likelihood estimation using backward lagged covariates to obtain a theoretically rigorous estimator, parametric convergence rates are not achievable. This contrasts with joint modelling approaches (Tsiatis and Davidian (2004)), where strong modelling assumptions on the joint distribution of the covariate process and event times facilitates likelihood based inferences which may achieve parametric rates of convergence for the regression parameter β.
Numerical studies reported in Section 4 show that small bias may be achieved for bandwidths between n−0.9 and n−0.4, with stable variance estimation and confidence interval coverage for bandwidths larger than n−0.7. Within this range, the bias diminishes as the sample size increases, as predicted by Theorem 1. In Section 4, an automatic bandwidth selection procedure is proposed, with both the corresponding model based variance estimators and confidence intervals exhibiting good performance.
3 Full Kernel Estimation With Forward and Backward Lagged Covariates
If data continue to be collected on subjects for whom an event has occurred, as in the recurrent events case, we may use full kernel to impute missing values using both forward and backward lagged covariates. Andersen and Liestol (2003) investigated scenarios where observation terminates at the time of the first event, as with classical right censored data, hence, did not consider the use of forward lagged covariates. Let Ni(t) be a recurrent event counting process and let Yi(t) = I(Ci ≥ t) be the at risk process for subject i up to time Ci, i = 1, …, n. Similarly to half kernel estimation, one may construct a smoothed partial likelihood score function using full kernel smoothing:
| (3.8) |
where and
| (3.9) |
One should recognize that the smoothed estimating function (3.8) is valid under both model (1.1) and under the weaker proportional rate model (1.2). The results provided below hold under the weaker assumption (1.2).
To state the main asymptotic findings for full kernel estimator β̃n solving (3.8), some additional notations and conditions are needed. For i = 1, …, n, Ni, Yi and Ci are independent realizations of random variables N, Y, and C. Denote
| (3.10) |
where the definition of λ*(t) is given in Section 2. We assume that the following conditions are satisfied:
-
(C1)
{Ni(·), Yi(·), Zi(·)}(i = 1, …, n) are independent and identically distributed.
-
(C2)
pr(C ≥ τ) > 0, where τ is a predetermined constant.
-
(C3)
N(τ) and N*(τ) are bounded by finite constants and μ0(t) and λ*(t) are twice continuously differentiable.
-
(C4)
For i = 1, …, n, Zi have bounded total variation, where for all j = 1, …, p, where Zij is the jth component of Zi and K is a constant. In addition, is twice continuously differentiable for s, t ∈ [0, τ]⊗2.
-
(C5)
is positive definite.
-
(C6)
K(z) is a symmetric density function satisfying . In addition, hn → 0 and nhn → ∞.
-
(C7)
.
Conditions (C1)–(C6) are similar in spirit to those for half kernel estimation in Section 2. Conditions (C1) and (C2) are standard for the proportional rate model (1.2). The assumption of bounded N(t) in (C3) is also conventional with recurrent events over finite time intervals. Conditions (C4) and (C5) are full kernel analogs for model (1.2) of half kernel conditions (A3) and (A4) for model (1.1). These guarantee finiteness and positive definiteness of the full kernel estimator’s variance-covariance matrix. The kernel requirements in (C6) are similar to those in (A5), with (C6) and (C7) indicating the allowable range of bandwidth for full kernel estimation is larger than that for half kernel estimation given in (A5). The implications of this weaker bandwidth requirement are discussed below.
The asymptotic properties of the full kernel estimator β̃n are detailed in the following theorem:
Theorem 2
Under conditions (C1)–(C6), the asymptotic distribution of β̃n satisfies
| (3.11) |
where
β0 is the true regression coefficient and D is a constant vector, which can be found in the Appendix. The asymptotic variance
Theorem 2 permits bandwidths yielding non-zero asymptotic biases in the standardized distribution of the estimator. If we further restrict the bandwidths under (C7), then the asymptotic bias vanishes. This result is stated in the following corollary:
Corollary 2
Under conditions (C1)–(C7), β̃n is consistent and converges to a mean zero normal distribution given in Theorem 2.
The variance estimate for β̃n may be obtained by expanding the estimating equation (3.8). With estimating A(β0) and estimating Σ̃(β0), we can do valid inference.
Corollary 3
Under conditions (C1)–(C7), the sandwich formula consistently estimates the variance of β̃n.
With full kernel estimation, the bias is of order . Taking hn = o(n−1/5), the maximum allowable bandwidth under (C7) giving negligible asymptotic bias, the estimator achieves o(n2/5) rate of convergence. One can easily show that the convergence rates in Theorem 1 hold for half kernel estimation based on recurrent events data where only backward lagged covariates are utilized. Thus, full kernel estimation using both forward and backward lagged covariates yields an optimal convergence rate which is superior to the optimal o(n1/3) rate for half kernel estimation giving negligible asymptotic bias. The practical gains associated with using both forward and backward covariates is examined in the simulations in Section 4.
4 Simulation Studies
We first study the performance of the half kernel estimator using backward lagged covariates in estimating equation (2.5) with classical right censored data. We generate 1,000 datasets, each consisting of n = 100, 400 or 900 subjects. The total number of covariate observation times for each subject was Poisson distributed with intensity rate 8. The covariate observation times are generated from uniform distribution Unif(0, 1). The covariate process is generated through a piecewise constant function
where follows a unit variance multivariate normal distribution with mean 0 and correlation e−|i−j|/20, i, j = 1, …, 20. The survival time is simulated from model (1.1) with λ0(t) = 1 and β0 = 1.5. The censoring time is generated from a uniform distribution with lower bound 0 and upper bound giving censoring percentages of 15% and 50%. The results for other choices of the model parameters are rather similar and are omitted.
Based on Theorem 1, to obtain a half kernel estimator with asymptotically negligible bias, we employ bandwidths in the range (n−1, n−1/3) when calculating β̂n using the smoothed likelihood score function. The kernel function is the Epanechnikov kernel, which is K(x) = 0.75(1 − x2)+. Further simulations (not reported) evidence that the use of other kernel function has little impact on the estimator’s empirical performance.
Table 1 summarizes the main findings over 1,000 simulations. We observe that as the sample size increases, the bias decreases and is small, that the empirical and model based standard errors agree reasonably well, and that the coverage is close to the nominal 0.95 level. The performance improves with larger sample sizes.
Table 1.
Simulation results with different censoring rate
| n | BD | censoring rate is 15% | censoring rate is 50% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RB | SD | SE | CP(%) | Bias | RB | SD | SE | CP(%) | ||
| Half Kernel | |||||||||||
| 100 | n−0.7 | 0.051 | 0.034 | 0.420 | 0.502 | 91 | 0.169 | 0.113 | 0.543 | 0.740 | 90 |
| n−0.6 | 0.019 | 0.013 | 0.346 | 0.384 | 91 | 0.084 | 0.056 | 0.451 | 0.584 | 91 | |
| auto | 0.042 | 0.028 | 0.434 | 0.385 | 93 | 0.047 | 0.031 | 0.595 | 0.500 | 90 | |
| 400 | n−0.7 | 0.040 | 0.026 | 0.299 | 0.321 | 93 | 0.046 | 0.031 | 0.365 | 0.423 | 92 |
| n−0.6 | −0.009 | −0.006 | 0.222 | 0.242 | 93 | 0.008 | 0.006 | 0.277 | 0.301 | 93 | |
| auto | 0.028 | 0.019 | 0.298 | 0.263 | 93 | 0.035 | 0.023 | 0.378 | 0.332 | 95 | |
| 900 | n−0.7 | 0.008 | 0.005 | 0.247 | 0.253 | 95 | 0.033 | 0.022 | 0.305 | 0.327 | 93 |
| n−0.6 | 0.006 | 0.004 | 0.181 | 0.188 | 94 | 0.007 | 0.005 | 0.220 | 0.236 | 94 | |
| auto | 0.014 | 0.010 | 0.244 | 0.216 | 94 | 0.020 | 0.013 | 0.306 | 0.260 | 93 | |
| Last Value | |||||||||||
| 100 | −0.157 | −0.104 | 0.232 | 0.220 | 85 | −0.086 | −0.057 | 0.339 | 0.309 | 90 | |
| 400 | −0.180 | −0.120 | 0.115 | 0.106 | 59 | −0.130 | −0.087 | 0.146 | 0.146 | 83 | |
| 900 | −0.178 | −0.119 | 0.073 | 0.070 | 30 | −0.137 | −0.091 | 0.098 | 0.095 | 69 | |
| Full Kernel | |||||||||||
| 100 | n−0.7 | 0.005 | 0.003 | 0.294 | 0.316 | 93 | 0.025 | 0.017 | 0.354 | 0.383 | 93 |
| n−0.6 | −0.053 | −0.035 | 0.242 | 0.247 | 93 | 0.011 | 0.007 | 0.298 | 0.305 | 94 | |
| auto | 0.039 | 0.026 | 0.311 | 0.278 | 93 | 0.018 | 0.012 | 0.359 | 0.335 | 91 | |
| 400 | n−0.7 | −0.003 | −0.002 | 0.204 | 0.209 | 94 | 0.015 | 0.010 | 0.247 | 0.247 | 95 |
| n−0.6 | −0.020 | −0.014 | 0.159 | 0.160 | 95 | −0.013 | −0.008 | 0.192 | 0.192 | 94 | |
| auto | −0.022 | −0.015 | 0.185 | 0.186 | 94 | 0.013 | 0.009 | 0.235 | 0.222 | 94 | |
| 900 | n−0.7 | 0.001 | 0.001 | 0.172 | 0.179 | 94 | 0.004 | 0.003 | 0.209 | 0.213 | 94 |
| n−0.6 | −0.018 | −0.012 | 0.126 | 0.135 | 95 | −0.003 | −0.002 | 0.223 | 0.231 | 94 | |
| auto | −0.004 | −0.003 | 0.146 | 0.151 | 96 | −0.005 | −0.004 | 0.206 | 0.185 | 94 | |
| Nearest Value | |||||||||||
| 100 | −0.196 | −0.130 | 0.159 | 0.155 | 73 | −0.190 | −0.126 | 0.204 | 0.188 | 76 | |
| 400 | −0.220 | −0.145 | 0.081 | 0.073 | 20 | −0.219 | −0.146 | 0.100 | 0.088 | 3 | |
| 900 | −0.218 | −0.146 | 0.056 | 0.048 | 2 | −0.220 | −0.146 | 0.065 | 0.058 | 7 | |
Note: “BD” represents different bandwidths, “Bias” is the empirical bias, “RB” is the “Bias” divided by the true β0, “SD” is the sample standard deviation, “SE” is the average of the standard error estimates and “CP” represents the coverage probability of the 95% confidence interval for β̂n.
We next study the properties of the full kernel estimator under model (1.1). The data generation is identical to that presented above, where covariate observation was terminated at the minimum of the failure and censoring times. To utilize full kernel estimation, if a failure occurs prior to censoring, then the covariate process continues to be observed beyond the event time until the right censoring time. This is equivalent to a recurrent events set-up. Following Corollary 1, the allowable bandwidth range for full kernel estimation with negligible bias is (n−1, n−1/5). The results presented in Table 1 enable a direct assessment of improvements provided by full kernel estimation with forward and backward lagged covariates over half kernel estimation which only employs backward lagged covariates.
Similarly to half kernel estimation, as the sample size increases, the bias is well controlled, the empirical and model based standard errors agree reasonably well, and the empirical coverage probability is close to 0.95. As predicted by the theoretical developments, full kernel estimation yields empirical gains over half kernel estimation. With the same bandwidth and same sample size, the standard error is markedly diminished when using both forward and backward lagged covariates relative to using only backward lagged covariates, with the magnitude of the bias being comparable.
We also propose a strategy for automatic bandwidth selection. The idea is to minimize the mean squared error, where the bias and variance are calculated separately. For half kernel method, the bias is of order hn as shown in the proofs in the Appendix. So we regress β̂(hn) with 30 equally spaced hn in the allowable range to get an estimate for the slope Ĉ. To calculate the variance, we randomly split the data into two parts, and calculate β̂1(hn) and β̂2(hn) respectively. We then choose hn to minize . For full kernel method, we use similar idea except that the bias is of order and we regress β̂(hn) with in the allowable range to calculate the bias. The results are summarized in Table 1. From the table, the automatic bandwidth procedure performs well relative to the fixed bandwidth results, both for half and full kernel estimation.
With longitudinal covariates in time to event analysis, a naïve approach is the last value carried forward approach. If data at a particular time point are missing, then the backward lagged covariate observed at the most recent time point in the past is imputed for the missing value. Andersen and Liestol (2003) discussed bias reduction strategies, in which the backward lagged covariate is only imputed if it falls in a window around the time point of interest. Last value carried forward is conceptually simple and its ease of implementation has lead to its use in practice. However, because backward lagged covariates are not weighted by their distance from the imputation time, such procedure lacks theoretical validity. To demonstrate that this approach may lead to substantially biased inferences, we studied its properties under the above simulation set-up.
The results in Table 1 exhibit that rather large bias may be incurred by the naïve last value carried forward analysis. Such biases do not attenuate as the sample size increases and the coverage probabilities may be much lower than the nominal 0.95 level. The coverage probability is worse with decreased censoring percentage. Heuristically, as the censoring rate decreases, more events are observed and the estimator’s variance decreases, yielding lower coverage probabilities.
To make fair comparison with full kernel approach, we adopt a nearest value method. In this approach, the nearest observation which could be either backward lagged covariates or forward lagged covariates is used in the calculation of partial likelihood. The results are similar to last value carried forward as both methods are biased but the nearest value approach has smaller variability as seen in Table 1.
Per the request of a referee, we have provided additional simulations comparing our approach and last value carried forward with two covariates, one time-dependent covariate and one time-independent covariate, to see the performance of our method in a multivariate regression case. The results presented at Table 2 indicate that last value carried forward does not generally control the type I error and that there may be either gain or loss of power with last value carried forward versus our approach with multiple covariates. This depends in part on the direction of the bias of the last value carried forward estimates and in part on their variances. The simulation set-up is similar to those in previous sections. The hazard function is generated from h(t) = 2eβ1X1(t)+β2X2, where X1(t) follows a multivariate normal distribution for 20 equally spaced piecewise constant function in (0, 1). It has mean μ(t) = 4sin(2πt) and variance covariance matrix with 1 at diagonal and e−|t1 − t2| off diagonal at time points t1 and t2. The time-independent covariate X2 follows a standard normal distribution. We also employed binomial X2, obtaining similar results which are omitted due to space constraints. In the simulation h = n−0.7 and we use Wald statistics to test the hypothesis β1 = 0. Four scenarios were investigated. In the first, β1 = 0, β2 = 0.5, which looks at the type I error control for time-dependent covariate in the presence of time-independent covariate; the second scenario is β1 = − 0.3, β2 = 0, 5, which looks at the power for testing time-dependent covariate with a time-independent covariate; the third is β1 =−0.15, β2 = 0.5, which looks at the power for testing time-dependent covariate at the presence of time-independent covariate with reduced signal strength; and the last scenario is β1 = −0.3, β2 = 0, which looks at the power for testing time-dependent covariate only.
Table 2.
Simulation results comparing power
| n | Our approach | last value carried forward | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | SE | CP | Power(%) | Bias | SD | SE | CP | Power (%) | |
| Case 1: β1 = 0, β2 = 0.5 | ||||||||||
| 100 | −0.017 | 0.263 | 0.244 | 92 | 7 | 0.137 | 0.080 | 0.073 | 56 | 44 |
| 400 | −0.002 | 0.183 | 0.181 | 94 | 5 | 0.129 | 0.039 | 0.035 | 6 | 94 |
| 900 | 0.001 | 0.159 | 0.155 | 94 | 5 | 0.126 | 0.025 | 0.023 | 0 | 100 |
| Case 2: β1 = − 0.3, β2 = 0.5 | ||||||||||
| 100 | 0.015 | 0.266 | 0.247 | 91 | 24 | 0.282 | 0.062 | 0.065 | 1 | 5 |
| 400 | 0.012 | 0.190 | 0.186 | 94 | 36 | 0.278 | 0.033 | 0.032 | 0 | 11 |
| 900 | 0.012 | 0.167 | 0.161 | 94 | 47 | 0.274 | 0.021 | 0.021 | 0 | 22 |
| Case 3: β1 = −0.15, β2 = 0.5 | ||||||||||
| 100 | 0.016 | 0.256 | 0.243 | 94 | 12 | 0.191 | 0.068 | 0.068 | 20 | 9 |
| 400 | 0.014 | 0.183 | 0.182 | 94 | 13 | 0.186 | 0.033 | 0.032 | 0 | 18 |
| 900 | 0.005 | 0.168 | 0.157 | 93 | 17 | 0.185 | 0.022 | 0.021 | 0 | 39 |
| Case 4: β1 = −0.3, β2 = 0 | ||||||||||
| 100 | 0.017 | 0.284 | 0.251 | 91 | 24 | 0.268 | 0.064 | 0.065 | 2 | 8 |
| 400 | 0.004 | 0.190 | 0.185 | 94 | 38 | 0.268 | 0.031 | 0.032 | 0 | 16 |
| 900 | 0.006 | 0.166 | 0.164 | 95 | 45 | 0.269 | 0.021 | 0.021 | 0 | 33 |
As can be seen in Table 2, last value carried forward continues to evidence bias, with reduced variance. The type I error is not controlled using last value carried forward approach when there are time-independent covariates. The power can either increase or decrease using last value carried forward approach as the bias can be either up or down when there are time-independent covariates. Our approach has better power when the model contains only time-dependent covariate, with the power improving as sample size increases.
Joint modelling of longitudinal and survival data has been proposed to incorporate the most commonly used first-choice assumptions from both subject areas. In the joint modelling, one assumes that there is a true, hypothetical unobserved value of the longitudinal outcome at time t, denoted by mi(t). That is, the observed covariate Zi(t) is assumed to be subject to measurement error. In contrast to the standard proportional hazards model, which assumes no measurement error, the hazard function for the event of interest is specified conditionally on mi(t) and not Zi(t). Specifically,
| (4.12) |
where wi is a vector of baseline covariates with a corresponding vector of regression coefficients γ. The parameter α quantifies the effect of the underlying longitudinal outcome on the risk of an event. A linear mixed effects model is specified for the longitudinal data:
| (4.13) |
where Zi(t) is the observed covariate, mi(t) is assumed to follow a linear mixed model, and εi(t) is assumed independent of mi(t), with mean 0 and variance σ2. To complete the model specification, the distribution of εi(t) must be specified up to σ 2, with normality commonly assumed. In the case that the measurement error σ2 = 0, the standard proportional hazards specification which conditions on Zi(t) is obtained.
The joint modelling relies heavily on the underlying assumptions in (4.13) and may result in invalid inferences under model misspecification. Moreover, due to the complexity of the model specification, the procedure may be computationally unstable with small and moderate sample sizes. We compare the performance of joint models to our approach and last value carried forward under the simulation set-up in Table 1. We fit the joint model using the R package JM (Rizopoulos (2010)), assuming normal measurement error. Note that JM cannot accommodate σ2 = 0. When we generate data from correctly specified models (4.12) and (4.13) with zero measurement error, as is assumed by the standard proportional hazards model, the program fails to converge.
We instead compared our proposed estimator with the joint modelling strategy using JM with small measurement error, giving approximately the same survival models. The longitudinal process is generated from the linear mixed model
where random intercept βi ~ N (−0.01, 0.72) and independently, the measurement error εij ~ N(0, 0.052). The number of measurements for each subject is Poisson distributed with intensity rate 8, and conditional on this, observation time tij ~ Unif(0, 2). We then generate the survival time based on hazard function
A uniformly distributed random variable is used to produce 15% censoring rate. For our method which is based on the usual proportional hazards model conditioned on the observed covariates, the data generation step for the event time is identical except we use Zi in the hazard model. For estimation, we use automatic bandwidth selection approach introduced earlier. From Table 3, we see that both methods perform well in terms of bias, variance and coverage probability in the correctly specified set-up. The efficiency gains predicted from joint modelling are reflected in the smaller empirical standard errors.
Table 3.
Summary statistics comparing our method and joint modelling method
| n | our method | joint modelling method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RB | SD | SE | CP(%) | Bias | RB | SD | SE | CP(%) | |
| correct model | ||||||||||
| 100 | 0.050 | 0.050 | 0.420 | 0.423 | 95 | 0.041 | 0.041 | 0.252 | 0.231 | 94 |
| 400 | −0.037 | −0.037 | 0.361 | 0.291 | 91 | −0.008 | −0.008 | 0.125 | 0.112 | 95 |
| 900 | −0.032 | −0.032 | 0.242 | 0.247 | 94 | −0.008 | −0.008 | 0.073 | 0.075 | 97 |
| misspecified model | ||||||||||
| 100 | 0.015 | 0.010 | 0.330 | 0.267 | 92 | −0.017 | −0.011 | 0.299 | 0.248 | 89 |
| 400 | 0.018 | 0.012 | 0.204 | 0.174 | 92 | −0.173 | −0.115 | 0.154 | 0.111 | 56 |
| 900 | 0.012 | 0.008 | 0.177 | 0.142 | 93 | −0.218 | −0.145 | 0.133 | 0.070 | 32 |
Note: see Table 1.
Next we generate data when the longitudinal model (4.13) is misspecified. The covariate process is generated through
follows a normal mixture model z = 0.4z1 +0.6z2, where z1 is a unit variance multivariate normal distribution with mean −1 and correlation e−|i−j|/20, and z2 is also a unit variance multivariate normal distribution with mean 1.5 and correlation 2−|i−j|/20, i, j = 1, … , 20. The survival time is simulated from model (1.1) with λ0(t) = 1 and β0 = 1.5. We use censoring rate = 15% to illustrate and the bandwidth selection is based on automatic procedure introduced earlier.
The results in Table 3 demonstrate that our method continues to provide unbiased estimates, the model based standard errors agree with the empirical standard errors, and our inferences provide coverage which agrees with the nominal level. On the other hand, JM exhibits substantial bias which does not diminish as the sample size increases, the empirical and model based standard errors do not agree, and the coverage probability may be much less than the nominal level, particularly for larger sample sizes. In addition, under sample size n = 900, JM failed to converge in 20 datasets, with the results in Table 2 based on those datasets where JM converged.
5 Cardiac Arrest Study
We now illustrate the proposed inferential procedure in Section 2 with a comparison to the last value carried forward approach and joint modelling method on data from a cardiac arrest study. A database of 58,132 patients who were hospitalized on the wards at the University of Chicago from November 2008 until August 2011 is utilized. During this period, there were 109 cardiac arrests on the hospital wards and we are interested in risk factors associated with cardiac arrest. Details of the study design, methods and medical implications can be found in Churpek et al. (2012).
Patients on the general hospital wards have vital signs, such as heart rate, blood pressure, and respiratory rate, collected routinely every few hours, and studies have found that abnormal vital signs are common before cardiac arrest on the wards as a signal of worsening condition (Churpek et al. (2012)). Importantly, the collection of vital signs for these patients is erratic, occurring at different time intervals for each patient. A statistical model that associates vital signs and time to cardiac arrest would yield improved detection of high-risk patients and earlier detection of clinical deterioration resulting in better patient outcomes.
To this end, we adopt model (1.1) to analyze the relationships between vital signs and time to cardiac arrest. Because heart rate has been shown to be positively correlated with cardiac arrest and is measured accurately in patients using an electronic monitor, we took the heart rate as the covariate and studied its effect on the time to occurrence of cardiac arrest. A last value carried forward analysis yields point estimate 0.041 with standard error 0.0042, which is highly statistically significant. However, because this analysis is ad hoc and lacks formal theoretical justification, it is worthwhile to assess potential biases using our proposed methods. We computed the half kernel estimates for model (1.1) with bandwidths hn = 3*(Q3 − Q1)*n−γ where Q3 is the 0.75 quantile, Q1 is the 0.25 quantile of the measurement times for heart rate, and γ= 0.5, 0.6, 0.7. We take n as total number of events of cardiac arrest after eliminating missing values, which is 107, due to the relatively low event rate. Thus, the effective sample size in this dataset, e.g., the number of events, is comparable to the effective sample size in the simulation studies in Section 4, owing to the very high censoring rate. Parameter estimators were obtained from estimating function (2.5) with different choices of bandwidths, confirming the ad hoc results from the last value carried forward approach. The resulting estimates and standard errors are 0.029 and 0.0037 when γ = − 0.5; 0.029 and 0.0040 when γ = − 0.6; 0.030 and 0.0047 when γ = − 0.7; and 0.030 and 0.0039 for automatic bandwidth selection procedure.
We can clearly see the positive association between heart rate and time to cardiac arrest, which has been verified in medical studies (Churpek et al. (2012)). For different choices of bandwidths, both point estimate and variance do not change much, which shows that our method is not sensitive to bandwidth selection. While the effect magnitude is somewhat diminished from the last value carried forward analysis, statistical significance is achieved at the 0.05 level for all bandwidth choices, confirming the ad hoc results.
We then fit the joint model using R package JM (Rizopoulos (2010)) with random intercept. The point estimate was 0.048, but standard errors were not computable due to the lack of positive definiteness of the Hessian matrix at convergence. This raises questions about whether the point estimate is the actual maximizer of the full likelihood function used to estimate the joint model. In addition to these computational stability issues, the joint model required two hours computing time, while the proposed approach and the last value carried forward method required several minutes, on the same computer.
6 Concluding Remarks
We have presented kernel weighting methods for estimation of proportional intensity models (1.1) and (1.2) with intermittently observed longitudinal covariates. The weighting techniques formalize the ad hoc last value carried forward approach by reducing the impact of covariates measured distant in time from the missing values. One may view the half kernel estimator based on backward lagged covariates as a theoretically justified adaptation of the “windowing” idea in Andersen and Liestol (2003). Our theoretical results show that this approach yields an estimator which cannot achieve parametric rates of convergence, unlike joint modelling (Tsiatis and Davidian (2004)), where much stronger modelling assumptions are invoked. Interestingly, we find that utilizing forward lagged covariates observed after the occurrence of an event via full kernel estimation may lead to improved rates of convergence relative to half kernel estimation but which are still slower than the parametric rate. Whether parametric rates of convergence are achievable without strong joint modelling assumptions is unclear and merits further investigation.
Both smoothed and non-smoothed covariates may be used in our estimation procedure. Our theoretical derivations assume that the probability that the covariates are observed when the event occurs is zero. Scenarios may arise in practice where covariates are observed at the time of events. The assumption is that the probability of this occurring has zero measure, such that the information in these covariates is asymptotically negligible and only the smoothed covariates contribute information. If the probability is non-zero, then in theory, the rate of convergence of the estimator is determined by covariates observed at event times and is the usual rate.
Modelling the hazard function conditionally on the current value is the standard form of the proportional hazards model; see Therneau and Grambsch (2001), for a discussion of the proportional hazards model with time-dependent covariates. All of the standard software have implemented the proportional hazards model with time-dependent covariates based on the specification in which the current value of the time-dependent covaraite is utilized. That said, there may be applications in which the relationship between the hazard and a complicated function of the covariate’s trajectory, such as the trend, may be of interest. To conduct such analyses, more complicated models are needed, e.g., joint models, in which the failure time and the time-dependent covariate are jointly modeled. The usual proportional hazards model which does not require modelling the time-dependent covariate may not be as amenable to capturing such covariate effects.
The standard form of the proportional hazards model is specified conditionally on the observed value of the covariate and does not permit measurement error. The goal of this paper is to provide methods for fitting the standard proportional hazards model with sparsely observed time-dependent covariates in the absence of measurement error. We note that even with time-independent covariates the presence of measurement error invalidates the standard partial likelihood estimators and more complicated models and estimation procedures are needed. With time-dependent covariates, the presence of measurement error necessitates the use of joint models and simultaneous estimation of the longitudinal and survival models via maximum likelihood, which is complicated both computationally and inferentially.
We note that in general when employing a standard proportional hazards model with “internal” (or endogenous) time-dependent covariate it is not possible to predict survival based on Z(t). Such “internal” covariates are measured on the individual being followed for the event of interest. For details, please see the discussion in Kalbfleisch and Prentice (2002). If the covariate is “external” (or exogenous), e.g., not measured at the individual level, then prediction may be possible. Both the half and full kernel methods provide consistent and asymptotically normal estimates of the regression parameters in the proportional hazards model, regardless of whether the time-dependent covariates are “internal” or “external”. If the covariates are “internal”, then prediction is not possible, while if they are “external” prediction is possible. These results regarding prediction are true for the usual partial likelihood estimator with time-dependent covariates when the covariates are fully observed. For the case of “internal” covariates, if prediction is desired, alternative modelling strategies, like joint modelling, are needed.
While the joint modelling approach has certain modelling advantages over the standard Cox model, in addition to potential improvements in efficiency, these gains depend heavily on strong assumptions about the model for the longitudinal covariates and considerable care is needed in the implementation of these full likelihood methods. In the cardiac data analysis, computational problems resulted in questionable results, while simpler partial likelihood procedures converged reliably. Minimal assumptions are required for the longitudinal covariates for the validity of the kernel weighted partial likelihood estimators, which only utilize assumptions on the model for the failure time, leading to the bias variance trade-off evidenced in the simulations in Section 4.
Additional simulations were performed to assess whether our proposed method might be severely underpowered relative to the last value carried forward approach for testing the effect of the time-dependent covariate. Results (omitted) demonstrate that the relative power of the two procedures depends in part on the magnitude and direction of the bias for last value carried forward and in part on the improved efficiency of last value carried forward. In certain scenarios, where the bias is strongly towards the null, last value forward may lose considerable power relative to our proposed methods. In these simulations, the time-dependent covariate had a strong and nonlinear trend, where the mean function for the time-dependent covariate is a sinusoidal function which oscillates strongly over the time interval of observation. Our proposed method performed well in this scenario with a moderate number of observation times for the time-dependent covariate. To further explore the efficiency issue, we conducted simulations in which the trajectory is completely observed. In this case, the naive last value carried forward analysis is valid as covariate values are observed at all event times. This may be viewed as a “gold standard” analysis. In such settings, our proposed method is unbiased but unsurprisingly may incur substantial efficiency loss relative to the “gold standard”, which is also unbiased. The efficiency loss in the simulations diminshes as the number of observations of the covariate process increases.
As mentioned previously, the methods of Cai and Sun (2003) and Tian, Zucker and Wei (2005) for the proportional hazards model with time-dependent regression parameter apply identical kernel weights to all individuals when smoothing the partial likelihood. These methods are not directly applicable in our setting, where different weights are needed for different individuals. Moreover, the methods for time-dependent regression parameters with time-dependent covariates require that the trajectory of the time-dependent covariate is fully observed. If the covariate is sparsely observed, then the methods are not applicable. It would be of interest to generalize our smoothed partial likelihood approach for the standard formulation of the Cox model with time-independent regression parameter to the time-dependent proportional hazards model with sparsely observed time-dependent covariates. This is a topic for future research.
When the observation times are informative, as might occur when there is more frequent monitoring of high risk subjects, the usual assumption of independent observation times is violated and our methods are not valid. Relevant literature on this topic includes Sun et al. (2005), Liu et al. (2008) and Sun et al. (2012), among others. Future work is needed to extend our methods to accommodate such informative observation times.
Supplementary Material
References
- Andersen P, Liestol K. Attenuation caused by infrequently updated covariates in survival analysis. Biostatistics. 2003;4:633–649. doi: 10.1093/biostatistics/4.4.633. [DOI] [PubMed] [Google Scholar]
- Andersen P, Gill R. Cox’s regression models for counting processes: a large-sample study. Ann Statist. 1982;10:1100–1120. [Google Scholar]
- Cai Z, Sun Y. Local linear estimation for time-dependent coefficients in Cox’s regression models. Scandinavian Journal of Statistics. 2003;30:93–111. [Google Scholar]
- Churpek M, Yuen T, Park SY, Hall JB, Edelson DP. Can vital signs predict cardiac arrest on the wards? a nested case-control study. Chest. 2012;141:1170–1176. doi: 10.1378/chest.11-1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degruttola V, Tu XM. Modelling progression of CD-4 lymphocyte count and its relation to survival time. Biometrics. 1994;50:1003–1014. [PubMed] [Google Scholar]
- Dupuy JF, Grama I, Mesbah M. Asymptotic theory for the Cox model with missing time-dependent covariate. Ann Statist. 2006;34:903–924. [Google Scholar]
- Faucett CL, Thomas DC. Simultaneously modelling censored survival data and repeatedly measured covariates: A Gibbs sampling approach. Statist Med. 1996;15:1663–1685. doi: 10.1002/(SICI)1097-0258(19960815)15:15<1663::AID-SIM294>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- Fleming TR, Harrington DP. Wiley series in probability and statistics. 2005. Counting processes and survival analysis. [Google Scholar]
- Gill RD, van der Laan MJ, Robins JM. Coarsening at random: Characterizations, conjectures and counterexamples. In: Lin DY, Fleming TR, editors. In Proc First Seattle Symposium in Biostatistics: Survival Analysis. Springer; New York: 1997. pp. 255–294. [Google Scholar]
- Henderson R, Diggle P, Dobson Angela. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;4:465–480. doi: 10.1093/biostatistics/1.4.465. [DOI] [PubMed] [Google Scholar]
- Hogan JW, Laird NM. Mixture models for the joint distribution of repeated measures and event times. Statist Med. 1997;16:239–257. doi: 10.1002/(sici)1097-0258(19970215)16:3<239::aid-sim483>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- Ibrahim JG, Chu H, Chen LM. Basic conectps and methods for joint models of longitudinal and survival data. J Clin Oncol. 2010;28:2796–2801. doi: 10.1200/JCO.2009.25.0654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalbeisch JD, Prentice RL. The statistical analysis of failure time data. Wiley; 2002. [Google Scholar]
- Liu L, Huang X, O’Quigley J. Analysis of longitudinal data in the presence of informative observational times and a dependent terminal event, with application to medical cost data. Biometrics. 2008;64:950–958. doi: 10.1111/j.1541-0420.2007.00954.x. [DOI] [PubMed] [Google Scholar]
- Polland D. Convergence of stochastic processes. Springer; New York: 1984. [Google Scholar]
- Rizopoulos D. Chapman and Hall/CRC Biostatistics Series. 2012. Joint models for longitudinal and time-to-event data: with applications in R. [Google Scholar]
- Rizopoulos D. JM: An R package for the joint modelling of longitudinal and time-to-event data. Journal of Statistical Software. 2010;35:1–33. [Google Scholar]
- Sun J, Park DH, Sun L, Zhao X. Semiparametric regression analysis of longitudinal data with informative observation times. J Amer Statist Assoc. 2005;100:882–889. [Google Scholar]
- Sun L, Song X, Zhou J, Liu L. Joint analysis of longitudinal data with informative observation times and a dependent terminal event. J Amer Statist Assoc. 2012;107:688–700. [Google Scholar]
- Therneau TM, Grambsch PM. Modeling survival data: extending the Cox model. Springer; New York: 2001. [Google Scholar]
- Tian L, Zucker D, Wei LJ. On the Cox model with time-varying regression coefficients. J Amer Statist Assoc. 2005;100:172–183. [Google Scholar]
- Tsiatis A, Degruttola V, Wulfsohn MS. Modelling the relationship of survival to longitudinal data measured with error. Applications to survival and CD4 counts in patients with AIDS. J Amer Statist Assoc. 1995;90:27–37. [Google Scholar]
- Tsiatis A, Davidian M. A semiparametric estimator for the proportional hazards model with longitudinal covariate measured with error. Biometrika. 2001;88:447–458. doi: 10.1093/biostatistics/3.4.511. [DOI] [PubMed] [Google Scholar]
- Tsiatis A, Davidian M. Joint modelling of longitudinal and time-to-event data: an overview. Statist Sinica. 2004;14:809–834. [Google Scholar]
- van der Vaart A, Wellner J. Weak convergence and empirical processes. Springer; New York: 1996. [Google Scholar]
- Wulfsohn MS, Tsiatis AA. A jiont model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- Xu J, Zeger SL. Joint analysis of longitudinal data comprising repeated measures and times to events. Journal of Applied Statistics. 2001;50:375–387. [Google Scholar]
- Yao F. Functional principal component analysis for longitudinal and survival data. Statist Sinica. 2007;17:965–983. [Google Scholar]
- Zeng D, Cai J. Asymptotic results for maximum likelihood estimators in joint analysis of repeated measurements and survival time. Ann Statist. 2005;33:2132–2163. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


