atSNP: transcription factor binding affinity testing for regulatory SNP detection

Abstract

Motivation: Genome-wide association studies revealed that most disease-associated single nucleotide polymorphisms (SNPs) are located in regulatory regions within introns or in regions between genes. Regulatory SNPs (rSNPs) are such SNPs that affect gene regulation by changing transcription factor (TF) binding affinities to genomic sequences. Identifying potential rSNPs is crucial for understanding disease mechanisms. In silico methods that evaluate the impact of SNPs on TF binding affinities are not scalable for large-scale analysis.

Results: We describe affinity testing for regulatory SNPs (atSNP), a computationally efficient R package for identifying rSNPs in silico. atSNP implements an importance sampling algorithm coupled with a first-order Markov model for the background nucleotide sequences to test the significance of affinity scores and SNP-driven changes in these scores. Application of atSNP with >20 K SNPs indicates that atSNP is the only available tool for such a large-scale task. atSNP provides user-friendly output in the form of both tables and composite logo plots for visualizing SNP-motif interactions. Evaluations of atSNP with known rSNP-TF interactions indicate that SNP is able to prioritize motifs for a given set of SNPs with high accuracy.

Availability and implementation: https://github.com/keleslab/atSNP.

Contact: keles@stat.wisc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide association studies have been instrumental in identifying single nucleotide polymorphisms (SNPs) associated with large numbers of phenotypes. The vast majority of association SNPs are in non-coding regions, suggesting that they may have regulatory roles in deriving the phenotype (Maurano et al., 2012). In particular, regulatory SNPs which alter binding affinity of transcription factors and affect gene expression constitute an important class of such SNPs (Pai et al., 2015). A standard in silico approach for identifying rSNPs is by evaluating how the SNP-driven nucleotide change impacts binding affinity of TFs to the region surrounding the SNP (Macintyre et al., 2010; Riva, 2012; Thomas-Chollier et al., 2011; Andersen et al., 2008). Specifically, the DNA sequences around each SNP are scored against a library of TF motifs with both the reference and the SNP alleles using position weight matrices (PWMs) (Stormo et al., 1982) of the motifs. SNPs with significantly different scores between the reference and SNP alleles are then hypothesized as rSNPs.

We describe atSNP, an R package that carries out the following tasks for every SNP-motif combination of the input data after extracting genome sequences of small windows (±30 bps) around the SNP positions: (i) computing affinity scores for both alleles; (ii) statistical testing for allele-specific affinity scores; (iii) statistical testing for changes in affinity scores between alleles. A few existing tools can perform various subsets of these tasks (Table 1). The most distinctive feature of atSNP is its ability to accommodate large scale analysis (e.g. over > 20 K SNPs). is-rSNP has the most similar functionality to atSNP; however, is-rSNP (both 1.0 and 2.0) can only analyze at most 20 SNPs at a time. Similarly, TRAP takes as input only one SNP. Although rSNP-mapper can take as input larger number of SNPs, it lacks critical calculations such as the significance of SNP-driven affinity change. FIMO is not designed for evaluating SNP impact on affinity scores; however, it enables P-value computation for affinity scores and can be used to compare scores under different alleles. However, due to computational reasons, FIMO can only accommodate outputting results thresholded by a small pre-specified significance level for large SNP sets. In our hands with a 24 AMD Opteron 2.2 GHz processor, a FIMO run for 26 100 SNPs against a single PWM without thresholding could not finish within 24 hours whereas atSNP required less than 5 minutes. The main computational burden of both FIMO and is-rSNP is the computation of the exact P-values by enumerating all possible sequences and computing their scores under the null hypothesis. atSNP utilizes an importance sampling technique to overcome this challenge (Supplementary Materials).

Table 1.

Comparison of existing in-silico rSNP detection tools

Method	Allele-specific scores	P-values for allele-specific scores	Between-allele scores	P-values for between-allele scores	User specified motif library	Scalability to >20 K SNPs	Visualization of SNP effects	Open source code
atSNP	✓	✓	✓	✓	✓	✓	✓	✓
is-rSNP (Macintyre et al., 2010)	✓	✓	✓	✓	✓
RAVEN (Andersen et al., 2008)	✓		✓
rSNP-MAPPER (Riva, 2012)	✓		✓
TRAP⋆ (Thomas-Chollier et al., 2011)	✓	✓	✓
FIMO⋆⋆ (Grant et al., 2011)	✓	✓			✓			✓

^⋆TRAP takes as input only one SNP at a time.

^⋆⋆FIMO scans sequences for occurrences of motifs and is not readily a rSNP tool.

2 Implementation

Supplementary Figure S1 summarizes the main inputs and outputs of atSNP. atSNP includes a motif library of 2065 PWMs from the ENCODE project (Kheradpour and Kellis, 2014) and the JASPAR core motif library (Mathelier et al., 2014). In addition, it allows user-defined motif libraries in a variety of formats, e.g. MEME format (Grant et al., 2011) or other PWM libraries from the JASPAR database (Mathelier et al., 2014). atSNP accesses genome data of the input organism through the Bioconductor BSGenome package (Pages, 2014) and thus can analyze data from a variety of organisms. It computes the binding affinity score for each subsequence overlapping the SNP position in either strand and reports the maximum of these as the affinity score of the sequence. In order to evaluate the significance of these scores, atSNP first estimates a null distribution for the scores by a first-order Markov model using the subsequences surrounding the SNP positions (default ± 30 bps of the SNP position). P-value computations for both the allele-specific scores and between-allele score differences are carried out using importance sampling algorithms adapted from Chan et al. (2010) (Supplementary Materials). We compared the P-values computed by atSNP with those computed by FIMO (Grant et al., 2011) and illustrated that the importance sampling method drastically improves computational time without sacrificing accuracy (Supplementary Materials).

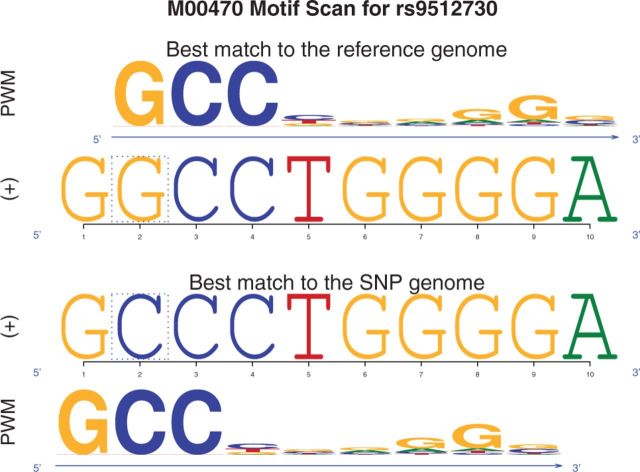
atSNP produces as output a data.table listing the affinity scores, P-values, and allele-specific matching positions for each SNP-motif pair. This R data structure provides powerful functionality for querying and integrating additional data sources. Furthermore, atSNP provides composite logo plots for directly visualizing the SNP effects on motif matches as in Figure 1.

Fig. 1.

A composite logo plot for rs9512730-M00470 (TFAP2) pair from atSNP. The SNP location is within the dashed box. The P-values for the binding affinity of the best matches with the SNP and reference alleles are 2.29e−3 and 4.9e−4, respectively. The P-value for the affinity change is 0.058 (ranked 1450th among all the 26 100 SNPs). If we compare the binding affinities of the reference and SNP allele sequences based on the matching position on the reference allele only, there is a big score change induced by the SNP. This is likely to be a false positive, because shifting 1 bp to the left results in a matching subsequence with the SNP allele. atSNP allows the matching positions on both alleles to be different and thereby avoids such potential false positives

3 Example

To demonstrate atSNP’s computation efficiency, we evaluated the regulatory potential of 26 100 SNPs from the Psychiatric Genomics Consortium (Gratten et al., 2014) against a library of 10 motifs. Genome subsequences around the SNP positions were obtained from the human genome version hg19 with the BSgenome package (Pages, 2014). atSNP ran to completion in 7 min and 15 s of wall clock time using 10 parallel threads on a server with 24 AMD Opteron 2.2 GHz processors and in 23 min and 4 s when using only a single thread. We also analyzed the same dataset with FIMO for a much simpler task of calculating P-values of subsequences overlapping each SNP position. FIMO required 2.5 h to complete at the P-value threshold of 0.1. Since is-rSNP does not support batch execution of large sets of SNPs, we did not include it in this run-time comparison. We further performed numerical comparisons and evaluations with known rSNP-TF interactions between atSNP and FIMO and is-rSNP and illustrated that atSNP’s results are both accurate and robust against false positives (Section 4 of Supplementary Materials). A sample SNP-motif interaction in Figure 1 also highlights that atSNP prevents potential false positives by allowing different matching positions with the reference and SNP alleles.

Funding

This research was supported by National Institutes of Health grants HG007019, HG003747, and U54AI117924.

Conflict of Interest: none declared.