Evaluating Continuous Tumor Measurement-Based Metrics as Phase II Endpoints for Predicting Overall Survival

Abstract

Background:

We sought to develop and validate clinically relevant, early assessment continuous tumor measurement–based metrics for predicting overall survival (OS) using the Response Evaluation Criteria in Solid Tumors (RECIST) 1.1 data warehouse.

Methods:

Data from 13 trials representing 2096 patients with breast cancer, non–small cell lung cancer (NSCLC), or colorectal cancer were used in a complete case analysis. Tumor measurements from weeks 0–6-12 assessments were used to evaluate the ability of slope (absolute change in tumor size from 0-6 and 6–12 weeks) and percent change (relative change in tumor size from 0–6 and 6–12 weeks) metrics to predict OS using Cox models, adjusted for average baseline tumor size. Metrics were evaluated by discrimination (via concordance or c-index), calibration (goodness-of-fit type statistics), association (hazard ratios), and likelihood (Bayesian Information Criteria), with primary focus on the c-index. All statistical tests were two-sided.

Results:

Comparison of c-indices suggests slight improvement in predictive ability for the continuous tumor measurement–based metrics vs categorical RECIST response metrics, with slope metrics performing better than percent change metrics for breast cancer and NSCLC. However, these differences were not statistically significant. The goodness-of-fit statistics for the RECIST metrics were as good as or better than those for the continuous metrics. In general, all the metrics performed poorly in breast cancer, compared with NSCLC and colorectal cancer.

Conclusion:

Absolute and relative change in tumor measurements do not demonstrate convincingly improved overall survival predictive ability over the RECIST model. Continued work is necessary to address issues of missing tumor measurements and model selection in identifying improved tumor measurement–based metrics.

The Response Evaluation Criteria in Solid Tumors (RECIST) is the current standard methodology for assessing changes in tumor size in clinical trials of solid tumors (1–2). RECIST categorizes change in tumor measurements into four groups: complete response (CR), complete disappearance of all lesions; partial response (PR), at least 30% reduction from baseline sum for target lesions; progressive disease (PD), at least 20% increase from the lowest sum of measurements (and at least 5mm absolute increase, in RECIST version 1.1) or new lesion recorded (with additional FDG PET assessment, in version 1.1); and stable disease (SD), neither sufficient shrinkage to qualify as PR/CR nor sufficient increase to qualify as PD. Concerns over the high failure rate in Phase III trials has led to pursuing alternatives to RECIST response as a Phase II endpoint.

In order to make more complete use of detailed tumor measurements, several alternative approaches have been proposed. These include the use of continuous tumor measurement–based metrics representing the absolute change in tumor size (eg, log ratio of the sum of tumor measurements at week 8 vs at baseline [3–5]); the relative change in tumor size (eg, between the baseline and first assessment or between the first and second assessments [6–7], and averaged overall assessments [8]); and time to tumor growth (eg, using a tumor size model [5]). Although some of these alternatives have been evaluated using clinical data, none has been evaluated with a large database across multiple studies. We previously reported that alternative cutpoints for defining the four RECIST-based groups (CR, PR, PD, and SD) and alternative classifications (eg, CR/PR vs SD vs PD or CR/PR/SD vs PD) provided no meaningful improvement over RECIST response in predicting overall survival (OS) (9). While Karrison et al. (3) and Jaki et al. (4) discussed their proposed endpoints in the context of designing phase II trials and the associated savings in sample size and Suzuki et al. (6) evaluated endpoints based on statistical significance of hazard ratio estimates, none of these directly evaluated the predictive ability of the endpoint on OS as the primary goal.

In this work, we seek to develop and validate simple, clinically relevant metrics for predicting OS based on continuous summaries of longitudinal tumor measurements. Specifically, we wish to evaluate the tumor measurement–based metrics alone, without adjusting for other patient characteristics, in order to understand their potential as phase II endpoints and to compare with the current RECIST-based response endpoints, which are based strictly on tumor measurement–based changes. To this end, our goal is not to develop an individual’s risk prediction model. The metrics we consider are motivated by clinical and intuitive appeal and are largely similar in principle to those previously proposed in the literature. We examine these metrics for their predictive ability in a large database, specifically data that were used to develop the RECIST version 1.1 guidelines (1–2). Predictive ability was assessed via discrimination using the concordance index (c-index [10]), as well as via measures of calibration, association, and likelihood.

Methods

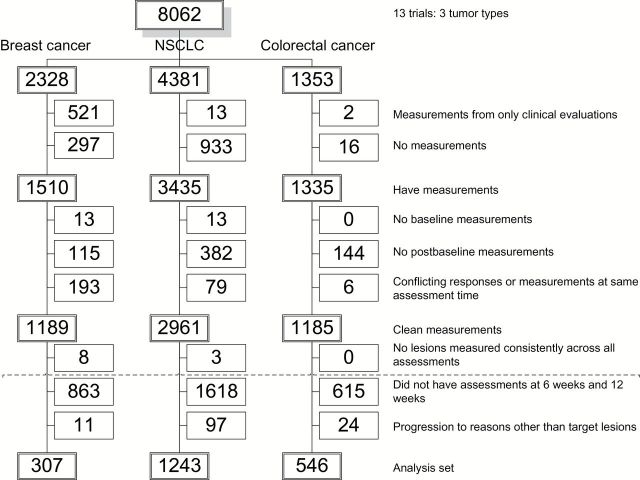
Data from the RECIST 1.1 data warehouse, representing 13 trials in three disease groups: breast cancer, non–small cell lung cancer (NSCLC), and colorectal cancer were used (1–2). The original RECIST data warehouse included 16 trials that are described in (1–2). Twelve of the 13 trials had assessments at six and 12 weeks; one trial had assessments at seven and 14 weeks. The raw data included 8062 patients with cycle-by-cycle, lesion-by-lesion measurement data. Patients were excluded for several reasons: having either no recorded measurements or measurements based on clinical evaluations only (n = 1782); lack of clean measurement data: no baseline measurements (n = 26), no postbaseline measurements (n = 641), and conflicting responses or measurements recorded for the same assessment time (n = 278); and having lesions that were not consistently measured across all assessments (n = 11). After these initial exclusions, a patient was assigned “protocol-compliant” status if all observed measurements were within two weeks of protocol-scheduled assessments while the patient remained on active treatment. The data were then split into training (60%) and validation (40%) sets, with the split stratified on survival status, progression status, and protocol-compliant status. Patients were subsequently excluded for the following additional reasons: missing assessments within +/- two weeks of week 6 or 12 (n = 3096) and having disease progression for reasons other than progression of target lesions (n = 132).

Figure 1 is a CONSORT diagram showing flow of patients from the raw dataset to the final analysis dataset. The final dataset included 2096 patients for whom consistent tumor measurements (millimeters, mm) were available, representing patients with breast cancer (307), NSCLC (1243), and colorectal (546) cancer.

Figure 1.

CONSORT Diagram showing the flow of patients from the original dataset to the final analysis dataset. NSCLC = non–small cell lung cancer.

A 12-week landmark analysis was conducted. Specifically only patients who were alive and progression-free at 12 weeks postbaseline and who had measurements available at baseline, six weeks, and 12 weeks were included in analyses. Measurements from baseline, six weeks, and 12 weeks were used. As reference for comparison, we fit a Cox model using the RECIST-based definition of response to represent the current practice. We also fit a Cox model with time-dependent progression status using data available over the entire follow-up (ie, no landmark analysis). This latter model represents the potentially best model because it utilizes all follow-up data, but practically does not suggest an obvious metric (eg, first slope or last slope) nor does it allow for early assessment (eg, at 12 weeks).

Cox proportional hazards models were used with a primary endpoint of OS. A separate model was fit for each disease group; each model was adjusted for average baseline size (mm/lesion), defined as the sum of all baseline measurements divided by the number of baseline lesions. The primary model assessment criterion was discriminatory ability measured by the concordance index, or c-index (10). The concordance index measures the ability of a model’s predictions to differentiate patients with different survival outcomes. It ranges from 0 to 1.0, where values of 0.5 to 1.0 reflect good discrimination, a value of 0.5 reflects no discrimination (ie, random prediction), and values of 0 to 0.5 reflect good “reverse” discrimination. For a more complete picture of predictive ability, we also summarized other aspects of predictive ability, namely measures of calibration (Hosmer-Lemeshow [HL], type Goodness-of-Fit, comparing the observed vs predicted 1-year survival probabilities within deciles of predicted probabilities [11]), association (hazard ratios and P values), and likelihood (Bayesian Information Criteria [BIC]). Nonparametric bootstrapping with 1000 replicates was used to construct 95% confidence intervals (CIs) of the c-indices and HL statistics for a single model and of differences in c-indices and HL statistics between any two models. Discriminatory ability and calibration of models were validated externally. Specifically, the training model estimates were first applied to the validation set to obtain predictions, and the c-index and HL statistic were then calculated. The proportional hazards (PH) assumption was assessed by the method of Grambsch and Therneau (12). All statistical tests were two-sided.

Metrics

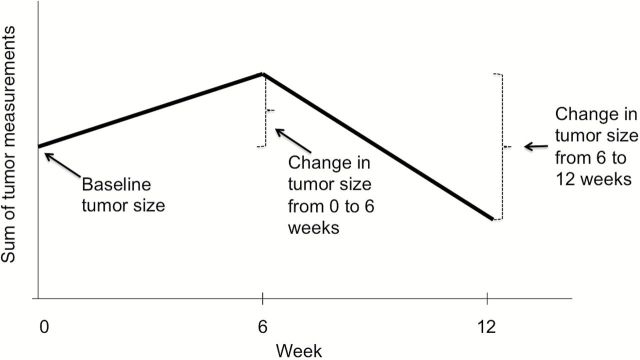
We considered two pairs of continuous metrics for predicting OS: slope (absolute change) and percent (%) change in tumor size. These metrics are simple to calculate and understand, clinically relevant, similar in principle to those previously proposed in the literature, and motivated by intuitive appeal. Specifically, if we consider continuous measurements at three timepoints, then the absolute (and relative) change in tumor size between any two consecutive timepoints, as well as the baseline tumor size, is a simple summary statistic that captures the essential features of the tumor size trajectory (Figure 2). Therefore, with m_t denoting the measurement at week t (or within a +/- 2-week window) and Δt the actual time difference (in weeks) between measurements, we considered first slope (units: mm/w; defined as: (m₆- m₀)/Δt) and last slope (units: mm/w; defined as (m_12- m₆)/Δt), and first percent change in slope (units: 10%change/w; defined as: (10*(m₆ – m₀)/(Δt * m₀)) and last percent change in slope (units: 10%change/w; defined as: (10*(m₁₂- m₆)/(Δt * m₆)). We also included linear spline terms, with knots at first slope and last slope (or first percent change and last percent change) equaling 0. Including the spline terms allows for the hazard ratio associated with first slope (or last slope, first percent change, or last percent change) to differ according to whether the first slope (or last slope, first percent change, or last percent change) is positive or negative. The slope and the percent change model specifications are given below.

Figure 2.

Hypothetical tumor size trajectory. Simple summary statistics that capture essential features of the trajectory include (absolute and relative) change in measurements at consecutive timepoints and baseline tumor size.

Slope Mode:

$$\begin{array}{l}log\lambda (t)\\ =log{\lambda }_0(t)+{\beta }_{1}aveBaseline+\\ {\beta }_{2}firstslope+{\beta }_3{\mathrm{(firstslope)}}^{+}+{\beta }_{4}lastslope+{\beta }_5{\mathrm{(lastslope)}}^{+}\end{array}$$

Percent (%) Change Model:

$$\begin{array}{l}log\lambda (t)\\ =log{\lambda }_0(t)+{\beta }_{1}aveBaseline+\\ {\beta }_{2}first\%change+{\beta }_3{\mathrm{(first\%change)}}^{+}\\ +{\beta }_{4}last\%change+{\beta }_5{\mathrm{(last\%change)}}^{+}\end{array}$$

In both models, λ(t) represents the hazard function for a patient, λ₀(t) represents the baseline hazard function, and aveBaseline is the average baseline size (mm/lesion). The firstslope, lastslope, first%change, and last%change are the metrics as previously defined; and (X)⁺ = X if X > 0 and = 0 otherwise, ie, the linear spline term.

Results

The median OS for the 307 breast cancer patients was 17.6 months, with a total of 205 deaths and a median survival of 532 days. The median OS for the 1243 NSCLC patients was 11.2 months, with a total of 670 deaths. The median OS for the 546 colorectal cancer patients was 15.2 months, with a total of 236 deaths. The average baseline tumor sizes were 34.82, 43.36, and 41.33mm for breast cancer, NSCLC, and colorectal cancer patients, respectively. The average changes in tumor size across all patients were -2.34, -3.68, and -3.24mm between baseline and first (6-week) assessment and -1.45, -1.07, and -1.76mm between the six- and 12-week assessment for breast cancer, NSCLC, and colorectal cancer, respectively; that is, we saw on average a decrease in tumor size over time across all patients. Detailed results for the training and validation set models are provided in Tables 1 and 2. We highlight results for the training set models below.

Table 1.

Summary of hazard ratios from slope and percent (%) change models

Model and metric	HR (P value)
	Breast	NSCLC	Colorectal
Slope model	training (n = 189)	training (n = 746)	training (n = 322)
Average baseline size, mm	1.00	1.00	1.00
	(.39)	(.16)	(.19)
First slope, mm/w	0.89	0.98	1.04
	(.0012)	(.19)	(.14)
(First slope)+*	1.10	1.50	0.93
	(.68)	(<.001)	(.44)
Last slope, mm/w	1.04	0.95	1.01
	(.46)	(.077)	(.71)
(Last slope)+*	2.01	1.26	1.54
	(.036)	(<.001)	(<.001)
Percent (%) change model	training (n = 182)	training (n = 734)	training (n = 320)
Average baseline size, mm	1.01	1.01	1.01
	(.048)	(.0067)	(.10)
First % change, 10%/wk	0.57	1.14	3.97
	(.14)	(.43)	(.0038)
(First % change)+*	2.69	2.61	0.28
	(.47)	(.48)	(.056)
Last % change, 10%/wk	1.06	1.22	1.83
	(.84)	(.26)	(.19)
(Last % change)+*	4.26	2.34	4.01
	(.20)	(.0035)	(.095)

* Linear spline term (X)⁺ defined as (X)⁺ = X if X > 0 and = 0 otherwise. HR = hazard ratio; NSCLC = non–small cell lung cancer.

Table 2.

Summary statistics for slope and percent (%) change models*

Statistic	Breast		NSCLC		Colon
	Slope	% change	Slope	% change	Slope	% change
c-index
Training (95% CI)†	0.58 (0.53 to 0.65)	0.55 (0.52 to 0.63)	0.58 (0.55 to 0.61)	0.57 (0.55 to 0.61)	0.62 (0.58 to 0.68)	0.64 (0.59 to 0.69)
Externally validated	0.47	0.45	0.56	0.58	0.52	0.55
RECIST‡	0.52		0.57		0.60
Time-dependent§	0.67		0.67		0.67
HL
Training	0.05	0.04	0.03	0.01	0.12	0.05
Externally validated	0.48	0.35	0.04	0.07	0.11	0.16
RECIST	0.05		0.01		0.04
BIC
Training	1125.73	1079.59	4981.90	4823.78	1365.74	1370.51
RECIST	2065.38		8845.70		2668.12

* Concordance (c-) index, Hosmer-Lemeshow goodness-of-fit statistic, and Bayesian Information Criteria, with comparison to RECIST model and time-dependent Cox model. BIC = Bayesian Information Criteria; CI = confidence interval; HL = Hosmer-Lemeshow; NSCLC = non–small cell lung cancer; RECIST = Response Evaluation Criteria in Solid Tumors.

† 95% CI for c-indices are bootstrap confidence intervals.

‡ RECIST model is fit to all data available from first 12 weeks in overall dataset (training and validation sets).

§ Time-dependent c-index is based on a Cox model with time-dependent progression status using all available data in overall dataset (training and validation sets), ie, using the time-dependent models described in the Methods section.

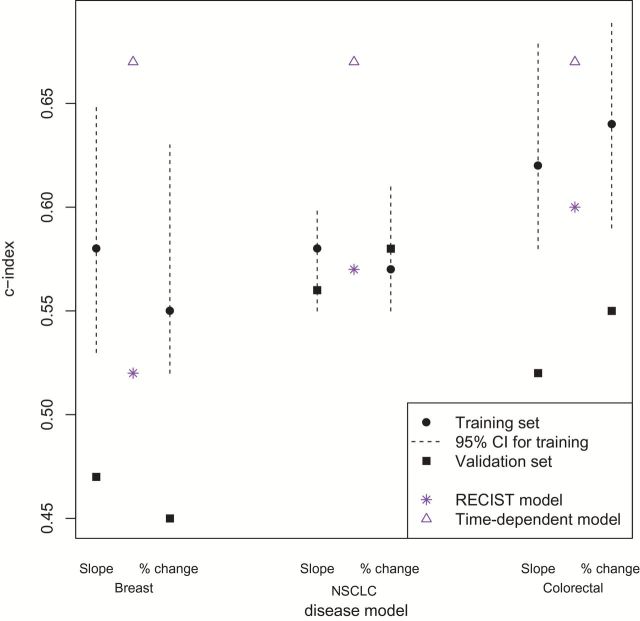
The distributions of average baseline size and the four metrics were roughly symmetric. No violations of the PH assumption were noted. For all three disease types, the slope and percent change models provided higher point-wise estimates for the c-indices than the RECIST models. The slope models performed slightly better than the percent change models for breast cancer and NSCLC patients. In particular, the pointwise c-indices for patients with breast cancer, NSCLC, and colorectal cancer in the slope models were 0.58 (95% bootstrap CI = 0.53 to 0.65), 0.58 (95% CI = 0.55 to 0.61), and 0.62 (95% CI = 0.58 to 0.68), respectively; and in the percent change models, 0.55 (95% CI = 0.52 to 0.63), 0.57 (95% CI = 0.55 to 0.61), and 0.64 (95% CI = 0.59 to 0.69). In comparison, the c-indices for the RECIST models were 0.52 (95% CI = 0.49 to 0.61), 0.57 (95% CI = 0.54 to 0.60), and 0.60 (95% CI = 0.55 to 0.61). However, for all three disease types, the bootstrap 95% confidence interval for the pairwise differences in c-indices comparing the slope vs RECIST, percent change vs RECIST, and slope vs percent change models included 0 (results not shown). The c-indices for the time-dependent models described in the Methods section (0.67 for all 3 diseases) were substantially higher than those for all three of the models (slope, percent change, and RECIST), suggesting theoretical potential for improvement in predictive ability (Tables 1 and 2; Figure 3).

Figure 3.

Concordance (c-) index across diseases using measurements from week 0-6-12 visits, for the slope model and the percent change model, in training (black solid circles) and external validation sets (black solid squares). The dotted lines represent 95% bootstrap confidence intervals (CIs) associated with the c-indices from the training set. For comparison, c-indices from the RECIST and time-dependent models are marked. Differences in disease-specific c-indices between models are not statistically significant, based on bootstrap 95% CIs of pairwise differences, including 0 (not shown). NSCLC = non–small cell lung cancer; RECIST = Response Evaluation Criteria in Solid Tumors.

In addition to model discrimination, we summarize other aspects of predictive ability for the models (Tables 1–2). Regarding calibration, all three models had similar goodness-of-fit statistics, with the slope model having slightly poorer calibration (larger HL statistic) than either the percent change or RECIST models. Again, the confidence intervals for the pairwise differences in HL statistics included 0. In terms of likelihood, the slope and percent change models had similar BIC, but the RECIST model had higher BIC than either the slope or percent change models.

Measures of association were assessed by the hazard ratios and P values (Table 1). In general, most hazard ratios are close to 1, although there is no uniform pattern of association (eg, all positive or all negative) between the metrics and the hazard for death across the models and disease groups. The one exception is with the last slope spline term in the slope models. The hazard ratio corresponding to this term is statistically significantly greater than 1 across all diseases and in both the training and validation set, which suggests that among patients with similar first slope values, the hazard ratio associated with an increase in last slope is higher for those for whom the last slope is positive (tumor growth) vs negative (tumor shrinkage).

The externally validated measures of discriminatory ability and calibration are presented in Table 2. The validated c-indices were lower than those from the training set, for all diseases and models, except for the percent change model in NSCLC. Specifically, for the slope and percent change models, the validated (training) c-indices were: 0.47 and 0.45 for breast cancer (training: 0.58 and 0.55), 0.56 and 0.58 for NSCLC (training: 0.58 and 0.57), and 0.52 and 0.55 for colorectal cancer (training: 0.62 and 0.64). The validated HL statistics were higher than those from the training set, for all diseases and models, except for the slope model in NSCLC. Specifically, for the slope and percent change models, the validated (training) HL statistics were: 0.48 and 0.35 for breast cancer (training: 0.05 and 0.04), 0.04 and 0.07 for NSCLC (training: 0.03 and 0.01), and 0.11 and 0.16 for colorectal cancer (training: 0.12 and 0.05).

Discussion

This work was motivated by the need to identify and evaluate clinically relevant, easily assessable alternative metrics with improved predictive ability for overall survival. Our goal was to identify alternative tumor measurement-based metrics, and not to develop a risk prediction model. Previously we found that alternative categorical tumor measurement metrics provided no improvement over the current RECIST metrics in predicting survival (9). In this work, we sought to improve predictive ability through the use of continuous tumor measurement–based metrics. The primary evaluation of predictive ability was discrimination (via the c-index), with secondary evaluations being calibration (goodness-of-fit), association (hazard ratios and P values), and likelihood (BIC). By reporting results of all of these measures, we hope to offer a more comprehensive understanding of the predictive ability of the metrics. Evaluating any single one of these measures alone, and specifically identifying a statistically significant association (eg, Suzuki et al. [6], Birchard et al. [13]), may be sufficient to identify a candidate for a new metric, but may not be sufficient to establish an improvement in predictive ability over RECIST. For example, from our results, we observe that although a metric is statistically significantly associated with the hazard of death, it does not necessarily demonstrate improved predictive ability over RECIST as assessed by discrimination.

The models for breast cancer perform poorly relative to those for NSCLC and colorectal cancer. One possible explanation is that breast cancer patients have longer overall survival and often receive multiple lines of therapy, and thus a patient’s overall survival experience is affected by multiple treatment regimens. Our metrics utilize tumor measurements recorded from only the initial treatment, which fundamentally limits their ability to predict OS. Further, 22% (521) of the initial pool of breast cancer patients were excluded from our analysis for having clinical examinations only; ie, response evaluation was exclusively by physical exam and not by imaging measurements.

The following consistent trends emerged within each disease group. First, the fact that the hazard ratio corresponding to the last slope spline term is consistently statistically significantly greater than 1 suggests that it may be important to differentiate between whether the last slope is positive or negative (ie, tumor grows or shrinks between 6 and 12 weeks) in predicting overall survival. Second, based on discrimination (c-index), the slope and percent change models have better discrimination than RECIST-based models; however, the 95% confidence intervals for the pairwise differences of c-indices consistently include 0. Moreover, based on likelihood (BIC), the percent change models are slightly better than or similar to the slope models (smaller or similar BIC), but both in turn have lower BIC than the RECIST model. Based on calibration (HL goodness-of-fit statistic), neither the slope nor percent change model yields better calibration than the RECIST model.

With the goal of early assessment, we additionally conducted a six-week landmark analysis using data available from baseline and six weeks only. However, these models performed no better than the 12-week models (results available upon request).

In addition to the two models we presented (slope and percent change), we explored models with other continuous tumor measurement–based metrics that were also motivated by considering the tumor size trajectory in Figure 1. Specifically, we considered models with the following predictors: time to first tumor growth, indicator of inflection (change in curvature of the tumor growth trajectory), number of inflection points, sign of first or last slope (positive vs negative vs zero), and number of cycles with stable disease (SD). These metrics suffer some methodological challenges (eg, time to first tumor growth is not well-defined if a patient’s tumor never grows). More importantly, however, none of these other metrics ultimately was brought forward, given concerns over a desire for model simplicity and interpretability, clinical relevance, and multicollinearity. Regarding multicollinearity, although there was evidence of a relationship between the first and last slopes (percent changes) (Supplementary Figure 1, available online), we kept both in the final model because of clinical relevance and improved discriminatory ability over a model with only first or last slope (percent change).

There are some important limitations to our analysis, many of which also apply to previous work on identifying alternative endpoints. First, our results are generalizable at most to the three disease groups we considered: breast cancer, non–small cell lung cancer, and colorectal cancer. Second, we conducted a landmark analysis and therefore only included patients who were alive and progression-free at 12 weeks. In contrast, we could have used a time-dependent Cox model with slope as the time-dependent covariate. However, the time-dependent model would neither allow for early (eg, 12-week) assessment of endpoint nor would it yield a well-defined and readily interpretable metric (eg, “slope between baseline and six weeks” has a well-defined interpretation, whereas “slope at time t” is not well defined). Third, we conducted a complete case analysis, which only included patients who had complete measurement data from baseline, week 6, and week 12. For purposes of evaluating the metrics, such a complete case analysis may introduce bias because those patients with incomplete measurement data might represent a sicker population. In particular, the generalizability of our results is still limited, as is the case with other previous work in this area (eg, [5,6]). We are currently exploring using nonlinear mixed effects models of tumor growth in order to impute missing measurements (eg, [14]) and will reevaluate our models based on the larger (imputed) dataset. Fourth, although we evaluated and compared the metrics based on measures of discrimination, calibration, likelihood, and association, we focused on discrimination (via the c-index). The question of what is the most appropriate approach to evaluate and compare non-nested predictors of survival remains open. We are currently employing a resampling-based approach to assess the “true positive (negative) rate” of our metrics. We believe this will serve as another measure of predictive ability, and one that can potentially directly inform on how these new metrics may address the concern over high failure rates in Phase III trials. Fifth, 85% of the patients from the raw dataset had to be excluded because of not having protocol-compliant measurement data, a fact that poses a major limitation not only to our models but to any model for predicting survival using these data (and likely using any real-world clinical trials data). To explore the potential effect of this attrition on our results, we conducted a sensitivity analysis that included only the subset of studies with a high degree of compliance (Supplementary Table 1, available online). Moreover, our models did not account for patients developing new lesions, progressing because of clinical reasons and not from growth of target lesions, and going off study because of toxicity with no measurements after that time. This remains an important challenge to address in order to make any model practically relevant. Finally, we note that as survival increases and effective second- and later-line therapies become available in many diseases, the ability for any metric based only on first-line therapies to predict OS will become increasingly difficult (15). Another reason for the relatively low predictive ability of these metrics could be how tumor size is measured. Measurements are typically done through CT imaging, which is based on tissue size and density but does not convey crucial information about function, which may potentially better predict survival. Functional-based measurements coupled with tumor measurement–based metrics may be used in the future for evaluating tumor burden in clinical trials.

In conclusion, the slope and percent change models do not demonstrate convincingly improved OS predictive ability over the RECIST model. Although point estimates of discrimination for the slope and percent change models are higher than those for the RECIST model, the 95% confidence intervals for pairwise differences in c-indices included 0. Ongoing work is addressing missing tumor measurements and model selection methods and assessing clinical utility of alternative endpoints.

Funding

National Cancer Institute (R21 CA167326).

The funding source had no role in the preparation of this manuscript.

Dr. Han was a graduate student at the University of Rochester, NY, when this work was completed and is now currently employed by Novartis Pharmaceuticals. Dr. Dong was a graduate student at the University of Pittsburgh, PA, when this work was completed and is now currently employed by Takeda Pharmaceuticals.

The authors wish to thank the other members of the RECIST Working Group for their valuable feedback: Janet Dancey, Elisabeth de Vries, Robert Ford, Steve Gwyther, Wendy Hayes, Otto Hoekstra, Erich Huang, Saskia Litiere, Yan Liu, Margaret Mooney, Larry Rubinstein, Larry Schwartz, Lesley Seymour, Lalitha Shankar, Patrick Therasse, and Helen Young.

The authors also thank the following organizations for making data available for the RECIST data warehouse: Amgen, AstraZeneca, Breast Cancer International Research Group (BCIRG), Bristol-Myers Squibb, European Organization for Research and Treatment of Cancer (EORTC) Breast Cancer Group and Gastrointestinal Group, Erasmus University Medical Center, Rotterdam, Netherlands, Genentech, Roche, Sanofi Aventis.

The authors are thankful to the Associate Editor, three reviewers, and the Senior Editor for many helpful suggestions and comments.

The authors take full responsibility for the analysis and interpretation of the data, the writing of the manuscript, and the decision to submit the manuscript for publication.