Comparison and calibration of a real-time virtual stenting algorithm using Finite Element Analysis and Genetic Algorithms

Abstract

In this paper, we perform a comparative analysis between two computational methods for virtual stent deployment: a novel fast virtual stenting method, which is based on a spring–mass model, is compared with detailed finite element analysis in a sequence of in silico experiments. Given the results of the initial comparison, we present a way to optimise the fast method by calibrating a set of parameters with the help of a genetic algorithm, which utilises the outcomes of the finite element analysis as a learning reference. As a result of the calibration phase, we were able to substantially reduce the force measure discrepancy between the two methods and validate the fast stenting method by assessing the differences in the final device configurations.

1. Introduction

Endovascular devices (stents, stent grafts, flow diverters) are widely adopted for restoring the patency of arteries and veins. Over the last decade, the development in stent technology has been rapid and has revolutionised the treatment of many cardiovascular diseases by offering a minimally invasive alternative to complex open heart surgical interventions  [1]. Progress on different designs, materials and surface processing allowed the use of stents for treating a wide variety of conditions, including stenosis and aneurysms of coronary  [2], carotid  [3], cerebral  [4], thoracic  [5] and peripheral arteries  [6] and, more recently, cardiac valve dysfunction  [7], [8]. As a consequence, interventional cardiologists currently have an extensive range of products at their disposal that enable them to reach complex cardiovascular districts from different access sites. This variety of available devices also aims at targeting diverse patient populations who might suffer from acquired or congenital heart diseases. In addition, every stent is associated with its own mechanical implantation performance, characterised by different foreshortening, dog-boning, deliverability and elastic recoil  [9]. Such increasing availability can make the choice of the most suitable device more complicated and, therefore, makes it desirable to accurately predict optimal stent placement, especially under patient-specific conditions  [10], [11], [12].

Computational models, like finite element (FE), have been widely employed in the past to study stent implantation. FE simulations supported the inexpensive testing of novel designs, materials, etc., and contributed towards better understanding of the mechanisms of stent expansion  [13], [14]. More recently, thanks to the advances in cardiovascular imaging and computational power, it has also been possible to include patient-specific anatomical models in the simulations, to study the interactions with complex geometries  [15], [16], [17] and the risk of structural failure in these environments  [18]. However, the complexity of such simulations still requires relatively high computational times, which limit the use of FE simulations to support daily clinical activities.

In this context, there have been a number of attempts to develop different computational methods to simulate stent deployment in “real-time”. These methods feature fast computational times, necessary for their usefulness in clinical settings; however, they still display considerable simplifications, especially in stent modelling, which is often based on fitting a generic cylinder inside the vessel, on the surface of which stent struts are subsequently drawn  [19], [20]. Even the approach proposed by Larrabide et al.  [21] that models the stent design explicitly is challenged by complex vascular geometries. Therefore, to the best of our knowledge, no virtual stent deployment method has yet been proposed, that is able to combine fast turnover times with sufficient accuracy.

Against this background, we developed a novel fast computational method to simulate stent deployment under patient-specific conditions, specifically designed to be subsequently used in clinical practice  [22]. This fast method is based on a spring–mass model and can potentially take into account different device designs as well as emulate deformable vasculature. Although the spring-mass method offers a convenient way to model mechanical behaviour in real-time due to its simplicity, the search for the appropriate springs constants is not straightforward. Moreover, the fast computational speed inevitably comes with a cost of reduced accuracy; therefore, the error has to be thoroughly estimated. Hence, the goal of this study is to perform a rigorous comparison of our fast method against FE analysis and to use FE outcomes as a learning base for fitting the required parameters. For that purpose, we conducted a series of experiments of increasing complexity, in order to evaluate the discrepancy in final device configurations and residual force estimation. Thereafter, we performed an optimisation step, in which the parameters of the fast method were calibrated with the help of a genetic algorithm which was guided by the FE results. We conclude the paper by presenting the post-calibration results and the outlook on further improvements.

2. Methods

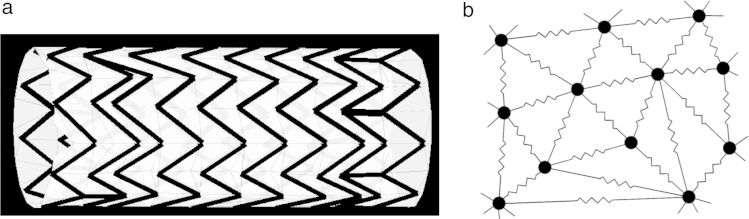
This study focuses on the analysis of a novel numerical fast method (FM) to simulate the process of stent expansion, as compared to detailed Finite Element (FE) analysis. The device employed in this comparison resembled a self-expanding stent graft that is widely used for the treatment of aortic aneurysms and dissections (Fig. 1(a)). The device consists of an external self-expanding nitinol wire structure (i.e., stent struts) that is helically attached along the entire surface of the ePTFE graft. The stent is characterised by 10 crowns, where the 2 terminal crowns are attached to the central spiral crown by 2 vertical bars. The device diameter is 38 mm and its length is 92.25 mm. The wire of the stent struts is 0.381 mm thick.

Fig. 1.

Stent graft model. (a) Reconstruction of the stent graft. (b) Schematic representation of a spring–mass mesh: the mesh consists of discrete mass points connected by lineal springs.

Image (b) adapted from Meier et al.  [23].

The assessment of FM was based on the comparative analyses of a stent graft expansion, with subsequent optimisation step, and is divided into four phases:

• 1.Verification of the numerical methods: a simple case of stent free expansion was tackled with both FM and FE methods in order to verify the convergence of the numerical solutions (Section  2.3).
• 2.First comparison of FM against FE: a comparative analysis of both numerical methods was performed by simulating the stent implantation within six models of different vessel sites of increasing complexity. For this initial comparison, the FM was implemented using standard stiffness parameters derived from literature data (Section  2.4).
• 3.Optimisation of FM: based on the results obtained during the first round of comparative analyses, the parameters of the FM were calibrated by means of a genetic algorithm (Section  2.5).
• 4.Second comparison of FM against FE: the post-calibrated FM was finally tested by repeating the six simulations of stent implantation and by comparing the new results against the unmodified FE analyses (Section  2.4).

In the next sections, a detailed description of both numerical methods and each procedural step is reported.

2.1. Fast method

The proposed FM operates on a simplified stent representation, in which the strut wires are approximated by straight lines (centrelines), that is, the struts are modelled without an explicit thickness. Additionally, the modelled struts are supplemented with a background mesh, that emulates the graft of the device. The two meshes are merged by creating an anisotropic grid using triangulation constraints, that is, the background mesh incorporates the elements of the stent struts (see schematic representation in Fig. 1(a)).

The mechanics of the device in FM is based on so-called spring–mass models that are widely used in surgery simulations and many other engineering applications  [23]. In this approach, the mesh is replaced by fictitious springs, as schematically depicted in Fig. 1(b). Each spring then behaves according to Hooke’s law: the restoring force $F$ acting on the node $i$ from its neighbours is determined in the following way

$$F_i=\sum _{j=1}^{n_i}{k}_{ij}({\delta }_j-{\delta }_i)\text{,}$$ (1)

where ${\delta }_i$ is the displacement of node $i$, $k_{ij}$ stands for the stiffness of the spring $(i-j)$ and $n_i$ indicates the number of vertices directly connected to the node $i$.

Application to stent deployment. The crimping of the stent creates spring forces acting in the structure, which allows the nodes of the mesh to recover their original configuration driven by these forces. The nodal movement takes into account its intertwinement with the neighbours by means of the nodal stiffness, the value of which is set to be equal to the sum of stiffness values of all springs connecting it to its immediate neighbours. In the first instance, we have set the stiffness of springs to be inversely proportional to the segment length before the deformation, as originally proposed by Batina  [24]. This setting takes into account the fact that mesh vertices located in close proximity to each other should exert stronger restoring force onto each other.

Subject to restoring forces, the new nodal displacement can be calculated at every time step as the restoring force divided by the stiffness of the node $K_{i,nodal}$:

$${\delta }_i=-\frac{F_i}{K_{i,nodal}}\text{,}$$ (2)

where the stiffness of the node is set to the sum of the stiffness of all edges emanating from this node $K_{i,nodal}={\sum }_{j=1}^{n_i}{k}_{ij}$. Eq. (2) is solved for displacements for all nodes of the structure on the vertex-to-vertex basis. The new nodal coordinates are determined by adding the calculated displacement $\delta$ to the old coordinates.

The deployment process starts with the crimping of the device which simulates its positioning in the catheter. In clinical practice, the chosen device is compressed into a 24FR (24×0.333 mm=8 mm) catheter system which results in an 80% reduction in diameter. Thereafter, the crimped device is aligned along the centreline of the target vessel at the relevant position for the start of the expansion process. The stent expansion procedure is performed in an iterative way on a vertex-to-vertex basis, according to Eq. (2). The coordinates of a vertex are updated after each iteration, as long as no contact between the vertex and the vessel occurred. The contact is defined to occur when the Euclidean distance between the vertex of the stent and any of the vessel vertices becomes smaller than a chosen parameter $ϵ$. To detect contact, a contact check is performed in every iteration of the deployment loop before the update of the coordinates of stent vertices (step “Check contact”). After the contact was detected, the displacements of the stent vertex in contact are still calculated in future iterations, to enable possible readjustments resulting from the tension of the neighbouring nodes. However, its position can only change if it is located within the $ϵ$-boundary of the vessel inner surface. The detailed pseudocode is shown below.

• 1.
  Calculate initial displacement of stent vertices by subtracting the load-free ($lf$) coordinates of vertices from the current crimped coordinates ($cr$). For a vertex $v_i={(x_i,y_i,z_i)}^{\prime }$ initial crimping delta ${\delta }_i^{cr}$ is found by:

  $${\delta }_i^{cr}=\left(\begin{array}{c}\hfill {\delta }_{x_i}^{cr}\hfill \\ \hfill {\delta }_{y_i}^{cr}\hfill \\ \hfill {\delta }_{z_i}^{cr}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill x_i^{cr}\hfill \\ \hfill y_i^{cr}\hfill \\ \hfill z_i^{cr}\hfill \end{array}\right)-\left(\begin{array}{c}\hfill x_i^{lf}\hfill \\ \hfill y_i^{lf}\hfill \\ \hfill z_i^{lf}\hfill \end{array}\right)\text{.}$$
• 2.Iterate until there is almost no change in expansion delta ${\delta }^{\exp }$, that is, stop when
  $max\{\left|{\delta }_{x_i}^{\exp }\right|,\left|{\delta }_{y_i}^{\exp }\right|,\left|{\delta }_{z_i}^{\exp }\right|\}\le ϵ$, where $i$ ranges over all nodes ($ϵ=10^{-6}$)

  • •
    Calculate restoring force$F_i$ for each node $i$ from Eq. (2)

    $$F_i=\sum _{j=1}^{n_i}{k}_{ij}({\delta }_j^{cr}-{\delta }_i^{cr})\text{.}$$
  • •
    Calculate expansion delta${\delta }_i^{\exp }$ for each node $i$ from force and nodal stiffness

    $${\delta }_i^{\exp }=-\frac{F_i}{\sum _{j=1}^{n_i}{k}_{ij}}\text{.}$$
  • •
    Check contact between the newly determined stent coordinates and the vessel:
    for each stent vertex $v_i$ and each potential vessel contact vertex $p_j\in P_i$
     if they are closer than $ϵ$: $\Vert (v_i+{\delta }_i^{\exp })-p_j\Vert <ϵ$
     add $i$ to set $C$ of nodes in contact: $C≔C\cup \left\{i\right\}$
  • •
    Update stent nodal coordinates for each node $i$ not in contact, $i\notin C$

    $$\left(\begin{array}{c}\hfill x_i^{cr}\hfill \\ \hfill y_i^{cr}\hfill \\ \hfill z_i^{cr}\hfill \end{array}\right):=\left(\begin{array}{c}\hfill x_i^{cr}\hfill \\ \hfill y_i^{cr}\hfill \\ \hfill z_i^{cr}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\delta }_{x_i}^{\exp }\hfill \\ \hfill {\delta }_{y_i}^{\exp }\hfill \\ \hfill {\delta }_{z_i}^{\exp }\hfill \end{array}\right)\text{.}$$
  • •
    Update crimping delta values ${\delta }_i^{cr}$ for each node $i\notin C$, by adding expansion displacement ${\delta }_i^{\exp }$ to the previous ${\delta }_i^{cr}$

    $${\delta }_i^{cr}=\left(\begin{array}{c}\hfill {\delta }_{x_i}^{cr}\hfill \\ \hfill {\delta }_{y_i}^{cr}\hfill \\ \hfill {\delta }_{z_i}^{cr}\hfill \end{array}\right):=\left(\begin{array}{c}\hfill {\delta }_{x_i}^{cr}\hfill \\ \hfill {\delta }_{y_i}^{cr}\hfill \\ \hfill {\delta }_{z_i}^{cr}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\delta }_{x_i}^{\exp }\hfill \\ \hfill {\delta }_{y_i}^{\exp }\hfill \\ \hfill {\delta }_{z_i}^{\exp }\hfill \end{array}\right)\text{.}$$
• 3.Output stent nodal coordinates

The FM was implemented in Matlab and executed on an Intel Core 2 Duo with a 2.66 GHz CPU with 4 GB of memory and without using any parallelisation.

2.2. Finite element analysis

All the FE analyses were performed using the FE code Abaqus 6.11/Explicit (Dassault Systemes Simulia Corp., Providence, RI, USA) on an Intel Xeon X5690 with 2 processors of 3.46 GHz and 24 GB of RAM; all simulations ran in parallel using 4 cores. The CAD model of the stent was meshed with beam and shell elements to discretise the stent struts and the stent graft, respectively. Following sensitivity analysis, the average length of the beam elements was 0.9 mm with a final mesh resulting in 2371 elements, while the average size of shell elements was 0.8 mm for a total of 13004 elements. The constitutive models used to characterise both the Nitinol stent struts and polyester graft were based on a previously validated study by our group  [25]. Each experiment consisted of three steps: crimping, positioning within the vessel model and deployment.

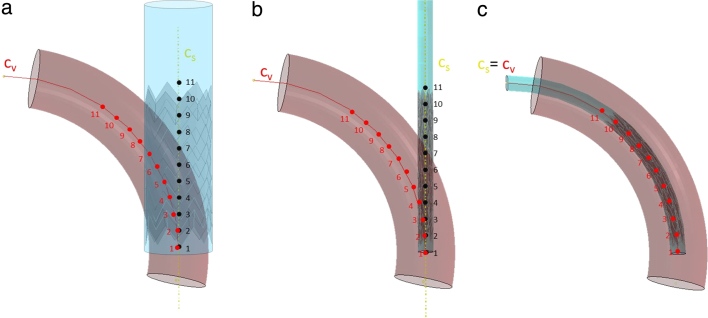
• 1.Crimping. The device was crimped to the size of the delivery catheter (8 mm diameter) by applying a radial displacement (15 mm) to a coaxial cylindrical surface. Such cylindrical surface mimicked the presence of the membrane sheath that constrains the stent into the delivery catheter (see Fig. 2(a)). Specific boundary conditions were assigned to the stents, in order to avoid rigid translation during the analysis: the device was constrained in its terminal section in both circumferential and axial direction (see Fig. 2(b)).
• 2.Positioning. In order to position the crimped stent and its cylindrical sheath within each virtual implantation site, we used the respective centrelines. Since the stent and the sheath were coaxial, their centreline ($C_s$) is unique. Such centreline was then aligned to the vessel centreline ($C_v$). We therefore subdivided the lines through a discrete number of points ($n=11$). A kinematic constrain was applied between the points of $C_s$ and the nodes of the cylinder laying on the plane passing through that point and cutting $C_s$ perpendicularly. Hence, the coordinates differences of the points of $C_s$ and $C_v$ were calculated. The resulting displacements and rotations were applied onto the points of $C_s$, causing the bending of the device (see Fig. 2(c)).
• 3.Deployment. The deployment of the stent was achieved by replicating the release from the delivery catheter and was implemented by gradually retrieving the virtual membrane sheath.

Fig. 2.

Crimping and initial positioning of the stent graft with FE method. (a) The stent before crimping. $C_v$ (in red) is the centreline of the vessel defined by 11 points. $C_s$ (in yellow) is the centreline of the stent and the coaxial cylinder. (b) After the cylindrical surface has crimped the stent, displacements and rotations are applied to the points of $C_s$ to make them reach the corresponding points of $C_v$ and to position the stent inside the vessel (c). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.3. Model verification: free expansion

To test the validity of the models and their overall performance, we set up the free expansion experiment with both FM and FE methods. In case of FM, from the initially crimped configuration (8 mm in diameter), the stent graft was subject to free expansion until it reached its load-free configuration. Since the released stent graft is supposed to recover its known load-free configuration, the expansion process can be tracked by the average distance to the target load-free stent. Therefore, the dynamics of the free expansion process was evaluated by analysing the convergence of four parameters:

• 1.Mean nodal distance metric is the average distance from the vertices of the current expanding stent to their counterparts in the load-free device. Such distance is defined as ${\overline{d}}_{\mathrm{nodal}}=\frac{1}{N}{\sum }_{i=1}^N\Vert v_i^0-v_i\Vert$, where $v_i^0$ is the position of the node $i$ in the load-free stent and $v_i$ — in the current expanding stent.
• 2.Mean angle difference between the load-free and the current expanding stent is measured as ${\overline{\epsilon }}_{\mathrm{angle}}=\frac{1}{M}{\sum }_{j=1}^M|{\theta }_j^0-{\theta }_j|$, where ${\theta }_j^0$ is the value of the angle $j$ in the load-free stent and ${\theta }_j$ — in the current expanding stent, and $M$ stands for the number of angular elements in the stent structure.
• 3.Mean strut length difference provides quantification of the error related to the stent strut length as a relative percentage of their initial length. It is defined as ${\overline{\epsilon }}_{\mathrm{length}}=\frac{1}{S}{\sum }_{k=1}^S\frac{|l_k^0-l_k|}{l_k^0}$, where $l_k^0$ is the length of the strut $k$ in the load-free stent and $l_k$ — in the current expanding stent and $S$ stands for the number of struts (expressed in %).
• 4.Mean nodal force takes into account the reaction forces causing the expansion process. It is measured as $\overline{F}=\frac{1}{N}{\sum }_{i=1}^N\Vert F_i\Vert$, where $F_i$ is the reaction force at the node $i$, with the index $i$ running from 1 to number of nodes $N$.

To set up the FE free expansion we used quasi-static conditions, in which the contribution of the kinetic energy to the total energy should be equal to zero, assuming that there are no inertial effects. Therefore, to verify the convergence of the FE analysis, the ratio Kinetic Energy/Internal Energy had to reach a value $<5\%$.

2.4. Comparative analysis: FM vs FE

As in the free expansion case, the device was crimped to 8 mm and then deployed, this time until it reached the vessel walls. The comparison was based on the analysis of the expansion of the stent graft under 6 different conditions:

• 1.deployment within a 34 mm straight cylindrical vessel;
• 2.deployment within a 20 mm straight cylindrical vessel;
• 3.deployment within a bent vessel (diameter=34 mm;curvature=0.01);
• 4.deployment within a C-shaped vessel (diameter=34 mm;curvature=0.02);
• 5.deployment within an W-shaped vessel (diameter=34 mm);
• 6.deployment within an anatomical model of a patient-specific dissected aorta. As it would be done in clinical practice, the graft was placed inside the true lumen to cover the initial tear entry and prevent blood from flowing into the false lumen. The vessel diameter was varying at the deployment site: in the distal location (with respect to the dissection entry) it was approximately of a round shape with 29 mm in diameter, whereas proximally the true lumen resembled an oval with dimensions of 13 and 28 mm. Hence, the geometry in the proximal end is quite irregular, exhibiting sharp corners that might be problematic to comply with for a stiff device.

In order to quantify the differences in outcomes of the two methods, the following parameters have been measured:

• 1.Residual distance is measured between the corresponding nodes of the deployed stent that was expanded with the two different methods: FM and FE. The difference has been calculated by comparing these distances to the vessel diameters.
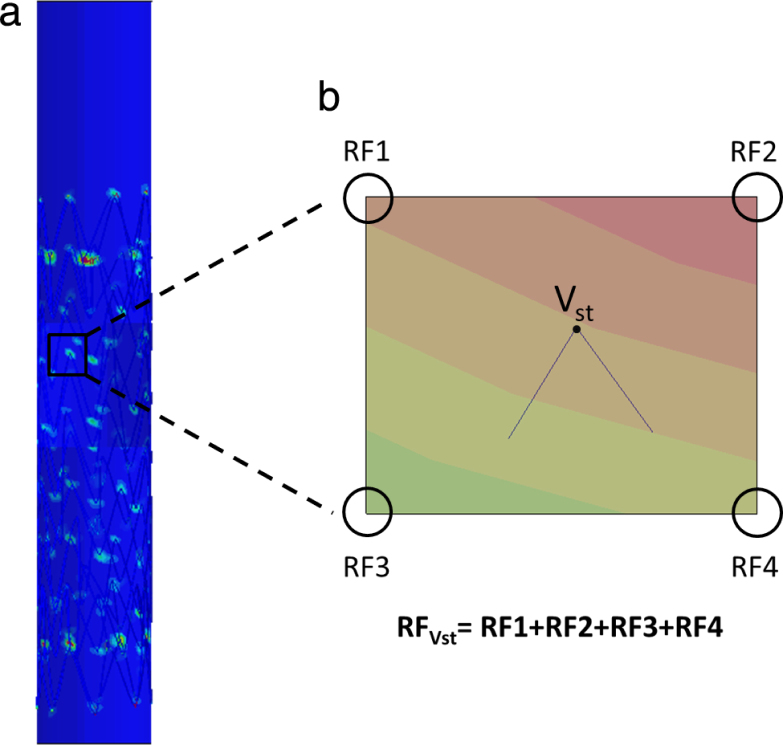
• 2.The distribution of residual forces in stent vertices is determined in the two different methods, FM and FE. While FM can directly output nodal forces, the residual forces (RF) in the FE method can be calculated only if the structure is constrained in all directions. For this reason, we derived the RF in the stent vertices through the reaction forces measured in each node of the vessel, which is always fully constrained. For each stent vertex in contact with the vessel, it was possible to find the 4 closest nodes of the vessel with the help of a specifically implemented automated method; these 4 nodes belong to the element of the vessel in contact with the vertex of the stent. The sum of these 4 reaction forces is equal and opposite of the RF in the stent’s vertices (see Fig. 3).
• 3.Relative error in struts length is calculated in relation to the original length of struts, i.e., in the load-free stent configuration.

Fig. 3.

Reaction forces measure in FE. (a) Reaction forces (RF) calculated in the vessel are represented by a colour map in the 20 mm cylindrical vessel. (b) The RF of the stent vertex $V_{st}$, which is in contact with the vessel, is calculated summing up the four RF of the four closest vessel nodes.

2.5. Calibration with genetic algorithms

In this section we aim at finding the optimal stiffness values for our fast stent model of the analysed stent device. In general, stiffness setting has significant implications on the expansion process. Without any modification to other parts of the expansion algorithm, alterations to the stiffness setting can lead to substantial degradation or even a complete loss of expanding properties of the modelled device. On the whole, instantiation of the stiffness values for spring–mass models is not a straightforward task. Several attempts have been reported in the literature, describing ways of finding the best stiffness parameters for spring–mass models for different applications; for the most part, they are of a heuristic nature  [26], [27].

We have chosen the framework of Genetic Algorithms (GAs) as a means to optimise stiffness setting of the given stent device. GAs draw inspiration from natural evolution  [28]. They simulate populations of individuals, each individual being represented by a certain number of genes that encode parameters of the investigated problem. The fitness of an individual is determined by a cost or fitness function that is formulated for a given problem setting. At the beginning of the optimisation process, the population is randomly initialised by assigning to individuals random values of genes that define them. In the course of an iteration, the fitness is assessed, and the new population is formed based on the fitness/cost function and the generic operators of mutation and crossover applied to selected individuals. Mutation means that when copying the genes from the current to a new generation, random changes might occur with a certain probability. In contrast, crossover combines genes from selected individuals to form an offspring. The aim of the algorithm is to make the population converge to a final population in which the best performing individuals will be as close as possible to the optimal solution of the problem. As a rule, GAs do not guarantee a convergence to the global optimum; however, they are able to find good approximative solutions by reaching local optima.

In our case, we used the known final FE configurations and reported residual forces as a reference for optimising the stiffness parameters of FM. Thus, the cost function for the GA formulation should take into account the discrepancy between the FM and FE outcomes in terms of the nodal distances and the value of forces. Our goal is to find stiffness parameters resulting in better alignment between the two methods.

Setup. In theory, the spring constant of an “ideal” spring can be found as $k=\frac{E{A}_0}{L_0}$, where $E$ is the Young’s modulus of the material, $A_0$ is the unstretched cross sectional area and $L_0$ is the unstretched length of the spring. This indicates that, all else being equal, $k$ is inversely proportional to the original length of the spring ($L_0$), scaled by $E{A}_0$. Therefore, in our model, we keep the inverse relation to the length, as was the case before, and will be only looking for the optimal scaling constant with the help of the GA. Additionally, we have differentiated between the scaling values for the background springs (wBg) and the springs representing stent struts (wStr). Hence, the springs constants in our setup will be calculated in the following way for a vertex $v_i={(x_i,y_i,z_i)}^{\prime }$ and $v_j={(x_j,y_j,z_j)}^{\prime }$:

$$k_{ij}^{Bg}=\frac{wBg}{\Vert v_i-v_j\Vert }\text{and}{k}_{ij}^{Str}=\frac{wStr}{\Vert v_i-v_j\Vert }+k_{ij}^{Bg}=\frac{wStr+wBg}{\Vert v_i-v_j\Vert }\text{.}$$ (3)

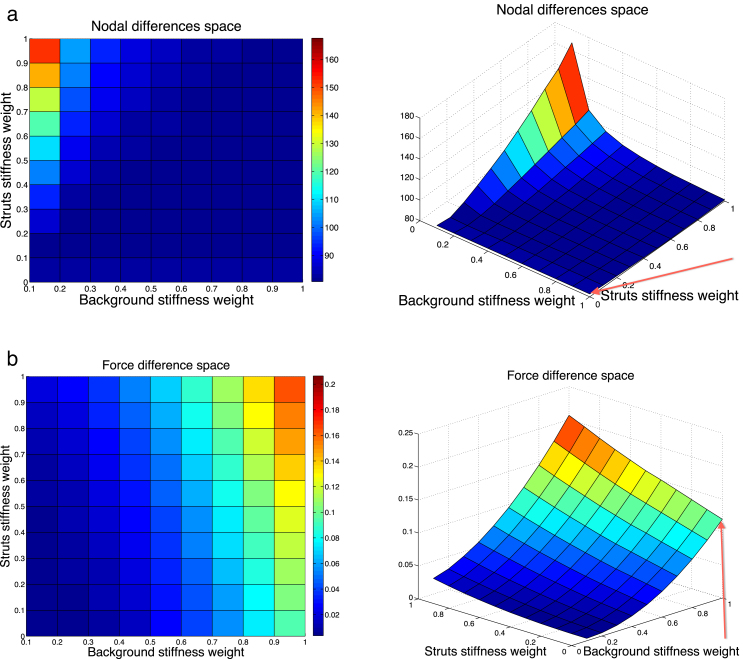
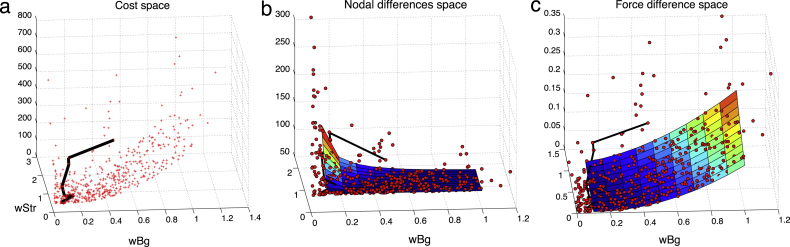
Therefore, the space our GA is operating within can be visualised as a 3D function defined by the two stiffness weights (wStr and wBg). Fig. 4 illustrates an approximative extract from this space for case 3 (bent vessel with diameter = 34 cm) for the intervals $wBg=[0.1\dots 1]$ and $wStr=[0\dots 1]$ along abscissa and ordinate axes, respectively, and the corresponding cost value along the $z$-axis. The graph shows the behaviour of the nodal (a) and force (b) difference as parameters vary. The squared error of the nodal distance ranges between 80 (blue) and 170 (red), whereas the squared force error lies between 0.015 (blue) and 0.2 (red) in these intervals. Note the difference of more than 3 orders of magnitude between the error measures.

Fig. 4.

Variation of the error space as a function of stiffness scaling. (a) Space of nodal differences. (b) Space of force differences. Baseline values from the previous section are indicated by red arrows: ${\overline{e}}_{\mathrm{nodal}}=82.7447$ and ${\overline{e}}_F=0.1196$. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

All the simulations in the initial comparison (pre-calibration) section were performed with the stiffness setting $wStr=0$ and $wBg=1$, which is located at the bottom right corner of the error space, indicated by the red arrows in Fig. 4. With the help of the graphs, we can see that this stiffness setting corresponds to a relatively low value with respect to the nodal difference; however, it maps to a fairly high point on the force difference space, compared to other values of the analysed interval. More precisely, the baseline squared error values are ${\overline{e}}_{\mathrm{nodal}}=82.7447$ and ${\overline{e}}_F=0.1196$.

Implementation. As already mentioned, we distinguish between two classes of springs: springs belonging to the stent struts and those of the background sheath.

Population: In each generation, there are 7 individuals in the population. Each individual is defined by a pair of genes that represent the two scalars we are looking for: the weight for the background sheath (wBg) and the (additional) weight for the struts stiffness (wStr), that is, an individual is represented as $ind=[wStr,wBg]$. The population is randomly initialised and then evolved for roughly 100 generations using the genetic operators described below.

Cost function: In each generation, for each of the 7 individuals in the population, the FM simulation with the stiffness values corresponding to the genes of the individual ($ind=[wStr,wBg]$) is run and then compared to the FE reference to determine the fitness of the individual. Both the nodal distances and the force values will be optimised simultaneously. Firstly, we compute the mean squared error of both values calculated from the convergence metrics defined in the previous section. More precisely, the mean squared difference in residual force magnitude is measured as

$${\overline{e}}_F=\frac{1}{N}\sum _{i=1}^N{(\Vert F_i^{FE}\Vert -\Vert F_i^{FM}\Vert )}^2\text{,}$$

where $F_i$ is the reaction force at the node $i$, with the index $i$ running from 1 to number of nodes $N$. The mean squared difference in nodal distance is calculated as

$${\overline{e}}_{\mathrm{nodal}}=\frac{1}{N}{\left(\frac{100}{2R}\right)}^2\sum _{i=1}^N{\Vert v_i^{FE}-v_i^{FM}\Vert }^2\text{,}$$

where $v_i$ is the position of the node $i$ in the final stent obtained with the fast ($v_i^{FM}$) and FE ($v_i^{FE}$) method, respectively; R indicates the radius of the vessel wall, that is, the error is estimated with respect to the vessel wall diameter. Thereafter, we combine two error measures into a single cost function in the following way:

$$f_{\mathrm{cost}}=\frac{1}{2}\left({\overline{e}}_{\mathrm{nodal}}\right)+\frac{5\cdot {10}^3}{2}\left({\overline{e}}_F\right)$$ (4)

to be able to optimise both metrics simultaneously. In order to bring them to relatively the same importance, we had to scale the force error to $5\cdot {10}^3$ due to the difference in magnitude of the two values.

Selection: At each generation, all individuals are sorted according to their performance with respect to the cost function. Two best performing individuals are kept for the next generation without alterations. The rest of the population is subject to generic operators of mutation and crossover.

Mutations: At each generation, the 3 best performing individuals undergo random mutations when creating new offsprings. The mutation operator is adding a random variable from the interval $[-1.5\dots 1.5]$ to each of the two genes. However, since stiffness cannot be negative, the value is corrected if the result of the addition turns out to be negative; the positive counterpart is taken instead.

Crossover: At each generation, the 2 fittest individuals are selected and crossed to create two offsprings by swapping the defining genes. To ensure the diversity in the population, at the end of the population forming, we perform an additional check to ensure that all individuals are different. This enables to explore the space of possible solutions in a better way and speed up the convergence.

The optimisation is performed once on the case of the bent vessel (diameter=34 cm) to capture the bending behaviour, and the resulting stiffness values are subsequently used in all post-calibration comparisons.

3. Results

In this section we report the outcomes of the numerical experiments described above: (1) verification with free expansion, (2) pre-calibration comparison, (3) FM optimisation using genetic algorithm and (4) post-calibration comparison.

3.1. Free expansion

Fig. 5 highlights the phases of the free expansion process simulated with both numerical methods. In particular, results of FM simulations are presented as the snapshots of the obtained stent configuration after a certain number of iterations, while FE analyses are shown throughout the simulation (30 s). Dynamics of the expansion process are plotted in Fig. 6, where the four metrics of convergence and the internal energy are plotted for FM and FE, respectively. The evolution of all plotted functions confirm the convergence of the results and the ability of both methods to expand the device to its load-free configuration.

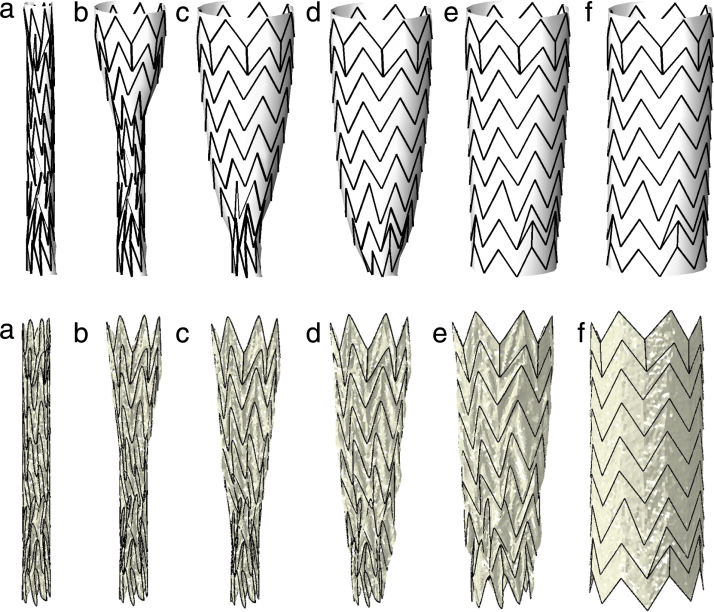
Fig. 5.

First row: free expansion of the stent graft device with the fast method: (a) initial crimped stent; (b) result after 10, (c) 50, (d) 150, (e) 250, (f) 500 iterations. Second row: free expansion of the stent graft device with the FE method, the crimped configuration is gradually released to the full expansion (from left to right).

Fig. 6.

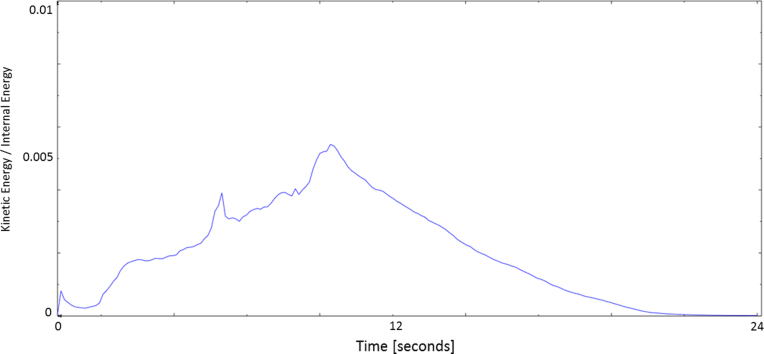
Convergence in the free expansion experiment.

(a) The convergence of the FE model in the free expansion experiment is achieved when the stent is fully deployed and the ratio kinetic energy/internal energy is below 0.05.

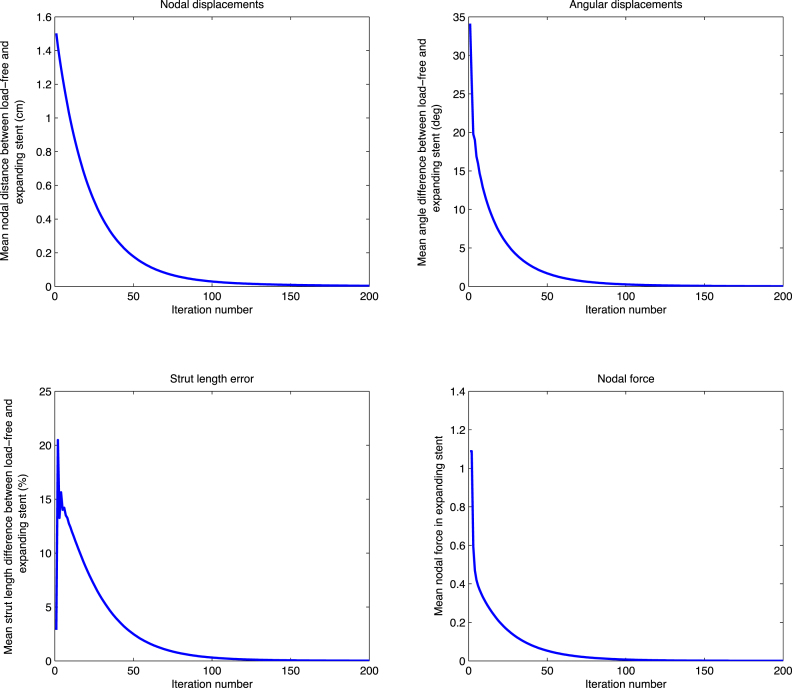
(b) Free expansion of the stent graft for 200 iterations with FM. Upper row: mean nodal distance and mean angle difference between load-free and expanding stent. Bottom row: mean strut length difference and mean nodal force in the expanding stent. FM reaches convergence after about 200 iterations and 2 s of execution time.

Specifically for the FM case, the nodal displacement ${\overline{d}}_{\mathrm{nodal}}$ (Fig. 6(b), upper left corner) converges completely after 200 iterations, while the measure of angular distance ${\overline{\epsilon }}_{\mathrm{angle}}$ (Fig. 6(b), upper right corner) and the measure of the residual nodal forces (Fig. 6(b), bottom right corner) exhibit a slightly faster convergence, being almost zero during the last 100 iterations. The trend related to the error of strut lengths (Fig. 6(b), bottom left corner) shows a different tendency, with the error first increasing up to 20% after few iterations and then decreasing in the course of the iterative process, until complete convergence is reached.

The analysis of the ratio between internal and kinetic energies of the FE model confirms the absence of any dynamic processes at the end of the free expansion phase when the stent graft completely recovers its original shape, as displayed in Fig. 6(a).

3.2. Pre-calibration comparison

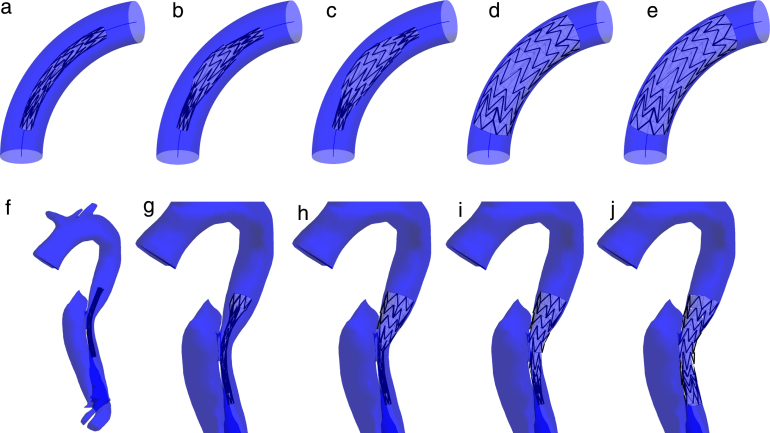
To assess the differences between the FM and FE methods, the stent graft configurations obtained with both methods were compared in six different deployment scenarios. Both methods are able to realistically capture the self-expansion of the stent graft until it reaches equilibrium in contact with the arterial wall. The process of expansion is visualised in Fig. 7 which displays two examples of different complexity. In order to mimic clinical practice, the deployment of the device was either initiated at the centre and progressed to both extremities (first row) or was started at the one end and progressed towards the other extremity (second row), as common for this type of stent grafts. In the case of FM, the final configuration was obtained after approximately 200 iterations of the virtual deployment algorithm and required around 20 s. The device was in a reasonably good opposition to the vessel wall and covered the initial tear completely. In both FM and FE simulations, the stent graft successfully covered the virtual vasculature lesion. These results confirmed the possibility to use both the techniques also in case of complex anatomical cases.

Fig. 7.

First row: deployment of the stent graft in a bent cylinder with FM. Results after (a) crimping and initial positioning along the centreline, (b) after 20, (c) 30, (d) 100, (e) 200 iterations of FM method. Second row: placement of a stent graft over a dissection entry. Result after (f) 1, (g) 20, (h) 50, (i) 80, (j) 150 iterations of FM expansion.

One of the most important outcomes of the comparative analysis is the fact that in all tested cases the use of FM is associated with a dramatic reduction in computational time when compared with FE, generally being in the order of seconds for FM and in the order of hours for FE. Table 1 reports the timings of the simulations for both methods. Free expansion is the fastest case, where FM reaches the load-free configuration in just 2 s, while simulations inside the vessels with the diameter of around 30 mm take approximately 30 s. Most of the execution time of the FM deployment algorithm is dedicated to the contact check and calculations of the implications the vessel wall has on the stent structure. Interestingly, in both methods, the highest computational time (i.e., curved vessels) is not associated with the most complex geometry (i.e., patient-specific case of aortic dissection). Another fact worth mentioning is the relation of the computational time to the diameter of the vessel in both methods. While the computational time of FM appeared to be directly related to the diameter of the vessel, no immediate relation was found for the FE simulations. Such outcome is probably related to the simplified contact model used by FM, which makes the stent-graft expansion terminate once the nodes come in contact with the vessel wall. On the contrary, it is well known that the contact algorithm used in the FE analyses increases the computational cost of the simulations.

Table 1.

Results of 7 stent deployment simulations with FM and FE.

Simulation setup	FM times (s)	$\overline{d}$ (%)	FE times
(1) Free expansion	2.01	0	2 h 3 min
(2) Straight vessel: 34 mm	28.60	2.73	1 h 33 min
(3) Straight vessel: 20 mm	8.55	7.13	7 h 4 min
(4) Curved vessel: bent	39.70	8.31	10 h 15 min
(5) Curved vessel: C-shaped	41.75	9.70	8 h 9 min
(6) Curved vessel: W-shaped	32.75	9.58	7 h 28 min
(7) Aortic dissection	19.44	10.50	4 h 30 min

The detailed results of all six simulations are reported in Fig. 8, Fig. 9, which illustrate the final deployed configurations for both numerical methods. The visual comparison enables the qualitative assessment of the differences of the two methods by means of overlaying the final deployed configurations of the devices (last column FM+FE). The visual comparison showed an overall good agreement in terms of device positioning. However, in the cases where the curvature is higher (i.e., curved C-shaped vessel and curved W-shaped vessel), it is possible to observe a larger difference in the arrangement of the extremities of the stent. Importantly, it is possible to observe that such differences seem to be associated with a different grade of vessel curvature rather than with a different opening size.

Fig. 8.

Resulting configurations after deployment in simplified vessel geometries. The columns correspond to (a) final device configuration inside the vessel obtained with FE, (b) FE reaction forces, (c) final configuration inside the vessel obtained with FM and (d) FM final configuration displayed in red overlaid with the FE result in black. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 9.

Resulting configurations after deployment in curved vessel geometries. The columns correspond to (a) final device configuration inside the vessel obtained with FE, (b) FE reaction forces, (c) final configuration inside the vessel obtained with FM and (d) FM final configuration displayed in red overlaid with the FE result in black. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

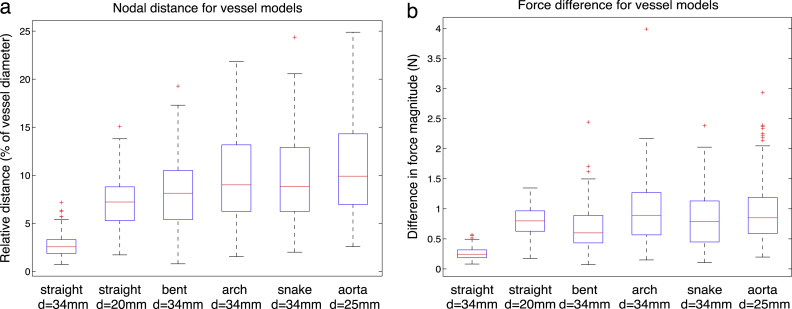
In order to quantify resulting differences, nodal distance and residual stent forces have been computed for each vertex of the stent struts. In Fig. 10, the difference between the two methods is reported in the form of box plots. In the simple straight geometries, the average nodal distance discrepancy is about 4%; however, it is increasing with more complex geometries, reaching about 10% for the patient-specific case. The smallest residual nodal distance is reported for the straight vessel ($d=34\mathrm{mm}$) with the mean of the nodal errors $\mu =3.78\%$ and the standard deviation $\sigma =1.20\%$, when fitted to the normal distribution. For the 20 mm straight vessel, the discrepancy between FM and FE is more pronounced ($\mu =7.13\%$, $\sigma =2.60\%$). In the narrow vessel the FM device exhibited a configuration very similar to the crimped one. The difference for the more narrow vessel is larger because the FM device does not have a chance to sufficiently open up before hitting the vessel wall and is still exhibiting a configuration very close to the crimped one, due to the unsophisticated FM contact model. Since the crimping procedures in both methods are different (and hence different crimped configurations), we are effectively comparing the difference in crimping as well. In fact, in a wider vessel, the difference in crimping is being gradually elevated in the course of the expansion, when the device is moving to its load-free configuration, resulting in a smaller difference. Overall, the nodal difference tends to increase with the increasing complexity of the vessel model, reaching its maximum in the case of the model of dissected aorta. Under patient-specific conditions, the highest average nodal distance of $\mu =10.50\%$, with respect to the vessel diameter (which is taken to be 2.5 cm as the result of averaging the round distal and oval proximal diameters) and $\sigma =4.64\%$. Such differences can be explained by observing that the middle part of the device was not completely complying to the vessel wall in the case of FM. The reason for the lack of opposition in the FM device is the fact that the FM contact is detected too soon in the complex oval vessel geometry, which shows the limitation of the FM contact model employed.

Fig. 10.

Difference between the two methods, FM and FE, for all vessel models, before stiffness learning. (a) Resulting nodal distance with the median value represented as a red line and the blue box outlining the 25th and 75th percentiles; the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually. (b) Resulting difference in force magnitude between the two methods.

With respect to the residual forces, the difference between the two methods is displayed in Fig. 10(b), with an average force difference lying below 1 N and an absolute maximum of 4 N highlighted in the case of the C-shaped vessel. The values were in the same order of magnitude as the ones reported by FE method. Even in the case of the narrow 20 mm vessel, the relation remained the same, which means that the forces reported by the fast method were consistent with the increase of crimping in the device. The general trend is that the FM reports force values larger than the FE method for all simulated cases. This outcome indicates that the stiffness of the springs used in the FM were initially set to a value which was too high for the investigated problem.

The final comparison metric was the discrepancy in struts’ length. As we noted in free expansion case, FM tended to distort the struts length at the beginning of the iterative process, correcting it in the course of the subsequent iterations (see Fig. 6(b), bottom left graph). Hence, in cases where the device deployment is terminated beforehand, there is usually a small error in struts’ length for the FM cases. For example, in the case of the 34 mm vessel, the majority of struts display an error of less than 3% of their original length. The aforementioned FM convergence dynamics leads to the higher error rate in the narrower 20 mm vessel, where the average is approximately 6%. On the contrary, the FE method does not distort the struts length in such extent; however, for the 20 mm vessel there is a non-zero error of about 2%. On the whole, the error in struts length is negligible and is indirectly incorporated in the nodal distance metrics, which was already discussed above.

Bearing in mind these initial results, the next sections report on the effect of modifying the FM spring stiffness setting, following the GA calibration.

3.3. Calibration with GAs

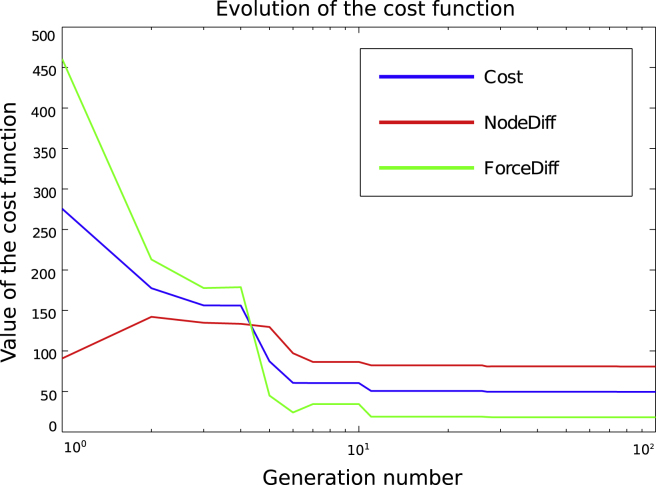
With the aim of reducing the differences between FM and FE and modifying the stiffness settings, we have performed multiple runs of the GA resulting in similar outcomes. As a rule, the convergence was achieved after 50 generations. The results of one typical run are reported here in detail. The very first, randomly assigned, population and the final population are captured in Table 2, together with the corresponding values of the cost function. The cost function fell from the initial best value of 275.6908 to 49.4124 during the simulation, which is displayed in Fig. 11. All individuals that were sampled during the evolution process can be seen in Fig. 12, which displays them as red crosses on the cost space (a) and as red circles on the nodal (b) and force (c) differences spaces. The evolution of the fittest individuals from each generation are plotted as a black line. The convergence towards the most optimal exemplar can be noticed by means of the increase in the concentration of red crosses and circles in the lowest interval of both parameters. In the course of the evolution, the fittest candidate emerges, defined by the pair [0.0688, 0.0874] with the ${\overline{e}}_{\mathrm{nodal}}=80.7917$, ${\overline{e}}_F=0.0036$ and ${\overline{f}}_{\mathrm{cost}}=49.4124$. Note that $wStr$ was defined as the additional stiffness weighting that would be added to the background stiffness weight (see Eq. (3)). Thus, the overall struts stiffness weight is the sum of the two values ($0.0688+0.0874=0.1562$), whereas the weight for the background stiffness remains 0.0874.

Table 2.

Population evolution.

Fig. 11.

Evolution of the cost function throughout 100 generations (abscissa is scaled logarithmically). Red, green and blue lines represent the evolution of nodal error, force error and the overall cost function, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 12.

Example run of the GA visualised in the space of weighting parameters for (a) the cost function, (b) nodal difference and (c) force difference functions. Red crosses and circles represent all the individuals that happened to be instantiated during the 100 generations. The black line shows the evolution of the best fitted individuals from each generation, converging on the one defined by the pair [0.0688, 0.0874]. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The optimal individual that emerges in the course of the GA is very sensitive to the definition of the cost function, in particular to the weightings that indicate importance of the two error measures. The value of weightings that was employed in our cost function was identified using testing and seems to result in both good simulation outcomes and stable convergence behaviour of the genetic algorithm.

3.4. Post-calibration comparison

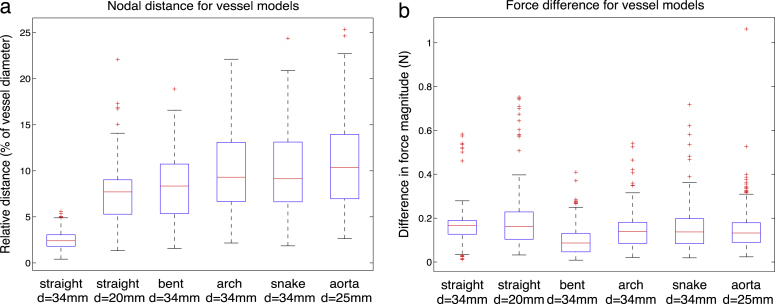
Fig. 13 shows the results of the simulations with the new stiffness values obtained with the GA in the previous section, with the strut stiffness weight set to 0.1562 and the weight for the background stiffness set to 0.0874. Compared to the pre-calibration result (Fig. 10), there is a considerable improvement in the force measurement: from an average difference in magnitude of 1 N to 0.18 N. However, the nodal distance exhibits only a small change, with inconsistent tendency: in some cases there has been a slight improvement, whereas others exhibit minor increase of the resulting discrepancy. This is of no concern, however, since the error in nodal distance was small in the first place.

Fig. 13.

Difference between the two methods FM and FE for all vessel models, after stiffness learning. (a) Resulting nodal distance with the median value represented as a red line and the blue box outlining the 25th and 75th percentiles. (b) Resulting difference in force magnitude. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

These results indicate that the stiffness scaling is not sufficient by itself. Further improvements in the FM algorithm could be achieved by modifying the contact model and possibly implementing a more sophisticated stiffness mechanisms, which potentially takes into account 3D stiffness or different settings for the background mesh, such as anisotropy. These will require further investigation.

4. Conclusions

This paper reported a comparative analysis of a novel fast virtual stenting method with the widely-used finite element analysis. A set of six in silico experiments were conducted and evaluated, resulting in the assessment of the novel FM. Further, using FE results as a learning base, we were able to optimise FM for the chosen stent device by calibrating stiffness parameters with the help of a genetic algorithm. Such calibrations of the FM have to be performed for each new stent device that is to be included in FM deployment simulations. In general, each stent features its own optimal FM stiffness coefficients that have to be previously determined with the help of the demonstrated method.

The obtained stiffness setting substantially improved the force measures reported by the FM and reduced the force discrepancy between the two methods. Overall, the results of all performed experiments indicated a good agreement between the FM and FE methods. More precisely, the mean difference in the nodal positioning ranged between 4% and 10% depending on the complexity of the case, being the highest for the patient-specific case of the aortic dissection with a very irregular geometry. Another quantitative measure of the validity of the FM was the mean force discrepancy, which after the calibration phase, lay below 0.2 N.

The obtained results are promising, especially considering the current limitations of the FM. In particular, the simplified contact model, which is likely to be responsible for high errors, especially in the case of narrow vessels and complex anatomical features. Improving the contact model algorithm would help reduce the errors, most probably at the cost of more expensive computation and longer execution time. Another limitation of the study is in the assumption of rigid vessel walls. Although the FM is already able to model the flexible vasculature, we decided to focus on the process of stent expansion, in order to eliminate possible interdependencies.

In conclusion, the computational fast method proposed here can be explored as an additional tool to facilitate clinical practice. While FE can provide more detailed and accurate analysis, the much faster computational time (in the order of seconds) and acceptable error ($<10\%$) associated with FM, bring high hope for its potential usefulness as an integral part of clinical practice.