Direct observation of an attosecond electron wave packet in a nitrogen molecule

Attosecond electron wave packet in a molecule is captured by the pump-probe method with a-few-pulse attosecond pulse train.

Abstract

Capturing electron motion in a molecule is the basis of understanding or steering chemical reactions. Nonlinear Fourier transform spectroscopy using an attosecond-pump/attosecond-probe technique is used to observe an attosecond electron wave packet in a nitrogen molecule in real time. The 500-as electronic motion between two bound electronic states in a nitrogen molecule is captured by measuring the fragment ions with the same kinetic energy generated in sequential two-photon dissociative ionization processes. The temporal evolution of electronic coherence originating from various electronic states is visualized via the fragment ions appearing after irradiation of the probe pulse. This observation of an attosecond molecular electron wave packet is a critical step in understanding coupled nuclear and electron motion in polyatomic and biological molecules to explore attochemistry.

INTRODUCTION

In chemistry, we seek to understand how chemical bonds form or break to control reactions or create new substances. The proton and electron transfer processes are well-known fundamental processes in photocatalysis and photosynthesis reactions (1, 2). Until now, ultrafast molecular dynamics has been investigated using two complementary approaches, namely, diffraction (3, 4) and spectroscopic methods (5–7). Time-resolved electron or x-ray diffraction can reveal the ensemble-averaged temporal evolution of nuclear and/or charge distributions in molecules. However, the temporal resolution is currently in the femtosecond range. The spectroscopic method enables us to investigate temporal evolution of nuclear and/or charge distributions in a single molecule.

With the recent advent of attosecond extreme ultraviolet pulses, research in observing and controlling ultrafast electronic motion in atoms and molecules in real time has been realized (8, 9). Thus far, the sub-femtosecond chemical reactions of a small molecule are controlled by inducing the charge localization using the carrier envelope phase–stabilized few-cycle pulse (5, 10, 11) or visualized by the correlated wave packet pairs (12). Correlated electron dynamics on the attosecond time scale have only been investigated in atomic targets (13, 14). Although some valuable insights on attosecond molecular response have been obtained without using attosecond pulses (15, 16), it is beyond doubt that the attosecond-pump/attosecond-probe method is the most direct and universal method to extract attosecond molecular dynamics (17, 18). To realize the attosecond-pump/attosecond-probe measurement, however, an intense attosecond pulse is required to achieve a focal intensity larger than 10¹⁴ W/cm² (19–21).

In the new research field of attochemistry, the electronic motion in a molecule will be manipulated before the onset of nuclear vibrational motion (8). This indicates that the chemical reactions should be steered within the time scale of electrons. Because the spectral bandwidth of an attosecond pulse covers energy levels of multiple electronic states, multiple states can be excited coherently to create an electron wave packet (EWP). Moreover, the generation process of an attosecond pulse via the high-harmonic generation (HHG) (22) itself intrinsically creates the EWP, and it is considered to be one of the straightforward ways to observe the molecular EWP on the attosecond time domain, but it is difficult to specify the relevant electronic states because the HHG process is induced by the highly nonlinear process of tunneling ionization and the strong driving light pulse perturbs the electronic states.

When the EWP is prepared between two electronic states with energy gap ΔE, the coherent oscillation between the two states occurs with a period of 2π/ΔE. Thus far, several probe schemes for observing molecular EWP have been proposed, and these schemes are based on photoelectron (23, 24) or high-harmonic (25, 26) spectroscopy. In the case of photoelectron spectroscopy, the probe pulse ionizes the electronic states forming the EWP to the same continuum state. Thus, the spectral bandwidth of the probe pulse must cover ΔE.

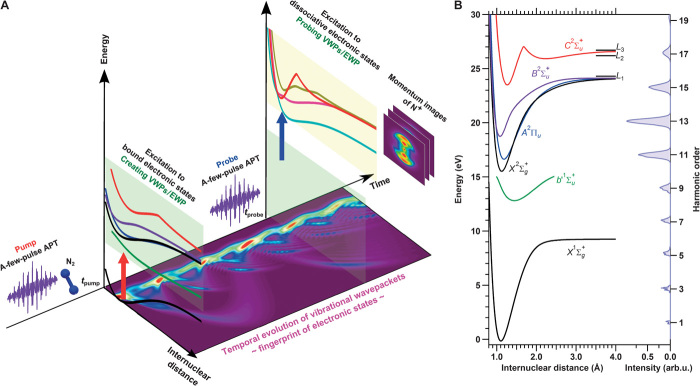
In contrast, here we present the direct observation of temporal evolution of the EWP in a nitrogen molecule by the attosecond-pump/attosecond-probe method using nonlinear Fourier transform spectroscopy (NFTS) (27). The scheme for observing the EWP in N₂ is shown schematically in Fig. 1A. The potential energy curves of electronic states relevant to the EWP formation are shown in Fig. 1B with the harmonic distribution of a-few-pulse attosecond pulse train (APT) composed of a few attosecond pulses in the envelope. The pump pulse creates a coherent EWP among the bound electronic states in N₂ and N₂⁺. Note that the latter involves the ejection of a photoelectron. The probe pulse excites all electronic states involved in the EWP to respective dissociative electronic states in N₂⁺ and triggers fragmentation to generate the N⁺ ion. The pump-probe delay-dependent kinetic energy (KE) distribution of N⁺ exhibits at least four characteristic oscillations from 500 as to 3.5 fs ascribed to the electronic motion or charge oscillation between two electronic states.

Fig. 1. Scheme for observing EWP in a nitrogen molecule.

(A) A-few-pulse APT excites electronic states (shaded light green) to prepare an EWP at the time t_pump. The a-few-pulse APT probe with time delay Δt excites relevant electronic states to the dissociative electronic states in N₂⁺ (shaded light yellow) to trigger the fragmentation (N⁺ + N) at the time t_probe. Momentum images of fragment N⁺ were recorded by scanning the delay Δt. The bottom image shows the numerically simulated nuclear wave packets related to the EWP obtained by considering the superposition of five electronic states $(\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+},\mathit{X}{}^2{\mathrm{\sum }}_{\mathit{g}}^{+},\mathit{A}{}^2\mathrm{\Pi }_{\mathit{u}},\mathit{B}{}^2{\mathrm{\sum }}_{\mathit{u}}^{+},\mathit{C}{}^2{\mathrm{\sum }}_{\mathit{u}}^{+})$. (B) Potential energy curves of electronic states relevant to the EWP formation and the harmonic distribution constituting the APT. L₁, L₂, and L₃ are dissociation limits. arb.u., arbitrary unit.

In the proposed method, the KE of the fragment ion is a measure of the EWP. We first discuss the coherent motion of the EWP created in the N₂⁺ electronic states. The pump pulse ionizes to create a superposition of two bound electronic states in N₂⁺, namely, an EWP. The probe pulse with delay Δt excites this EWP to another coherent superposition of multiple dissociative electronic states, in which N₂⁺ dissociates into N⁺ + N. There are several quantum pathways in the present pump-probe study that lead to the ejection of N⁺ with the same KE. These pathways allow us to observe the temporal evolution of the EWP. Therefore, when we scan the delay Δt and record the fragment N⁺ with an appropriate KE, a periodic modulation of the ion yield associated with the temporal evolution of the EWP appears because of the coherence of quantum pathways.

We have also observed a coherent motion of the EWP created between an electronic state in N₂ and an electronic state in N₂⁺. The probe process in this case is similar to that described above. The only difference is that the excitation process with the probe pulse accompanies the ionization of N₂ to induce dissociations. This is described in detail in section 2 of the Supplementary Materials.

RESULTS

Vibrational wave packet assignment

We conducted an NFTS measurement to observe the attosecond electronic responses by scanning the delay Δt between the pump-APT and the probe-APT (the experimental setup is described in Materials and Methods). Figure 2A shows the delay-dependent N⁺ signals at a KE, E = 0.2 eV. Figure 2B shows the Fourier power spectrum of Fig. 2A, which exhibits four peaks from 500 as to 3.5 fs. The observed frequency peaks are ascribed to the signals associated with the electronic motion in N₂ because these periods are much shorter than the vibrational period of N₂.

Fig. 2. Attosecond electron responses in the pump-probe measurement.

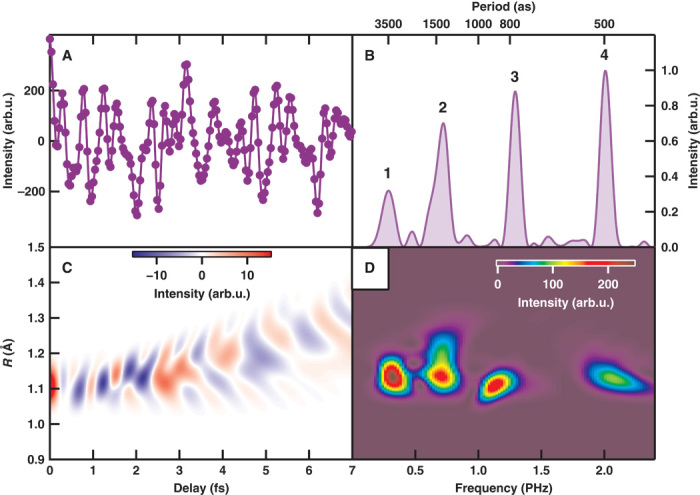
(A) Temporal evolution of fragment ion intensity at E = 0.2 eV. (B) Fourier power spectrum of (A). (C) Numerical simulation of the nuclear correlation function $\text{Re}[{\displaystyle \mathrm{\sum }_{\mathit{i}<\mathit{j}}}{\mathrm{\Psi }}_{\mathit{i}}^{*}(\mathit{R},\mathrm{\Delta }\mathit{t}){\mathrm{\Psi }}_{\mathit{j}}(\mathit{R},\mathrm{\Delta }\mathit{t})]$ composed of four pairs of electronic states. (D) Fourier power spectrogram of (C).

The relevant electronic states in the pump and probe steps of the EWP should be identified to clarify the origin of the observed electronic responses. If the relevant electronic state is not a dissociative state, the pump process leads to the formation of a vibrational wave packet (VWP). Then, the electronic state can be identified by recording the vibrational motion of each electronic state because the unique temporal evolution of the VWP is a fingerprint of the electronic state.

We measured the delay-dependent KE distribution of N⁺ exhibiting the temporal evolution of VWPs as shown in Fig. 3A. Figure 3B shows the Fourier power spectrogram of Fig. 3A. The observed nuclear motion T_vib ~54 fs (~18.5 THz) is ascribed to the VWP motion in $\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$ state in N₂. As shown schematically in Fig. 3C, peaks B and C originate from N⁺ generated by the excitation with the 11th- and higher-order harmonics at the outer turning point to the $5{}^2\mathrm{\sum }_{\mathit{g}}^{+}$ state and dissociate into different dissociation limits (L₄ for peak B and L₃ for peak C).

Fig. 3. Temporal evolution of VWPs for assigning EWP.

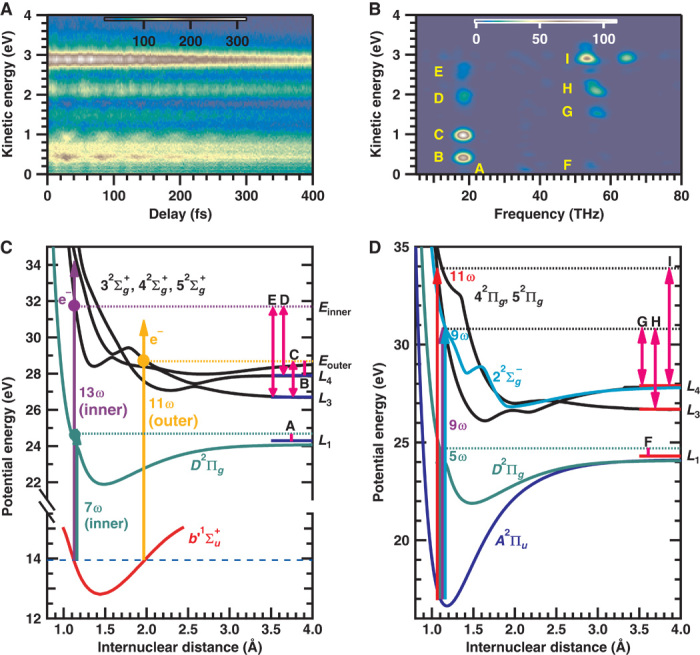
(A) Delay-dependent KE distribution of N⁺. (B) Frequency-KE spectrogram of (A). (C) Probe scheme of the VWP prepared in the $\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$ state. (D) Probe scheme of the VWP prepared in the ${\mathit{A}}^2{\mathrm{\Pi }}_{\mathit{u}}$ state.

On the other hand, peaks D and E originate from N⁺ generated by the excitation with the 13th- and higher-order harmonics at the inner turning point to the $3{}^2\mathrm{\sum }_{\mathit{g}}^{+}$ state and dissociate into L₄ for peak D and L₃ for peak E. The weak peak A around E = 0.2 eV is assigned to N⁺ generated by the excitation with the seventh- or higher-order harmonics at the inner turning point to the D²Π_g state and dissociate into L₁.

The observed nuclear motions T_vib = 15 to 20 fs (50 to 67 THz) are ascribed to the VWPs in the electronic states in N₂⁺. Peaks G to I in Fig. 3B originate from the VWP of the A²Π_u state, and the probe scheme of each peak is shown in Fig. 3D. Peak F around E = 0.2 eV originates from N⁺ generated by the excitation with the fifth-order harmonic to the D²Π_g state and dissociates into L₁. On the basis of the VWP measurement, we found that five electronic states $(\mathit{b}\prime {}^1\mathrm{\sum }_{\mathit{u}}^{+},\mathit{X}{}^2\mathrm{\sum }_{\mathit{g}}^{+},{\mathit{A}}^2{\mathrm{\Pi }}_{\mathit{u}},\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}, \text{and} \mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+})$ can be probed to generate N⁺ with the same KE of 0.2 eV (see sections 3 and 4 in the Supplementary Materials). In the above VWP assignment, it is difficult to absolutely exclude the existence of other dissociation channels because the assignment is based on the calculated potential energy curves of highly excited electronic states.

EWP assignment

We will now assign the peaks shown in Fig. 2B to the EWP created on pairs of electronic states. Peak 4, which exhibits the fastest oscillation at T_EWP = 500 as (ΔE = 8.3 eV), can be ascribed to the EWP created between the A²Π_u and $\mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states. The oscillation period T_EWP = 3.5 fs (ΔE = 1.2 eV) for peak 1 is ascribed to the EWP between the $\mathit{X}{}^2\mathrm{\sum }_{\mathit{g}}^{+}$ and A²Π_u states. On the other hand, peaks 2 and 3 can be ascribed to the EWP between the electronic state in N₂ and the electronic state in N₂⁺. Peak 2 (T_EWP = 1.4 fs, ΔE = 3.1 eV) is ascribed to the EWP between the $\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$ and A²Π_u states. Finally, peak 3 (T_EWP = 770 as, ΔE = 5.4 eV) can be ascribed to the EWP between the $\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$ and $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states. On the basis of the energy difference ΔE, peaks 2 and 3 can also be ascribed to the EWPs between the $\mathit{X}{}^2\mathrm{\sum }_{\mathit{g}}^{+}$ and $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states and between the $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ and $\mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states, respectively. However, peak 2 for ($\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$, A²Π_u) and peak 3 for ($\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$, $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$) are considered to be major contributions because the transition probabilities for ($\mathit{X}{}^2\mathrm{\sum }_{\mathit{g}}^{+}$, $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$) and ($\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$, $\mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$) are much smaller than those for ($\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$, A²Π_u) and ($\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$, $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$). Figure 2C shows the frequency spectrogram calculated from the nuclear correlation function $\text{Re}[{\displaystyle \sum _{\mathit{i}<\mathit{j}}}{\mathrm{\Psi }}_{\mathit{i}}^{*}(\mathit{R},\mathrm{\Delta }\mathit{t}){\mathrm{\Psi }}_{\mathit{j}}(\mathit{R},\mathrm{\Delta }\mathit{t})]$, where Ψ_k(R, Δt)(k = i, j) are the nuclear wave functions. The Fourier transform of Fig. 2C is shown in Fig. 2D, and it qualitatively reproduces the experimental result shown in Fig. 2B. The discrepancy in the relative intensity of peaks between the experimental result shown in Fig. 2B and the numerical simulation shown in Fig. 2D can be ascribed to the difference in the transition probabilities.

Figure 4A shows the numerically simulated temporal evolution of the nuclear correlation function between the A²Π_u and $\mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states, $\text{Re}[{\mathrm{\Psi }}_{\mathit{A}}^{*}(\mathit{R},\mathrm{\Delta }\mathit{t}){\mathrm{\Psi }}_{\mathit{C}}(\mathit{R},\mathrm{\Delta }\mathit{t})]$. In the figure, the EWP between the electronic states oscillates with a period of 500 as. Figure 4B shows the correlation function integrated over the internuclear distance and the charge oscillation between two electronic states.

Fig. 4. Numerically simulated snapshot of the electron spatial distribution of the EWP between the A²Π_u state and the $\mathit{C}{}^2{\mathrm{\sum }}_{\mathit{u}}^{+}$ state.

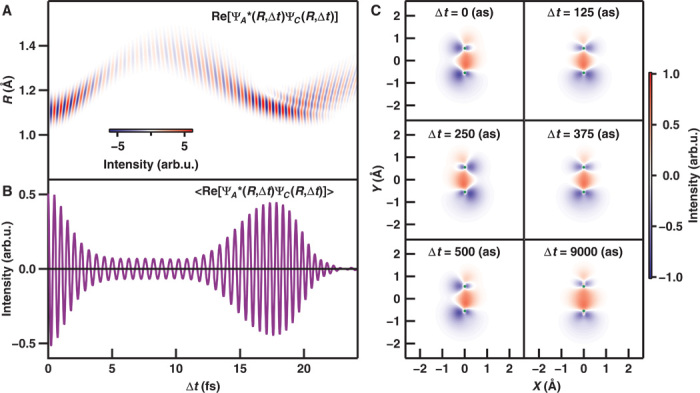
(A) Nuclear correlation function $\text{Re}[{\mathrm{\Psi }}_{\mathit{A}}^{*}(\mathit{R},\mathrm{\Delta }\mathit{t}){\mathrm{\Psi }}_{\mathit{C}}(\mathit{R},\mathrm{\Delta }\mathit{t})]$. (B) Nuclear correlation function integrated over the internuclear distance $\langle \text{Re}[{\mathrm{\Psi }}_{\mathit{A}}^{*}(\mathit{R},\mathrm{\Delta }\mathit{t}){\mathrm{\Psi }}_{\mathit{C}}(\mathit{R},\mathrm{\Delta }\mathit{t})]\rangle$. (C) Snapshots of differential electron density between the A₂Π_u and $\mathit{C}{}^2{\mathrm{\sum }}_{\mathit{u}}^{+}$ states in N₂⁺, where the green circles indicate the positions of nitrogen atoms with an equilibrium geometry of N₂.

The temporal evolution of the differential electron density map (EDM) between the A²Π_u and $\mathit{C}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$ states shown in Fig. 4C reveals the variation of the electron spatial distribution where the reference electron density is set to that of ${\mathit{X}}^2{\mathrm{\sum }}_{\mathit{g}}^{+}$ state (see section 5 in the Supplementary Materials). The EDM oscillates with a period of 500 as, and the nuclear motion on this time scale is negligible. Thus, the distributions at Δt = 0 as and Δt = 500 as are identical, and the distribution at Δt = 250 as is also the same, but with opposite phase. However, the EDM at Δt = 9000 as is similar to that at Δt = 125 as because both the nuclear correlation functions are almost zero.

CONCLUSION

Here, we observed the EWP among five bound electronic states in N₂ using the attosecond-pump/attosecond-probe method by detecting fragment ions as a good measure of electron motions. The pump and probe processes of the EWP among these five electronic states are securely identified by measuring the coherent temporal evolution of the VWP in each electronic state. The combination of an intense a-few-pulse APT with a moderate spectral bandwidth and NFTS makes it possible not only to visualize attosecond electron motion in molecules but also to assign electronic states.

Compared with conventional methods (23–26) for observing EWP, the proposed approach has distinct advantages in that (i) the probe process of each electronic state can be unambiguously identified, (ii) the eigenenergy of final states excited by the probe pulse can be different for each electronic state, and (iii) the EWP formed in the singly charged electronic states can be probed without further ionization to generate the second photoelectron.

Direct observation of an EWP in a diatomic molecule is key to exploring coupled nuclear electron motions in more complex molecules. However, the complex molecule will accompany complicated photoelectron spectra, and it will be difficult to elucidate the key electronic states leading to a target chemical reaction. Although attosecond electron motion in molecules can be monitored by detecting ions and photoelectrons in coincidence, the repetition rate of available attosecond light sources is still insufficient to perform attosecond-pump/attosecond-probe measurement. The detection of fragment ions and the identification of the relevant electronic state from nuclear motion by a-few-pulse APT in the present study provide a powerful alternative method for observing attosecond electron motion in complex molecules. The development of wavelength tunable attosecond pulses well matched to the potential energy of the electronic states in molecules can further extend the potential of the proposed scheme for investigating attosecond electron motion and/or coupled nuclear electron motion.

MATERIALS AND METHODS

A-few-pulse APT generation and characterization

The experimental setup for attosecond-pump/attosecond-probe measurement of an EWP in a nitrogen molecule is shown in fig. S1. The experimental setup is composed of three primary components: (i) an intense a-few-pulse APT generator, (ii) a high-throughput, high-stability interferometer with an attosecond time scale, and (iii) a counting velocity map imaging ion spectrometer.

An APT is generated using a sub–15 fs TiS laser system [800 nm, 12 fs, 40 mJ per pulse (maximum), 100 Hz] (28). The output of a femtosecond laser system is loosely focused (f = 5 m) onto a static gas cell filled with Xe gas to generate intense high harmonics (29). The resultant harmonic intensity distribution at the focal region is shown in fig. S2 where the throughput of XUV optics [Si plane mirror, SiC concave mirror, XUV grating, and XUV CCD (charge-coupled device)] is taken into account. By tuning the central wavelength of fundamental light, the harmonic distribution is tuned with three configurations. When the central wavelength of fundamental light is in a blue-shift configuration, the resultant harmonic energy is also blue-shifted as shown in fig. S2A. On the other hand, when the central wavelength of fundamental light is in a red-shift configuration, the harmonic distribution is also red-shifted as shown in fig. S2C.

The temporal profile of APT is characterized in situ by measuring an interferometric autocorrelation trace using a nitrogen molecule as a nonlinear medium (30). By recording the fragment ions originating from two-photon nonsequential dissociative ionization as a function of delay, the interferometric autocorrelation trace is obtained as shown in fig. S3A. The resultant pulse duration of each attosecond pulse is 250 as, and the duration of the APT envelope is 4.2 fs in which the attosecond bursts repeated each half-cycle of the fundamental laser. This short APT envelope suggests that the number of attosecond pulses in the envelope is a few as shown in fig. S3B. Therefore, the generated APT can be referred to as “a-few-pulse APT.” The probability of two-photon processes with a-few-pulse APT is given in fig. S3C. For the purpose of using lower-order harmonics (first through seventh), a thin metal filter, which is usually inserted to block the fundamental light and lower-order harmonics, is not inserted. The unconverted fundamental light is significantly attenuated to avoid multiphoton absorption as described in the following. The resultant pulse duration of a-few-pulse APT is somewhat chirped by the attosecond chirp. The magnitude of the chirp is estimated to be 1.3 × 10⁻³² fs² (19).

Excitation with APT

Molecules pumped with the APT can be excited by multiple attosecond pulses in the train. The effect of an attosecond burst on the VWP is negligible because the envelope of APT (~4 fs) is much shorter than the vibrational period of N₂ and N₂⁺ (14 fs in the shortest). Note that the VWP can only be created when the spectral bandwidth of light source can cover several vibrational states. On the other hand, for observing the EWP, the carrier frequency of light source should be larger than the energy difference of electronic states relevant to the formation of EWP. Our a-few-pulse APT satisfies these conditions. The effect of an attosecond burst on the EWP between the A²Π_u and $\mathit{C}{}^2{\mathrm{\sum }}_{\mathit{u}}^{+}$ states exhibiting 500-as oscillation is numerically simulated, and the probability of internuclear distance is plotted as a function of delay in fig. S4. When the EWP is created by the single pulse excitation, the periodic change of 500 as in the probability of internuclear distance is clearly seen in fig. S4A. On the other hand, when the EWP is created by a-few-pulse APT, the same periodic structure can be observable, although the modulation contrast is lower than the single pulse excitation case shown in fig. S4B.

High-throughput, high-stability delay line

The generated intense a-few-pulse APT propagates about 6 m downstream, and the APT passes through a pinhole (2 mmØ). Because the beam diameter of high harmonics is about 3 mmØ, the contribution of the long trajectory is eliminated by the pinhole. At the same time, the significant portion of co-propagated fundamental light is truncated by the pinhole. After passing through the pinhole, the APT pulse is injected into a high-throughput, high-stability interferometer (31). The APT beam is spatially split by a pair of Si plane mirrors. The incident angle for the Si mirror is set to the Brewster angle of the fundamental laser pulse. One of the Si mirrors is mounted on a high-precision piezo linear one-axis translation stage.

The delay between the two replicas of a-few-pulse APT is precisely adjusted by moving the piezo stage. Two types of piezo stages were used for the pump-probe measurement. For measuring the interferometric autocorrelation trace or extracting electronic responses of nitrogen molecules, the delay was scanned every 35.6 as from −7 to +7 fs corresponding to moving the piezo stage (P-621.1CL, Physik Instrumente) in 20-nm steps. On the other hand, in measuring the temporal evolution of VWPs, the delay was scanned every 2 fs from 0 to 400 fs corresponding to moving the piezo stage (P-628.1CL, Physik Instrumente) in 1120-nm steps.

The instability of the delay can be suppressed to be smaller than 10 as/hour by actively regulating the temperature of the piezo stage by a Peltier module sandwiched with Cu plates with 0.001°C precision using a high-precision temperature controller (ILX Lightwave, LDT-5910C) because the thermal expansion of the position sensor of the piezo stage decreases the stability of the interferometer. The temperature regulation increases the stability of the interferometer by one order of magnitude. The delay zero is experimentally confirmed by measuring the interferometric autocorrelation trace of the APT.

Velocity map imaging ion spectrometer

Replicas of the APT pulses with a fixed delay are propagated to a SiC concave mirror (f = 100 mm) passing through a velocity map imaging spectrometer (VMIS) (32) and are focused onto a molecular beam of nitrogen molecules. The focal intensity is about 1 × 10¹⁴ W/cm² for both the pump and probe pulses. The molecular beam is injected from a high-speed piezo valve (33) integrated into the rear of a repeller electrode in the VMIS (34). The central part of the molecular beam of nitrogen is skimmed by a pinhole (0.5 mmØ) of the repeller electrode. The density of the molecular beam can be high enough to induce the distortion of the momentum image due to a space charge effect with the intense a-few-pulse APT. In the actual measurement, to avoid image distortion, the sample density is set two orders of magnitude lower than the onset density of the space charge effect.

Data acquisition conditions and data analysis

The opening time of the piezo valve can be as short as 20 μs with a repetition rate of 100 Hz to ensure that the operating pressure of the VMIS chamber remains much lower than 10⁻⁴ Pa. For robust operation of the high-speed piezo valve, it is water-cooled using a recirculating water chiller. The resultant ions at the focal region are extracted by three-parallel electrodes satisfying a Wiley-Mclaren condition (35) to a two-dimensional position-sensitive detector (Photonis) composed of two microchannel plates (MCPs; 120 mmØ) in a Chevron configuration and a phosphor screen (P47). The phosphorus lifetime of P47 (~60 ns) is short enough to extract only one fragment species by imposing a pulsed gate voltage to the MCPs with a duration of 100 ns. The phosphorus image on the phosphor screen is image-relayed onto a scientific CMOS camera (Andor, Neo5.5). As an active area, 1200 × 1200 pixels are set and are read out with a 2 × 2 binning to improve the signal-to-noise ratio. The momentum images are read out at 50 Hz, corresponding to the acquisition of one image per two laser pulses, limited by the bandwidth of the frame grabber board (~250 MB/s).

A total of 5000 momentum images are recorded for each delay, and the counting analysis is performed for each momentum image so as to compensate for the incident angle–dependent detection efficiency and the inhomogeneity of the electron multiplication gain in the MCP detector (36). After the counting analysis (37), the number of counts per pixel is accumulated for each delay. Because the resultant momentum image is a two-dimensional projection of a Newton momentum sphere, the original Newton momentum sphere is reconstructed by an inversion method (pBASEX) (38).

Here, the temporal evolution of the fragment signal shown in Figs. 2 and 3 is obtained after integration over the angle measured from the laser polarization. The angular distribution of the fragment is used to securely assign the probe processes of each VWP because the angular distribution reflects the symmetry of the electronic states.

SUPPLEMENTARY MATERIALS

Supplementary materials for this article are available at http://advances.sciencemag.org/cgi/content/full/1/8/e1500356/DC1

Experimental setup and conditions

Observation of an electron wavepacket through kinetic energy distribution measurement

Potential energy curves of N₂ and N₂⁺

Vibrational wavepacket

Electron wavepacket

Movie S1. Temporal evolution of the differential EDM.

Fig. S1. Experimental setup.

Fig. S2. Spectrum of fundamental light and high harmonics.

Fig. S3. Interferometric autocorrelation trace of a-few-pulse APT.

Fig. S4. APT pump effect on the internuclear density.

Fig. S5. Potential energy curves of the A²Π_u state and the final states excited from the A²Π_u state.

Fig. S6. Franck-Condon factors of the electronic states in N₂ and N₂⁺.

Fig. S7. Potential energy curves and vibrational distributions of the b¹Π_u and $\mathit{b}\prime {}^1{\mathrm{\sum }}_{\mathit{u}}^{+}$ states.

Fig. S8. Frequency-filtered delay KE spectrogram.

Fig. S9. Numerical simulation of temporal evolution of VWP.

Table S1. Spectroscopic constants of electronic states in N₂ and N₂⁺(44).

Table S2. Energy of N₂⁺ dissociation limits relevant to the probe process of the vibrational and electron wavepacket (39).

Table S3. Probe process of vibrrational wavepacket in $\mathit{X}{}^2\mathrm{\sum }_{\mathit{g}}^{+}$.

Table S4. Probe process of vibrrational wavepacket in A²Π_u.

Table S5. Probe process of vibrrational wavepacket in $\mathit{B}{}^2\mathrm{\sum }_{\mathit{u}}^{+}$.

Table S6. Assignment of observed electron wavepacket at E = 0.2 eV.

References (39–52)