StringTie enables improved reconstruction of a transcriptome from RNA-seq reads

Abstract

Methods used to sequence the transcriptome often produce more than 200 million short sequences. We introduce StringTie, a computational method that applies a network flow algorithm originally developed in optimization theory, together with optional de novo assembly, to assemble these complex data sets into transcripts. When used to analyze both simulated and real data sets, StringTie produces more complete and accurate reconstructions of genes and better estimates of expression levels, compared with other leading transcript assembly programs including Cufflinks, IsoLasso, Scripture and Traph. For example, on 90 million reads from human blood, StringTie correctly assembled 10,990 transcripts, whereas the next best assembly was of 7,187 transcripts by Cufflinks, which is a 53% increase in transcripts assembled. On a simulated data set, StringTie correctly assembled 7,559 transcripts, which is 20% more than the 6,310 assembled by Cufflinks. As well as producing a more complete transcriptome assembly, StringTie runs faster on all data sets tested to date compared with other assembly software, including Cufflinks.

Over the past decade, numerous studies have revealed an increasing degree of diversity in the transcriptomes of higher eukaryotes¹. Most transcribed elements are never translated into proteins and are encoded by a myriad of non-protein-coding RNA genes (ncRNAs) that have complex patterns of expression and regulation². Further complicating the picture, more than 90% of transcripts of multiexon protein-coding genes, and about 30% of ncRNAs, undergo alternative splicing^3,4. We currently have a far from complete picture of the exonintron structure of all transcripts in the human genome. For non-human species, the landscape of alternative splicing is even less clear.

In recent years, gene discovery methodology has been revolutionized by RNA-seq, a high-throughput assay that sequences transcribed genes⁵. Previous efforts to model genes de novo, through recognition of splice sites, coding regions and other signals, have been superseded by more accurate methods that use RNA-seq data as input. An RNA-seq run can produce more than 200 million short reads, each of which is 100–150 base pairs (bp). Assembling these short reads into full transcripts is a complex task. Not only do different transcripts have highly variable sequence coverage, but also alternative transcripts from the same locus can share exons, making it difficult to assemble multiple isoforms unambiguously. Determining the quantities of all of these transcripts is also challenging, even if we assume that the transcript structures are known. Exon sharing among transcripts, ambiguous read mappings due to close paralogs and low levels of gene expression are all factors that make the quantification task difficult⁶. In addition, incorrectly assembled transcripts are a major obstacle to correct isoform abundance estimation.

Although a growing number of methods have been developed to solve either the transcript identification problem (e.g., Trinity⁷, Oases⁸), the expression quantification problem (e.g., RSEM⁹, eXpress¹⁰) or both (e.g., IsoInfer¹¹, Scripture¹², Cufflinks¹³, SLIDE¹⁴, IsoLasso¹⁵, iReckon¹⁶, Traph¹⁷), much work remains to produce consistent, highly accurate solutions. A recent study¹⁸ of the current transcript reconstruction methods showed that even in cases where these methods identified all constituent exons of a transcript, they often failed to assemble the exons into complete isoforms. Moreover, the expression of multiple isoforms and novel splice variants greatly affects the accuracy of transcriptome reconstruction. As a result, more accurate methods for identifying novel transcripts are needed to reproduce more complete transcriptomes. Here, we report a transcriptome assembly method named StringTie that correctly identified 36–60% more transcripts than the next best assembler (Cufflinks) on multiple real and simulated data sets. Using simulated data, we show that the expression levels produced by StringTie also showed higher agreement with the true values.

There are two main approaches to the transcriptome assembly problem. A reference-based or genome-guided transcriptome assembly algorithm uses alignments of reads to the genome that are produced by a specialized spliced-alignment tool, such as TopHat2 (ref. 19) or GSNAP²⁰, to identify clusters of reads that represent potential transcripts. It then builds transcript assemblies from these alignments. If paired-end reads are available, they improve the ability of the assembler to link together exons belonging to the same transcript. A de novo assembly approach does not need a reference genome and can, in theory, reconstruct transcripts even from regions that are missing from a reference. This second approach is technically more difficult because the presence of multicopy gene families, large variations in expression levels and large numbers of alternatively spliced variants make assembly very challenging without a reference genome. Owing to these factors, de novo transcriptome assembly is generally less accurate than genome-guided assembly, and de novo methods are primarily used for RNA-seq data sets from organisms that lack a sequenced genome²¹.

StringTie uses a genome-guided transcriptome assembly approach along with concepts from de novo genome assembly to improve transcript assembly. Specifically, the inputs to StringTie can include not only spliced read alignments, but also the alignments of contigs that StringTie pre-assembles from read pairs. For clarity, we use the name StringTie+SR to describe results that use both types of input data.

Using a mapping of reads to the reference genome, genome-guided transcript assemblers cluster the reads and build graph models representing all possible isoforms for each gene. One such model is a splice graph, in which nodes represent exons or parts of exons, and paths through the graph represent possible splice variants (Supplementary Fig. 1). Cufflinks¹³, which is the most widely used transcript assembler, uses an overlap graph, in which the sequenced fragments are nodes and two nodes are connected if they overlap and have compatible splice patterns. Cufflinks and other transcriptome assembly programs, such as Scripture¹², IsoLasso¹⁵, SLIDE¹⁴ and iReckon¹⁶, use various criteria to parse these graphs. Cufflinks uses a parsimony-based algorithm that generates the minimal number of transcripts that will explain all reads in the graph. Although the parsimony principle is appealing, it does not consider transcript abundance, and it may not reconstruct the correct set of isoforms, as illustrated in Supplementary Figure 2. Obviously, if the wrong transcripts are generated, then their expression levels cannot be correct.

Rather than finding a minimal set of transcripts and then estimating their expression levels separately as Cufflinks does, StringTie assembles transcripts and estimates their expression levels simultaneously. StringTie first groups the reads into clusters, then creates a splice graph for each cluster from which it identifies transcripts, and then for each transcript it creates a separate flow network to estimate its expression level using a maximum flow algorithm.

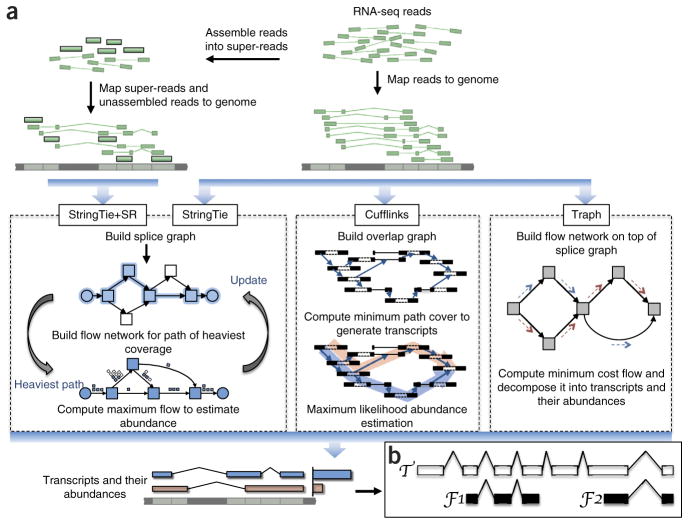
The maximum flow problem is a well-studied problem in optimization theory, but until now it has not been used to solve the transcript quantification problem. A flow network is currently used for transcriptome assembly and quantification by only one other method, Traph¹⁷ (note, Traph uses a fundamentally different flow network formulation; for example, it solves a minimum rather than maximum flow problem; see Supplementary Discussion for details). Figure 1 illustrates the main differences between StringTie, StringTie+SR, Cufflinks and Traph.

Figure 1.

Transcript assembly pipelines for StringTie, Cufflinks and Traph. (a) Overview of the flow of the StringTie algorithm, compared to Cufflinks and Traph. All methods begin with a set of RNA-seq reads that have been mapped to the genome. An optional secondary input to StringTie is a set of pre-assembled super-reads, designated as StringTie+SR. StringTie iteratively extracts the heaviest path from a splice graph, constructs a flow network, computes maximum flow to estimate abundance, and then updates the splice graph by removing reads that were assigned by the flow algorithm. This process repeats until all reads have been assigned. (b) Annotated transcript T for which read data covers only the fragments F1 and F2. An assembler is given credit for a correct reconstruction of T if it correctly assembles F1 and F2.

Although StringTie can be run using known gene coordinates to guide the assembly process, here we focus on how accurately it can assemble and quantify transcripts, regardless of whether prior annotation is known. We evaluated StringTie when it was run without annotation, and compared its performance with Cufflinks¹³, IsoLasso¹⁵, Scripture¹² and Traph¹⁷, which along with MITIE²² are the only transcriptome assemblers than can be run without annotation. We attempted to include MITIE, but excessive running time prevented inclusion; after one month of computation, MITIE did not produce results for any of the data sets included in this study. It is impossible to know with certainty which transcripts are actually present in real data, so for initial comparisons of different assemblers we used simulated data. Simulation allows us to evaluate how well each assembler captures both the structure and the quantity of each gene and transcript, because the exact composition of a simulated data set is known. We used Flux Simulator²³ to generate 150 million 75-bp paired-end reads, extracted from all RefSeq human transcripts as provided by the UCSC Genome Browser²⁴. Limitations of simulated data include an imperfect ability to model sample preparation protocols and the distribution of reads across the genome²⁵. Flux Simulator tries to overcome these limitations by the use of parameterized models that reproduce the common sources of systematic bias in each of the main steps in sample preparation.

To test the ability of the different programs to assemble reads correctly in different experimental setups, we simulated two data sets with different characteristics and different read distributions. We generated the first data set (Sim-I) using the exact parameters specified for a directional human RNA-seq protocol provided on the Flux Simulator web page (http://sammeth.net/confluence/display/ SIM.) We generated a second data set (Sim-II), in which we replaced the empirical fragment size distribution from Sim-I with a parameterized normal N(250,20) distribution, because some transcriptome assemblers¹³ assume a normal distribution. Both data sets follow the default error model for reads and incorporate the biases from common library preparations as modeled by Flux Simulator.

We mapped the simulated reads from each data set to the GRCh37/ hg19 human reference genome using TopHat2 (ref. 19). The two resulting BAM alignment files were used as inputs for StringTie, Cufflinks, Traph, Scripture and IsoLasso. We also assembled the paired reads into “super-reads” using the MaSuRCA assembler²⁶, which uses a k-mer index of all reads to extend every read in both directions as long as this extension is unique. If two paired reads were merged into the same super-read, we then aligned the full fragment to the genome (as if it were one longer read). We include results from a separate run of StringTie, denoted StringTie+SR, in which the input consists of a mixture of aligned super-read fragments and alignments of unassembled reads.

To compute the accuracy of the transcriptome assemblers, we considered a transcript to be correctly identified if its full intron chain was identified (i.e., all intron boundaries matched exactly) and if the start of the first exon and the end of the last exon were <100 bp from the actual start and end, respectively. We allowed this flexibility at the boundaries of the transcript to reflect the drop-off in coverage that often occurs near the ends of transcripts, and also the uncertainty (in the annotation) about the precise boundaries of the 3′ and 5′ UTR regions for many genes. We considered multi-exon transcripts to be correctly assembled only if their strand was also correctly identified, and when strand-specific RNA-seq data were used, we also required that single-exon transcripts were assigned to the correct strand. The Cuffcompare program from the Cufflinks package uses the same matching criteria to label correctly assembled transcripts. If the read data only partially covered a transcript (making it impossible to identify the full transcript from the input data alone), then we considered the corresponding prediction to be correct if all partially covered parts of the transcript were identified.

For example, the annotated transcript T had relatively few reads covering it (Fig. 1b). These reads covered only the exons and partial exons shown as fragments F1 and F2. We considered T to be correctly identified if a program’s output contained those two fragments. We defined the sensitivity of a program as the number of transcripts that are identified correctly out of all the ones that were expressed in the simulation experiment. We defined the precision (or positive predictive value) of a program as the percentage of predicted transcripts or transcript fragments (such as F1 and F2 in Fig. 1b) that matched the true transcripts.

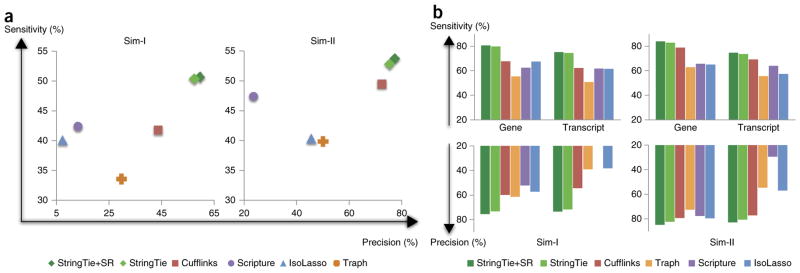
A comparison of StringTie, StringTie+SR, Cufflinks, Scripture, IsoLasso and Traph on the two simulated data sets is shown in Figure 2. All programs had the same input, except for StringTie+SR, which used the assembled super-reads as described above. Note that Scripture had very low precision on both data sets because it tends to predict a far larger number of splice variants for each gene than the other methods. On Sim-I, StringTie+SR found 20% more true transcripts than the next-best programs, with 34% fewer false positives. Not surprisingly, StringTie’s improvement is much higher on Sim-I than on the cleaner Sim-II data set, where the fragment sizes followed a distribution that matched the built-in assumptions of Cufflinks. Cufflinks in particular performed far better on Sim-II compared with Sim-I, with sensitivity and precision just slightly below StringTie. All other programs, however, were substantially lower than StringTie for both precision and sensitivity on both data sets.

Figure 2.

Transcriptome assemblers’ accuracies in detecting expressed transcripts from two simulated RNA-seq data sets. (a) Transcriptome assemblers’ accuracies in detecting expressed transcripts from two simulated RNA-seq data sets. In data set Sim-I (left), the fragment sizes follow an empirical distribution based on Illumina sequences, and in Sim-II (right) the fragment sizes follow a parameterized normal distribution. StringTie+SR pre-assembles the reads into super-reads when possible. (b) Accuracy of transcriptome assemblers on gene loci from the same two data sets, considering only those transcripts that were completely covered by input reads. Scripture’s precision on Sim-I was 17.7%, below the 20% minimum shown here.

In principle, the other programs can also be provided with the aligned super-reads as input, as done for StringTie+SR. We tried this strategy with Cufflinks (the best assembler other than StringTie), and both its sensitivity and precision declined substantially on Sim-I, whereas on Sim-II it made only marginal improvements (results not shown). By contrast, StringTie+SR performed better than StringTie alone on both data sets, though only by a small amount. The limited improvement is a consequence of the fact that the assembled super-reads used here simply filled in the gap between a pair of reads.

The accuracies shown in Figure 2a represent all transcripts, including those that were only partially covered by reads. We looked at how well the assemblers did for those transcripts that were fully covered by reads, that is, transcripts present at relatively higher levels in a given sample (Fig. 2b). Figure 2b and Supplementary Table 1 present the accuracy of all six programs on these fully covered transcripts. Assembly accuracy was defined as above for transcripts, and we introduce an analogous definition of gene-level accuracy; we considered a gene to be correctly identified if at least one of its transcripts was correctly assembled. Thus gene-level accuracy was always higher than transcript-level accuracy.

In most cases, the assemblers’ accuracies in Figure 2b followed the same ranking as in Figure 2a, which included partially covered transcripts. StringTie+SR and StringTie performed the best on both sensitivity and precision, followed by Cufflinks. For Sim-II, StringTie+SR showed an increase of more than 5% over Cufflinks in both sensitivity and precision. On Sim-I this increase was more than twice as great on both measures. On both data sets, StringTie and StringTie+SR predicted at least one transcript perfectly matching the annotation for over 80% of the genes.

It is worth noting that Cufflinks is designed to eliminate isoforms expressed at very low levels, on the assumption that those isoforms may be incompletely spliced precursors or other artifacts. By default, the Cufflinks threshold for filtering out low-abundance transcripts is set to 10% of the most abundant isoform (computed separately for each gene). We tried lowering this threshold for Sim-I and Sim-II, which slightly increased Cufflinks’ sensitivity while reducing its precision by a comparable amount. Like Cufflinks, StringTie was also designed to eliminate assembled transcripts with very low levels of expression. Figure 2a,b shows StringTie’s accuracy when this filtering threshold was set to 10%, the same level as used by Cufflinks. Interestingly, lowering the threshold to 5% for StringTie still yielded better sensitivity and precision than Cufflinks yielded at the 10% threshold (Supplementary Figs. 3 and 4). All other results presented here use the 10% filter for both Cufflinks and StringTie (Supplementary Discussion and Supplementary Fig. 5).

Assembly of reads reproduces the exon-intron structure of genes, but we also need to estimate how much of each transcript was present in the original cells. To evaluate the transcript quantification performance of each program, we compared the estimated expression with the known amounts of each transcript in the simulated data. Quantification is measured by the number of pairs of reads (“fragments” where one or both ends of a fragment are sequenced), which are normalized based on the total number of fragments sequenced (measured in millions) and by the length of the transcript (measured in kilobases), giving an estimate measured as fragments per kilobase of transcript per million fragments (FPKM). With the exception of Scripture, all programs tested here use FPKM values to estimate transcript abundances. StringTie also reports a read per base coverage for each exon of a predicted transcript. Scripture produces RPKM values, which count reads instead of fragments. As has been pointed out previously¹³, FPKM is preferable to RPKM in the case of paired-end RNA-seq experiments, where in some cases one of the two reads belonging to a fragment might be unmapped, possibly leading to underestimates of expression. We obtained very similar results whether using FPKM or RPKM values (Supplementary Table 2).

We computed the Spearman correlation coefficient between the true and estimated expression levels for each set of transcripts. Specifically, we compared the expression level of each predicted transcript with the true transcript that it matched. The Spearman correlation first converts all values to ranks; that is, the FPKM values f₁, f₂, f₃, … from largest to smallest are converted to rank values 1, 2, 3, …, and these ranks are then correlated to compare each method’s predictions with the true ranks. We found similar results using Pearson correlation coefficients (Supplementary Table 3) with a log-transformed version of abundances, that is, log₂(x + 1), to prevent the correlation values from being dominated by the most abundant transcripts and to avoid problems with zero abundance counts.

Because the predicted transcripts do not always match the true transcripts, we compared the quantification values as follows. First, if a predicted transcript P failed to match any true expressed transcript, than we matched P with a transcript that had an expression level of zero. Second, if a true transcript T was not covered (even in part) by any prediction, then we matched T with a prediction that had an expression level of zero. If multiple predicted transcripts (transfrags) were contained within a single true transcript, then we summed all the reads assigned to the predicted transfrags and correlated this sum with the expression level of the true transcript. Table 1 shows the correlations between true and predicted expression levels for StringTie and the four other transcriptome assemblers tested in this paper.

Table 1.

Transcriptome assemblers’ performances on simulated and real data

Data set	Measure	StringTie+SR	StringTie	Cufflinks	Traph	Scripture	IsoLasso
Sim-I	ρall	0.648	0.646	0.551	0.080	−0.361	0.162
	ρpredicted	0.871	0.878	0.826	0.432	−0.228	0.500
Sim–II	ρall	0.799	0.787	0.720	0.310	−0.435	0.000
	ρpredicted	0.913	0.907	0.883	0.524	−0.301	0.258
Kidney	Genes	10,773	10,659	7,774	n/a	7,813	2,785
	Transcripts	13,900	13,720	9,245	n/a	13,833	3,191
Blood	Genes	9,198	8,938	6,073	n/a	6,533	3,526
	Transcripts	11,489	10,990	7,187	n/a	11,213	4,124
Lung	Genes	10,913	10,779	8,566	n/a	7,070	3,590
	Transcripts	14,055	13,706	10,370	n/a	12,559	4,187
Monocytes	Genes	9,005	8,859	6,351	n/a	6,244	3,020
	Transcripts	11,059	10,748	7,502	n/a	1,1046	3,528

Results on simulated data show the Spearman correlation coefficient between the real and predicted number of reads (measured by RPKM values for Scripture and FPKM values for all other programs) for each of the assemblers considered in this study. Rows labeled “ρ_all” include all true and predicted transcripts. Rows labeled “ρ_predicted” include all predictions but exclude true transcripts that were not predicted by a given program. For the four real data sets, shown are the number of genes and transcripts exactly matching known annotation. Traph was unable to process any of the real data sets.

StringTie+SR and StringTie had similar performance, and both were substantially better than Cufflinks (Table 1). Traph and IsoLasso performed far worse, and Scripture’s expression levels consistently had a negative correlation with the true values. Scripture’s negative correlation values are a result of its strategy of predicting far more transcripts than are present in the actual data. (For example, on the Sim-II data, Scripture produced ~60 times as many incorrectly assembled transcripts as StringTie. Scripture’s estimated RPKM values for these incorrectly assembled transcripts were also much higher than the estimated FPKM values of the other assemblers; for details see Supplementary Table 4.) All programs performed better when considering only the genes they predicted, ignoring genes that were present but that they failed to predict (Table 1,ρ_predicted versus ρ_all). However, the trends for these genes remained the same, with StringTie well ahead of Cufflinks, and the other programs far behind (Supplementary Discussion and Supplementary Figs. 6 and 7).

Real data provide a better test of each program’s performance because they have properties that are not accurately captured by simulations. Repetitive regions in the human genome, wide variance in GC content, isoform length and alternative splicing complexity are all factors that influence performance²⁷. However, we have no way of knowing, for real data sets, precisely what genes and isoforms were expressed nor do we know their expression levels. Nonetheless, we do have several well-curated sets of human genes, for which the exon-intron structure has been evaluated and validated in multiple experiments. If a predicted transcript matches one of these ‘known’ genes from end to end, then it is reasonable to infer that the gene was indeed present in the real data, although its expression level remains uncertain. Therefore, for our experiments on real data sets, we focused on measuring how many of these well-curated genes were correctly predicted. We evaluated each transcriptome assemblers’ predictions against a merged collection of all annotated protein coding and noncoding genes (Online Methods).

Our real data included three human RNA-seq data sets from the ENCODE project²⁸, all of them strand-specific, and one unstranded RNA-seq data set that we generated for this study using nuclear RNA from a human kidney cell line. We downloaded the ENCODE data sets from the UCSC genome browser (http://genome.ucsc.edu/cgi-bin/hgFileUi?db=hg19&g=wgEncodeCshlLongRnaSeq), and we chose them to represent three different tissues: whole B cells in blood (GEO accession GSM981256), the cytosol of fetal lung fibroblasts (GSM981244) and CD14-positive monocytes (GSM984609). These samples contained 90 million 76-bp paired-end reads, 145 million 101-bp paired-end reads and 120 million 76-bp paired-end reads, respectively. For our own data set, we used an RNA-seq library, prepared with the standard unstranded Illumina TruSeq method and sequenced to yield ~180 million 100-bp paired-end reads with an average fragment length of 177 bp. We mapped reads using TopHat2, and assembled super-reads using MaSuRCA. Aligned paired reads outputted by TopHat2 were provided to StringTie, Cufflinks, Scripture, IsoLasso and Traph. For StringTie+SR, reconstructed fragments from super-reads assembled by MaSuRCA were aligned by TopHat2 and provided as additional input. Note that Traph would not run on any of these data sets and was not included in the results below.

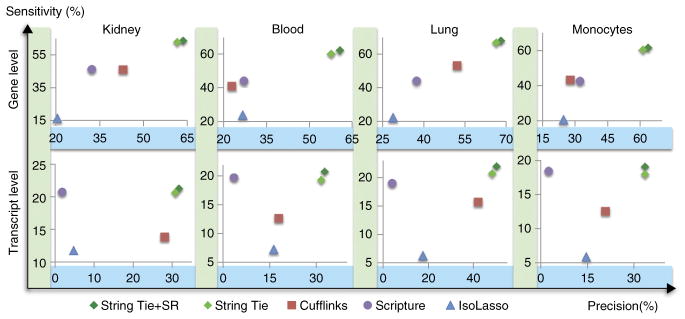
Many of the transcripts produced by the various assemblers did not match any annotated genes. Supplementary Table 5 shows the total number of transcripts predicted by each transcriptome assembler. Because these were real data, we could not determine which if any of these were false-positive predictions, both because the annotation databases were incomplete and because we did not know which genes were truly present in the sample. Nevertheless, we can evaluate sensitivity for known genes. If we counted all predictions not matching the annotation as false positives, then all methods would be equally penalized for excessive gene predictions. Using this approach, StringTie had substantially greater sensitivity than all competing methods at detecting genes in the current human genome annotation (Fig. 3). It obtained this relatively high sensitivity while at the same time having a lower apparent false-positive rate (i.e., better precision) than Cufflinks, which was the next-best assembler on all four real data sets.

Figure 3.

Accuracy of transcript assemblers at assembling known genes, measured on real data sets from four different tissues. Known genes are defined as those annotated in either the RefSeq, UCSC or Ensembl human gene databases. Gene level sensitivity (y axis) measures the percentage of genes for which a program got at least one isoform correct, whereas transcript sensitivity measures the percentage of known transcripts that were correctly assembled. Precision (x axis) is measured as the percentage of all predicted genes (transcripts) that match an annotated gene (transcript).

As in the simulation experiment, we considered a gene to be identified correctly if the assembler predicted the correct intron chain for at least one isoform. Overall, StringTie+SR and StringTie performed very similarly, and both outperformed all other programs on all four data sets, as measured both by sensitivity and precision at identifying annotated transcripts. Figure 3 shows the accuracy of the various programs on fully covered transcripts; these were transcripts for which all internal exons were fully covered by reads in the input alignment, and each intron had at least one spliced read aligned across it. (See Supplementary Table 6 for the exact number of fully covered transcripts in each data set.) Because many overlapping splice variants are present at most loci, the number of transcripts covered by reads is less than the number actually present in the sample. This explains the low absolute sensitivity for all programs at the transcript level.

Table 1 shows the number of correctly identified genes and transcripts by the programs tested on all four real data sets. StringTie+SR correctly predicted 27% more genes than were predicted by the next most sensitive program. Compared with Cufflinks, StringTie+SR and StringTie predicted 48% and 44% more known transcripts, on average, in these four data sets. Notably, on the blood data set StringTie+SR predicted 60% more transcripts than Cufflinks (11,489 versus 7,187, an increase of 4,302). All programs were run using their default parameters. Changing these parameters tended to increase sensitivity while lowering precision, although in some cases we were able to obtain a slightly better accuracy (Supplementary Table 7). However, the improvements in accuracy were not consistent across all four data sets when using the same set of parameters, and they were never close to the levels achieved by StringTie.

Table 1 also shows that on all four data sets, Scripture produced almost as many transcripts (though fewer genes) matching the annotation as StringTie+SR. As reflected by Scripture’s performance on the simulated data, this sensitivity at the transcript level derived from its strategy of predicting a near-exhaustive list of all possible splice variants for a given gene. This is reflected in the statistic that whereas the other programs assembled an average of 1.6–2.0 transcripts per locus, Scripture predicted an average of 21.6 transcripts per locus across the four real data sets.

StringTie and StringTie+SR took less than 30 min to complete on the two sets of simulated data, whereas the other four programs took between 81 min (Cufflinks) and 48 h (Traph). On the real data sets, StringTie required from 35–76 min and was more than three times faster than the fastest of the other four programs, and in some cases over 50 times faster. Wall clock and CPU times for all assemblers on all data sets are shown in Supplementary Tables 8 and 9, respectively.

All of the transcriptome assemblers have a large memory footprint. These memory requirements are usually unavoidable for transcrip-tome assembly owing to the vast amount of RNA-seq data that need to be processed in memory at once. For example, in highly expressed transcripts, the bundle of reads that come from the same gene locus can easily total over 2 million reads. To store and analyze these reads requires alignment start and end positions, positions of mismatches and indels, strand information and mate pair information. On the four real data sets used here, the maximum memory used by StringTie varied between 1.6 gigabytes (GB) and 12 GB. Cufflinks, IsoLasso and Scripture had memory requirements ranging from 6.4 to 26.6 GB on the same data (Supplementary Table 10).

It is feasible that StringTie was superior to Cufflinks because it did a better job at identifying the dominant transcript for a gene locus. Alternatively, it might have had an advantage on genes with larger numbers of exons or genes with more isoforms. To tease apart these hypotheses, we analyzed the genes that were found by StringTie but not by Cufflinks, and vice versa, on all four of the real data sets. Approximately 70% of the transcripts correctly identified by Cufflinks were also found by StringTie (Supplementary Table 11). Cufflinks found an average of ~2,000 transcripts that StringTie missed, whereas StringTie assembled ~5,000–8,400 transcripts that Cufflinks missed. On all data sets, the transcripts found uniquely by StringTie had a significantly higher number of exons than the ones uniquely identified by Cufflinks (two-sample t-test, P < 4.6 × 10⁻⁹ on all four data sets; Supplementary Fig. 8). The StringTie-only transcripts also tended to be expressed at lower levels (Supplementary Fig. 9). We also looked at genes for which either StringTie or Cufflinks identified at least one correct isoform. Among these, StringTie had a higher proportion of genes with three or more correctly assembled isoforms (Supplementary Fig. 10). Thus, StringTie was better at reconstructing at least three types of genes: (i) those at low abundance; (ii) those with more exons and (iii) those with multiple isoforms.

StringTie uses a network flow algorithm to assemble and quantify RNA-seq reads. Compared with other leading methods on both simulated and real data, StringTie was substantially more accurate at both assembly and quantitation of gene transcripts, recovering more expressed transcripts while demonstrating higher precision than the other programs. The main reason for StringTie’s accuracy is the network flow algorithm. StringTie can also use aligned de novo assembled fragments that combine pairs of reads into a longer sequence. This optional preprocessing step provides a modest additional improvement in accuracy. The main reason underlying the greater accuracy of StringTie most likely derives from its optimization criteria. By balancing the coverage (or flow) of each transcript across each assembly, it incorporates depth of coverage constraints into the assembly algorithm itself. When assembling a whole genome, coverage is a crucial parameter that must be used to constrain the algorithm; otherwise an assembler may incorrectly collapse repetitive sequences. Similarly, when assembling a transcript, each exon within an isoform should have similar coverage, and ignoring this parameter may produce sets of transcripts that are parsimonious but wrong. Genes with a large number of splice variants are especially difficult to reconstruct precisely (see Supplementary Fig. 11 for an example of a complex multi-isoform gene showing that of those programs tested, StringTie assembled three of the isoforms correctly, and none of the other programs captured any of the isoforms).

StringTie is a transcript assembler that uses the optimization technique of maximum flow in a specially constructed flow network to determine gene expression levels, and does so while simultaneously assembling each isoform of a gene. And unlike other transcript assemblers, it incorporates alignment to both a genome and a de novo assembly of reads. We envisage that users could replace Cufflinks with StringTie in most RNA-seq analysis pipelines and expect substantial improvements in transcript assembly coupled with faster performance.

ONLINE METHODS

RNA-seq library preparation and sequencing

Nuclear RNA was prepared from HEK293T (kidney) cells. Briefly, cells were lysed on ice for 5 min in 10 mM Tris-HCl pH 7.5, 10 mM NaCl, 0.2 mM EDTA, 0.05% NP-40, and nuclei were spun at 2,500g for 3 min and then resuspended in QIAzol for RNA isolation using the miRNeasy kit according to the manufacturer’s instructions (Qiagen). The RNA-seq library was created using the Illumina TruSeq RNA Sample Preparation Kit v2 with the standard protocol, and sequenced on one lane of the HiSeq 2000 platform (100 bp, paired-end). Data are available at NCBI as accession number SRP041943. The database of annotated protein coding and noncoding genes (41,409 genes and 171,904 transcripts in total) was produced by merging all annotated genes from the RefSeq database²⁹, the UCSC Browser²⁴ and the Ensembl database³⁰.

Identification and quantification of transcripts

StringTie’s approach to reconstructing the transcriptome is depicted in Figure 1 and, in more detail, in Supplementary Figure 12. The initial step is similar to other reference-based transcriptome assemblers, in the sense that it relies on the output of a specialized spliced-alignment program. However, StringTie incorporates several key innovations, notably (i) a network flow algorithm to reconstruct transcripts and quantitate them simultaneously; and (ii) the capacity to include longer assembled reads, representing the full fragments from which the initial paired-end reads were sequenced.

To reconstruct the fragments from their end sequences, we use a de novo assembly algorithm that creates “super-reads.” Using the super-read software from the MaSuRCA genome assembler²⁸, we extend every read in both directions as long as this extension is unique. We then identify pairs of reads that belong to the same super-read and extract the sequence containing the pair plus the sequence between them; that is, the entire sequence of the original DNA fragment. Thus, for example, if the original RNA-seq data comprised paired 100-bp reads from a 300-bp fragment library, these steps will convert many of those pairs into single, 300-bp super-reads. We then map the super-reads to the reference genome. Note that the true super-read might be much longer than the fragment, but we currently limit StringTie to the fragment length. This restriction allows us to treat super-reads as single reads in the algorithm, and therefore no special adjustment is required to evaluate their contribution to transcript expression levels.

The advantage of using super-reads is twofold. First, when a gene sequence is nonrepetitive, as coding sequences tend to be, we usually can reconstruct fragments even if they span multiple exons. Second, more of the longer sequences will map unambiguously to the genome, simplifying the assembling of transcripts. We have designed StringTie to be run on any input BAM file, regardless of whether it contains aligned read pairs or a combination of these plus super-reads.

After the super-reads are mapped to the reference genome, StringTie next builds an alternative splice graph (ASG) at each gene locus from all overlapping reads at that locus. Note that if more than a certain percentage of the reads (by default 95%) aligned in a gene locus are multi-mapped, then StringTie will skip processing that locus. The ASG captures all possible transcripts that are consistent with the mapped reads^15,17, where nodes in the graph correspond to contiguous regions of the genome that are uninterrupted by any spliced read alignment, and directed edges correspond to reads that align across two such nodes in the correct 5′ to 3′ order. Note that the nodes do not necessarily correspond to whole exons in the transcripts; they may be only partial exons, as illustrated by node 4 in Supplementary Figure 12 (see also node 1 in Supplementary Fig. 1). We add a source and a sink (nodes s and t) to the ASG so that any path from source to sink represents a possible transcript.

After building the ASG, StringTie iterates through the following two steps (steps 4 and 5 in Supplementary Fig. 12):

1. First it searches for the heaviest path, defined as the path with the highest “path-compatible” read per base coverage, from source to sink. Once a potential heaviest path is found, this path will constitute an assembled transcript predicted by StringTie.

2. Second, StringTie estimates the coverage level of the transcript by solving a maximum-flow problem that determines the maximum number of fragments that can be associated with the chosen transcript.

   After the expression level of the transcript is computed, StringTie removes the fragments that contributed to it, and updates the per-base read coverage in the ASG.

StringTie ends the iteration through the two steps above when the coverage of the heaviest path in the ASG drops below some fixed threshold (by default, set to 2.5 reads per bp).

To find the heaviest path in the ASG, we use a heuristic algorithm that starts at the node with the highest coverage (measured as average reads per base) and then extends the path first to the source and then to the sink by choosing the adjacent node with the highest number of compatible fragments with the path built so far. Note that an adjacent node might have a higher coverage then the one chosen to extend the path, but it will not be chosen if the fragments covering that node are not be compatible with the path chosen up to that point. Because every node in the splice graph is consulted at most once, our algorithm for finding the heaviest path has a running time complexity of O(n), where n represents the number of nodes in the splice graph.

The heaviest path in the ASG represents an assembled transcript, although no coverage is yet associated with it. Although we employ a heuristic approach to identify a transcript from the ASG, determining its coverage is essential to finding the set of all paths that represent expressed transcripts. To determine the coverage of a transcript, StringTie uses a flow network design that we formally describe next.

Basic definitions

Formally, a network is defined to be any finite collection of points, called nodes, together with a collection of directed edges (or arcs) that connect particular pairs of these nodes. By convention, we do not allow an arc to connect a node to itself, but we do allow more than one arc to connect the same two nodes. We will be concerned only with connected networks in the sense that every node can be reached from every other node by following a sequence of arcs, where the direction of the arcs is ignored. In linear programming, if a network is disconnected, then the problem it describes can be treated as a number of separate problems, one for each connected subnetwork.

The underlying structure of a flow network is a directed graph, with its vertices representing network nodes, and arcs representing the (existing or possible) connections between nodes. Mathematically, a flow network is defined as a quadruple N = (G, s, t, c), where G = (V, E), with E ⊆ V × V, is a directed graph with a set of vertices V and a set of directed edges E, s ∈ V and t ∈ V are the source and the sink of the network, respectively, and c : E →R⁺ is a function that associates a positive capacity to each edge in the graph. We say that a function f : E →R⁺ is a flow over the network N if the following two conditions are satisfied:

1. 0 ≤ f((u, v)) ≤ c ((u, v)), for every (u, v)∈E,

2. Σ_{(u, v) ∈E} f((u, v)) = Σ_{(v, u) ∈E} f((v, u)), for every v∈V, v ≠ s, t.

The value of the flow is the quantity ||f|| = Σ_{(s, v) ∈E} f((s, v)). It is not hard to show that ||f|| = Σ_{(v, t) ∈E} f((v, t)). The maximum flow problem is to find a flow f with maximum value in N. Condition 1 above can be extended such that a lower bound can be required for the flow going through an edge:

$$l_{(u,v)}\le f((u,v))\le c((u,v)),\text{for}\text{every}(u,v)\in E$$

In other words, we want to require that only some edges with capacities larger than l_e be used. It has been shown in the literature that this problem can be reduced to a standard maximum flow problem³¹. The maximum flow problem is a well-studied problem in the field of optimization theory and can be solved in strong polynomial time, with O(VElog(V²/E) complexity, where V and E represent the number of nodes and edges, respectively³².

As described above, in traditional flow networks there is an implicit assumption that flow is conserved on every edge; i.e., if f_uv units flow into an edge (u, v)∈E at node u, then exactly the same f_uv units will reach node v. Many practical applications violate this conservation assumption. For example, we can imagine a water distribution network model as a flow network, where if some quantity of water is shipped across an open canal linking two nodes, some is lost due to evaporation and seepage during transit, and the amount reaching the destination will only be a fraction of the amount that left the origin. These cases can be still modeled with a flow network where we associate a positive multiplier p_uv associated with edge (u, v)∈E such that if a packet of f_uv units of flow enter node u, then by the time it reaches node v, the packet contains p_uv f_uv units of flow. If 0 < p_uv < 1, edge (u, v) is said to be lossy, and if 1 < p_uv < ∞ is said to be gainy. In the flow network presented above p_uv = 1 for all edges (u, v)∈E. If p_uv ≠ 1 for at least one edge, the flow network is called a generalized flow network, or a flow network with multipliers. Just as in the standard maximum flow problem, in the generalized maximum flow problem, the goal is to send as much flow as possible between two nodes, subject to the edge capacity constraints. Also, flow can be ‘lost’ or ‘gained’ as it is sent through the network. The maximum generalized flow problem is a special case of linear programming, and it can be solved by general-purpose linear programming techniques such as the primal simplex method³³. Several combinatorial methods that solve the program in polynomial time are also described in the literature³⁴.

Flow network design in StringTie

StringTie uses the generalized flow network concept introduced above to compute the coverage associated with a transcript path in the ASG. We start building the network by first creating nodes corresponding to all the nodes in the ASG. We then connect any two nodes by an edge if an alignment mapping (of a super-read, or of an unassem-bled pair of reads) starts at one node and ends at the other (Supplementary Fig. 13). The number of such alignments determines the capacity of an edge. More specifically, if a fragment aligns in n places, than that fragment alignment will contribute 1/n to the edge capacity. We then split the nodes in the flow network into two nodes each, as follows. For each node v in the ASG, with the exception of the source and sink, we introduce nodes vⁱⁿ and v^out that “enter” and “exit”, respectively, the initial ASG node. We connect these two nodes with a new edge, and we set the capacity of that edge equal to the number of fragments that align to the initial node in the ASG. We also associate with this edge a multiplier that controls the biased distribution of fragments aligning to any given node in the ASG. Such biases are often encountered in the reads produced by next-generation sequencing technologies; for example, it is common to observe more reads near the 3′ end of a transcript than the 5′ end.

Special care needs to be taken to make the distribution of sequencing reads more uniform²⁵. In StringTie we attempt to reduce this coverage bias by normalizing the distribution of reads entering and exiting a node in the ASG. Formally, for each edge connecting a pair of nodes vⁱⁿ and v^out in the network, we associate the following multiplier, or bias factor:

$$b_v=\frac{{\sum }_{u\in \mathit{ASG}}w(f_{uv})}{{\sum }_{u\in \mathit{ASG}}w(f_{vu})}$$ (1)

where f_xy is a fragment starting at node x and ending at node y, and w(f_xy) represents the weight associated with the fragment f_xy. Similarly to Cufflinks, we define w(f_xy) =1/n, where n represents the number of fragment f_xy mappings. Note that in the case of paired-end reads, the sequence of the fragment f_xy may not be completely known, but the two paired reads clearly define the nodes x and y. Practically, the bias b_v ensures that the proportion of fragments f_uv associated with a transcript path in the ASG is equal to the proportion of fragments f_vu that correspond to the same transcript.

With the exception of the edges connecting an ‘entering’ and an ‘exiting’ node, all the edges have multipliers equal to 1. Supplementary Figure 13 shows an example of the flow network associated with the transcript containing nodes 1, 3 and 5 in the ASG depicted in Supplementary Figure 12. Note that the edge connecting nodes 1^out and 5ⁱⁿ is not present in the ASG, because there is no splice variant that skips exon 3 and connects exons 1 and 5 directly. However, we add this edge to the flow network to account for the fragment that starts and ends at nodes 1 and 5 in the ASG.

The intuition behind this flow network design is that StringTie tries to stitch compatible fragments together that will explain a maximal number of reads for the underlying transcript path. In our implementation, two fragments (single reads or pairs of reads) are considered to be compatible if one fragment starts in the same node as the other one ends. The maximum flow in this network, where the flow follows the bias factor restrictions imposed by equation (1) above, represents the expression level associated with the predicted transcript. As discussed above, the generalized maximum flow problem can be solved efficiently in polynomial time. In contrast, Cufflinks formulates abundance estimation as an expectation-maximization (E-M) computation, which cannot be solved in polynomial time. In Supplementary Software 1 we provide pseudocode that introduces the bias factors in the classical breadth-first search implementation of the maximum flow algorithm.

StringTie is implemented in C++ and is freely available as open source software at http://ccb.jhu.edu/software/stringtie (also see Supplementary Software 1).