Calculations show that these molecules form membrane-like structures at low temperatures in a liquid methane environment.
Keywords: Titan, abiogenesis, exobiology, liposome, physical chemistry, quantum chemistry, computational chemistry, molecular dynamics
Abstract
The lipid bilayer membrane, which is the foundation of life on Earth, is not viable outside of biology based on liquid water. This fact has caused astronomers who seek conditions suitable for life to search for exoplanets within the “habitable zone,” the narrow band in which liquid water can exist. However, can cell membranes be created and function at temperatures far below those at which water is a liquid? We take a step toward answering this question by proposing a new type of membrane, composed of small organic nitrogen compounds, that is capable of forming and functioning in liquid methane at cryogenic temperatures. Using molecular simulations, we demonstrate that these membranes in cryogenic solvent have an elasticity equal to that of lipid bilayers in water at room temperature. As a proof of concept, we also demonstrate that stable cryogenic membranes could arise from compounds observed in the atmosphere of Saturn’s moon, Titan, known for the existence of seas of liquid methane on its surface.
INTRODUCTION
Studies of protobiology and the formation of cells on Earth generally focus on nucleic acids; indeed, it is generally believed that ribonucleic acids were the precursors to terrestrial life (the “RNA world” hypothesis) (1). However, recent research has shown that RNA catalysis depends on establishing high local concentrations, meaning that compartmentalization was likely a coequal or an earlier phase than RNA (2). This supports a “lipid world” hypothesis, in which lipid membranes played an important role as a very early evolutionary step in creating life on Earth (3). Lipid bilayers, without additional cellular machinery, have been observed to grow, divide, aid polymerization reactions, and even synthesize RNA from polymerase enzymes (4–6).
Terrestrial cell membranes are composed of a bilayer of phospholipids: surfactants composed of nonpolar lipid chains and oxygen-laden polar heads. The polar heads form surfaces compatible with water, allowing the membrane to separate the aqueous world outside and the aqueous life within. The lipid tails of the phospholipids aggregate by van der Waals forces, thus stabilizing the membrane. A vesicle made from such a membrane is known as a liposome.
The role of self-assembled surfactants in evolutionary biology on Earth raises the question of whether nonaqueous conditions can support any analogous structure. Experimental studies have been performed to create vesicles in nonpolar solvents. This has included the consideration of nonionic ethers (7), esters (8), surfactants (9), and inverted phospholipids (10). Inverse phospholipid membranes have even been considered as biological possibilities in liquid methane (7–16).
Liquid methane is of particular interest because it is the only liquid other than water that forms seas on the surface of a planetary body in our solar system. This body is Saturn’s moon, Titan (11, 12). Whether Titan can support any form of cell membrane is not certain. However, we do observe that Titan’s surface hosts an unknown process that consumes hydrogen, acetylene, and ethane, all of which continually flow down from the atmosphere but do not accumulate (13–15). This makes liquid methane a very interesting solvent to consider for cell membrane alternatives.
However, the phospholipid membranes, which are so strong and elastic in water, do not perform as well in liquid methane. The nonpolar tails of phospholipids would seem to be compatible with nonpolar liquid methane, and the polar heads with each other; does this suggest that an inverse membrane to those formed in water could exist in methane? Unfortunately not; this phospholipid hypothesis neglects the fact that the tails of phospholipids are long-chain hydrocarbons, which will be rigid at cryogenic temperatures. Furthermore, the phospholipid head component atoms, oxygen and phosphorus, are not available in any form in the methane seas of Titan and presumably not in any similar liquid methane environment. Inverted-phase liposomes are therefore not a viable option. The idea of using polarity to prevent dissolution, however, is valid if any suitable materials exist.
As a proof of concept for vesicle formation in a methane-rich environment, we began our search for polar materials using those that form naturally when ultraviolet light interacts with a methane- and nitrogen-containing atmosphere (12). From spectroscopic observations by the Cassini orbiter, we know the most common polar compounds in the upper portion of Titan’s methane-nitrogen atmosphere, as shown in Table 1 [(12), p. 167]. Lower in the atmosphere, all of these species condense into aerosols, preventing further observation by Cassini. Laboratory experiments to reproduce the methane-nitrogen atmosphere have generally produced a tar-like residue of molecules, called tholins (17). These tholins have been found to consist of hydrocarbons, nitriles, and amines (17). Therefore, we have also included primary nitriles and amines of lengths propyl-hexyl in our study, although the abundance of the tholins relative to the Cassini-observed species is uncertain.
Table 1. Polar nitrogen compounds found on Titan and their abundance in the upper atmosphere as measured by Cassini [(12), p. 167].
Given the challenges of experimental studies at cryogenic temperatures, we adopted a molecular simulation approach to screen for the most promising candidates for self-assembly into a structure reminiscent of a membrane. We considered only short ligands, given the fact that longer ligands offer no advantage at such cold temperatures. Our candidate molecules are all much shorter than typical phospholipids, which involve carbon chains 15 to 20 atoms long. Liquid methane is cold enough to solidify almost any substance: a four-membered carbon chain, butane for example, is far below its freezing point of 133 K in liquid methane. At such temperatures, it might seem almost impossible for a flexible organic membrane to form, let alone one with similar flexibility to that of a lipid bilayer. However, low temperature also allows small molecules to aggregate differently than they would at 300 K. Our normal intuition needs to be adjusted for a colder world.
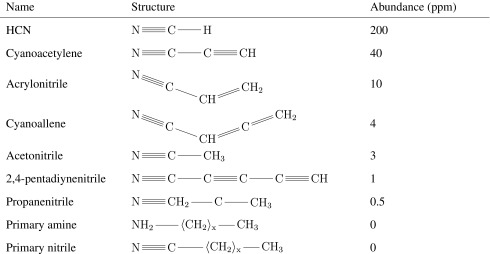
We hypothesized that liquid methane membranes would rely on the polarity of nitrogen-containing groups (“azoto” groups) to hold them together, in the same way that terrestrial liposomes rely on the nonpolarity of alkyl groups. Therefore, we referred to these structures as “azotosomes.” A comparison between the liposome and proposed azotosome structures is shown in Fig. 1.
Fig. 1. Liposomes and azotosomes.
(A) Liposome in polar solvent. Polar heads are braced by nonpolar lipid tails. (B) Azotosome in nonpolar solvent. Nonpolar tails are braced by polar nitrogen–rich heads.
The key physical requirements of a membrane are that it be flexible and stable. The most common measure of cell membrane flexibility is the area expansion modulus Ka (also known as the dilational, stretch, or area compressibility modulus) (18, 19). The area expansion modulus of terrestrial cell membranes at room temperature is 0.24 to 0.50 J/m2 (18, 19). As we will show, several of our azotosome candidates lie within this range. The most common measure of stability is the decomposition energy or stability time scale (20). In general, lipid bilayers on Earth are metastable (21). We will show that some of our azotosome candidates have high decomposition energies relative to the cryogenic environment, resulting in very long stability time scales.
Synthesizing azotosomes for experimental study would be a challenging project, akin to the first synthesis of liposomes and with the added difficulty of cryogenic conditions. However, the molecules that compose azotosomes are similar to molecules routinely studied on Earth, making the properties of azotosomes accessible through standard molecular simulation. Molecular dynamics (MD) has been used for decades to simulate bilayer membranes (20, 22–24) and polymer vesicles (polymersomes) (25). The values of Ka calculated by MD have been found to agree closely with experiments (18), supporting our use of the technique for these new membranes.
To provide the molecular forces in our simulations, we used Optimized Potentials for Liquid Simulations (OPLS), which are well-known and effective models for liquid hydrocarbons, small organic molecules (26, 27), and polymersomes (25). We validated OPLS models for our molecules by confirming the OPLS-generated structures and pairwise binding energies against quantum mechanical calculations (27), as described in Materials and Methods. Only the molecules that OPLS modeled faithfully in terms of bond lengths, angles, and binding energies were passed on for study as azotosome candidates.
RESULTS
The errors in OPLS models for the bond lengths, bond angles, and dihedral (torsion) angles for the compounds we tested are provided in Table 2. Calculations for the three most highly unsaturated compounds—cyanoacetylene, cyanoallene, and 2,4-pentadiynenitrile—were not considered further because their OPLS models exhibited errors in the average bond lengths of greater than 0.04 Å, which we considered to be unacceptably large. Being highly unsaturated, these species are the least likely to be stable when they leave the upper atmosphere anyway, so their unsuitability for OPLS modeling is unlikely to be important here. For the remaining compounds, the average difference between the OPLS and ab initio structures for the bond lengths was 0.008 Å, 0.6° in the angles and 0.3° in the dihedrals (where present).
Table 2. Error in OPLS-optimized structures.
Average difference, for each species, between its OPLS structure and the structure obtained via ab initio optimization with Onsager’s self-consistent reaction field (SCRF) model of an implicit solvent.
| Species |
Δ(bond length) (Å) |
Δ(bond angle) (°) |
Δ(dihedral) (°) |
| Propanenitrile | 0.00 | 0.5 | 0.0 |
| Butanenitrile | 0.01 | 0.5 | 0.1 |
| Pentanenitrile | 0.01 | 0.4 | 0.1 |
| Hexanenitrile | 0.00 | 0.6 | 0.2 |
| Aminopropane | 0.01 | 0.7 | 0.7 |
| Aminobutane | 0.01 | 0.6 | 0.6 |
| Aminopentane | 0.01 | 0.6 | 0.4 |
| Aminohexane | 0.01 | 0.5 | 0.2 |
| Hexane | 0.01 | 0.3 | 0.0 |
| Methane | 0.02 | 1.5 | 0.0 |
| HCN | 0.01 | 0.0 | 0.0 |
| Acrylonitrile | 0.01 | 1.2 | 0.0 |
| Acetonitrile | 0.00 | 0.0 | 0.0 |
| Cyanoacetylene | 0.05 | 6.3 | 0.0 |
| Cyanoallene | 0.08 | 9.5 | 0.0 |
| 2,4-Pentadiynenitrile | 0.06 | 75.8 | 0.0 |
Ab initio binding energies were generated in vacuum and in implicit solvent. The difference between these energies was between 0.1 and 1.3 kcal/mol for all species under evaluation with an average of 0.6 kcal/mol. The difference between the OPLS and ab initio binding energies ranged from 0.2 to 0.9 kcal/mol, averaging 0.6 kcal/mol. In general, values for the OPLS-generated binding energy for a given species fell between the ab initio values with and without solvent, which supports the use of the OPLS models. OPLS pairwise binding energies would be expected to fall between those of ab initio in vacuum and ab initio in solvent because the OPLS pairwise calculations are “solvent-like” due to the nonpolarizability of the OPLS model. This makes the OPLS model experience a partial solvent effect, even when only a pair of molecules is present. An outlier among the molecules we studied was HCN, which had an OPLS binding energy that was 1.8 kcal/mol above the value for the binding energy predicted by an ab initio representation with an implicit solvent, suggesting that the OPLS model of HCN is inaccurate.
However, as we shall show later, HCN does not self-assemble into an azotosome because of its small size. Its excessive binding energy will thus be irrelevant because it will not be considered further due to its lack of self-assembly. Binding energies found by the three methods (OPLS and ab initio calculations for the system in vacuum and solvent) are provided in Table 3.
Table 3. Pairwise binding energies.
OPLS and ab initio calculations produced similar results.
| Species |
OPLS (kcal/mol) |
DFTvacuum (kcal/mol) |
DFTsolvent (kcal/mol) |
| Propanenitrile | −6.4 | −7.5 | −6.2 |
| Methane | 0.0 | 0.0 | 0.0 |
| HCN | −4.1 | −3.0 | −2.3 |
| Acrylonitrile | −5.6 | −6.0 | −4.9 |
| Acetonitrile | −5.9 | −6.3 | −5.0 |
Each azotosome begins the simulation as a grid of molecules, and then self-assembles into its preferred structure. Species that OPLS could not represent accurately were removed from consideration, as was HCN, which did not form an ordered layer, and hexane, which formed a solid. The area expansion moduli of the remaining azotosomes, and also a plain hexane bilayer with no functional head, are shown in Table 4. Given the accuracy of the OPLS binding energies, we expect these values of Ka and ∆E to be accurate to within 20%.
Table 4. Flexibility Ka of nitrile and amine azotosomes, and activation energy ΔE to remove a molecule from each azotosome.
| Species | Ka (J/m2) | ΔE (kcal/mol) |
| Acrylonitrile | 0.26 | 17.1 |
| Acetonitrile | 0.37 | 5.8 |
| Propanenitrile | 0.10 | 7.6 |
| Butanenitrile | 0.13 | 6.4 |
| Pentanenitrile | 0.55 | 8.4 |
| Hexanenitrile | 0.26 | 6.0 |
| Aminopropane | 0.22 | 5.2 |
| Aminobutane | 0.19 | 6.7 |
| Aminopentane | 0.28 | 7.7 |
| Aminohexane | 0.30 | 7.7 |
| Hexane bilayer | 2.20 | — |
All of our azotosomes have flexibilities similar to those of known terrestrial cell membranes: 0.13 to 0.55 J/m2 for the azotosomes versus 0.24 to 0.50 J/m2 for terrestrial liposomes. With respect to thermal fluctuations, azotosomes will appear stiffer than Earth liposomes because the thermal fluctuations on Titan are smaller than those on Earth. However, with respect to mechanical stress, cryogenic azotosomes and room temperature liposomes will respond surprisingly alike.
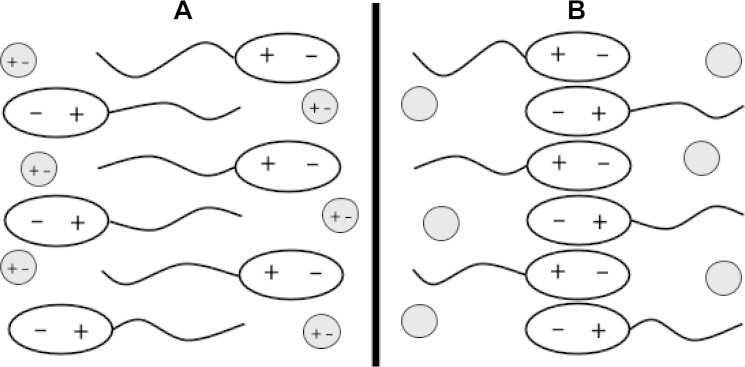
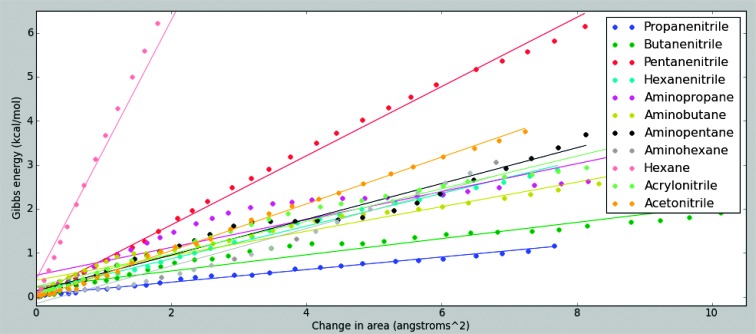
The comparison between hexane and hexanenitrile is instructive. Plain hexane forms a layer eight times stiffer than hexanenitrile. Furthermore, the hexane bilayer is brittle, as shown in Fig. 2. After a small amount of stretching, it appears to snap. In contrast, the hexanenitrile layer stretches smoothly throughout. The only difference between these two compounds is that hexanenitrile has a polar nitrogen head.
Fig. 2. Stretching a hexanenitrile azotosome and a hexane bilayer.
The slope of the linear fit is proportional to the area modulus Ka.
The key difference between the pure hydrocarbon layer and an azotosome is the structure resulting from the polar nitrogen head. We believe that it is this structure that allows a cryogenic azotosome to have the flexibility of a room temperature lipid bilayer.
The dissociation energy barriers for each azotosome are also given in Table 4. Acetonitrile, butanenitrile, hexanenitrile, aminopropane, and aminobutane have ΔE values well below 8 kcal/mol, indicating unstable azotosomes. Propanenitrile, pentanenitrile, aminopentane, and aminohexane azotosomes have energy barriers close to 8 kcal/mol. They should be considered possible candidates because their values lie within a 20% uncertainty that we feel is appropriate here. Acrylonitrile azotosomes show high barriers to decomposition (17 kcal/mol) that are sufficient to ensure their stability over long time scales.
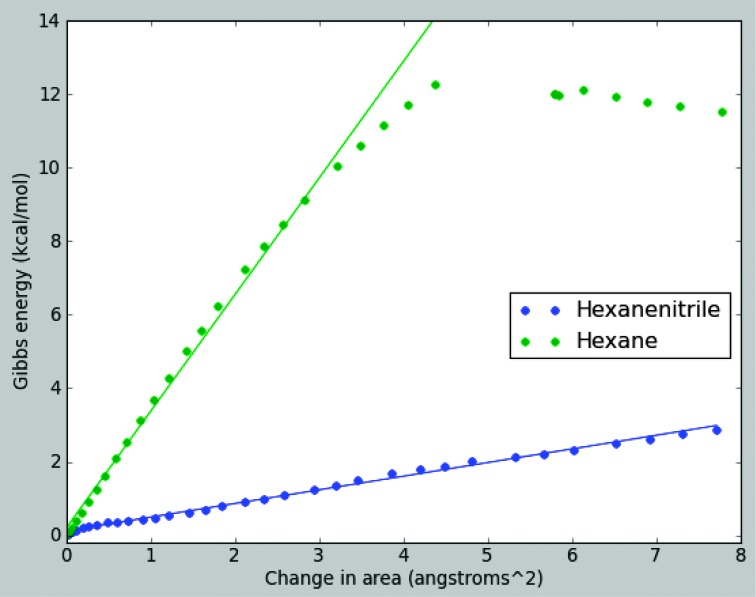
The geometry of the acrylonitrile molecule appears to favor the azotosome and hamper other states (Fig. 3). This aligns with the fact that acrylonitrile is known experimentally to have a somewhat disordered solid phase (28). Like all the azotosomes studied here, acrylonitrile azotosomes are symmetrical with respect to the plane of the membrane, implying that—like a lipid bilayer—they should be able to form vesicles of many sizes.
Fig. 3. States of acrylonitrile.
(A) Azotosome. Interlocking nitrogen and hydrogen atoms reinforce the structure. (B) Solid. Adjacent nitrogen atoms create some unfavorable repulsion. (C) Micelle. Adjacent nitrogen atoms make this highly unfavorable. (D) Azotosome vesicle of diameter 90 Å, the size of a small virus particle.
The calculation of free energies, required to determine Ka, also allowed us to derive the total free energy of decomposition for each azotosome. These values are shown in Table 5. All of these free energies are positive, indicating that the azotosome state is preferable to the dissolved state. These free energy values are concentration-dependent, because ΔGdissolve is always negative at infinite dilution. The concentration created by dissolving one azotosome molecule in each box is about 0.1%, which is higher than we might expect in Titan’s seas. However, the real concentrations are currently unknown, so they may or may not be high enough to make azotosomes thermodynamically stable. There is no trend in ΔG with respect to the number of carbon atoms in the chain. ΔG appears to be determined by the way in which the molecules fit together, rather than any simple property of the molecules themselves.
Table 5. Gibbs free energy of decomposition.
The net mechanical work required to remove a molecule from the membrane, within 20% uncertainty. These values are concentration-dependent.
| Species | ΔG (kcal/mol) |
| Acrylonitrile | 7.6 |
| Acetonitrile | 17.4 |
| Propanenitrile | 6.4 |
| Butanenitrile | 7.1 |
| Pentanenitrile | 13.4 |
| Hexanenitrile | 11.5 |
| Aminopropane | 5.9 |
| Aminobutane | 6.7 |
| Aminopentane | 9.6 |
| Aminohexane | 6.2 |
DISCUSSION
In a cold world without oxygen, we suggest that the vesicles needed for compartmentalization, a key requirement for life, would be very different to those found on Earth. Rather than long-chain nonpolar molecules that form the prototypical terrestrial membrane in aqueous solution, we find membranes that form in liquid methane at cryogenic temperatures do so from the attraction between polar heads of short-chain molecules that are rich in nitrogen. We have termed such a membrane an azotosome. We find that the flexibility of such membranes is roughly the same as those of membranes formed in aqueous solutions. Despite the huge difference in temperatures between cryogenic azotosomes and room temperature terrestrial liposomes, which would make almost any molecular structure rigid, they exhibit surprisingly and excitingly similar responses to mechanical stress.
On the basis of our criteria of thermodynamic stability, or at least metastability, the azotosome appears to be a realizable cryogenic membrane. Starting from all the known molecular components in the atmosphere of such a world, Titan, we were able to select a couple of candidate molecules that were capable of exhibiting properties that appear to be important for vesicle formation. For example, an acrylonitrile azotosome has good thermodynamic stability, high energy barrier to decomposition, and area expansion modulus similar to that of phospholipid cell membranes in oxygen-rich solutions. Acrylonitrile exists in Titan’s atmosphere at a concentration of 10 ppm and could plausibly be formed on any celestial body with a nitrogen-methane atmosphere.
The availability of molecules with an ability to form cell membranes does not by itself demonstrate that life is possible. However, it does direct our search for exotic metabolic and reproductive chemistries that would be similarly compatible under cryogenic conditions. As our understanding of conditions that could nurture extraterrestrial life expands, so does our probability of finding it, perhaps within the liquid methane habitable zone.
MATERIALS AND METHODS
The first property of azotosomes we investigated was their flexibility, as measured by the area expansion modulus Ka. One procedure that has been used to calculate this property is simulation of the spontaneous fluctuation of a membrane’s area over a lengthy MD run (18). However, this method relies on random sampling of rare events and thus has problems with accuracy, overestimating Ka by a factor of ≥2(18). Instead, we indented the membrane by a given amount and calculated the area expansion modulus from the resistance to stretching (18). This is directly comparable to the nanoindentation method, which is used to find Ka experimentally, and comparison of such simulations and experiments on terrestrial liposomes has shown them to yield equivalent results (18).
The second criterion that we used to assess azotosomes was their stability. One procedure that has been used to study liposome stability is to simulate the membrane over a lengthy MD run and observe whether it dissociates spontaneously (20). Waiting for dissociation is, unfortunately, only effective for the weakest membranes because MD typically covers only nanoseconds of simulated time. A superior procedure is to find the time scale of dissociation via the activation energy (29). By the Arrhenius law, the rate of a process with activation energy ΔE is proportional to exp(−ΔE/kBT), where kB is the Boltzmann constant and T is the absolute temperature (29). If the time scale of the process without an energy barrier, t0, is known, then the time scale of the process with the barrier is given by t = t0exp(ΔE/kBT).
The dependence of the time scale on ΔE is exponential, so the uncertainty in the time scale will be greater than the underlying uncertainty in the energy barrier. Fortunately, we only require the time scale’s order of magnitude. For a molecule to move 1 Å at 94 K with no energy barrier takes on the order of t0 = 1 ps. If an activation energy of 8 kcal/mol is required, for instance, this gives a time scale of 1 ps × exp(8 kcal/mol/kBT) = 235,000 s (three Earth days). In the absence of model error, this time scale is sufficiently long that it could lead us to suggest that an azotosome is sufficiently stable if it has a decomposition energy barrier higher than 8 kcal/mol. With a 20% uncertainty, corresponding to the error between the OPLS and ab initio binding energies of the azotosome components, a more conservative cutoff would be to use a barrier of 10 kcal/mol, corresponding to a decomposition time of more than 100 Earth years.
Optimized Potentials for Liquid Simulations (OPLS)
MD creates a deterministic simulation of the time evolution of a system, which is then sampled to provide both thermodynamic and kinetic properties. The model we chose to represent the energetics of the system is a set of interatomic potentials known as OPLS. The OPLS force field, originally developed by Jorgensen and co-workers, is a widely used model designed to represent the interactions between liquid hydrocarbons and other simple organic molecules (26). OPLS has a long history of accuracy in describing the liquid state properties of organic compounds (27), and Discher et al.’s review paper on polymersomes endorses it as the best choice for simulating those membranes (25).
The OPLS description of the potential energy takes the following form:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
where (Eq. 1) E is the potential energy; rN is the N interatomic distances in a system containing N atoms; Ebonds is the bond-stretching energy; Eangles is the angle-changing energy; Edihedrals is the dihedral twisting energy; Enonbonded is the pairwise van der Waals and Coulombic energy; (Eq. 2) Kr is the spring constant of a given bond (assumed to be harmonic); r is the bond length; r0 is the equilibrium bond length; (Eq. 3) kθ is the spring constant of a given angle (assumed to be harmonic); θ is the angle; θ0 is the equilibrium angle; (Eq. 4) V1 to V4 are the energy coefficients of the cosines of increasing frequency, which define the dihedral interaction; ϕ is the torsion angle about the dihedral with an eclipsed configuration = 0; (Eq. 5) Aij and Bij are the Lennard-Jones coefficients of the i-j pair interaction; rij is the pair distance; ke is the Coulomb constant; qi and qj are the atomic charges; and (Eq. 6) Aii, Ajj, Bii, and Bjj are the Lennard-Jones parameters of pure i-i and j-j interactions.
OPLS force field verification
We confirmed the accuracy of the OPLS model for our molecules using quantum mechanics calculations. We used the Gaussian 09 quantum mechanics program with the Berny optimization algorithm (30), using the M062X/aug-cc-pVDZ level of theory and an implicit hydrocarbon solvent (31). To calculate the binding energies, we compared the energy of an optimized, free-floating molecule to the energy of an optimized pair of molecules. For the quantum binding energy, we corrected for basis set superposition error as needed (32). We confirmed the OPLS structures and pairwise binding energies of each of the molecules studied here against these quantum mechanical calculations, and we excluded any OPLS models that had errors in bond distances of more than 0.04 Å, in bond angles (1°), in dihedral angles (2°), and in binding energies (1 kcal/mol). Dihedrals that are free rotors (for example, rotation about an alkane C-C bond) were not included in the error averages because their angles do not contribute significantly to the energy. These data are listed in Results. We performed these tests using ab initio calculations with the computationally exacting, but particularly accurate, M062X/aug-cc-pVDZ level of theory (33). This “Minnesota functional” is known to yield accurate pairwise binding energies for van der Waals and polar systems (34).
Once the veracity of the OPLS-generated structures was confirmed against ab initio simulations, the binding energies were also validated in a similar manner. Two sets of ab initio–generated binding energies were created for comparison, one in vacuum and one in implicit solvent. The solvent-based energies are closer to experimental conditions, whereas the energies in vacuum were used essentially as error bounds. The OPLS models with in-solvent binding energy errors greater than 1 kcal/mol were excluded.
MD procedure for membrane flexibility
To find the flexibility and energy barriers of our candidate azotosomes, we need to calculate all possible routes by which a molecule can leave its azotosome and then sum the relevant properties of these routes according to the probability of their occurrence. The properties we chose as relevant here are the potential energy and the force on the test molecule in the direction of the membrane. To prepare all these possible routes, we began with a representative section of membrane, a 6 × 6 x-y grid of molecules, for each candidate species.
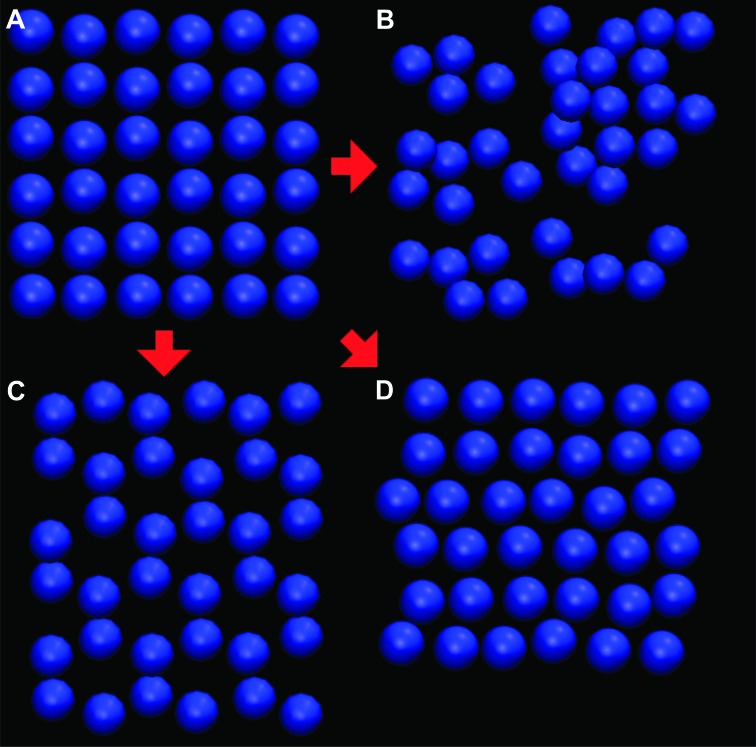
This piece of membrane was then expanded periodically to simulate a two-dimensional membrane of arbitrary extent. The surrounding space was filled with methane solvent. The edge molecules (those for which x = 0 or y = 0) were held fixed in the z direction to keep the membrane in place. The membrane was allowed to equilibrate, self-assembling into its desired structure as shown in Fig. 4.
Fig. 4. Nitrogen head positions in selected azotosomes.
(A) Initial grid. (B) Aminopentane (amorphous). (C) Pentanenitrile (hexagonal). (D) Acrylonitrile (close packed hexagonal).
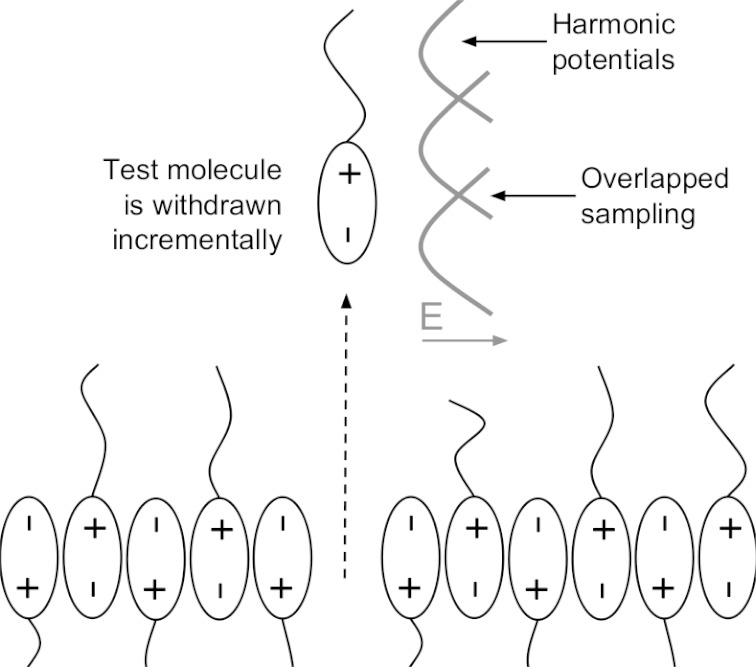
Next, a test molecule (at the location x,y = 3,3) was incrementally withdrawn in the z direction. At each increment, the test molecule was allowed to move freely in the [x,y] directions. In the z direction, it was loosely restrained by a harmonic potential, allowing it to sample nearby z locations, but not to leave the vicinity. This procedure, known as “umbrella sampling,” allows a sampling of all possible configurations and also provides a measure of whether the sampling was adequate—we can simply check whether we have enough samples from each small increment in the z direction. A schematic of this process is shown in Fig. 5.
Fig. 5. Umbrella sampling of the azotosome decomposition process.
The test molecule is incrementally withdrawn from the membrane in the z direction.
This procedure is necessary because of the azotosomes’ high barriers to decomposition. If the barriers to decomposition were low, the system would naturally sample the decomposed states within the simulated time. Umbrella sampling forces the simulation to reach these states even if they would require a very long time to arise from inherent fluctuations.
At each of the millions of MD steps, the potential energy function was evaluated, and the force required to hold the test molecule away from the membrane was calculated. This yielded profiles of force and potential energy as a function of distance from the membrane, which are provided separately in the Supplementary Materials. The force profiles were integrated over distance to yield free energy profiles, as shown in Fig. 6. The change in area was calculated by measuring the deflection of the indented nitrogen atom at the center of the sheet and finding the area of the rectangular pyramid formed between it and the restrained nitrogen atom at the corners of the sheet. This procedure proved to be very robust with respect to changes in the overall sheet size. The deflection of the indented atom was measured relative to the equilibrium state of the membrane, that is, relative to the point of minimum free energy.
Fig. 6. Stretching the azotosomes.
The slope of the fit line is proportional to the area modulus Ka.
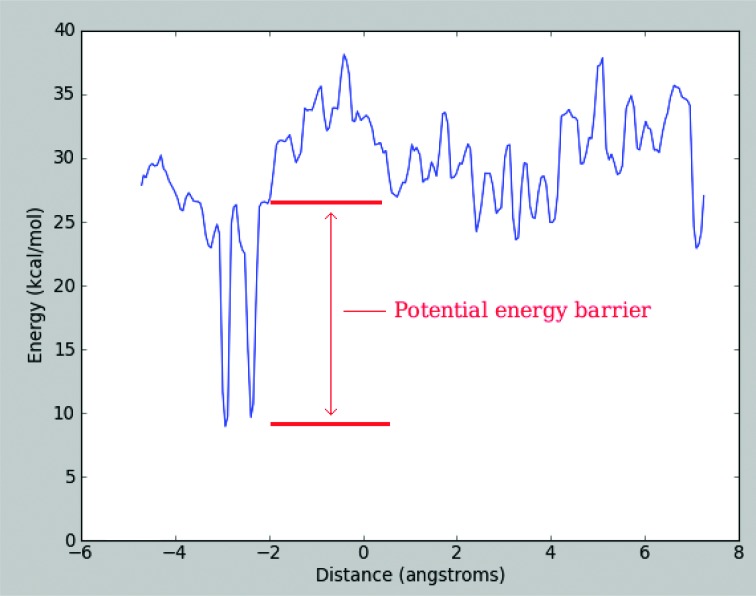
The potential energy barrier for each azotosome was calculated by finding the largest single uninterrupted increase in the potential energy during the decomposition of each azotosome. The concept of a rate-determining, Arrhenius-style energy barrier relies on the barrier being uninterrupted. If there is a stable intermediate state at which the system can reequilibrate, then it is not one barrier, but two smaller barriers, with a drastic increase in the implied rate of reaction. Because we used umbrella sampling, with its fine-grained view of the energy profiles, we were able to divide them into very fine sections (0.05 Å) and make sure that there were no intermediate states within our barriers. An example barrier (acrylonitrile) is shown in Fig. 7.
Fig. 7. Potential energy profile for the decomposition of acrylonitrile.
The largest instantaneous energy barrier is the activation energy to decompose the azotosome.
A few of the fine 0.05-Å sections, almost all at the beginning and end where no umbrella sampling overlap could occur, had fewer than 500 samples. We removed these sections for consideration as barriers because (500 samples) × (2 fs per sample) is smaller than the time scale of our NPT equilibration (1000 fs). This has the effect of making our energy barrier calculations more conservative because the sampling frequency of a section is inversely related to its energy.
All MD runs were performed using the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS; distribution March 2014) (35). Standard OPLS parameters were used unchanged from the Jorgensen 2008 data sets (36). Typical best practices for the MD simulation of membranes were followed. For example, a constant-temperature, constant-pressure (NPT) ensemble was applied using the Nose´-Hoover thermostat and barostat, the barostat being anisotropic (37). The anisotropic barostat allows the membrane the freedom to change or lose its structure, increasing the realism of the simulation (20). The temperature was set to 94 K and the pressure to 1.45 atm, similar to the conditions on the surface of Titan (17). Verlet integration was used with a time step of 2 fs (37). The particle-particle particle-mesh algorithm was used to add long-range Coulombic interactions, which are significant in membrane simulations (38). The short-range forces, Coulombic interactions, and Lennard-Jones forces were computed pairwise with a cutoff radius of 8 Å (38). Each membrane was initialized as a flat x-y plane with periodic boundary conditions in x, y, and z, as shown in Fig. 3. The initial simulation cell size was 21 × 21 × 42 Å. The position of the test molecule was altered in increments of 0.2 Å, starting at 2 Å below its starting position in the membrane and ending 10 Å above, giving 60 simulations per species tested. Data collection was then performed for 1 ns at each increment. The z-directional restraint on each molecule was exerted on its terminal nitrogen atom or, in a nonpolar molecule, on its terminal carbon. This allowed each molecule to rotate if it experienced an asymmetric force, giving it access to the maximum number of degrees of freedom. The restraints on the edge molecules were absolute (z forces were set to zero), whereas the restraint on the test molecule was imposed as a harmonic force with a spring constant of 10 kcal/mol-Å. This moderate restraint allowed the test molecule to cover the 0.2-Å range and overlap with the ranges of other simulations, providing continuous sampling of the properties of the system.
Correction (25 March 2015): The acknowledgments section has been updated.
Acknowledgments
We thank several Cornell faculty colleagues: F. Escobedo, S. Daniel, and N. Hairston for reading this manuscript and for their helpful suggestions and revisions. We thank David Usher for suggesting the term azotosome, and him and David Shalloway for discussions that led to the concept of nitrogen-containing reverse vesicles and micelles. Funding: We gratefully acknowledge the financial support of the Templeton Foundation. Author contributions: J.S. performed the MD simulations and wrote the drafts of the paper, J.L. provided consultation on the Titan environment and guided the simulations to conform with it, and P.C. provided consultation on the MD simulations and supervised the simulations and the writing of the paper. Competing interests: The authors declare that they have no competing financial interests. Data and materials availability: The data reported in this paper and the custom code used to create it are located at the repository https://github.com/jminuse/azotosome-paper.
REFERENCES AND NOTES
- 1.Orgel L. E., The origin of life—A review of facts and speculations. Trends Biochem. Sci. 23, 491–495 (1998). [DOI] [PubMed] [Google Scholar]
- 2.Strulson C. A., Molden R. C., Keating C. D., Bevilacqua P. C., RNA catalysis through compartmentalization. Nat. Chem. 4, 941–946 (2012). [DOI] [PubMed] [Google Scholar]
- 3.Segré D., Ben-Eli D., Deamer D. W., Lancet D., The lipid world. Orig. Life Evol. Biosph. 31, 119–145 (2001). [DOI] [PubMed] [Google Scholar]
- 4.Deamer D., A giant step towards artificial life? Trends Biotechnol. 23, 336–338 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Peretó J., López-García P., Moreira D., Ancestral lipid biosynthesis and early membrane evolution. Trends Biochem. Sci. 29, 469–477 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Walde P., Surfactant assemblies and their various possible roles for the origin(s) of life. Orig. Life Evol. Biosph. 36, 109–150 (2006). [DOI] [PubMed] [Google Scholar]
- 7.Kunieda H., Shigeta K., Suzuki M., Phase behavior and formation of reverse vesicles in long-polyoxyethylene-chain nonionic surfactant systems. Langmuir 15, 3118–3122 (1999). [Google Scholar]
- 8.Mollee H., De Vrind J., De Vringer T., Stable reversed vesicles in oil: Characterization studies and encapsulation of model compounds. J. Pharm. Sci. 89, 930–939 (2000). [DOI] [PubMed] [Google Scholar]
- 9.Li H., Hao J., Wu Z., Phase behavior and properties of reverse vesicles in salt-free catanionic surfactant mixtures. J. Phys. Chem. B 112, 3705–3710 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Tung S.-H., Lee H.-Y., Raghavan S. R., A facile route for creating “reverse” vesicles: Insights into “reverse” self-assembly in organic liquids. J. Am. Chem. Soc. 130, 8813–8817 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Norman L. H., Is there life on…Titan? Astron. Geophys. 52, 1.39–1.42 (2011). [Google Scholar]
- 12.I. Müller-Wodarg, C. A. Griffith, E. Lellouch, T. E. Cravens, Titan: Interior, Surface, Atmosphere, and Space Environment (Cambridge University Press, Cambridge, UK, 2014), vol. 14. [Google Scholar]
- 13.McKay C., Smith H., Possibilities for methanogenic life in liquid methane on the surface of Titan. Icarus 178, 274–276 (2005). [Google Scholar]
- 14.Strobel D. F., Molecular hydrogen in Titan’s atmosphere: Implications of the measured tropospheric and thermospheric mole fractions. Icarus 208, 878–886 (2010). [Google Scholar]
- 15.Clark R. N., Curchin J. M., Barnes J. W., Jaumann R., Soderblom L., Cruikshank D. P., Brown R. H., Rodriguez S., Lunine J., Stephan K., Hoefen T. M., Le Mouélic S., Sotin C., Baines K. H., Buratti B. J., Nicholson P. D., Detection and mapping of hydrocarbon deposits on Titan. J. Geophys. Res.: Planets 115 (2010). [Google Scholar]
- 16.Schulze-Makuch D., Fairén A. G., Davila A., Locally targeted ecosynthesis: A proactive in situ search for extant life on other worlds. Astrobiology 13, 674–678 (2013). [DOI] [PubMed] [Google Scholar]
- 17.Sarker N., Somogyi A., Lunine J. I., Smith M. A., Titan aerosol analogues: Analysis of the nonvolatile tholins. Astrobiology 3, 719–726 (2003). [DOI] [PubMed] [Google Scholar]
- 18.Hofsäß C., Lindahl E., Edholm O., Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophys. J. 84, 2192–2206 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sen S., Subramanian S., Discher D. E., Indentation and adhesive probing of a cell membrane with AFM: Theoretical model and experiments. Biophys. J. 89, 3203–3213 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ayton G., Smondyrev A. M., Bardenhagen S. G., McMurtry P., Voth G. A., Calculating the bulk modulus for a lipid bilayer with nonequilibrium molecular dynamics simulation. Biophys. J. 82, 1226–1238 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lasic D., On the thermodynamic stability of liposomes. J. Colloid Interface Sci. 140, 302–304 (1990). [Google Scholar]
- 22.Van der Ploeg P., Berendsen H., Molecular dynamics simulation of a bilayer membrane. J. Chem. Phys. 76, 3271 (1982). [Google Scholar]
- 23.Venable R. M., Zhang Y., Hardy B. J., Pastor R. W., Molecular dynamics simulations of a lipid bilayer and of hexadecane: An investigation of membrane fluidity. Science 262, 223–226 (1993). [DOI] [PubMed] [Google Scholar]
- 24.Goetz R., Gompper G., Lipowsky R., Mobility and elasticity of self-assembled membranes. Phys. Rev. Lett. 82, 221 (1999). [Google Scholar]
- 25.Discher D. E., Ortiz V., Srinivas G., Klein M. L., Kim Y., Christian D., Cai S., Photos P., Ahmed F., Emerging applications of polymersomes in delivery: From molecular dynamics to shrinkage of tumors. Prog. Polym. Sci. 32, 838–857 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jorgensen W. L., Maxwell D. S., Tirado-Rives J., Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236 (1996). [Google Scholar]
- 27.Hobza P., Kabeláč M., Šponer J.. Mejzlík P., Vondrášek J., Performance of empirical potentials (AMBER, CFF95, CVFF, CHARMM, OPLS, POLTEV), semiempirical quantum chemical methods (AM1, MNDO/M, PM3), and ab initio Hartree–Fock method for interaction of DNA bases: Comparison with nonempirical beyond Hartree–Fock results. J. Comput. Chem. 18, 1136–1150 (1997). [Google Scholar]
- 28.Yokoyama Y., Ohashi Y., Crystal structure of acrylonitrile. Bull. Chem. Soc. Jpn. 71, 345–348 (1998). [Google Scholar]
- 29.Hu Y., Jun Y.-S., Biotite dissolution in brine at varied temperatures and CO2 pressures: Its activation energy and potential CO2 intercalation. Langmuir 28, 14633–14641 (2012). [DOI] [PubMed] [Google Scholar]
- 30.Li X., Frisch M. J., Energy-represented direct inversion in the iterative subspace within a hybrid geometry optimization method. J. Chem. Theory Comput. 2, 835–839 (2006). [DOI] [PubMed] [Google Scholar]
- 31.Tomasi J., Mennucci B., Cammi R., Quantum mechanical continuum solvation models. Chem. Rev. 105, 2999–3093 (2005). [DOI] [PubMed] [Google Scholar]
- 32.Simon S., Duran M., Dannenberg J., How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers? J. Chem. Phys. 105, 11024–11031 (1996). [Google Scholar]
- 33.Walker M., Harvey A. J., Sen A., Dessent C. E., Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions. J. Phys. Chem. A 117, 12590–12600 (2013). [DOI] [PubMed] [Google Scholar]
- 34.Plumley J. A., Dannenberg J., A comparison of the behavior of functional/basis set combinations for hydrogen-bonding in the water dimer with emphasis on basis set superposition error. J. Comput. Chem. 32, 1519–1527 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Plimpton S., Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995). [Google Scholar]
- 36.W. Jorgensen, OPLS All-Atom Parameters for Organic Molecules, Ions, Peptides & Nucleic Acids (Yale University, New Haven, CT, 2009). [Google Scholar]
- 37.Tuckerman M. E., Alejandre J., López-Rendón R., Jochim A. L., Martyna G. J., A Liouville-operator derived measure-preserving integrator for molecular dynamics simulations in the isothermal–isobaric ensemble. J. Phys. A: Math. Gen. 39, 5629 (2006). [Google Scholar]
- 38.Pollock E., Glosli J., Comments on P3M, FMM, and the Ewald method for large periodic Coulombic systems. Comput. Phys. Commun. 95, 93–110 (1996). [Google Scholar]