Abstract
Preterm birth is a strong contributor to perinatal mortality, and preterm infants that survive are at risk for long-term morbidities. During most of pregnancy appropriate mechanical function of the cervix is required to maintain the developing fetus in utero. Premature cervical softening and subsequent cervical shortening are hypothesized to cause preterm birth. Presently, there is a lack of understanding of the structural and material factors that influence the mechanical function of the cervix during pregnancy. In this study we build finite element (FE) models of the pregnant uterus, cervix, and fetal membrane based on magnetic resonance imagining (MRI) data in order to examine the mechanical function of the cervix under the physiologic loading conditions of pregnancy. We calculate the mechanical loading state of the cervix for two pregnant patients: 22 weeks gestational age with a normal cervical length and 28 weeks with a short cervix. We investigate the influence of 1) anatomical geometry 2) cervical material properties, and 3) fetal membrane material properties, including its adhesion properties, on the mechanical loading state of the cervix under physiologically relevant intrauterine pressures. Our study demonstrates that membrane-uterus interaction, cervical material modeling, and membrane mechanical properties are factors that must be deliberately and carefully handled in order to construct a high quality mechanical simulation of pregnancy.
Keywords: finite element, preterm delivery, preterm birth, short cervix, cervical tissue
1. Introduction
Preterm birth is a critical health problem affecting more than 15 million infants per year in the U.S. and caused 1 million deaths in 2013 (World Health Organization 2014). Preterm infants account for 35% of all perinatal deaths and $26 billion in health care costs (National Research Council 2007). Although multiple etiologies lead to preterm birth, a short cervix as measured by transvaginal ultrasound is associated with increased risk of preterm birth (Iams 2014). Thus, ultrasound measurement of cervical length is a key component of clinical algorithms to prevent preterm birth (Iams 2014; Berghella 2012).
Although the clinical significance of a short cervix is well known, there is no clinical consensus to what extent a short cervix is causally related to preterm birth or a consequence of a different pathogenesis. Limiting clinical investigation of cervical shortening is a lack of understanding of the deformation mechanisms leading to a short cervix. The structural antecedents of cervical shortening are not known, so prediction of cervical shortening is not possible. An improved understanding of deformation mechanisms leading to a short cervix is urgently needed to elucidate the etiology of a short cervix and its relation to preterm birth.
Here we present a finite element (FE) study to calculate the stress and strain in the cervix during pregnancy. The models in our study are based on anatomical geometry from MRI and cervical mechanical properties of human cervical tissue (Myers, Hendon, et al. 2015; Myers, Socrate, et al. 2010; Myers, Paskaleva, et al. 2008; Yao, Yoshida, et al. 2014). Principal stress and strain patterns in the cervix and lower uterine segment are calculated as a function of cervical length, cervical tissue properties and interaction with the fetal membrane. We pay particular attention to the top of the cervix, called the internal cervical os, because cervical shortening is initiated at this location (Zork, Vink, et al. 2014; Zilianti, Azuaga, et al. 1995).
An important variable affecting the stress pattern in the cervix is the three-dimensional anatomy of cervix and uterus during pregnancy (House, McCabe and Socrate 2013). Large geometric changes occur with fetal growth, and these changes are poorly understood because pregnancy is a protected environment (House, Bhadelia, et al. 2009). Anatomical geometry is irregular, asymmetric, and different for every pregnancy, and external forces on the uterus and cervix vary between patients as a result of these geometric differences. Those factors make it difficult to discern the detailed mechanical stress state of the organs. Previous studies have investigated the mechanical loading state of the cervix through finite element models with CAD-based (House and Socrate 2006; House, Feltovich, et al. 2012; Paskaleva 2007) and 2D (Mahmoud, Wagoner Johnson, et al. 2013) geometry measured from medical images. Our study builds upon past knowledge using anatomy-based models with fewer simplifying geometric assumptions. These new models can help elucidate the effects of asymmetry and anatomical irregularity on resulting stress and strain patterns.
In addition to the complexity of the pelvic geometry, the material response to loading of the tissue plays an equally important role in the mechanical function of the cervix. Material properties of ex-vivo tissue samples of the uterus and fetal membrane have been reported by others, with tensile modulus ranging from 0.5 to 2 MPa for the uterus (Pearsall and Roberts 1978) and 2 to 30 MPa for the fetal membrane (Benson-Martin, Zammaretti, et al. 2006; Oyen, Calvin and Cook 2004). The material characteristics of the cervix have been measured by our research group (Yao, Yoshida, et al. 2014; Fernandez, Vink, et al. 2013; Myers, Socrate, et al. 2010, 2009; Myers, Paskaleva, et al. 2008), where the tissue material response to loading is nonlinear, time-dependent, and anisotropic. In this study we consider steady state mechanical loading of the cervix. We investigate five cervical material models, two neo-Hookean and three fiber composite models, where material parameters are obtained from fitting model equations to equilibrium tension and compression data (Myers, Paskaleva, et al. 2008; Myers, Socrate, et al. 2010). One of the most salient features of the equilibrium behavior of cervical tissue is the nonlinearity between tension and compression, where the tensile stiffness is orders of magnitude higher than the compressive stiffness. To account for this nonlinearity, we explore three fiber composite cervical material models, specifically: a non-dispersed fiber model with preferentially aligned collagen fibers directed circumferentially around the cervical canal, an ellipsoidal continuously distributed collagen network model with circumferential preferential alignment, and a random, continuously distributed collagen network model where collagen fibers are recruited in the direction of principal tensile loading.
In this study, we describe the methodology we used to create a 3D finite element model of the lower uterine segment (LUS), fetal membrane, and cervix of two pregnant patients: one at 22 weeks of gestation with a normal cervix length (38 mm) and one at 28 weeks with a short cervix (9 mm). A “short cervix” is defined as a (non-dilated) cervical length ≤ 25mm. We simulate the effects of the intrauterine pressure (IUP), which at baseline levels is clinically called the uterine tone. IUP is prescribed as a variable hydrostatic pressure applied to the interior of the fetal membrane. We then model the interaction between the membrane and the uterus and cervix for IUP values spanning the full physiological range (Buhimschi, Buhimschi, et al. 2004). FE results for the two patients are given, and our analysis contrasts the cervical stress and strain patterns between the normal and short cervix geometries using random continuous fiber distribution models for both the LUS and the cervix. Then, we shift focus to the the normal cervix model to compare material models for the cervix that feature different levels of complexity and mechanical properties. Lastly, we consider the effect of membrane adhesion and membrane stiffness on the cervix’s loading state. Through this modeling effort we show that the positioning, symmetry, and shape of the organs play a large role in the mechanical stress state of the cervix, where asymmetric features drive large concentrations of stress and strain. We also show that adhesion of the fetal membrane to the LUS and cervix reduces the load on the cervix and that the choice of material model for the cervix will influence the stress and strain in the cervix. These results are examples of the countless opportunities for the study of pregnancy that detailed biomechanical models such as ours make possible.
2. Methods
2.1 Patient Demographic
Eligible patients were recruited and consented under an IRB-approved research protocol at the Columbia University Medical Center. Exclusion criteria included women with premature membrane rupture, placenta accreta/previa, chorioamnionitis, placental abruption, concerning fetal or maternal status and preterm labor. Patient demographics and obstetric history are given in Table 1.
Table 1.
Patient demographics
| Normal Cervix Patient | Short Cervix Patient | |
|---|---|---|
| Age | 32 | 25 |
| Gestation Time at Scan | 22 weeks | 28 weeks |
| Gravida | 1 | 3 |
| Parity | 0 | 1 |
| Delivery | 39 weeks, 1 day | 39 weeks, 2 days |
2.2 Data Acquisition and Pulse Sequence
MRI data sets were acquired using a 1.5 Tesla GE HDxt scanner with a 12 channel phased array torso coil. The pulse sequence was a Sagittal T2 Cube, 3D Fast Spin Echo sequence with TR=2000 ms, TE=103 ms, receiver BW ± 15.6 kHz, and Echo Train Length=60. The slice thickness was 2.2 mm (interpolated to 1.1mm) with a field of view (FOV) of 26 cm and image matrix of 256 × 256 for each slice. The resulting zero-filled voxelized data had a resolution of 1.1 × 0.5 × 0.5 mm3 in the sagittal, axial, and coronal directions, respectively. To cover the entire uterus and cervix 90 sections were acquired in approximately 6 minutes acquisition time with no breath holding. This pulse sequence achieved high image resolution and a large FOV while minimizing patient discomfort.
2.3 Segmentation of MRI Data
The MRI image stack was loaded into the Simpleware ScanIP software (Version 6.0, Exeter, UK). We identified the uterus and cervix within the image volume, and manually segmented the organ in each image slice. In general, fluids and tissues with increased water content show up brighter on T2 images while tissues with low proton density, or fibrous tissues, show up darker (Hashemi 2010). Cervical stroma was noticeably darker on the scans than the cervical mucous plug, amniotic fluid, and the bladder. The uterine wall could be seen as a slightly darker band within the images surrounding the fetus and placenta. In areas where the uterus was not clearly visible due to patient movement or low contrast, the tissue was assumed to be continuous with constant thickness and to connect to the visible regions of tissue in agreement with all other anatomical constraints.
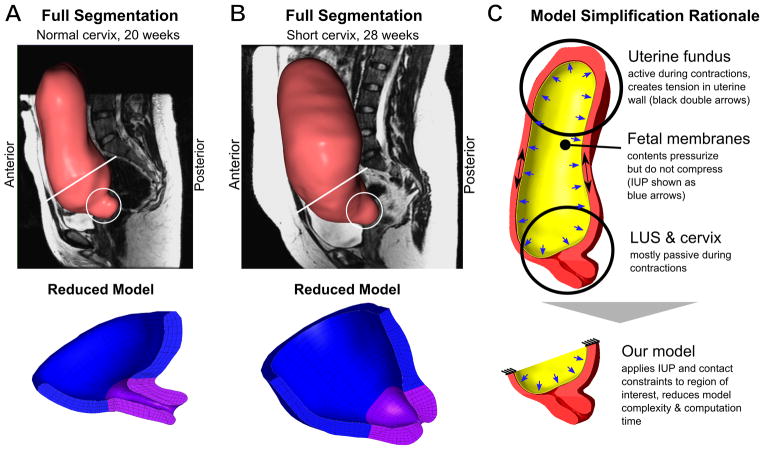
Each segmented pixel on a given slice generated a voxel in the 3D model, and adjacent voxels connected to form the 3D shape of the segmented volume. After segmenting each slice, we employed Gaussian smoothing filters (with radius between 0.5 and 5 mm) to reduce noise in the segmented model. A smooth surface was required for successful volume element formation. The segmented volumes are shown for each patient with a representative sagittal MRI slice in Figures 1A–B.
Figure 1.
3D Geometry of (A) Normal and (B) Short Cervix Pregnancy at 20 and 28 Weeks, respectively. Circles indicate the location of the cervix. (C) Translation from whole uterine geometry to partial model of LUS and cervix.
2.4 Volume Meshes
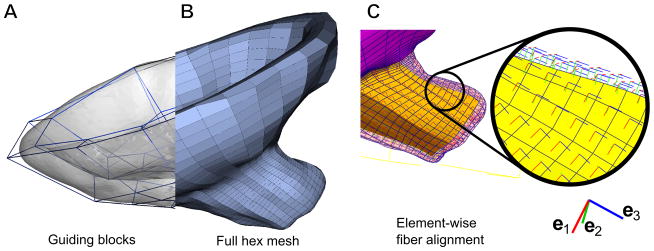
For computational efficiency, we developed a partial model to focus on the interaction between the fetal membrane, LUS, and the cervix. See Section 2.5.1 and Figure 1C for details on how the partial model accounts for uterine loading. Surface meshes for the LUS and cervix were imported into IA-FEMesh1 for the creation of the volumetric finite element meshes. Within the software, we positioned structural guiding blocks (Figure 2A) around the surface mesh previously created. We then seeded the boundaries of these blocks to specify the mesh density for the model, and generated hexahedral elements (2B). Near the cervical canal, we increased the mesh density to improve model accuracy and output resolution.
Figure 2.
(A) Surface mesh shown in translucent gray with guiding blocks for IA-FEMesh shown as blue framework of polyhedra. (B) Resulting hexahedral mesh of the LUS and cervix. (C) Local fiber coordinates in each hexahedral element. Each local e1 points circumferentially around the inner cervical canal.
To create a volume mesh for the fetal membrane, a mask representing the interior of the uterus was generated. A surface mesh was fitted to that volume, then extruded inward 0.5 mm to form a thin volumetric mesh representing the membrane. We chose 0.5 mm thickness because it is representative of reported literature values for fetal membrane thickness (Jabareen, Mallik, et al. 2009; Frigo, Lang, et al. 1998; Benson-Martin, Zammaretti, et al. 2006). Figures 1A-B show the completed meshes, and mesh statistics are given in Table 2.
Table 2.
Mesh properties
| Normal LUS + Cervix | Normal Membrane | Short LUS + Cervix | Short Membrane | |
|---|---|---|---|---|
| Hexahedral Elements | 5332 | 2450 | 2652 | 2180 |
| Min, Max, Mean Volume (mm3) | 1.0, 216.5, 17.5 | 1.9, 14.4, 3.6 | 0.23, 331, 31.9 | 0.03, 5.3, 25.4 |
| Min, Max, Mean Jacobian | 0.06, 144, 14.6 | 0.7, 12.9, 3.3 | 0.002, 36.7, 3.6 | 0.003, 3.0, 0.62 |
2.5 Building the FE Model
Model assembly and model calculations were done with the FEBio2 finite element package. Volume meshes were imported and assembled within FEBio’s PreView program (Maas, Ellis, et al. 2012). For both the normal and short cervix models, we defined the cervix as the region of tissue from the external os to the internal os and partitioned these elements separately from the rest of the LUS. In the short cervix model, the transition from the lower uterine segment to the shortened cervix was defined to be the histological internal os (Figure 1).
Models were built to investigate the effect of three different factors on the mechanical stress state of the cervix: 1) geometry of the anatomy, 2) cervical material model, and 3) fetal membrane mechanical properties including adhesion to the uterine wall. To investigate geometric considerations, the cervical stress state of the normal and short cervix models were compared using the same cervical material model and model parameters. To investigate different forms of the cervix material model (models described in Section 2.5.2) and the effect of membrane properties (described in Section 2.5.3), the normal cervix model was used as a platform for comparison.
2.5.1 BCs and Loads
In pregnancy, the upper portion of the uterus contracts, resulting in increased IUP which must be balanced by stress in the cervix and LUS. The IUP during uterine contraction and pushing is three to four times greater than the IUP of passive loading conditions (Buhimschi, Buhimschi, et al. 2004). In contrast to the uterine fundus, the LUS and cervix are primarily mechanically passive during labor (Cunningham, Leveno, et al. 2010). For those reasons, we replicated the dominant loading forces in the LUS and neglected passive interactions with ligaments, though ligament effects may be included in subsequent models. In order to constrain the geometry in 3D space, the top edge of the LUS was fixed while the remaining portion was left free to deform (Figure 1C). To investigate the response of the model under varied biologically relevant loading conditions, the interior side of the fetal membrane was subjected to a prescribed pressure that sweeps the range of 0–13 kPa, covering the IUP ranges of pregnancy and delivery. The figures in this paper were generated using an IUP of 8.6 kPa (representing contraction pressure) unless otherwise specified (Buhimschi, Buhimschi, et al. 2004).
2.5.2 Tissue Material Models and Material Parameters
All of the material properties used in the simulations are listed in Table 3. Each cervical material model described in this section was chosen to represent a different kind of fiber organization. Fetal membrane and uterine tissue were each modeled as a neo-Hookean material and their moduli were based on studies in the literature (Benson-Martin, Zammaretti, et al. 2006; Oyen, Calvin and Cook 2004; Pearsall and Roberts 1978).
Table 3.
Material models and properties used in the LUS, fetal membrane, and cervix. For material fits to experimental data, see Figure 3 and (Myers, Hendon, et al. 2015; Gan, Yao, et al. 2014). Material properties are defined as in the FEBio 2.0 software. For fiber stiffness parameters ξi, subscripts indicate correspondence to a local basis direction in each element. In this study, direction e1 indicates a basis vector aligned circumferentially around the cervical canal. The EFD model is rotationally symmetric around this preferential direction. For the SFD model, the same property is specified for every orthogonal direction. Subscript NH refers to a neo-Hookean material model.
| Location | Material Model | Properties |
|---|---|---|
| LUS | SFD | ENH = 0.006 MPa, νNH = 0.3, β = 3, ξ = 0.1 MPa |
| Fetal membrane | NH | ENH = 20 MPa, νNH = 0.3 |
| Cervix | NH-tensile | ENH = 0.966 MPa, νNH = 0.3 |
| Cervix | NH-compressive | ENH = 0.004 MPa, νNH = 0.3 |
| Cervix | NFD | ENH = 0.002 MPa, νNH = 0.3, β = 3, ξ = 0.15 MPa |
| Cervix | EFD | ENH = 0.002 MPa, νNH = 0.3, βi = 3, |
| Cervix | SFD | ENH = 0.002 MPa, νNH = 0.3, |
Neo-Hookean Material Model
The simplest kind of material model used in our study was a hyperelastic neo-Hookean (NH) containing no fibers. It is an isotropic material, similarly stiff in tension and compression. The strain energy per unit reference volume for a neo-Hookean material is given by
| (1) |
In the expression above, μ and λ are the Lamé constants from linear elasticity, and J = det F is the Jacobian where F is the deformation gradient (Holzapfel 2000). The Young’s modulus and Poisson’s ratio are related to the Lamé constants by ENH = μ(3 + 2μ/λ)/(1 + μ/λ) and νNH = 1/[2(1 + μλ)], respectively. We investigated two neo-Hookean models for cervical material behavior, one fitted to compression data and the other fitted to tensile data. The two NH models served as points of comparison by approximating the possible extremes of non-pregnant tissue response.
Fiber Composite Material Models
Fiber composite models have been described by several authors (Holzapfel 2000; Lanir 1983; Ateshian 2009, 2007), and applied specifically to describe human cervical tissue material behavior by our group (Myers, Hendon, et al. 2015). For more information on the models in this section, one may consult those works as well as the FEBio documentation (Maas, Rawlins, et al. 2014).
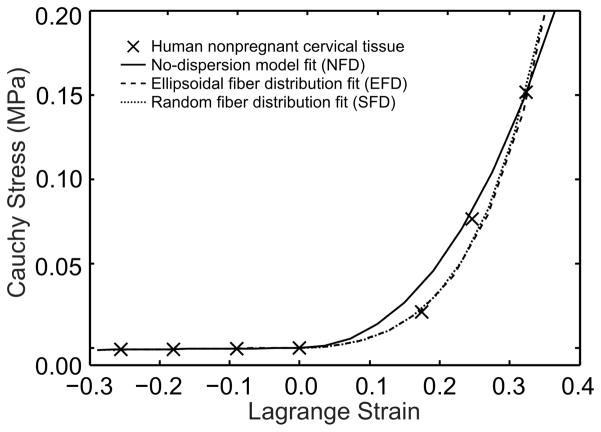
To explore the effects of modeling different fiber distributions, we chose three model configurations: no fiber dispersion (NFD), preferentially aligned ellipsoidal fiber distribution (EFD), and a random or spherical fiber distribution (SFD). Each model was independently fitted to experimental data from tension and compression tests on human non-pregnant cervical tissue. The curve fits are in Figure 3.
Figure 3.
Curve fits for three fiber composite models to tension and compression data from experiments on non-pregnant human cervical tissue specimens done by our group (Myers, Hendon, et al. 2015; Myers, Socrate, et al. 2010; Myers, Paskaleva, et al. 2008). The fits were done using a combination of manual iteration and least-squares regression. The final material property values are listed in Table 3.
Tension-compression nonlinearity in fiber composite material models occurs because the fibers only sustain tension while a neo-Hookean ground substance is used to provide the required compressive support. Fibers were modeled in each case to undergo affine deformation with the ground substance. The total strain energy for each fiber composite material in this study is the sum of the strain energy density of a neo-Hookean ground substance and that of a particular fiber configuration ΨFibers:
| (2) |
The Cauchy stress tensor is then
| (3) |
The simplest fiber composite model we utilized has fibers directed along only the local e1 direction of each element in the reference configuration. Organ-level fiber directionality was achieved by using a custom python script to prescribe the orientation of a local basis {ei} in each element with respect to the global coordinate system according to manually defined anatomical landmarks and the orientation of the hexahedral element faces within the model. The resulting model featured a local e1 axis (and therefore fibers) in each element, circumferentially oriented around the cervical canal (Figure 2C). The fiber strain energy density for this NFD model – called the Fiber with Exponential Power Law model in FEBio – has the form
| (4) |
The Cauchy stress for non-dispersed fibers is then
| (5) |
| (6) |
where is the current fiber direction, given an initial fiber direction nr (equal to e1 in this model), and In = nr · FTF·nr is the square of the fiber stretch. In this model, ξNFD > 0 is the fiber “modulus” with units of stress, βNFD ≥ 2 is a unitless stiffening parameter, and H(·) is a unit step function that is zero-valued for negative arguments and unity-valued for positive.
While a fiber model with no dispersion is highly appropriate in some circumstances (for example, when modeling ligaments), it may not be the closest reflection of collagen fiber alignment in the cervix, which is more dispersed (Gan, Yao, et al. 2015; Aspden 1988). For that reason, we fitted two distinct distributed fiber composite models to tension-compression data from non-pregnant human tissue. The first model assumed an ellipsoidal distribution of fiber stiffness as a function of spherical angles θ and ϕ, while the second model prescribed a random (or spherical) distribution. The strain energy density for ellipsoidal or spherical fiber distributions is given by the integral
| (7) |
where H and In are as previously defined. The fiber strain energy in this material is governed by the power law defined in FEBio in the form
| (8) |
where ξEFD(nr) is the fiber stiffness distribution function. For this model, it is written in the form of the ellipsoid
| (9) |
where ξ1 and ξ2,3 are the lengths of the semi-major axis (in the local e1 direction) and both semi-minor axes (e2 and e3), respectfully, of the ellipsoid defining the fiber distribution. The unit vector nr points in the direction of fibers passing through dA and is given in terms of the spherical coordinates θ and ϕ by nr = sin ϕ cos θe1 + sin ϕ sin θe2 + cos ϕe3.
The Cauchy stress tensor for EFD fibers is given by
| (10) |
| (11) |
where βEFD ≥ 2 is the fiber stiffening parameter taken as a constant, In = nr · FTF·nr is the fiber stretch squared and is the current direction of the fibers that were directed along nr in the reference configuration.
Implicit in our ellipsoidal model was the assumption of an equal fiber dispersion in all directions perpendicular to the semi-major fiber axis e1 (equivalent to setting ξ2 = ξ3). The ratio of ξ1 to ξ2 for our EFD model was fitted to x-ray diffraction fiber orientation density data of cervical stroma from (Aspden 1988). Note that the spherical fiber dispersion is simply the spherically symmetric case of an ellipsoidal fiber distribution, and was achieved by setting ξ1 = ξ2 = ξ3 in the relations above.
2.5.3 Fetal Membrane and Contact
Two contact scenarios were investigated. With the exception of the adhesion comparison, all simulations were carried out using FEBio’s “tied” contact interface, which constrains two adjacent surfaces to deform and translate together without sliding relative to each other. We took this type of contact to represent a healthy pregnancy in which the fetal membrane is still attached to the decidua parietalis. In contrast, a “facet-to-facet” sliding contact interface was used to represent the interaction between a detached membrane and the decidua. In both cases, an augmented Lagrangian method was used to enforce the contact interface.
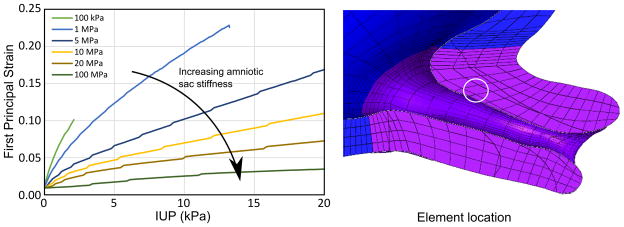
To determine the effect of the fetal membrane stiffness on mechanical loading in the cervix, we varied the modulus ENH of the membrane and plotted the resulting strains in an element located near the cervical internal os (Figure 10). For all other simulations in this study, the Young’s modulus ENH of the membrane was set to 20MPa, which represents a median value of stiffnesses reported in the literature for high strains (Benson-Martin, Zammaretti, et al. 2006; Oyen, Calvin and Cook 2004).
Figure 10.
First principal strain in a representative element within the internal os for increasing IUP while parameterizing the fetal membrane modulus from 0.1 to 100 MPa. With increasing membrane stiffness, strain levels in the cervix decrease. Literature values for membrane stiffness vary between 1 and 40 MPa.
2.5.4 Simulation Steps and Solving
Each simulation was done in two stages. The first stage was an initialization process to ensure good surface alignment between the uterus and fetal membrane volume meshes. This step applied no load to the model but gradually increased the contact penalty from 0 to 100% of its value (scaling the Lagrange multiplier increment). The second step in the simulation linearly increased the IUP applied to the interior of the fetal membrane from 0 kPa to 13 kPa in a minimum of 100 time steps.
The simulations were carried out in FEBio 2.0 on a Windows 7 PC with an Intel Core i7 processor and 32 GB of RAM. The exact convergence times varied between 10–60 minutes, depending on material model and material properties.
3. Results
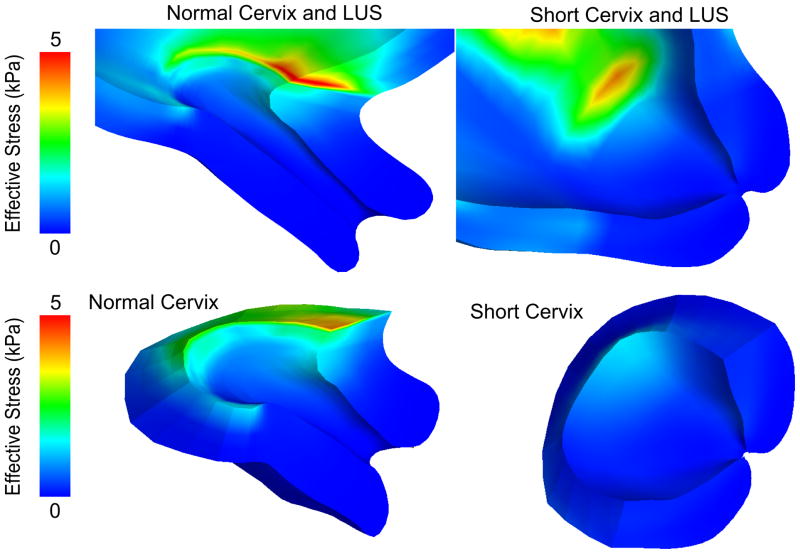
Significant differences exist in the loading of the cervix between the normal and short cervix models (Figures 4, 5, and 6). Whereas the lower half of the normal cervix remains unloaded, the short cervix model exhibits large strains (0.04–0.06) throughout its length (Figure 5). Material model comparisons show that the mechanical responses of the fiber composite models fall in between the two neo-Hookean models. The fiber composite models with dispersion are able to resist membrane loading in a manner that produces smaller stress and/or strain concentrations than the neo-Hookean and NFD models. Finally, our simulations of the interaction between the fetal membrane and the lower uterine segment confirm the load-sharing role of the membrane during pregnancy, and show how increased membrane stiffness shields the cervix from loading.
Figure 4.
Stress results for the normal and short cervix model using a random continuous distributed fiber model in the cervix, with an IUP of 8.6 kPa corresponding to the peak IUP during uterine contraction. Effective stress levels in the cervix are highest near the LUS.
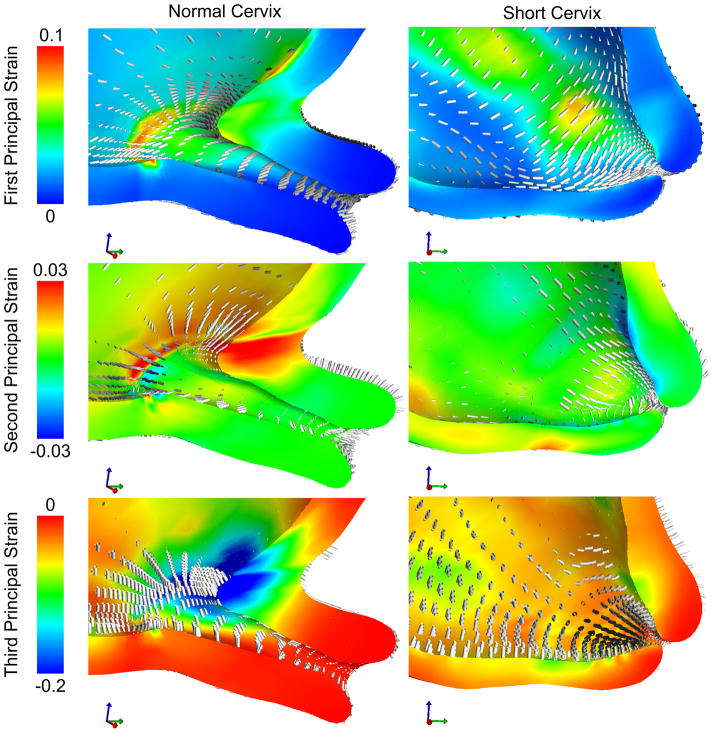
Figure 5.
Strain results for the normal and short cervix model using a random continuous distributed fiber model in the cervix, with an IUP of 8.6 kPa corresponding to the peak IUP during uterine contraction. Circumferential first principal strains around the cervical canal are observed in both models. Strain levels in the short cervix model on the order of 0.04 to 0.06 are present in locations along the whole length of the histological cervical canal. In the normal cervix model, these large strains do not propagate farther than the 1/3 of the cervix closest to the internal os.
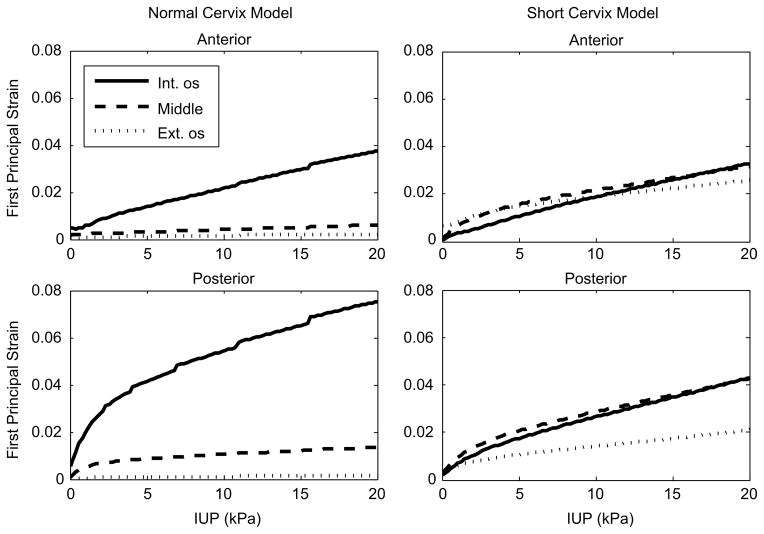
Figure 6.
First principal strains from representative elements near the internal os, middle, and external os of the anterior and posterior cervical canal of the normal and short cervix models. Notice that higher strain levels persist farther toward the external os in the short cervix model, while strains quickly drop off in the normal cervix model as the distance from the internal os increases.
3.1 Normal and Short Cervix Models
The effective stress (Figure 4) and first principal strain (Figure 5) in the cervix are compared between the short and normal cervix models using a randomly distributed continuous fiber cervical material model. The geometry of the anatomy and the placement of the cervix within the pelvis drive the patterns of stress and strain within the cervix, where asymmetric stress concentrations are observed in both models at the internal os, the initial site of cervical shortening. For both models, circumferential first principal tensile strains are seen in the posterior cervix, while longitudinal strains appear in the anterior cervix. In the normal cervix model, the internal os experiences the highest principal strain on the order of 0.05 to 0.1, while strains in the inferior-posterior half of the cervix are under 0.02. In contrast, the short cervix model has strains on the same order of magnitude (0.04–0.06) over the whole cervix from the internal os to the external os. This difference in cervical strain distribution between the models is shown for characteristic element locations as IUP is increased (Figure 6). In both models, strains are not uniform when going around the internal os and vary by an order of magnitude or more due to anatomical geometric asymmetry.
Von Mises (effective) stresses within the inner uterine wall layer tend to be higher than the stresses in the outer layer of the wall, by a factor ranging from 2 to 10 in different locations. On the inside of the uterus, these stresses are compressive normal to the uterine wall from the contact with the fetal membrane. Near the outer wall, the dominant stresses are oriented tangent to the uterine wall and balance the high pressure inside the uterus.
The normal cervix model predicts stress concentrations in the LUS near the interface between the LUS and cervix. These stress concentrations are expected due to the step change in material properties at the interface between the cervix and uterus, and are measured to be approximately 7 to 10 times the average stress in the cervix for both neo-Hookean models and the non-dispersed fiber model, but only 3 times the average cervical stresses for the distributed fiber composite models. The short cervix model also features the expected stress concentrations at the material boundary for the SFD material. Future models will feature a more gradual property change, but it is noted that the precise location of this division can only be known through histology.
3.2 Cervical Material Models
Comparisons between material models are given for the normal cervical geometry. The choices of cervical material model and model parameters strongly impact the magnitude of stress within the cervix and the corresponding strain under an applied IUP (Figures 7 and 8).
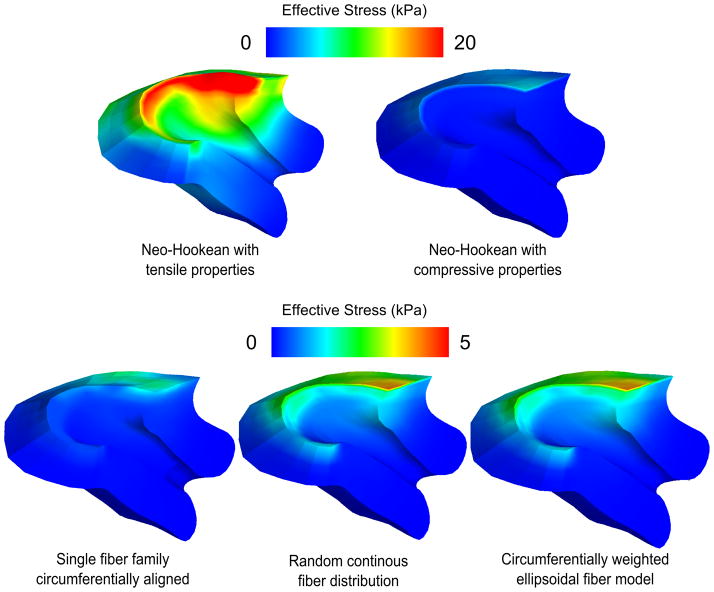
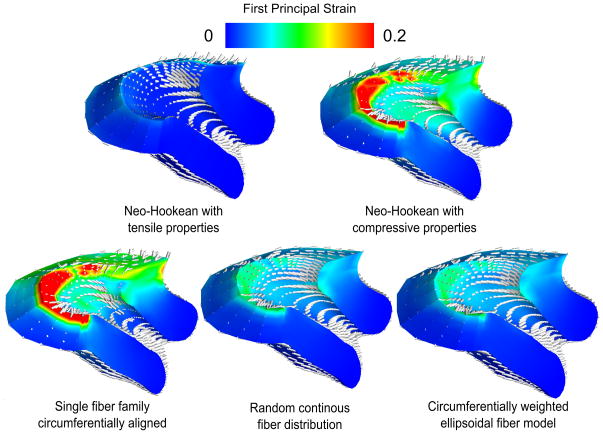
Figure 7.
Effective stress at IUP=8.6 kPa for five different cervical material models. The neo-Hookean models put upper and lower bounds on stress response, while the fiber composite models replicate the tension-compression nonlinearity of the tissue. Note the similarity between the random continuous model and the ellipsoidal model. Out of all the models, the single fiber family model predicts the lowest stresses at the top of the cervix. The two distributed fiber models predict more load bearing by the upper cervix on both the posterior and anterior sides.
Figure 8.
First principal strains IUP=8.6 kPa for five different cervical material models. The single fiber family model with no dispersion produces high strains perpendicular to the fiber direction because of the tension-compression nonlinearity of the material model. The continuous fiber distribution models do not produce the effect as strongly due to having at least some fibers in each direction.
All of the fiber composite model stress and strain predictions lie in between those of the compressive and tensile neo-Hookean models. The NFD model shows concentrated tensile strains greater than 0.2 around the internal os and large regions of tensile strain on the order of 0.2 within the cervix in directions perpendicular to the fiber alignment. The EFD and SFD models have the most uniform strain distributions of all, with first principal strains at levels under 0.15 throughout. Moving from an EFD model to an SFD model does not significantly change the resulting strain predictions.
3.3 Fetal Membrane Adhesion
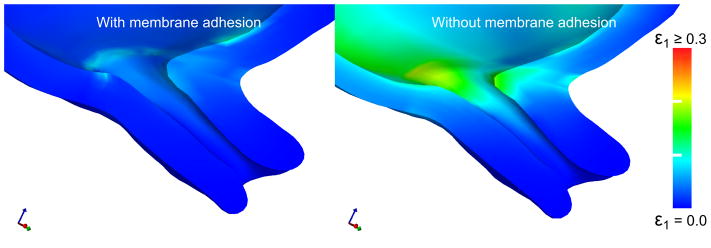
Load sharing occurs between the fetal membrane and the LUS when the membrane is fully adhered to adjacent LUS surfaces. With a NH membrane modulus of 10 MPa, effective stress levels on the uterus and cervix are under 1 kPa with adhesion at an IUP of 8.6 kpa. These levels are two orders of magnitude lower than the effective stresses in the no-adhesion case. Adhesion reduces the peak first principal strain level near the internal os by 60% under IUP loading (Figure 11). When membrane adhesion is enforced, high strains occur in the membrane over the entrance to the cervical canal, but membrane strains are reduced in regions of the membrane that are adhered to the uterine wall. With no membrane adhesion, such a phoneomenon does not occur. The degree of load sharing is highly dependent on the material properties of the fetal membrane. A parameterized study of adhesion with varying amniotic sac modulus (100kPa to 100MPa in 6 steps) shows that higher membrane stiffness leads to lower cervical strain (Figure 10).
Figure 11.
First principal strain in the cervix and LUS under the assumptions of an attached fetal membrane and a detached fetal membrane with no friction. In both cases, the IUP is set to the level experienced in a uterine contraction during labor. Detachment of the fetal membrane before delivery increases the mechanical load on the cervix, inducing deformation. Simulations use the random continuous fiber model for the cervix, with IUP=8.6 kPa (typical peak contraction value).
4. Discussion
In this work we detail a method to generate an anatomically accurate finite element model of the pregnant pelvis derived from MRI data. We explore the effects of geometry, cervical material properties, membrane properties, and membrane contact assumptions on the stress and strain generated in the cervix for two patients in their second trimester of pregnancy. The results illustrate that asymmetries of the uterus and cervix impact the magnitude and direction of stress and strain in the cervix. We also demonstrate that cervical material characteristics, particularly the collagen ultrastructure and tissue stiffness parameters, contribute significantly to the level of dilation in the cervix. Lastly, we have demonstrated that the fetal membrane contributes to the load-bearing of the uterine contents during pregnancy, where a fully-adhered fetal membrane results in lower mechanical loading in the cervix than in the case of a membrane which is free to slide in its contact with the decidua.
4.1 Anatomical Geometry
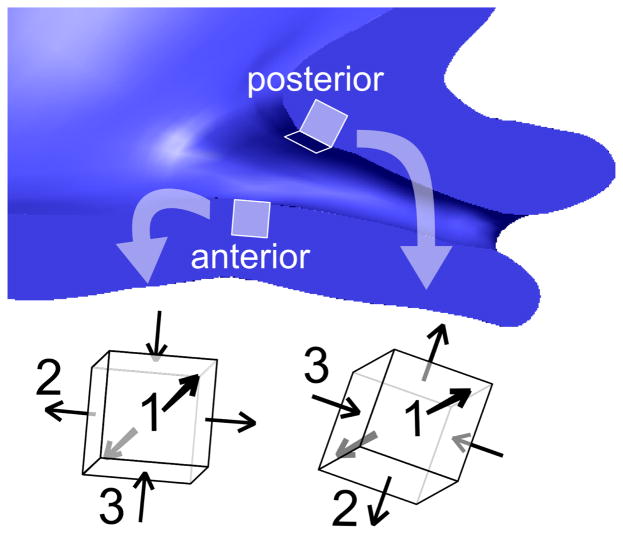
Our patient-specific models show a stress concentration at the level of the internal os of the cervix, matching findings from previous CAD-based models (House and Socrate 2006; House, Feltovich, et al. 2012). In the results presented here, this stress and strain concentration is not centered on the cervical opening, but is instead offset due to the asymmetry of the cervical canal and the uterus. Therefore, regions of high stress will vary between patients, and may vary between pregnancies. Interrogating an element at the posterior and at the anterior internal os (Figure 9) we find that both locations have a first principal strain in tension oriented circumferentially around the cervical canal (see anterior and posterior directions 1). The posterior element is subjected to more compression along the axis of the cervical canal (posterior direction 3) because of the acute angle between the cervix and the posterior part of the LUS wall. The anterior element experiences compression from the fetal membrane but it occurs in the radial direction from the canal to the exterior surface of the cervix (see anterior direction 3). This example illustrates how it is possible for non-obvious strain effects to arise from irregular or asymmetric geometry.
Figure 9.
Principal strain directions in two representative locations, one anterior and one posterior to the internal os. The directions of the principal strains depend on the orientation of the cervix within the pelvis due to physical interaction with the LUS.
4.2 Cervical Material Properties
Based on ex-vivo mechanical tests of human tissue specimens we know that the material behavior of the tissue is nonlinear, anisotropic, and time-dependent. It is currently unknown how each of these tissue material behavior complexities plays a role in keeping the cervix shut during pregnancy. By comparing results from the different model choices, we highlight the large difference in the cervical stress and strain for two neo-Hookean models, one based on tension data and the other on compression data, and three fiber composite models (Figures 7, 8). Our findings suggest that by incorporating cervical collagen directionality and dispersion we gain additional mechanical insight into the role of the collage ultrastructure in maintaining the fetus.
In our results we find that it is key to account for the distributed nature of the collagen fiber network. A cervical material model with a single fiber family with no dispersion creates high stress and strain concentrations in directions perpendicular to the fiber. Collagen dispersion creates tensile load carrying capability in multiple directions, as illustrated by the results for both continuous fiber models. The randomly oriented and ellipsoidal fiber models predict remarkably similar outcomes, with the addition of the preferred directionality not resulting in significantly lower strains. Further studies with additional material property and collagen ultrastructure measurements based on pregnant tissue samples need to be conducted to understand the exact role of the cervical collagen stiffness and dispersion during pregnancy.
4.3 Adhesion between the Chorion and Decidua
In normal pregnancy, the fetal membrane is firmly adhered to the lower uterus and cervix with the aid of the fetal fibronectin protein (van Baaren, Y, et al. 2013). However, in some cases of cervical shortening, lack of adhesion can be seen on vaginal sonography. To investigate how the adhesion of the fetal membrane to the uterus affects the stress and strain inside the cervix, we equipped our model with two distinct contact conditions: first, a no-slip tied contact interface, representing complete adhesion; and second, a frictionless sliding interface representing detached fetal membrane. Our model demonstrates that load sharing can occur between the fetal membrane and cervix in the case of the model with adhesion. Peak and average stress and strain levels were approximately 60% lower with adhesion acting between the membrane and uterus 11. These results demonstrate that the interaction between the cervix and membrane could play an important role in cervical shortening, and also that membrane adhesion is a key consideration when building finite element models of pregnancy.
Membrane stiffness and material model choice is another important factor to consider, because a stiffer membrane will result in lower cervical deformation (Figure 10). In the future, our simulations will incorporate material models based on new experimental data from mechanical testing of amnion (Mauri, Perrini, et al. 2014), which will better replicate the macroscopic mechanical response of the complex membrane microstructure (Mauri, Perrini, et al. 2013).
4.4 Limitations
All biomechanical models of pregnancy will require simplifying assumptions, but we would like to address some of ours that we believe to be the most important. First, In-vivo imaging of the abdomen produces geometry of an already loaded configuration, where imaging in an unloaded configuration is impossible. The reference configuration used to calculate stresses and strains therefore represent a loaded geometry, and the results presented in this paper should be viewed as an approximation or extrapolation. Regardless of this fact, the over-all trends of stress and strain should not be affected dramatically and our comparisons between different material models and loading conditions are valid. Additionally, it was not possible to measure the cervical material properties of the patients scanned in this study. For that reason, we used mechanical properties previously published by our group. We used non-pregnant properties for these simulations because we hypothesize that the cervix has not drastically softened at the gestational ages of our subjects. In animal models of pregnancy, the cervix softens gradually in early pregnancy and to a greater extent in late pregnancy (Timmons, Akins and Mahendroo 2010). We are currently working to understand the rate of softening in human cervix during pregnancy. Note also that our models are mechanical simulations of two specific pregnancies, so continued work on many additional patient scans is required before drawing conclusions about the effects of geometric and material factors on any patient population. Lastly, we have neglected any influence of the pubovescical, uterosacral, and cardinal ligaments, which may have some effect on the loading state. Our model includes the LUS, cervix, and the portion of the fetal membrane present in the lower uterus. The components accounted for in the model should create a representative stress and strain configuration in the cervix under the loading conditions of interest, but it is not designed to accurately reproduce deformation far from the cervix and the internal os.
5. Conclusion
We present here a method for incorporating realistic anatomical geometry, fetal membrane contact, IUP interaction, and cervical collagen ultrastructure and material behavior into a mechanical simulation of pregnancy. In this study, we calculate the stress and strain in the LUS and cervix under physiological IUP levels in anatomically derived finite element models for two pregnant patients. Capturing the irregular geometry of the LUS and cervix is an important part of an accurate modeling strategy. This study employs detailed cervix and LUS anatomy and analyzes the interaction between that anatomy and the fetal membrane at physiological IUP levels. We also included cervical material ultrastructure – based on what is known about collagen fiber organization in the tissue – by way of fiber composite material models and element-wise fiber directionality. We believe that these are the dominant factors affecting the mechanical stress and strain state within the cervix, particularly near the internal os. Key mechanical and structural factors for cervical performance are the specific geometry of the LUS and cervix, the mechanical properties of the cervix, the fetal membrane material and adhesion, and how these components collectively resist loading from IUP. When constructing biomechanical simulations of pregnancy, one ought not to neglect modeling membrane-uterus interaction, and one should carefully consider all relevant material model choices, because both of these decisions have a large impact on simulation outcome.
In future studies, our model will serve as a useful platform for analysis of mechanically-based interventions for preterm delivery. Additionally, it lays a necessary foundation before moving toward simulation of hypothesized biomechanical activation of cervical remodeling in pregnancy.
Acknowledgments
The authors acknowledge the support of the Office of the Provost at Columbia University and the Columbia University Medical Center Irving Institute for Clinical and Translational Research, which is supported by the National Center for Advancing Translational Sciences, National Institutes of Health through Grant No. UL1 TR000040. We would also like to express our gratitude to Noah Zweben, a mechanical engineering undergraduate student at Columbia University, for his hard work helping to construct the models.
Footnotes
Version 1.0. http://www.ccad.uiowa.edu/MIMX/Projects/IA-FEMesh
Version 2.1.0. http://www.febio.org
References
- Aspden R. Collagen organization in the cervix and its relation to mechanical function. Coll Relat Res. 1988;8:103–112. doi: 10.1016/s0174-173x(88)80022-0. [DOI] [PubMed] [Google Scholar]
- Ateshian GA. Anisotropy of fibrous tissues in relation to the distribution of tensed and buckled fibers. J Biomech Eng. 2007;129(2):240–9. doi: 10.1115/1.2486179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA. Modeling the matrix of articular cartilage using a continuous fiber angular distribution predicts many observed phenomena. J Biomech Eng. 2009;131(6):1–34. doi: 10.1115/1.3118773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson-Martin J, Zammaretti P, Bilic G, Schweizer T, Portmann-Lanz B, Burkhardt T, Zimmermann R, Ochsenbein-Kölble N. The Young’s modulus of fetal preterm and term amniotic membranes. Eur J Obstet Gynecol Reprod Biol. 2006;128(1–2):103–7. doi: 10.1016/j.ejogrb.2005.12.011. Available from: http://www.ncbi.nlm.nih.gov/pubmed/16442204. [DOI] [PubMed] [Google Scholar]
- Berghella V. Progesterone and preterm birth prevention: translating clinical trials data into clinical practice. Am J Obstet Gynecol. 2012;206(5):376–86. doi: 10.1016/j.ajog.2012.03.010. Available from: http://www.ncbi.nlm.nih.gov/pubmed/22542113. [DOI] [PubMed] [Google Scholar]
- Buhimschi CS, Buhimschi IA, Malinow AM, Weiner CP. Intrauterine pressure during the second stage of labor in obese women. Obstet Gynecol. 2004;103(2):225–230. doi: 10.1097/01.AOG.0000102706.84063.C7. [DOI] [PubMed] [Google Scholar]
- Cunningham FG, Leveno KJ, Bloom SL, Hauth JC, Rouse DJ, Spong CY. Williams obstatrics. Chapter 6. New York, NY: The McGraw-Hill Companies; 2010. Parturition. Available from: http://mhmedical.com/content.aspx?aid=6050050. [Google Scholar]
- Fernandez MJ, Vink JS, Yoshida K, Wapner R, Myers KM. Direct Measurement of the Permeability of Human Cervical Tissue. J Biomech Eng. 2013;135(2):021024. doi: 10.1115/1.4023380. [DOI] [PubMed] [Google Scholar]
- Frigo P, Lang C, Sator M, Ulrich R, Husslein P. Membrane thickness and PROM - High-frequency ultrasound. Prenat Diagn. 1998;18(4):333–337. [PubMed] [Google Scholar]
- Gan Y, Yao W, Myers KM, Hendon CP. An automated 3d registration method for optical coherence tomography volumes. Engineering in Medicine and Biology Society (EMBC), 2014 36th Annual International Conference of the IEEE; IEEE; 2014. pp. 3873–3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan Y, Yao W, Myers KM, Vink JY, Wapner RJ, Hendon CP. Analyzing three-dimensional ultrastructure of human cervical tissue using optical coherence tomography. Biomed Opt Express. 2015;6(4):1090–1108. doi: 10.1364/BOE.6.001090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashemi R. Mri : the basics 2010 [Google Scholar]
- Holzapfel GA. Nonlinear solid mechanics. Vol. 24. Wiley; Chichester: 2000. [Google Scholar]
- House M, Bhadelia RA, Myers KM, Socrate S. Magnetic resonance imaging of three-dimensional cervical anatomy in the second and third trimester. Eur J Obstet Gynecol Reprod Biol. 2009;144:S65–S69. doi: 10.1016/j.ejogrb.2009.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- House M, Feltovich H, Hall TJ, Stack T, Patel A, Socrate S. Three-dimensional, extended field-of-view ultrasound method for estimating large strain mechanical properties of the cervix during pregnancy. Ultrason Imaging. 2012;34(1):1–14. doi: 10.1177/016173461203400101. Available from: http://uix.sagepub.com/lookup/doi/10.1177/016173461203400101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- House M, McCabe R, Socrate S. Using imaging-based, three-dimensional models of the cervix and uterus for studies of cervical changes during pregnancy. Clin Anat. 2013;26(1):97–104. doi: 10.1002/ca.22183. Available from: http://dx.doi.org/10.1002/ca.22183. [DOI] [PubMed] [Google Scholar]
- House M, Socrate S. The cervix as a biomechanical structure. Ultrasound Obstet Gynecol. 2006;28(6):745–9. doi: 10.1002/uog.3850. Available from: http://www.ncbi.nlm.nih.gov/pubmed/17063451. [DOI] [PubMed] [Google Scholar]
- Iams JD. Clinical practice. Prevention of preterm parturition. N Engl J Med. 2014;370(3):254–61. doi: 10.1056/NEJMcp1103640. Available from: http://www.ncbi.nlm.nih.gov/pubmed/24428470. [DOI] [PubMed] [Google Scholar]
- Jabareen M, Mallik AS, Bilic G, Zisch AH, Mazza E. Relation between mechanical properties and microstructure of human fetal membranes: an attempt towards a quantitative analysis. Eur J Obstet Gynecol Reprod Biol. 2009;144(Suppl 1):S134–41. doi: 10.1016/j.ejogrb.2009.02.032. Available from: http://www.ncbi.nlm.nih.gov/pubmed/19282091. [DOI] [PubMed] [Google Scholar]
- Lanir YT. Constitutive equations for fibrous connective tissues. J Biomech. 1983;16(1):1–12. doi: 10.1016/0021-9290(83)90041-6. [DOI] [PubMed] [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: Finite Elements for Biomechanics. J Biomech Eng. 2012;134(1):011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas SA, Rawlins D, Weiss J, Ateshian GA. Febio theory manual. Musculoskeletal Research Laboratories, University of Utah; Salt Lake City, UT: 2014. [Google Scholar]
- Mahmoud H, Wagoner Johnson A, Chien EK, Poellmann MJ, McFarlin B. System-level biomechanical approach for the evaluation of term and preterm pregnancy maintenance. J Biomech Eng. 2013;135(2):021009. doi: 10.1115/1.4023486. Available from: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3705860&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauri A, Perrini M, Ehret AE, De Focatiis DSA, Mazza E. Time-dependent mechanical behavior of human amnion: Macroscopic and microscopic characterization. Acta Biomater. 2014:25–31. doi: 10.1016/j.actbio.2014.09.012. Available from: http://dx.doi.org/10.1016/j.actbio.2014.09.012 http://www.ncbi.nlm.nih.gov/pubmed/25240983. [DOI] [PubMed]
- Mauri A, Perrini M, Mateos JM, Maake C, Ochsenbein-Koelble N, Zimmermann R, Ehrbar M, Mazza E. Second harmonic generation microscopy of fetal membranes under deformation: normal and altered morphology. Placenta. 2013;34(11):1020–6. doi: 10.1016/j.placenta.2013.09.002. Available from: http://www.ncbi.nlm.nih.gov/pubmed/24070621. [DOI] [PubMed] [Google Scholar]
- Myers KM, Hendon CP, Gan Y, Yao W, Yoshida K, Fernandez M, Vink J, Wapner RJ. A continuous fiber distribution material model for human cervical tissue. J Biomech. 2015 doi: 10.1016/j.jbiomech.2015.02.060. Available from: http://www.sciencedirect.com/science/article/pii/S0021929015001529. [DOI] [PMC free article] [PubMed]
- Myers KM, Paskaleva AP, House M, Socrate S. Mechanical and biochemical properties of human cervical tissue. Acta Biomater. 2008;4(1):104–116. doi: 10.1016/j.actbio.2007.04.009. [DOI] [PubMed] [Google Scholar]
- Myers KM, Socrate S, Paskaleva A, House M. A study of the anisotropy and tension/compression behavior of human cervical tissue. J Biomech Eng. 2010;132(2):021003. doi: 10.1115/1.3197847. [DOI] [PubMed] [Google Scholar]
- Myers KM, Socrate S, Tzeranis D, House M. Changes in the biochemical constituents and morphologic appearance of the human cervical stroma during pregnancy. Eur J Obstet Gynecol Reprod Biol. 2009;144(Suppl 1):S82–9. doi: 10.1016/j.ejogrb.2009.02.008. [DOI] [PubMed] [Google Scholar]
- National Research Council. Preterm birth: Causes, consequences, and prevention. Washington, DC: The National Academies Press; 2007. [PubMed] [Google Scholar]
- Oyen ML, Calvin SE, Cook RF. Uniaxial stress-relaxation and stress-strain responses of human amnion. J Mater Sci: Mater Med. 2004;15(5):619–24. doi: 10.1023/b:jmsm.0000026102.85071.1f. Available from: http://www.ncbi.nlm.nih.gov/pubmed/15386971. [DOI] [PubMed] [Google Scholar]
- Paskaleva A. Biomechanics of Cervical Function in Pregnancy - Case of Cervical Insufficiency [dissertation] MIT; 2007. [Google Scholar]
- Pearsall GW, Roberts VL. Passive mechanical properties of uterine muscle (myometrium) tested in vitro. J Biomech. 1978 doi: 10.1016/0021-9290(78)90009-x. Available from: http://www.sciencedirect.com/science/article/pii/002192907890009X. [DOI] [PubMed]
- Timmons B, Akins M, Mahendroo M. Cervical remodeling during pregnancy and parturition. Trends Endocrin Met. 2010;21(6):353–361. doi: 10.1016/j.tem.2010.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Baaren GJ, YJ, Grobman WA, Bossuyt PM, Opmeer BC, Mol BW. Cost-effectiveness analysis of cervical length measurement and fibronectin testing in women with threatened preterm labor. Am J Obstet Gynecol. 2013;209(5):436.e1–436.e8. doi: 10.1016/j.ajog.2013.06.029. [DOI] [PubMed] [Google Scholar]
- World Health Organization. Preterm birth: Fact sheet no. 363. 2014 http://www.who.int/mediacentre/factsheets/fs363/en/. Online; updated 2014 Nov 17; cited 2015 Mar 11.
- Yao W, Yoshida K, Fernandez MJ, Vink RJ, Wapner JS, Ananth CV, Oyen ML, Myers KM. Measuring the compressive viscoelastic mechanical properties of human cervical tissue using indentation. J Mech Behav Biomed Mater. 2014;34(C):18–26. doi: 10.1016/j.jmbbm.2014.01.016. [DOI] [PubMed] [Google Scholar]
- Zilianti M, Azuaga A, Calderon F, Pagés G, Mendoza G. Monitoring the effacement of the uterine cervix by transperineal sonography: a new perspective. J Ultrasound Med. 1995;14(10):719–724. doi: 10.7863/jum.1995.14.10.719. [DOI] [PubMed] [Google Scholar]
- Zork N, Vink JS, Yoshida K, Cremers S, Jiang H, Ananth C, Wapner R, Kitajewski J, Myers KM. 746: The affect of parity on the distribution of collagen crosslinks in the human cervix. Am J Obstet Gynecol. 2014;210(1):S366–S367. doi: 10.1016/j.ajog.2014.09.036. Available from: http://linkinghub.elsevier.com/retrieve/pii/S0002937813018449. [DOI] [PMC free article] [PubMed] [Google Scholar]