Super-resolution reconstruction in frequency, image, and wavelet domains to reduce through-plane partial voluming in MRI

Abstract

Purpose:

To compare and evaluate the use of super-resolution reconstruction (SRR), in frequency, image, and wavelet domains, to reduce through-plane partial voluming effects in magnetic resonance imaging.

Methods:

The reconstruction of an isotropic high-resolution image from multiple thick-slice scans has been investigated through techniques in frequency, image, and wavelet domains. Experiments were carried out with thick-slice T2-weighted fast spin echo sequence on the Academic College of Radiology MRI phantom, where the reconstructed images were compared to a reference high-resolution scan using peak signal-to-noise ratio (PSNR), structural similarity image metric (SSIM), mutual information (MI), and the mean absolute error (MAE) of image intensity profiles. The application of super-resolution reconstruction was then examined in retrospective processing of clinical neuroimages of ten pediatric patients with tuberous sclerosis complex (TSC) to reduce through-plane partial voluming for improved 3D delineation and visualization of thin radial bands of white matter abnormalities.

Results:

Quantitative evaluation results show improvements in all evaluation metrics through super-resolution reconstruction in the frequency, image, and wavelet domains, with the highest values obtained from SRR in the image domain. The metric values for image-domain SRR versus the original axial, coronal, and sagittal images were PSNR = 32.26 vs 32.22, 32.16, 30.65; SSIM = 0.931 vs 0.922, 0.924, 0.918; MI = 0.871 vs 0.842, 0.844, 0.831; and MAE = 5.38 vs 7.34, 7.06, 6.19. All similarity metrics showed high correlations with expert ranking of image resolution with MI showing the highest correlation at 0.943. Qualitative assessment of the neuroimages of ten TSC patients through in-plane and out-of-plane visualization of structures showed the extent of partial voluming effect in a real clinical scenario and its reduction using SRR. Blinded expert evaluation of image resolution in resampled out-of-plane views consistently showed the superiority of SRR compared to original axial and coronal image acquisitions.

Conclusions:

Thick-slice 2D T2-weighted MRI scans are part of many routine clinical protocols due to their high signal-to-noise ratio, but are often severely affected by through-plane partial voluming effects. This study shows that while radiologic assessment is performed in 2D on thick-slice scans, super-resolution MRI reconstruction techniques can be used to fuse those scans to generate a high-resolution image with reduced partial voluming for improved postacquisition processing. Qualitative and quantitative evaluation showed the efficacy of all SRR techniques with the best results obtained from SRR in the image domain. The limitations of SRR techniques are uncertainties in modeling the slice profile, density compensation, quantization in resampling, and uncompensated motion between scans.

1. INTRODUCTION

Spatial resolution in magnetic resonance imaging (MRI) is limited by the constraints in MRI hardware, scan time limitations, and patient motion. Improved spatial resolution may be achieved at the cost of a reduced signal-to-noise ratio (SNR) and/or increased scan time. A trade-off is normally made between these factors.¹ Improvements in scanner hardware and software, and technologies like parallel imaging, have pushed the limits and enabled higher spatial resolutions, shorter acquisition times, and higher SNRs. Averaging at the acquisition level may be used to improve SNR, however, this increases the scan time and makes the scans more susceptible to motion. Other techniques like Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction (PROPELLER)² aim to improve resolution and SNR while reducing the susceptibility to motion by collecting k-space data in concentric rectangular strips rotated around the k-space origin. Nevertheless, most MRI acquisitions are still lengthy, susceptible to motion, and are acquired at relatively low resolutions to maintain high SNR.

In fact, 2D sequences with highly anisotropic voxel spacing (thick slices) are often used to achieve high SNR in T2-weighted (T2W) imaging and when imaging moving subjects like fetuses. The remarkably high SNR and in-plane resolution of these thick-slice scans make them visually appealing to the radiologist. The effect of partial voluming in the slice select direction is often overlooked as the images are only evaluated in the slice plane view clinically. Normally, these thick-slice scans are acquired in two or three different slice select directions to provide different radiologic views of the anatomy; however, all such scans are contaminated with partial voluming in the slice select direction, so should be used carefully despite their appealing 2D appearance. The use of these scans in computer-aided analysis is very limited due to their anisotropic resolution and significant through-plane partial voluming.

There has been an interesting body of work on postacquisition fusion of thick-slice anisotropic 2D MRI scans. This includes simple averaging of volumes, selective combination in the Fourier domain,³ wavelet fusion,⁴ and super-resolution reconstruction (SRR) in the image domain.^5–7 Super-resolution MRI closely follows the concepts of super-resolution reconstruction in digital image and video processing with techniques in frequency, image, and wavelet domains.⁸ In an early work, Greenspan et al.⁹ achieved enhanced MRI resolution in the slice-select direction using an iterative error back projection algorithm. Also very early on, the MRI community acknowledged that MRI data, which are collected (sampled) in the frequency domain (i.e., k-space), are inherently band-limited, so resolution enhancement is not achievable in-plane or in true 3D MRI acquisitions.^10,11 This has been explained by the fact that Fourier encoding excludes aliasing in the frequency and phase encoding directions.^6,9 Super-resolution, on the other hand, relies on aliasing in the signal encoding directions, as described by Candès and Fernandez-Granda.¹²

The advantage of specific data acquisitions for SRR in terms of lower acquisition time, higher SNR, and higher spatial resolution was considered theoretically and by experiments in Ref. 9 and more recently in Ref. 6 through detailed analysis and experiments. Plenge et al.⁶ showed that for certain imaging contrasts and sequences, such as T2-weighted MRI, SRR provides better trade-offs between SNR, acquisition time, and spatial resolution compared to direct high-resolution acquisitions. The relatively long repetition times required for T2W MRI make it less efficient to reduce slice thickness during acquisition rather than through SRR. For a more comprehensive review of image-based SRR methods in MRI, we refer to Refs. ⁵ and ⁷, and for a review and comparison of frequency and wavelet domain techniques we refer to Ref. 4. In this paper, we do not repeat or verify those experiments and findings. Instead, for the first time, we evaluate and compare all three classes of super-resolution MRI techniques through carefully designed phantom experiments to study the effect of partial voluming and verify our findings in a neuroimaging application to detect thin radial bands of white matter abnormalities in T2W brain MRI of pediatric patients diagnosed with tuberous sclerosis complex (TSC).

We argue that the most prominent application of SRR techniques is when the MRI data are acquired as thick 2D slices; which is often performed to maintain high SNR, for example, in fast spin echo imaging, and/or to minimize the acquisition time to reduce the effect of subject motion, for example, in single shot fast spin echo imaging in fetal MRI.^13–15 Super-resolution fetal MRI is an exemplary application of SRR in the image domain which includes models of “motion” incorporated into the SRR formulation. This formulation of motion-robust super-resolution MRI (Ref. ¹³) follows the concepts of forward modeling and inverse problem solution in super-resolution image reconstruction, and has been extended to other challenging applications like diffusion-weighted MRI,¹⁶ tongue MRI,¹⁷ and 4D thoracic MRI.¹⁸

The focus of this paper is on interpretation, evaluation, and comparison of SRR in frequency, image, and wavelet domains with an emphasis on correcting partial voluming effects in the slice select direction. We have considered motion-free scenarios to focus on resolution enhancement rather than motion estimation or correction. For this purpose, we focused on 2D fast spin echo (FSE) MRI, conducted physical phantom experiments with a controlled imaging protocol for quantitative evaluation, and examined in a clinical neuroimaging application for a realistic evaluation of the extent of partial voluming in routinely performed thick-slice MRI acquisitions. The results indicate that SRR can be used for postacquisition fusion of these scans for improved computer-aided analysis. An overview of the methods is presented in Sec. 2 and is followed by the results and conclusion in Secs. 3 and 4.

2. METHODS

2.A. Super-resolution reconstruction in the frequency domain

Thick-slice two-dimensional MRI scans, acquired at anisotropic spatial resolutions, often comprise the collection of high-frequency k-space samples in the phase and frequency encoding directions of each plane. The effective in-plane resolution of these scans is high, at nominal values between 0.4 and 0.8 mm, generating pixel sizes as small as 0.16–0.64 mm². There is, however, no high-frequency k-space sampling in the slice select direction in these scans. When multiple 2D scans with different slice select directions are available, the k-space data from those scans can be combined to provide a dense sampling of the k-space cube involving high-frequency k-space samples in different directions. Examples of these multiple 2D scans are orthogonal acquisitions with axial, coronal, and sagittal slice select directions,^3,9 and acquisitions with rotated slice select directions.¹⁹ The fusion of k-space data from these scans provides dense sampling of the center of k-space and covers high-frequency corners of the k-space as well, thus simultaneously improves SNR and spatial resolution in 3D.

Fusion of k-space data from multiple scans is performed through several steps. In the first step, the 2D k-space data (in k_x, k_y, z domain) are transformed into 3D k-space (k_x, k_y, k_z) domain by considering the slice profile. This operation corresponds to a 1D Fourier transform along the slice select direction in case of a sinc RF pulse. Applying this operation to each acquisition fills the k-space such that the center of the k-space is more densely sampled compared to the outer parts. This irregular sampling can result in blurring in the reconstructed image which can be corrected using a carefully chosen density compensation function (DCF).²⁰ Here, in this work, we calculate and apply a density compensation function suggested by Pipe and Menon²¹ as it results in sharp reconstructions. This method uses DCF suggested by Jackson et al.²² as the initial point and then iteratively optimizes the sharpness of the point spread function (PSF) in a given field of view (FOV) (rectangular in this work). The weight of each point (W_i) is calculated iteratively using the following equation that involves convolution with the Kaiser-Bessel function (C):

$${\displaystyle W_{i+1}=\frac{W_i}{W_i\otimes C}.}$$ (1)

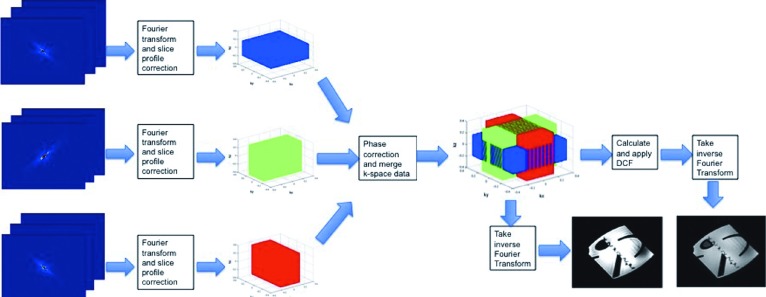
The iterations stop when the overall sampling density is between 0.99 and 1.01. The maximum number of iterations is set to be 100 but in our experiments the algorithm always stopped before reaching to the maximum iterations condition. When the 3D k-space is reconstructed, we use the inverse nonuniform FFT as suggested by Fessler and Sutton²³ in order to transform from 3D k-space (k_x, k_y, k_z) into the 3D image space (x, y, z). Figure 1 demonstrates this algorithm.

FIG. 1.

This figure demonstrates the steps of super-resolution reconstruction in the frequency domain. The k-space data of all 2D input scans are merged after initial Fourier transform, slice profile correction, and phase correction. A density compensation function is then calculated and applied to the merged k-space data. Inverse nonuniform FFT is applied to the corrected k-space data to generate the SRR image.

2.B. Super-resolution reconstruction in the image domain

Super-resolution reconstruction in image domain is established based on a forward model of 2D slice acquisition. A complete forward model for each slice includes subject motion, slice selection, blurring due to PSF of MRI acquisition, and sampling,^13,24 and can be written as follows:

$${\displaystyle {\mathbf{y}}_k={\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{S}}_k\mathbf{x}+{\mathbf{v}}_k,}$$ (2)

where y_k is the vector of voxels of the kth 2D slice, x is a vector of the high-resolution uniformly sampled volumetric image voxels, v_k is the noise, S_k is a matrix representing the slice selection operation which includes slice geometry (orientation) and slice profile, B_k is a matrix representing the PSF of the MRI signal acquisition process, and D_k is a sampling operation. Slice selection is performed through selective excitation by the application of a shaped RF pulse and a refocusing gradient for postexcitation rephasing.

The matrix operation S_k models the slice selection geometry involving slice orientation and slice profile. Note that the model in Eq. (2) is not limited to orthogonal scans. In fact, each slice in this model can have a unique geometry and an arbitrary orientation. For an arbitrary slice select direction, defined by the normal vector of the slice plane equation, the voxels of slice k, defined by vector $\overrightarrow{r}$, can be described by

$${\displaystyle \left|{\overrightarrow{\mu }}_{sk}.\overrightarrow{r}-s_{0k}\right|<\mathrm{\Delta }{s}_k/2,}$$ (3)

where ${\overrightarrow{\mu }}_{sk}$ is the normal vector of the slice plane which defines the slice orientation, s_0k is the slice origin in the scanner coordinate system, and Δs_k is the slice thickness. This corresponds to a rectangular slice profile generated by a sinc RF pulse envelope function.

SRR in image domain is formulated as the inverse problem of finding x in Eq. (2) given the acquired slices y_k. This inverse problem can be formulated and solved through maximum a posteriori (MAP) estimation to minimize an error norm function f(.) between observed and estimated slice acquisitions and a regularization term g(.) on the reconstructed image,

$${\displaystyle \hat{\mathbf{x}}=\underset{\mathbf{x}}{arg\hspace{0.17em}min}\left[\sum _{k=1}^{n}f\left({\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{S}}_k\mathbf{x}-{\mathbf{y}}_k\right)+\lambda g\left(\mathbf{x}\right)\right],}$$ (4)

where λ is the regularization weight that is chosen based on the number of input images and the super-resolution factor discussed below. Under normal conditions, when SNR>3, the noise v_k is considered to be additive, white, and Gaussian^6,25 and so will be the slice errors in the first term in Eq. (4). With a Gaussian distribution of error, f is defined to be the l₂-norm function based on maximum likelihood estimation.^6,13,24

The SRR inverse problem is naturally ill-posed. Regularization is thus used to solve an underdetermined problem in the MAP formulation in Eq. (4). The effect of regularization on reconstruction as a function of slice thickness (super-resolution factor) was studied in Ref. 24, in which it was shown that for SRR from three orthogonal scans no regularization was needed for a super-resolution factor of 2. On the other hand, when the problem was underdetermined due to higher super-resolution factors, regularization played an important role. The simplest assumption to regularize an underdetermined inverse problem is to assume a quadratic model for the image prior.²⁴ By assuming an exponential quadratic model of the probability density function of x, this translates to minimizing the l₂-norm of the reconstructed image gradient; however, this tends to generate over-smooth reconstructed images. To maintain image edge information and avoid over-smoothing, edge-preserving regularization using total variation (TV) and bilateral TV can be used.^14,18,26,27 These techniques maintain edges by promoting sparsity in the solution.

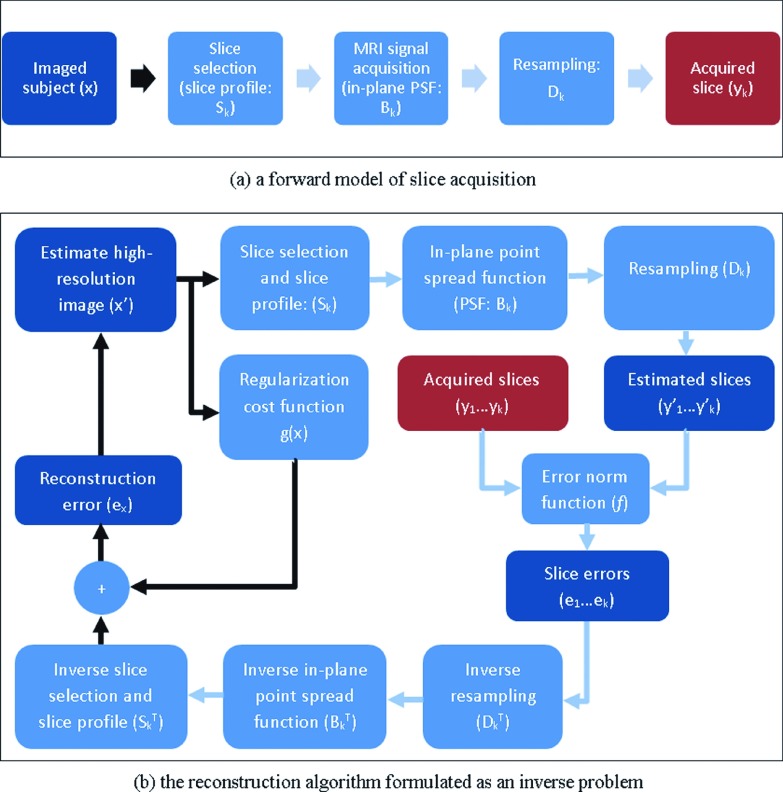
The matrices in Eq. (4) are large and typically sparse, so a closed-form solution to the inverse problem is prohibitive. The minimization is thus performed through numerical optimization by methods like gradient descent or conjugate gradient. The matrices D_k, B_k, and S_k and their transposes are implemented as corresponding image operators which are first applied sequentially to the estimated high-resolution image for the calculation of the slice error vectors, and their inverse is applied to the error vectors to generate an updated version of the reconstructed image. Figure 2(a) shows a forward model of slice acquisition and Fig. 2(b) shows the flowchart of the corresponding reconstruction algorithm. This algorithm iteratively finds a solution to the minimization problem in Eq. (4). For the experiments in this study, we chose λ = 0.05 and used a gradient descent algorithm for optimization.

FIG. 2.

This figure shows a forward model of 2D slice acquisition in (a) and the corresponding SRR algorithm in the image domain in (b). The arrows show the flow of the data, where the black arrows show the data in the high-resolution image space and the blue (or gray) arrows show the data in the space of the slices. Matrices are implemented as image operators. The inverse problem is solved through gradient descent minimization of the reconstruction error obtained from transformed slice errors and a regularization term.

2.C. Super-resolution reconstruction in the wavelet domain

Aganj et al.⁴ proposed a fusion approach based on 3D wavelet decomposition of orthogonal anisotropic MRI scans to reconstruct an isotropic high-resolution 3D image, and showed that it outperformed state-of-the-art frequency domain fusion methods. The idea is to decompose a MRI scan by a 3D wavelet transform with eight blocks denoted by LLL, LLH, LHL, …, HHH, in the XYZ coordinate system, where L stands for low-frequency, and H stands for high-frequency information in each of X, Y, and Z directions. An anisotropic scan with axial (Z) slice select direction has useful information in its **L blocks and virtually no information in its **H blocks. For a scan with coronal (Y) slice select direction, there is useful information in four *L* blocks and virtually no information in the *H* blocks. Instead of fusing original images, the wavelet-decomposed blocks with useful information are thus combined. The combined images are then used through inverse 3D wavelet transform to reconstruct a SRR image. For this process, the original scans are first resampled into a common isotropic-resolution space and then decomposed and recombined using the referenced approach in the wavelet domain.

Haar wavelets were used in Ref. 4 to account for a rectangular-shape slice profile. This translates to assuming a rectangular PSF in the slice select direction. In this study, we examined Haar and reverse biorthogonal wavelet basis functions as possible approximations of the slice profile. Obviously, one of the disadvantages of the wavelet domain SRR is the difficulty in modeling the slice profile by a wavelet basis function. Although the ideal slice profile can be modeled by the Haar wavelet, in practice the slice profile might deviate from the perfect slice profile. The original implementation of the wavelet domain image fusion can be obtained from http://www.nitrc.org/projects/wlfusion.

2.D. Slice profile

The slice profile is very much dependent on the RF pulse type for each MRI sequence. The slice profile generated by a shifted and truncated sinc pulse envelope function may be approximated by a rectangular function, and that of a truncated Gaussian may be approximated by a Gaussian function.¹³ When fast RF pulse types are used in fast MR acquisitions such as single-shot fast spin echo (SSFSE) and echo-planar imaging (EPI), the slice profile is compromised and approximation may pose errors. Under these conditions, an actual model of the slice profile may be computed by solving the Bloch equations by taking into account the RF pulse parameters and shape, or may be measured experimentally.²⁸

In image-based SRR, the slice profile and the in-plane PSF have been approximated by separable 3D Gaussian functions^{14,15,18,29,30} following Greenspan et al.⁹ who experimentally found Gaussian slice profiles to produce high-quality reconstructions and Noll et al.³¹ who found Gaussian functions to be good models of slice profile for through-plane interpolation. Jiang et al.³⁰ modeled the slice profile of a SSFSE sequence by a Gaussian function with full width at half maximum (FWHM) equal to the slice thickness. The in-plane PSF was approximated by a Gaussian with FWHM of 1.2× the in-plane spacing in Ref. 14 and by the convolution of two identical Gaussians with FWHM of 0.6× the in-plane spacing in Ref. 18. In this study, we conducted experiments with both rectangular and Gaussian slice profiles with FWHM equal to the slice thickness. A rectangular slice profile is described by Eq. (3) as a boxcar function and a Gaussian slice profile is achieved by multiplying a Gaussian kernel to the boxcar function.

2.E. Evaluation methods

Spatial resolution is the detail an image holds. By this definition, spatial resolution is not defined by the number of voxels or the spacing in an image, but it quantifies how close lines can be to each other and still be visibly resolved in the image. Partial volume effect is defined as the loss of apparent signal from small structures because of limited spatial resolution of the imaging system. If the size of the structure to be imaged is less than twice the FWHM resolution in x, y, and z dimensions of the imaging system, the resultant signal is underestimated. Higher spatial resolution decreases the partial volume effect as it better resolves the structures. Following these definitions, we use several methods to evaluate the effectiveness of SRR methods for resolution enhancement in this study.

The first step is visual assessment, which aims at detecting how well image features and structures can be visually resolved. Second, since a reference image with minimal partial voluming can be acquired in the controlled phantom study, we calculate three image similarity measures between each original or reconstructed image and the high-resolution reference image. These similarity measures are (1) peak signal-to-noise ratio (PSNR), (2) structural similarity image metric (SSIM),³² and (3) mutual information (MI).³³ These similarity metrics quantify the differences between the reference gold standard scan and the reconstructed images and thus provide an objective evaluation of SRR. It is interesting to correlate these metrics with perceptual evaluation of image quality with a focus on resolution. For this purpose, an expert blindly ranks each set of images in terms of delineation and detection of image structures and edges in different regions of interest.

Expert’s evaluation is performed by visualizing nine images (reference and different methods) simultaneously on a 27-in., 8-bit monitor using the visualization tool of the Computational Radiology Kit (crkit: http://crl.med.harvard.edu/software/CRKIT/index.php). Images are presented in NIfTI format with locked cursor in three planes, and the expert is asked to rank images from 1 to 8 based on their similarity to the reference image (1 is best, 8 is worst) with the option to rank images equally if they appear to have similar quality. The rankings are then averaged and correlated with the similarity metrics. We should note that various quantitative measures, such as perceptual evaluation models,^34,35 have been used to evaluate MR image artifacts, such as blur, aliasing, and noise; but the focus here was on resolution, therefore we design the phantom study to compare images with a high-resolution scan. Expert evaluation is similarly performed to compare reconstructed images to the high-resolution reference scan.

The third stage involves the evaluation of image intensity profiles, which are profiles of intensity values on lines defined on the image. This analysis shows how points and edges appear in the image. We compare all images and all intensity profiles to the reference image and its intensity profiles, respectively.

In the neuroimaging application, we use automatic segmentation and visual assessment to evaluate and compare the appearance of anatomic features and abnormalities on the original and reconstructed images. First, an expert radiologist blindly ranks the resampled original and SRR images based on the delineation of structural details and tissue boundaries in the out-of-plane (sagittal) views. Different images are displayed simultaneously on an 8-bit monitor with locked cursor using the visualization tool in crkit. The focus of this evaluation is on the resolution of images rather than signal-to-noise ratio, image artifacts, or sharpness, therefore the radiologist is asked to assess the delineation of tissue boundaries and narrow structures that extend in various directions (not just one direction) and provide an overall rank. Second, by blindly comparing the resampled original scans and the SRR image, an expert counts the number of missing radial lines in seven regions of interest for every case. This is performed in three axial planes, two coronal planes, and two sagittal planes and the average of missing structures is calculated.

2.F. Phantom imaging

Phantom imaging was specifically designed and performed for controlled quantitative evaluation and comparison of SRR methods and did not aim to replicate or simulate any clinical study. For American College of Radiology (ACR) phantom imaging, FSE MRI was performed with 32 channel body matrix and spine coils on a Siemens Skyra 3 Tesla scanner (Siemens, Erlangen, Germany) with repetition time (TR)/echo time (TE) = 15 490/90 ms, flip angle (FA) = 160, bandwidth (BW) =  195 Hz/pixel, echo train length (ETL) = 100, number of excitations (NEX) = 1, FOV = 320 × 320 mm², matrix size = 448 × 448, in-plane resolution of 0.7 mm, and slice thickness of 1.4 mm. In addition to thick-slice scans using these parameters, a high-resolution reference image was acquired with NEX = 4. The in-plane resolution of 0.7 mm was deemed appropriate to study the three 4 × 4 pinhole structures of the phantom with diameters and distances of 1.1, 1.0, and 0.9 mm. To study the effect of partial voluming and resolution enhancement, we positioned the ACR phantom in an oblique orientation in the scanner with approximate angles of 45° with respect to the scanner axes.

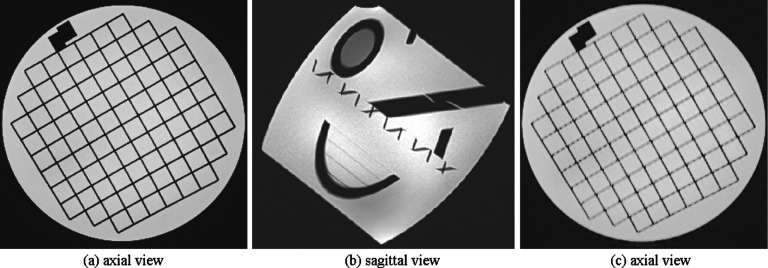
Figure 3 shows the rationale behind oblique placement of the phantom. If the ACR phantom is placed parallel to the table and imaged in the axial slice select direction, the edge of structures will be parallel to the slice select direction and thus the edges will be amplified and delineated with high SNR in the axial view (a). This is an ideal imaging scenario; however, it is not always possible to choose a slice select direction that is exactly parallel to the edge of anatomic structures. In fact, anatomic edges and tissue boundaries do not follow straight lines and often involve curves that are hard to follow in 3D. Therefore, to replicate more realistic anatomic imaging scenarios, we put the ACR phantom in an oblique orientation (b). This position results in an axial slice like (c) which has blurred edges due to partial voluming in the slice select direction. We acquired thick-slice FSE scans in the axial, coronal, and sagittal slice select directions with respect to the scanner coordinates. The high-resolution reference scan was acquired by choosing the slice select direction to be parallel to the structure edges, i.e., axial to the phantom axes.

FIG. 3.

This figure shows the rationale behind oblique imaging in this study. If the MR signal is averaged in the slice select direction through thick-slice acquisition in a direction that is parallel to the image edges and perpendicular to the fine structural details, image features will be delineated with high SNR (a). This is an ideal imaging scenario; however, it is not always possible to image in this direction, mainly because anatomic structures do not follow straight lines and often follow curves. To have a more realistic model, we put the ACR phantom in an oblique orientation in the scanner (b). This position results in an axial slice like (c) which has blurred edges due to partial voluming in the slice select direction.

2.G. Neuroimaging

The clinical neuroimaging protocol performed at our institution for the evaluation of brain abnormalities in patients diagnosed with TSC includes a sagittal T1-weighted 3D MPRAGE sequence with isotropic resolution of 1 mm as a reference for brain anatomy, a fluid-attenuated inversion recovery (FLAIR) sequence for the detection of brain lesions, and two thick-slice high-resolution T2W FSE MRI scans in the axial and coronal planes for the detection of brain lesions and subcortical white matter abnormalities typical to TSC. While the MPRAGE and FLAIR scans are used for overall evaluation of the brain anatomy and abnormalities, the high-SNR, high-resolution T2W scans play a critical role in the evaluation of small lesions and the narrow radial bands of white matter abnormalities in these patients.

We retrospectively applied SRR to T2-weighted MRI scans of ten pediatric patients with TSC who underwent clinical neuroimaging for the evaluation of brain abnormalities. The clinical MRIs for these patients were all performed on a Siemens Skyra 3 Tesla scanner using a 32-channel head coil. The T2-weighted FSE sequence was performed in the axial and coronal planes of the brain with typical values of TR/TE = 14 070/89 ms, ETL = 19, slice thickness = 2 mm, FA = 120, NEX = 2, BW = 195 Hz/pixel, FOV = 204 × 172 mm², matrix size = 512 × 218, and in-plane resolution of 0.4 × 0.6 mm. By using SRR, we reconstructed a T2-weighted image with isotropic resolution of 0.5 mm for each patient.

3. RESULTS

3.A. Qualitative and quantitative evaluations with the ACR phantom

Figures 4(a)–4(c) show a section of the ACR phantom that includes pinhole structures, of the three original FSE scans acquired in the axial, coronal, and sagittal slice select directions with respect to the scanner coordinate system. This section was chosen to be perpendicular to the long axis of the pin structures for best visualization. Partial voluming due to 1.4 mm slice thickness in the slice select direction, which was oblique to the axis of the structures (Fig. 3), obviously affects the appearance of the structures and makes it difficult to distinguish between the dots. This figure shows that the SRR methods provided much better structural details than the original images. It is observed that there are differences between the SRR images, but visually it is hard to decide which technique performed best.

FIG. 4.

Visual comparison of the original fast spin echo scans in three orthogonal slice acquisition directions in (a)–(c), with (d) and (e): image domain super-resolution reconstructed scans with rectangular and Gaussian slice profiles, respectively, (f): SRR in the frequency domain, (g) and (h): wavelet fusion with Haar and reverse biorthogonal wavelet basis functions, respectively, and (i) the original high-resolution scan used as the reference scan here. This comparison indicates that image fusion techniques can generate images that delineate fine structures of the images when compared to the original scans; but there are also differences between these techniques, for example, the pinhole structures are better highlighted in (e) when compared to (d) but image edges in the structure at the top of the image are better reconstructed in (d). It is hard to conclude which technique performed best.

Table I shows a quantitative comparison of the original scans and the reconstructed images resampled to the space of the reference image. The image similarity has been compared based on PSNR, SSIM, and MI similarity measures. The highest similarity value in each row has been highlighted in bold. The results indicate that all reconstruction methods generated scans that were more similar to the reference scan as compared to the original scans, and that the SRR in the image domain with rectangular slice profile and the wavelet fusion performed the best in terms of the similarity metrics. The similarity measures for SRR methods are, however, rather close to each other. In addition to technical differences, variations in image contrast in the reference image and the reconstructions can be regarded as a source of difference.

TABLE I.

Image similarity metrics: PSNR, SSIM, and MI computed between each original or reconstructed scan and the reference scan. The highest similarity value in each row has been highlighted in bold. The results indicate that all reconstruction methods generated scans that were more similar to the reference scan as compared to the original scans. Overall, the highest values were obtained from image-based SRR with a rectangular slice profile. The last three rows show the average expert rankings and the average rankings of features of types A and B in the images, respectively. The average expert evaluation suggests that SRR with Gaussian slice profile generated the best results.

	Axial	Coronal	Sagittal	SRR rect.	SRR Gauss	k-space	WL Haar	WL rbio
PSNR	32.22	32.156	30.654	33.265	32.321	32.381	33.07	33.122
SSIM	0.922	0.924	0.918	0.931	0.929	0.932	0.932	0.937
MI	0.842	0.844	0.831	0.871	0.866	0.861	0.863	0.861
Expert	6.1	6.4	6.9	2.6	2.1	3.4	2.3	2.3
Type A	5.3	5.5	7.2	1.5	1.3	4.0	3.0	3.0
Type B	7.0	7.3	6.8	3.5	2.8	3.0	1.8	1.8

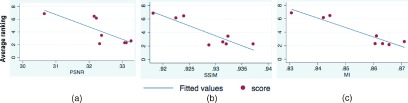
PSNR assumes a linear relationship between intensity values. MI is robust to nonlinear intensity relationships. While both measures quantify the relationships between intensity values, SSIM measures local structural similarity. We calculated the correlation of these similarity metrics with average expert rankings of the resolution of images in seven regions of interest that involved structures with different shapes, sizes, and angles, corresponding to (A) orthogonal views of the pin and grid structures, and (B) out-of-plane views of oblique edges and structures. The average expert rankings (ranging from 1 for best to 8 for worst image quality) have been shown in the last rows of Table I (average, A, and B). Figure 5 shows the scatter plots of average expert rankings with the similarity metrics, linear fitted lines, and their correlation coefficients. This figure shows that the MI similarity metric had the highest correlation coefficient with the expert rankings (CC = − 0.943).

FIG. 5.

Scatter plots, fitted lines, and correlation coefficient (CC) of average expert ranking of images versus similarity metrics (PSNR, SSIM, and MI). The highest correlation was observed between expert’s evaluation and MI. The PSNR showed the lowest correlation to expert’s perceptual ranking of images. The expert rankings suggest comparable perceptual resolution of all four image-based and wavelet-domain SRR methods and a marked improvement over original images resampled at higher resolution (a) CC=-0.776 (b) CC=-0.890 (c) CC=-0.943.

3.B. Evaluation with image intensity profiles

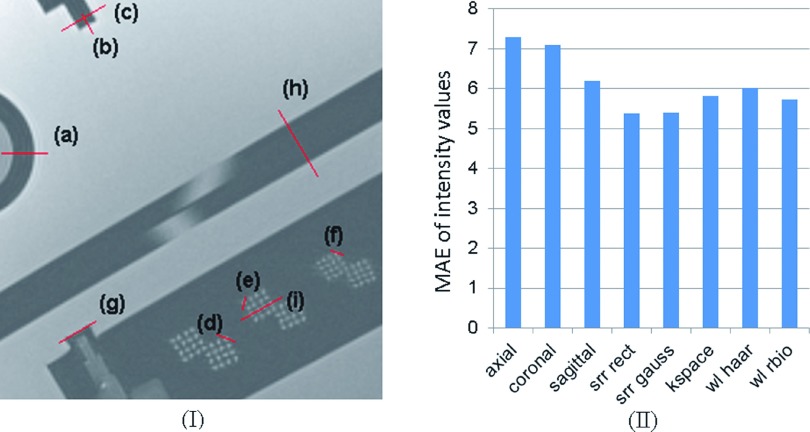
We defined nine lines to evaluate image intensity profiles on the original and SRR images and compared them to the reference image. These lines have been shown by (a)–(i) on a section of the reference image in Fig. 6(I). Figure 6(II) shows mean absolute error (MAE) of all intensity profiles computed between each image and the reference image. According to this analysis, all SRR techniques provided improvement over the intensity profiles of the original thick-slice scans, and the image-based SRR method, in average, seemed to generate the closest intensity profiles to the reference scan.

FIG. 6.

(I) visualizes the position of designated intensity profile lines (a)–(i) on the selected reference MR slice of the ACR phantom; the intensity profiles are shown in Fig. 7. (II) shows the MAE of intensity values between the reference intensity profile and the intensity profile of each image. This analysis indicates that image-based SRR performs the best among others.

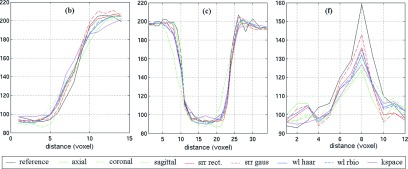
Representative intensity profiles of the original and SRR images and the reference image have been shown in Fig. 7. These lines show that the reference image always had the sharpest changes in intensity profiles over the image edges. This analysis also shows that depending on the type, direction, and size of the image edge structures, the original thick-slice scans may or may not delineate image details. This shows the importance of the slice select direction in which the partial voluming has the largest effect.

FIG. 7.

Intensity profiles of the selected lines (b), (c), and (f) shown in Fig. 6(I) computed over the reference image, three original scans (axial, coronal, and sagittal), and five reconstructed scans using SRR in image, frequency, and wavelet domains. The reference image intensity profile (black) shows the sharpest changes over actual image edges in all graphs; and the reconstructions normally follow it more closely than the original scans. The statistical analysis of MAE of intensity values between all lines and the reference (shown in Fig. 6) indicates that all SRR techniques resulted in improvements in intensity profiles compared to the original scans. This analysis also shows that image-based SRR performed slightly better than the other techniques, so was chosen to study partial voluming effect and its reduction in our neuroimaging application.

The analyses performed here show comparable performance of SRR techniques but also indicate that image-based SRR outperforms the frequency-domain and wavelet domain techniques. On the other hand, the computational burden of image-based SRR is significantly higher than the other techniques. Typical reconstruction times for one SRR image in our experiments was about 3 h, 1 h, and 10 min for image-domain, frequency-domain, and wavelet domain methods, respectively. It is possible to highly parallelize the slice error minimization process in the image-domain approach and significantly accelerate the reconstruction. Also, more efficient computations may be developed for density compensation, which is responsible for the computation burden of the frequency-domain approach. The wavelet-domain SRR, on the other hand, may be used to generate a SRR image in near real time before a scan session ends.

3.C. Application to neuroimaging of tuberous sclerosis complex

The axial and coronal T2-weighted MRI scans acquired clinically for TSC patients are both considered very useful due to their very high SNR and high in-plane spatial resolution of 0.4 × 0.6 mm². These scans allow diagnostic-quality assessment of the white matter and cortical lesions and especially the thin radially oriented subcortical and deep white matter hyperintensities that are typically observed in these patients. Although the radiologists only looked at the high-quality high-resolution planar views of these images, we retrospectively processed the images and looked at the out-of-plane views, which showed the effect of partial voluming as a result of 2 mm slice thickness.

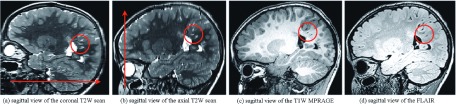
Figure 8 shows the sagittal views of the axial and coronal FSE scans of one of the cases in (a) and (b), and the closest MPRAGE and FLAIR slices in (c) and (d), respectively. It is observed that partial voluming had a strong effect on the visualization of the structures. The arrows in these images show the slice select direction and the circles highlight some of the thin structures, including the radial hyperintensity bands in the coronal scan that were visualized with details on this image because their main axis was parallel to the slice select direction. These structures are much better visualized by the T2W contrast than by the contrast in MPRAGE or FLAIR scans, but may become obscured by partial voluming in the slice select direction (b).

FIG. 8.

This figure shows the out-of-plane sagittal views of (a) the axial and (b) the coronal FSE scans of a TSC patient, (c) the corresponding sagittal view of a T1W MPRAGE scan, and (d) the corresponding sagittal view of a FLAIR scan of the same patient; the arrows show the slice select direction on the FSE scans; circles highlight some of the thin structures with axis that were almost exactly parallel to the slice select direction in the coronal FSE scan so could be appropriately visualized on the coronal FSE scan despite the 2 mm slice thickness. Image (b), on the other hand, shows that these thin structures may easily be obscured by partial volume effect when they are not parallel to the slice select direction. Although the details of the anatomy have been visualized on the high-resolution MPRAGE and FLAIR scans, many of these structures, such as the abnormal radial bands of white matter, are best visualized by T2W FSE scan.

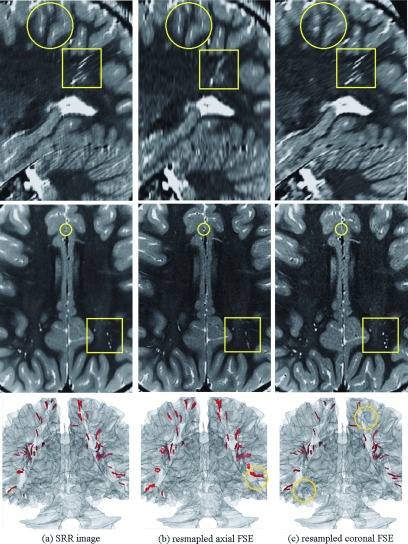
We reconstructed a high-resolution image at isotropic resolution of 0.5 mm³ from the axial and coronal FSE scans using the SRR technique. For comparison, we resampled both axial and coronal FSE scans to the space of the SRR image by using cubic b-spline interpolation. Sagittal and axial sections of these images have been shown in Fig. 9, where (a), (b), and (c) correspond to SRR, resampled axial, and resampled coronal images, respectively. Circles and squares highlight some of the differences between these images, caused by partial voluming. It is clearly observed in both axial and sagittal views of (c) that the radial lines (highlighted by squares) were separately visualized (with high SNR and contrast) on the coronal scan because their axes were exactly parallel to the slice select direction in this scan [also see Figs. 8(b) and 9(c)], but were mixed and obscured on the axial scan (b). Partial voluming, in fact, enhanced the contrast of these structures on the coronal scan. On the other hand, the structures highlighted by circles were visualized on the axial scan in (b) but were obscured on the coronal scan in (c).

FIG. 9.

From top to bottom, this figure shows sagittal and axial views and a 3D rendered segmentation of the brain and the hyperintensity radial bands of white matter abnormalities on (a) SRR image, (b) resampled axial FSE, and (c) resampled coronal FSE scans. The circles and squares highlight some of the differences between images due to partial volume effects in the slice select direction. Collectively visual comparison shows that thin structures can be easily obscured and overlooked in thick-slice FSE scans, but are better delineated in 3D using SRR by fusing thick-slice scans. The 3D rendering also shows how some radial lines were missed and some were visualized on the axial and coronal scans in (b) and (c), but were generally better segmented and visualized on the 3D rendered SRR image (a). The circles on the 3D rendered images highlight some of the structures that were missed or mixed due to partial voluming.

While some of the structures were visualized with fine details on the coronal image (c), such as the ones highlighted by the squares, others, such as those highlighted by circles, were obscured by partial voluming in this image. These structures were better visualized on the axial (b) and SRR (a) images. To evaluate the 3D visibility of all structures on the SRR and the original scans, we segmented the white matter tissue and used automatic intensity-based thresholding followed by connected component analysis to segment the hyperintense radial bands of white matter in the images. The last row in Fig. 9 shows triangular-mesh surface model rendering of the radial bands on a transparent surface model rendering of the white matter tissue. The comparison of this figure for the three images shows that many lines in the superior part of the brain were obscured and not detected on the coronal image (c), and many lines in the posterior part of the brain were obscured or mixed in the axial image (b). These have been highlighted by circles. On the other hand, the highest number of hyperintensity lines was detected and visualized on the SRR image (a).

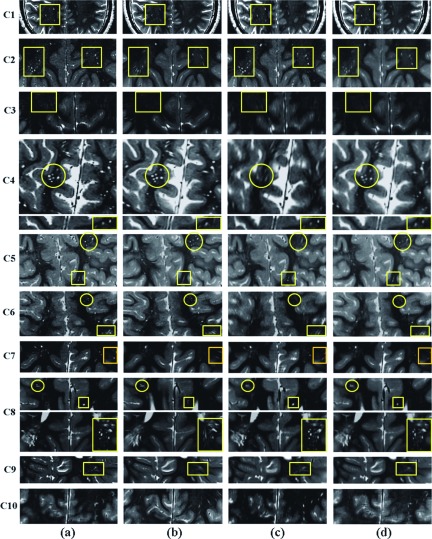
Figure 10 shows the results of SRR in all ten TSC patients. For each patient, the SRR image is shown in (a), the resampled axial image is shown in (b), the resampled coronal image is shown in (c), and the average of the resampled axial and coronal images is shown in (d) for comparison. We observed that SRR improved the resolution and reduced partial voluming effects in all cases except in C10. Uncompensated motion between scans in C10 compromised the quality of SRR. The squares in this figure highlight the structures that were visualized with anatomic details on the SRR but were severely affected by partial voluming effects in the axial image. Some of these structures were severely affected by partial voluming in both coronal and axial images, e.g., cases C6, C7, and C9. Circles, on the other hand, highlight some of the structures that were severely affected by partial voluming in the coronal image but visualized with anatomic details on the SRR image.

FIG. 10.

Selected slices of SRR image (a), and resampled axial (b), coronal (c), and the average of axial and coronal images (d) of ten TSC patients. This figure shows that the details of the anatomy and the radial hyperintensity lines of white matter abnormalities were much better delineated with SRR as compared to the original and average scans in 9 out of 10 cases. Uncompensated motion between the scans in C10 compromised the quality of SRR. The squares in this figure highlight the structures that were visualized with details on the SRR images but were severely affected by partial voluming effects in the axial images. Some of these structures were severely affected by partial voluming in both coronal and axial images. Circles, on the other hand, highlight some of the structures that were visualized with details on the SRR and axial images but were severely affected by partial voluming in the coronal image.

For visual perceptual evaluation of image resolution in the resampled out-of-plane views, an expert radiologist blindly ranked the original and the reconstructed images in the resampled sagittal view. The focus in this evaluation was on resolution rather than noise or image artifacts or sharpness; therefore, the radiologist evaluated the delineation of small structures and tissue interfaces in the images and ranked the images accordingly. The results, summarized in row 1 of Table II, showed that SRR images ranked first in all cases. The difference in scores between the SRR images and the resampled axial and coronal scans was statistically significant. In the second evaluation, an expert counted the number of obscured structures (due to partial voluming) in seven regions of interest in the axial, coronal, and sagittal planes of the SRR and resampled original images of each case. Average values are shown in row 2 of Table II. The difference between the average values for SRR and the original images was significant (at alpha threshold of 0.05).

TABLE II.

Statistics of radiologist expert blind ranking and “obscured structure” counting of the SRR and the original images of ten neuroimaging cases resampled at high resolution in the out-of-plane (sagittal) view. SRR consistently ranked first in all comparisons and showed the lowest average number of obscured structures. Paired two-tailed t-tests showed significant differences between the scores. The asterisk shows a statistically significant difference at p < 0.05.

Blinded expert evaluation	SRR	Axial	Coronal
Average ranking (1–3)	1∗	2.6	2.4
Average no. of obscured structures	1.11∗	2.28	2.53

4. CONCLUSIONS

The analysis, experimental results, and comparisons in this study show that all super-resolution image reconstruction techniques improved the appearance of image structures in the out-of-plane views of the original thick-slice scans. The analyses also show that the performance of the techniques depends on their parameters, including the models of PSF and slice profile in image-based SRR and wavelet fusion, and density compensation in k-space fusion. Previous studies showed that SRR is capable of improving the trade-off between resolution, SNR, and acquisition time.^6,19 We argue that the most prominent application of these techniques is when isotropic high-resolution imaging is not possible or optimal due to scan time limitations, due to contrast properties, or to avoid motion. The rationale behind calling these techniques super-resolution is that they follow the concepts of super-resolution reconstruction in image and video processing.⁸

Super-resolution, by definition, is considered extrapolation in the frequency domain, as compared to compressed sensing, which is considered interpolation in the frequency domain.¹² Accordingly, SRR in MRI is feasible through shifted sampling in the slice select direction,^29,30 and does not necessarily require the acquisition of orthogonal scans or scans with rotated slice select directions. Motion-robust super-resolution methods^13–15,36 are not restricted to any specific type of acquisition but rely on subject motion and motion correction to render the information-rich sampling required for high-resolution reconstruction. The acquisition of two or three scans with orthogonal slice select directions or multiple rotated slice stacks¹⁹ provides better coverage of the k-space but successful reconstruction is still dependent upon proper modeling of the slice profile in image-based SRR or density compensation in the frequency-domain approach. While more realistic or experimental models of slice profile and in-plane point spread function can be incorporated into the techniques in image and frequency domain, models of slice profile in the wavelet domain are limited to wavelet basis functions.

Image-based SRR seems to be the most flexible and generic framework for the fusion of 2D slice acquisitions as it may allow incorporation of complex models of motion, slice profile, slice geometry, and point spread function, but k-space SRR also shows great potential if precise PSF models and density compensation are achieved. While motion can be incorporated at the slice level in image-based SRR,^13,36 only scan-level rigid-body motion can be incorporated into the wavelet and k-space fusion approaches. Consequently, image-based SRR has been successfully applied to applications like fetal brain MRI, where robust estimation strategies could also be effectively used due to the relatively large number of images used in the reconstruction.^13,14 Image-based SRR has been extended to 4D MRI applications such as diffusion-weighted MRI (Refs. ¹⁶ and ²⁶) and 4D thoracic MRI.¹⁸

From an application viewpoint, while thick-slice MRI scans, such as T2-weighted FSE and FLAIR, may provide diagnostic-quality, appealing views of the anatomy with very high SNR, they should be used carefully, considering that small structures may easily get obscured by partial voluming in slices that may be 2 mm or thicker. Advantage of thick-slice scans is the time saving per sequence and their high SNR. Through averaging signal over the slice thickness, the thick-slice scans provide more information in each planar view for the radiologist assessment, for example, through projecting the direction of radial bands into the plane; but this is gained at the increased risk of missing small structures or abnormalities due to partial voluming. Super-resolution reconstruction enables thick-slice scans, acquired in orthogonal views, to be retrospectively fused to generate images with isotropic high spatial resolutions for improved computer-aided analysis. The use of high spatial resolution T2-weighted imaging through super-resolution or other high-resolution imaging techniques remains to be investigated in detail in quantitative evaluation of radial bands, lesions, and tubors in the classification and prognosis of TSC and other complex disorders, which may lead to improved strategies for the management and treatment of these disorders.