To transfer or not to transfer? Kinematics and laterality quotient predict interlimb transfer of motor learning

Abstract

Humans can remarkably adapt their motor behavior to novel environmental conditions, yet it remains unclear which factors enable us to transfer what we have learned with one limb to the other. Here we tested the hypothesis that interlimb transfer of sensorimotor adaptation is determined by environmental conditions but also by individual characteristics. We specifically examined the adaptation of unconstrained reaching movements to a novel Coriolis, velocity-dependent force field. Right-handed subjects sat at the center of a rotating platform and performed forward reaching movements with the upper limb toward flashed visual targets in prerotation, per-rotation (i.e., adaptation), and postrotation tests. Here only the dominant arm was used during adaptation and interlimb transfer was assessed by comparing performance of the nondominant arm before and after dominant-arm adaptation. Vision and no-vision conditions did not significantly influence interlimb transfer of trajectory adaptation, which on average was significant but limited. We uncovered a substantial heterogeneity of interlimb transfer across subjects and found that interlimb transfer can be qualitatively and quantitatively predicted for each healthy young individual. A classifier showed that in our study, interlimb transfer could be predicted based on the subject's task performance, most notably motor variability during learning, and his or her laterality quotient. Positive correlations suggested that variability of motor performance and lateralization of arm movement control facilitate interlimb transfer. We further show that these individual characteristics can predict the presence and the magnitude of interlimb transfer of left-handers. Overall, this study suggests that individual characteristics shape the way the nervous system can generalize motor learning.

if you exclusively learned to write with your dominant hand and have to write for the first time with your nondominant hand, you may write legibly. Such performance necessarily reflects an interlimb transfer of the learned skill. Understanding generalization of motor learning is important since it reveals the local or global nature of the underlying processes (Harris 1963; Poggio and Bizzi 2004; Seidler and Noll 2008; Carroll et al. 2014; Sarwary et al. 2015). By studying goal-directed upper-limb movements in sensorimotor adaptation paradigms, previous work showed that interlimb transfer is generally limited (Dizio and Lackner 1995; Criscimagna-Hemminger et al. 2003; Wang and Sainburg 2004a,b; Taylor et al. 2011; Joiner et al. 2013; Mostafa et al. 2014) although it can be absent (Martin et al. 1996; Kitazawa et al. 1997). This suggests that sensorimotor adaptation is largely specific to the effector, but it remains unclear why interlimb transfer varies across studies. In fact little is known about the factors that determine whether, and to what extent, adaptation to a particular condition generalizes to other conditions. In the present study, we considered that interlimb transfer may be determined by environmental conditions but also by individual characteristics.

Malfait and Ostry (2004) suggested that sensorimotor adaptation could generalize across limbs when task conditions allow the conscious perception of a perturbation/movement error. Berniker and Kording (2008) then suggested that generalization depended on the perceived source of motor errors, adaptation generalizing mostly if the error is assigned to a change in the environment. Sensory feedback, which is critical to perceive errors and adapt (Della-Maggiore et al. 2004; Scheidt et al. 2005; Hwang et al. 2006; Franklin et al. 2007; Sarlegna et al. 2010), may thus influence interlimb transfer. In fact, previous work showed that the availability of visual feedback was important for the generalization (Shabbott and Sainburg 2010; Taylor et al. 2013) and the interlimb transfer of visuomotor adaptation (Cohen 1973), which may be linked to a strategic processing of motor errors (Malfait and Ostry 2004; Berniker and Kording 2008; Taylor et al. 2011). One aim of the present study was thus to test whether different environmental conditions, with or without vision, influence the conscious perception of motor errors and interlimb transfer of adaptation.

While environmental conditions do seem to influence interlimb transfer, individual characteristics may also influence interlimb transfer. Currently, between-subject differences are often thought of as reflecting noise and discarded by averaging data from a group of participants, but heterogeneity of performance is inevitable as it reflects natural variations of genetic, environmental, and biological factors (Kanai and Rees 2011). Interindividual differences may be a key to understand the processes underlying sensorimotor adaptation. For example, Wu et al. (2014) recently showed that the more subjects were variable in a prelearning phase, the better they learned a novel arm-reaching task. Although variability can be seen as antagonistic to performance, this study provided evidence that increased variability can relate to better performance. The functional aspect of variability may be linked to the exploration of multiple solutions, at both brain activity and behavioral levels (Deco et al. 2011; Garrett et al. 2011). A second aim of the present study was thus to examine the possibility that interlimb transfer depends on individual characteristics such as movement kinematics, in particular variability of movement trajectory, or the conscious perception of motor errors. The laterality quotient (LQ) (Oldfield 1971) has also been shown to influence interlimb transfer of motor learning (Chase and Seidler 2008), and we investigated this issue first by testing the influence of the degree of handedness on interlimb transfer in right-handers and then by assessing interlimb transfer in left-handers.

Several studies showed that interlimb transfer can only be observed from the dominant arm (DA) to the nondominant arm (NDA) (Criscimagna-Hemminger et al. 2003; Galea et al. 2007) although transfer has also been found to be bidirectional (Wang and Sainburg 2004a; Sarwary et al. 2015). In the present study, we thus used a paradigm allowing us to assess, for each individual, transfer of sensorimotor adaptation from the DA to the NDA. We specifically addressed the interlimb transfer of adaptation to new limb dynamics by using a rotating platform that could generate Coriolis forces on the entire arm while subjects perform unconstrained arm reaching movements (Dizio and Lackner 1995).

MATERIALS AND METHODS

Experiment on Healthy Right-Handed Young Adults

Subjects.

Twenty subjects with no known sensorimotor impairment participated. Ten young adults (5 males, 5 females, mean age: 24.6 yr) were tested with direct vision of the limb and workspace throughout the experiment (VP group). Ten other young adults (5 males, 5 females, mean age: 23.3 yr) had no visual feedback, only proprioceptive feedback of hand movement as the room was in darkness (P group).

All 20 subjects were right handed (LQ ≥70%). The LQ, i.e., the degree of handedness, was assessed by asking subjects to complete the 10-item version of the Edinburgh Inventory (Oldfield 1971). This questionnaire assesses hand dominance in daily activities (e.g., writing, throwing), LQ ranging from −100 (left handed) to 100 (right handed). LQ was 80 ± 10% on average for the P group and 87 ± 11% for the VP group.

All subjects had normal or corrected-to-normal vision and were naive to the purpose of the experiment. Participants gave their informed consent before the study, which was approved by the Institutional Review Board of the Institute of Movement Sciences and performed in accordance with the ethical standards of the Declaration of Helsinki.

Experimental setup.

Participants sat in a bucket seat (adapted from a car seat) at the center of a motorized rotating platform and were asked to reach toward flashed visual targets (Fig. 1A). An adjustable headrest was used to restrain the head. On a horizontal board, at waist level, a visual and tactile landmark indicated the starting hand position. Visual targets were low-intensity red light-emitting diodes (3 mm in diameter). Three targets were positioned on a 37-cm radius circular array at 0° (straight-ahead), 20° (to the right), and −20° with respect to start position.

Fig. 1.

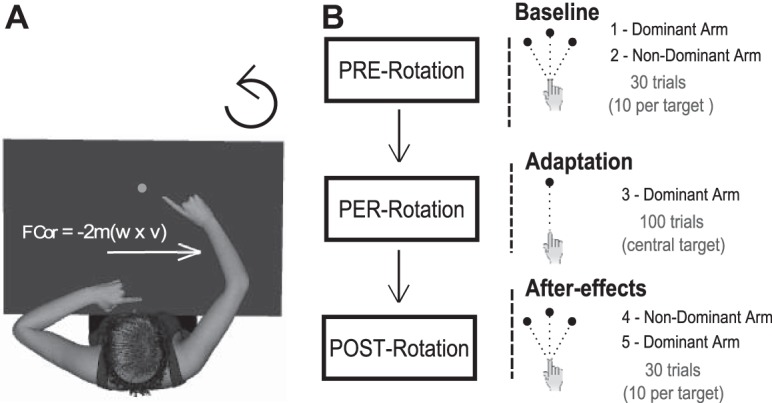
A: experimental setup. B: illustration of the experimental protocol.

Infrared active markers were taped to the right and left index fingertips whose positions were sampled at 350 Hz using an optical motion tracking system (Codamotion cx1 and MiniHub; Charnwood Dynamics, Leicestershire, UK). As in Sarlegna et al. (2010), the experimenter controlled the tracking system, the motorized platform, and the presentation of the visual targets from an adjacent room by using a customized software (Docometre) governing a real-time acquisition system ADwin-Pro (Jäger, Germany).

Procedure.

At the beginning of each trial, participants had to actively position their hand at the starting location (Fig. 1A). They were asked to reach as fast and accurately as possible with their hand toward the visual target that was illuminated for 0.3 s. No explicit instructions were given with respect to hand path. However, participants were required to “reach in one movement” and not to correct after their finger contacted the horizontal board. At 1.6 s after trial onset, an auditory 100-ms tone informed the subject to go back slowly to the starting location. At 7.4 s after trial onset, a 600-ms tone signaled to the participant that the trial had ended and that the next trial would start immediately. Peak velocity (PV) of the targeted, outward reaching movement was ∼10 times greater than that of the backward arm movement toward the start position. All participants were familiarized with the task during a preliminary phase.

The experimental session consisted of three phases (Fig. 1B).

1) PRE-rotation test (baseline): participants executed 30 reaching movements with the DA then with the NDA (10 trials per target for each hand, in a pseudorandom order which was similar for all 20 participants) while the platform remained stationary, providing baseline reaching performance in the normal force field. After the PRE-test, the rotating platform was accelerated in 80 s up to a constant velocity of 120°/s, i.e., 20 rpm.

2) PER-rotation (adaptation) phase: participants performed 100 movements with the DA to the central target while the platform was rotating counterclockwise at 120°/s, generating clockwise Coriolis forces on the moving limb. Coriolis forces (F_cor; see Dizio and Lackner 1995) are the product of the arm mass (m), platform's angular velocity (w) and tangential arm velocity (v) according to the equation: F_cor = −2m(w × v). After the adaptation phase, the rotating platform was slowed to a stop within 80 s.

3) POST-rotation test: once the platform was stationary, participants executed 30 reaching movements with the nonexposed NDA first and then with the DA (10 trials per target for each hand). The first presented target was the central one (then left, right. . .).

Participants were instructed not to move any body part, including their head and opposite arm, during or between trials, and an infra-red camera allowed continuous monitoring of subject's behavior. A 60-s delay was used between the end of the platform's acceleration and deceleration phases and the first reach trial to allow the vestibular semicircular canals to return to their resting discharge frequency. The PER-rotation test lasted ∼20 min, the complete reaching task lasting ∼45 min.

At the end of the experimental session, the subject, still in the bucket seat, filled a questionnaire that combined open-choice, multichoice, and forced-choice questions related to awareness and credit assignment of errors. We wished to determine whether subjects consciously perceived errors in movement trajectory during the first trials of the PER-rotation phase, asking first “Did you feel something in particular in the first trials of the PER-rotation phase?” and “Were you surprised by your performance in the first trial of the PER-rotation phase?” If the subject talked about motor errors, he or she was considered to be aware of his or her errors; otherwise he or she was not. Then we showed a top view of each subject's arm trajectory in the first trial of the PER-rotation phase and asked subjects to fill a questionnaire to determine whether errors were assigned to internal and/or external factors. We thus asked, in a counterbalanced order, “Did you associate the errors you made early in the PER-rotation phase to external factors?” and “Did you associate the errors you made in the PER-rotation phase to yourself (e.g., internal factors such as fatigue, inattention. . .)?” Subjects here had to answer “Strongly disagree,” “Somewhat disagree,” “Somewhat agree,” or “Strongly agree.” At last subjects were asked to circle whether errors were more associated to “Internal” or “External” factors.

Kinematic data analysis.

Data were analyzed using Matlab (Mathworks, Natick, MA). A few trials (1.6%) had to be discarded because they were not properly performed by the subjects or were corrupted by noise. Position data from the markers on the right and left index fingertips were low-pass filtered with a dual-pass, no-lag Butterworth (cut-off frequency: 8 Hz; order: 2). Movement onset was defined as the first time tangential hand velocity reached 3 cm/s and movement offset as the first time hand velocity dropped below 3 cm/s.

Initial direction was computed as the angle between the vector from the start position to the target position and the vector from the start position to the hand position at 150 ms after movement onset. Initial movement direction at 150 ms was considered the most critical dependant variable because it mostly reflects the initial motor plan, before online corrective feedback loops substantially influence movement execution (Prablanc and Martin 1992; Saunders and Knill 2003; Sarlegna et al. 2004; Franklin and Wolpert 2008). Besides, 150 ms corresponded to the mean time (averaged across healthy right-handed subjects) of PV, and therefore, the time at which the magnitude of the Coriolis forces acting on arm movements is maximum during platform rotation. As in Dizio and Lackner (1995), we computed the lateral endpoint error, i.e., the perpendicular deviation (in cm) between the index fingertip at movement end and the straight line connecting the starting point (i.e., movement onset) to the target, and the maximum perpendicular deviation (in cm) between the index fingertip and the straight line connecting the hand position at movement onset and the target (Malfait and Ostry 2004). For all the measures, we assigned positive values to rightward deviations and negative values to leftward deviations.

To assess adaptation and interlimb transfer, we employed a proceduresimilar to that used by Dizio and Lackner (1995). First, to assess adaptation of the DA, we compared the mean of the 10 trials of the PRE-test (baseline) with the first two trials and the last trial of the PER-rotation phase (to observe the effects of the velocity-dependent force field and the final adaptation, respectively) and the first two trials of the POST-test (to observe an aftereffect and reaadaptation) for movements toward the central target (0°). To assess whether adaptation differed between groups, we fitted exponential curves to each individual data of initial direction y = a × e^−bx + c, in which a represents the amplitude of the initial error, b the time constant, and c the offset. To assess interlimb transfer of DA adaptation to the NDA, we compared the 10 NDA movements toward the central target (0°) of the PRE-test to the first NDA movement of the POST-test for movements toward the central target.

The level of adaptation was assessed for both initial direction and lateral endpoint error using the formula (first adaptation trial − final adaptation)/(first adaptation trial − baseline) with final adaptation referring to the mean of the last 10 trials of the adaptation phase and baseline referring to the mean of the 10 trials towards the central target in the preadaptation phase.

Statistical analysis.

Repeated-measures ANOVAs were used to assess the significance of DA adaptation and interlimb transfer. To assess DA adaptation, we conducted 6 × 2 [PHASE (PRE-, PER-Initial, PER-2nd trial, PER-Final, POST-Initial, POST-2nd trial) × VISION (P and VP groups)] ANOVAs, and to assess interlimb transfer, we used 2 × 2 [PHASE (PRE-, POST-Initial) × VISION (P and VP groups)] ANOVAs.

All data had a normal distribution as verified with the Kolmogorov-Smirnov method. The variance homogeneity across experimental groups was also confirmed using Levene test. Newman-Keuls tests were used for post hoc analysis. For all tests, the significance threshold was set at 0.05.

The transfer value of each subject was defined using the formula $t_i=\frac{X_i-{\mu }_i}{{\text{SE}}_i}$, where, for each subject i, X is the initial direction of the first POST-test NDA trial, μ_i is the initial direction averaged across NDA baseline movements, and SE is the standard error of the baseline. We used the standard error instead of the standard deviation as it is more appropriate for relatively small samples (Chin and Lee 2008). We used the transfer value to assess the impact of different factors on transfer (i.e., the 3 variables used in the classification model). As data analysis showed significant interlimb transfer with a mean leftward shift (i.e., the values of the aftereffects were negative), we multiplied for ease of understanding the t-scores by −1 so that any increase in the t-score would correspond to an increase in interlimb transfer. The aftereffects on the DA were computed with the same method.

Classification model.

A linear discriminant analysis, a form of classification model, was used to separate subjects in a qualitative manner according to their aftereffects on the NDA. Two classes were considered: “Transfer” and “No transfer.” Each subject was assigned to a class based on the difference in NDA initial direction between PRE- and POST-tests. Specifically, the 10 NDA movements toward the central target in the PRE-test were used to compute a 99% confidence interval (CI): $C{I}_i=\left[{\overline{x}}_i-t_{\alpha }\frac{{\sigma }_i}{\sqrt{n}};\hspace{0.17em}{\overline{x}}_i+t_{\alpha }\frac{{\sigma }_i}{\sqrt{n}}\right]$, where for each observation i, x̄ designates the mean of the baseline, t_α is the value of the Student distribution for a 99% CI in function of the degree of freedom α, σ is the standard deviation of the mean of the baseline, and n is the number of trials. Based on Dizio and Lackner (1995), we expected a negative shift in NDA initial direction; thus, if the initial direction of the first NDA movement of the POST-test fell below the lower bound of the CI, the subject was assigned to the “Transfer” class. If the initial direction fell within the CI or above the upper bound, the subject was assigned to the “No transfer” class.

Three variables were eventually selected (see below) to perform the linear discrimination: variability (standard deviation) of the mean initial direction across the last 10 trials in the PER-rotation phase, mean PV across all 100 trials in the PER-rotation phase, and LQ (Oldfield 1971).

A fivefold cross-validation method was used to assess the accuracy of the classification model, i.e., 80% of the observations was used to build the model (training dataset, n = 16) and predict the remaining 20% of the observations (test dataset, n = 4) in an iterative manner until all the observations were tested once. Thirty iterations of the fivefold cross validation were run to have a better estimate of the model performance.

To evaluate the efficiency of the model, a receiver operating characteristic (ROC) curve was employed. A ROC curve displays the probabilities in term of sensitivity and specificity of the model at each decision threshold (i.e., a value ranging from 0 to 1 above which the observation is assigned to the class 1). In our study, sensitivity [true positive (TP) rate] measured the proportion of actual “Transfer” subjects who are correctly classified by the model. Specificity [true negative (TN) rate] measured the proportion of actual “No transfer” subjects who are correctly classified. FP and FN are the false positive and negative rate.

$$\text{sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}}\times 100\%$$

$$\text{specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}}\times 100\%$$

Selection of the variables.

The variables used for the linear discrimination analysis were selected among a set of 57 variables with a backward stepwise method, i.e., by eliminating the least necessary variable one by one (and by evaluating the resulting errors through cross validation). As the backward stepwise method cannot be performed if there are more observations than variables, the selection was applied first on multiple sets of 9 to 12 variables. For each set, we kept the variables that contributed the most to the prediction of transfer. We reiterated the selection until we got the 12 best variables.

The variables were the LQ and kinematic variables. In the adaptation phase, the kinematic variables representing the errors resulting from the force field (i.e., initial direction at PV and at 150 ms, maximum perpendicular deviation, lateral endpoint) were determined across the first and last 10 trials, as well as across the 100 trials, while other variables were determined across the 100 trials, except for the area under the curve (first 10 and 10 last only).

1) From the adaptation phase

i) The variability and the mean of lateral endpoint error, PV, maximum curvature, initial direction at PV, and at 150 ms.

ii) The mean of reaction time, movement time, difference in PV between the PER-rotation and the NDA POST-rotation phase, area under the curve with respect to a straight trajectory (first 10 and 10 last trials only), perpendicular deviation throughout the trajectory, peak acceleration, and time to PV.

iii) Amplitude and slope of the exponential fit of the adaptation curve (i.e., unknown a and b).

2) From the baseline, the mean and standard deviation of maximum perpendicular deviation, initial direction of the DA and NDA at lateral endpoint, PV, and 150 ms (10 trials).

3) From the NDA POST-rotation phase, the reaction time, movement time, time to PV, and PV of the first trial.

To determine whether the variables used for the linear discrimination analysis could determine the amount of interlimb transfer, we performed a multiple regression analysis using the transfer value (see Statistical analysis) as the dependent variable.

Experiment with Left-Handed Individuals

We tested left-handers to both test the robustness of the model on new data and test whether our findings on right-handers were valid for right-handers and left-handers.

Subjects.

Nine young left-handed individuals (7 males, 2 females, mean age: 23.4 ± 3 yr old) performed the experiment in darkness, like the P group of the main experiment. Mean LQ was −70 ± 37%. One subject was a self-declared left-hander, who preferred to write or draw with the left hand but had a LQ of +10%. Participants gave their informed consent before the study, which was approved by the Institutional Review Board of the Institute of Movement Sciences and performed in accordance with the ethical standards of the Declaration of Helsinki.

Procedure.

The experimental procedure was the same as for the right-handed subjects of the P group except that subjects were tested with a clockwise platform rotation. This was done so that the biomechanical consequences of the perturbation were matched for left- and right-handers. The left DA was tested during the adaptation phase while interlimb transfer was tested as the difference in right NDA performance between trials immediately before and after the PER-rotation phase. Apart from the arm used, data analysis was similar for right- and left-handers. For the sake of understanding, results of left-handers were flipped so that they corresponded to the other right-handed subjects.

RESULTS

Adaptation of the Right DA to the Novel Force Field

A classical pattern of adaptation was observed in the right-handed group. Figure 2, A and B, shows that DA movements were generally straight and accurate in both groups in the PRE-test. However, the counterclockwise rotation generated Coriolis forces that clearly perturbed, rightward, the hand path on the initial trial of the PER-rotation phase in the VP and P groups. Indeed, when considering only movements toward the central target, a 2 × 6 {VISION (VP, P) × PHASE [PRE-test (mean of 10 trials), PER-Initial, PER-2, PER-Final, POST-1, and POST-2]} ANOVA only showed an effect of the experimental PHASE on initial direction [F(5,90) = 6.7; P < 0.0001], revealing that initial direction was substantially shifted to the right compared with baseline (by 6.4° on average across groups, Fig. 2, C and D). Also, when subjects first encountered the biomechanical consequences of the platform rotation on the arm movement, visual feedback was used to adjust online the last portion of the arm trajectory compared with subjects without vision. Indeed, a 2 × 6 ANOVA on the lateral endpoint error revealed an effect of VISION [F(1,18) = 21.2; P < 0.001], PHASE [F(5,90) = 36.0; P < 0.001], and an interaction [F(5,90) = 3.1; P < 0.02; Fig. 2D], which revealed that endpoint error in the first two trials of the PER-rotation phase differed from baseline in the P group (mean shift of the first trial = 4.6 cm; P < 0.001) but not in the VP group (P = 0.24). As trials were repeated, subjects gradually compensated for the rightward deviation to restore straight, accurate movement performance. The t-tests for independent samples did not reveal any significant difference in adaptation between the P and VP groups for any of the three parameters of the exponential fit of the initial direction data (see materials and methods).

Fig. 2.

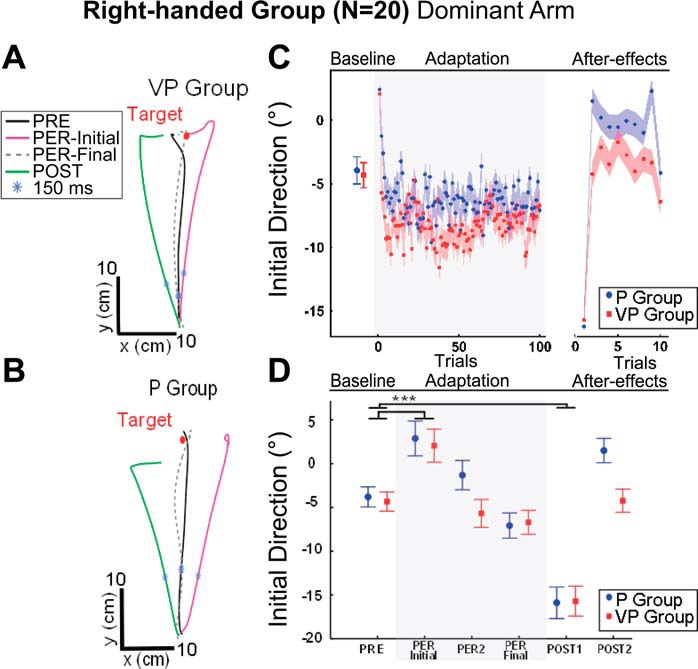
Adaptation of the dominant arm (DA) movements toward the central target. A and B: top view of DA hand paths for a representative subject of the vision-proprioception (VP) group (A) and proprioception (P) group (B). C: mean initial direction (degree) of the central target averaged for the PRE-test (baseline) for each trial across the adaptation phase and the POST-test for the P (blue) and VP (red) groups. Shaded blue and red areas represent means ± SE. D: mean initial direction (degree) for the P (blue) and VP (red) groups in the PRE-test (baseline); the 1st, 2nd, and last trial of the PER-rotation phase; and the 1st and 2nd trials of the POST-test. For each PRE-test, all 10 trials were averaged to obtain a baseline reference. Error bars represent means ± SE. *P < 0.05, ***P < 0.001, significant difference.

Once the rotation stopped, and after the left NDA was tested in the normal force field, substantial aftereffects were observed on the right DA. In the first trial of the POST-test, toward the central target, DA trajectory differed from baseline with an 11.8° shift in initial direction and a 4.6 cm shift in lateral endpoint on average across groups. Similar findings were observed when initial direction was computed at 150 ms or at PV. Overall, PV and movement time was similar in PRE-, PER-, and POST-tests and across experimental groups (mean in P group = 2.4 ± 0.9 m/s and 423 ± 16 ms; mean in VP group = 2.6 ± 0.9 m/s and 429 ± 16 ms).

We tested different target directions in PRE- and POST-tests to assess whether the force-field adaptation of DA movements toward the central target generalized to movements performed in other directions. For the lateral, right, and left targets, separate 2 × 3 ANOVAs {VISION (VP, P) × PHASE [baseline (mean of 10 trials), POST-1 and POST-2]} on initial direction revealed only a significant effect of experimental PHASE [left target: F(2,36) = 11.0; P < 0.001; right target: F(2,36) = 4.3; P < 0.05]. Post hoc analyses revealed that for the left target, initial direction in the first trial of the POST-test tended to differ (P = 0.06) from baseline (mean shift = −3.0°) and for the right target, the shift was significant (mean = −2.6°; P < 0.05), indicating intralimb generalization (across movement directions).

Interlimb Transfer of Dynamic Adaptation to the left NDA

Figure 3, A and B, shows how movement trajectory of the left NDA was influenced by adaptation of the right DA movements: a 2 × 2 [VISION (VP, P) × PHASE (PRE-, POST-test)] ANOVA showed that NDA initial direction differed between baseline and the first trial of the POST-test by −2.8° [F(1,18) = 5.6; P < 0.05], as illustrated on Fig. 3C. There was no significant VISION effect [F(1,18) = 0.1; P = 0.76] and no significant interaction [F(1,18) = 0.0; P = 0.99], indicating that interlimb transfer of force-field adaptation was not influenced by vision. It should be noted that the mean difference POST-PRE in initial direction was negative (leftward shift), which is consistent with a representation of the limb dynamics in extrinsic coordinates. Also, the mean interlimb transfer represented 20% of the mean aftereffect observed on the DA movements toward the central target (Fig. 3D). We found no significant aftereffects on initial direction for the left [F(1,18) = 0.61, P = 0.44] and right targets [F(1,17) = 0.01, P = 0.90], indicating that adaptation of DA movements toward a single target only generalized, to a significant but limited extent, to NDA movements toward the same target (and to DA movements toward different targets).

Fig. 3.

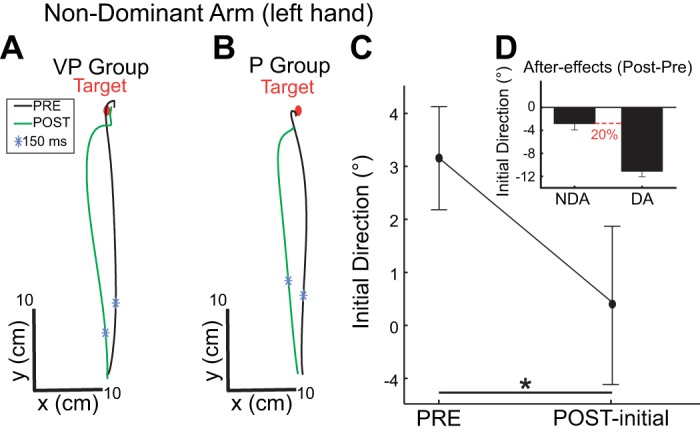
Interlimb transfer of force-field adaptation in the right-handed group. A and B: top view of nondominant arm (NDA) hand paths for a representative subject of the VP group (A) and the P group (B) in the PRE-test (representative trial in black) and in the POST-test (1st trial in green). C: initial direction in baseline and the 1st trial of the POST-test with the NDA for both groups (no groups effect). D: aftereffects (POST: baseline at initial direction) for the left NDA and the right DA. Error bars represent SE. *P < 0.05, significant difference.

The analysis of lateral endpoint errors revealed slightly different results since an interaction [F(1,18) = 7.9, P < 0.05] indicated a significant transfer only for the P group. Indeed, on the first trial of the POST-test, visual feedback mechanisms enabled subjects with vision (VP group) to correct the trajectory errors induced by the aftereffect on the NDA and reach more accurately the target at the end of the movement compared with subjects without vision. Maximum perpendicular deviation occurred on average 264 ± 84 ms after movement onset in the P group and after 239 ± 90 ms in the VP group. The 2 × 2 [VISION (VP, P) × PHASE (PRE-, POST-test)] ANOVA revealed an interaction [F(1,18) = 6.18, P < 0.05], which showed that the difference between PRE- and POST-test trials was significant only for the P group, not for the VP group. Vision thus appears to influence interlimb transfer only when considering late or terminal kinematic features of the movement, as in some previous studies (Cohen 1973), but this really highlights the efficiency of visual feedback mechanisms to minimize motor errors.

Awareness and Assignment of Motor Errors

The possible link between conscious assignment of errors (i.e., to internal or external factors) and interlimb transfer was investigated using debriefing questionnaires at the end of the reaching experiment. Three subjects out of 10 in the P group and 1 subject out of 10 in the VP group reported not being aware of trajectory errors in the first trials of the PER-rotation phase. A Mann-Whitney nonparametric test showed that the transfer value did not differ according to the awareness of errors (P = 0.25). When asked “Did you associate the errors you made in the first trials of the PER-rotation phase to external factors?,” all 20 subjects agreed. When subjects were asked whether they would associate these errors to internal factors, six subjects (4 of the P group, 2 of the VP group) agreed but interlimb transfer was similar for subjects who agreed or not [t(18) = −1.2, P = 0.25]. When forced to choose whether errors were mostly due to internal or external factors, only one subject (from the VP group) out of 20 assigned his errors to internal factors.

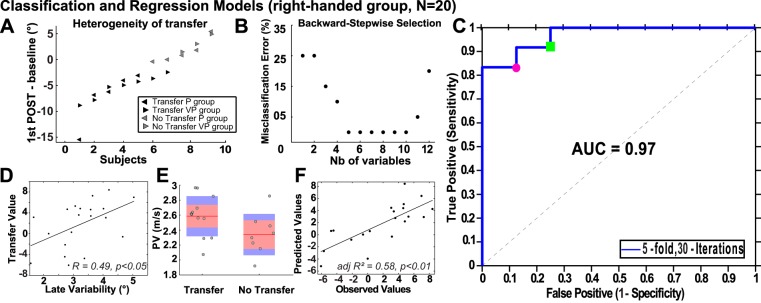
Heterogeneity of DA-to-NDA Interlimb Transfer Across Subjects

Most studies on interlimb transfer have determined whether transfer was significant based on group averages. However, the goal of the present study was to explore interindividual differences and Fig. 4A shows a substantial heterogeneity in interlimb transfer across subjects. We determined whether transfer occurred for each subject based on their baseline confidence interval (see Statistical analysis). This method revealed that 12 out of 20 subjects were classified as “Transfer” subjects. Four subjects presented little difference in initial direction between PRE- and POST-tests, and four subjects seemed to produce an opposite pattern of transfer compared with the ensemble average, but for statistical reasons, we grouped the eight subjects who did not perform as the ensemble average and classified them as “No transfer” subjects.

Fig. 4.

Individual characteristics determining interlimb transfer. A: difference, for each subject, in initial direction between the 1st trial of the POST-test of the NDA and the baseline in the P group (left-pointed triangles) and the VP group (right-pointed triangles). Subjects classified with significant interlimb transfer according to their baseline 99% confidence interval (CI) are in black while other subjects are in grey. B: misclassification error (MCE) in percentage as a function of the number (Nb) of variables. The MCE reaches the minimum when 5 variables are used and then overfitting occurs with >10 variables. C: receiving operator characteristics (ROC) curve of the linear discriminant analysis, with additional results at 2 decision thresholds (red circle: 0.25, green square: 0.21). AUC, area under the curve. D: correlation between variability of initial direction in the last 10 trials of the adaptation phase (x) and the transfer value (y). E: peak velocity in the classes “Transfer” and “No Transfer.” Each data point represents a subject. The distribution is represented by a boxplot where the red line is the mean, the red shaded area the 95% interval, and the blue area the SE. F: observed transfer values as a function of the values predicted by the multiple regression (dependent variable: transfer value; independent variables: variability, laterality quotient, and peak velocity).

Classification Model of Interlimb Transfer Based on Individual Characteristics

To determine whether the presence of interlimb transfer could be linked to any characteristic of the subjects, we first employed a qualitative approach and used a linear discriminant analysis to find the combination of variables that best characterizes the interclass differences (here “Transfer” vs. “No transfer”). A backward-stepwise method was first used to find the variables which could best discriminate the two different classes of behaviour (Fig. 4B; see materials and methods). For the sake of simplicity, we selected the best three variables, i.e., variability of DA initial direction in the last 10 trials of the PER-rotation phase, LQ (Oldfield 1971), and mean DA PV across all 100 trials of the PER-rotation phase. Figure 4C shows the ROC of the linear discriminant analysis based on these three variables: the area under the curve was 97%, which indicates strong discriminating ability at different decision thresholds. Such thresholds influence the sensitivity and specificity of the classification model, but both were well balanced as high sensitivity was not obtained at the cost of low specificity. In other words, the classification model using a linear combination of the three variables could accurately predict observations from the classes “Transfer” (class 1) and “No transfer” (class 0). For instance, at the threshold 0.25 (red circle), the sensitivity was equal to 0.83 and specificity was 0.88 (10/12 “Transfer” subjects and 7/8 “No transfer” subjects were well detected). At the threshold 0.21 (green square), sensitivity was 0.92 and specificity was 0.75 (11/12 “Transfer” subjects and 6/8 “No transfer” subjects were well detected, respectively). Combinations of two variables could also well discriminate the classes “Transfer” and “No transfer”: for instance, area under the curve when LQ was removed from the analysis was 79%.

Supplemental Video S1 (Supplemental Material for this article is available online at the Journal website) shows how “Transfer” and “No transfer” subjects were discriminated with three individual characteristics. The variable with the highest coefficient in the discriminant function of the classification model was the variability of DA initial direction over the 10 last adaptation trials, followed by the LQ and the mean PV during adaptation. Figure 4D shows a positive linear correlation between the transfer value and the variability (r = 0.49; P = 0.03). The transfer value was correlated with other measures of motor variability such as variability of DA direction at PV across the adaptation phase (r = 0.59; P < 0.01), variability of DA initial direction across the adaptation phase (r = 0.56; P < 0.05).

The positive correlation between LQ and the transfer value was marginally significant (P = 0.06). There was no significant correlation between PV and the transfer value (r = 0.18; P = 0.44) but PV marginally differed [t(18) = 2; P = 0.06] between the “Transfer” class (mean = 2.6 ± 0.3 m/s) and the “No Transfer” class (mean = 2.3 ± 0.3m/s; see Fig. 4E). No effect of VISION was observed on the three variables (variability: P = 0.45; PV: P = 0.33; LQ: P = 0.24). The three variables were not significantly correlated to each other.

We also investigated the link between interlimb transfer and the level of adaptation. However, the level of adaptation (see materials and methods) when considering initial direction and lateral endpoint error could not be linked to interlimb transfer as the level of adaptation did not significantly differ across classes of transfer [t(18) = −0.36, P = 0.71; t(18) = 0.88, P = 0.39; respectively] and there was no significant correlation with the amount of transfer (r = 0.05, P = 0.8; r = −0.10, P = 0.7; respectively).

The Amount of Interlimb Transfer Can Be Determined Based on Individual Characteristics

To examine whether the magnitude of interlimb transfer could be predicted based on the three variables of the model, we used a multiple regression analysis. Figure 4F shows that the variables could predict the observed transfer value [F(3,16) = 7.5; r² = 0.58; adjusted r² = 0.50; P < 0.01]. All the variables contributed significantly to the model (P < 0.01 for variability and PV; P < 0.05 for LQ). The equation of the multiple regression was as follows: 46 + 2.8 × variability + 0.2 × LQ + 0.08 × PV.

We tested whether the aftereffects on the right DA could be predicted by the variables listed in the materials and methods, with the exception of variability of DA initial direction in the baseline as it was used to assess the DA aftereffects. We applied a multiple regression with stepwise selection (forward and backward) similar to the methods used to predict interlimb transfer but none of the (combination of) variables could predict the DA aftereffects.

Interlimb Transfer of Dynamic Adaptation in Left-Handers

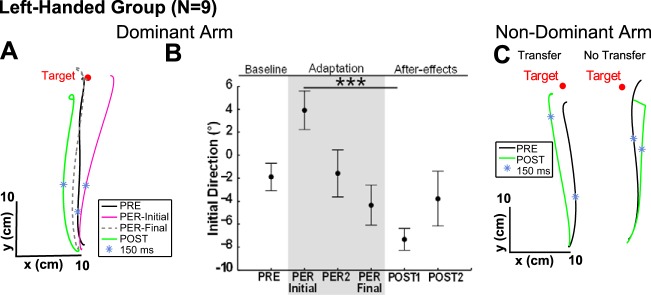
Adaptation of the left DA.

To test the influence of handedness on interlimb transfer and to test our qualitative and quantitative models of transfer, we repeated the experiment with nine left-handed subjects. Figure 5, A and B, shows a classical pattern of adaptation in initial direction. A one-way ANOVA {PHASE [PRE-test (mean of 10 trials), PER-Initial, PER-2, PER-Final, POST-1, and POST-2]} revealed an effect of the experimental phase [F(5,35) = 5; P < 0.01]. The first trial of the PER-rotation, adaptation phase differed from all other trials (all P < 0.05; the difference with baseline being marginally significant, P = 0.05). The mean shift in initial direction of the first trial compared with baseline was 5.8 ± 6° and the mean aftereffect, on initial direction, was −5.4 ± 5.2°.

Fig. 5.

Adaptation and interlimb transfer in left-handers. A: top view of DA hand paths for a representative subject. B: initial direction (in degree) for the DA averaged across subjects in the PRE-test (baseline); the 1st, the 2nd, and the last trial of the PER-rotation phase; and the 1st and second trials of the POST-test. ***P < 0.001, significant difference. Error bars represent SE. C: top view of NDA hand paths for 2 representative subjects

Interlimb transfer of dynamic adaptation to the right NDA.

On average, initial direction was similar in PRE-test (mean = −1.7 ± 3.5°) and POST-test (mean = 0.1 ± 6.2°) such that there was no significant interlimb transfer for the group [t(8) = −0.76; P = 0.4]. However, for four subjects out of nine, initial direction in the first trial of the POST-test differed from the 99% confidence interval of the NDA PRE-test (baseline), indicating interlimb transfer. For these four “Transfer” subjects interlimb transfer (mean = −6.3 ± 3.9°) was consistent with a representation of limb dynamics in extrinsic coordinates. In the “No transfer” class, the mean shift between PRE- and POST-test was 1.9 ± 1.8° (see Fig. 5C).

Test of the classifier on left-handed individuals.

Testing left-handers gave us the opportunity to test the robustness of the model on new data and to investigate whether the LQ had an influence on transfer among left-handers (in other words, does the extent of handedness and handedness itself matter to interlimb transfer?).

With respect to the individual characteristics that were identified as determining interlimb transfer, variability of initial direction during the last 10 trials of the adaptation phase did not significantly differ between left and right-handers [mean variability = 3.4 ± 1.2°; t(27) = −0.9; P = 0.4]. Although all subjects were instructed that they should reach as fast and as accurately as possible left-handers were faster than right-handers during the adaptation phase [mean PV = 3.2 ± 0.3 vs. 2.5 ± 0.3 m/s; t(27) = −7; P < 0.001]. This advantage in left-handers in term of movement speed is consistent with previous work (Kilshaw and Annett 1983).

The large difference in PV between right and left-handers greatly reduced the classifier's accuracy because the discriminant function is very sensitive to out-of-range data. Hence, only LQ and variability were used for the classifier, which was built with the data of the 20 right-handed subjects (training dataset) and tested on the 9 left-handed subjects. At the threshold 0.58, the model misclassified only one “Transfer” subject.

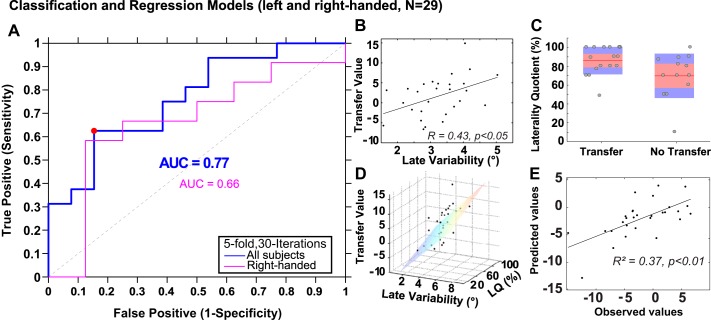
Next, we pooled the data of the left- and right-handers and ran the cross-validation on all the subjects to consider the distribution of the two variables. We ran a fivefold 30-iteration cross validation on 29 subjects: 16 were in the class “Transfer,” 13 in the class “No Transfer.” The area under the curve indicated 77% of good discrimination, which was higher that when the 2 variables were tested on the 20 right-handers (Fig. 6A). At the threshold 0.58, the sensitivity and the specificity were equal to 0.62 and 0.85, respectively (i.e., 10/16 “Transfer” subjects and 11/13 “No Transfer” subjects were well detected; the misclassified subjects were 6 right and 2 left-handers).

Fig. 6.

Classification and regression models for both right- and left-handers. A: in blue, the ROC of the left DA classification model built with 2 variables (laterality quotient and variability) for all (both right- and left-handed) subjects (n = 29). A result is shown at the decision threshold 0.58 (blue circle). In pink, the ROC for the right-handers (n = 20) only. B: correlation between variability and the transfer value. C: representation of the laterality quotient distribution between the classes “Transfer” and “No transfer.” Each data point represents a subject. The red line is the mean, the red shaded area the 95% interval, and the blue area the SE. D: transfer value as a function of variability (°) and laterality quotient (%). The regression model is represented by the hyperplan. E: observed transfer values as a function of the predicted transfer values based on the multiple regression (dependent variable: transfer value; independent variables: variability and laterality quotient).

When considering more quantitative aspects, Fig. 6B shows that variability was correlated to the transfer value (n = 28, r = 0.43; P < 0.05). Figure 6C shows that the LQ was marginally significant to discriminate the classes “Transfer” and “No Transfer” (P = 0.08). Altogether, variability and LQ were useful to discriminate “Transfer” and “No transfer” subjects (Fig. 6D).

Finally, we conducted a multiple regression analysis to examine whether the magnitude of interlimb transfer could also be predicted by variability and LQ with both right and left-handers in the data set. Figure 6E shows that the observed transfer value could be predicted [F(2,26) = 10.3; r = 0.65; r² = 0.42; adjusted r² = 0.37; P < 0.01], with a combination of the two variables. The equation of the multiple regression was as follows: 15.2 +2.9 × variability + 0.1 × LQ.

DISCUSSION

Conflicting results have been reported on the interlimb transfer of sensorimotor adaptation (Imamizu and Shimojo 1995; Morton et al. 2001; Anguera et al. 2007; Galea et al. 2007) and we sought to identify the factors that determine interlimb transfer. We first used an experimental approach that showed, on average in healthy right-handed subjects, significant interlimb transfer of force-field adaptation. Interlimb transfer was similar irrespective of the sensory feedback conditions (vision/proprioception and proprioception only), the conscious perception of motor errors, and the level of adaptation. Previous studies already reported a similar level of adaptation irrespective of visual feedback conditions (Franklin et al. 2007; Hinder et al. 2008; Arce et al. 2009), and our study appears to extend these findings to the interlimb transfer of sensorimotor adaptation. More importantly, the present study suggests that an individualized approach can reveal the critical factors determining interlimb transfer. Three main predictors of interlimb transfer were identified in the right-handed group: variability, PV, and LQ. When left-handers were tested, interlimb transfer could also be qualitatively and quantitatively predicted with variability and LQ. Taken together these results suggest that beyond the environmental conditions, interlimb transfer is determined by quantitative features of the adaptation phase and by the subjects' degree of lateralization.

Variability of Motor Execution and PV are Key Predictors of Interlimb Transfer

When considering our results averaged across subjects, they are in line with previous studies that reported significant, but limited, interlimb transfer of sensorimotor adaptation. Our results are also consistent with studies that reported interlimb transfer of adaptation to novel limb dynamics reflecting a central representation of limb dynamics in extrinsic coordinates (Dizio and Lackner 1995; Criscimagna-Hemminger et al. 2003; Malfait and Ostry 2004). However, when we looked at interlimb transfer for each individual, we uncovered a substantial heterogeneity. A classification model revealed that a key predictor of interlimb transfer is the variability of initial movement direction during the last part of the adaptation phase. Recent studies have highlighted how motor variability at the execution level could enhance motor learning, first in songbirds (Ölveczky et al. 2005; Tumer and Brainard 2007) and more recently in humans with arm-reaching tasks (Wu et al. 2014). A direct link between our study and that of Wu et al. (2014) cannot be firmly established yet since they investigated the link between baseline performance and motor adaptation while we investigated the link between motor adaptation and transfer. However, our results seem to relate to their findings, suggesting that overall, variability may reflect action exploration, which in turn could facilitate sensorimotor adaptation.

There are multiple types of variability and for instance motor variability at the execution level differs from variability in task goal (Ranganathan and Newell 2013). Increasing the variability in task goal is also well known to improve motor learning (Braun et al. 2009; Kitago and Krakauer 2013) as it stimulates problem-solving capacities. However, adaptation with multiple target directions to a visuomotor rotation (Wang and Sainburg 2004b) and a novel force field (Mattar and Ostry 2007) was not found to facilitate interlimb transfer. These findings raise the question as to why variability of movement execution is so beneficial to adaptation and interlimb transfer.

Although motor variability has often been considered as noise, it is now thought to be beneficial to learning since it would reflect action exploration (Kanai and Rees 2011; Herzfeld and Shadmehr 2014; Wu et al. 2014). Variability presumably allows the nervous system to develop a general knowledge of the relationship between efferent signals and their actual consequences, which in turn would enable the selection of the most appropriate movement strategy. New experiments are necessary to clarify how exactly variability facilitates sensorimotor adaptation and its generalization.

PV during the adaptation phase also seemed to determine intermanual transfer in our study. Kitazawa et al. (1997) previously showed that the velocity of reaching had a substantial influence on sensorimotor adaptation and our study seems to extend this finding to the interlimb transfer of force-field adaptation. Indeed, we observed a greater PV in so-called “Transfer” subjects compared with “No transfer” subjects. This could be related to the notion that fast movements, with a high PV, are mostly controlled based on feedforward control mechanisms because there is less time to process peripheral sensory feedback during movement execution. Minimizing errors of fast movements thus relies more on the update of motor planning processes, which would facilitate interlimb transfer. One hypothesis to experimentally test is that manipulating movement speed should influence interlimb transfer such that an increased movement speed would result in an increased interlimb transfer.

LQ Influences the Interlimb Transfer of Sensorimotor Adaptation

LQ, a quantitative assessment of handedness in everyday activities (Oldfield 1971), was the second most important predictor of interlimb transfer in our study. Many studies with healthy subjects and stroke patients (Wang and Sainburg 2004a; Mutha et al. 2012; Sainburg 2014) support the idea that, in right-handers, the left hemisphere is specialized for the control of limb dynamics. While the control of dominant hand movements involves greater activation of the contralateral hemisphere compared with the ipsilateral one (Dassonville et al. 1997; Volkmann et al. 1998; Pool et al. 2014), movements of the nondominant hand are controlled by a more balanced pattern of hemispheric activation (Kawashima et al. 1993; Kim et al. 1993; Ziemann and Hallett 2001). There is also neuropsychological evidence that damage to the dominant left hemisphere can impair the motor function of both right and left hands (Haaland and Harrington 1996; Sainburg 2014). This body of work suggests that, for our right-handed participants, the internal representation of the right hand dynamics was updated during the adaptation phase primarily in the left hemisphere. The contribution of the left hemisphere to the control of the NDA may be the basis of interlimb transfer in right-handers, an idea consistent with a study (Criscimagna-Hemminger et al. 2003) that showed interlimb transfer of force-field adaptation in a split-brain patient. In our study with right-handers, the fact that the amount of interlimb transfer increased with the LQ may be explained by a greater activation of the contralateral (left) hemisphere in strongly lateralized subjects when using the dominant (right) hand (Dassonville et al. 1997; Pool et al. 2014) and/or by more involvement of the ipsilateral (left) hemisphere in strongly lateralized subjects when using the nondominant (left) hand (Verstynen et al. 2004).

One might argue, contrarily, that less neural asymmetry and more bilateral brain activity in general might favor interlimb transfer. When Chase and Seidler (2008) investigated interlimb transfer of adaptation to a visuomotor rotation, they observed in left-handers that interlimb transfer increased as the degree of handedness decreased. Also, when they studied whether learning a sequence of finger movements with one hand transferred to the other hand, they found that, in right-handers, interlimb transfer increased as the degree of handedness decreased. We presume that there are differences between adapting to a novel dynamic environment and adapting to a visuomotor rotation (Krakauer et al. 1999; Rabe et al. 2009) or learning a sequence of finger movements. However, these and our findings collectively highlight the importance of handedness for interlimb transfer.

Although all left-handers could adapt to the novel force field with their left DA, we did not observe significant interlimb transfer on the right NDA, perhaps because of a small sample size. However, a large heterogeneity was found across subjects and a subject-by-subject analysis indicated that transfer was in fact observed in a few subjects. These “Transfer” subjects could be discriminated from so-called “No transfer” subjects based on the LQ as well as variability of initial direction during late adaptation. The fact that PV was not found to be a significant predictor of transfer likely results from the finding that left-handers were faster than right-handers, which is consistent with previous work (Kilshaw and Annett 1983). Because LQ was found to influence interlimb transfer of all, right- and left-handed individuals, our findings suggest that it is the extent of handedness that influences intermanual transfer of sensorimotor adaptation.

In summary, LQ and other subjects' characteristics such as movement kinematics are important for interlimb transfer, which does not result solely from environmental conditions. These individual characteristics should be carefully considered as they could explain the large heterogeneity of results in the literature.

GRANTS

This work benefited from the financial support of the Institute of Movement Sciences (ACI), Aix-Marseille University (International Relations Grant), the Royal Society (International Exchange Grant), and Centre National de la Recherche Scientifique (PICS, DEFISENS, and AUTON Programs).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H.Z.L., J.-L.V., F.B., and F.R.S. conception and design of research; H.Z.L. and F.R.S. performed experiments; H.Z.L. analyzed data; H.Z.L., J.-L.V., R.C.M., J.C., L.B., C.B., and F.R.S. interpreted results of experiments; H.Z.L. prepared figures; H.Z.L. and F.R.S. drafted manuscript; H.Z.L., J.-L.V., R.C.M., J.C., L.B., C.B., and F.R.S. edited and revised manuscript; H.Z.L., J.-L.V., R.C.M., J.C., F.B., L.B., C.B., and F.R.S. approved final version of manuscript.