Abstract
Introduction
Computational modeling of skeletal muscle requires characterization at the tissue level. While most skeletal muscle studies focus on hyperelasticity, the goal of this study was to examine and model the nonlinear behavior of both time-independent and time-dependent properties of skeletal muscle as a function of strain.
Materials and Methods
Nine tibialis anterior muscles from New Zealand White rabbits were subject to five consecutive stress relaxation cycles of roughly 3% strain. Individual relaxation steps were fit with a three-term linear Prony series. Prony series coefficients and relaxation ratio were assessed for strain dependence using a general linear statistical model. A fully nonlinear constitutive model was employed to capture the strain dependence of both the viscoelastic and instantaneous components.
Results
Instantaneous modulus (p<0.0005) and mid-range relaxation (p<0.0005) increased significantly with strain level, while relaxation at longer time periods decreased with strain (p<0.0005). Time constants and overall relaxation ratio did not change with strain level (p>0.1). Additionally, the fully nonlinear hyperviscoelastic constitutive model provided an excellent fit to experimental data, while other models which included linear components failed to capture muscle function as accurately.
Conclusions
Material properties of skeletal muscle are strain-dependent at the tissue level. This strain dependence can be included in computational models of skeletal muscle performance with a fully nonlinear hyperviscoelastic model.
1. Introduction
The passive properties of skeletal muscle play a key role in force transmission throughout the tissue under active generation and passive stretch (Brown et al., 2012; Gillies and Lieber, 2011; Huijing, 1999; Smith et al., 2011). In tendon transfer procedures, the detachment and re-attachment of a muscle requires the estimation of resting length with manual tensioning, which can lead to deficiencies in contractile function (Fridén and Lieber, 2002, 1998). As skeletal muscle is non-linear (Calvo et al., 2010; Takaza et al., 2012) and time dependent (Meyer et al., 2011; Myers et al., 1998), this makes manually detecting proper resting length via passive muscle tension a challenge. To improve simulations such as finite element analyses, which can aid in surgical procedures by identifying proper muscle tension, we must first develop a complete understanding of the time and strain dependent properties of skeletal muscle.
As the modeling approaches for soft biological tissues such as skeletal muscle continue to advance, the formulation of constitutive relationships for these materials become more complex. This is derived from a need for a more complete understanding of the material behavior of these tissues, enabling simulations to accurately predict both local and global tissue function. While computational models of skeletal muscle have been developing since the introduction of the Hill model in 1938 (Hill, 1938), there have been relatively few studies of muscle tensile material properties at the tissue level (Abraham et al., 2012; Takaza et al., 2012), with the majority of studies evaluating compressive properties (Böl et al., 2014; Pietsch et al., 2014; Van Loocke et al., 2009, 2008, 2006). Studies of the structural response of individual muscle fibers (Meyer et al., 2011) and intact muscles (Calvo et al., 2010; Gras et al., 2012; Myers et al., 1998) are more prevalent. Since skeletal muscle is a highly organized collection of fibers and a collagenous connective matrix, which plays a key role in force transmission (Meyer and Lieber, 2011), it may be difficult to extrapolate whole muscle behavior from results of studies of individual fibers. Likewise, variations in anatomical structure between muscles from different locations in the body makes inference of the response of one muscle from the study of another a dubious proposition at best.
Many recent investigations into skeletal muscle properties have focused on hyperelastic material properties (Böl et al., 2014; Calvo et al., 2010; Gras et al., 2012; D. A. Morrow et al., 2010; Pietsch et al., 2014; Takaza et al., 2012). However, the number of studies examining the time dependency are limited to compressive conditions (Bosboom et al., 2001; Pietsch et al., 2014; Van Loocke et al., 2009, 2008, 2006), single fiber (Bensamoun et al., 2006; Meyer et al., 2011) or whole muscle investigations (Anderson et al., 2002; Best et al., 1994; Grover et al., 2007), or utilize a linear or quasi-linear viscoelastic response (Gras et al., 2013, 2014; Myers et al., 1998). Thus, to the author's knowledge, there have been no previous modeling efforts which have included nonlinear tissue level strain dependent viscoelastic behavior for skeletal muscle in tension. However, when developing such a model, one must take care to ensure that any efforts can be implemented into future computational analyses. This is typically done through the development of an energy based formulation instead of a stress based formulation, which prevents stress integration in a finite element simulation (Odegard et al., 2008).
Thus, the goals of this study were to (1) examine the time and strain dependent material properties of skeletal muscle tissue subjected to consecutive stress relaxation cycles and to (2) implement a fully nonlinear hyperviscoelastic model to capture muscle nonlinearity in both time independent modulus and viscoelastic relaxation behavior under passive tensile conditions.
2. Methods
2.1 Specimen Preparation
Longitudinal (along the fiber direction) load-relaxation tests were performed on nine tibialis anterior (TA) muscle samples harvested from nine New Zealand White rabbits (one sample per animal). The handling of all study animals was performed with approval from the Mayo Clinic Institutional Animal Care and Use Committee. Specimens were cut from the muscle midbelly away from surrounding fascia and aponeurosis to a thickness of 3.6 mm using a razor tissue punch with the long axis coinciding with muscle fiber direction (Figure 1). Specimens were 22.0 ± 4.1 mm long and 5.4 ± 1.0 mm wide as measured with digital calipers. All testing was completed within two hours of sacrifice to mitigate the effects of post-mortem rigor (Van Ee et al., 2000; Van Loocke et al., 2006). Testing was performed at room temperature, and specimens were kept moist continually using a saline mist spray.
Figure 1.
Midbelly specimens were excised from the tibialis anterior (A) along the fiber direction (vertical arrow), loaded, and tested in a material testing system with thin film grips (B). Samples were cut into rectangular strips and the apparent dog bone shape (B) is a result of tissue compression at the grips and not changes in cross sectional area with sample length.
2.2 Stress Relaxation Tests
Load-relaxation tests were performed on an MTS 858 material test device (MTS, Eden Prairie, MN) with specimens mounted in thin film clamps (Imada, Northbrook, IL) (Figure 1). A pre-stress condition corresponding to 0.1% of the ultimate stress of the muscle by direction (D. A. Morrow et al., 2010) was applied. Specimen length was calculated as grip to grip length and strain was calculated from crosshead displacement per previous work on rabbit skeletal muscle (D. A. Morrow et al., 2010). Samples were subject to five load-relaxation cycles of 0.7 mm (mean strain of 0.031 ± 0.002 standard error of mean) followed by a 300-second relaxation period (Abraham et al., 2012). Operating in this range ensured that tissue remained below the ultimate strain (D. A. Morrow et al., 2010) and would not be strained to the point of creating damage or plastic deformation (Meyer et al., 2011). Force measurements were sampled at 20 Hz using a 1-kgf load cell (Transducer Techniques, Temecula, CA). As the relaxation behavior of muscles under stress relaxation has been shown to be strain-rate insensitive (Abbott and Lowy, 1956), all material tests were performed at a uniform rate of displacement. Tissues were elongated at a rate of 3.8 mm/sec, corresponding to 0.1 fiber-lengths/sec (Lieber and Blevins, 1989).
2.3 Raw Data Analysis
First Piola-Kirchoff stress (P) was calculated as the reaction force divided by the initial cross-sectional area and converted into Second Piola-Kirchoff by where F is the deformation gradient. The relaxation ratio of each individual zeroed stress relaxation step was calculated as the mean stress over the final one second of relaxation divided by the peak stress from that step. Material elongation was determined using crosshead displacement. Green strain was calculated as the mechanical correlate to S (Equation 1, where eG is one dimensional Green strain and e is engineering strain). All relaxation data was processed in Matlab (The Mathworks, Inc., Natick, MA) using a first order Savitsky-Golay filter (sgolayfilt) as it is highly effective in reducing high frequency noise.
| (1) |
2.4 Linear Viscoelastic Prony Series
Calculated stress relaxation data for each strain increment (five steps each and nine specimens for a total of 45 stress relaxation steps) were fitted to a constitutive formulation for viscoelastic materials (Shetye et al., 2014; Van Loocke et al., 2008) (Equation 2, where S(eG, t) is the stress at time t and strain level eG, E(t) is the time dependent elastic modulus, and τ is an integration variable). A three-term linear Prony series (Ghoreishy, 2012; Maikos et al., 2008; Shetye et al., 2014; Troyer et al., 2012; Van Loocke et al., 2008) was utilized to describe the time dependent elastic modulus (Equation 3, where E0 is the instantaneous modulus, En are relaxation coefficients, and τn are time constants). A nonlinear optimization (lsqnonlin) in Matlab applied the Levenberg-Marquardt unbounded local optimizing algorithm to fit experimental and model data. This approach varied all seven of the material properties from Equation 3 to minimize the residuals between the model output and experimental data at each time point (Calvo et al., 2010; Kauer et al., 2002; Lei and Szeri, 2007; Shetye et al., 2014; Wheatley et al., 2015). Additional weight was given to the peak response to ensure a good fit throughout loading and initial relaxation by mutiplying the peak error by the total number of data points in each step (Wheatley et al., 2015). The E0 initial parameter value was set to 10 kPa, the En terms were initially set to values of 0.5, 0.25, and 0.15, respectively, while the τn terms were set to 0.1s, 10s, and 100s, respectively. These values were determined by performing the optimization under a range of initial values and comparing the results to locate the optimal fits. The En terms were set to decreasing values as a large portion of tissue relaxation typically occurs over very short time periods in studies of biological tissues (Troyer et al., 2012; Van Loocke et al., 2009, 2008; Wheatley et al., 2015). Each parameter was then scaled within the optimization such that all initial values remain on the same order of magnitude, which improves the fitting procedure (Lei and Szeri, 2007; Wheatley et al., 2015).
| (2) |
| (3) |
2.5 Fully Nonlinear Hyperviscoelastic Modeling
Experimental data was then averaged together to generate a single set of mean stress relaxation data in addition to the nine individual specimens. These data were fit to a fully nonlinear hyperviscoelastic model. Here the hyperelasticity was characterized by an isotropic polynomial strain energy density (SED) function (Holzapfel, 2000; Wheatley et al., 2015) (Equation 4, where is the stretch dependent strain energy density, λi are the stretches in the longitudinal (λ1) and transverse (λ2, λ3) directions, respectively, and a2i are material constants). The Poisson's ratio (v) of unbathed skeletal muscle was assumed to be 0.47, per a previous study of fresh skeletal muscle under uniaxial tension (Takaza et al., 2012). The resulting transverse strain was driven by the Poisson effect (), resulting in a simplification of the three stretches to only a longitudinal stretch and strain dependence shown in Equation 5.
| (4) |
| (5) |
The instantaneous modulus E0 was then calculated as a function of stretch from the SED equation (Equation 6) (Holzapfel, 2000). Previous studies have applied a polynomial expression to identify the dependence of Prony series parameters on stretch level for compressed muscle (Van Loocke et al., 2009) and spinal cord (Shetye et al., 2014). However, we chose to employ a simple exponential function for the purpose of minimizing the number of optimized parameters while still maintaining a robust, non-linear function. Thus, the relaxation coefficients and time constants were given exponential dependence on longitudinal stretch (Equations 7 and 8, where αn, βn, μn, and ωn are material properties). A stretch and time dependent hyperviscoelastic tangent modulus (E(λ(τ),t), which directly incorporates the strain energy density function through E0 and the viscoelastic nonlinearity through En and τn(λ), can then be defined (Equation 9). The complete nonlinear constitutive relationship for second Piola-Kirchoff stress is then developed (Equation 10), highlighting the coupling between stretch and time dependence of the tangent modulus. It should be noted that this tangent modulus characterizes the stiffness behavior at a particular deformation and is highly nonlinear, thus it should not be confused a linear elastic Young's modulus.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The fitting procedure was similar to the optimization performed for single step data, but it included all five consecutive relaxation steps and the expanded constitutive relation outlined above. Ten separate optimizations were performed, each of the nine individual specimens in addition to an averaged set of mean experimental data. The nine individual specimens provided statistical measurement of variability, while the set of mean experimental data was used to develop a single set of constitutive parameters as averaging parameters from multiple specimens is an ineffective approach in constitutive mode ling (D. Morrow et al., 2010; Robertson and Cook, 2014). The initial parameter values were structured similarly to the linear Prony series fitting, where initial En values of 0.5, 0.25, and 0.15 were used along with initial τn values of 0.1s, 10s, and 100s. This was achieved by setting all βn and ωn initially to a value of zero, which results in no initial strain dependence. All initial parameter values can be found in Table 1. To verify uniqueness and global minima, the optimization was repeated with each parameter either reduced by 50% or increased by 100%.
Table 1.
Initial parameter values for the fully hyperviscoelastic model fitting. Each parameter was scaled such that the initial values all shared the same order of magnitude. All αn, βn, and ωn parameters are unit less.
| Parameter | a2 [kPa] | a4 [kPa] | α 1, 2, 3 | β 1, 2, 3 | μ1, 2, 3 [s] | ω 1, 2, 3 |
|---|---|---|---|---|---|---|
| Initial Value | 10 | 1000 | 0.5, 0.25, 0.15 | 0 | 0.1, 10, 100 | 0 |
While the fully nonlinear hyperviscoelastic model provides a highly robust approach, justification for employing such a complex constitutive formulation is needed. Specifically, it was unclear if both the hyperelasticity and nonlinear viscoelasticity were both necessary. Thus, the outlined optimization procedure to fit mean experimental data was employed with four separate models combining linear and nonlinear components from Equations 2 through 7. These models included the fully nonlinear model (FNM), a model including a linear instantaneous modulus and nonlinear viscoelasticity (LINV, Equations 2, 3, 7, and 8), a nonlinear instantaneous modulus and linear viscoelasticity approach (NILV or often referred to quasilinear viscoelasticity or QLV, Equations 2-6), and a fully linear model (FLM, Equations 4-10) (Equation 2).
2.4 Statistics
The goodness of fit for each load-relaxation cycle was evaluated with the goodnessOfFit function in Matlab (Wheatley et al., 2015). In brief, the “fit” value was determined from the normalized mean square (Equation 11), where and are the model and experimental stress values, respectively, at the data ith point and n is the total number of data points. Fits range from -∞ (worst) to 1 (perfect). Additionally, the overall percent error and peak percent error (percent difference between peak response at the end of loading) were calculated.
| (11) |
Muscle behavior was assessed by comparing the dependence on strain of all Prony series terms (Equation 3) and the relaxation ratio with a general linear model, with significance set at p<0.05 for all tests. This was performed in Minitab Statistical Software (Minitab Inc., State College, PA). The coefficients of variation (CV) was determined for all statistical measures in the linear Prony series model to identify the accuracy of all fits. The CV was also calculated for all statistical measures and parameter values for the fully nonlinear model for five consecutive steps for all nine individual specimens.
3. Results
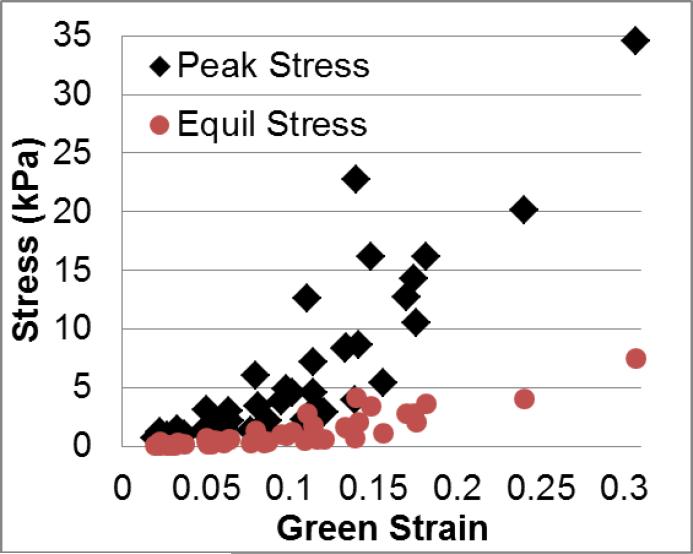
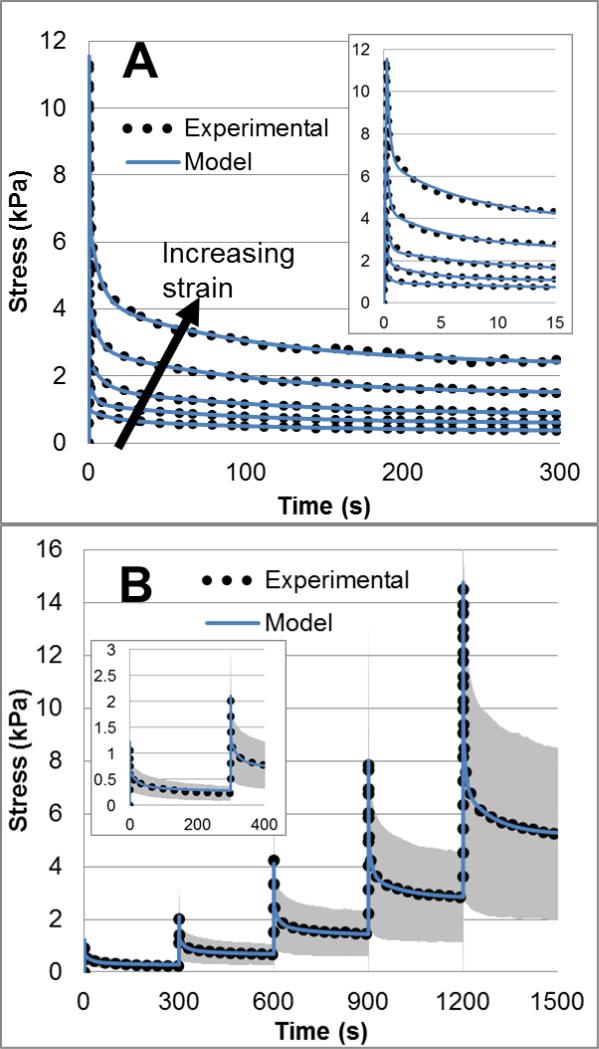
The peak and equilibrium stresses for all specimens show a nonlinear stress-strain relationship (Figure 2). As each specimen was displaced 0.7 mm, variations in gauge length provide a more continuous stress-strain graph than if each specimen was strained at identically discrete intervals. Using a nonlinear optimization algorithm in MATLAB proved to be an excellent way to fit experimental data both visually (Figure 3) and by numerical analysis (Table 2), with both low percent error values and fit values close to the optimal value of 1. The optimizing process also showed an excellent ability to fit both the peak response as well as the shape of the relaxation behavior. The optimization procedure was successful for both the linear model fit to individual zeroed stress relaxation steps (Figure 3A and Table 2) as well as the nonlinear model fit to five consecutive steps (Figure 3B and Table 2).
Figure 2.
Stress-strain data for all peak (black diamonds) and equilibrium (red circles) data from all nine samples. Note the nonlinear behavior for both peak and equilibrium responses in addition to the dispersed strain values.
Figure 3.
Viscoelastic Prony fitting to five isolated stress relaxation steps of a single specimen (A), with loading and initial relaxation shown inset. Arrow indicates curves go from lowest strain level on bottom to highest on top. Nonlinear hyperviscoelastic fitting to mean experimental data (B) with initial steps shown inset for clarity.
Table 2.
Numerical optimization results for the linear Prony series fit to each normalized individual step and the fully hyperviscoelastic model optimized to all nine specimens.
| Linear Model (Equations 2-3) Isolated Steps (45 individual steps) | Nonlinear Model (Equations 4-10) Full Steps (9 specimens with 5 steps each) | ||
|---|---|---|---|
| Complete Response Error | Mean (%) | 2.73 | 4.93 |
| CV | 0.45 | 0.28 | |
| Peak Response Error Only | Mean (%) | 2.53E-5 | 6.65 |
| CV | 1.28 | 0.25 | |
| Fit Value | Mean | 0.967 | 0.999 |
| CV | 0.022 | 7.6E-4 | |
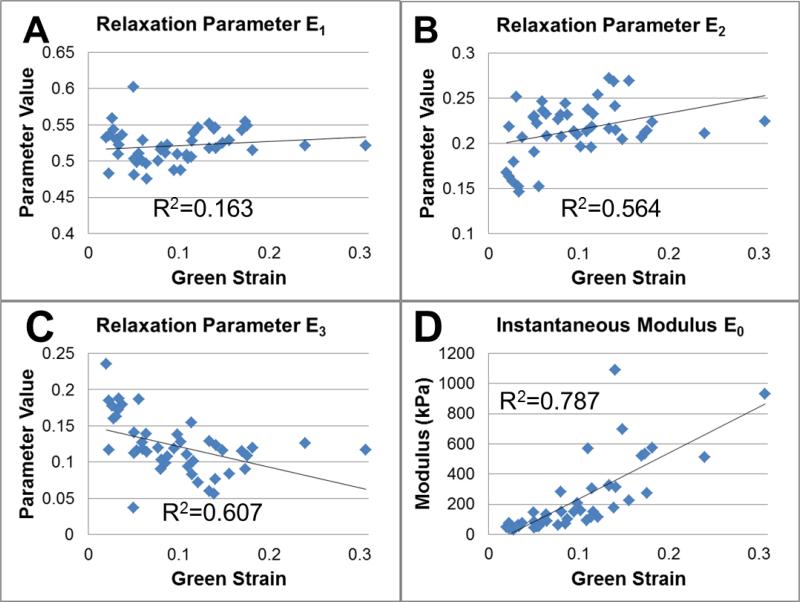
Prony series relaxation coefficients and the instantaneous modulus for all five steps of all nine specimens were plotted (45 total) were plotted against Green strain to provide visual inspection of the dependence of modulus and relaxation behavior on strain level (Figure 4). Here a positive slope corresponds to increases with increasing strain, while a negative slope conversely suggests a decrease. The general linear model analysis of all Prony series coefficients showed that muscle relaxation behavior exhibited strain dependence (Figure 4), as changes in relaxation parameters were observed (E2 positive slope, p<0.0005 and E3 negative slope, p<0.0005) with increasing strain level. The instantaneous modulus E0 also had a positive slope (p<0.0005). Alternatively, the analysis showed no changes in the E1 relaxation parameter (p=0.157) rate parameters (p=0.184, p=0.205, and p=0.157 for τ1, τ2, and τ3, respectively). The mean values (and coefficients of variation in percent) for the rate parameters were found to be 0.109 (0.060) seconds, 5.29 (0.44) seconds, and 108 (0.54) seconds. The relaxation ratio showed no dependence on strain (p=0.777) and had a mean value of 0.211 with a coefficient of variation of 0.18.
Figure 4.
Viscoelastic Prony series coefficients which were found to have a significant dependence on deformation level. The second relaxation parameter E2 (B) had a positive slope (p<0.0005), while the third relaxation parameter E3 (C) had a negative slope (p<0.0005). The instantaneous modulus E0 (D) also increased with strain (p<0.0005).
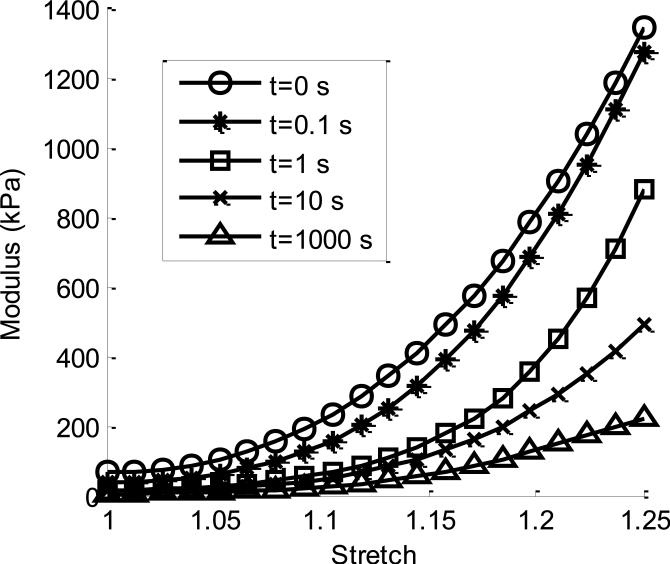
The mean data fit yielded a single set of constitutive parameters (Table 3), which can be utilized in computational modeling efforts. This single optimization resulted in a 2.97% error between the mean data and model, with a fit value of 0.999 and mean peak errors of 2.40% (Table 4). Multiplying initial parameters by 50% and 200% did not significantly affect either the model fit or optimized parameters. A visual representation of the model tangent stiffness provides a useful method to highlight the dependence of material behavior on both strain level and relaxation time (Figure 5).
Table 3.
Optimized hyperviscoelastic constitutive parameters fitted to mean experimental data with coefficient of variation percent in parentheses.
| SED Ψ | Relaxation Coefficients En | Rate Coefficients τn | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a2 [kPa] | 6.62 (0.52) | α 1, 2, 3 | 0.641 (0.089) | 0.124 (0.53) | 0.114 (0.47) | μ1, 2, 3 [s] | 0.202 (0.25) | 12.2 (1.2) | 262 (2.1) |
| a4 [kPa] | 3820 (0.85) | β 1, 2, 3 | 2.27 (2.6) | −3.67 (2.7) | −1.46 (8.6) | ω 1, 2, 3 | 9.78 (1.1) | −11.6 (2.8) | 5.25 (3.3) |
Table 4.
Fitting comparisons between linear and nonlinear models, showing overall mean error, mean error of the five peak values, and the normalized mean square error goodness of fit value.
| Fully Nonlinear Model | Linear Instantaneous, Nonlinear Viscoelastic | Nonlinear Instantaneous, Linear Viscoelastic | Fully Linear Model | |
|---|---|---|---|---|
| Complete Response Error (%) | 3.20 | 15.1 | 4.08 | 33.0 |
| Peak Response Error Only (%) | 3.39 | 18.3 | 5.58 | 106 |
| NMSE Fit Value | 1.00 | 0.984 | 0.999 | 0.937 |
Figure 5.
Tangent modulus behavior for the implemented fully nonlinear hyperviscoelastic constitutive model. This model exhibits dependence on both stretch level (x-axis) as well as relaxation time (various curves). The instantaneous response (circle markers, t=0 s) and equilibrium behavior (triangle markers, t=1,000 s) along with intermediate times are shown, highlighting the evolution of modulus behavior over time.
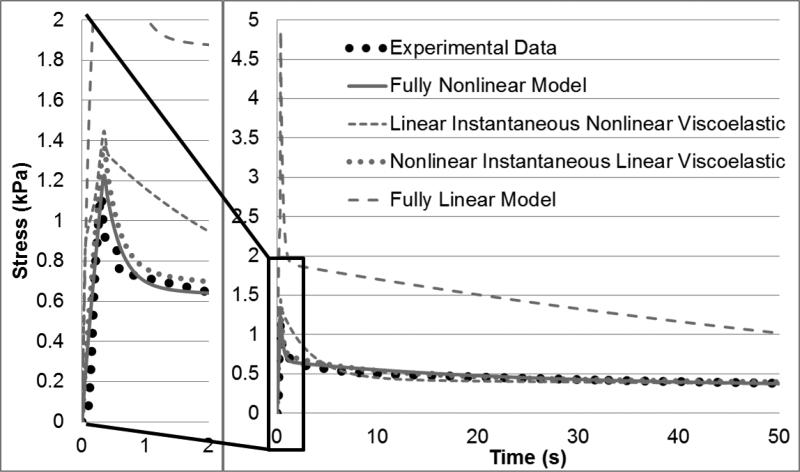
The model justification results (Figure 6 and Table 4) show that the fully nonlinear model (FNM) far outperformed the others. The fully linear model (FLM) failed to capture any sufficient material behavior with an error of over 30% (Table 4). While the two models combining linearity and nonlinearity (linear instantaneous nonlinear viscoelastic - LINV and nonlinear instantaneous linear viscoelastic – NILV) did an improved job predicting experimental behavior overall, particularly the NILV model (Table 4), Figure 6 highlights an inability to match experimental data under highly transient conditions. Specifically, the LINV model over predicted the stress and showed an initial relaxation at a slower rate than observed experimentally before good agreement beyond roughly five seconds of relaxation. The NILV model, however, showed a good relaxation shape but failed to match the overall stress level. The FNM was able to combine both the proper stress level and relaxation shape of the experimental data, providing an optimal fit when compared to the other simulations.
Figure 6.
Comparison of various linear and nonlinear models fitted to averaged experimental data with only the first fifty seconds of the first step shown. Initial loading and relaxation (from 0-2 seconds) is further highlighted on left.
4. Discussion
4.1 Experimental Data Analysis
The experimental data shown in this work provides a more continual stress-strain relationship (Figure) when compared to studies for which each specimen is strained to identical discrete values. This allows for a more detailed investigation of the effect of strain level on passive skeletal muscle mechanics. The analyzed experimental data from this work can be compared to previously published works which studied the time dependent behavior of skeletal muscle in tension (Abraham et al., 2012; Best et al., 1994; Meyer et al., 2011). These investigations similarly showed a large portion of the relaxation occurs over a short time period, after which the tissue slowly transitions into an equilibrium state. Abraham et al., (2013) comparably investigated stress relaxation of excised New Zealand White Rabbit tibialis anterior, albeit it at a single 10% strain step and observed a steady state modulus of roughly 70 kPa for excised tissue compared to an equilibrium modulus value of around 20 kPa at 10% strain from our raw data. The fully nonlinear hyperviscoelastic model similarly predicts an equilibrium tangent modulus of 24 kPa at 10% strain from our data.
Data from Takaza et al., (2013) and Morrow et al., (2010) suggest a stress level of between 5 and 40 kPa at 10% strain in constant rate testing loaded at 0.05%/s. Best et al., (1994) show a stress level of ~350 kPa at 10% strain, at a much higher strain rate (667%/s), which certainly contributed to higher stress values. Our data shows stress values of roughly 5-10 kPa for peak and 2-3 kPa for equilibrium stress at 10% strain. However, as Meyer et al., (2011) showed with a single muscle fiber that superposition does not hold and consecutive stress relaxation cycles result in stresses lower than a single cycle, this may account for the discrepancies between our data and other literature. Specifically, the increased stiffness observed by Abraham et al would be a result of a single stress relaxation step at 10% strain, compared to 3-4 smaller steps of roughly 3% strain, while the constant rate elongation tests would see a compounding effect, resulting in increased stresses.
4.2 Linear Prony Series Viscoelasticity
Analyzing the optimized linear Prony series coefficients as well as the relaxation ratio provides insight into the transient performance of skeletal muscle as a function of strain (Figure 4). Outside of a study by Meyer et al., (2011) who investigated viscoelasticity of single fibers, there is limited published data to compare with our data. The first result to note is that the relaxation ratio exhibited no dependence on strain level, which appears to agree with the findings of Meyer et al., (2011) under consecutive stress relaxation steps on single fibers. The strong increase in instantaneous modulus with strain further supports the well-documented tensile hyperelasticity of skeletal muscle in the fiber direction (Calvo et al., 2010; Lu et al., 2010; Takaza et al., 2012).
The changes observed in Prony series coefficients with strain shows the course under which this relaxation occurs differs as a function of material strain. Specifically, the increases in the second relaxation coefficient coupled with a decrease in the third relaxation coefficient implies that with increasing strain the total rate of relaxation is increasing. This is simplified by the fact that the rate parameters did not change with strain level. These findings differ from Meyer et al., (2011) who found increasing stress relaxation steps resulted in a slower relaxation rate. However, the highly collagenous extracellular matrix (Gillies and Lieber, 2011; Light and Champion, 1984; Listrat et al., 2000) supports a large portion of muscular force transmission (Huijing, 1999; Lieber et al., 2003; Meyer and Lieber, 2011) and as such could certainly affect the relaxation behavior of the tissue. Previous studies have suggested that collagen fibers play a role in the time dependent response of the meniscus (Zhu et al., 1994) and cartilage (Li et al., 2005), thus it is no surprise that the viscoelastic behavior of muscle differs between the fiber and tissue level.
4.3 Fully Nonlinear Viscoelastic Model
To the author's best knowledge, this work presents the first fully nonlinear hyperviscoelastic model of tissue level skeletal muscle under tensile strain. Previous works have evaluated the viscoelastic nonlinearity of a single muscle fiber (Bensamoun et al., 2006; Meyer et al., 2011), have utilized a linear or quasi-linear viscoelastic response (Gras et al., 2013, 2014; Myers et al., 1998), or investigated other biological tissues such as spinal ligaments (Troyer and Puttlitz, 2011), the spinal cord (Shetye et al., 2014), and skeletal muscle in compression (Van Loocke et al., 2009). Meyer et al., (2011)'s investigation of single fiber viscoelasticity was very effective in capturing the strain dependent viscosity of the mouse single fiber. We chose to employ a hyperelastic model as fiber bundle behavior exhibits nonlinear stiffness when compared to individual fibers or groups of fibers (Meyer and Lieber, 2011). This SED based hyperelastic relationship (Equation 3) is also advantageous over stress based functions (Meyer et al., 2011; Shetye et al., 2014; Van Loocke et al., 2009) which must be integrated to calculate strain energy within an analysis (Odegard et al., 2008). Thus, this constitutive formulation provides a simpler model to incorporate in finite element analyses. The fully hyperviscoelastic model exhibited not only the robustness to match various strain levels, but the accuracy to capture both the peak responses (average error of 3.29% for the five peaks) and the relaxation shape (3.20% overall error and a 0.999 total fit value). This novel formulation is capable of combining a technically sound continuum mechanics based hyperelastic SED function (Equation 3, which is polyconvex and positive definite) and a flexible exponential viscoelastic definition (Equations 6 and 7). The optimized coefficients (Table 3) can be directly incorporated into analyses in which the fully nonlinear behavior of the tissue is of importance, such as repeated loading simulations or analyses involving inhomogeneous deformation.
One possible concern from the optimized parameter values in Table 3 are the negative values for the β1, ω2, and ω3 parameters. As this hyperviscoelastic model was applied numerically, there remains the mathematical possibility for a negative modulus based on the constitutive parameter values, which is clearly not physically reasonable. This can be investigated by identifying the role of each parameter within the constitutive model. The a2 and a4 parameters describe the nonlinear behavior of the strain energy density function, and as such can be related to a stiffness or modulus term. The αn terms behave similarly to the En terms from Equation 3, where they reduce a certain amount of the modulus over time, corresponding to each time constant, which are largely described with the μn terms. The remaining βn and ωn terms characterize the strain dependence of the αn and μn terms, respectively, through an exponential function (Equations 7 and 8). We can see that positive βn and ωn values result in increases in relaxation with increases in stretch level, while negative βn and ωn values conversely result in decreases in relaxation with increases in stretch level. Thus, the negative values observed in Table 3 are not concerning from a physical standpoint, as all an, αn and μn parameters remain positive.
A three term Prony series was selected for this work as it provides an excellent fit to experimental data while minimizing the total number of parameters. While increasing the number of Prony series terms increases the fitting potential, this is offset with computational capabilities, as minimizing the total number of parameters improves the accuracy of the optimization procedure (Wheatley et al., 2015). However, some studies have employed higher order series (Salisbury et al., 2015; Shetye et al., 2014; Van Loocke et al., 2009, 2008) with good success. Conversely, lower order Prony series have also been utilized effectively in studies of biological tissues (Chang et al., 2015; Sandino et al., 2015). However, the third order series allows for rate parameters dispersed at decade values (roughly 0.1s, 1s, and 100s for μn, Table 3), which are able to capture the short term, intermediate, and long term relaxation behavior of the tissue. It is uncertain exactly how increasing or decreasing the Prony series order would affect the model, but the effectiveness of the utilized approach remains clear.
This highly nonlinear tangent modulus (Figure 5) further supports the well documented nonlinear response of skeletal muscle in longitudinal tension (Calvo et al., 2010; Lieber, 2010; D. A. Morrow et al., 2010; Takaza et al., 2012). The nonlinear shape also continues throughout relaxation, as highlighted by the various curves at increasing relaxation times, suggesting that skeletal muscle tensile non-linearity exists both in the instantaneous and equilibrium state. Figure 5 also provides further evidence of a short and steep initial relaxation phase, as from zero relaxation (circle) to 0.1 seconds (asterisk) a significant portion of the tangent modulus is reduced. This is then followed by a more drastic decrease from 0.1 to 1 second (square), particularly at lower stretch values. Conversely, the changes in material behavior occurring between 10 (x) and 1000 seconds (triangle, when the material has reached equilibrium) represent a similar reduction in modulus, yet this occurs over a much longer time period. Furthermore, the fact that this modulus remains positive throughout complete relaxation and over a range of stretch values confirms the notion that the numerical application of this model obeys natural physical conditions.
The model justification study (Figure 6 and Table 4) highlighted the improved fitting of the fully nonlinear model over other approaches. Specifically, the models incorporating linear instantaneous behavior had inferior agreement, while the NILV (also known as quasi-linear viscoelasticity or QLV) model was able to produce a reasonable overall fit to the data (~4% error, Table 4), yet it struggled at lower strains as the first step saw over 15% total error and over 20% peak error. Thus it was clear that for complete accuracy, a fully nonlinear model is unmatched by its linear counterparts. As finite element analyses naturally develop more complex constitutive formulations and discrete physiological components to improve clinical significance, the inclusion of a fully nonlinear response may one day be a standard approach.
4.4 Study Limitations and Improvements
While this study effectively explores the strain-dependent changes in the temporal response of muscle tissue, further studies will be needed to establish a full understanding of tissue behavior. Specifically, single cycle load-relaxation studies over a range of strain levels and rates are needed to completely assess the extent to which muscle tissue does not adhere to the principle of superposition and to identify strain rate dependence. These data could also be used to validate the proposed hyperviscoelastic model. It should also be noted that this work represents the response of a single muscle (in this case the New Zealand White Rabbit tibialis anterior with a sample size N=9) and that further experiments to identify nonlinear viscoelastic muscle behavior for different muscles would greatly aid in the confirmation of the proposed model. It remains unclear how muscle curvature, pennation angle, possible changes in fiber type among other physiological characteristics may affect the viscoelastic response.
As this work only proposed an isotropic model, future studies should be performed to identify the viscoelastic behavior in the transverse direction as muscle is anisotropic (D. A. Morrow et al., 2010; Takaza et al., 2012). However, from a computational standpoint, a simplified isotropic model allows for good global accuracy while minimizing computational cost (Ahamed et al., 2015). Muscle studies in compression have identified transverse anisotropy under carefully controlled conditions (Böl et al., 2014) in addition to differences between the time dependent behavior as a function of loading orientation (Pietsch et al., 2014; Van Loocke et al., 2009, 2008), yet it is unclear how these properties translate, if at all, to tension. Development of data sets including shear and volumetric loading conditions would provide a full picture of passive muscle behavior in tension. These data could then be incorporated by expanding the SED function from Equation 3 and subsequently applying independent viscoelastic behavior for each term. This would broaden the current implementation to include transverse isotropy in addition to shear and volumetric behavior for use in a more complex three dimensional finite element model. Additionally, the ability of the utilized hyperviscoelastic constitutive model to predict any strain rate dependence remains unclear. The inclusion of any plastic strain, such as non-recoverable changes in length under in vitro tensile conditions, could also be added to improve finite element implementation. While there may be some concern over the use of second Piola-Kirchoff stress over Cauchy stress, all data analysis was performed in the reference configuration and a push-forward operation could be performed to more closely reflect the local material behavior if desired (Holzapfel, 2000). Finally, while the employed stretch level viscoelastic dependence (Equations 6 and 7) proved very effective at matching experimental data, a different formulation could possibly improve this model.
5. Conclusion
This study shows that the viscoelastic response of skeletal muscle depends significantly upon strain level as evaluated by comparison of the relaxation response of five consecutive load-relaxation cycles. Furthermore, a novel fully nonlinear model including both an explicit hyperelastic strain energy density function and a strain dependent viscoelastic formulation provided an excellent fit to experimental data. To capture the complete range of muscle tensile behavior, the non-linearity of both the time dependent and time independent properties must be modeled.
Acknowledgements
The authors would like to gratefully acknowledge the National Institutes of Health: National Institute of Child Health & Human Development for financial support [R01HD31476-12].
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
6. Conflicts of Interest
The authors have no conflicts of interest to report.
References
- Abbott BC, Lowy J. Stress relaxation in muscle. Proc. R. Soc. Lond. B. Biol. Sci. 1956;146:281–288. doi: 10.1098/rspb.1957.0011. [DOI] [PubMed] [Google Scholar]
- Abraham AC, Kaufman KR, Haut Donahue TL. Phenomenological consequences of sectioning and bathing on passive muscle mechanics of the New Zealand white rabbit tibialis anterior. J. Mech. Behav. Biomed. Mater. 2012;17:290–295. doi: 10.1016/j.jmbbm.2012.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahamed T, Rubin MB, Trimmer BA, Dorfmann L. Time-dependent behavior of passive skeletal muscle. Contin. Mech. Thermodyn. 2015 [Google Scholar]
- Anderson J, Li Z, Goubel F. Models of skeletal muscle to explain the increase in passive stiffness in desmin knockout muscle. J. Biomech. 2002;35:1315–1324. doi: 10.1016/s0021-9290(02)00170-7. [DOI] [PubMed] [Google Scholar]
- Bensamoun S, Stevens L, Fleury MJ, Bellon G, Goubel F, Ho Ba Tho MC. Macroscopic-microscopic characterization of the passive mechanical properties in rat soleus muscle. J. Biomech. 2006;39:568–578. doi: 10.1016/j.jbiomech.2004.04.036. [DOI] [PubMed] [Google Scholar]
- Best TM, McElhaney J, Garrett WE, Myers BS. Characterization of the passive responses of live skeletal muscle using the quasi-linear theory of viscoelasticity. J. Biomech. 1994;27:413–419. doi: 10.1016/0021-9290(94)90017-5. [DOI] [PubMed] [Google Scholar]
- Böl M, Ehret AE, Leichsenring K, Weichert C, Kruse R. On the anisotropy of skeletal muscle tissue under compression. Acta Biomater. 2014;10:3225–34. doi: 10.1016/j.actbio.2014.03.003. [DOI] [PubMed] [Google Scholar]
- Bosboom EMH, Hesselink MKC, Oomens CWJ, Bouten CVC, Drost MR, Baaijens FPT. Passive transverse mechanical properties of skeletal muscle under in vivo compression. J. Biomech. 2001;34:1365–1368. doi: 10.1016/s0021-9290(01)00083-5. [DOI] [PubMed] [Google Scholar]
- Brown SHM, Carr JA, Ward SR, Lieber RL. Passive mechanical properties of rat abdominal wall muscles suggest an important role of the extracellular connective tissue matrix. J. Orthop. Res. 2012;30:1321–1326. doi: 10.1002/jor.22068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvo B, Ramírez A, Alonso A, Grasa J, Soteras F, Osta R, Muñoz MJ. Passive nonlinear elastic behaviour of skeletal muscle: Experimental results and model formulation. J. Biomech. 2010;43:318–325. doi: 10.1016/j.jbiomech.2009.08.032. [DOI] [PubMed] [Google Scholar]
- Chang C-T, Chen Y-H, Lin C-CK, Ju M-S. Finite element modeling of Hyper-viscoelasticity of peripheral nerve Ultrastructures. J. Biomech. 2015 doi: 10.1016/j.jbiomech.2015.04.004. [DOI] [PubMed] [Google Scholar]
- Fridén J, Lieber RL. Evidence for muscle attachment at relatively long lengths in tendon transfer surgery. J. Hand Surg. Am. 1998;23:105–110. doi: 10.1016/S0363-5023(98)80097-X. [DOI] [PubMed] [Google Scholar]
- Fridén J, Lieber RL. Tendon transfer surgery: clinical implications of experimental studies. Clin. Orthop. Relat. Res. 2002:S163–S170. [PubMed] [Google Scholar]
- Ghoreishy MHR. Determination of the parameters of the Prony series in hyper-viscoelastic material models using the finite element method. Mater. Des. 2012 [Google Scholar]
- Gillies AR, Lieber RL. Structure and function of the skeletal muscle extracellular matrix. Muscle Nerve. 2011;44:318–31. doi: 10.1002/mus.22094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gras L-L, Laporte S, Viot P, Mitton D. Experimental characterization of post rigor mortis human muscle subjected to small tensile strains and application of a simple hyper-viscoelastic model. Proc. Inst. Mech. Eng. H. 2014;228:1059–68. doi: 10.1177/0954411914555422. [DOI] [PubMed] [Google Scholar]
- Gras LL, Mitton D, Viot P, Laporte S. Hyper-elastic properties of the human sternocleidomastoideus muscle in tension. J. Mech. Behav. Biomed. Mater. 2012;15:131–140. doi: 10.1016/j.jmbbm.2012.06.013. [DOI] [PubMed] [Google Scholar]
- Gras LL, Mitton D, Viot P, Laporte S. Viscoelastic properties of the human sternocleidomastoideus muscle of aged women in relaxation. J. Mech. Behav. Biomed. Mater. 2013;27:77–83. doi: 10.1016/j.jmbbm.2013.06.010. [DOI] [PubMed] [Google Scholar]
- Grover JP, Corr DT, Toumi H, Manthei DM, Oza AL, Vanderby R, Best TM. The effect of stretch rate and activation state on skeletal muscle force in the anatomical range. Clin. Biomech. 2007;22:360–368. doi: 10.1016/j.clinbiomech.2006.10.009. [DOI] [PubMed] [Google Scholar]
- Hill AV. The Heat of Shortening and the Dynamic Constants of Muscle. Proc. R. Soc. B Biol. Sci. 1938 [Google Scholar]
- Holzapfel GA. Nonlinear Solid Mechanics. Wiley; Chichester, West Sussex, England: 2000. [Google Scholar]
- Huijing PA. Muscle as a collagen fiber reinforced composite: A review of force transmission in muscle and whole limb. J. Biomech. 1999 doi: 10.1016/s0021-9290(98)00186-9. [DOI] [PubMed] [Google Scholar]
- Kauer M, Vuskovic V, Dual J, Szekely G, Bajka M. Inverse finite element characterization of soft tissues. Med. Image Anal. 2002;6:275–287. doi: 10.1016/s1361-8415(02)00085-3. [DOI] [PubMed] [Google Scholar]
- Lei F, Szeri AZ. Inverse analysis of constitutive models: Biological soft tissues. J. Biomech. 2007;40:936–940. doi: 10.1016/j.jbiomech.2006.03.014. [DOI] [PubMed] [Google Scholar]
- Li LP, Herzog W, Korhonen RK, Jurvelin JS. The role of viscoelasticity of collagen fibers in articular cartilage: Axial tension versus compression. Med. Eng. Phys. 2005;27:51–57. doi: 10.1016/j.medengphy.2004.08.009. [DOI] [PubMed] [Google Scholar]
- Lieber RL. Skeletal muscle structure and function: implications for rehabilitation and sports medicine. Williams & Wilkins; 1992. [Google Scholar]
- Lieber RL. Skeletal Muscle Structure, Function, and Plasticity. Lippincott Williams and Wilkins; Philadelphia, PA.: 2010. [Google Scholar]
- Lieber RL, Blevins FT. Skeletal muscle architecture of the rabbit hindlimb: functional implications of muscle design. J. Morphol. 1989;199:93–101. doi: 10.1002/jmor.1051990108. [DOI] [PubMed] [Google Scholar]
- Lieber RL, Runesson E, Einarsson F, Fridén J. Inferior mechanical properties of spastic muscle bundles due to hypertrophic but compromised extracellular matrix material. Muscle and Nerve. 2003;28:464–471. doi: 10.1002/mus.10446. [DOI] [PubMed] [Google Scholar]
- Light N, Champion AE. Characterization of muscle epimysium, perimysium and endomysium collagens. Biochem. J. 1984;219:1017–1026. doi: 10.1042/bj2191017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listrat A, Lethias C, Hocquette JF, Renand G, Menissier F, Geay Y, Picard B. Age-related changes and location of types I, III, XII and XIV collagen during development of skeletal muscles from genetically different animals. Histochem. J. 2000;32:349–356. doi: 10.1023/a:1004013613793. [DOI] [PubMed] [Google Scholar]
- Lu YT, Zhu HX, Richmond S, Middleton J. A visco-hyperelastic model for skeletal muscle tissue under high strain rates. J. Biomech. 2010;43:2629–2632. doi: 10.1016/j.jbiomech.2010.05.030. [DOI] [PubMed] [Google Scholar]
- Maikos JT, Elias RAI, Shreiber DI. Mechanical properties of dura mater from the rat brain and spinal cord. J. Neurotrauma. 2008;25:38–51. doi: 10.1089/neu.2007.0348. [DOI] [PubMed] [Google Scholar]
- Meyer GA, Lieber RL. Elucidation of extracellular matrix mechanics from muscle fibers and fiber bundles. J. Biomech. 2011;44:771–773. doi: 10.1016/j.jbiomech.2010.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer GA, McCulloch AD, Lieber RL. A Nonlinear Model of Passive Muscle Viscosity. J. Biomech. Eng. 2011 doi: 10.1115/1.4004993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow D, Donahue T, Odegard G, Kaufman K. A method for assessing the fit of a constitutive material model to experimental stress–strain data. Comput. Methods Biomech. Biomed. Engin. 2010;13:247–56. doi: 10.1080/10255840903170686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow DA, Haut Donahue TL, Odegard GM, Kaufman KR. Transversely isotropic tensile material properties of skeletal muscle tissue. J. Mech. Behav. Biomed. Mater. 2010;3:124–129. doi: 10.1016/j.jmbbm.2009.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers BS, Woolley CT, Slotter TL, Garrett WE, Best TM. The influence of strain rate on the passive and stimulated engineering stress--large strain behavior of the rabbit tibialis anterior muscle. J. Biomech. Eng. 1998;120:126–132. doi: 10.1115/1.2834292. [DOI] [PubMed] [Google Scholar]
- Odegard GM, Haut Donahue TL, Morrow DA, Kaufman KR. Constitutive modeling of skeletal muscle tissue with an explicit strain-energy function. J. Biomech. Eng. 2008;130:061017. doi: 10.1115/1.3002766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pietsch R, Wheatley BB, Haut Donahue TL, Gilbrech R, Prabhu R, Liao J, Williams LN. The Anisotropic Compressive Properties of Porcine Muscle Tissue. J. Biomech. Eng. 2014;136:111003. doi: 10.1115/1.4028088. [DOI] [PubMed] [Google Scholar]
- Robertson D, Cook D. Unrealistic statistics: How average constitutive coefficients can produce non-physical results. J. Mech. Behav. Biomed. Mater. 2014;40C:234–239. doi: 10.1016/j.jmbbm.2014.09.006. [DOI] [PubMed] [Google Scholar]
- Salisbury C, Cronin D, Lien F-S. Deformation Mechanics of a Non-linear Hyper-viscoelastic Porous Material, Part I: Testing and Constitutive Modeling of Non-porous Polychloroprene. J. Dyn. Behav. Mater. 2015 [Google Scholar]
- Sandino C, McErlain DD, Schipilow J, Boyd SK. The poro-viscoelastic properties of trabecular bone: a micro computed tomography-based finite element study. J. Mech. Behav. Biomed. Mater. 2015;44:1–9. doi: 10.1016/j.jmbbm.2014.12.018. [DOI] [PubMed] [Google Scholar]
- Shetye SS, Troyer KL, Streijger F, Lee JHT, Kwon BK, Cripton PA, Puttlitz CM. Nonlinear viscoelastic characterization of the porcine spinal cord. Acta Biomater. 2014;10:792–797. doi: 10.1016/j.actbio.2013.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LR, Gerace-Fowler L, Lieber RL. Muscle extracellular matrix applies a transverse stress on fibers with axial strain. J. Biomech. 2011;44:1618–1620. doi: 10.1016/j.jbiomech.2011.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takaza M, Moerman KM, Gindre J, Lyons G, Simms CK. The anisotropic mechanical behaviour of passive skeletal muscle tissue subjected to large tensile strain. J. Mech. Behav. Biomed. Mater. 2012;17:209–220. doi: 10.1016/j.jmbbm.2012.09.001. [DOI] [PubMed] [Google Scholar]
- Troyer KL, Puttlitz CM. Human cervical spine ligaments exhibit fully nonlinear viscoelastic behavior. Acta Biomater. 2011;7:700–709. doi: 10.1016/j.actbio.2010.09.003. [DOI] [PubMed] [Google Scholar]
- Troyer KL, Shetye SS, Puttlitz CM. Experimental Characterization and Finite Element Implementation of Soft Tissue Nonlinear Viscoelasticity. J. Biomech. Eng. 2012 doi: 10.1115/1.4007630. [DOI] [PubMed] [Google Scholar]
- Van Ee CA, Chasse AL, Myers BS. Quantifying skeletal muscle properties in cadaveric test specimens: effects of mechanical loading, postmortem time, and freezer storage. J. Biomech. Eng. 2000;122:9–14. doi: 10.1115/1.429621. [DOI] [PubMed] [Google Scholar]
- Van Loocke M, Lyons CG, Simms CK. A validated model of passive muscle in compression. J. Biomech. 2006;39:2999–3009. doi: 10.1016/j.jbiomech.2005.10.016. [DOI] [PubMed] [Google Scholar]
- Van Loocke M, Lyons CG, Simms CK. Viscoelastic properties of passive skeletal muscle in compression: Stress-relaxation behaviour and constitutive modelling. J. Biomech. 2008;41:1555–1566. doi: 10.1016/j.jbiomech.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Van Loocke M, Simms CK, Lyons CG. Viscoelastic properties of passive skeletal muscle in compression-Cyclic behaviour. J. Biomech. 2009;42:1038–1048. doi: 10.1016/j.jbiomech.2009.02.022. [DOI] [PubMed] [Google Scholar]
- Wheatley BB, Fischenich KM, Button KD, Haut RC, Haut Donahue TL. An optimized transversely isotropic, hyper-poro-viscoelastic finite element model of the meniscus to evaluate mechanical degradation following traumatic loading. J. Biomech. 2015;48:1454–60. doi: 10.1016/j.jbiomech.2015.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu W, Chern KY, Mow VC. Anisotropic viscoelastic shear properties of bovine meniscus. Clin. Orthop. Relat. Res. 1994:34–45. [PubMed] [Google Scholar]