Systematic Review and Meta-Analysis of Studies Evaluating Diagnostic Test Accuracy: A Practical Review for Clinical Researchers-Part II. Statistical Methods of Meta-Analysis

Abstract

Meta-analysis of diagnostic test accuracy studies differs from the usual meta-analysis of therapeutic/interventional studies in that, it is required to simultaneously analyze a pair of two outcome measures such as sensitivity and specificity, instead of a single outcome. Since sensitivity and specificity are generally inversely correlated and could be affected by a threshold effect, more sophisticated statistical methods are required for the meta-analysis of diagnostic test accuracy. Hierarchical models including the bivariate model and the hierarchical summary receiver operating characteristic model are increasingly being accepted as standard methods for meta-analysis of diagnostic test accuracy studies. We provide a conceptual review of statistical methods currently used and recommended for meta-analysis of diagnostic test accuracy studies. This article could serve as a methodological reference for those who perform systematic review and meta-analysis of diagnostic test accuracy studies.

INTRODUCTION

Meta-analysis of diagnostic test accuracy studies is a useful method to increase the level of validity by combining data from multiple studies. Ideally, an analytic method used for this type of meta-analysis should estimate diagnostic accuracy with the least bias, incorporating various factors known to affect the results. Several different methods have been proposed for meta-analysis of diagnostic test accuracy studies (1,2,3,4,5,6,7), but there is still considerable uncertainty regarding the best method to synthesize those studies (8). These methods provide either summary points of different accuracy parameters (for example, sensitivity, specificity, positive and negative likelihood ratios, and diagnostic odds ratio [DOR]; for definitions, please refer to Part I of this two-part review) or a summary receiver operating characteristic (SROC) curve (9).

There are several unique characteristics of meta-analysis of diagnostic test accuracy studies compared to therapeutic/interventional studies (8,10). The most important difference is that diagnostic accuracy of a test is generally measured by a pair of summary points, namely, sensitivity and specificity. Although a DOR is a single dimensional parameter for a diagnostic accuracy, it does not provide meaningful practical information for clinical practice (8). Second, a binary medical diagnosis (i.e., presence vs. absence of a target disease condition) is usually based on a certain diagnostic criterion or a threshold that is chosen from a wide range of values or findings. Different studies have different thresholds or criteria that greatly influence the estimation of summary points. In general, a threshold of a diagnostic test that is changed to increase sensitivity results in decreased specificity, and vice versa (3). Third, between-study heterogeneity of diagnostic test accuracy studies is generally larger than that of therapeutic/interventional studies. Imaging scanners and protocols vary greatly between institutions. Even in the same institution, several different scanners and protocols for imaging diagnosis may exist. Moreover, diagnostic imaging studies often greatly differ in their design, conduct, population, and reference standards (1).

Sophisticated statistical methodologies have been evolving to deal with these unique characteristics of diagnostic meta-analysis, especially during recent decades. Some of the most recent methods may not yet be familiar to many radiology researchers or practitioners who want to understand or perform meta-analysis of diagnostic test accuracy studies (11). Although it may be difficult to arrive at a formal unified consensus on the "standard" method to perform meta-analysis of diagnostic test accuracy studies, general recommendations regarding the appropriate statistical methods are available (12,13,14,15). In this review, we summarize the methodological differences between therapeutic/interventional meta-analysis and meta-analysis of diagnostic test accuracy studies (Table 1). In addition, we compare the different statistical methods used to compute summary points of diagnostic accuracy and obtain SROC curves, and further discuss their appropriate use.

Table 1. Comparison of Meta-Analysis of Therapeutic/Interventional Studies and Diagnostic Test Accuracy Studies.

	Therapeutic/Interventional Study	Diagnostic Test Accuracy Study
Number of outcome variables	Single outcome	Pair of outcomes, sensitivity and specificity, which generally inversely correlated
Analysis of heterogeneity between studies	Chi-square test (Cochrane Q statistic): p < 0.1 generally indicates significant heterogeneity Higgins' I2 statistic: rough guide to interpretation is as follows (10);  0% to 25%, might not be important  25% to 50%, may represent low heterogeneity  50% to 75%, may represent moderate heterogeneity  75% to 100%, high heterogeneity	Cochrane Q or Higgins' I2 statistics alone may not be informative as they do not consider threshold effect Visual evaluation of coupled forest plot or SROC plot to find threshold effect Spearman correlation analysis between sensitivity and false positive rate: r ≥ 0.6 generally indicates considerable threshold effect (12)
Meta-analytic summary	Summary point and its 95% CI obtained with  Fixed-effects model: when study heterogeneity does not exist  Random-effects model: when existence of study heterogeneity is suspected	Summary point  Summary sensitivity and specificity and their 95% CIs obtained with bivariate model: recommended Summary plot (SROC curve)  Moses-Littenberg model: not recommended  HSROC curve: recommended

CI = confidence interval, HSROC = hierarchical summary receiver operating characteristic, SROC = summary receiver operating characteristic

Overview of a Choice of Meta-Analytic Methods

As summarized in Table 2, the meta-analytic summary measures can be categorized into summary points (e.g., summary sensitivity, specificity, and DOR) and summary lines (i.e., SROC curves) (1,8). It is appropriate to calculate summary points if the sensitivities and specificities of primary studies do not vary substantially across studies. In general, but not always, this situation occurs when all studies use the same diagnostic threshold (i.e., cut-off value or criterion to categorize the test results as positive or negative) in similar clinical settings. However, such a situation is ideal and rarely occurs in real-world practice or clinical research (11). If there is evidence of a lack of heterogeneity in sensitivity and specificity across studies, two univariate meta-analyses for these measures using either fixed- or random-effects models could be considered. However, if sensitivity and specificity vary markedly and/or there is an evidence of a threshold effect between studies, summary points alone should be avoided, since the summary points such as summary sensitivity, specificity or DOR do not correctly reflect the variability between studies and may miss important information regarding heterogeneity between studies (1). In this case, it is more appropriate to construct a summary line such as a SROC curve to show how the different sensitivities and specificities of primary studies are related to each other. The SROC curve can be calculated with several different methods, as discussed below. Of note, the Diagnostic Test Accuracy Working Group of the Cochrane Collaboration and the Agency for Healthcare Research and Quality (AHRQ) currently recommend the use of hierarchical models (15,16).

Table 2. Statistical Methods for Meta-Analytic Summary Statistics of Diagnostic Test Accuracy Studies.

Method	Summary Measures	Weighting	Comments Summary point
Summary point
Separate pooling	Summary sensitivity, specificity, LR+, LR-, and DOR	Fixed effects or random effects	Not recommended:  Conducts separate meta-analyses for each summary point  Ignores threshold effect as well as correlation between sensitivity and specificity
Hierarchical methods (bivariate/HSROC model)	Summary sensitivity, specificity, LR+, LR-, and DOR	Random effects	Recommended:  Accounts for correlation between sensitivity and specificity  For practical reasons, bivariate model is preferred for computing summary points, while HSROC model is preferred for constructing HSROC curve
Summary line (SROC analysis)
Moses-Littenberg model	SROC curve, AUC, and Q*	Similar to fixed effects	Not recommended:  Does not account for variability between studies  Does not weight studies optimally  Ignores correlation between sensitivity and specificity
Hierarchical model	HSROC curve, AUC, confidence region, and prediction region	Random effects	Recommended:  Accounts for within- and between-study heterogeneity  Accounts for correlation between sensitivity and specificity

AUC = area under the ROC curve, DOR = diagnostic odds ratio, HSROC = hierarchical summary receiver operating characteristic, SROC = summary receiver operating characteristic

Methods to Compute Summary Points of Diagnostic Accuracy Parameters

Separate Pooling of Sensitivity and Specificity

Since sensitivity and specificity are proportions, we can pool these parameters separately by calculating a weighted average using either fixed- or random-effects model, similar to the calculation of a pooled estimate in meta-analysis of therapeutic/interventional studies that have a single proportional outcome. Separate pooling of sensitivity and specificity is still widely used in many meta-analyses of diagnostic test accuracy. Nevertheless, this separate pooling method is applicable only if the sensitivity and specificity are independent of each other, a condition that is rarely satisfied. In fact, sensitivity and specificity are generally correlated, and hence, a separate pooling would inadvertently produce inaccurate results by ignoring the correlation. Moreover, these pooling methods do not have meaningful results unless the studies use the same explicit diagnostic threshold, and thus sensitivity and specificity do not vary widely across studies (1,3).

In separate pooling methods, either fixed- or random-effects model could be used. A fixed-effects model assumes that the true effect for a test accuracy (in both magnitude and direction) is the same (i.e., fixed) across studies and between-study variations or heterogeneities are due solely to random error (i.e., a sampling error). Under this assumption, the underlying common effect is estimated through a weighted average of study results. Specifically, in a fixed-effects model, pooling is made by only considering the weights of included studies using either an inversevariance method, in which the weight (w_i) is based on the variance of normal approximation for a proportion (w_i = n / p [1 - p]), or the study size alone (w_i = n) (1). On the contrary, a random-effects model provides an estimate of the average effect of a diagnostic test accuracy by assuming that the between-study variation or heterogeneity is due to not only random variation (i.e., random error) but also from inherent differences in the magnitudes of test accuracy (usually known as a tau-squared, τ²) between studies, for example, due to differences in the study populations or procedures used (note that a random-effects model does not assume a variation of direction of the study's test accuracies). In the random-effects model, these two sources of variation are considered together in calculating a weight (w_i^*) for each of the included studies in terms of w_i^* = (τ² + w_i^-1)^-1. Here, τ² is the estimated variation or heterogeneity between the effects for test accuracy observed in different studies. The simplest, and hence most commonly used, method of pooling in a random-effects model is the DerSimonian and Laird method (17).

As noted in Part I of this review (9), heterogeneity is almost always presumed in diagnostic test accuracy systematic reviews, and hence, a use of a random-effects model is recommended by default. A use of a fixed-effects model is only appropriate when there are too few studies to estimate between-study variations or when there is no evidence for heterogeneity. A routine use of Cochran's Q-test or Higgins' I² statistic, however, is not recommended in a diagnostic test accuracy review to assess an existence and degree of heterogeneity since they do not account for variation due to a threshold effect. Instead, the Cochrane handbook suggests graphical representation of the magnitude of heterogeneity; for example, the amount of heterogeneity due to the threshold effect in meta-analyzed studies could be examined by estimating the degree of closeness of observed study results to the SROC (15), as well as by calculating how much larger 95% prediction regions are compared with 95% confidence regions (18).

Pooling of a DOR

Diagnostic odds ratio is a single parameter of diagnostic accuracy, hence, it is relatively straightforward to compute pooled summary estimates of DOR. This parameter is also often reasonably constant regardless of variation in the threshold (1). Therefore, DOR can be pooled in the same way as the odds ratio, a common proportional outcome in therapeutic/interventional studies, using either the fixed-effects model with an inverse-variance method or the DerSimonian and Laird random-effects model. The main disadvantage of using DOR as a summary measure is that it is less intuitive and more difficult to interpret in a clinically relevant way. Specifically, it does not distinguish between the ability to detect diseased cases (sensitivity) and the ability to detect non-diseased cases (specificity). The same DOR may also be achieved by different combinations of sensitivity and specificity. For this reason, DOR is not only rarely used as a summary statistic in primary studies for diagnostic test accuracy but also not recommended as an outcome index for its meta-analysis. One exception is studies with the specific aim to analyze the diagnostic association between sensitivity and specificity (19).

Joint Modeling of Sensitivity and Specificity

A joint modeling of both sensitivity and specificity to preserve the two-dimensional nature of diagnostic accuracy using hierarchical models is currently regarded as the optimal method for obtaining summary statistics for meta-analysis of diagnostic test accuracy studies by several authoritative bodies such as the Diagnostic Test Accuracy Working Group of the Cochrane Collaboration or the AHRQ (3,11,15,16). These models are highly recommended when there is a threshold effect in meta-analysis (20).

There are currently two analytical models available for hierarchical modeling: the bivariate model (3) and the hierarchical summary receiver operating characteristic (HSROC) model (21). The HSROC model is occasionally referred to as the Rutter and Gatsonis HSROC model, after the inventors of this model (3,8,21). Both models utilize a hierarchical structure of the distributions of data in terms of two levels, and provide equivalent summary estimates for sensitivity and specificity under the special condition, as described below. At the first level, a within-study variability (i.e., random sampling error) is considered by assuming a binomial distribution for the sensitivity and 1-specificity of each study, respectively. For example, the number of test positives (y_ij) for each study (i) in each disease group (j) is assumed to follow a binomial distribution of y_ij ~ B(n_ij, π_ij), j = 1, 2, where n_ij and π_ij represent the total number of tested subjects and the probability of a positive test result, respectively. The first level is the same in both models. However, they differ at the second level when modeling a between-study difference (i.e., heterogeneity). In the HSROC model, the probability of a subject in study i with disease status j being positive for a test (π_ij) is modeled with a cut-off point (i.e., the proxy of threshold) (θ_i) and an accuracy parameter (i.e., a natural logarithm of DOR) (α_i) that incorporate both the sensitivity and specificity of the study i in the form of a logit (π_ij) = (θ_i + α_i X_ij) exp (-β X_ij). In here, logit implies a natural logarithm of odds (odds is defined as the ratio of a probability being a success to a probability being a failure), the variable X_ij represents a dummy variable for the true disease status of the subject in study i with disease status j, and the parameter β is a scale parameter that is assumed to be a normally distributed random effect for a test accuracy, which can be used for modeling a possible asymmetry in the ROC curve. The between-study variation is, in fact, allowed in the HSROC model by assuming that parameters θ_i and α_i are independently and normally distributed with a mean threshold of Θ and a mean accuracy of Λ, respectively. Covariates (Z_i) that affect unexplained heterogeneity across studies, if any, can be taken into account in the HSROC model by assuming the mean of the parameters θ_i and α_i as a function of the covariates, namely, Θ + YZ_i and Λ + λZ_i, respectively. Whereas, in the second level of the bivariate model, the logit-transformed sensitivity and specificity of the study i are assumed to have a bivariate normal distribution with means µ_A and µ_B, variances σ²_A and σ²_B, respectively, and the covariance σ_AB between logit sensitivity and specificity. This means that the bivariate model allows for a potential correlation between sensitivity and specificity and manages the differences in the precision of the sensitivity and specificity estimates using the five parameters, namely, µ_A, µ_B, σ²_A, σ²_B, and their correlation ρ_AB = σ_AB / (σ_Aσ_B). Like the HSROC model, the bivariate model can also take into account the effect of covariates that affect sensitivity and specificity by replacing the means of µ_A and µ_B with linear predictors in the covariates. This means that explanatory variables can be added to the bivariate model, which leads to separate effects on sensitivity and specificity. Conceptually, the bivariate model is similar to the HSROC model except that the relationship between sensitivity and specificity is addressed by the correlation of its logit transformation in the former and the threshold in the latter. Further mathematical details are beyond the scope of this review, and interested readers are encouraged to read more technical articles (3,7,8).

Both the bivariate model and Rutter and Gatsonis HSROC model could be used to estimate the SROC curve, the summary values of sensitivity and specificity, 95% confidence regions of the summary values, and its 95% prediction regions of the SROC curve. In the absence of covariates or when the same covariates are used for sensitivity and specificity (in the bivariate model) or for the cut-off point and accuracy parameters (in the HSROC model), the two models are mathematically equivalent and provide equivalent estimates of expected sensitivity and specificity (22). When there are covariates, the bivariate model is easier to use due to its ability to incorporate the covariates into the model, as compared to the HSROC model. The bivariate model is preferred for the estimation of a summary value of sensitivity and specificity, as well as for evaluating how their expected values may vary with study level covariates; whereas, the HSROC model is favored for the estimation of the SROC curve for assessing test accuracy and determining how the curve's position and shape may vary with study level covariates (15).

Methods to Obtain SROC Curves

It is recommended to summarize the results of primary studies with varying diagnostic thresholds, with a SROC curve, rather than using summary points such as summary sensitivity or specificity (1). This is because the sensitivity and specificity of a diagnostic accuracy test usually vary with variation in the threshold (i.e., threshold effect). Graphical examination is an easy way to evaluate the threshold effect. When pairs of sensitivity and specificity extracted from each primary study are plotted on a ROC space, a between-study heterogeneity as well as a relationship between sensitivity and specificity can be observed. The horizontal axis of the ROC space uses a false positive rate, that is 1-specificity, while the vertical axis uses sensitivity of primary studies. A SROC curve could be derived from this plot using various statistical modeling methods.

Moses-Littenberg SROC Curve

The Moses-Littenberg method is the simplest and previously the most commonly used model for deriving a SROC in meta-analysis of diagnostic tests (5). This is a sort of fixed-effects model since it does not provide estimates of the heterogeneity between studies; hence, it should be used solely for exploratory purposes. The Moses-Littenberg model fits a straight regression line to the logits of sensitivity and 1-specificity of each study, and uses the estimated intercept and slope in a form of back-transformed values to construct the SROC curve (Fig. 1). A brief description on construction of the Moses-Littenberg SROC curve is as follows: First, the pairs of logit-transformed sensitivity and 1-specificity estimates from each study are used to compute D = logit (sensitivity) - logit (1-specificity) and S = logit (sensitivity) + logit (1-specificity). Note that the variable D is the natural logarithm of DOR itself, while the variable S is a quantity related to the overall proportion of positive test results. Note that, because S increases as the overall proportion of test positives increases, S can be considered as a proxy for a test threshold. Second, a simple linear regression model D = α + βS + ε is fitted using D as a dependent variable and S as an independent variable. Third, use the parameter estimates of α and β to estimate an expected value of sensitivity using the following formula: E (sensitivity) = 1 / [1 + exp {-(α + [1 + β] logit [1-specificity]) / [1 - β]}]. Finally, an SROC curve can be derived by drawing a curve using the expected values of sensitivity across a chosen range of possible values of specificity on the original ROC coordinates. Note that the range of specificities over which the curve is drawn is usually confined to the range observed in the data. An explanation of a more detailed mathematical theory can be found elsewhere (23).

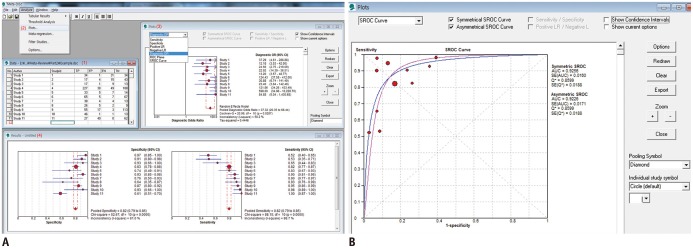
Fig. 1. Examples of forest plot, separate pooling of sensitivity and specificity, and construction of Moses-Littenberg SROC curve (method currently not recommended) using Meta-disc software.

A. Use of Meta-disc. First, data are entered in data window (1). In analyze tab, choose Plots function (2). Then, select plot to draw from new pop-up window (3). Results can be reviewed in Results window (4). B. Moses-Littenberg SROC curve. SROC curves and summary estimates, including area under ROC curve (AUC) and Q^* index are presented. SROC = summary receiver operating characteristic

In the Moses-Littenberg model, the area under the ROC curve (AUC) and an index termed Q^* are provided as global summary measures of the SROC curve. If a test is perfectly accurate, the value of AUC is 1.0, and decreases toward 0.5 as the diagnostic performance of the test decreases. However, since ROC curves of different shapes can have the same AUC, it is inappropriate to interpret the AUC alone when the shape of the ROC curve is unknown. If the test results in the diseased and non-diseased groups have a logistic distribution with equal variance in both groups, the symmetric ROC curves can be obtained in which all points on the curve have a common DOR. When the DOR changes with threshold, the SROC curve becomes asymmetrical (4). Q^* is a point where the SROC curve intersects the diagonal that runs from the top left to the bottom right of the ROC plot, in where sensitivity equals specificity. If Q^* is located in the upper left corner on the SROC curve, it indicates that the test has a good diagnostic performance. The point Q^* can also be calculated by Q^* = (√DOR / [1 + √DOR]). However, the use of Q^* to compare different diagnostic tests is controversial because the range of estimates of sensitivity and specificity from primary studies may not include values near the Q^* point (1,23). Since Q^* often gives a wrong impression of accuracy if SROC curves are asymmetric, and it may bear little relation to the values observed in primary studies used in the meta-analysis, a use of Q^* is generally discouraged (15).

Although the Moses-Littenberg method allows for the correlation between sensitivity and specificity and is convenient for less mathematically or statistically complex meta-analyses, it has several limitations. First, this method is not statistically rigorous because the model's independent variable S is not a fixed but a random variable. Thus, its inherent measurement error violates the basic assumptions of linear regression such as homogeneity of variance and covariates measured without error. Second, since the analysis is based on the DOR, summary measures of sensitivity and specificity are not directly estimated. Third, this method does not take into account the withinand between-study heterogeneity in test accuracy (8). In addition, this method can lead to improper SROC curves where sensitivity decreases as 1-specificity increases if there are outlying studies that influence the determination of the slope of the regression line (15).

Hierarchical Models

As discussed earlier, hierarchical models, namely, the bivariate model and HSROC model, are multivariate methods that jointly analyze sensitivity and specificity. These models utilize the within-study binomial structure of the data while accounting for both within- and between-study heterogeneity; hence, they are currently the most statistically rigorous and recommended methods for dealing with a threshold effect (3,7). Both models produce a HSROC curve as well as summary points of sensitivity and specificity, together with their confidence and prediction region (Fig. 2). As explained earlier, the HSROC model directly estimates HSROC parameters such as accuracy (α_i), threshold (θ_i), and shape parameter (β) as random-effects variables, which enables direct construction of a HSROC curve. On the other hand, in the bivariate model, recalculation of HSROC parameters is required by transforming the estimated parameters of the bivariate model, and subsequently, a HSROC curve can be fitted. For these reasons, the HSROC model is preferred for estimating a HSROC curve. In the HSROC space, the confidence region and prediction region are used to describe an uncertainty of the summary sensitivity and specificity (24). The confidence region relates to the summary estimates of sensitivity and specificity jointly in the HSROC space while it also accounts for their inverse association based on the included studies. However, this region does not represent the between-study heterogeneity (1). On the other hand, the prediction region refers to potential values of sensitivity and specificity that might be observed in a future study by describing the full extent of the uncertainty of the summary points, which therefore can reflect the between-study heterogeneity. The prediction region is a region within which, assuming the model is correct, there is a 95% confidence for the true sensitivity and specificity of a future study (22). Therefore, the prediction region can predict the summary sensitivity and specificity of a similar prospective diagnostic accuracy study (1).

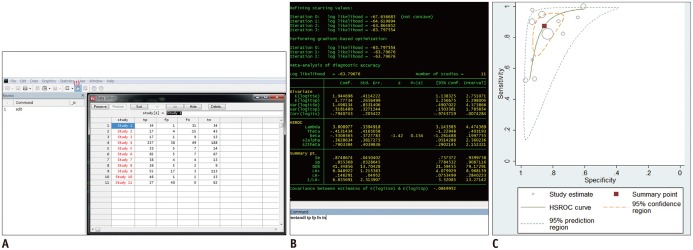
Fig. 2. Example of meta-analysis with hierarchical modeling (method currently recommended). Metandi module in STATA is used.

A. Data input. Simply click data editor button (1) and enter data in Data Editor window (2). B. Calculation of summary estimates. Summary estimates of sensitivity, specificity, DOR, LR+, and LR- can be obtained using command "metandi tp fp fn tn". C. HSROC curve is obtained using command "metandiplot tp fp fn tn". Circles represent estimates of individual primary studies, and square indicates summary points of sensitivity and specificity. HSROC curve is plotted as curvilinear line passing through summary point. 95% confidence region and 95% prediction region are also provided. DOR = diagnostic odds ratio, HSROC = hierarchical summary receiver operating characteristic, LR = likelihood ratio

Software Programs

There are several statistical software programs available for meta-analysis of diagnostic test accuracy studies. The RevMan program (downloadable at http://tech.cochrane.org/revman/download) provides a coupled forest plot, as well as the Moses-Littenberg SROC curve; the Meta-disc program (downloadable at http://www.hrc.es/investigacion/metadisc_en.htm) is also quite straightforward to use and enables a separate pooling of sensitivity and specificity, drawing of the Moses-Littenberg SROC curve, and metaregression analysis using covariates (Fig. 1). However, since they do not provide hierarchical modeling, the methods provided by these software programs are no longer recommended.

Well-established software programs for hierarchical modeling include an open-access program language (R) or commercial statistical softwares (SAS or STATA). The available software programs for diagnostic meta-analysis with the bivariate model or the HSROC model include R (mada package), STATA (midas or metandi modules) or SAS (nlmixed procedure or metadas macros) (24,25). The HSROC curves can be plotted through the RevMan using the parameter estimates obtained from these softwares as input values. The Diagnostic Test Accuracy Working Group of the Cochrane Collaboration has developed practical tutorials for the 'metadas' macro of the SAS, as well as the 'metandi' command of the STATA (http://srdta.cochrane.org/softwaredevelopment).

CONCLUSION

The need for meta-analysis of diagnostic test accuracy studies has noticeably increased in recent decades with the rapid advances in diagnostic imaging tests and increased understanding of evidence-based medicine in the field. At the same time, the statistical methodology for meta-analysis of diagnostic test accuracy studies has been constantly evolving. Authoritative bodies such as the Cochrane Collaboration and the AHRQ currently recommend the use of hierarchical models; hence, the bivariate and HSROC models are expected to be used more frequently in meta-analysis of diagnostic test accuracy studies. As a result, it is imperative for radiology researchers or practitioners to have a good understanding of the methodology and should strive towards a good conceptual grasp of the methods. At the same time, given the complexity of the new statistical methods, it is crucial for clinical researchers to closely collaborate with experienced biostatisticians.