Abstract
Osteoporosis is a progressive bone disease that is characterized by a decrease in bone mass and the deterioration in bone microarchitecture. This study investigates the feasibility of characterizing bone microstructure by analyzing the frequency spectrum of the photoacoustic (PA) signal from the bone. Modeling and numerical simulation of PA signal were performed on trabecular bone simulations and CT scans with different trabecular thicknesses. The resulting quasi-linear photoacoustic spectra were fittted by linear regression, from which the spectral parameter slope was quantified. The simulation based on two different models both demonstrate that bone specimens with thinner trabecular thicknesses have higher slope. Experiment on osteoporotic rat femoral heads with different mineral content was conducted. The finding from the experiment was in good agreement with the simulation, demonstrating that the frequency-domain analysis of PA signals can provide an objective assessment of bone microstructure and deterioration. Considering that PA measurement is non-ionizing, non-invasive, and has sufficient penetration in both calcified and non-calcified tissues, this new bone evaluation method based on photoacoustic spectral analysis holds potential for clinical management of osteoporosis and other bone diseases.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.5120) Photoacoustic imaging, (170.6935) Tissue characterization
1. Introduction
Osteoporosis, widely recognized as a major health issue, is a progressive bone disease that is characterized by a decrease in bone mass and density which can lead to an increased risk of fracture. In osteoporosis, the bone mineral density (BMD) is reduced, bone microarchitecture (BMA) deteriorates, and the amount and variety of proteins in bone are altered. Todate, most of the clinically available diagnostic methods are based on the use of either X-ray or ultrasound (US) [1]. The BMD provided by dual X-ray absorptiometry (DXA) is considered as the “gold standard” for osteoporosis diagnosis. BMD, however, can only explain 60-80% of the variability in bone strength [2]. It has been demonstrated that other mechanical factors, including microarchitecture and post-yield mechanical properties that cannot be tested by DXA, are also important in determining the fracture risk of bone [3, 4]. Non-ionizing and non-invasive quantitative ultrasound (QUS) technologies provide a practical and low-cost alternative for DXA. QUS assessment of bone structure and strength is mainly performed in the transmission mode and based on the measurement of two key parameters including speed of sound (SOS) and broadband ultrasonic attenuation (BUA). These parameters are strongly correlated with BMD but less reflective of the information of bone microstructure [5–7].
Photoacoustic (PA) imaging and sensing, an emerging hybrid technology involving both light and sound, has excellent sensitivity to the chemical and physiological information in biological samples and has been explored for potential application in the diagnosis of osteoporosis [8–15]. Most of the previous research on PA evaluation bone were focused on either the chemical components or ultrasound properties of bone. There is no thorough research yet to explore the feasibility of PA technique in characterizing trabecular bone microstructure which is highly related to bone health. Recently studies from our group and others have demonstrated that the frequency domain power distribution of radio-frequency (RF) PA signal contains information representative of histological microstructures in biological samples [16–20]. To quantitatively evaluate microstructures for potential tissue characterization, a new technique named photoacoustic spectral analysis (PASA), based on frequency domain analysis of PA signals, has been extended from the framework of ultrasound spectral analysis. To extract the main features of the PA signal from a target tissue in the frequency domain, the power spectrum of the radio-frequency PA signal is computed. The power spectrum, after calibration by removing the system impulse response, is fitted by linear regression which leads to three spectral parameters including midband fit, intercept, and slope. The PA spectral parameters are highly relevant to the microstructures of optical absorbers in phantoms and biological tissues [16, 17]. Imaging and sensing the PA spectral parameters also show protential for assessment of cancerous tumors and liver conditions [20, 21]. PASA may offer fundamental advantages for addressing a number of practical problems faced by conventional PA imaging. For example, PASA separates the effects from system components and tissue properties on image features, and delivers system-independent quantitative results. Moreover, performing linear fitting of the averaged power spectrum provides a cogent means of addressing the stochastic nature of tissue microstructures, and can lead to quantitative and repeatable measurements.
In this study, we have, for the first time, examined the feasibility of the newly developed PASA technique in characterizing the microstructures of trabecular bone, and in differentiating bone loss and preservation from normal. Both theoretical modeling and experimental measurements on well-established animal models were conducted. Compared to the other two spectral parameters (i.e. midband fit and intercept), slope is more sensitive to the tissue heterogeneity, and can better reflect the histological microstructures and the spatial distributions of the optical absorbing chemical components in porous trabecular bone. Moreover, slope is less susceptible to the variation in light fluence and, hence, is more reliable for quantitative imaging and objective tissue characterization. Therefore, in this study, the PA spectral parameter slope of each bone specimen was quantified and correlated with the BMD of the bone.
2. Simulation
To evaluate the feasibility of PASA in characterizing trabecular bone microstructures, we first conducted simulations on bone models. Two different models both reflecting the changes in bone microarchitectures were used. The first model, as shown in Fig. 1(A), was based on artificial bones with different levels of bone loss. The porous feature in sample 6 was generated by a computer, with the white area showing the trabeculae and the dark area showing the pores. To represent bone loss at different severities, the samples from 1 to 5 experienced different levels of erosion which gradually reduced the trabecular thickness. The mean trabecular thickness (MTT), for bone samples 1-6 were 0.24, 0.27, 0.31, 0.37, 0.44 and 0.51 mm respectively. The MTT of each sample was quantified following the indirect indices of mean trabecular plate thickness method [22]. The RF PA signal from each sample in Fig. 1(A) were simulated using the k-wave toolbox of Matlab which was developed by the Cox group [23]. To reduce the computational cost, the simulations were performed in a two- dimensional space. However, the conclusions from two-dimensional and three-dimensional simulations are the same, because both follow the same relationship between the PA spectral parameters and the physical sizes of optical absorbers [17].
Fig. 1.
(A) Six artificial trabecular bone samples showing different levels of bone loss. (B) Normalized power spectral density (PSD) and linear fit (R2 = 0.90, 0.90, 0.92, 0.92, 0.94, 0.96, respectively, for samples 1-6) of each bone sample. (C) The spectral parameter slope quantified from the power spectrum of each bone sample presented as a function of the mean trabecular thickness (MTT).
In simulation, the speed of sound and the density were set as 1500 m/s and 1000 kg/m3, and 3200 m/s, 1900 kg/m3, respectively, for water and trabecular bone [23]. The optical absorption coefficient and the Gruneisen parameter of trabeculae are both relevant to the absolute value of the PA signal amplitude. However, since none of them affects the shape of PA signal waveform, these two parameters do not impact the PA spectral parameter slope. Therefore, both of them were set as 1 in simulation. For each bone sample, we simulated the RF PA signals that are received at 50 different positions evenly distributed around the sample. Then the power spectra of the 50 RF PA signals were averaged. The averaging over 50 positions can further emphasize the main features of the power spectrum, and makes the linear fit and the PA spectral parameters less susceptible to the stochastic tissue microstructures. In Fig. 1(B), the normalized power spectrum of the six bone samples following different levels of bone loss are compared. As the bone loss increases (i.e. more bone erosion), the high frequency components of the PA power spectrum increase, which meets our expectation well. When trabeculae are the dominant PA sources in trabecular bone, thicker trabeculae produce PA signal with lower high frequency components. By performing a linear fit of each power spectrum, the spectral parameter slope was quantified. In Fig. 1(C), the slope as a function of the MTT, as well as the rational fitting, is presented. As expected, smaller MTT (or severer bone loss) leads to higher spectral parameter slope.
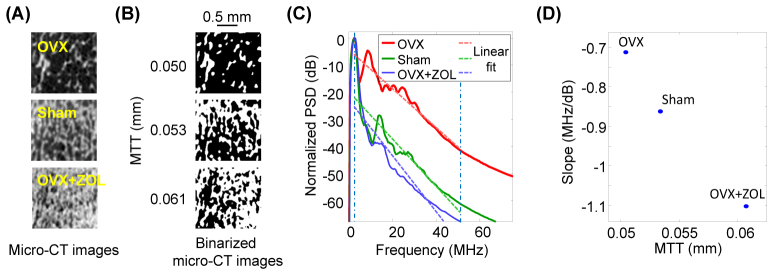
The second bone model for simulation was based on the high resolution micro-CT images acquired from three rat bones with different BMD. The details of rat models of bone loss and preservation are in section 3.2. As shown in Fig. 2(A), the micro-CT images were from three rat tibia (OVX, Sham, and OVX + ZOL). Each amplitude image was binarized, as shown in Fig. 2(B), with the white area showing the trabeculae and the dark area showing the pores. They represent different levels of MTT (0.050, 0.058, 0.061 mm, respectively). The second model for simulation offers only three different levels of trabecular thicknesses. However, compared to the first artificial bone model, the scond model, which is based on real bone specimens, is more realistic and may better reflect the spongy feature of trabecular bone. The RF PA signals from each bone sample in Fig. 2(B) were also simulated using the same Matlab k-wave toolbox [23]. With the RF PA signals received at 50 positions evenly distributed around the sample, the power spectra were averaged, as shown in Fig. 2(C), and a linear fit of the power spectra was performed to draw the quantified PA spectral parameter slope of each bone sample. Same as the finding from the first model, the simulation from this second model suggests that thinner MTT leads to higher spectral parameter slope again, as shown in Fig. 2(D).
Fig. 2.
(A) Micro-CT images of three rat tibia bones (OVX, Sham, and OVX + ZOL) with different trabecular microstructures, i.e. different mean trabecular thickness (MTTs). (B) Binarized micro-CT images of the three rat tibia bones. Their qualified MTTs were 0.050, 0.053, 0.061 mm respectivly. (C) Normalized power spectral density (PSD) and linear fit (R2 = 0.95, 0.86, 0.85, respectively, for OVX, Sham, and OVX + ZOL) of each bone sample. The leads to quantified spectral parameter slope. (D) The spectral parameter slope quantified from the power spectrum of each bone sample.
3. Experiment and analysis
3.1 Experiment setup
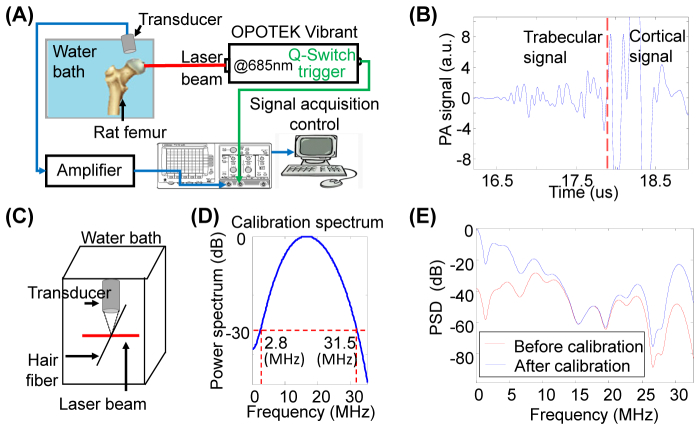
As show in the schematic of the experiment setup in Fig. 3(A), an OPO system (Vibrant B, Opotek) pumped by an Nd:YAG laser (Brilliant B, Bigsky) was used to provide laser pulses with a repetition rate of 10 Hz and a pulse width of 5.5 ns. The laser beam with 2 mm in diameter illuminating the bone surface generates PA signals which were received by a 20 MHz focused transducer (V317, Panametrics). Working at 685-nm wavelength, the light fluence on the bone surface was 19.2 mJ/cm2 which was within the ANSI safety limit. The bone sample and the transducer were immersed in a water bath for acoustic coupling. The PA signals from the bone specimen were recorded by a digital oscilloscope (TDS 540B, Tektronics). An example PA signal from a rat femur is shown in Fig. 3(B). This A-line includes both signal from the trabecular architecture and signal from the cortical structure. In this study, we tried to avoid the strong signal from the cortical bone and focus on the trabecular bone only. To achieve this, the direction of light illumination and the direction of PA signal detection were arranged with an angle between them larger than 90 degrees. In this case, the strong PA signal from the cortical bone at the light illuminated side arrived at the transducer later than the PA signal from the trabecular part. As shown in Fig. 3(B), the trabecular signal can be differentiated from the signals generated in cortical layers based on their difference in time of flight.
Fig. 3.
Experimental setup for PA measurement of bone. (B) Typical RF PA signals from a rat femur. Trabecular signal and cortical signal was distinguished base on the time flight. (C) Geometry for measuring the RF PA signal from a thin hair fiber (i.e. a point source) to be used for calibration. (D) The power specrum of the PA signal from the point source that was used later in calibrating the PA measurement from each bone specimen. (E) Power spectra density (PSD) of the trabecular signal in (B) before and after calibration.
The calibration measurement used for PA spectral analysis was performed on a hair fiber with a diameter of 70 μm, as shown in Fig. 3 (C). The PA signal from the hair fiber was generated using the same light illumination geometry as those for the measurement on bone specimens. The hair fiber was placed at the focal point of the transducer. With a small size comparable to the acoustic wavelength at the center frequency of the transducer, the hair fiber illuminated by a narrow laser beam formed a point source leading to a broadband PA signal, as shown in Fig. 3(D). To account for the system response, the measurement from each bone was calibrated by dividing the PA power spectrum from the bone by the PA power spectrum from the point source. The PSD of the PA signal in Fig. 3 (B) before and after calibration was shown in Fig. 3(E). After calibration for each bone sample, the linear regression was performed in the spectral range of 2.8-31.5 MHz which was determed by the −30 dB of the power spectrum from the point source, as shown in Fig. 3(D).
3.2 Animal model
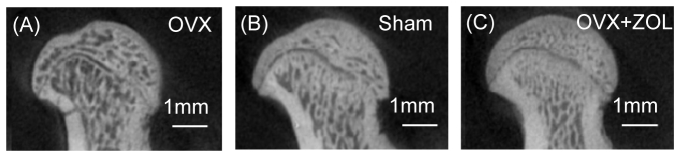
In this study, well-established rat models of bone loss and preservation were employed. 3-4 month female Sprague-Dawley rats were subject to sham surgery (Sham, N = 4), ovariectomy (OVX, N = 4), or OVX plus weekly Zoledronic Acid (OVX + ZOL, N = 4, 1.6 µg/kg/wk i.p.) [24]. The OVX rat model is required by the FDA for the evaluation of agents used to treat or prevent postmenopausal osteoporosis, and the model has been validated based on the early bone turnover that produces bone loss following estrogen withdrawal. 4 weeks after surgery, rats were euthanized, and femora were dissected and subject to PA assessment. Significant reduction in bone mass in the femoral heads was evident in the OVX rats, while rats from the OVX + ZOL group provide a model of bone preservation. Using the setup shown in Fig. 3, PA measurement was performed ex vivo on the femoral head. To validate the findings from PA measurements, the bone specimens were also scanned by a micro-CT (GE Healthcare eXplore Locus RS). The microCT images, as shown in Fig. 4, verified that the MTT of OVX diminished significantly, resulting in 56.0% reduction; while for OVX + ZOL rats, the MTT increased about 18.1% over the sham controls.
Fig. 4.
Example micro-CT images of femur bones of female rats subject to (A) OVX, (B) Sham, and (C) OVX + ZOL with mean trabecular thickness (MTT) 0.10, 0.22 and 0.26 mm, demonstrating the decrease and increase in MTT for the bones in the OVX and OVX + ZOL groups, respectively, in comparion to the normal controls.
3.3 Experiment results
Figure 5(A) shows the examples of calibrated PA power spectral density (PSD), as well as the east-square linear fit, from the three bone groups (i.e. OVX, Sham, OVX + ZOL). The linear fit enabled the extraction of the spectral parameters including the slope that were further analyzed. In comparison with the sham control (normal), the power spectra from the OVX bones containing less and thinner trabeculae have stronger high frequency components; while the OVX + ZOL bones containing higher amount and larger size of trabeculae show weaker compared in Fig. 5(B), suggesting that, at 685-nm wavelength, the osteoporosis bones (OVX) have larger slope than the bones from the other two groups with higher BMD. Although with considerable overlap, the measurements from the sham and the OVX + ZOL groups also show noticeable difference. The finding from the experiment on the rat models of bone loss and preservation has a good agreement with that from the simulations.
Fig. 5.
PASA of rat femur bone specimens. (A) Examples of power spectral density (PSD) of the RF PA signal of three groups (OVX, Sham, OVX + ZOL) after calibration by removing the system response. The corresponding linear fit (R2 = 0.24, 0.78, 0.68, respectively, for OVX, Sham, and OVX + ZOL) in the spectral range of 2.8-31.5 MHz leads to quantified spectral parameter slope. (B) The quantified spectral parameter slope of the three groups of bones.
4. Conclusion and discussion
The results from this study suggest the feasibility of a novel PASA technique, by quantitatively analyzing the frequency spectrum of the RF PA signal measured from the bone, in objective assessment of bone microarchitecture. The MTT, an important factor determining the bone strength, can be correlated with the spectral parameter slope quantified from the PA power spectrum. Considering the unique advantages of PA measurement, including high sensitivity, being non-ionizing and non-invasive, and sufficient penetration in both calcified and non-calcified tissues, this new PASA technique holds potential for clinical translation to clinic. However, studies involving larger number of samples from animal models and human patients are necessary to verify these findings.
In this work exploring the relationship between PA spectral parameter and bone microstructure, simulations based on k-space algorithm were conducted, which helped us to understand the findings from the experiment. k-space algorithm can deal with the complications during PA signal propagation through the bone including ultrasonic scattering, reflection, and refraction at the numerous interfaces. However, k-space algorithm does not consider shear waves, various propagating acoustic modes, frequency dependent acoustic velocity and material attenuation which all affect the propagation and detection of PA signal from the bone. Therefore, future study based on more accurate modeling is needed to fully understand how each bone parameter affects PA signal in time and frequency domain.
As another limitation of this work, neither the simulation nor the experiment has considered the soft tissue covering the bone. As a major impact, the ultrasonic attenuation in the soft tissue overlying the bone may change the PA power spectrum and the spectral parameter slope. As an example, considering that the mean thickness of the soft tissue over human calcaneus bone is 8.5 +/− 1.5 mm [25] and the ultrasonic attenuation coefficient in soft tissue is about 0.54 (dB/(MHz·cm)) [26], the PA spectral parameter slope is estimated to decrease about 0.46 +/− 0.08 (dB/MHz) as a result of the ultrasonic attenuation in overlying soft tissue. When the thickness of overlying soft tissue in known, this impact, however, can be largely compensated, especially when PASA is performed in conjunction with QUS [27].
Considering that both PASA and QUS involve broad band ultrasonic detection, PASA is a natural complement to QUS techniques which have been extensively studied and have already led to clinical instruments. In future clinical settings, PASA could be combined with QUS to realize PA-QUS dual measurement of bone. It is worth noting that the parameter slope of BUA quantified in QUS reflects the relationship between the attenuation of sound signals through bone and its frequency. The spectral parameter slope as quantified in PASA refers to the descent rate of the PA spectral magnitude with respect to the frequency. Therefore, these two shopes, although with the same unit of dB/MHz, have different physical meanings, and may have different correlations with bone microstructure. Unlike QUS, the ultrasonic signal in PASA is not produced by the transmit probe but instead by the laser light illumination in bone. The frequency components of the initial pressure waves in a trabecular bone are mainly determined by its microstructal features. Therefore, it is reasonable to expect that the PA signal from bone could carry richer and more direct information of bone microstructure. Before being received by the transducer, the PA signal from a bone would also be affected by the ultrasonic attenuation in the trabecular and cortical parts of the bone as well as in the overlying soft tissues. In bones with higher BMD, the ultrasound attenuation is stronger, especially in the high frequency range, which also affects the shape of the power spectrum of the received PA signal. Therefore, the PA spectral parameter slope is a combination of not only bone microstructures but also its ultrasonic properties. In order to separate these two aspects, the bone ultrasonic properties which could be quantified by QUS may be introduced into the procedure of PASA to achieve better accuracy for bone characterization. In comparison with DEXA, QUS has lower device and operating costs. In this proof-of-principle study, the light source for PASA was from an Nd:YAG laser pumped OPO which significantly increased the cost of this bone evaluation device. In the future, the PASA of bone can be implemented inexpensively by using high-power laser diodes which has already been adapted to biomedical PA imaging and sensing [28, 29].
Acknowledgments
This research was supported by National Institute of Health under grant numbers R01AR060350 and R01CA186769, and R21AR061594, National Natural Science Foundation of China under grants number 61201425, Natural Science Foundation of Jiangsu Province under grants number BK20131280, and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References and links
- 1.Pisani P., Renna M. D., Conversano F., Casciaro E., Muratore M., Quarta E., Paola M. D., Casciaro S., “Screening and early diagnosis of osteoporosis through X-ray and ultrasound based techniques,” World J. Radiol. 5(11), 398–410 (2013). 10.4329/wjr.v5.i11.398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Albanese C. V., De Terlizzi F., Passariello R., “Quantitative ultrasound of the phalanges and DXA of the lumbar spine and proximal femur in evaluating the risk of osteoporotic vertebral fracture in postmenopausal women,” Radiol. Med. (Torino) 116(1), 92–101 (2011). 10.1007/s11547-010-0577-1 [DOI] [PubMed] [Google Scholar]
- 3.Hayes W. C., Piazza S. J., Zysset P. K., “Biomechanics of fracture risk prediction of the hip and spine by quantitative computed tomography,” Radiol. Clin. North Am. 29(1), 1–18 (1991). [PubMed] [Google Scholar]
- 4.Glüer C. C., Wu C. Y., Jergas M., Goldstein S. A., Genant H. K., “Three quantitative ultrasound parameters reflect bone structure,” Calcif. Tissue Int. 55(1), 46–52 (1994). 10.1007/BF00310168 [DOI] [PubMed] [Google Scholar]
- 5.Töyräs J., Nieminen M. T., Kröger H., Jurvelin J. S., “Bone mineral density, ultrasound velocity, and broadband attenuation predict mechanical properties of trabecular bone differently,” Bone 31(4), 503–507 (2002). 10.1016/S8756-3282(02)00843-8 [DOI] [PubMed] [Google Scholar]
- 6.Liu C., Ta D., Fujita F., Hachiken T., Matsukawa M., Mizuno K., Wang W., “The relationship between ultrasonic backscatter and trabecular anisotropic microstructure in cancellous bone,” J. Appl. Phys. 115(6), 064906 (2014). 10.1063/1.4865173 [DOI] [Google Scholar]
- 7.Njeh C. F., Boivin C. M., Langton C. M., “The role of ultrasound in the assessment of osteoporosis: a review,” Osteoporos. Int. 7(1), 7–22 (1997). 10.1007/BF01623454 [DOI] [PubMed] [Google Scholar]
- 8.Lashkari B., Mandelis A., “Coregistered photoacoustic and ultrasonic signatures of early bone density variations,” J. Biomed. Opt. 19(3), 036015 (2014). 10.1117/1.JBO.19.3.036015 [DOI] [PubMed] [Google Scholar]
- 9.Lashkari B., Yang L., Mandelis A., “The application of backscattered ultrasound and photoacoustic signals for assessment of bone collagen and mineral contents,” Quant. Imaging Med. Surg. 5(1), 46–56 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang L., Lashkari B., Tan J. W., Mandelis A., “Photoacoustic and ultrasound imaging of cancellous bone tissue,” J. Biomed. Opt. 20(7), 076016 (2015). 10.1117/1.JBO.20.7.076016 [DOI] [PubMed] [Google Scholar]
- 11.Feng T., Kozloff K. M., Tian C., Perosky J. E., Hsiao Y.-S., Du S., Yuan J., Deng C. X., Wang X., “Bone assessment via thermal photo-acoustic measurements,” Opt. Lett. 40(8), 1721–1724 (2015). 10.1364/OL.40.001721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Steinberg I., Eyal A., Gannot I., “Multispectral photoacoustic method for the early detection and diagnosis of osteoporosis,” in SPIE BiOS(International Society for Optics and Photonics, 2013), pp. 85656G–85656G–85659. [Google Scholar]
- 13.Steinberg I., Gannot I., Eyal A., “Investigation of a dual modal method for bone pathologies using quantitative ultrasound and photoacoustics,” in SPIE BiOS(International Society for Optics and Photonics, 2015), pp. 93230R–93230R–93236. [Google Scholar]
- 14.Pifferi A., Torricelli A., Taroni P., Bassi A., Chikoidze E., Giambattistelli E., Cubeddu R., “Optical biopsy of bone tissue: a step toward the diagnosis of bone pathologies,” J. Biomed. Opt. 9(3), 474–480 (2004). 10.1117/1.1691029 [DOI] [PubMed] [Google Scholar]
- 15.Moilanen P., Zhao Z., Karppinen P., Karppinen T., Kilappa V., Pirhonen J., Myllylä R., Haeggström E., Timonen J., “Photo-acoustic excitation and optical detection of fundamental flexural guided wave in coated bone phantoms,” Ultrasound Med. Biol. 40(3), 521–531 (2014). 10.1016/j.ultrasmedbio.2013.10.018 [DOI] [PubMed] [Google Scholar]
- 16.Yang Y., Wang S., Tao C., Wang X., Liu X., “Photoacoustic tomography of tissue subwavelength microstructure with a narrowband and low frequency system,” Appl. Phys. Lett. 101(3), 034105 (2012). 10.1063/1.4736994 [DOI] [Google Scholar]
- 17.Xu G., Dar I. A., Tao C., Liu X., Deng C. X., Wang X., “Photoacoustic spectrum analysis for microstructure characterization in biological tissue: A feasibility study,” Appl. Phys. Lett. 101(22), 221102 (2012). 10.1063/1.4768703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang S., Tao C., Wang X., Liu X., “Quantitative detection of stochastic microstructure in turbid media by photoacoustic spectral matching,” Appl. Phys. Lett. 102(11), 114102 (2013). 10.1063/1.4798272 [DOI] [Google Scholar]
- 19.Strohm E. M., Gorelikov I., Matsuura N., Kolios M. C., “Modeling photoacoustic spectral features of micron-sized particles,” Phys. Med. Biol. 59(19), 5795–5810 (2014). 10.1088/0031-9155/59/19/5795 [DOI] [PubMed] [Google Scholar]
- 20.Kumon R. E., Deng C. X., Wang X., “Frequency-domain analysis of photoacoustic imaging data from prostate adenocarcinoma tumors in a murine model,” Ultrasound Med. Biol. 37(5), 834–839 (2011). 10.1016/j.ultrasmedbio.2011.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu G., Meng Z.-X., Lin J. D., Yuan J., Carson P. L., Joshi B., Wang X., “The Functional Pitch of An Organ: Quantification of Tissue Texture with Photoacoustic Spectrum Analysis,” Radiology 271(1), 248–254 (2014). 10.1148/radiol.13130777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Parfitt A. M., Mathews C. H., Villanueva A. R., Kleerekoper M., Frame B., Rao D. S., “Relationships between surface, volume, and thickness of iliac trabecular bone in aging and in osteoporosis. Implications for the microanatomic and cellular mechanisms of bone loss,” J. Clin. Invest. 72(4), 1396–1409 (1983). 10.1172/JCI111096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cox B. T., Kara S., Arridge S. R., Beard P. C., “k-space propagation models for acoustically heterogeneous media: Application to biomedical photoacoustics,” J. Acoust. Soc. Am. 121(6), 3453–3464 (2007). 10.1121/1.2717409 [DOI] [PubMed] [Google Scholar]
- 24.Glatt M., Pataki A., Evans G. P., Hornby S. B., Green J. R., “Loss of vertebral bone and mechanical strength in estrogen-deficient rats is prevented by long-term administration of zoledronic acid,” Osteoporos. Int. 15(9), 707–715 (2004). 10.1007/s00198-004-1588-3 [DOI] [PubMed] [Google Scholar]
- 25.Chappard C., Camus E., Lefebvre F., Guillot G., Bittoun J., Berger G., Laugier P., “Evaluation of error bounds on calcaneal speed of sound caused by surrounding soft tissue,” J. Clin. Densitom. 3(2), 121–131 (2000). 10.1385/JCD:3:2:121 [DOI] [PubMed] [Google Scholar]
- 26.Culjat M. O., Goldenberg D., Tewari P., Singh R. S., “A review of tissue substitutes for ultrasound imaging,” Ultrasound Med. Biol. 36(6), 861–873 (2010). 10.1016/j.ultrasmedbio.2010.02.012 [DOI] [PubMed] [Google Scholar]
- 27.Oelze M. L., O’Brien W. D., Jr., “Frequency-dependent attenuation-compensation functions for ultrasonic signals backscattered from random media,” J. Acoust. Soc. Am. 111(5), 2308–2319 (2002). 10.1121/1.1452743 [DOI] [PubMed] [Google Scholar]
- 28.Allen T. J., Cox B. T., Beard P. C., “Generating photoacoustic signals using high-peak power pulsed laser diodes,” in Photons Plus Ultrasound: Imaging and Sensing 2005, Oraevsky A. A., Wang L. V., eds. (Spie-Int Soc Optical Engineering, Bellingham, 2005), pp. 233–242. [Google Scholar]
- 29.Karppinen P., Salmi A., Moilanen P., Karppinen T., Zhao Z. M., Myllyla R., Timonen J., Haeggstrom E., “Phase-delayed laser diode array allows ultrasonic guided wave mode selection and tuning,” J. Appl. Phys. 113(14), 144904 (2013). 10.1063/1.4801394 [DOI] [Google Scholar]