Effect of finite metallic grating size on Rayleigh anomaly-surface plasmon polariton resonances

Abstract

Rayleigh anomalies (RAs) and surface plasmon polaritons (SPPs) on subwavelength metallic gratings play pivotal roles in many interesting phenomena such as extraordinary optical transmission. In this work, we present a theoretical analysis of the effect of finite metallic grating size on RA-SPP resonances based on the combination of rigorous coupled wave analysis and finite aperture diffraction. One-dimensional arrays of gold subwavelength gratings with different device sizes were fabricated and the optical transmission spectra were measured. As the grating size shrinks, the broadening of the RA-SPP resonances is predicted by the theoretical model. For the first order RA-SPP resonances, the results from this model are in good agreement with the spectra measured from the fabricated plasmonic gratings.

1. Introduction

Extraordinary optical transmission (EOT) through periodic subwavelength diameter airholes [1] or narrow slits [2] in metal film has been the subject of intensive research in plasmonics for many years. The mechanisms underlying the EOT in these grating or photonic crystal systems can be attributed to the complex interaction among surface plasmon polaritons (SPPs), Rayleigh Anomalies (RAs), waveguide modes, and even the Fabry-Perot (FP) resonances inside the airholes or slits [1–9]. Interestingly, RAs originated from the observations by Wood as early as 1902 [10] and were physically interpreted by Rayleigh [11] and Fano [12] as the passing-off of a spectral diffraction order, and are associated with both plasmonic and dielectric gratings. For the simplest structure consisting of a thin metallic grating on top of a glass substrate as shown in Fig. 1 (a), waveguide modes and F-P resonances inside the slits are not supported, therefore, the EOT phenomenon is described by the coupling of RAs on one side of the film with SPP Bloch waves (SPP-BWs) on the opposite side [6, 8]. Nevertheless, such theoretical analysis was based on infinitely large metallic grating size and experimental characterization used very large gratings (millimeter size), which can be a good approximation to the modeling. Driven by chip-scale optical interconnects and lab-on-chip sensing applications using subwavelength gratings [13, 14], it is becoming increasingly urgent to minimize the footprint of integrated photonic devices. Assuming an infinite size metallic grating in modeling is invalid and implementing a large size device is not practical for these new applications. However, to take this ‘finiteness’ into account is quite troublesome. Finite element analysis (FEA) calculations can be useful but if the grating size is quite large (but finite), large computer resources and long calculation time are required. There are a few semi-analytic methods that basically treat the finite grating as an array of electromagnetic radiators or scatters [15, 16]. Nevertheless, they are too complicated and are not adequate for large gratings either.

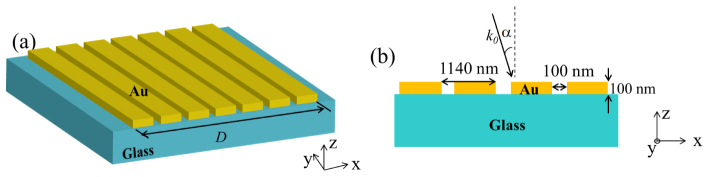
Fig. 1.

(a) Schematic illustration of the finite Au grating on a glass substrate (b) cross-sectional view of the structure with geometric parameters.

In the past years, guided-mode resonance filters (GMRFs) using dielectric gratings with finite grating periods and finite input beam size have been analyzed using different numerical approaches [17–19]. In this paper, we present the theoretical study of the effect of finite size on RA-SPP resonances in metallic gratings that are not presented in dielectric GMRFs. The analysis is based on the combination of the finite aperture diffraction and the transmission spectrum of the infinite metallic grating obtained by the rigorous coupled wave analysis (RCWA) [20]. In an effort to verify the theoretical analysis, experimental data of the transmission properties of the gold(Au)/glass grating are presented and compared with the simulation results. The comparison clearly confirmed that the broadening in RA-SPP resonances matched very well with the modeling as the size of the grating shrinks.

2. Simulation and theoretical analysis

Our proposed structure consists of a one-dimensional (1-D) periodic Au array structure on a glass substrate with refractive index n of 1.502 as shown in Fig. 1(a). The Au film thickness is 100 nm, the grating period is 1140 nm and the gap width is 100 nm, as shown in the cross-sectional view in Fig. 1 (b). When a transverse-magnetic (TM) plane wave excites the plasmonic grating from the top with an incident angle of α, the grating with periodicity p will add additional photon momentum in integer multiples of G = 2π/p in the x direction. In this case, SPPs are excited under the phase matching condition [21],

$$k_{SPP}=k_0\sin \alpha \pm iG =\mathrm{Re}\left|\frac{\omega }{c}\sqrt{\frac{{\epsilon }_{Au}{\epsilon }_d}{{\epsilon }_{Au}+{\epsilon }_d}}\right|,$$ (1)

where ω, c, and k₀ are the angular frequency, velocity, and momentum of light in free space, ε_d and ε_Au are the dielectric permittivity of the dielectric medium and Au, respectively. i is an integer which denotes specific SPP mode, and α is the incident angle. Besides SPP waves, RAs are excited as well, which come from the diffracted wave propagating parallel to the grating surface. RAs occur under the condition [22],

$$k_{RA}=k_0\sin \alpha \pm iG =\mathrm{Re}\left|\frac{\omega }{c}\sqrt{{\epsilon }_d}\right|.$$ (2)

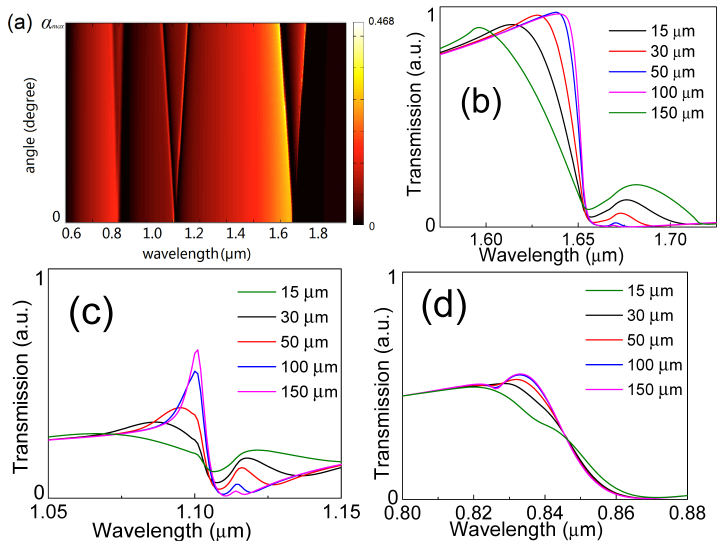
The coupling between RAs and SPPs on metal/dielectric interfaces leads to EOT with narrow spectral features at specific wavelengths [23]. Figure 2(a) shows the simulation results of the total transmitted optical power using RCWA from 600 nm to 1900 nm by scanning the incident angle α from 0 to 3.2°, with a simulation step of 0.016°. In the wavelength range of 1000 nm to 1900 nm, two Fano Resonances are formed due to the first order RA-SPPs for surface-normally incident TM light: one at the top air-Au interface at 1634 nm, and the other at the bottom Au-glass interface at 1076 nm. Higher order RA-SPPs can also be observed, and a minimum transmission of second order RA-SPPs at the Au-glass interface is shown at 823 nm. With an incident angle of the incoming light, symmetry is broken and each pair of RA-SPPs splits into a high and low-energy branch from Eq. (1). The wavelength separation between the two branches increases with the incident angle α, as shown in Fig. 2(a).

Fig. 2.

(a) RCWA simulation of total transmitted power with different angular incidences. Summary of the simulated results for grating sizes D from 15 μm to 150 μm are shown in the plots of (b) first order RA-SPP at Au/glass interface (c) first order RA-SPP at Au/air interface (d) second order RA-SPP at Au/glass interface.

In the next step, we will consider the effect of finite size of the grating. As 100nm Au film is almost completely opaque to visible and near-infrared wavelength, we can treat the structure as an infinite grating with an aperture window of D, where D is the size of the grating as shown in Fig. 1(a). When a plane wave U(x) passes through a finite grating, the electric field is modulated by both effects of the infinite plasmonic grating and the aperture window.Therefore, the near-field electric field amplitude can be expressed as

$$E(x)=g_{gr}(x)f_{ap}(x)U(x),$$ (3)

where g_gr(x) denotes the transfer function due to the infinite grating, and f_ap(x) is the aperture window function. Based on Fraunhofer diffraction theory [24], the electric field measured at the far field becomes the spatial Fourier transform of the near-field distribution, which is

$$E(\theta )\propto {F\left[g_{gr}(x)f_{ap}(x)U(x)\right]|}_{f_x=\frac{x}{\lambda z}=\frac{\theta }{\lambda }},$$ (4)

where θ is the angular divergence of the diffracted light. Since F[U(x)] ~δ(f_x−α/λ), Eq. (4) becomes

$$\begin{array}{l}E(\theta )\propto {F\left[g_{gr}(x)f_{ap}(x)\right]|}_{f_x=\frac{\theta -\alpha }{\lambda }}\\ ={\displaystyle \int G_{gr}\left(\frac{\theta -\alpha }{\lambda }-\xi \right)F_{ap}(\xi )d\xi },\end{array}$$ (5)

where G_gr(f_x) and F_ap(f_x) denote the spatial Fourier transforms of g_gr(x) and f_ap(x), respectively, and F_ap is a well-known sinc function. With that, we can solve the transmitted intensity I(θ) at the far field by calculating the convolution given by

$$I(\theta )\propto {\left|{\displaystyle \int G_{gr}\left(\frac{\theta -\alpha }{\lambda }-\xi \right)\sin c(D\xi )d\xi }\right|}^2.$$ (6)

Considering that, for subwavelength grating, only zeroth-order diffraction mode exists in the long wavelength range and its diffraction angle is equal to the incident angle, we can write G_gr(θ/λ−α/λ) ~G₀(α)δ(θ/λ−α/λ), where |G₀(α)|² represents the transmitted optical power when the incidence angle is α [see Fig. 2(a)]. Therefore. Equation (6) can be further approximated as

$$I(\theta )\propto {\left|G_0(\alpha )\right|}^2\sin {\text{c}}^2\left[D\left(\frac{\theta -\alpha }{\lambda }\right)\right].$$ (7)

Using this combined analytical-numerical approach, the overall transmission spectra of the finite plasmonic grating are plotted in Figs. 2(b)-2(d). The broadening of RA-SPP resonances due to the reduction of the grating size can be clearly seen from the simulation results, especially for the fundamental resonances in Figs. 2(b) and 2(c).

3. Experiment

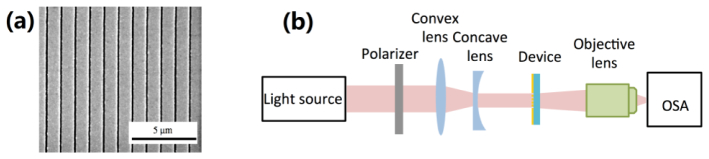
To verify our calculation, we fabricated an array of subwavelength Au gratings on a glass substrate. Au thin film was deposited onto the glass substrate by thermal evaporation with a deposition rate of 5 Å/sec, resulting in a film thickness of 100 nm. An array of Au gratings was fabricated by focused-ion beams (FIB) with grating sizes of 15 μm, 30 μm, 50 μm, 100 μm, and 150 μm. The nano-scale structures were patterned by gallium ion beams with ion energy and current controlled at 30 kV and 30 pA, respectively. Figure 3(a) shows the scanning electron microscopy (SEM) image of the fabricated plasmonic grating. Controlling the width of the gap and minimizing the fabrication defects are crucial for obtaining sharp RA-SPP resonances for the device. During the fabrication process, the geometrical dimensions are precisely controlled and smooth Au slits were obtained using FIB. Figure 3(b) shows the experimental setup of measuring the transmission spectrum. A broadband supercontinuum white light source (NKT Photonics) with free-space collimated beam was used as input source. A polarizer was used to generate a linearly TM polarized light with electric field polarized perpendicular to the slit direction. The beam size was reduced to ~500 μm by using a free-space convex and a concave lenses. Compared with the size of the plasmonic gratings, the beam spot size is much larger. Therefore, the incident light can be approximated as a plane wave. The device was mounted on a five axis stage, which allowed precise adjustment of the linear translations as well as the incident angle within 0.0029 ˚. The output light was then focused through a 40 × objective lens (NA = 0.65) and coupled into an optical spectrum analyzer (HP70951A).

Fig. 3.

(a) SEM image shows the fabricated grating with smooth slits; and (b) Transmission measurement setup

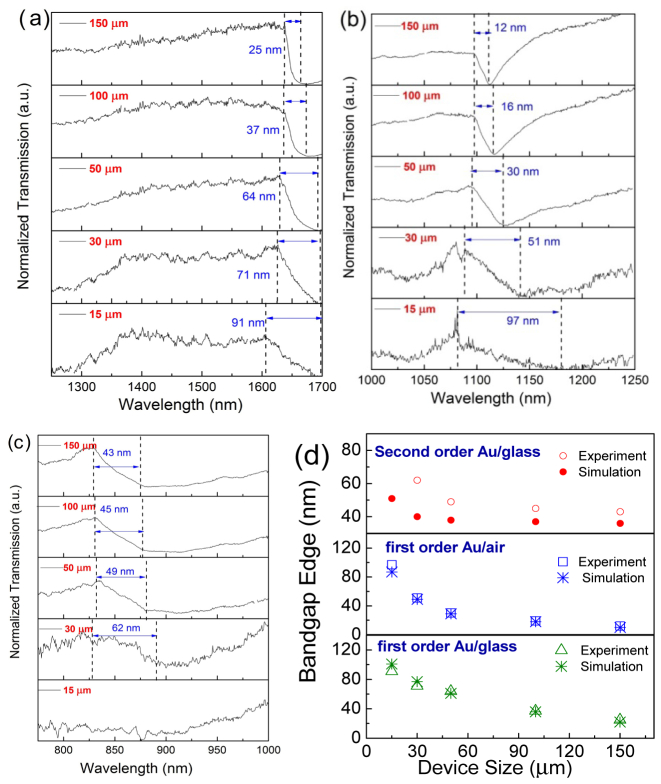
The normalized optical transmission spectra were measured for the gratings size of 15 μm, 30 μm, 50 μm, 100 μm, and 150 μm. Figures 4(a)-4(c) shows the zoomed-in transmission at the wavelength range of 1250-1700nm, 1000-1250nm, and 750-1000nm, respectively. As predicted by the modeling in Section 2 and Figs. 2(b)-2(d), when the size of the grating shrinks, the RA-SPP resonances became less pronounced. The RA-SPP resonances with the sharpest transition edge always occur on the 150 μm plasmonic grating. In order to quantitatively compare our model with experimental results, we summarized the transition edge of the RA-SPP resonances in Fig. 4(d) representing the first-order RA-SPPs at Au/glass (~1634 nm) and Au/air interfaces (~1076 nm), and the second order RA-SPPs at the Au/glass(~823 nm) interface. The bandwidth of the transition edge is accounted as the wavelength range from the maximum transmission (RA) to the minimum transmission (SPP-BW). For the first-order RA-SPPs at Au/glass and Au/air interfaces, the modeling results of the bandwidth of the transition edge matched very well with the experimental results. However, when we compare the shape of the transmission spectra, the small peaks of the transition edge in the simulation results in Figs. 2(b) and 2(c) due to the low-energy branch were not observed in the experimental results in Figs. 4 (a) and 2(b). This is possibly due to the fluctuation of the light source or the measurement error at low optical power as the grating size shrinks. The measured transition edges of the higher order RA-SPPs within 750-1000nm are broader than the modeling results. We must point out that the modeling results have underestimated the higher order RA-SPP broadening by approximating Eq. (6) to Eq. (7). In addition, thermally evaporated Au film shows higher imaginary part of the dielectric permittivity than bulk Au adopted in the simulation, which results in the higher loss at shorter wavelength range since the electro-magnetic waves penetrate deeper into the metal.

Fig. 4.

Measured spectra showing the transmission within (a) first order Au/glass within 1250-1700 nm. (b) first order Au/air within 1000-1250 nm and (c) second order Au/glass within 750-1000 nm (d) Summary of the simulated and experiment results of transitional edges vs. device size.

4. Conclusion

We presented a simple method to investigate the effect of finite grating size on RA-SPP resonances of plasmonic gratings based on the combination of RCWA and finite aperture diffraction. As predicted by this model, the transition edges of RA-SPP resonances are broadened as the grating size shrinks due to the angular dependence of RA-SPP resonances, which agrees very well with experimental results quantitatively. This study points out the theoretical limit of miniaturizing subwavelength plasmonic gratings for optical sensing and optical modulation.