Assessment of the best flow model to characterize diffuse correlation spectroscopy data acquired directly on the brain

Abstract

Diffuse correlation spectroscopy (DCS) is a non-invasive optical technique capable of monitoring tissue perfusion. The normalized temporal intensity autocorrelation function generated by DCS is typically characterized by assuming that the movement of erythrocytes can be modeled as a Brownian diffusion-like process instead of by the expected random flow model. Recently, a hybrid model, referred to as the hydrodynamic diffusion model, was proposed, which combines the random and Brownian flow models. The purpose of this study was to investigate the best model to describe autocorrelation functions acquired directly on the brain in order to avoid confounding effects of extracerebral tissues. Data were acquired from 11 pigs during normocapnia and hypocapnia, and flow changes were verified by computed tomography perfusion (CTP). The hydrodynamic diffusion model was found to provide the best fit to the autocorrelation functions; however, no significant difference for relative flow changes measured by the Brownian and hydrodynamic diffusion models was observed.

1. Introduction

Near-infrared spectroscopy (NIRS) methods based on the quantification of light absorption at specific wavelengths have been developed for measuring key physiological parameters, such as tissue perfusion, blood volume and oxygenation [1–3]. For example, blood flow can be measured by manipulating arterial oxygenation saturation or injecting a light-absorbing contrast agent [4–6]; however, these techniques only enable single time-point measurements. An alternative approach that provides continuous blood flow monitoring is diffuse correlation spectroscopy (DCS) [3]. This method indirectly measures changes in blood flow by monitoring light intensity fluctuations caused by the movement of erythrocytes in tissue [7,8]. More specifically, the propagation of photons through extravascular tissue, where they endure multiple scattering events that randomize their direction, and within vessels, which contain moving erythrocytes, induces decorrelation of the light that manifests as intensity fluctuations. Blood flow is assessed by characterizing light intensity decorrelation using a model that describes the movement of erythrocytes.

Currently, the most common approach for analyzing DCS data is by modeling erythrocyte motion as a Brownian diffusion-like process, which has previously been shown in various species (swine, rodent and human) to provide a better characterization of the normalized temporal intensity autocorrelation function than the expected random flow model (R_FM) [9], which describes the motion of erythrocytes as ballistic [4,10–13]. To explain this unexpected finding, Carp et al. proposed a hybrid model, referred to as the hydrodynamic diffusion model (H_DM), that accounts for both the possibility of multiple light-scattering events within a vessel, characteristic of diffusive motion, and light-scattering events across vessels, characteristic of random ballistic motion [14]. Furthermore, Carp et al. demonstrated that the DCS measurements are best fit by the H_DM for data acquired on premature newborns [14].

Although DCS has been shown to be a promising tool for blood flow monitoring, the most appropriate flow model for characterizing perfusion is still debatable. The purpose of the current study was to compare the ability of the three flow models to characterize DCS data acquired directly on the exposed cerebral cortex of juvenile pigs. This approach removes signal contributions from the extracerebral tissues (scalp and skull) that can alter the shape of DCS autocorrelation curves due to partial volume errors caused by tissue heterogeneity [15]. In addition, cerebral blood flow (CBF) was independently measured by computed tomography perfusion (CTP) for comparison to the flow estimates obtained by each of the three flow models.

1.1 Diffuse correlation spectroscopy

To assess dynamics of light scatterers, DCS measures the normalized intensity autocorrelation function, g₂(ρ,τ) given by [16]:

$$g_2(\rho ,\tau )\equiv \frac{\langle I\left(\rho ,t\right)I\left(\rho ,t+\tau \right)\rangle }{{\langle I(\rho ,t)\rangle }^2}$$ (1)

where <I(ρ,τ)>, ρ and τ represents the average detected intensity, the source-detector distance (SDD) and the correlation time, respectively. Equation (1) is related to the electric field autocorrelation function by the Siegert relation [17]:

$$g_2(\rho ,\tau )=1+\beta \frac{{\left|G_1\left(\rho ,\tau \right)\right|}^2}{{\langle I(\rho ,t)\rangle }^2}$$ (2)

where, β is the coherence factor of the detection channel and G₁(ρ,τ) is the electric field autocorrelation function. Previously shown, G₁(ρ,τ) satisfies a diffusion equation [7,17]. Assuming a point light source with unit intensity, the analytical solution to the correlation diffusion equation for a semi-infinite homogenous medium is given by [4,16,19]:

$$G_1(\rho ,\tau )=\frac{3{{\mu }_s}^{\prime }}{4\pi }\left[\frac{\exp \left(-k_D{r}_1\right)}{r_1}-\frac{\exp \left(-k_D{r}_2\right)}{r_2}\right]$$ (3)

where, r₁ = [ρ² + (z₀)²]^1/2, r₂ = [ρ² + (z₀ + 2z_b)²]^1/2, z₀ = (µ_s')⁻¹ is the effective depth of the source, and z_b = 2D(1 + R_eff)/(1-R_eff) is the distance above the tissue surface at which the fluence vanishes, where D is the diffusion coefficient given as (3µ_s')⁻¹ and R_eff is the effective reflection coefficient calculated to be 0.493 for the refraction indices of tissue and air [20]. Furthermore, in Eq. (3), k_D is given by:

$$k_D^2=3{\mu }_a{{\mu }_s}^{\prime }+{\mu }_s^{2\prime }{k}_0^2\alpha \langle \Delta r^2\left(\tau \right)\rangle$$ (4)

The coefficients µ_a and μ_s' are the absorption and reduced scattering coefficient, respectively, k₀ is the wavenumber of light in the medium, α is the proportion of moving scatters (predominantly red blood cells) to all scatterers and is related to the blood volume, and <Δr²(τ)> is the mean-square displacement of the moving scatterers during a correlation time τ. In the analysis of measured g₂(ρ,τ), the specific expression for <Δr²(τ)> is given by one of the following flow models.

1.2 Random flow model

The random flow model (R_FM) is based on the assumption that photon scattering events associated with motion occur from scatterers that are uncorrelated (i.e., in separate vessels). In this case, the mean-square displacement is given by:

$$\langle \Delta r^2\left(\tau \right)\rangle =V^2{\tau }^2$$ (5)

where, V is the velocity of the moving erythrocytes. The product αV² is referred to as the random blood flow index (BFI_R).

1.3 Brownian diffusion model

The Brownian diffusion model (B_DM) assumes incoherent motion caused by multiple interactions of moving scatterers, such as erythrocytes within the same vessel. It is the most commonly used model in DCS analysis and the Brownian displacement formula is given by:

$$\langle \Delta r^2\left(\tau \right)\rangle =6D_B\tau$$ (6)

where, D_B is the effective diffusion coefficient, and αD_B is referred to as the Brownian blood flow index (BFI_B).

1.4 Hydrodynamic diffusion model

Carp et al. proposed using the Langevin formula for red blood cell mean squared displacement to account for the occurrence of both Brownian and random flow motion [14]:

$$\langle \Delta r^2\left(\tau \right)\rangle =6D_H\left\{\tau -{\tau }_C\left[1-\exp \left(-\frac{\tau }{{\tau }_C}\right)\right]\right\}$$ (7)

where D_H is the effective hydrodynamic diffusion coefficient and τ_c is the time scale required to establish diffusive motion. Unlike the Brownian diffusion model, τ_c accounts for possible ballistic motion at short delay times. For the hydrodynamic diffusion model (H_DM), the two fitting parameters are τ_c and αD_H, the hydrodynamic blood flow index (BFI_H).

2. Methods

2.1 Experimental procedure

Animal experiments were conducted in accordance with the guidelines of the Canadian Council of Animal Care (CCAC) and approved by the Animal Use Committee at Western University. Juvenile pigs (~6 weeks old) were obtained from a local supplier on the day of the experiment. Following anesthetic induction with 5% isoflurane, the animals were tracheotomized and mechanically ventilated on a mixture of oxygen and medical air. A catheter was inserted into a femoral artery for blood gas analysis. After surgery, the isoflurane was reduced to 3-4% and the animal was transported to the computed tomography (CT) suite where the experiments were conducted using a portable NIRS/DCS system.

The animal was placed prone on the bed of the CT scanner on top of a heated blanket used to maintain rectal temperature between 38 and 39 °C throughout the experiment. To place the optical probes directly on the brain, a rectangular piece of scalp tissue (~10 cm²) located laterally to the midline on the right hemisphere was first excised. A caustic pencil was used to cauterize the incised scalp tissue to prevent bleeding. Lastly, a handheld dremel was used to drill two burr holes, which were the size of optical fibers, into the skull parallel to the midline. Care was taken to ensure that the dura mater was not punctured by the dremel. Contact pressure on the dura was minimized since the fibers fit tightly in the holes, which carried their weight. Furthermore, the distance to the dura could be measured on the CT images (Fig. 1) and used to guide the distance that the fibers were inserted. The burr holes were 7 mm apart, with the exception of one animal for which the separation was 20 mm. A scout CT scan with an anatomical marker on top of the skull was used to define the location of the burr holes.

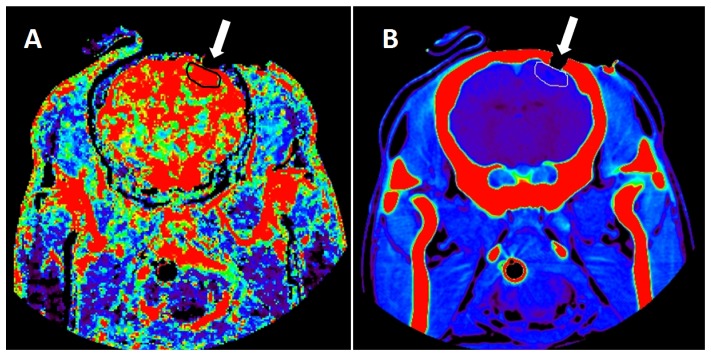
Fig. 1.

A CT image of a single slice for a blood flow map (A) and the corresponding anatomical map (B). The ROI, shown in black for A and white for B, was manually drawn on the superficial cortex using in-house software. The burr hole, which exposed the cortex and held the optical fiber, is identified by the white arrow.

Following surgery, the emission and detection fibers were placed in the posterior and anterior burr holes, respectively. The head of the pig was covered by an opaque blanket to reduce ambient light contamination. During the experiment, arterial oxygen saturation, heart and respiration rates, mean arterial pressure, and rectal temperature were continuously monitored. Arterial blood samples were obtained to measure arterial pH, partial carbon dioxide tension (paCO₂), partial oxygen tension (paO₂) and blood glucose concentration. Samples were acquired before and after each set of measurements to assess physiological stability during the data acquisition period. Intermittent dextrose injections were administered to maintain normal blood glucose levels (between 5 and 7 mmol/L).

Two sets of CT, time-resolved (TR)-NIRS, and DCS data were acquired in each experiment: first at normocapnia (paCO₂ between 38 and 42 mmHg) and then at hypocapnia (paCO₂ between 20 and 25 mmHg). Each capnic level was maintained by adjusting the ventilation volume and rate. The sequence of data acquisition during normocapnia consisted of CT perfusion, TR-NIRS measurements of optical properties and DCS. For the hypocapnic condition the sequence of data acquisition was reversed in order to avoid removing the optical probes from the burr holes between the two conditions.

2.2 Computed tomography

The dynamic CT protocol consisted of a bolus injection of 1.0 mL/kg of iodine-based contrast agent (iopamidol [370-Isovue®], Bracco S.p.A., Milan, Italy) at a rate of 3 mL/s into the cephalic vein once during each capnic condition. The first five animals were scanned by a Lightspeed QXi multislice scanner (General Electric Company, Waukesha, WI) and the last three animals were scanned by the Revolution CT scanner (General Electric Company, Waukesha, WI) due to scanner availability. Each scan (slice thickness = 2.5 mm, current = 200 mA, energy = 80 kVp, FOV = 140 × 140 × 40 mm) provided sixteen coronal slices, once every second, for a period of 40 s. The field of view covered the entire head of the pig. Functional maps of CBF were calculated using the clinical CT perfusion software package (PERFUSION 5, General Electric Healthcare Worldwide), which was developed and validated in house [21]. Region of interest (ROI) analysis was performed using an in-house developed software that performed pixel thresholding to remove signal contributions from large vessels that can lead to overestimation of CBF [22]. Five sequential slices between the burr holes that were visible on the anatomical CT images were chosen as they correspond to the “banana-shaped” path of the near-infrared light between the emission and detection optical fibers, as seen in Fig. 1. For each slice, an ROI (~5 cm diameter) was drawn on the cerebral cortex near the skull, since NIRS is most sensitive to superficial tissue. The CBF values were obtained by averaging over the ROIs in the five slices.

2.3 Optical methods

2.3.1 Time-resolved NIRS

The TR-NIRS systems consisted of a picosecond pulsed diode laser (LDH-P-C 764, PicoQuant, Germany) emitting at 764 nm, with an average output power and pulse repetition rate of 1.4 mW and 80 MHz, respectively. The light was attenuated using electronically controlled variable neutral density filters (NDC-50C-4M, Thorlabs) and coupled to a multimode emission fiber used for both DCS and TR-NIRS (emission probe: N.A. = 0.22, core = 400 µm; Fiberoptics Technology, Pomfret, CT). A 2-m fiber (N.A. = 0.22, core = 400 μm; Fiberoptics Technology, Pomfret, CT) was used to detect light at a SDD of 7-mm. The TR-NIRS detection fiber was coupled to a fast hybrid photomultiplier detector with Peltier cooling (PMA Hybrid, PicoQuant, Germany). The output of the detector was sent to a multichannel picosecond event timer and time-correlated single-photon counting (TCSPC) module (HydraHarp 400, PicoQuant, Germany). The system was given at least a 2-hour warmup period to stabilize the laser and detection system before acquiring data [23]. Under each capnic condition, a distribution of times of flight of photons (DTOF) was recorded for 30 seconds. At the end of the study, the instrument response function (IRF) was measured to account for systemic temporal dispersion [24].

Tissue optical properties (μ_a and μ_s') were acquired for each condition to reduce inter-subject variability when extracting blood flow indices from DCS [4,25]. A three-parameter fitting routine, described in detail elsewhere [26], was used to extract estimates of μ_a, μ_s' and an amplitude scaling factor during normocapnia. The model used to fit the DTOF was the solution of the diffusion approximation for a semi-infinite homogenous medium convolved with the measured IRF. The short SDD was calibrated with a phantom of known optical properties. The fitting range was set to 95% and 30% of the peak DTOF value for the ascending and descending sides, respectively. The measured μ_s' for normocapnia was fixed when analyzing the DTOF acquired during hypocapnia to reduce the number of fitting parameters to μ_a and amplitude scaling factor.

2.3.2 Diffuse correlation spectroscopy

The light source of the DCS system consisted of a continuous-wave laser (DL785-100-S, CrystalLaser, Nevada) emitting at 785 nm with a maximum output power of 100 mW and a coherence length >5 m. As with the TR-NIRS system, the emitted light was attenuated by electronically controlled variable neutral density filters and coupled to the multimode emission fiber. A single-mode fiber (SMF-28e + , N.A. = 0.14, length = 4 m, core = 8.2 µm, single-mode cutoff wavelength at 1260 nm) was placed in the anterior burr hole of the animal and was used for detecting the temporal light intensity fluctuations. The SMF was tightly wrapped into a 5-cm coil to increase the losses of the higher-order modes before being coupled to the input-channel of the avalanche photodiode of a single photon counting module (SPCM-AQ4C, Excelitas Canada Inc, QC, Canada) [27,28]. The output of the SPCM was sent to a photon correlator board (DPC-230, Beker & Hickl, Germany) that computed the normalized intensity autocorrelation functions (g₂).

For each animal, two g₂ curves were acquired, one during normocapnia and one during hypocapnia, over an acquisition period of 90 s. The μ_a and μ_s' measured by TR-NIRS were used in the DCS fitting routine. Each g₂ curve was analyzed three times using the solution of the diffusion approximation for a semi-infinite homogenous medium including one of the three flow models (B_DM, R_FM and H_DM). The start and end limits for the fitting were defined by correlation times of 0.6 µs and 1 ms, respectively. In the fitting procedure, the coherence factor β was set to the value determined by averaging the first 10 data points of each g₂ curve.

2.4 Statistical analysis

All errors are given as the standard errors of the mean (SEM), unless stated otherwise. All statistics were computed with the IBM SPSS Statistics 20 software package. For the measured physiological parameters, a multivariate analysis of variance (ANOVA), which included pH, paCO₂, paO₂, cGlu, ctHb, MAP, HR, temperature, and SpO₂, was computed to determine significant changes between capnic conditions. For two experiments, the TR-NIRS data set was not experimentally collected due to overheating of the detector and therefore were determined by the average optical properties of the remaining animals during normocapnia. For the hypocapnia optical properties, the μ_a values were estimated from the average change in absorption from normocapnia to hypocapnia measured by all animals in this study. A one-way ANOVA compared capnic conditions for measured μ_a and BFI values, and, for the former, a post-hoc test [Tukey’s honest significant difference (HSD)] identified any significant light absorbing outliers between subjects.

A direct comparison between the sums of squares (SS) determined the best fit of the B_DM and R_FM, since both models included one fitting parameter. However, the extra fitting parameter (τ_c) included in the H_DM is expected to reduce the variance in the fit of the measured g₂(ρ,τ). Therefore, an F-test was used to compare whether the improvements by the H_DM to fit the measured g₂(ρ,τ) curves, due to the additional fitting parameter, exceeded the reduction in variance similarly to the approach used by Carp et al. [14]. The degree of freedom used in the F-test was determined by the number of correlation bins that the individual fit required, which was 164. For the H_DM to better characterize the data compared to either the B_DM or the R_FM, the calculated F-number had to exceed a critical F-value of 3.9, as determined by the finv function in MATLAB (Mathworks, Natick, MA) for a p<0.05.

Linear regression analysis was performed to assess the correlation between CBF measured by CTP, and the blood flow index obtained by each of the three DCS models and τ_c for the H_DM. A Bland-Altman plot was used to assess the difference in the percent flow reductions measured by DCS and CTP [29]. For the Bland-Altman plot, a one-sample t-test identified differences between the two modalities (DCS and CTP), and a linear regression was used to determine any proportionality bias.

3. Results

3.1 Physiological parameters and optical properties

Eleven juvenile pigs (ten females, one male) were used in the study with an average weight of 16.0 ± 0.7 kg; however, only nine animals were scanned by CTP due to limited access to the CT scanner for the first two experiments.

Table 1 lists the physiological parameters measured during normocapnia and hypocapnia. A multivariate ANOVA indicated significant differences between capnic conditions for blood pH [p<0.001, partial-η² = 0.84, power = 1.00] and arterial carbon dioxide pressure (paCO₂) [p<0.001, partial-η² = 0.98, power = 1.00] as expected. All other physiological parameters, including blood glucose concentration, temperature and arterial oxygen saturation, did not change. Their mean values were 4.0 ± 0.2 mmol/L, 38.4 ± 0.1 °C, and 95 ± 1%, respectively.

Table 1. Measured physiological parameters.

Condition	*pH	*paCO2 [mmHg]	paO2 [mmHg]	ctHb [g/dL]	MAP [mmHg]	HR [bpm]
Normocapnia	7.45 ± 0.01	40.2 ± 0.3	182 ± 11	10.2 ± 0.3	43.6 ± 1.9	128 ± 8
Hypocapnia	7.62 ± 0.02	22.1 ± 0.4	213 ± 12	9.8 ± 0.4	38.1 ± 1.9	121 ± 7

Note: Data are presented as average ± SEM. paCO₂, partial pressure of carbon dioxide in the blood; paO₂, partial pressure of oxygen in the blood; MAP, mean arterial blood pressure; HR, heart rate. * p<0.05 between conditions.

Figure 2 presents the average µ_a values measured by TR-NIRS during normocapnia and hypocapnia. No significant difference between the two conditions was observed [p>0.55, partial-η² = 0.02, power = 0.09]. Following surgery, visible hemorrhaging in the emission burr hole was observed in one animal, which resulted in high μ_a values, as confirmed by a Tukey HSD post-hoc analysis (Fig. 2). Consequently, the data from this animal were removed from further analysis, unless stated otherwise. The mean μ_s' for all animals was 10.7 ± 1.3 cm⁻¹.

Fig. 2.

Average µ_a values for the 10 animals included in this study and the µ_a value of the excluded outlier. Absorption values are presented for normocapnic (black) and hypocapnic (grey) conditions. The large µ_a for the outlier was attributed to excessive blood in the emission burr hole. Error bars represent the SEM.

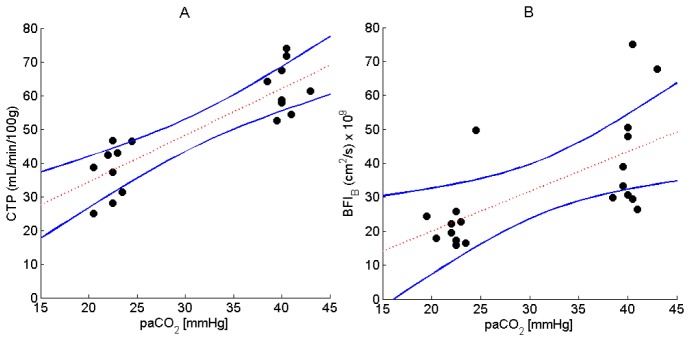
Figure 3 presents CBF values measured by CTP and the BFI_B derived from the DCS data, both plotted as a function of paCO₂. The outlier identified in Fig. 2 was excluded from the DCS data. The results from the B_DM are presented since it is the model most commonly used to analyze DCS data. Regression analysis resulted in a slope of 1.4 ± 0.20 mL/min/100g/mmHg (CI_95%: 0.94, 1.8, p<0.001), an intercept of 7.1 ± 6.6 mL/min/100g (CI_95%: −6.8, 21.1, p>0.29) and correlation coefficient (R) of 0.86 for CBF versus paCO₂. Likewise, the line of best fit from Fig. 3(B) had a slope of (1.2 ± 0.3) x 10⁻⁹ cm²/s/mmHg [CI_95%: (0.45, 1.86) x 10⁻⁹, p<0.003], an intercept of (1.7 ± 10.9) x 10⁻⁹ cm²/s [CI_95%: (−21.2, 24.6) x 10⁻⁹, p>0.88] and R of 0.63.

Fig. 3.

Measured flow by (A) CTP (N = 9) and (B) DCS using the B_DM (N = 10), during normocapnia and hypocapnia. The line of best fit and CI_95% are represented by the dashed red line and blue lines, respectively.

Table 2 lists the mean CBF values measured by CTP and corresponding BFI values derived from the DCS data using each of the three flow models. All values (CBF, BFI_B, BFI_R and BFI_H) were significantly different (p<0.05) between the two capnic conditions.

Table 2. Measured hemodynamic parameters.

Condition	*CBF [mL/min/100g]	*BFIB [10−9 cm2/s]	*BFIR [10−3 cm2/s]	*BFIH [10−9 cm2/s]	*τc [µs]
Normocapnia	62.5 ± 2.5	47.6 ± 4.9	37.2 ± 8.0	70.0 ± 8.2	2.72 ± 0.34
Hypocapnia	37.7 ± 2.6	27.9 ± 4.1	12.5 ± 3.3	38.2 ± 6.4	3.52 ± 0.29

Note: Values represent the average ± SEM. CBF, cerebral blood flow quantified by CTP; BFI_B, blood flow index determined by the Brownian flow model; BFI_R, blood flow index determined by the random flow model; BFI_H, blood flow index determined by the hydrodynamic flow model; τ_c, the time scale for the randomization of velocity vectors associated with RBC scattering events. * p<0.05 between conditions.

Included in Table 2 is τ_c from the H_DM, which was also significantly different (p<0.05) between conditions. Not given in Table 2 are the average value of β, which was 0.152 ± 0.002 for all models; no significant differences were observed between capnic conditions.

3.2 Example of the best-fit of the flow models

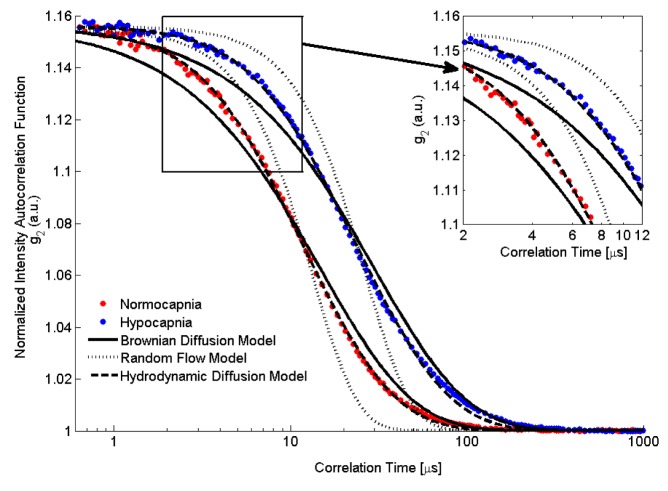
Figure 4 shows normalized intensity autocorrelation curves obtained on the exposed cerebral cortex of one animal during normocapnia (blue) and hypocapnia (red).

Fig. 4.

DCS autocorrelation curves during normocapnia (red dots) and hypocapnia (blue dots) from one animal. Also shown are the best-fit to the three DCS flow models: BFI_B (solid line), BFI_R (dotted line) and BFI_H (dashed line). Data were acquired with a count rate of ~600 kHz for a total acquisition time of 30 seconds. To visually enhance the differences between the fits of the three models, a portion of the graph is displayed that focuses on correlation times between 2 to 12 µs, which encompass the initial decay of the measured intensity autocorrelation functions.

The normalized intensity autocorrelation curves decayed faster during normocapnia than during hypocapnia, reflecting the higher blood flow in the former condition. For the example shown in Fig. 4, the blood flow reductions measured by BFI_B, BFI_R and BFI_H were 48.9%, 74.0% and 50.0%, respectively. Figure 4 illustrates the poor fit of the R_FM model. A statistical analysis by the F-test, as was described earlier, indicated that the fit of the H_DM was significantly better than for the B_DM for all autocorrelation curves. No differences were observed in the extracted BFI values by including more of the tail component of the correlation curves in the fitting routine (data not shown).

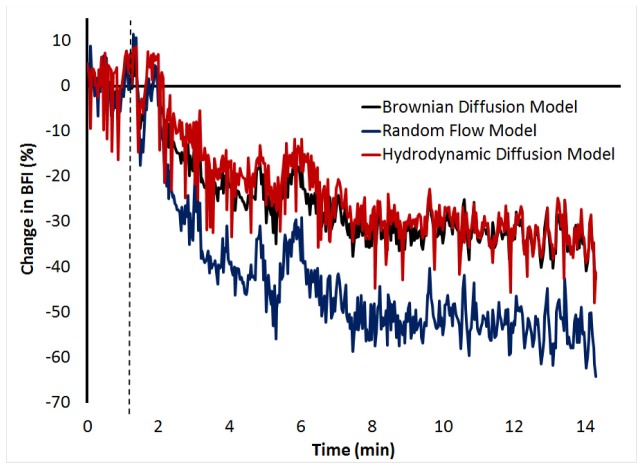
To further investigate the fits of the three DCS flow models, Fig. 5 presents continuous BFI values during the transition from normocapnia to hypocapnia. The BFI was determined from autocorrelation curves generated every two seconds. The flow reductions measured by the three models were 34.1%, 54.6% and 34.6% for the B_DM, R_FM and H_DM, respectively.

Fig. 5.

Real-time change in BFI measured during the transition from normocapnia to hypocapnia in one pig. DCS data were acquired at a count rate of 780 ± 3 kHz and analyzed by each flow model. The dashed line represents the end of the normocapnic period before the respirator was adjusted to induce hypocapnia.

3.3 Computed tomography perfusion comparison

Linear regression between CBF values measured by CTP and corresponding BFIs measured by each of the three DCS models was conducted on eight experiments after the outlier was removed (Fig. 2). Linear regression was also conducted between CTP CBF and τ_c. The resulting regression slopes, intercepts and R-values are listed in Table 3.

Table 3. Linear relationships between CTP and corresponding DCS indices from all three flow models.

Parameter	Units	Slope (CI95%)	Intercept (CI95%)	R-value
BFIB	10−9 cm2/s	*1.03 ± 0.23 (0.54, 1.52)	−13.9 ± 12.1 (−39.9, 12.1)	0.78
BFIR	10−3 cm2/s	*1.24 ± 0.33 (0.52, 1.95)	−36.8 ± 17.7 (−74.8, 1.1)	0.70
BFIH	10−9 cm2/s	*1.66 ± 0.36 (0.89, 2.44)	−27.9 ± 19.1 (−68.9, 13.0)	0.78
τc	µs	*-0.030 ± 0.015 (−0.061, −0.001)	*4.86 ± 0.76 (3.24, 6.48)	0.46

Note: BFI_B, blood flow index determined by the DCS Brownian flow model; BFI_R, blood flow index determined by the DCS random flow model; BFI_H, blood flow index determined by the DCS hydrodynamic flow model; CI_95%, 95% confidence intervals. Estimated slope and intercept ( ± SEM) for linear regression between CTP and BFI for each flow model along with the correlation coefficient (R) and p-values calculated by SPSS. * represents coefficients that are significantly different (p<0.05) from the null.

Table 3 demonstrates that the BFI values from each of the three models were correlated with CBF measured by CTP as indicated by a slope significantly different (p<0.01) from the null but a y-intercept not significantly different from zero. The displacement time constant τ_c, from the H_DM also correlated with CBF, but its R-value was not as strong and the y-intercept was significantly different from the zero.

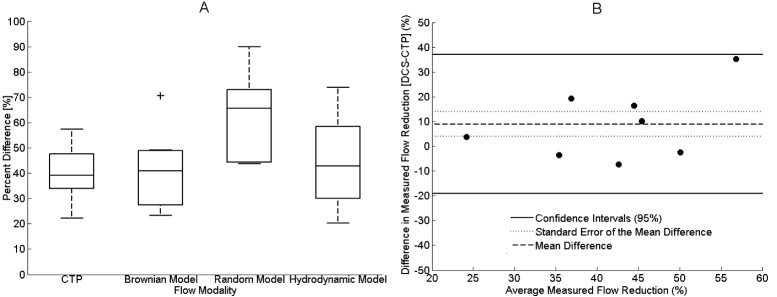
Figure 6 presents the relative CBF decrease from normocapnia to hypocapnia as measured by CTP and DCS. The box-plot presents the results from all three DCS flow models, whereas only the results from the B_DM are presented in the Bland-Altman plot. In Fig. 6(A), the average CBF change measured by CTP was −39.7 ± 3.7%, which was only significantly different from the change in BFI_R (−63.2 ± 4.7%) and not from the BFI changes measured by the other two models (−41.0 ± 4.3% for BFI_B and −44.2 ± 5.0% for BFI_H). In Fig. 6(B), the mean difference between BFI_B and CTP, indicated by the solid line, was 9.0 ± 5.1%, which was not significant (CI_95%: −19.1 and 37.0, as indicated by the two solid lines).

Fig. 6.

(A) Box plots of the reductions in flow from normocapnia to hypocapnia measured by CTP (N = 9) and the three DCS flow models (N = 10). The center line, box edges, error bars, and the cross represents the median, 1st and 3rd quartiles, CI_95%, and outliers, respectively. (B) Bland-Altman plot comparing the reductions in CBF measured by CTP and BFI_B (N = 8; due to listwise deletion). Each symbol represents a single animal. The mean difference between the two modalities, the standard error of the mean, and the CI_95% are indicated by the solid line, the dotted line and the dashed line, respectively.

In Fig. 6(B) the animals that did not undergo CTP and the optical outlier for DCS were removed due to listwise deletion. For clarity, Table 4 summarizes all of the pigs in this study with their acquired modalities (CTP, TR-NIRS and DCS) and SDD.

Table 4. A summary of all animals with acquired modalities.

Animal #	CTP	TR-NIRS	DCS	SDD [mm]
1	No	Yes	Yes	7
2	No	Yes	Yes	7
3	Yes	No (Unstable System)	Yes	7
4	Yes	No (Unstable System)	Yes	7
5	Yes	Yes	Yes	7
6	Yes	Yes	Yes	20
7	Yes	Yes	Yes	7
8*	Yes	Yes	Yes	7
9˟	Yes	Yes	Yes	7
10	Yes	Yes (Identified Outlier)	Yes (Removed Outlier)	7
11^	Yes	Yes	Yes	7

Note: ˟, * and ^ represents the animal used in Fig. 1, Fig. 4 and Fig. 5, respectively. An unstable TR-NIRS system occurred by an overheated detector prior to acquisitions. The identified outlier was described in detail above by Fig. 2.

4. Discussion

The main aims of this study were to assess which DCS flow model best characterized ‘brain’ autocorrelation curves and to compare measured flow reductions obtained with the different models to an independent measure of CBF. These experiments were conducted with the optical probes placed directly on the exposed cortex in order to collect DCS data without any signal contamination from extracerebral tissues. To verify that the interrogated cortical region was relatively homogeneous with regards to blood flow, the autocorrelation curves were re-analyzed using only the early portion (i.e., between correlation times of 0.3 and ~10 µs) since this range is considered more sensitive to deeper propagating photons [30]. No significant differences in blood flow indices were observed compared to the larger range of correlation times (0.6 μs to 1 ms) used in the Methods section, indicating that it was reasonable to consider the exposed cerebral cortex as a homogenous medium [31].

Of the three models used to characterize normalized intensity autocorrelation functions, the hybrid model, H_DM, which accounts for both diffusive and ballistic motion, provided the best fit as determined by the F-test. This was evident at early correction times, which represents the transition from the ballistic to diffusion regime (Fig. 4). This finding is in agreement with Carp et al., who found that the H_DM provided a superior fit to DCS data acquired from premature infants [14]. The additional constant τ_c, which represents the time scale to transition from ballistic to diffusive motion, was found to be significantly greater (~29%) at hypocapnia compared to normocapnia. This inverse relationship with CBF would be expected considering that within a given period fewer interactions between RBCs within a vessel would occur as flows decreases. Despite the better fit provided by the H_DM, differences in blood flow indices from this model and the more commonly used B_DM were small. No significant differences were observed between the two models in terms of absolute BFI values and relative changes. This agreement indicates that the ballistic range of photons detected by DCS is relatively small, suggesting that most detected photons undergo correlated scattering events (i.e. scattering events occurring within a single vessel).

A practical limitation with using the H_DM is the addition of an extra fitting parameter, τ_c, which leads to a greater sensitivity to noise in the measured autocorrelation curves. This was demonstrated visually by the continuous monitoring example shown in Fig. 5, in which data were acquired every two seconds. To characterize the noise sensitivity of each model, the coefficient of variation of the BFI over the baseline period was computed. The coefficient for BFI_H was 38.5% larger than for BFI_B. Furthermore, the linear regression analysis between the blood flow indices and CBF measurements from CTP showed less uncertainty and a tighter confidence interval range for the B_DM than the H_DM (Table 3). Therefore, the B_DM model, which is more robust and provides similar BFI measurements to the H_DM, is the more practical model to use, particularly for data with a lower signal-to-noise ratio, such as the real-time DCS monitoring displayed in Fig. 5.

For the second aim of this study, CTP was used to measure CBF at normocapnia and hypocapnia. The latter causes a substantial reduction in CBF because of the tight coupling between cerebrovascular tone and arterial blood carbon dioxide tension. Hypocapnia rather than hypercapnia was used in these experiments because decreases in blood flow are clinically relevant to the management of critical care patients due to the incidence of delayed cerebral ischemia. Flow reductions caused by hypocapnia are not as great as caused by ischemia; however, the good agreement with the CTP results is further evidence of the ability of DCS to measure CBF changes accurately. The cerebral vascular reactivity measured with the B_DM was (−2.3 ± 0.2)% per mmHg of paCO₂, which is in good agreement with our previous study, which used the same animal model (juvenile pigs) and a contrast-enhanced NIRS technique to measure CBF [32]. Likewise, these findings confirm previous validation studies involving both animal models and human subjects that have shown a good correlation between BFI_B and CBF changes measured by other modalities [12,33]. Considering that the DCS data in the current study were collected directly on the brain, this agreement is evidence that DCS is relatively insensitive to extracerebral signal contamination in applications in which the scalp and skull are thin. These would include animal models, such as piglets and rats [4,13], but more importantly, also applies to newborns [34,35].

A possible limitation with this study is the potential for CTP to overestimate CBF due to the presence of pixels with extremely high flow estimates. These ‘vascular’ pixels are attributed to high contrast enhancement in vessels and were removed in the current study by setting perfusion thresholds [22]. This procedure has been shown to significantly improve the correlation with CBF measurements from positron emission tomography [36] and from magnetic resonance imaging [37]. Another potential limitation was the possibility of variations in CBF between measurements from the different modalities. To minimize this, paCO₂ was monitored frequently to ensure it remained stable during each capnic level.

5. Conclusion

In summary, contributions from the superficial layers (scalp and skull) were eliminated by exposing the cerebral cortex of juvenile pigs and acquiring DCS directly on the brain. In agreement with Carp et al., the flow model that demonstrated the best fit to the intensity autocorrelation functions was the hybrid flow model, as evident at early correlation times. However, BFI values from the B_DM and the H_DM were very similar and both were in agreement with the CBF changes measured by CTP, indicating that the diffusion-like flow of erythrocytes dominates. Furthermore, the B_DM is the more practical model for characterizing DCS data due to its greater robustness.