Calculation of crystalline lens power using a modification of the Bennett method

Abstract

We present a method for measuring lens power from extended depth OCT biometry, corneal topography, and refraction using an improvement on the Bennett method. A reduced eye model was used to derive a formula for lens power in terms of ocular distances, corneal power, and objective spherical equivalent refraction. An error analysis shows that the formula predicts relaxed lens power with a theoretical accuracy of ± 0.5 D for refractive error ranging from −10 D to + 10 D. The formula was used to calculate lens power in 16 eyes of 8 human subjects. Mean lens power was 24.3 D ± 1.7 D.

1. Introduction

The crystalline lens is a dynamic focusing element that accounts for approximately one third of the dioptric power of the relaxed eye. Together with corneal power and ocular distances, crystalline lens power is one of the parameters that determine the refractive state of the eye. The significant contribution of lens power to the refractive state of the eye has prompted a great amount of interest to measure lens power and its age-dependence, and to determine how changes in lens power correlate with changes in ocular dimensions in the development of the refractive state of the eye [1–6]. Lens power is also essential to the study of accommodation, since changes in lens shape produce a change in lens power which allows the eye to shift focus from far to near during accommodation.

Lens power can be calculated from measurements of lens thickness and radii of curvature. Values of the lens radii of curvature can be derived from images of the Purkinje reflexes (phakometry) [7–9], or from cross-sectional or three-dimensional images of the lens acquired using Scheimpflug imaging [10,11], or optical coherence tomography (OCT) [12–14]. Scheimpflug and OCT images must be corrected for distortions caused by refraction of light at the corneal and lens surfaces. The lens power calculations are generally performed with an assumed value for the equivalent refractive index [15, 16], a value shown to change with age [16]. The calculated lens power is highly sensitive to errors caused by the uncertainty in the value of the equivalent refractive index. For instance, for a lens with an anterior radius of 10 mm and posterior radius of −6 mm, an uncertainty of only ± 0.01 in refractive index produces an uncertainty of ± 2.7 D in lens power. Alternatively, for a precision of ± 0.5 D in lens power calculation, one would need to know the equivalent index with a precision of ± 0.002 [17]. In the study of Dubbelman [16] the variability of the equivalent refractive index obtained experimentally among individuals of the same age is on the order of ± 0.005. This suggests that the uncertainty in the refractive index alone introduces an uncertainty on the order of ± 1.3 D in the lens power calculated directly from measurements of curvature.

Another approach to calculate the lens power is the method developed by Bennett [18], which eliminates the need for measurements of lens curvatures. The Bennett method requires measurement of corneal power, anterior chamber depth, lens thickness, axial eye length, and the subject’s refraction. A paraxial model of the eye constructed from the measured biometric parameters is used to calculate lens power. The calculation relies on an estimate of the position of the principal planes of the lens. Lens power is calculated by assuming that the ratio of anterior to posterior lens radius is fixed, equal to the value used in the Emsley-Gullstrand model. With this assumption, the position of the lens principal planes relative to the lens vertices depends only on the lens thickness. Error analyses show that the Bennett method provides a measurement of lens power with an accuracy that is on the order of ± 1 D, better than the accuracy provided by phakometry [19–21].

Rozema, Atchison, and Tassignon [21] recently published a detailed study comparing the lens power obtained with the Bennett method with values obtained from phakometry and using simplified versions of the Bennett method. The simplified methods assume that the crystalline lens is a thin lens placed either at the anterior vertex of the lens (Stenström method), or at the mid-point between the two principal planes of the lens (Bennett-Rabbetts method). Rozema, Atchison, and Tassignon improved on these methods by finding the position of the thin lens that matches the calculated lens power to the lens power obtained using phakometry for a set of emmetropic eyes. However, the prediction error in lens power was found to increase significantly when the method was applied to a data set that includes myopic eyes. The prediction error was also found to be strongly correlated with axial eye length. These analyses suggest that the optimal position of the thin equivalent lens varies with the refractive state of the eye.

In this paper, we present a modified version of the Bennett method where we replace the thick lens model used in the Bennett method with a thin lens approximation. We demonstrate that there is a position of the thin lens that eliminates the prediction error in lens power. We also show that the position of the thin equivalent lens depends on the ratio of anterior to posterior curvature and on the conjugate ratio of the lens (ratio of image to object distance for the lens). We demonstrate the application of this method to the calculation of lens power based on ocular biometry using an extended-depth optical coherence tomography system [22], and measurements of corneal topography and refraction.

2. Lens power calculation from biometry

2.1 Equivalent thin lens position

Table 1 defines all variables used in the subsequent equations for the given schematic of the eye (Fig. 1). The known ocular parameters are: the radii of curvature of the anterior and posterior cornea, the anterior chamber depth, the lens thickness, the vitreous depth, and the refractive error of the eye. Similar to the Bennett method, the lens power s obtained by applying the conjugation formulae to the lens:

$$L_0=\frac{n}{s{\text{'}}_L}-\frac{n}{s_L}$$ (1)

In the crystalline lens, the distance between the principal planes is small ($\overline{H_3{H}_4}$< 0.2 mm, calculated using the age-dependent data of Dubbelman et al [16]) for a normal range of lens shapes and refractive indices. To simplify the expressions, the lens can be approximated as a thin lens, with lens center O. Bennett and Rabbetts modeled the lens as a thin lens with lens center located at the mid-point between the two principal planes of the lens [21, 23]. Instead of using the midpoint, we demonstrate below that there is an optimal position of the lens center that minimizes the error in the lens power calculation. This position depends on the conjugate ratio (ratio of image to object distance, s’_L/s_L).

Table 1. List of variables (in alphabetical order).

ACD:	Anterior chamber depth: Distance from posterior corneal vertex to anterior lens vertex
b:	Coefficient of the calculation of lens power
CCT:	Central corneal thickness
H1, H3, H4:	Corneal object principal point, Lens object principal point, Lens image principal point
K, K1, K2:	Total corneal power, Anterior corneal surface power, Posterior corneal surface power
ΔL	Prediction error in lens power: ΔL = L-L0
L0, L:	Total lens power - Actual, Total lens power - Estimated
L3, L4:	Anterior lens surface power, Posterior lens surface power
LT:	Central lens thickness
ML	Lens magnification, ML = s’L/sL
n, nK, nL:	Refractive indices: aqueous and vitreous, cornea, lens equivalent refractive index
O:	Lens center for the thin lens model of the lens
R:	Refraction in the anterior corneal plane
R1, R2, R3, R4:	Radius of curvature: Anterior cornea, Posterior cornea, Anterior lens, Posterior lens
SEQ:	Spherical Equivalent Refraction
sK:	Distance from retinal conjugate to object principal point of cornea
s'K:	Distance from image principal point of cornea to primary image
sL:	Distance from object principal point of lens to primary image
s'L:	Distance from image principal point of lens to retina
V1, V3, V4	Vertex: Anterior cornea, Anterior lens, Posterior lens
VD	Distance from posterior lens vertex to retina
vL:	Distance from lens anterior vertex to primary image
v'L:	Distance from lens posterior vertex to retina

Fig. 1.

Schematic representing the primary image formed by the cornea, which is subsequently imaged by the crystalline lens onto the retinal plane. Variable definitions can be found in Table 1. The figure shows the case of a myopic eye (the retinal conjugate is located at a finite distance in front of the eye). Solid vertical lines correspond to principal planes. Dashed vertical lines show the planes passing through the object, image, and surface vertices.

The assumption that the lens is a thin lens with center O introduces a small error in the object and image distances, s_L and s'_L, equal to the distances from the lens principal points to the lens center. The resulting estimated lens power is:

$$L=\frac{n}{s{\text{'}}_L-\overline{H_{4}O}}-\frac{n}{s_L-\overline{H_{3}O}}$$ (2)

Since the distances $\overline{H_{4}O}$ and $\overline{H_{3}O}$ are much smaller than the distance s_L' and s_L the fractions can be replaced with their first order Taylor series approximation:

$$L=n\left[\frac{1}{s{\text{'}}_L}\left(1+\frac{\overline{H_{4}O}}{s{\text{'}}_L}\right)-\frac{1}{s_L}\left(1+\frac{\overline{H_{3}O}}{s_L}\right)\right]$$ (3)

Combining Eqs. (1) and (3) gives:

$$L=L_0+n\left(\frac{\overline{H_{4}O}}{s{{\text{'}}_L}^2}-\frac{\overline{H_{3}O}}{{s_L}^2}\right)$$ (4)

Using Eq. (4), and the relation $\overline{H_{4}O}=\overline{H_4{H}_3}+\overline{H_{3}O}$, we find that the prediction error in lens power, ΔL = L-L₀, produced when we approximate the crystalline lens by a thin lens located at a position O is:

$$\Delta L=L-L_0=n\left(\frac{\overline{H_{3}O}-\overline{H_3{H}_4}}{s_L{\text{'}}^2}-\frac{\overline{H_{3}O}}{{s_L}^2}\right)$$ (5)

From Eq. (5), we can see that there is a position of the lens center, O, for which the prediction error is equal to zero:

$$\overline{H_{3}O}=\frac{\overline{H_3{H}_4}}{1-\frac{s{{\text{'}}_L}^2}{{s_L}^2}}$$ (6)

Since the ratio s_L’/s_L is the magnification M_L, of the lens, we can write Eq. (6) as:

$$\overline{H_{3}O}=\frac{\overline{H_3{H}_4}}{1-{M_L}^2}$$ (7)

The position of the lens center can be expressed in terms of the anterior vertex, V₃, of the lens, by using the formulas for the distance from vertices to principal planes in a thick lens [25]:

$$\overline{V_3{H}_3}=\frac{n}{n_L}LT\frac{L_4}{L_0}$$ (8a)

$$\overline{V_4{H}_4}=-\frac{n}{n_L}LT\frac{L_3}{L_0}$$ (8b)

Combining Eqs. (7) and (8a, 8b) gives:

$$\overline{V_{3}O}=LT\frac{1}{1-{M_L}^2}\left(1-\frac{n}{n_L}\times \frac{L_3+L_4\times {M_L}^2}{L_0}\right)$$ (9)

An error analysis shows that if we ignore the contribution of the thickness term in the expression of the lens power (i.e., we make the approximation L₀ = L₃ + L₄ in Eq. (9)) the shift in position of the lens center is less than 0.1 mm which we consider negligible. If we neglect the thickness term in the expression of lens power, L₀, we can write Eq. (9) in the following form:

$$\overline{V_{3}O}=bLT$$ (10)

Where b is equal to:

$$b=\frac{1}{1-{M_L}^2}\left(1-\frac{n}{n_L}\frac{L_3+L_4\times {M_L}^2}{L_3+L_4}\right)$$ (11)

Or, in terms of the radii of curvature (where R₄<0):

$$b=\frac{1}{1-{M_L}^2}\left(1-\frac{n}{n_L}\frac{{M_L}^2-\frac{R_4}{R_3}}{1-\frac{R_4}{R_3}}\right)$$ (12)

Equations (10) and (12) show that the distance from the anterior lens vertex to the optimal thin lens position is proportional to the lens thickness, with a proportionality constant that depends on the conjugate ratio of the lens and on the ratio of posterior to anterior lens radius.

2.2. Estimated lens power

The object and image distances in Eq. (2) can be expressed in terms of the vertices (see Fig. 1):

$$s{\text{'}}_L=v{\text{'}}_L+\overline{H_4{V}_4}$$ (13a)

$$s_L=v_L+\overline{H_3{V}_3}$$ (13b)

Combining Eqs. (2), (10), and (13) gives the following expression for the estimated lens power, where b is given by Eq. (12):

$$L=\frac{n}{v{\text{'}}_L-(b-1)LT}-\frac{n}{v_L-bLT}$$ (14)

In Eq. (14) the distance v’_L is the vitreous depth and the distance v_L is the distance from the anterior surface of the lens to the primary image formed by the cornea. If we assume that the cornea is a thin lens located at the anterior principal plane of the cornea, we have v_L = s’_K-ACD-CCT-$\overline{H_1{V}_1}$. The distance s’_K is found by applying the conjugation formula to the cornea: n/s’_K = 1/s_K + K. If we use the approximation 1/s_K = R, we obtain:

$$v_L=\frac{n}{R+K}-ACD-CCT-\overline{H_1{V}_1}$$ (15a)

where:

$$\overline{H_1{V}_1}=-\frac{1}{n_K}CCT\frac{K_2}{K}$$ (15b)

Finally, we arrive at an equation for lens power dependent on the measured parameters (VD, R, K, K₂, ACD, CCT, and LT) and the parameter b:

$$L=\frac{n}{VD-(b-1)\times LT}-\frac{n}{\frac{n}{R+K}-ACD-CCT\left(1-\frac{1}{n_K}\frac{K_2}{K}\right)-b\times LT}$$ (16)

2.3 Value of the b coefficient

The b coefficient (Eq. (11)) depends on the value of the refractive indices, the ratio of the posterior to anterior radii of curvature of the lens, and on the square of the magnification of the lens. The ratio of anterior to posterior lens radius of curvature changes with age and with accommodation [26–28]. Using age-dependent in vivo data from Dubbelman et al [16] to represent the relaxed lens and age-dependent in vitro data from Borja et al [27] to represent the maximally accommodated lens, the ratio of posterior to anterior lens varies from −0.51 to −0.72. For the calculation of lens power, we use in Eq. (12) a fixed value of R₄/R₃ = −0.6 located in the mid-point of the range and a fixed value of the equivalent index n_L = 1.43. The value of b is then given by:

$$b=\frac{0.650-0.584{M_L}^2}{1-{M_L}^2}$$ (17)

With this assumption, the only remaining source of inter-individual variability of the coefficient b is the lens magnification. An approximate expression of the magnification in terms of the measured ocular distances and refractive error can be obtained by assuming that the lens is a thin lens with a lens center located at the mid-point of the lens vertices. The object and image distances (s_L, s’_L) of the lens in the expression of the magnification are then replaced with v_L – LT/2 and v’_L + LT/2, respectively, where the distance v’_L is the vitreous depth and v_L is given by Eq. (15). The approximate expression of the magnification then becomes:

$$M_L=\frac{VD+\frac{LT}{2}}{\frac{n}{R+K}-ACD-CCT\left(1-\frac{1}{n_K}\frac{K_2}{K}\right)-\frac{LT}{2}}$$ (18)

To evaluate the error in the magnification predicted by the approximate expression of Eq. (18), we generated an age-dependent model of the relaxed paraxial eye with four surfaces and adjusted the vitreous depth to vary the refractive error at the corneal plane, from −10 D to + 10 D (axial ametropia). Dimensions of the cornea, lens, and anterior chamber depth were obtained from the in vivo Scheimpflug data of Dubbelman et al [16]. The parameters of the eye model are shown in Table 2. Figure 2 shows the exact (M_L = s’_L/s_L) and approximate (Eq. (18)) values of M_L for a 20 year old relaxed eye for refractive errors ranging from −10 D to + 10 D (left) and for an emmetropic eye as a function of age (right). Over the range of refractive errors, the maximum relative difference between the approximate and exact value of M_L² is 3.5% (0.464 vs 0.481). The value of M_L is found to be approximately independent on age. This analysis demonstrates that a close estimate of the value of M_L can be calculated from the measured biometric data.

Table 2. Eye model parameters for the error analysis (based on data from refs [16]. and [27]).

Parameter	Age-dependent relaxed Eye	20 year old accommodated
Anterior Corneal Radius (mm)	7.8	7.8
Posterior Corneal Radius (mm)	6.5	6.5
Corneal Thickness (mm)	0.55	0.55
Refractive index, air	1	1
Refractive index, cornea	1.376	1.376
Refractive index, aqueous	1.336	1.336
Refractive index, vitreous	1.336	1.336
Equivalent refractive index, lens	1.441 - (0.00039 × Age)	1.433
Anterior Chamber Depth (mm)	3.87 - (0.01 × Age)	2.75
Anterior Lens Radius (mm)	12.9 - (0.057 × Age)	7.26
Posterior Lens Radius (mm)	−6.2 + (0.012 × Age)	−4.67
Lens Thickness (mm)	2.93 + (0.024 × Age)	4.16

Fig. 2.

(Left) Exact and approximate conjugate ratio squared for a relaxed 20 year old eye (Dubbelman eye model) as a function of the refractive error. (Right) Exact and approximate conjugate ratio squared vs age for the relaxed age-dependent emmetropic Dubbelman eye model.

2.4 Error analysis

To evaluate the error in the lens power predicted by Eq. (16) with the coefficient b predicted by Eq. (17) and magnification provided by Eq. (18), we used the age-dependent model of the relaxed paraxial eye with refractive error ranging from −10 D to + 10 D (see Section 2.3 and Table 2). In addition, we modeled an accommodated 20 year old eye by using curvature, thickness and refractive index acquired from isolated lenses [27], corresponding to a fully accommodated state. The parameters of the two eye models are shown in Table 2. Equation (16) was applied to calculate lens power. The value produced by the calculation was compared to the actual effective power of the lens obtained using the thick lens power formula.

Figure 3 shows the value of prediction error in lens power for the relaxed emmetropic eye as a function of age, as well as for the 20 year old relaxed and accommodated eyes and for the 60 year old eye in terms of refractive error. For the 20 year old eye, the prediction error ranges from −0.14 to −0.16 D in the relaxed state and 0.30 to 0.65 D in the accommodated state. In the 60 year old eye, the predicted error ranges from 0.13 to 0.48 D. The calculations show that for a range of ± 10 D of ametropia and an age range of 20 to 60 years, the predicted error is within ± 0.5 D for the relaxed eye. For the accommodated eye, the method overestimates the lens power by 0.3 D to 0.65 D, depending on the refractive error.

Fig. 3.

(Left) Predicted error the approximate constant b for the relaxed emmetropic eye vs age. (Right) Prediction error for the 20 year old relaxed and accommodated, and the 60 year old model in terms of refractive error.

Figure 4 shows the predicted error of the change in lens power for the 20 year old eye in terms of refractive error. The change in lens power is 9.7 D. The prediction error monotonically increases from 0.46 D to 0.79 D as the refractive error changes from −10 to + 10 D. For an emmetropic eye, the prediction error is 0.59 D. These values correspond to a relative error ranging from 4.7% to 8.1% of the total change in lens power (less than 10%).

Fig. 4.

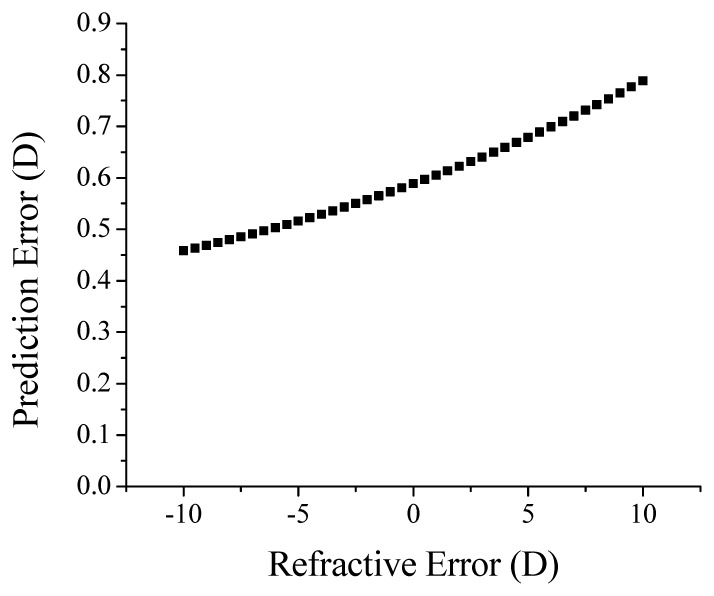
Predicted error of the change in lens power for the 20 year old vs refractive error. The change in lens power is 9.1 D.

3. Measurement of lens power using whole eye OCT

3.1 Methods

Using the method described above, applied to whole-eye OCT images, we calculated the lens power of 16 eyes in 8 subjects enrolled in a study approved by the University of Miami’s Institutional Review Board. Age ranged from 21 to 31 years (mean = 24.5 ± 3.3 years). Objective spherical equivalent refraction measured using a commercial autorefractor (AR-1, Nidek, Japan) ranged from −5.8 to + 3.8 D (mean = −2.3 ± 2.8 D). Refraction was measured without cycloplegia. For the anterior and posterior corneal radius of curvature, we used the mean value of the flattest and steepest meridian in the central 3 mm zone acquired using a commercial anterior segment biometry system (Pentacam, Oculus, Germany). Corneal thickness, anterior chamber depth, lens thickness, and vitreous depth were obtained using a custom built extended-depth spectral domain OCT system with a central wavelength of 840 nm and an axial resolution of 8 µm in air. A detailed description of the OCT system has been previously published [22]. A typical image acquired with this OCT system is shown in Fig. 5. The OCT system is coupled to an accommodation target that allows the operator to adjust the accommodative demand. The target was adjusted to lie at the subject’s uncorrected far point. The OCT system was aligned under guidance of a live display of the cross-sectional image until the lens thickness was perceived to be maximal. The A-line that corresponds to the corneal apex was selected from the recorded B-scan for all measurements. The ocular distances were determined by finding the position of the intensity signal peaks corresponding to corneal and lens surfaces and the retinal pigment epithelium.

Fig. 5.

Image acquired using the extended-depth SD-OCT system. The image of the whole eye is acquired by using an optical switch and three reference arms. The switch allows the capture of the entire anterior segment in two successive frames and of the retina in a third frame. The vitreous is not imaged.

The OCT image was processed to convert optical distances into geometrical distances using the following group refractive indices at 840 nm [22]: cornea = 1.387, aqueous humor = 1.342, crystalline lens = 1.415, vitreous = 1.341, retina = 1.380. The precision of ocular distance measurements was evaluated in a study on 1 subjects where 28 images were acquired in sequence. The standard deviation of the measurements was +/− 0.002 mm for the cornea, +/− 0.012 mm for the anterior chamber depth, +/− 0.018 mm for the lens, and +/− 0.011 mm for the vitreous depth.

The measured values were entered in Eq. (16) to calculate the lens power. The value of b was calculated using Eqs. (17) and (18). Corneal power was calculated by applying the formula for the power of a thick lens with a refractive index of 1 for air, 1.376 for the cornea, and 1.336 for aqueous.

3.2. Results

The values measured in the 16 eyes are summarized in Table 3. These values were used to find the parameters required to calculate lens power using Eq. (16) (Table 4). Lens power is shown in Fig. 6 against axial eye length. All data is plotted on the same graphs, without separation of left and right eyes. Lens power ranged from 21.66 D to 27.60 D, with a mean of 24.30 ± 1.70 D. Lens power was found to decrease as axial eye length increases, consistent with the findings of Iribarren et al [3] who show a statistically significant increase in lens power with a decrease in axial eye length. However, the sample size of the present study is too small to make any definite conclusions as to the relation between lens power and ocular components.

Table 3. Data collected on 16 eyes of 8 subjects. See definition of symbols in Table 1.

Subject # and eye	Age (years)	SEQ, R (D)	R1 (mm)	R2 (mm)	CCT (mm)	ACD (mm)	LT (mm)	VD (mm)
1 OD	22	−4.07	7.74	6.37	0.488	3.783	3.438	18.302
1 OS	22	−5.62	7.79	6.44	0.481	3.773	3.432	18.927
2 OD	26	−5.07	7.53	6.19	0.526	3.224	3.709	17.265
2 OS	26	−5.81	7.50	6.18	0.533	3.303	3.660	17.714
3 OD	26	−3.76	7.52	6.00	0.523	3.039	3.475	17.352
3 OS	26	−2.96	7.47	5.94	0.518	2.991	3.552	16.959
4 OD	31	−0.63	7.46	6.23	0.475	3.331	3.670	16.138
4 OS	31	−0.88	7.41	6.08	0.476	3.406	3.679	15.924
5 OD	21	−1.75	7.68	6.40	0.540	3.215	3.567	15.970
5 OS	21	−0.13	7.68	6.39	0.537	3.175	3.618	15.942
6 OD	21	−5.13	7.86	6.49	0.523	3.622	3.452	18.567
6 OS	21	−4.88	7.81	6.47	0.522	3.705	3.425	18.540
7 OD	23	−1.13	7.83	6.41	0.525	2.968	3.797	16.438
7 OS	23	−0.62	7.73	6.34	0.509	3.048	3.752	16.336
8 OD	26	1.50	7.61	6.40	0.549	2.797	3.994	14.689
8 OS	26	3.81	7.58	6.36	0.534	2.873	3.921	14.607
AVG	24.5	−2.32	7.64	6.29	0.516	3.266	3.634	16.854
STD	3.3	2.79	0.14	0.17	0.024	0.318	0.174	1.329

Table 4. Calculated values used in the equations for lens power.

Subject # and eye	K (D)	K2 (D)	H1V1 (mm)	ML	b	L (D)
1 OD	42.41	−6.28	0.053	0.695	0.712	21.66
1 OS	42.16	−6.21	0.051	0.676	0.706	22.23
2 OD	43.59	−6.46	0.057	0.659	0.701	25.45
2 OS	43.79	−6.47	0.057	0.664	0.702	24.52
3 OD	43.46	−6.67	0.058	0.675	0.705	24.26
3 OS	43.73	−6.73	0.058	0.683	0.708	24.18
4 OD	44.09	−6.42	0.050	0.718	0.720	22.70
4 OS	44.28	−6.58	0.051	0.710	0.717	23.56
5 OD	42.83	−6.25	0.057	0.659	0.701	27.43
5 OS	42.82	−6.26	0.057	0.690	0.710	25.09
6 OD	41.79	−6.16	0.056	0.665	0.702	23.37
6 OS	42.07	−6.18	0.056	0.677	0.706	22.62
7 OD	41.89	−6.24	0.057	0.671	0.704	25.75
7 OS	42.45	−6.31	0.055	0.688	0.709	24.62
8 OD	43.28	−6.25	0.058	0.683	0.708	27.66
8 OS	43.44	−6.29	0.056	0.725	0.723	24.35
AVG	43.01	−6.36	0.055	0.684	0.708	24.34
STD	0.81	0.18	0.003	0.020	0.007	1.70

Fig. 6.

Lens power vs axial eye length for 16 eyes of 8 subjects.

Anterior segment distances and predicted lens power obtained from our study were in good agreement with the age-dependent biometric data of Dubbelman [16] at the age corresponding to the average age of our subjects (24.5 years) (Dubbelman / present study): Anterior chamber depth: 3.08 / 3.27 mm, lens thickness: 3.52 / 3.63 mm, lens power: 24.1 / 24.3 D.

4. Discussion

We demonstrate a modified version of the Bennett method that relies on a thin lens approximation. In the original Bennett method, the positions of the principal planes of the lens are calculated by assuming that the ratio of posterior to anterior radius of the lens is the same as that of the relaxed Gullstrand eye model. The position of each principal plane of the lens is then calculated from the lens thickness and two fixed constants. We use a thin lens model and demonstrate that there is a position of the thin lens that produces a zero prediction error (Eq. (6)). In first approximation, the distance from the anterior lens vertex to the optimal thin lens position is proportional to the lens thickness, with a proportionality constant that depends on the conjugate ratio of the lens and on the ratio of posterior to anterior lens radius (Eq. (12)).

A theoretical error analysis using eye models of different ages, accommodative states, and refractive errors suggests that the theoretical prediction error is within ± 0.5 D for the relaxed eye if the distance from anterior vertex to lens center is assumed to be independent of the lens shape. This approach provides a direct simple expression of lens power in terms of ocular distances, corneal power and refraction with a single coefficient that depends on ocular dimensions and refractive error (b, Eq. (6)). The modified method significantly reduces the theoretical prediction error compared to the methods that use a fixed position for the thin lens relative to the anterior lens vertex [21], particularly in ametropic and accommodated eyes. In principle, the error could be further reduced by using an age- and accommodation- dependent estimate of the ratio of posterior to anterior lens radius, which can be calculated for instance using the biometric data of Dubbelman et al [16, 28].

Similar to the Bennett method, the proposed modified method requires a measurement of lens thickness, which is not always available [21]. When lens thickness is unknown, an estimate of lens power can be calculated by using a fixed value or an age-dependent model for lens thickness. In that case, vitreous depth is estimated by subtracting lens thickness, anterior chamber depth and corneal thickness from the axial eye length (see example in Appendix). For instance, when the error analysis using the eye models described above is repeated using a fixed value of thickness equal to 4 mm, the theoretical prediction error for the relaxed lens power remains within +/−1 D over a wide range of refractive errors (−10 D to + 10 D).

In the calculation of the prediction error in lens power as a function of refractive error, the ametropic eye was modeled by changing only the axial eye length (axial ametropia). If instead we model ametropia by changing only the corneal shape (refractive ametropia), we find that the prediction error in lens power is independent of refractive error. Indeed, in that case both the vitreous depth, VD, and the quantity R + K remain constant as the refractive error changes. The approximate values of M_L (Eq. (18)) and b (Eq. (17)), and the predicted value of the lens power (Eq. (16)), will therefore remain constant and equal to the value obtained for the emmetropic eye.

Comparing the lens power predicted with our method to that of Bennett, we find that the Bennett method produces lens power values that are lower by −2.18 D on average. This difference stems mostly from the fact that the Bennett method calculates the corneal power from the anterior corneal radius only, using the standard keratometric index of 1.3375. Use of the standard keratometry formula produces an overestimation of corneal power by approximately 1.2 D on average in normal corneas. The remaining difference is due to differences in the location of the principal planes of the lens. The difference in methods of calculation of corneal power accounts for most of the difference between our lens power values and the values of Rozema et al [21, 24]. Our values are in closer agreement with values obtained using a keratometric index of 1.3315 [3], which is derived assuming a two-surface model of the cornea, with a value of anterior to posterior radius of curvature provided by the Gullstrand model eye (0.889). Recent studies show that the ratio of posterior to anterior radius of curvature is on the order of 0.82 to 0.84 [29, 30], corresponding to a keratometric index of 1.328 to 1.329. This value is in good agreement with the data that obtained in our study. According to Table 3, the mean ratio of posterior to anterior curvature is 0.824 ± 0.013, corresponding to a keratometric index of 1.328. This observation also brings to attention the fact that special care must be taken when comparing values of lens power obtained using the Bennett method in different studies. Use of different methods to calculate corneal power may produce significant differences in the calculated lens power. Studies that relied on the standard keratometric index of 1.3375 will tend to underestimate the lens power.

Another factor that may cause differences in published values of lens power is the difference in the position of the posterior boundary that is used as a reference for the measurement of axial eye length. In our study we used the inner boundary of the retinal pigment epithelium (RPE) as a reference, since this boundary is adjacent to the photoreceptors. In measurements acquired using ultrasound or commercial optical biometry systems, the inner limiting membrane (ILM) serves as the reference surface. Axial eye length measured with these devices must therefore be corrected by adding the retinal thickness (approximately 0.2 mm) [31]. Without this correction, the lens power will be slightly overestimated.

The extended depth OCT provides all of the ocular distances needed for determining lens power using equation [16], with high precision and in a single measurement. In principle, since the OCT system provides cross-sectional images of the corneal and lens contours, we could have calculated the lens power from OCT images and refraction only, without resorting to a separate measurement of corneal topography. However, accurate measurements of corneal and lens shape from OCT images requires the development and validation of image processing algorithms for segmentation, curve fitting, motion compensation, and distortion correction [10, 14, 32]. Ideally, these algorithms must be applied to three-dimensional OCT images to take into account ocular surface asymmetry. These techniques are beyond the scope of the present study, which presents an alternative method to calculate lens power without requiring measurements of the lens radii of curvature.

The uncertainty in the equivalent index produces a large uncertainty in the lens power calculated with the lens maker formula, as discussed in the introduction. According to Eq. (12), the expression of b also depends on the equivalent refractive index. However, the influence of this dependence on the lens power is minimal. For instance, for the 20 year old relaxed lens, the change in lens power is only 0.26 D when the refractive index is changed from 1.40 to 1.44.

The extended-depth OCT system provides high precision measurements of the ocular distances, including lens thickness with a single device. The advantage of this approach compared to A-scan optical or ultrasound biometry, is that visualization of the image during the measurement helps ensure proper alignment of the eye. We estimate that the alignment precision for a trained operator is within +/−0.2 mm. An error analysis shows that within this range, alignment errors produce an error that is below the 5.2 μm per pixel axial digital resolution of our images. In addition, we can select the A-line from the two-dimensional image along which ocular distances are measured, and we can use individual values of the refractive index for each ocular medium to convert from optical to geometrical distances. Together, these advantages help increase accuracy and precision of the calculation of lens power.

One limitation is that the method relies on a paraxial model of the eye. The paraxial retinal conjugate is assumed to coincide with the far point of the eye determined by spherical equivalent refraction. The calculation ignores the effect of ocular aberrations which may shift the best focus of the eye away from the paraxial focus. The method provides a mean value of lens power calculated using spherical equivalent refraction and mean corneal power across the central 3mm diameter optical zone. Another limitation is that refraction and OCT imaging were performed without cycloplegia. The measured lens power may therefore not correspond to the fully relaxed accommodative state. Some of the variations in lens power and lens thickness found between the 16 subjects could be due in part to the fact that some of the subject accommodated during refraction or imaging. However, the range and average values of the lens power are consistent with previous studies performed under cycloplegia.

5. Conclusion

We present an improved modification on the Bennett method to calculate lens power from corneal topography, refraction, and ocular biometry. The estimated theoretical uncertainty in the predicted relaxed lens power is within ± 0.3 D for refractive error ranging from −10 D to + 10 D. The estimated relative theoretical prediction error for the change in lens power during accommodation is on the order of 10%. A preliminary study on 8 subjects provides values of lens power that are in close agreement with previously published values.

6. Appendix

The appendix illustrates the steps involved in the calculation of lens power from biometric data. The data from subject 1-OD (Table 3) is used as an example.

6.1. General method

Step 1: Calculate K₁, K₂, and K:

$$K_1=\frac{n_K-1}{R_1}=\frac{1.376-1}{0.00774}=48.58D$$

$$K_2=\frac{n-n_K}{R_2}=\frac{1.336-1.376}{0.00637}=-6.28D$$

$$K=K_1+K_2-\frac{CCT}{n_K}{K}_1{K}_2=48.58-6.28+\frac{0.000488}{1.376}\times 48.58\times 6.28=42.41D$$

Step 2: Calculate M_L using the measured distances and calculated value of K:

$$\begin{array}{l}{M}_L=\frac{VD+\frac{LT}{2}}{\frac{n}{R+K}-ACD-CCT\left(1-\frac{1}{n_K}\frac{K_2}{K}\right)-\frac{LT}{2}}=\\ \frac{18.302+\frac{3.438}{2}}{\frac{1336}{-4.07+42.41}-3.783-0.488-0.053-\frac{3.438}{2}}=0.695\end{array}$$

Step 3: Calculate b using the calculated value of M_L:

$$b=\frac{0.650-0.584{M_L}^2}{1-{M_L}^2}=\frac{0.650-0.584\times {0.695}^2}{1-{0.695}^2}=0.712$$

Step 4: Calculate v_L using the measured distance and the calculated value of K and K_2:

$$\begin{array}{l}{v}_L=\frac{n}{R+K}-ACD-CCT\left(1-\frac{1}{n_K}\frac{K_2}{K}\right)\\ =\frac{1336}{-4.07+42.41}-3.783-0.488\left(\text{1}+\frac{\text{1}}{\text{1.376}}\frac{6.28}{42.41}\right)=30.522mm\end{array}$$

Step 5: Calculate lens power using lens thickness, vitreous depth (v'_L = VD) and the calculated values of b and v_L:

$$\begin{array}{l}L=\frac{n}{v{\text{'}}_L-(b-1)\times LT}-\frac{n}{v_L-b\times LT}=\\ \frac{1336}{18.302-(0.712-1)\times 3.438}-\frac{1336}{30.522-0.712\times 3.438}=21.66D\end{array}$$

6.2 Alternative method 1 - posterior corneal radius missing

If the posterior corneal radius is not measured, then an estimate can be calculated by assuming that the ratio of posterior to anterior corneal radius is 0.81 for an average normal cornea. For the example above, we obtain R₂=6.27 mm, which gives K₂=-6.38 D and K=42.31 D. The final value of lens power is 21.81 D, 0.15 D larger than the value obtained when the measured posterior radius is used in the calculation.

6.3. Alternative method 2 - lens thickness missing

If the lens thickness is unavailable, lens power can be estimated by using a fixed value (i.e., 4 mm), or the age-dependent model (Table 2). In that case, vitreous depth is calculated by subtracting lens thickness, anterior chamber depth and corneal thickness from the measured axial eye length. For the example above, the axial eye length is 26.01 mm and the age-dependent model of Table 2 (age = 22 years) gives a thickness of 2.93+0.024*22=3.46 mm. Estimated vitreous depth is 26.01-0.488-3.783-4 =17.74 mm if we use the fixed value (LT=4 mm) and 26.01-0.488-3.783-3.46=18.28 mm if we use the age-dependent model (LT=3.46 mm). Using these values in Steps 1-5 gives 22.43 D with the fixed value and 21.69 D with the age-dependent model. The prediction error is +0.77 D with the fixed value and +0.03 D with the age-dependent model.

Author Disclosure

The University of Miami and authors MR, FM, JMP, and AH stand to benefit from intellectual property in the OCT technology used in this study.