Enhancing the executive functions of 3-year-olds in the dimensional change card sort task

Abstract

Executive functions (EFs) enable flexible thinking, something young children are notoriously bad at. For instance, in the dimensional change card sort (DCCS) task, 3-year-olds can sort cards by one dimension (shape), but continue to sort by this dimension when asked to switch (to color). This study tests a prediction of a Dynamic Neural Field (DNF) model that prior experience with the post-switch dimension can enhance 3-year-old’s performance in the DCCS task. In Experiment 1A, a matching game was used to pre-expose 3-year-olds (n=36) to color. This facilitated switching from sorting by shape to color. In Experiment 1B, 3-year-olds (n=18) were pre-exposed to shape. This did not facilitate switching from sorting by color to shape. The DNF model was used to provide a mechanistic explanation for this asymmetry.

Executive functions (EFs) enable humans to think and behave in a flexible, goal-directed fashion. EF is an umbrella term for a set of interactive control processes that include working memory, inhibition, and attention switching. EFs contribute to children’s reasoning (Carlson, Moses, & Breton, 2002), arithmetic (Blair & Razza, 2007), reading (van der Sluis, de Jong, & van der Leij, 2008), and social (Clark, Prior, & Kinsella, 2002) abilities. Moreover, the establishment of robust EFs in early childhood is predictive of positive developmental outcomes, and EF deficits at 3 years of age are predictive of negative outcomes in health, wealth, and criminal activity involvement nearly 30 years later (Moffit et al., 2011). Not surprisingly, then, EF interventions that positively impact individual development are in great demand.

To date, efforts to develop early interventions to improve EFs have yielded mixed results. Interventions that have trained children’s task-switching abilities have transferred to other EFs such as working memory and inhibitory control (Karbach & Kray, 2009). Interventions that have trained children’s working memory abilities, by contrast, have not (for reviews, see Diamond, 2012; Shipstead, Hicks, & Engle, 2012). One potential reason that EF intervention efforts have yielded mixed results is that theories of EF development do not predict what contexts training should transfer to because they do not specify the mechanisms by which experience generalizes across contexts (Simmering & Perone, 2013; see also Gibson et al., 2012). For example, theories of EF development do not explain how the same working memory system is used in multiple task contexts. This limitation hinders their ability to specify the types of experience acquired in one context that should influence working memory in another context.

Here, we test a novel prediction of a Dynamic Neural Field (DNF) model of EF development that specifies how experience in one context can facilitate children’s performance in a canonical probe of EF in early development – the Dimensional Change Card Sort (DCCS) task. In the DCCS, children sort a collection of two-dimensional cards (e.g., red stars and blue circles) to target cards that match on one dimension (e.g., red circle and blue star). After sorting by one dimension, children are instructed to switch the dimension used to sort the same cards. Under these standard conditions, 4-year-old, but not 3-year-old, children flexibly switch attention across dimensions and sort correctly during the post-switch phase (Zelazo, 2006).

The standard DCCS task conditions require children to flexibly switch the dimension to which they attend across the pre- and post-switch phases of the task. A number of studies have shown that 3-year-old children can pass the DCCS task when the standard conditions are simplified or modified such that selective dimensional attention is not required (Brace, Morton, & Munakata, 2006; Brooks, Hanauer, Padowska, & Rosman, 2003). Other studies have shown that 3-year-old children can pass the DCCS task under the standard conditions if they are explicitly pre-trained to attend to the bi-dimensionality of the cards they sort in the DCCS task (Mack, 2007; Ramscar, Dye, Gustafson, & Klein, 2013). No previous study has shown that children can pass the DCCS task under the standard conditions without explicit pre-training. The DNF model predicts that flexible attention switching under the standard conditions of the DCCS task can be induced via prior experience with the label for and features distributed over the feature dimension used in the post-switch phase of the task. Below, we describe the DNF model and basis of this prediction. We then test this prediction with children.

A Dynamic Neural Field Model of Executive Function Development

DNF models embody a set of concepts linking brain and behavioral dynamics in real time and over development (for a review, see Spencer, Perone, & Johnson, 2009). The central component of a DNF model is the neural field. Neural fields consist of populations of neurons selectively tuned to continuous dimensions (e.g., hue). The dynamics of neural fields are governed by local excitatory / lateral inhibitory interactions. For example, a blue stimulus excites neurons selectively tuned to the specific hue. These neurons, in turn, excite neurons tuned to similar hues in a graded fashion. This excitation also leads to broad inhibition surrounding the excitation, creating a local excitatory / lateral inhibitory activation profile called a “peak” of activation. One important feature of DNFs is that activity within neural fields creates long-term Hebbian memories that influence their activity at a future point in time. For example, the neuronal response to a blue stimulus will create a long-term memory that strengthens the neuronal response to similar hues at a future point in time.

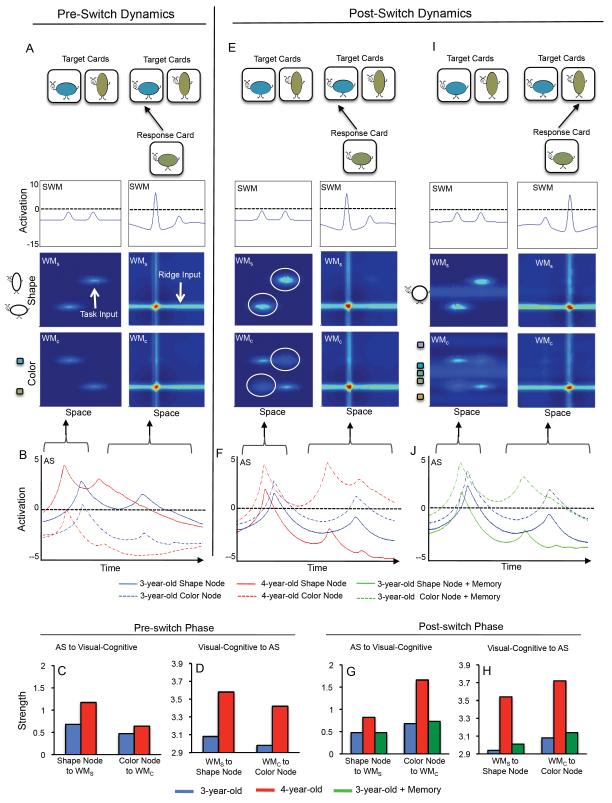
Buss and Spencer’s (2014) model of EF development consists of coupled visual-cognitive and dimensional attention systems. The left panel of Figure 1A shows the architecture of the model. The visual-cognitive system consists of three interactive working memory fields. Shown at the top of 1A is the spatial working memory (SWM) field. SWM represents the presence of stimuli at specific locations. SWM is coupled to a shape working memory (WM_S) field and a color working memory (WM_C) field, both of which are shown just below SWM. These fields are sensitive to ‘what’ is ‘where’, that is, they respond to features distributed along metrically organized feature dimensions such as hue (y-axis) at spatially specific locations (x-axis). The connection of WM_S and WM_C to SWM enables the model to represent objects as a color and a shape at a particular location (e.g., red + star on the left). The attention system (AS) consists of competitive nodes that respond to the labels “shape” and “color” that control attention switching across dimensions (1B). These nodes are coupled to WM_S and WM_C via a weight matrix that represents learned associations between the labels (e.g., ‘color’) and the feature values (e.g., blue) the labels represent.

Figure 1.

Shows DNF model dynamics for 3- and 4-year-old models in DCCS task. Panel A shows the model dynamics during the pre-switch phase. Initially, the model is situated in front of target cards depicting a short, blue object and a tall, green object. This generates task inputs in SWM (see “bumps”) and WM_S and WM_C (see light blue patches). The model is instructed to sort the short, green object depicted on the response card by shape. This leads the shape node in the attention system (AS) to become active for the 3- and 4-year-old models (see solid blue and solid red lines in B). Consequently, the strength of the connectivity between the AS and the visual-cognitive system is stronger for shape than color node (compare left portion to right portion of C-D). It is also stronger for the 4-year-old than 3-year-old model (compare red bars to blue bars in C-D). This reflects the stronger connectivity in the 4-year-old than 3-year-old model (see text). These interactions between the AS and visual-cognitive system lead the model to sort by shape by forming activation peaks in WM_S, WM_C, and SWM at the left location. Note that the arrows shown from the AS to the visual-cognitive system indicate the window of time that AS activity corresponds to the onset of a trial (left portion of A) and the sorting of the card (right portion of A).

Panel E shows the DNF model dynamics during the post-switch phase. The model is instructed to sort the short, green object by color. This leads the color node in the AS to become active for the 3- and 4-year-old models (see dashed blue and dashed red lines in F). During the post-switch phase, the strength of the connectivity between the AS and visual-cognitive system is stronger for color than for shape (compare right portions of G-H). It is also stronger for the 4-year-old than the 3-year-old model (compare red to blue bars in G-H). Importantly, for the 3-year-old model, this connectivity is too weak for WM_C to overcome the robust Hebbian memories acquired from sorting by shape during the pre-switch phase in WM_S (see white circles). The 3-year-old model continues to sort the short, green object to the left location by shape. The 4-year-old model sorts by color (not shown).

Panel I shows the 3-year-old model during the post-switch phase after it has acquired experience in the form of Hebbian memories with the dimensional label ‘color’ in the AS and 5 objects that differ in color (see distributed light blue patches in WM_C) and share one shape (see light blue ridge in WM_S). This experience primes WM_C to respond more strongly during the post-switch phase. It also creates a stronger pattern of connectivity from the AS to the visual-cognitive system for color than shape (green bars in G) and from the visual-cognitive system to the AS for color (green bars in H) than in the 3-year-old model alone for color (blue bars in G-H). This is also reflected in the strength of the color node in the AS, which is stronger for the 3-year-old + memory model than 3-year-old model alone (compare dashed green line to dashed blue line in the AS in J). The 3-year-old model switches attention across dimensions and sorts the short, green object to the right location based on color in the post-switch phase.

Buss and Spencer (2014) created 3-year-old and 4-year-old models by making two changes to the AS. First, older models had stronger excitatory and inhibitory interaction strengths within the AS making the shape and color nodes more competitive (winner-take-all interactions) and better able to maintain excitatory interaction once one of a node ‘won’ the competition. Second, the older model had a more selective weight matrix between the AS and the visual-cognitive system—the color node, for instance, projected greater activation to WM_C and less activation to WM_S. Buss and Spencer used the 3- and 4-year-old models to quantitatively simulate developmental changes in children’s performance in the DCCS task across 14 variants of the task and to generate and test novel behavioral predictions. Our goal here was to probe ways to facilitate the performance of the same 3-year-old model used by Buss and Spencer. Note that all model details including equations and parameter settings can be found in Buss and Spencer (2014).

Figure 1 illustrates how the 3- and 4-year-old models perform the DCCS task. 1A shows the DNF model during the pre-switch phase of the task. The very top shows target cards present at left (short, blue object) and right (tall, green object) locations. These target cards provide task input to SWM and generate “bumps” of activation at left and right locations in SWM.

The target cards also provide task input to WM_S and WM_C. As indicated by the light blue patches of activity in these fields, the target card depicting the tall, green object generates an increase in activation at the tall value in WM_S (see “task input” in Figure 1A) and at the green value in WM_C. Similarly, the target card depicting the short, blue object generates an increase in activation on the left side of WM_S and WM_C.

At the onset of the pre-switch phase, the DNF model is instructed to sort by shape. This selectively activates the shape node in the AS. The activation of the shape node is shown in 1B for the 3-year-old model (solid blue line) and 4-year-old model (solid red line). Because the shape node is activated, this node sends stronger activation to WM_S than the color node sends to WM_C. This difference in input strength from the AS to the visual-cognitive system is quantified in 1C: the activation from the shape node to WM_S is stronger than the activation of the color node to WM_C for both the 3-year-old model (blue bars) and 4-year-old model (red bars). This raises the baseline activity of neurons within WM_S, effectively priming the system to selectively attend to the shape dimension. Note that the strength difference in 1C is greater for the 4-year-old model because the nodes have stronger excitatory / inhibitory interactions and because the weight matrix connecting the AS to the visual-cognitive system is more selective.

Figure 1D shows that the priming effect also has an impact on the AS. In particular, because the AS and the visual-cognitive system are reciprocally connected, the priming leads to an increase in the strength of activation WM_S sends back to the shape node. This feedback from the visual-cognitive system to the AS is stronger for shape than color for both the 3- and 4-year-old models, although the activation strengths are greater for the 4-year-old model due to the more selective weight matrix.

Next, the model is presented with a response card depicting a short, green object (right panels in 1A). This provides a ridge of input across all spatial locations activating all neurons tuned to the short feature in WM_S and the green hue in WM_C (see “ridge input” in 1A). Recall that because of the task instructions, WM_S is primed to respond more strongly to shape stimuli than WM_C is to color stimuli. Consequently, the overlap of the ridge input from the response card with the task input from the target input in WM_S creates an activation peak at the left location associated with the short stimulus (see red ‘hot spot’ of activation in WM_S). This peak is a real-time neuronal representation of the shape of the short object at the left location. The peak excites neurons tuned to the left location in WM_C and SWM, leading to peaks in both fields, effectively ‘binding’ the short feature in WM_S to the green feature in WM_C. Consequently, the model sorts the response card to the left location, correctly attending to the shape on the card.

There are two influences on attention switching during the post-switch phase. The first is a Hebbian memory. The presence of peaks in the working memory fields creates Hebbian memories that accumulate slowly over trials. These Hebbian memories facilitate the re-formation of peaks at previously active sites in the working memory fields. Sorting the response cards in the pre-switch phase leads to the accumulation of Hebbian memories in WM_S and WM_C at sites associated with the sorting responses (e.g., at short and green feature values). This can be seen in the left panels of 1E which shows the state of the model at the onset of the post-switch phase. In WM_S, there is co-operation between the Hebbian memories and task inputs (white circles) because the model sorted response cards based on a match in shape (i.e., short objects to the left and tall objects to the right). Consequently, the model is primed to continue sorting by shape. In WM_C, by contrast, there is competition: Hebbian memories (white circles) accumulated at sites that did not overlap with the task inputs because the model sorted response cards to target cards that did not match in color.

The second influence on attention switching during the post-switch phase is the state of the AS. At the onset of the post-switch phase, the model is instructed to sort by color instead of shape. As is shown in 1F, this selectively activates the color node for the 3-year-old model (dashed blue line) and 4-year-old model (dashed red line). Consequently, the activation sent from the color node to WM_C (see 1G) is stronger than the activation sent from the shape node to WM_S for both the 3-year-old model (blue bars) and 4-year-old model (red bars). The activation returned from WM_C to the color node is also stronger than the activation returned from WM_S to the shape node (1H). Importantly, the degree to which WM_C is primed to respond to color is less for the 3-year-old model than the 4-year-old model due to weaker excitation / inhibition within the AS and a less selective weight matrix between the AS and the visual cognitive system.

This weaker priming has consequences in the post-switch phase because the system must overcome the response biases created during the pre-switch phase. In particular, when the 3-year-old model is presented with the short, green response card in the right panels of 1E, it sorts the card based on shape. The color priming was not sufficient to overcome the cooperation between Hebbian memories and task input in WM_S. By contrast, the 4-year-old model sorts correctly during the post-switch phase (not shown; see Buss & Spencer, 2014 for example simulations) because the color priming effect is much stronger (see 1G and 1H).

In summary, the 3-year-old model fails the DCCS task because there is strong cooperativity within the pre-switch working memory field (in this case, WM_S) and the AS activity is weak and not yet selective. But what if we could somehow boost attention to the post-switch dimension, in this example, color? One way to do this is to give the model experience with different hue values in the context of the label ‘color’. These experiences should leave distributed Hebbian memories within WM_C and stronger ‘color’ memories in the AS, effectively ‘boosting’ the degree to which the model is primed to respond to color during the post-switch phase of the task. Such a boost might be sufficient to tip the scales toward the color dimension during the post-switch phase.

Figure 1I implements this idea in the 3-year-old model (see the appendix for additional simulation details). In these simulations, the color node was initialized with a slightly stronger Hebbian memory reflecting recent experiences with the label ‘color’, priming the color node to respond more strongly to ‘color’ than it would without this experience. The model was also initialized with Hebbian memories for a collection of objects experienced outside the context of the DCCS task that all shared the same shape but varied in color. Importantly, we did not use any of the feature values used in the DCCS task. The resultant Hebbian memories are shown in the left panels of 1I. There is a localized memory on the shape dimension (light blue ridge at center of shape dimension in WM_S). This reflects the one shape shared by all colors experienced prior to the DCCS task. There are distributed memories on the color dimension (light blue patches along entire color dimension in WM_C). This reflects the variable colors the model was exposed to prior to the DCCS task. These memories elevate the neural activity across the color dimension in WM_C, priming WM_C to respond more robustly to color stimuli than it would without this prior experience.

This priming had a big impact on the performance of the 3-year-old model in the DCCS task. This is evident in the right panels of 1I which show performance during the post-switch phase. When the model is presented with the short, green response card at the onset of the post-switch phase and is instructed to sort by color, the label input and Hebbian memories in the AS and WM_C combine to create a stronger boost for color. The model sorts the short, green card to the right by color.

The influence of the Hebbian memories on the model’s dynamics is evident in the reciprocal interaction between the AS and visual-cognitive system. In particular, the slight increase in the Hebbian memories at the start of the simulation creates stronger activation from the color node to WM_C (1G) and stronger activation from WM_C to the color node (1H) during the post-switch phase for the 3-year-old model with Hebbian memories (green bars) relative to the standard 3-year-old model (blue bars). This can also be seen in 1J, which shows the stronger activation of the color node for the model with prior experience (dashed green line) relative to the standard 3-year-old model (dashed blue line). This slight initial boost for color is sufficient to tip the balance during the post-switch phase of the task and the 3-year-old model correctly switches attention from shape to color.

Quantitative Model Predictions

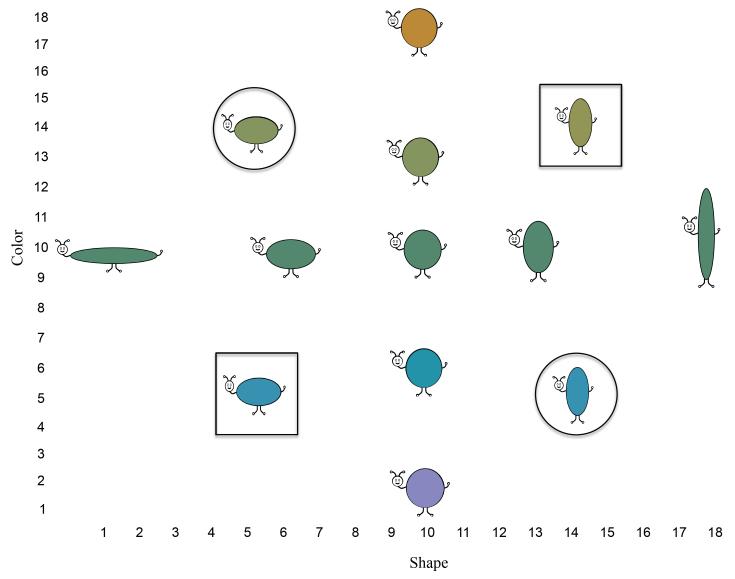
We quantitatively probed this prediction using the 3-year-old model, parameters, and simulation method from Buss and Spencer (2014). The distribution of the stimulus inputs is shown in Figure 2. The inputs were sampled from a set of 18 equidistant metric steps on the shape and color dimensions, which were distributed over 100 neurons in the model. Each metric step in the model for color and for shape was separated by 4 neurons. Each object consisted of one feature from the shape dimension and one feature from the color dimension. For example, stimulus s5c5 is the fifth feature on the shape and color dimensions. The values s5c5 and s14c14 (squares) were used as target cards. The values s14c5 and s5c14 (circles) were used as response cards. The model was instructed to sort each response card three times by shape during the pre-switch phase and each response card three times by color during the post-switch phase. When sorting by shape during the pre-switch phase, sorting response card s14c5 to target card s14c14 and response card s5c14 to s5c5 was the correct response because they share the same shape. When sorting by color during the post-switch phase, sorting response card s14c5 to target card s5c5 and response card s5c14 to s14c14 was the correct response because they share the same color. The model was run through the DCCS task 100 times under these standard conditions. To pass the DCCS task, it was required to correctly sort 5 of the 6 cards during the post-switch phase. The model passed at a rate of 30% (Figure 3). The model was also run through a memory + standard condition 100 times. It was initialized with Hebbian memories for five colors that spanned the color dimension (1, 6, 10, 13 and 18), all paired with the same shape (10). The strength of the memories for the five colors was set to .2 (the strength of the memory for the single shape shared by all colors was set to .6). The model passed at a rate of 81% (Figure 3).

Figure 2.

Shows buggle stimulus set. Each buggle consist of one value along a continuous, metrically organized color (hue) and shape (aspect-ratio) dimension. The entire shape dimension consisted of 18 equidistant metric steps. The entire color dimension consisted of 1-180° of a 360° color space (CIE*Lab, 1976), equally parsed to create 18 equidistant metric steps. The objects with squares were used as target (or response) cards, and the objects with circles were used as response (or target) cards. The objects sharing shape 10 but varying in color were used in the color memory game to expose children to what would be the post-switch dimension in Experiment 1A. The objects sharing color 10 but varying in shape were used in the shape memory game to expose children to what would be the post-switch dimension in Experiment 1B. The same shape and color values were used as input to the DNF model.

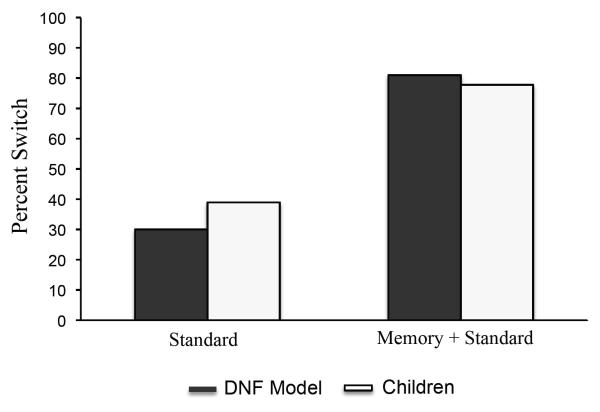
Figure 3.

Shows the percent of DNF model simulations (black bars) and children (white bars) that passed the post-switch phase of the DCCS task under the standard conditions and in the memory + standard condition in Experiment 1A.

Previous studies have shown that children can pass the DCCS task when the standard conditions are simplified (Brace et al, 2006) or children are explicitly pre-trained to attend to the features on both dimensions on the response cards used in the DCCS task (Mack, 2007; Ramscar et al, 2013). The DNF model predicts that attention switching in 3-year-old children can be induced by experience with the post-switch dimension even when the features used in the DCCS task are not part of that experience and the pre-exposure happens in a different task context. We tested this prediction in Experiment 1A.

Experiment 1A

Method

Participants

Eighteen 3-year-old (9 girls, M = 42.5 months, SD = 2.84) children participated in a memory game + standard DCCS condition. One additional child participated but was excluded for failing to sort 5 of 6 cards correctly during the pre-switch phase (see Zelazo, 2006). Eighteen 3-year-old children (10 girls, M = 41.30 months, SD = 2.30) participated in the standard DCCS task only. Four additional children participated but were excluded due to fussiness (n = 2) and failing to sort 5 of 6 cards correctly during the pre-switch phase (n = 2). Children were recruited from birth records and local child care facilities.

Stimuli, Design, and Procedure

The stimulus set from which the target, sorting, and memory game (described below) cards were derived were buggles (see Figure 2; Perone & Spencer, 2014). The set is a collection of objects that consist of one value along continuous color (hue) and shape (aspect-ratio) dimensions. On the color dimension, 18 equidistant colors were sampled from 1-180° of a 360° continuous color space (CIE*Lab, 1976). The shape dimension was parsed into 18 equidistant steps. Each metric step was defined by a proportional change in height and width, with total area held constant.

The color and shape values used were the same as those used in the DNF model. For the DCCS task, there were two sets of cards. For one set, s5c5/s14c14 were target cards and s14c5/s5c14 were response cards. For the other set, s5c14/s14c5 were target cards and s5c5/s14c14 were sorting cards. The set of cards used was counterbalanced across children. The goal of the standard condition was to ensure that 3-year-old children pass the DCCS at rates comparable to that observed in the literature with this new, metrically organized stimulus set. Given this goal, it was important for half of the children to sort by shape during the pre-switch phase and the other half of the children sort by color.

The standard conditions followed Zelazo’s (2006) protocol. The experimenter told the child the pre-switch rule (“We are going to play the shape game”). The experimenter showed the child how to sort one card by the pre-switch dimension and ensured that the child could do so with another card. During the pre-switch phase, the experimenter presented each response card, labeled it along the pre-switch dimension (“Here’s a blue buggle.”), and asked the child to sort the card (“Can you put it where it goes?”). If the child sorted incorrectly, the pre-switch rules were re-stated. At the onset of the post-switch phase, the experimenter explained the post-switch rule (“Now we are going to play the color game”) but did not show the child how to sort the cards by the post-switch rule. The post-switch phase was otherwise identical to the pre-switch phase. Children sorted each response card three times each. The order of the cards was random with the constraint that no more than two identical cards were presented on consecutive trials.

Children in the memory + standard condition played a memory game much like those sold commercially or played with a standard deck of cards. The goal of the memory game was to expose children to what would be the post-switch dimension in the DCCS task in an engaging task appropriate for the age group. For all children in the memory + standard condition, the pre-switch dimension was shape and the post-switch dimension was color. During the memory game, children matched 5 pairs of cards depicting the same shape and color values used in the DNF model. The same shape (10) was used for all cards but the colors spanned the color dimension (1, 6, 10, 13, 18; see Figure 2).

The experimenter and child sat at a table with the matching cards spread out face up within reaching distance. The experimenter familiarized the child with each matching pair of cards by showing the child each card and its match together. The experimenter said to the child, “Look! These two are the same color” to help ensure the child was engaged in the familiarization phase. The experimenter only labeled the dimension (i.e., color) and did not label any of the individual color values (e.g., blue). After the child was familiar with each pair, the experimenter flipped all the cards over so that they were face down and scrambled them. The experimenter then explained to the child that they were going to try to find the colors that matched. The experimenter provided a demonstration by turning over two non-matching cards, one at a time, and said “These two aren’t the same color.” The experimenter then flipped the two non-matching cards back over and told the child it was his/her turn. The child and experimenter took turns flipping over pairs of cards. If the pair was a match, then the cards were removed from the game. If the pair was not a match, both cards were flipped back over. Each child was required to find four of the five matches during the game. The experimenter randomly selected non-matching pairs of cards during his/her turn, until only four cards remained in the game. The experimenter then selected a matching pair to allow the child to uncover the final matching pair. It is notable that children may solve the memory game via trial and error or randomly flipping over cards rather than finding matches by relying on memory of the colors of previously flipped over cards. However, previous studies have shown that children of this age form working memories even for rapidly presented stimuli (Simmering, 2012); thus even if children’s performance was based on trial-and-error, they likely formed memories for the color values. Once all the matches were found, the DCCS task was administered.

Results

Children were considered to pass the post-switch phase of the DCCS task if they correctly sorted 5 of the 6 cards presented during the post-switch phase (Zelazo, 2006). Only 7 of 18 (38.9%) children passed the standard condition of the DCCS task with our metrically organized stimulus set (Figure 3), replicating previous findings (Zelazo, Müller, Frye, & Marcovitch, 2003). Of the 7 children who passed, 3 sorted by color during the pre-switch phase and 4 sorted by shape during the pre-switch phase. The rate of passing did not differ by pre-switch dimension χ² (1,N=18) = .234, p =.629. Results for the memory + standard condition were strikingly different: 14 of 18 children (77.8%) passed the DCCS task (Figure 3). A Chi-square analysis revealed that significantly more 3-year-old children passed in the memory game + standard condition than in the standard condition alone, χ² (1,N=36) = 5.60, p =.018. Thus, 3-year-old children flexibly switched attention from the shape to the color dimension under the standard conditions of the DCCS task after acquiring prior experience with the post-switch dimension.

Discussion

The results of Experiment 1A are consistent with the DNF model prediction that experience with colors prior to the DCCS task can induce flexible attention switching from shape to color in 3-year-old children. Previous studies have shown that children can pass the DCCS task when the standard conditions are simplified (Brace et al, 2006) or children are explicitly pre-trained to attend to the features on both dimensions on the response cards used in the DCCS task (Mack, 2007; Ramscar et al, 2013). Here, however, children’s flexibility was induced under the standard conditions without explicit task-specific pre-training or simplification.

One open question is whether flexible attention switching in the DCCS can also be induced for the shape dimension. Our simulations of the DNF model treated the color and shape dimensions equivalently. That is, the metric organization of the colors and shapes were identical for both dimensions in the model. Nevertheless, previous studies have observed asymmetries in children’s DCCS performance based on the dimension they sort by during the post-switch phase. For example, Fisher (2011) found that 3-year-old children failed a version of the DCCS task when they were asked to switch from a dimension with distinct features (e.g., star and flower) to a dimension with similar features (e.g., pink and red), but not when they were asked to switch from similar features to distinct features. Although children failed our DCCS task under the standard conditions regardless of whether they were sorting by color or by shape during the post-switch phase, it is possible that a memory game for the shapes used here would not influence children in the same way as color did. Thus, in Experiment 1B we tested whether experience with values distributed over the shape dimension could induce flexible attention switching from color to shape.

Experiment 1B

Method

Participants

Eighteen 3-year-old children (8 girls, M = 41.36 months, SD = 4.84) participated in this study. Nine additional children participated but were excluded due to fussiness (n = 2), experimenter error (n = 6), or failing the pre-switch phase (n = 1). Children were recruited from birth records, university community, and child care facilities.

Stimuli, Design, and Procedure

The stimuli, design, and procedure were identical to Experiment 1A with two exceptions. First, children matched by shape instead of color during the memory game with the same metric distribution of values over the shape dimension as was used for the color dimension in Experiment 1A (see Figure 2). Second, children sorted by color during the pre-switch phase of the DCCS task and shape during the post-switch phase.

Results

One child was excluded from the final analysis because she/he failed the pre-switch phase of the task. Eight of 18 (44.4%) children passed the post-switch phase of the task (Figure 4). A Chi-square analysis revealed that the number of 3-year-old children that passed the shape memory game + standard condition was not significantly different than the number of children that passed under the standard conditions alone, χ² (1,N=36) = .11, p = .74, but was significantly less than the number of children who passed in the color memory game + standard condition, χ² (1,N=36) = 4.21, p = .04. Thus, the experience provided during the shape memory game prior to participating in the DCCS task did not facilitate 3-year-old children’s ability to flexibly switch attention from color to shape.

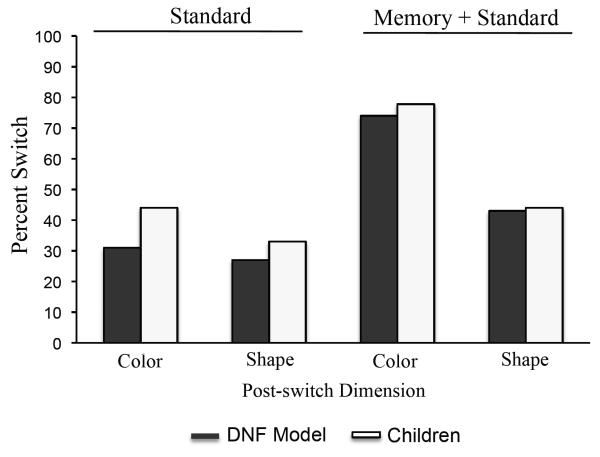
Figure 4.

Shows results across Experiments 1A and 1B. The left portion shows the percent of DNF model simulations (black bars) and children (white bars) that passed the post-switch phase of the DCCS task under the standard conditions when the post-switch dimension was color and when the post-switch dimension was shape (Experiment 1A). The right portion shows the percent of DNF model simulations (black bars) and children (white bars) that passed the post-switch phase of after the color memory game (Experiment 1A) and the shape memory game (Experiment 1B).

Discussion

The results indicate that experience with the color and shape dimensions used here do not influence children’s ability to flexibly switch attention across dimensions in the DCCS task in the same way. Why might this be? For insight, we return to results from Fisher (2011) showing that 3-year-old children failed a version of the DCCS task when they were asked to switch from a dimension with distinct features to a dimension with similar features, but not when they were asked to switch from similar features to distinct features. Buss and Spencer (2014) quantitatively simulated results from this study by changing the metric distribution of features used in the DNF model. When model inputs were compressed along one dimension making the inputs less distinctive along that dimension, the model failed the DCCS task if this less distinctive dimension was used as the post-switch dimension. By contrast, when the less distinctive dimension was the pre-switch dimension, the model correctly switched rules in the post-switch phase.

Based on these findings, we hypothesized that the asymmetry in the present study might reflect a similar asymmetry in the distinctiveness of the color and shape dimensions. In particular, we hypothesized that the shape dimension was less distinctive, that is, adjacent steps along the shape dimension were compressed relative to steps along the color dimension. The critical question here is how this asymmetry might impact the memories carried forward from the shape memory game to the DCCS task.

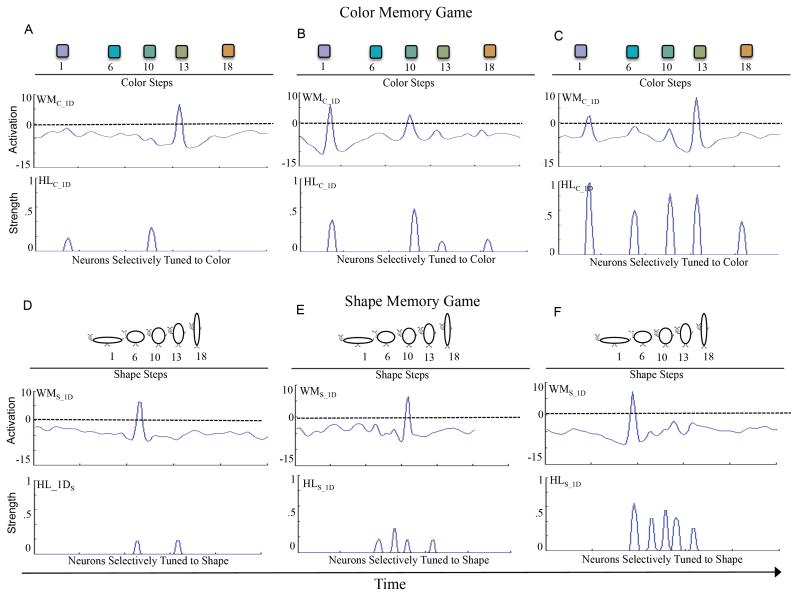
To explore this, we constructed a simplified, one-dimensional DNF model that enabled us to probe how experience with a distributed versus compressed set of stimuli would influence working memory peaks and Hebbian memories across a series of learning trials comparable to what children might experience in the memory game (for model details, see appendix). Figure 5 shows these simulations. The top of 5A shows the metric organization of colors used in Experiment 1A. Each metric step on the 18 step dimension is separated by 4 neurons in a neural population of 100 neurons selectively tuned to color. With this separation of values in color space, there is substantial neural territory devoted to each color. The middle panel of 5A shows a working memory field for color (WM_{C_1D}), and the bottom panel shows an associated Hebbian layer for color (HL_{C_1D}). This model was presented with the five color values used in the color memory game in a random order across 30 learning trials, much like successively flipping over cards in the color memory game while seeking matches. 5A shows the model early in learning. The model is maintaining a working memory for color 13 and has accumulated Hebbian memories for colors 1 and 10 on previous trials. 5B shows the model a bit later in learning. Now, the model is maintaining a working memory for color 1 but, critically, it is also maintaining a working memory for color 10 that was presented in the just-recent past. This enables the model to form robust Hebbian memories for both items. This learning process continues across trials, leading to strong Hebbian memories for all colors from the memory game (5C).

Figure 5.

Shows simulation of a one-dimensional DNF model of the color memory game (top portion) and shape memory game (bottom portion). The top of panel A shows the metric organization of the color values used in the color memory game. This is the input to a one-dimensional working memory field for color (WM_{C_1D}), shown just below. WM_{C_1D} is coupled to a Hebbian layer for colors (HL_{C_1D}). Panel A also shows the model early in learning, after exposure to just a couple of colors in the color memory game. At this time, the model has acquired a couple weak memories in HL_{C_1D}. Panel C shows the model a bit later in learning. Now, the model has acquired more memories in HL_{C_1D}, some of which are robust. It is also maintaining multiple items in WM_{C_1D}, which helps the model acquire even more robust memories in HL_{C_1D}. By the end of learning, late in the color memory game, the model has acquired robust memories in HL_{C_1D} for all the colors in the color memory game.

The top of panel D shows the metric organization of the shape values used in the shape memory game. These are noticeably closer than those used in the color memory game, even though the distribution is the same. These values were input into a one-dimensional working memory field for shape (WM_{S_1D}). Panel D also shows the model early in learning, after exposure to just a couple of shapes in the shape memory game. The model has a couple of weak memories in the associated Hebbian layer, HL_{S_1D}. Panel E shows the model a bit later in learning. The model has acquired memories for several shapes in HL_{S_1D}. Notice that WM_{S_1D} is only maintaining one item, as compared to two in WM_{C_1D} at the same time in learning in the color memory game (see B). This is because the closeness of the shape values creates interference in WM_{S_1D}, effectively limiting it to remembering only one item at a time. This, in turn, hinders the ability of the model to form robust memories in HL_{S_1D} during the course of the shape memory game (F).

Figure 5D-F shows what emerges when the model is presented with shapes that are less distinctive, that is, with shapes that are compressed together along the metric feature dimension (see top panel of 5D). In particular, each metric step on the 18 step dimension is separated by just 1.5 neurons in a neural population of 100 neurons selectively tuned to shape. With this small step size in shape space, there is little neural territory devoted to each shape. This has a dramatic impact on learning about shapes in the model. 5D shows the model early in learning. At this point, the model is maintaining a working memory of shape 6 and has accumulated Hebbian memories for shapes 1 and 6. A bit later in learning, the model is still only maintaining one shape in working memory (5E). This contrasts with the same model learning about colors in 5B—that model was able to maintain multiple colors in working memory at the same point in learning. What is the source of this difference? The close proximity of shape values leads to working memory peaks that inhibit each other. When a new working memory peak is formed, the lateral inhibition surrounding it effectively knocks out any existing working memory peaks that are close by (see inhibitory troughs surrounding peaks in 5D-F). This interferes with the formation of Hebbian memories, ultimately leading to weak Hebbian memories for the individual shapes over learning (5F). These weaker Hebbian memories for shapes, relative to those for colors (5C), may be insufficient to prime the shape dimension in the DCCS task. These simulations are consistent with recent evidence showing that young children’s performance in a working memory task was poorer for similar items than dissimilar items (Simmering & Cooper, 2014).

To probe whether this account might explain the asymmetry we observed across Experiments 1A and 1B, we conducted a second set of quantitative simulations. In particular, we re-simulated the model, testing the hypothesis that weaker Hebbian memory strengths for less distinctive shapes relative to stronger Hebbian memory strengths for colors could account for the pattern of behavioral results observed in Experiments 1A and 1B.

Quantitative Model Simulations of Dimensional Asymmetry

To re-simulate the DNF model and test whether the asymmetry across Experiments 1A and 1B might reflect differences in the distinctiveness of the colors versus shapes used in our stimulus set, we used the metric organization of the color and shape dimensions shown in Figure 5. The 18 metric steps on the color dimension were distributed as in Experiment 1A with each step separated by 4 neurons as illustrated in 5A. The 18 metric steps on the shape dimension, by contrast, were each separated by 1.5 neurons as illustrated in 5D. Recall that the metric organization of the stimulus inputs were identical on the shape and color dimensions in our previous simulations. Moreover, Buss and Spencer (2014) showed that the metric distribution of inputs can have an impact on performance in the standard DCCS task. Thus, the first set of simulations below tested whether the DNF model produces the same pattern of results in the standard task (see Figure 3) with the distribution of inputs compressed along the shape dimension (see Figure 5).

Next, we simulated the color memory game + standard condition using inputs compressed along the shape dimension. The goal of these simulations was to examine whether the novel prediction from Experiment 1A was replicated with the new input distribution for shape when color was the post-switch dimension in the DCCS task. The strength of the memories for the five colors was set to .2 (the strength of the memory for the single shape shared by all colors was set to .0375). Finally, we simulated the shape memory game + standard condition. Here, we once again used inputs compressed along the shape dimension. The strength of the initial Hebbian memories for the shapes used in the shape memory game were reduced relative to the colors used in the color memory game to reflect the weaker learning revealed in our previous simulations (see Figure 5). The strength of the memories for the five shapes was set to .025 (the strength of the memory for the single color shared by all shapes was set to .3). All simulation sets consisted of 100 simulations of the 3-year-old model from Buss and Spencer (2014).

Simulation results are shown in Figure 4 along with children’s performance from Experiments 1A and 1B. The DNF model performed similarly to children across all conditions. Specifically, the model with compressed inputs along the shape dimension showed low rates of passing under the standard conditions regardless of whether color or shape was the post-switch dimension. For the color memory game + standard, the DNF model correctly switched and sorted by color in the post-switch phase as before, replicating the novel prediction from Experiment 1A. By contrast, for the shape memory game + standard, the DNF model failed to switch to shape in the post-switch phase. Thus, the close metric separation for shapes did not influence the model’s performance under the standard conditions or the color memory + standard condition. For the shape memory game + standard condition, by contrast, the model, like children, failed to switch attention to shape. These simulations provide support for the hypothesis that the asymmetry in our empirical results might arise from a shape dimension that is less distinctive.

General Discussion

The present study showed that experience with a metrically organized feature dimension in a memory-matching game can enhance attention switching in the DCCS task. This is the first demonstration that young children can pass the DCCS task under the standard conditions without simplification (Brace et al., 2006; Brooks et al., 2003) or explicit pre-training to attend to the bi-dimensionality of the cards (Mack, 2007; Ramscar et al., 2013). In Experiment 1A, children played a game prior to the DCCS task that involved matching colors sampled from a wide range of the color dimension used here but that were not the colors used in the DCCS task itself. This experience over the color dimension induced flexible attention switching from shape to color in the DCCS task. A different pattern of results emerged in Experiment 1B. Children did not flexibly switch attention from color to shape in the DCCS task after experience with shapes sampled from the shape dimension. These results mark an important step toward understanding how attention switching can be facilitated across contexts, highlighting the role of stimulus features and how learning carries forward across situations. We discuss these contributions below.

What are the mechanisms by which experience over a dimension might influence attention switching across contexts? It has long been known that memories for auditory and visual features generalize over continuous dimensions based on a similarity gradient (Pavlov, 1937; Spence, 1937; for a discussion, see McLaren & Mackintosh, 2002). An old literature exploring developmental change in children’s dimensional attention abilities showed that children’s attention could be shifted from the featural to dimensional level by exposing them to multiple values distributed over a dimension, much like we did here. For example, Tighe and Tighe (1969) gave children who were in their first grade of elementary school a cylinder, showed them a series of different sized cylinders, and asked them to judge whether their cylinder matched the one shown to them. This enabled the children to represent relations between previously unseen values along that same size dimension in a transposition task (see also, Tighe & Tighe, 1968).

More recently, Perry and Samuelson (2013) induced attention to dimensions in children who were holistic attenders via a categorization task that required attention to a single dimension. In a pre-test, children were classified as dimensional or holistic attenders based on performance in a standard triad classification task with stimuli that varied on size and brightness. Children then did a categorization task during which they learned to sort stimuli into two categories based on attention to one dimension, either size or brightness. Children received feedback about their responses and were required to reach a performance criterion of 100% across multiple trials. Perry and Samuelson found that some of the children who had initially been classified as holistic attenders were able to attend dimensionally in a triad classification post-test that followed category learning.

The DNF model provides an account of how experience over a dimension can generate attention at the dimensional level across contexts. The model connects neural populations involved in processing dimensional labels such as ‘color’ and ‘shape’ in the AS to neural populations involved in remembering feature values distributed over those same dimensions in the visual-cognitive system. Experience provided with the label ‘color’ and values distributed over the color dimension during the memory game primed these systems to respond more robustly when exposed to those labels and similar features at a future point in time, as in the DCCS task. Importantly, the experience provided during the memory game led to changes in the activation passed back and forth between the AS and visual-cognitive systems—the same systems responsible for developmental change in dimensional attention in simulations reported by Buss and Spencer (2014). These simulation results raise the possibility that experience with labels and distributed features may be central to developmental changes in dimensional attention.

One alternative explanation of children’s enhanced performance in the DCCS task is that the act of matching in the memory game, rather than exposure to the colors, improved children’s ability to sort correctly during the DCCS task. Interestingly, the asymmetry in results across Experiments 1A and 1B suggests this alternative is unlikely. In particular, children’s performance in the DCCS task when switching from color to shape was not enhanced by the memory-matching game in Experiment 1B, even though children still identified matches.

Critically, results from Experiment 1B also suggest that the metric organization of a dimension influences children’s ability to carry forward experiences across contexts and, ultimately, whether or not flexible attention switching can be induced across contexts. Similar asymmetries in children’s DCCS performance have been observed in previous studies (e.g., Fisher, 2011). Inspired by simulations of such asymmetries (see Buss & Spencer, 2014), we hypothesized that the shape stimuli used here were metrically compressed—less distinctive—relative to the color stimuli. Simulations of the DNF model demonstrated the viability of this hypothesis—the model effectively captured the full range of children’s performance across conditions.

One intriguing possibility raised by these simulations is that the influence of the shape memory game on children’s DCCS performance might be enhanced via more intensive experience with the shape dimension. It is well known that the neuronal resources dedicated to stimulus representation can be increased via experience. For example, Recanzone, Merzenich, Jenkins, Grajski, and Dinse (1992) found that the neural territory devoted to the representation of one finger in somatosensory cortex increases in an experience dependent fashion in monkeys. Similarly, Ditye et al. (2013) found that improvements in adults’ ability to make subtle perceptual discriminations of color-motion conjunctions is associated with increased cortical matter as a result of intensive practice performing discriminations. It is possible that the similarities in the shapes used here, variations in ovals, were compressed relative to the entire shape dimension. The entire shape dimension might reflect children’s experience with canonical shapes such as star, triangle, and circle. Giving children extended experience discriminating the shape variations in our stimuli might expand the representational space devoted to variations in oval. This might, in turn, enable experience with shape to induce flexible attention switching from color to shape in the DCCS task. Alternatively, it might be possible to make the shape changes across the dimension more dramatic. While this is conceptually possible, in our stimulus set shapes 1 and 18 are already quite stretched (see Figure 2).

The DNF model provides novel insights into the influence of dimensional experience across contexts. The model has several distinct advantages relative to other neural network models that have been used to capture developmental change in children’s performance in the DCCS task (for an extensive comparison of theories, see Buss & Spencer, 2014). For instance, Morton and Munakata (2002) proposed a connectionist model consisting of a bank of nodes for each feature value (e.g., red, blue, circle, star) and a bank of nodes for each label. These input units feed into a hidden layer, which, in turn, feeds into an output layer that generates a sorting response (left or right). Across a series of trials, a robust latent (long-term) memory develops and competes with an active (working) memory generated by the post-switch sorting cards and labels. Developmental differences in DCCS performance arise when ‘older’ models generate a sufficiently robust active memory for the post-switch rule that can overcome the strength of the latent memory accumulated during the pre-switch phase.

The processes in the DNF model involved in children’s DCCS performance bear some resemblance to those proposed by Morton and Munakata (2002). For example, competition between memories generated from sorting during the pre-switch phase and what the child is asked to sort by in the post-switch phase play an important role in both models’ account of young children’s performance. But there are also important differences between models that are relevant to the current results (for additional contrasts, see Buss & Spencer, 2014). In particular, the connectionist model represents feature values independent of the dimensions along which they are distributed. Thus, it is unclear how experience with features not present in the DCCS task could influence later sorting as was evident here. The DNF model, by contrast, represents features in neural populations tuned to continuous metric dimensions. This unique feature led to the novel prediction tested in the present study. Further, this aspect of the model was central to our account of why children showed an asymmetry in responding across experiments.

In conclusion, our work highlights the utility of theoretically guided efforts to enhance children’s EF abilities. The DNF model led to a key insight about the nature of generalization across contexts, which led to the first empirical demonstration of successful switching by 3-year-old children in the standard DCCS task without simplification or task-specific training. The model provided a mechanistic account of asymmetries in the influence of dimensional experience across contexts as well, highlighting the importance of understanding how the details of the stimulus and task come together to influence children’s behavior. The DNF model also inspired a new paradigm for future investigations of how specific types of dimensional experience with features and labels influence young children’s cognitive flexibility in the DCCS task. One exciting possibility is that the experience acquired in the memory game might generalize to contexts beyond the DCCS. For example, might experience acquired in the memory game enhance children’s working memory for colors?

Perhaps most importantly, our work may shed new light on efforts to train flexible dimensional attention in children. Effective attention switching abilities are necessary for children to meet the challenges they face each day. In the classroom, children are constantly asked to switch attention across dimensions as they shift from one learning context to another. For instance, children must switch from attending to the size dimension while learning mathematics to the color dimension while painting during art. We gave children experience with a dimensional label and stimuli that spanned one metric dimension. The intriguing possibility is that this might be an effective way to help children learn dimensional attention skills as they extract the pattern of associations that maps a dimensional label like ‘color’ to a distributed set of features. Such training might be an important advance in efforts to foster EFs across a range of contexts, including the out-of-lab contexts so critical to positive developmental outcomes.

Appendix

The simulations in the main text used the equations, parameters, and simulation method from Buss and Spencer (2014) with the following exception: to generate the novel prediction described in Figure 1, we made three changes relative to the original report. The first change was the addition of memory (m) nodes that were coupled to the color node, i_color, and to the shape node, i_shape. The addition of the m nodes were required to implement experience with the label ‘color’ or ‘shape’ acquired during the memory game prior to the Dimensional Change Card Sort (DCCS) task. The equations for the m nodes associated with the color and shape nodes are identical. For simplicity, we only describe the equation for the m node associated with i_color. The equation is:

$${\stackrel{.}{m}}_{i_{\mathit{color}}}\left(t\right)=\begin{array}{ccc}\hfill \{\begin{array}{c}(-m_{i_{\mathit{color}}}(t)+g(i_{\mathit{color}},t\left)\right)∕{\tau }_{m\_\mathit{build}}\hfill \\ (-m_{i_{\mathit{color}}}(t\left)\right)∕{\tau }_{m\_\mathit{decay}}\hfill \end{array}\phantom{\}}\hfill & \hfill \hfill & \hfill \text{if}{\mathrm{i}}_{\text{color}}\left(t\right)>0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \text{otherwise}\hfill \end{array}$$

where ${\stackrel{.}{m}}_{i_{\mathit{color}}}\left(t\right)$ (t) is the rate of change of activation of m as a function of time, t. The constants τ_{m_build} and τ_{m_decay} set the time scale along which the memory trace accrues and decays, respectively. τ_{m_build} was set to 5,000 and τ_{m_decay} was set to 200,000. Activation of the m node accrues only when i_color is suprathreshold. Otherwise, activation of the m node decays. This thresholding is dictated by the gating function, g, which takes on a sigmoidal shape over the activation variable i_color. The gating function is:

$$g(i_{\mathit{color}},t)=\left[\frac{1}{1+\exp \left[-\beta \left(i_{\mathit{color}}\right(t)-i_{\mathit{color}0})\right]}\right]$$

where β (set to .1) is the slope of the sigmoid function and i_color0 is the threshold (zero). Experience with the label ‘color’ was implemented by initializing the m node associated with i_color to .05. The m node evolves from this initial condition. Note that input from the m node to i_color was scaled by a strength parameter, c_icolorm, set to .75.

The second change relative to the Buss and Spencer (2014) simulations was the initializations of the Hebbian layers associated with WM_C and WM_S. This initialization was required to implement prior experience with the post-switch dimension acquired in the memory game prior to the DCCS task. The Hebbian layers were initialized with Gaussian pattern inputs distributed over the feature dimension, y, and distributed homogeneously across the spatial dimension, x. The strength of the five color inputs to the Hebbian layer associated with WM_C was set to .1 with width 2, and the strength of the memory for the single shape shared by all colors to the Hebbian layer associated with WM_S was set to .3 with width 2. The slightly stronger input for the single shape was set to reflect the more intensive exposure to the single shape relative to the five colors. All strengths of the Hebbian inputs for the quantitative simulations are described in the text.

The third change relative to the Buss and Spencer (2014) simulations was the parameters of the AS. Preliminary simulations of the model revealed that the original Buss and Spencer parameters for the AS were not sensitive to changes in how the Hebbian layers were initialized. This was not surprising given that Buss and Spencer never explored this aspect of the model. One reason why the model was not influenced by these initial conditions was that the AS tended to show ‘all-or-none’ behavior. Thus, we examined whether we could make the parameters for the 3-year-old AS and the 4-year-old AS show less all-or-none activation dynamics, while still simulating the standard DCCS task. To do this, we increased excitation and decreased inhibition. This can be seen in Table A1, where the parameters of the AS we manipulated are shown next to the same parameters from Buss & Spencer in parentheses. As can be seen in the table, the 4-year-old model still had stronger excitation and inhibition overall, but the resultant values for these two models were much closer together than in Buss and Spencer.

The change in activation dynamics for the attentional nodes, of course, also changed the activation passed back-and-forth between the AS and the WM fields. Thus, we had to modify the strength of these projections to compensate (see Table A1). For the 3-year-old model, we had to increase the strength of the projection to and from the nodes to the ‘relevant’ dimension (e.g., ‘color’ node to color dimension). The projection for the ‘mismatched’ dimension (e.g., ‘color’ node to shape dimension) were set to .01. For the 4-year-old model, by contrast, we had to decrease the strength of the projection to and from the nodes to the ‘relevant’ dimension. The ‘mismatched’ projections were all set to a value of .001. Finally, now that the AS dynamics were more excitable overall, we reduced the strength of the direct input to the nodes that specified which game was being played (e.g., input to the ‘color’ node during the color game).

Once we had verified that the new parameters effectively simulated performance in the standard task for both ages, we then explored the influence of prior experience (i.e., initializing the Hebbian layers). These simulations are shown in Figure 1 in the main text.

Table A1.

Attentional System Parameters (Buss & Spencer parameters)

	3-year-old	4-year-old
cii_excite	3 (1)	3.2 (5)
cii_inhib	2 (5)	3 (20)
ciw_colorcolor	0.05 (.005)	.057 (.3)
ciw_colorshape	0.01 (.0025)	0.001 (.001)
ciw_shapeshape	0.05 (.005)	0.057 (.3)
ciw_shapecolor	0.01 (.0025)	0.001 (.001)
cwi_colorcolor	2 (1)	2.8 (3)
cwi_colorshape	0.01 (.5)	0.001 (.1)
cwi_shapeshape	2 (1)	2.8 (3)
cwi_shapecolor	0.01 (.5)	0.001 (.1)
Si_color	0.2 (1)	0.2 (1)
Si_shape	0.2 (1)	0.2 (1)

Simulations of Dimensional Asymmetry

The asymmetry in the strength and metric separation of the inputs across the shape and color dimensions for the simulations in Experiment 1B was motivated by the simulations of the one-dimensional DNF model of working memory described in the text and shown in Figure 5. The equations and parameters for this model are described below.

Working Memory (WM)

The simulations in the manuscript in Figure 5 showed a one-dimensional working memory field for color (WM_{C_1D}) and the same for shape (WM_{S_1D}). The equations (and parameters) governing these fields are identical. For simplicity, only the equations for WM_{C_1D} are shown. WM_{C_1D} consists of an excitatory layer (w) and an inhibitory layer (v). The excitatory layer is also coupled to a Hebbian layer (HL). Each layer is described below. The excitatory layer of WM_{C_1D} is given by the following equation:

$${\tau }_e\stackrel{.}{w}(y,t)=-w(y,t)+h_w+s(y,t)+\int c_{\mathit{ww}}(y-y^{\prime })g\left(w\right(y^{\prime }),t){\mathit{dy}}^{\prime }-\int c_{\mathit{wv}}(y-y^{\prime })g\left(v\right(y^{\prime }),t){\mathit{dy}}^{\prime }-a_{\mathit{wv}\_\mathit{global}}\int g\left(v\right(y^{\prime }),t){\mathit{dy}}^{\prime }+\int c_{\mathit{wm}}(y-y^{\prime })m(y^{\prime },t){\mathit{dy}}^{\prime }+\int c_r(y-y^{\prime })\xi (y^{\prime },t){\mathit{dy}}^{\prime }$$

where $\stackrel{.}{w}(y,t)$ is the rate of change of activation in the excitatory layer of WM_{C_1D} across the continuous behavioral dimension, y, as a function of time, t. τ_e is the time constant along which excitatory activation evolves. Activation within WM_{C_1D} is influenced by its current state, w(y,t), and its negative neuronal resting level, h_w. The stimulus input takes the form of a Gaussian distributed over the behavioral dimension, y:

$$s(y,t)=a\exp \left[-\frac{{(y-\mu )}^2}{2{\sigma }^2}\right]\chi \left(t\right)$$

with stimulus position centered at μ, strength α (set to 10), and width σ (set to 1). The gating function, χ(t), is set to 1 when the stimulus is present. For simulations of the shape memory game and color memory game, an input was randomly selected from a set of 5 every 2000 time steps for 60,000 time steps. For the shape memory game, the metric distance between each step was 1.5. For the color memory game, the metric distance between each step was 4. See text for additional details.

WM_{C_1D} dynamics are influenced by local excitatory within-layer interactions, +∫c_ww(y–y′)g(w(y′),t)dy′. These interactions are specified by the convolution of a Gaussian profile, c_ww(y–y′), which determines the neighborhood across which excitatory interactions propagate and a nonlinear gating function, g(w(y′),t)dy′, dictating that only neurons with above threshold activation (>0) participate in the interactions.

The Gaussian convolution was defined by:

$$c(y-y^{\prime })=a\exp \left[-\frac{{(y-y^{\prime })}^2}{2{\sigma }^2}\right]$$

where a sets the amplitude and σ sets the width (i.e., standard deviation) of the connection matrix function.

The gating function is given by the following equation which takes a sigmoidal shape over the activation variable, w:

$$g(w,t)=\left[\frac{1}{1+\exp \left[-\beta \left(w\right(t)-w_0)\right]}\right],$$

where β (set to .5) is the slope of the sigmoid function and u₀ is the threshold (zero).

WM_{C_1D} dynamics are also influenced by two inhibitory components. The first is a local inhibitory component, −∫ c_wv(y–y′)g(v(y′),tdy′. Inhibitory interactions are projected across a neural neighborhood specified by a Gaussian, c_wv(x–x′), and only above-threshold activity in the inhibitory layer contribute to interactions. The second is a global inhibitory component, _a_{wv_global} ∫g(v(y′),t)dy′, where the sum of suprathreshold activity within the inhibitory layer across the behavioral dimension, x, at time, t, is weighted by a_{wv_global}.

The last contribution to WM_{C_1D} dynamics is spatially correlated noise, which is presented by convolving a field of white noise with a Gaussian kernel, ∫c_r(y–y′)ξ(y′,t)dy′, with strength, a_r, set to .1 and width, σ_r, set to 2.

Inhibitory Layer

The excitatory layer is reciprocally coupled to an inhibitory layer, v. The equation for the inhibitory layer is:

$${\tau }_i\stackrel{.}{v}(y,t)=-v(y,t)+h_v+\int c_{\mathit{vw}}(y-y^{\prime })g\left(w\right(y^{\prime }),t){\mathit{dy}}^{\prime }+\int c_r(y-y^{\prime })\xi (y^{\prime },t){\mathit{dy}}^{\prime }$$

where $\stackrel{.}{v}(y,t)$ specifies the rate of change of activation for each neuron along the behavioral dimension, y, as a function of time, t. τ_i is the time constant along which inhibitory activation evolves. Activation in the inhibitory layer is influenced by its current state, v(y,t), and its negative neuronal resting level, h_v. The inhibitory layer receives excitatory inputs from WM_{C_1D}, +∫c_vw(y–y′)g(w(y′),t)dy′. These inputs are projected across a neural neighborhood specified by a Gaussian projection, c(y–y′), to which only suprathreshold neurons in WM_{C_1D} contribute as dictated by the gating function, g. An independent source of spatially correlated noise is also added to the inhibitory layer, +∫c_r(y–y′)ξ(y′,t)dy′.

Hebbian Layer (HL)

Activation in WM_{C_1D} is influenced by traces in a Hebbian layer (HL), which implement a form of Hebbian learning. The equation for the HL is:

$${\stackrel{.}{m}}_w(y,t)=\{\begin{array}{cc}(-m_w(y,t)+g(w(y,t))∕{\tau }_{m\_\mathit{build}}\hfill & \text{if}w(x,t)>0\hfill \\ (-m_w(y,t\left)\right)∕{\tau }_{m\_\mathit{decay}}\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

where ${\stackrel{.}{m}}_w(y,t)$ is the rate of change of activation for each site, y, in HL as a function of time, t. The constants τ_{m_build} and τ_{m_decay} set the time scale along which activation traces accrue and decay, respectively. τ_{m_build} was set to 10,000 and τ_{m_decay} was set to 40,000. Activation in HL only accrues when there is suprathreshold activation in WM_C. Otherwise, activation in HL decays. Model parameters for WM_{C_1D} are shown in Table A2.

Table A2.

One-dimensional Model Parameters

w		v		m
τe	40	τi	5	cwm	3.5
hw	−4	hv	−4	σwm	1
cww	1.4	cwv	1
σww	1	σwv	10
cvw	2	awv_global	0.01