High geothermal heat flux measured below the West Antarctic Ice Sheet

First direct measurements of heat flux from Lake Whillans may explain abundance of subglacial lakes and ice streams in region.

Abstract

The geothermal heat flux is a critical thermal boundary condition that influences the melting, flow, and mass balance of ice sheets, but measurements of this parameter are difficult to make in ice-covered regions. We report the first direct measurement of geothermal heat flux into the base of the West Antarctic Ice Sheet (WAIS), below Subglacial Lake Whillans, determined from the thermal gradient and the thermal conductivity of sediment under the lake. The heat flux at this site is 285 ± 80 mW/m², significantly higher than the continental and regional averages estimated for this site using regional geophysical and glaciological models. Independent temperature measurements in the ice indicate an upward heat flux through the WAIS of 105 ± 13 mW/m². The difference between these heat flux values could contribute to basal melting and/or be advected from Subglacial Lake Whillans by flowing water. The high geothermal heat flux may help to explain why ice streams and subglacial lakes are so abundant and dynamic in this region.

INTRODUCTION

Mass loss from the West Antarctic Ice Sheet (WAIS) is projected to have a significant impact on eustatic sea level rise (1, 2), and its basal melting component drives a continental-scale, hydrologic system, including subglacial lakes and wetlands that comprise largely unexplored aquatic habitats (3–6). Basal melting of the WAIS is influenced by thermal conditions near the base of the ice, including the geothermal heat flux rising from underlying crustal rocks (7, 8). Despite its importance, the geothermal heat flux below the WAIS has not previously been measured directly. Instead, measurements have been completed adjacent to the ice sheet margins (9, 10) and the heat flux below the WAIS has been estimated from global seismic data (11), space-borne geomagnetic measurements (12), inferred crustal age and composition (13), temperature measurements made within the ice itself (14), and models of ice dynamics (15).

RESULTS

Geothermal heat flux measurements

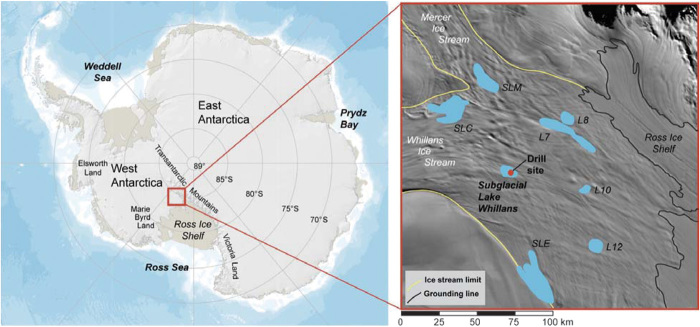
We present the first direct measurement of the heat flux (q) into the base of the WAIS, derived as the product of the thermal gradient (dT/dz) and thermal conductivity (λ) within sediments located under the ice (q = −λ dT/dz, where the negative sign results in a positive heat flux when elevation is positive-up). These data were collected as part of the Whillans Ice Stream Subglacial Access Research Drilling (WISSARD) project, which was developed to explore the hydrology, biogeochemistry, microbiology, and geology of a large West Antarctic ice stream (Fig. 1). A custom hot water drill was developed to penetrate >800 m through the ice above Subglacial Lake Whillans (SLW), followed by sediment coring, fluid and microbial sampling, and subsequent instrumentation of the borehole (5, 16). SLW is located near the confluence of the Mercer and Whillans Ice Streams (Fig. 1B) and was selected among dozens of nearby lakes [identified from seismic, ground-penetrating radar, and Global Positioning System (GPS) surveys (3, 4)] based on evidence of recent hydrologic activity, accessibility with the hot water drilling system, and inferred subglacial connection to the grounding line at the edge of the nearby Ross Ice Shelf (Fig. 1).

Fig. 1. Site maps.

Maps showing the location of West Antarctica and SLW, where the data and samples described in this study were collected. (A) Antarctic map showing geographic regions and location of field area below the confluence of the Whillans and Mercer Ice Streams. Grounded ice is shown in gray, and ice shelves are shown in tan. (B) Overview of the Whillans Ice Plain showing the surface morphology and position of the WAIS grounding line (39), the lateral limits of ice streams (yellow lines) (30), and the outlines of subglacial lakes (16, 40), identified as follows: SLC, Subglacial Lake Conway; SLM, Subglacial Lake Mercer; SLW, Subglacial Lake Whillans; SLE, Subglacial Lake Engelhardt; L7, Lake 7; L8, Lake 8; L10, Lake 10; and L12, Lake 12.

The WISSARD geothermal tool (GT) was developed for this project to measure the thermal gradient in the sediment below the SLW borehole (fig. S1). The tool is composed of a 2-m-long lance topped with a weight stand, three autonomous temperature sensor/logger probes attached to the outside of the lance, and bottom water and tilt sensors attached at the top of the weight stand. The tool was field tested on the McMurdo Ice Shelf and then transported to SLW for deployment. Sediment thermal conductivity was determined with the transient needle probe method (17), using core recovered from below SLW with a multicorer (16). Details concerning GT design and operation, probe calibration, acquisition of thermal conductivity data, processing of both data types, and resolution and assessment of uncertainties are included in Materials and Methods.

The WISSARD hot water drill penetrated the WAIS on 27 January 2013, and the GT was run twice 3.6 to 3.8 days later, after deployment of a camera, a conductivity-temperature-depth (CTD) profiler, a water sampler/filtering system, and a coring system and reaming of the borehole to maintain an adequate diameter for experimental systems (16). The Whillans Ice Stream was flowing laterally at ~1 m/day during WISSARD operations; thus, although numerous instruments were deployed through the same ice hole, tools that penetrated into the sediment below the hole over a period of days encountered relatively undisturbed material. During both GT deployments, the lance penetrated 1.10 to 1.13 m below ground surface (bgs), placing the deepest sediment sensor (T_S1) at 0.78 to 0.81 m bgs. Shallower sensors did not provide useful sediment data, mainly because they did not penetrate deeply enough and achieve stability below mudline. The tool was left in the sediment long enough to achieve partial equilibration, and in situ (equilibrium) temperatures were determined by fitting observational data to a radial equilibration model (Fig. 2; Materials and Methods). Equilibrium temperatures at a depth in the sediment below SLW from the two GT deployments are identical within measurement uncertainties, −0.39 ± 0.01°C at ~0.80 m bgs. The bottom water temperature was determined independently with a dedicated sensor and the upper sediment sensor (which did not penetrate the lake bottom) during the second deployment, while the GT was stationary in the sediment, yielding −0.56 ± 0.01°C during both tool deployments. Fifteen measurements of thermal conductivity were made on sediments recovered with the gravity multicorer, collected 0.2 to 0.4 m bgs, yielding values of 1.16 to 1.58 W/m K (mean λ = 1.36 ± 0.12 W/m K, corrected to in situ conditions), consistent with regional samples and measurements (9, 10). Examples of complete thermal conductivity measurement records are presented in Materials and Methods. The product of the thermal gradient and thermal conductivity indicates an upward heat flux below the WAIS at SLW of 285 ± 80 mW/m² (Table 1; uncertainties explained in Materials and Methods).

Fig. 2. Thermal data and interpreted values.

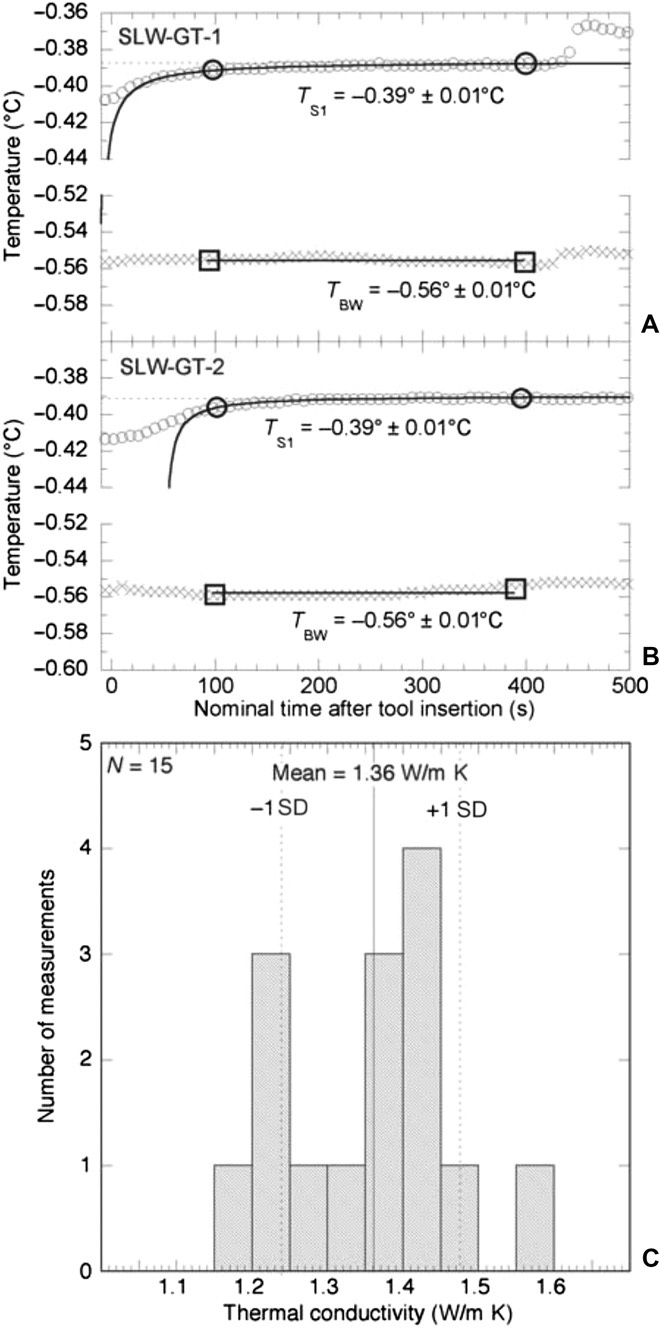
Processing details and complete field records are included in Materials and Methods and the Supplementary Materials, respectively. (A) Temperature-time record after probe penetration during the first tool deployment below SLW, as modeled to derive equilibrium temperature. Every fourth data point is shown for clarity. The solid curve shows the fit of data from sensor T_S1 (open circles) to an analytical model for tool equilibration in sediments after penetration. The large circles show the range of T_S1 data fit with the model. The horizontal dotted line shows the equilibrium temperature for T_S1. Record from the bottom water probe, T_BW (x symbols), was averaged over the interval shown (between large squares) to calculate bottom water temperature. (B) Temperature-time record after probe penetration during the second tool deployment below SLW, as modeled to derive equilibrium temperature. Symbols are the same as in (A). (C) Compilation of thermal conductivity values determined on sediment core recovered using the gravity multicorer.

Table 1. Summary of results from two deployments of the WISSARD GT at SLW.

Values reported in this table are discussed in Materials and Methods. T_BW, temperature of bottom water in SLW; T_S1, equilibrium temperature of the deepest sensor on the lance of the GT; z_S1, depth below the bottom of SLW.

	GT-1	GT-2	Uncertainty
Date, time (local)	31 Jan 2013, 1035	31 Jan 2013, 1600	—
TBW (°C)	−0.555	−0.556	±0.01
TS1 (°C)	0.387	−0.390	±0.01
zS1 (m)	0.81	0.78	±0.08
ΔT/Δz (°C/m)	0.207	0.213	+0.04, −0.07
λ (W/m K)	1.36	1.36	±0.12
q (mW/m2)	280	290	80

Glacial heat flux measurements

To complement geothermal heat flux measurements and constrain the basal heat budget for SLW, we deployed a distributed temperature sensing (DTS) system in the WISSARD drill hole within the ice at the end of 2013 field operations (Fig. 3). The DTS uses Raman backscatter and time of travel of a laser beam to determine temperature along an optical fiber (18). Information about DTS system configuration, deployment, calibration, processing, and resolution is provided in Materials and Methods. The DTS system yielded initial temperature data indicative of the thermal disturbance associated with drilling and refreezing throughout the borehole (2013 data, Fig. 3A). The system was reactivated and sampled 1 year later, after much of the frozen-in borehole had recovered to a temperature profile consistent with steady-state conditions (2014 data). There remained two small thermal anomalies in the 2014 borehole data, at 100 to 130 m below ice surface (bis), and 730 to 760 m bis, depth intervals at which there was extensive ice melting during hot water drilling and reaming operations. The rest of the profile is consistent with a simple one-dimensional advection-conduction model having an ice accumulation rate of ~0.19 m/year, Peclet number of ~4.6 (Materials and Methods). The thermal gradient at the base of the ice, as determined both with this model and from a linear fit of DTS data from the depth interval of 600 to 730 m bis (above the depth of the deepest thermal anomaly), is 0.050 ± 0.005°C/m (Fig. 3B). When combined with an ice thermal conductivity of 2.10 ± 0.050 W/m °C, this gradient suggests a conductive heat flux upward through the basal ice of 105 ± 13 mW/m².

Fig. 3. DTS data.

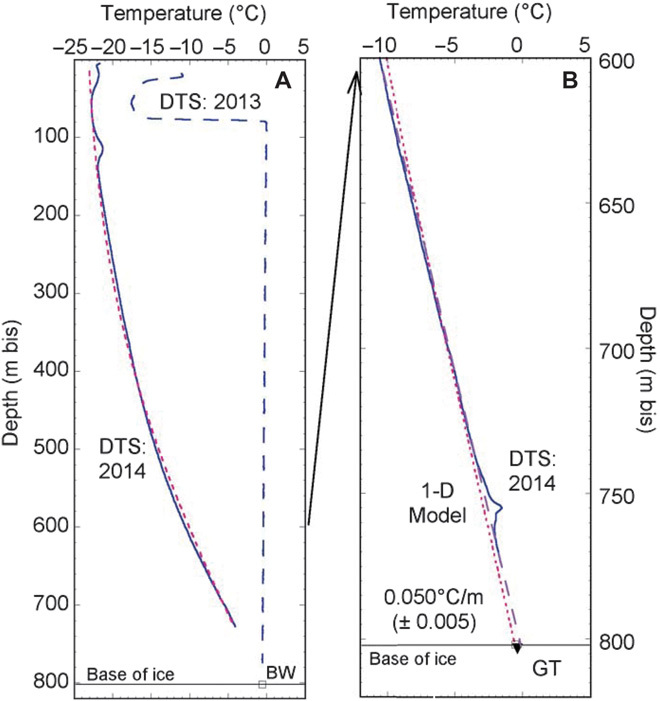
SLW and geothermal temperature data and interpretations are also shown, with temperature values plotted relative to top of ice. (A) DTS records from 2013 [immediately after deployment, conditions strongly perturbed by drilling (dashed blue line)] and 2014 [after a year of freezing and conductive equilibration (solid blue line)]. Base of ice is at 802 m bis, as is the temperature measured in SLW with the bottom water sensor in the GT (BW, open square). Result shown for a one-dimensional advection-conduction model (Pe ~ 4.6, ice accumulation rate of ~0.19 m/year), fitted to DTS data from 200 to 700 m bis (dotted pink line). (B) Detail of the deepest 200 m of 2014 DTS record (solid blue), with extrapolation of fit from one-dimensional advection-conduction model (pink dotted line) and linear fit of depth interval from 600 to 730 m bis (dashed purple line). The thermal gradient range shown for the base of the ice incorporates the values determined from the advection-conduction model (0.049°C/m) and the linear fit (0.052°C/m). The positive thermal anomaly at ~760 m bis is coincident with a zone of excessive melting during borehole operations, which had not reached thermal equilibrium when data were collected in 2014. The inverted triangle indicates the in situ sediment temperature determined with the GT.

Implications of high heat flux below SLW

The difference between the geothermal heat flux below SLW and the basal ice heat flux above the lake is ~180 mW/m², equivalent to a melt rate of ~1.8 cm/year, which is ~10% of the apparent ice accumulation rate. Alternatively, some of this excess geothermal heat could increase the temperature of water within SLW and/or warm fluids that flow toward the Ross Ice Shelf through the subglacial hydrologic system. Previous considerations of the basal heat budget in the SLW area included basal freezing at a rate of several millimeters per year, using 70 mW/m² for the geothermal heat flux (19), and basal freezing was invoked to explain the stoppage and slowdown of ice streams in the region (20). Our observation of high geothermal heat flux suggests that other mechanisms, such as long-term evolution of subglacial water drainage, may play a predominant role in slowing down and stopping ice streams in this area.

A heat flux of 285 ± 80 mW/m² is considerably greater than inferred for this area from geophysical studies or calculated at other sites in this part of the WAIS (Fig. 4). The most reliable regional borehole geothermal and marine heat flux measurements made in the Victoria Land Basin and nearby Transantarctic Mountains give values of 60 to 115 mW/m² (10). The heat flux estimated for West Antarctica using a global seismic model is ~80 to 125 mW/m², with values at the highest end of this range located hundreds of kilometers northeast of SLW (between Ellsworth Land and Marine Byrd Land), and lower values calculated around SLW (11) (Fig. 4A). A later analysis using satellite magnetic data suggests heat flux up to 150 mW/m² for parts of West Antarctica, with the highest values adjacent to the Transantarctic and Ellsworth Mountains to the east of SLW (12). A geothermal heat flux measurement from a single location cannot be used to test or calibrate large-scale models, but the models provide important context for interpreting the observation, and the data help to illustrate how regional calculations could smooth out local variations.

Fig. 4. Comparison of measured and modeled geothermal heat flux.

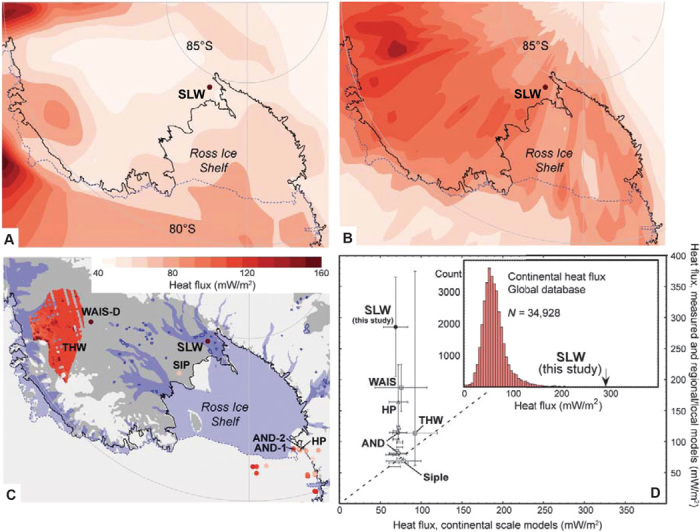
(A) Map of geothermal heat flux from a model based on space-borne geomagnetic data (12). (B) Map of geothermal heat flux from a model based on global seismic model data (11). (C) Compilation of regional geothermal heat flux values and estimates, superimposed on the map of the same area shown in (A) and (B), using the same color scale. Labeled symbols/areas are for this study (SLW), WAIS divide [WAIS-D (14)], ANDRILL sites 1 and 2 [AND-1 and AND-2 (10, 41)], Siple Dome [SIP (42)], Hut Point Peninsula [HP (43)], and Thwaites Glacier [THW (15)]. Additional values were tabulated by Morin et al. (10). Also shown are the grounding line (thick black line), areas with elevation lower than 500 m below mean sea level (gray), subglacial lakes (dark blue dots and outlines), and ice streams (surface velocity >50 m/year, pale blue areas). (D) Cross plot of observed/calculated versus modeled geothermal heat flux values, with labels corresponding to same values shown in (C). Horizontal bars show the results of geophysical calculations (11, 12) for equivalent locations (lower and higher values, respectively). Vertical bars show the uncertainties associated with each measurement or modeled estimate. Inset plot shows the global compilation of continental heat flux values (22), excluding 25 values <0 (inverted gradients) and 160 values >400 mW/m².

A global compilation and interpolation based on observations and geological correlations suggests a mean heat flux for West Antarctica of ~100 mW/m² (13), considerably lower than that measured at SLW. There is indirect evidence of elevated heat flux below the Thwaites Glacier, northeast of SLW, calculated using radar data and a hydrologic model, with regional values of 100 to 130 mW/m² and localized areas of heat flux >200 mW/m² (highest estimate of 375 mW/m²) thought to be associated with active volcanism (15) (Fig. 4C). A geothermal heat flux of 140 to 220 mW/m² was inferred at the WAIS-Divide ice core site, using thermal data from the ice sheet and a one-dimensional model of ice dynamics [(14); see Materials and Methods]. Measured and modeled heat flux values from the Prydz Bay region of East Antarctica are ~30 to 120 mW/m², up to three times greater (and more variable) than estimated on the basis of basement rock ages and inferred rates of crustal heat production (21). Looking at continental heat flux on a global basis, the value determined below SLW ranks 169th out of >35,000 reported continental values, higher than >99.5% of global measurements (Fig. 4D), with the highest values coming from areas of active hydrothermal and volcanic activity (22). West Antarctica is tectonically complex, comprising microcontinental blocks that have experienced both convergence and divergence over the last 200 million years (23, 24). The SLW drilling site is located within the West Antarctic Rift System, a region of faulted and thinned continental crust and active volcanism (25). Thermal perturbations associated with orogenesis could have accompanied crustal thinning (23, 26), interactions with a mantle plume (27), or shear heating of the mantle in response to glacio-isostatic adjustment (28). However, deep-seated heat sources should result in heat flux through the crust that is elevated at a regional scale. In contrast, available data and models suggest that heat flux below the WAIS is highly variable on a local basis (Fig. 4).

DISCUSSION

The spatial extent of elevated geothermal heat flux below the WAIS is not indicated by our data, although the alignment of areas having rapid ice movement, subglacial lakes, and/or high heat flux (Fig. 4C) may indicate a causal link [for example, (29)]. Much of the negative mass balance of continental ice sheets is driven by the rapid flow of ice streams that terminate at ice shelves and outlet glaciers [for example, (30, 31)]. Basal boundary conditions, including bed topography and interactions with warm ocean water [for example, (2, 32)], are important in controlling the rates of ice stream discharge. Geothermal heat flux remains a critical but poorly constrained variable in many models of dynamic ice sheets (33, 34), and it may help to determine ice stream locations and discharge rates (8) and the associated development of subglacial hydrologic systems (3). Meltwater production from the grounded part of the entire Antarctic Ice Sheet is thought to be ~65 giga–metric tons/year on the basis of continental-scale estimates of the geothermal heat flux (34). Every additional 100 mW/m² of excess geothermal heat applied to the base of the WAIS (about half of that inferred in this study of SLW based on the difference between geothermal and basal ice heat fluxes) would be equivalent to an increase in meltwater of ~19 giga–metric tons/year.

We do not hypothesize that elevated heat flux below the WAIS explains the instability of the ice sheet, nor that heat flux measured at SLW is regionally representative; however, locally elevated basal heat flux may help researchers to understand why parts of some ice sheets have been so sensitive to recent changes in climate and oceanic conditions [for example, (30)]. The SLW drill site was not placed at random, but it is located in a highly dynamic and hydrologically active setting; thus, the finding that heat flux is elevated in this location is perhaps not as surprising as it seems initially.

The elevated heat flux value measured below SLW also has important implications for the subglacial biosphere (5). The enhanced creation and discharge of meltwater resulting from excess subglacial heating could transport nutrients, carbon, and biomass across vast distances within the ice-covered hydrologic system. SLW and other lakes in this region drain and fill on multiannual cycles (3, 16), but some subglacial lakes that are less hydrologically dynamic could develop stable stratification and accumulate excess geothermal heat at depth, providing more variable (and potentially more habitable) conditions for the development and evolution of microbial ecosystems (5, 6).

MATERIALS AND METHODS

GT design, operation, and calibration

Tool overview and specs

The WISSARD GT uses autonomous sediment temperature probes (containing sensor, logger, and batteries) attached to a lance, with bottom water and tilt probes attached to a weight stand (fig. S1). The bottom water probe has a 2-cm-long sensor tube housing a thermistor sensor at the tip (nominally 30 kilohms at 25°C, 105 kilohms at 0°C). The probes on the lance use thermistors housed in a longer sensor tube (fig. S1B), designed to be bent and fitted to a Delrin outrigger fin that holds the sensor 10 cm from the lance. The offset from the lance minimizes the thermal disturbance to the sensor generated by the lance during the 5 to 8 min that the temperature probes are left stationary in the sediment during deployment. Adjacent outrigger fins and temperature probes are arranged on the lance with a 15° circumferential offset so that the penetration of a deeper outrigger does not disturb the sediment penetrated by a shallower outrigger. As described in the text, only data from the deepest sediment sensor and the bottom water sensor were used in this study. The probes have a nominal accuracy and precision of 0.001°C and were calibrated before and after use using a stirred fluid (water-antifreeze) bath in the laboratory (fig. S2).

The tool weighs up to 550 kg (field adjustable) and is lowered by wireline using a winch on the ice surface, so that gravity drives the lance and sensors into the sediment at the bottom of a borehole. The system was designed with a maximum diameter of 25 cm, small enough to pass down and up through a hole through an ice sheet made with a hot-water drill before the hole freezes in from the sides. Unfortunately, freezing in of the upper part of the ice borehole at the water-air interface required reducing GT diameter by removing the weight stand and attaching circular weights from the multicorer to the top of the lance (fig. S1). As a result, the tool weighed ~200 kg when deployed for this study.

Calibration of temperature probes

All GT temperature probes were calibrated in the laboratory before and after deployment below SLW using a stirred fluid bath (a 50:50 mixture of tap water and ethylene glycol) across a nominal temperature range of −3° to 30°C. At each calibration point, the fluid temperature in the bath was held steady for 20 to 40 min, as determined with a NIST (National Institute of Standards and Technology)–traceable resistance temperature device (RTD), and logged to a computer. The bath maintained a relatively steady temperature by simultaneous heating and cooling, resulting in an SD of ≤0.001°C at each stability point. Probe records were even more stable than the stirred bath, having additional thermal mass that reduced high-frequency variability. Calibration included six stability points before deployment at SLW and seven calibration points after deployment.

After each calibration session, data were downloaded from the probes, aligned in time with RTD data, and then plotted to select intervals for calibration calculations. Factory probe temperatures were calculated by the operating software on the basis of batch coefficients relating circuit resistance to sensor temperature. Apparent probe temperatures were cross-plotted against RTD temperatures and then fit with first-, second-, and third-order polynomials to reduce the residual misfit between the two. Residual errors using a third-order polynomial fit between probe and RTD temperatures, determined before and after deployment in the field, were ≤0.002°C at all calibration points (fig. S2). Data recovered after each GT deployment below SLW were processed to apply the corrections determined by calibration, generating the results reported herein.

Operation of autonomous temperature probes and GT

The temperature probes are constructed to permit serial communication through the pressure case, using the tool tip and pressure housing (separated by a ceramic disc) for serial communication. Temperature probes were programmed in the field for autonomous operation just before GT deployment. The internal clock of each probe was synchronized to the computer clock, the sampling interval was set to 2 s, and the probes were programmed to begin measurement and logging at the same time. Probes were installed on the GT after programming and then removed from the tool after deployment and recovery, and data were downloaded to the field computer.

The full record from deployments helps to illustrate the field operations (fig. S3). Once the individual probes were launched, the GT was assembled and hoisted into the air with a crane and then moved to the drilling platform (fig. S1A). The GT load was transferred to the winch cable, and the GT was lowered down the borehole through the ice. As the GT passed through the upper interval of the borehole, ambient air temperatures dropped below the logger range, but temperatures came back up into the measurable range once the tools encountered water in the borehole. (Temperatures encountered in the borehole were not apparent at the surface because the GT probes are autonomous, with no borehole to surface communication.) The GT was held ~10 m above the base of SLW, in the water-filled borehole, and then the winch was allowed to free fall until the load cell indicated that the GT had penetrated the lake bed, and a few extra meters of cable were unspooled to make sure that the GT would not be disturbed while in the sediment. After sufficient data were collected, the cable was slowly retrieved, paying careful attention to the load cell to avoid excessive cable strain.

The GT was recovered with clear indication of penetration into sediments below SLW: thick and sticky mud coating the tool up to 1.13 m from the tip (fig. S1B). This places the central sensor (T_S2) at 0.19 m bgs (not deep enough to produce useful sediment data), and the remaining sediment sensor (T_S3) 0.43 m above the bottom of the lake. Data were downloaded from the individual temperature probes and then plotted for a quick assessment of tool performance. The central sediment sensor, T_S2, was found to have suffered an electronic fault and was replaced. The GT was cleaned before it was run down the hole, removing all traces of mud from the first deployment. The second deployment was accomplished ~6 hours later following the same steps as during the first deployment, resulting in a similar record of temperature versus time (fig. S3B). During the second GT deployment, the mudline on the tool indicated penetration of 1.10 m from the tip, placing T_S1 at a depth of 0.78 m bgs and the sensor T_S2 at 0.16 m bgs. Although sensor T_S2 showed some evidence of frictional heating, it did not stabilize and did not appear to have been buried deeply enough to provide useful data. This is consistent with the inferred penetration depth during both deployments. The consistency of GT penetration depths indicated by mudline marks, along with penetration limits encountered during coring (16), suggests that there may be a significant lithologic change at ~1.1 m bgs, with an increase in sediment strength that limited tool penetration.

Processing of GT data

Processing of subglacial thermal data followed procedures developed for marine settings (35), using a graphical (interactive) program developed for tools deployed during scientific ocean drilling (36). The GT penetrates into the sediment and is left in place long enough to achieve partial equilibration, but not so long as to risk loss in sticky and reconsolidating sediments surrounding the tool. The final sediment temperature around each sensor is calculated using an analytical model that represents the equilibration of an infinitely thin cylinder (“line source”) after the frictional heating associated with insertion. Early time data after tool insertion are generally not well represented by the idealized analytical model because of the finite heat capacity of the tool and the differences in sediment properties around the sensor caused by tool insertion, and thus are not used in the fitting procedure. Remaining data are shifted in time to achieve the statistical best fit between observations and the model, and the analytical model is extrapolated to infinite time to calculate the equilibrium temperature.

Sediment temperature values were essentially stable 5 to 7 min after penetration below SLW (Fig. 2), so equilibrium temperatures extrapolated from fitting to an analytical model differ little from simple averages of measured values from the final 3 min of each deployment. In addition, changing the assumed thermal conductivity of sediment around the probes within a reasonable range (based on needle probe measurements from recovered core, described below) had little influence on inferred equilibrium temperatures because temperatures were virtually equilibrated. Bottom water temperatures were averaged from the same period that the sediment temperatures were determined. The thermal gradient values used to calculate heat flux were based on the difference between equilibrium temperatures in SLW bottom water and at ~0.80-m depth below the bottom of the lake. Uncertainties in individual temperature values and in gradient calculations are described below.

Sediment thermal conductivity data acquisition and processing

Sediment thermal conductivity was determined from a section of core by the needle probe method with constant heating (17), as summarized in this section. Sediment was recovered from below SLW with a multicorer using a 6-cm-diameter polycarbonate liner. A section of this core was analyzed in the laboratory. Measurements were made every 1 cm, beginning and ending 2 cm from the ends of the sediment core. For each measurement, a 1.6-mm-diameter hole was drilled through the core liner, with care taken to not drill into the sediment. A 5-cm-long needle probe was inserted through the hole and into the core material. The needle probe contains a loop of heater wire along its complete length and two thermistor sensors, one in the center of the needle (placed near the center of the sediment core diameter) and one near the needle base, which remains outside of the core liner during measurement.

Once the needle is pushed inside the core, the internal temperature is monitored until it is sufficiently stable to proceed with the measurement (drift ≤0.04°C/min). A thermal conductivity determination is made by recording temperature data for two periods. First, data are recorded without applying any current to the needle probe to record the rate of temperature drift so that measurements made during heating can be corrected. Next, a constant current is applied to the needle probe to generate heat at a known rate during the period of measurement. Both the drift and heating measurements lasted 200 s. The relative change in temperature during heating is used to calculate the thermal conductivity:

$$\mathrm{\Delta }\mathit{T}=\frac{\mathit{q}}{4\mathrm{\pi }\mathit{k}}\text{ln}(\mathit{t})+\mathit{C}$$

where ΔT is the relative temperature rise (recorded as the difference between internal and external temperature sensors), q is the rate of heating, k is thermal conductivity, and C is a constant representing the background drift rate of the sample. A time window of 10 to 75 s was used for calculation of the slope on a plot of ΔT versus ln(t) (fig. S4). Early data are typically neglected because the data do not follow a semi-log slope due to nonidealities in the experimental system and configuration, and later time data can be influenced by the thermal wave around the needle reaching the limit of the core liner. Thermal conductivity data were corrected for the difference between in situ and laboratory temperatures, an adjustment of −0.193%/°C.

Uncertainties in geothermal heat flux determinations

Individual temperature values

Calibrated temperature values recorded with the autonomous probes are accurate to within ±0.002°C. The extrapolation of sediment temperatures to equilibrium values results in similarly small errors because the instruments had nearly equilibrated before removal from the sediment (Fig. 2). Bottom water temperature records show modest variation during the same time as the probes were in the sediment. We assign an uncertainty in final temperature values (both sediment and bottom water) of ±0.01°C, which is consistent with the stability of observations.

Tool depth of penetration

The best indication of tool penetration depth is the limit of sticky mud observed to be coating the GT after each deployment. The outrigger mounts acted as “stand-offs” during recovery, preventing the probe lance from rubbing against the borehole wall and protecting the mud caked onto the side of the tool. Because the mudline was located between successive outrigger mounts, the marks were particularly well protected during recovery, and the mud could not have been scraped off from all around the lance and mounts, as would have been required for the mudline indicators to suggest shallower-than-actual penetration. In particular, there is a space just aft (above, when tool is hanging) of the outrigger mount fin, where there is a ~1-cm gap between the exposed sensor tube and the upper body of the mount. This area was packed in with mud above the bottom temperature sensor (T_S1) after both deployments (see fig. S1, B and C). There was no mud packed in this same location above the second sensor (T_S2) after either deployment. This suggests that the tool did not penetrate so far that the aft end of the T_S2 outrigger fin was buried in the mud.

The GT penetration depths inferred (1.13 and 1.10 m, corresponding to T_S1 depths of 0.81 and 0.78 m, respectively) are consistent with (i) the depth limit of penetration of other instruments, all of which appear to have encountered a hard layer/boundary at this depth (16), and (ii) the thermal records from outrigger probes in position T_S2 on the lance (fig. S1A). The T_S2 probes both gave evidence of sediment penetration, but to a depth that was insufficient to ensure an accurate measurement of ambient sediment conditions. The sensor tubes are ~39 cm long and should be fully buried to generate accurate readings. Heat can be conducted vertically along the sensor tube, leading to errors if the tube is not fully buried in the sediment. Even with complete burial, there can be disturbance of the shallowest sediment, such that the effective depth of individual sensors remains uncertain. For this reason, we assign a depth uncertainty of ±0.08 m, which is ~10% of the inferred depth of penetration.

Potential for changes in SLW temperature, impact from earlier deployments, or stratification

The minimum temperature determined with a CTD soon after penetration of SLW was −0.55°C, close to the freezing point of SLW fluid (16) and within 0.01°C of the −0.56°C value measured with the bottom water sensor on the GT during both deployments (T_BW), suggesting that there was little change in SLW temperature in the days before GT deployment. A T_BW perturbation associated with drilling and other operations (ΔT₀) would propagate downward into the sediment below SLW as

$$\mathrm{\Delta }\mathit{T}(\mathit{z}\mathit{t})=\mathrm{\Delta }{\mathit{T}}_0\mathit{e}\mathit{r}\mathit{f}\mathit{c}\left[\frac{\mathit{z}}{\sqrt{\mathrm{\alpha }\mathit{t}}}\right]$$

where z is depth below the lakebed, α is sediment diffusivity, and t is time since start of the perturbation. The temperature perturbation at 0.80-m depth in the sediment after 3.6 days (the time between end of initial borehole operations and the first GT deployment) would be 13% of the initial perturbation (fig. S5). This is equivalent to 0.004°C on the basis of a maximum water perturbation of 0.03°C, the difference between freezing temperature of −0.53°C and T_BW measured with the GT of −0.56°C. This potential error is within the uncertainty listed for equilibrium sediment temperatures.

The initial deployment of the GT is unlikely to have had an impact on the measurements during the second deployment, considering similar calculations. On the basis of the measured ice sliding rates during SLW operations below the ice, the two measurements were too far apart after 6 hours (~0.3 m) for there to have been significant lateral propagation of heat between measurement locations.

CTD data suggest that the densest water is found at the base of SLW, resulting mainly from elevated salinity (16). Water at the top and at the bottom of the lake is cooler than water in the middle. Temperatures measured with the bottom water sensor and the shallowest sediment probe (T_BW and T_S3, respectively) during the second deployment were identical within the stated uncertainty (±0.01°C, fig. S3B) despite these instruments being separated vertically by ~1.2 m (fig. S1), and sensor T_S3 was located ~45 cm above mudline. SLW is a highly dynamic environment, with water moving into and through the lake and with an upper lake boundary that is moving laterally. Although there is stratification of the lake based mainly on salinity (16), mixing helps to explain why water found near the base of the lake is relatively cool. For every excess geothermal heat input of 100 mW/m² into the base of SLW, there would be warming of ~0.4°C/year if the lake did not turn over, mix, and/or was not replenished by inflowing water.

Perturbations due to advection by pore fluid flow

Upward fluid advection through sediment below SLW could raise the measured thermal gradient close to the upper sediment boundary at the base of the lake if the seepage rate were sufficiently high. However, diffusion appears to be the dominant mode of solute transfer from shallow sediments to the water column in SLW (5), suggesting that thermal conditions in shallow sediments are conductive. In addition, the clay-rich matrix of the subglacial diamicton recovered on the geothermal probe and during sediment coring should prevent fluid flow at rates that would generate a significant thermal perturbation, as shown with the following analysis. The influence of upward fluid advection on a thermal profile is quantified through consideration of the Peclet number, β, the ratio of advective to conductive heat transfer: β = ρcqL/λ, where ρ is fluid density, c is heat capacity, q is specific discharge (volumetric flow rate per unit area), L is layer thickness, and λ is sediment thermal conductivity. Assuming a conductive/advective layer thickness of 5 m, the temperature at a depth below the upper boundary will vary according to the following formula:

$$\mathit{T}(\mathit{z})=\frac{{\mathit{e}}^{\mathrm{\beta }\frac{\mathit{z}}{\mathit{L}}}-1}{{\mathit{e}}^{\mathrm{\beta }}-1}({\mathit{T}}_{\mathrm{L}}-{\mathit{T}}_0)+{\mathit{T}}_0$$

where T₀ is temperature at the top of the layer, and T_L is temperature at the base of the layer (37). Increasing the temperature at 0.80-m depth such that the apparent thermal gradient is raised by 5 to 50% from the conductive (background) condition requires a flow rate of ~0.3 to ~3 m/year. Given the low shear strength of the recovered sediments (16), the excess pressure available to drive vertical fluid flow in this location can be no more than ~10 kPa, and thus, sediment permeability would have to be 6 × 10⁻¹⁵ to 6 × 10⁻¹⁴ m², values more appropriate for silty sand or fine sand.

Thermal conductivity

Thermal conductivity values measured with the needle probe method are generally considered to be accurate within ±5 to 10%. We verified the function of the experimental system through measurements of a core liner filled with unflavored gelatin, which yielded values consistent with water (±5%). We assign an uncertainty in thermal conductivity determinations of 0.12 W/m °C, relative to a mean measured value of 1.36 W/m °C (±9%), on the basis of the SD of measured values (corrected for in situ temperature).

Accumulated uncertainties

The heat flux apparent from the two separate GT deployments is 280 and 290 mW/m², respectively, with a mean of 285 mW/m². Limits on geothermal heat flux values were calculated by minimizing or maximizing individual values used to make this calculation, on the basis of the uncertainties listed above, yielding a final uncertainty for the heat flux determination of ±80 mW/m² (±28%). We consider this to be a conservative estimate because it is based on “worst case” scenarios for each component of the determination (combining all errors that make heat flux greater, and all errors that make heat flux lower). An analysis using propagation of Gaussian errors suggests a smaller uncertainty, ±16%.

DTS data acquisition, processing, and modeling

Data acquisition and processing

DTS observations were made using a fiber-optic cable (DNS-3454) consisting of two 50/125-μm multimode fibers and two 9-μm single-mode fibers (not used), inserted in a 2-mm-diameter, gel-filled stainless steel tube (for deployment under elevated pressure), wrapped in six 0.6-mm-diameter stainless steel braided cables (to provide strength under tension), and sheathed in an outer polyethylene jacket having a 4.5-mm diameter. The DTS cable was lowered to ~780 m bis (about 20 m above the base of the ice) and allowed to freeze in place, along with additional thermistor sensors, seismometers, and geophones, after completion of other operations in the SLW borehole (16). Independent calibration calculations were completed for data collected in 2013 and 2014, on the basis of the duration of measurements and the availability of independent temperature measurements and estimates.

DTS temperature measurements were made over a 10-hour period in February 2013, with 29 traces of backscatter intensity integrated over 10-min sampling windows and a spatial sampling resolution of 1.01 m. The water-filled part of the borehole was expected to be close to the pressure freezing temperature during these measurements. Measurements were calibrated using a pressure freezing point depression coefficient of 7.55 × 10⁻⁸°C/Pa, as inferred from the final CTD cast in the borehole before DTS emplacement (16), through comparison to the DTS signal from the air/water interface, 100 m below the air/water interface, and the bottom of the fiber-optic cable. The temperature resolution for this data set was calculated as the SD of the individual trace temperatures 25 m below the water/air interface (±0.0167°C) and at the bottom of the cable (±0.027°C). The calibration coefficients and calculated resolutions are consistent with the manufacturer’s specifications and with results from other DTS installations in ice shelves (38).

The DTS was used again in January 2014 for an 11-hour period, with 346 traces of backscatter intensity integrated over a 1-min sampling window. Because of relatively short DTS integration times in 2014, temperature resolution is calculated to be ±0.076°C at the air/water interface and ±0.085°C at the bottom of the cable. Independent temperature measurements within the borehole were not available in 2014, so the means of the 2013 calibration parameters were used to derive a set of preliminary 2014 temperatures. The preliminary temperature profile reached a minimum ice temperature of −22.74°C and a bottom hole temperature of −0.85°C. These preliminary data were adjusted using a slope and offset correction, assuming a minimum ice temperature of −23.10°C, consistent with previous estimates of mean annual temperature, and a freezing temperature for SLW of −0.55°C. This secondary correction had little impact on the measured thermal gradient, which is the critical value used in the present study, particularly in the region of interest near the bottom of the borehole.

Modeling of DTS data

The equation used to fit 2014 DTS data in Fig. 3 is based on this solution to a one-dimensional conduction-advection model:

$$\mathit{T}(\mathit{z})={\mathit{T}}_{\mathrm{T}}+({\mathit{T}}_{\mathrm{B}}-{\mathit{T}}_{\mathrm{T}})\times \mathit{e}\mathit{r}\mathit{f}\left[\frac{\mathit{z}}{{\mathit{z}}_{\mathrm{T}}}{\left(\frac{\mathit{P}\mathit{e}}{2}\right)}^{1/2}\right]/\mathit{e}\mathit{r}\mathit{f}\left[\frac{{\mathit{P}\mathit{e}}^{1/2}}{2}\right]$$

where T is temperature; z is elevation above the base of the ice; subscripts “T” and “B” refer to top and bottom, respectively; and Pe is Peclet number, which is the ratio of heat advection to conduction (vz_T/ κ, where v is ice accumulation rate and κ is ice thermal diffusivity). Parameters used to fit the 2014 DTS data are listed in table S1. The value of Pe was allowed to vary to minimize the misfit of the model (defined as the sum of the square residual error between measured and modeled temperature values), using data from 200 to 700 m bis (to avoid intervals having local melt/freezing anomalies associated with drilling or reaming of the hole).

Estimated geothermal heat flux from Fudge et al. (14)

The supplement to Fudge et al. (14) describes two mechanisms of heat loss, requiring input at the base of the ice to close the energy budget: conductive heat flux and basal melting. These authors do not estimate geothermal heat flux explicitly in their paper, perhaps because this was not a primary focus of their work. Instead, they were interested in estimating the basal melt rate to explain the unexpectedly young ice at depth in the WAIS Divide ice core.

The conductive heat escape from the ice base at WAIS Divide can be calculated from ice temperatures and thermal conductivity and is about 70 mW/m². Given the high vertical velocity at 3300-m depth, the estimated basal melt rate is 0.7 to 1.5 cm/year, equivalent to 70 to 150 mW/m². Together, these two heat sinks require a geothermal heat input of 140 to 220 mW/m².

Correction (20 July 2015): The list of WISSARD Science Team members has been updated in the Acknowledgments.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/6/e1500093/DC1

Fig. S1. WISSARD GT deployed below SLW.

Fig. S2. Example calibration results from two autonomous probes used with the WISSARD GT deployed below SLW.

Fig. S3. Complete records from GT deployments below SLW.

Fig. S4. Example records from needle-probe thermal conductivity determinations made on a core sample recovered from the bottom of SLW.

Fig. S5. Calculations of the thermal disturbance that could occur as a function of time owing to an abrupt change in bottom water temperature or an adjacent tool insertion.

Table S1. Physical parameters used to fit the 2014 DTS data to a one-dimensional, steady-state conduction-advection model.