The valence-fluctuating ground state of plutonium

Determination of plutonium’s fluctuating electronic and magnetic ground state resolves long-standing “missing” magnetism puzzle.

Abstract

A central issue in material science is to obtain understanding of the electronic correlations that control complex materials. Such electronic correlations frequently arise because of the competition of localized and itinerant electronic degrees of freedom. Although the respective limits of well-localized or entirely itinerant ground states are well understood, the intermediate regime that controls the functional properties of complex materials continues to challenge theoretical understanding. We have used neutron spectroscopy to investigate plutonium, which is a prototypical material at the brink between bonding and nonbonding configurations. Our study reveals that the ground state of plutonium is governed by valence fluctuations, that is, a quantum mechanical superposition of localized and itinerant electronic configurations as recently predicted by dynamical mean field theory. Our results not only resolve the long-standing controversy between experiment and theory on plutonium’s magnetism but also suggest an improved understanding of the effects of such electronic dichotomy in complex materials.

INTRODUCTION

Plutonium (Pu) is known for the instability of its nucleus, allowing it to undergo fission. The electronic cloud surrounding the Pu nucleus, however, is equally unstable because of the near degeneracy of multiple electronic configurations allowed by its special position in the periodic table. Pu belongs to the actinide series in which the 5f electron shell is progressively filled. In the early part of this series stretching from Th to Np, the 5f electrons are delocalized and thus contribute to bonding between neighboring atoms similar to the 5d series. Atomic volumes decrease with increasing atomic number Z, reflecting the increased screening of the positive nuclear charge with each additional electron. In contrast, for much larger and heavier actinides (Am and beyond), the 5f electrons are well localized and do not participate in bonding, and their atomic volumes decrease much slower with Z, as in the 4f lanthanide series. The 5f electrons of Pu—situated between Np and Am—exist in the abyss between these two opposing tendencies, making Pu the most electronically complex element in the periodic table, with intriguingly intricate properties for an allegedly simple elemental metal that have defied understanding since the 1940s (1, 2).

Because of this complexity, Pu exhibits a record-high number of six allotropic phases with large volumetric changes between these phases of up to 25%, and mechanical properties ranging from brittle α-Pu to ductile δ-Pu (3). The radius of Pu atoms in the face-centered cubic (fcc) δ phase is midway between that of Np and Am. δ-Pu exhibits a temperature-independent, Pauli-like magnetic susceptibility and a Sommerfeld coefficient of the specific heat that are an order of magnitude larger than in any other elemental metal (4) because of the strong electronic correlations that emerge from the delicate interplay of itinerant and localized electronic degrees of freedom (5). Even beyond Pu, it is recognized that the understanding of strong electronic correlations is a key issue for complex materials in general (6). However, the description of their electronic ground state continues to pose a significant challenge to theory, precisely because such materials exist in between the well-understood extremes of electron localization/delocalization (7).

The conundrum of Pu’s electronic instability becomes most clear from the drastic disagreement between conventional electronic structure theory and experiments (4). The large, temperature-independent magnetic susceptibility of Pu implies the absence of a net static magnetic moment expected if the 5f electrons were localized and is consistent with muon spin rotation experiments that set an upper limit for a static or even slowly fluctuating (on a time scale of microseconds and longer) moment of ≤10⁻³ μ_B/Pu (8). In contrast, conventional theories that succeed in correctly accounting for the structural and volumetric changes between the various phases of Pu predict static magnetic moments varying from 0.25 to 5 μ_B/Pu (4).

Resolving the ground state of the δ phase of Pu, which shows notoriously complex behavior despite its high-symmetry fcc crystal structure with only a single element, presents an excellent opportunity to isolate the effects of strong electronic correlations and make progress on their understanding. A promising solution was recently proposed by a dynamical mean field theory (DMFT) calculation of Pu’s electronic structure (9) and consists of modeling the ground state as a quantum mechanical admixture of localized and itinerant electronic configurations. The question of whether the ground state of δ-Pu is indeed a true quantum mechanical superposition may only be answered via observation of the associated virtual valence (charge) fluctuations among the distinct 5f⁴ (Pu⁴⁺), 5f⁵ (Pu³⁺), and 5f⁶ (Pu²⁺) electronic configurations. Here, we reveal these valence fluctuations via inelastic neutron scattering, thus resolving the long-standing controversy about its electronic complexity and “missing magnetism.”

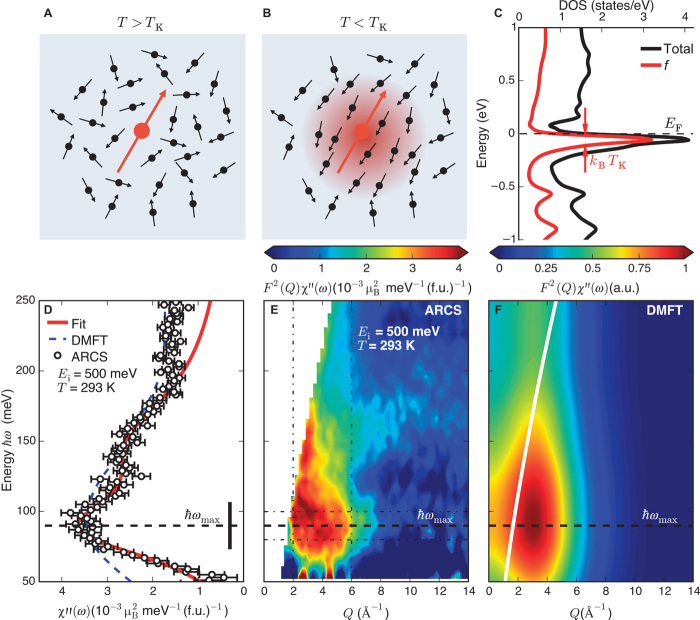
In the presence of strong electron-electron correlations, the f-electron wave function is typically well localized, giving rise to magnetic moments as shown in Fig. 1A. Because the aforementioned theories reproduce the correct experimental densities for Pu via 5f electron localization, they predict a magnetically ordered state. However, below a Kondo temperature T_K, itinerant conduction electrons tend to align their spins antiparallel with respect to the 5f magnetic moment that in turn becomes compensated (Fig. 1B) (10). Through this dynamic interaction in the spin degrees of freedom, the f electron becomes hybridized with the conduction electrons, effectively leading to its delocalization into the Fermi conduction sea where it forms a heavy quasiparticle. This results in a strongly modified electronic density of states that then includes the electronic f level as a quasiparticle resonance with a width of k_BT_K (k_B is the Boltzmann constant) at the Fermi level E_F (Fig. 1C).

Fig. 1. Visualization of the valence-fluctuating ground state of δ-Pu by means of neutron spectroscopy.

(A) Above a characteristic Kondo temperature T_K, the f-electron wave function in f-electron materials such as Pu is typically well localized, resulting in the formation of a magnetic moment (red). (B) For temperatures T < T_K, the conduction electrons (black) tend to align their spins antiparallel with respect to the magnetic moment that in turn becomes quenched, resulting in hybridization of the f electron with the conduction electrons. (C) On the basis of our DMFT calculations for δ-Pu (see the text), this leads to a strongly modified electronic density of states (DOS) that then includes the electronic f level as a “quasiparticle resonance” with a width of k_BT_K (k_B is the Boltzmann constant) at the Fermi level E_F. The DMFT calculation shows that the hybridization of 5f and conduction electrons drives a quantum mechanical superposition of different valence configurations, where the 5f electrons are continuously hopping into and out of the Fermi sea via the quasiparticle resonance, resulting in virtual valence fluctuations. Here, we use the spin fluctuations that arise from the repeated virtual ground state reconfiguration of the Pu ion from a magnetic (A) to a nonmagnetic (B) state to visualize the valence fluctuations by measuring the dynamic magnetic susceptibility χ″(ω) of δ-Pu by means of neutron spectroscopy. (D) χ″(ω) obtained from our measurements carried out at room temperature (T = 293 K) shows a maximum at the energy $\mathrm{\hslash }{\mathrm{\omega }}_{\text{max}}={({\mathit{E}}_{\mathrm{s}\mathrm{f}}^2+{\mathrm{\Gamma }}^2)}^{1/2}$ (black dashed line) that is determined by the characteristic spin fluctuation energy E_sf = k_BT_K and the lifetime τ of the fluctuations via τ = ℏ/2Γ. The red solid line is a fit χ″(ω) to Eq. 1 as described in the text. The broken blue line was calculated via DMFT. The vertical black bar represents the energy resolution of the experiment. (E and F) Full energy (hω) and momentum transfer (Q) dependence of the magnetic scattering as observed in our experiment and calculated by DMFT, respectively. The vertical and horizontal dash-dotted lines in (E) denote the integration ranges used for the energy and momentum transfer cuts shown in (D) and Fig. 2, respectively. The white solid line in (F) denotes the boundary beyond which no experimental data are available. f.u., formula units; a.u., arbitrary units.

Our DMFT calculations, which treat the effects from all important energy scales, notably the Kondo interaction, atomic multiplet effects and crystal field splitting equally, and the electronic band structure in a self-consistent way (11), demonstrate that the quantum mechanical mixing of the different valence configurations dominates the physics of Pu. Notably, the 5f electrons are continuously hopping into and out of the Fermi sea via the quasiparticle resonance, resulting in virtual valence fluctuations. We note that each of the quantum mechanically admixed 5f states hybridizes with the conduction electrons. For example, the main resonance peak at E_F (see Fig. 1C) is predominantly due to fluctuations between an f⁵ state with total spin J = 5/2 and the f⁶ state with total spin J = 0, whereas the two lower resonances at about 0.6 and 0.9 eV are due to fluctuations between higher total spin states of the f⁵/f⁶ configurations (9).

Core-hole photoemission spectroscopy (12) and resonant x-ray emission spectroscopy (RXES) measurements (13), both of which probe the valence configuration on a very short time scale (τ ≈ 1 fs), find a multivalence ground state in δ-Pu suggested by DMFT calculations (9), with reasonable agreement for the occupation of the 5f⁴, 5f⁵, and 5f⁶ states (Table 1). Because these measurements only allow an essentially instantaneous snapshot of the electronic configuration, the corresponding virtual valence fluctuations remained hidden. In contrast, neutron spectroscopy is sensitive to the expected time scale of about 0.01 ps upon which spin fluctuations develop from virtual interconfigurational excitations of the Pu ion from the magnetic f⁵ (J = 5/2) to the nonmagnetic f⁶ (J = 0) state.

Table 1. Average occupation of the 5f states in δ-Pu.

The occupation of the 5f states in δ-Pu is shown as calculated by DMFT and measured by RXES (13) and core-hole photo-emission spectroscopy (CHPES) (12), respectively. We also list the corresponding effective moment μ_eff of the three 5f states based on the intermediate coupling scheme (21).

δ-Pu 5f state	f4	f5	f6
Occupation (DMFT) (%)	12	66	21
Occupation (RXES) (%)	8(2)	46(3)	46(3)
Occupation (CHPES) (%)	6(1)	66(7)	28(3)
Effective moment μeff (μB)	2.88	1.225	0

The physics of spin fluctuations driven via valence fluctuations is captured by the Anderson impurity model (AIM) that describes the interaction of a magnetic impurity with a “bath” of conduction electrons (14), and of which the Kondo impurity problem is a special case (15). We note that whereas δ-Pu is actually a dense Kondo lattice in which interactions between a periodic array of Kondo “impurities” lead to lattice effects, previous work on Kondo lattice compounds has shown that generally 80 to 90% of the magnetic fluctuation spectrum is still correctly described by the AIM (16). For temperatures T < T_K, the 5f spin dynamics of a Kondo impurity are those of a localized, damped oscillator with a characteristic spin fluctuation energy E_sf = k_BT_K, resulting in dynamic magnetic susceptibility of the following form (16–19):

$${\mathrm{\chi }}^{″}(\mathrm{\omega })\infty \frac{\mathrm{\chi }(\mathit{T})(\mathrm{\hslash }\mathrm{\omega })\mathrm{\Gamma }}{{(\mathrm{\hslash }\mathrm{\omega }-{\mathit{E}}_{\mathrm{s}\mathrm{f}})}^2+{\mathrm{\Gamma }}^2}.$$ (1)

Here, ℏω is the energy transferred to the material with h = 2πℏ being the Planck constant, and χ(T) describes the temperature dependence of the susceptibility. Γ is inversely proportional to the lifetime τ of the fluctuations via τ = ℏ/2Γ. Earlier DMFT results yield T_K ≈ 800 K (9), and we therefore would expect to observe a spin resonance characterized by E_sf = 66 meV.

RESULTS

Figure 1D shows the dynamic magnetic susceptibility χ″(ω) of δ-Pu derived from our experiment with an incident neutron energy E_i = 500 meV and at room temperature (T = 293 K) (11). A clear resonance-like feature is characterized by a spin fluctuation energy E_sf = 84(1) meV, in good agreement with the earlier DMFT results (9). This corresponds to a Kondo temperature T_K = 975 K. There is another feature with a higher spin fluctuation energy of about 146 meV. It arises because of Kondo lattice effects that are accounted for in our state-of-the-art, self-consistent DMFT calculations (11), as illustrated by the calculated χ″(ω) in Fig. 1D (dashed blue line). We note that the position of the main peak, the linear fall off at low frequencies, and the broad distribution of the spectral weight extending to high energies are all very robust features of both the DMFT calculations and the experimental data. Notably, theory and experiment are in quantitative agreement if one takes into account their respective uncertainties as detailed in (11). Figure 1E shows the momentum (Q) and energy (ℏω) transfer dependence of the observed magnetic scattering that is given by F²(Q)χ″(ω), where F(Q) is the magnetic form factor for Pu. To confirm that the observed dynamic susceptibility is not an experimental artifact, we performed a second experiment with an incident energy E_i = 250 meV. Apart from differences in the experimental resolution, the same χ″(ω) is obtained (11). We note that crystal field excitations or intermultiplet transitions would, in principle, lead to similar forms of χ″(ω) but can be ruled out from the arguments described in (11). We have also computed F²(Q)χ″(ω), which is in excellent agreement with our measurements (Fig. 1F).

Using Eq. 1, we fit the dynamic susceptibility (red solid line in Fig. 1D) and extract the lifetime of the intertwined valence and spin fluctuations. We note that each of the two maxima is hereby fitted separately via the Lorentzian peak shape described by Eq. 1. The lifetime of both features agrees within the error bars, where for the main feature with E_sf = 84 meV, we obtain τ = 0.015(4) ps [Γ = 28.4(9) meV]. This explains why the magnetic fluctuations were not previously observed by the muon spin rotation measurements that only probe longer time scales down to 1 ps. Further, by integrating the observed intensities appropriately (11), we determine the size of the fluctuating moment as μ = 0.6(2) μ_B. Using the effective moment of the 5f⁴, 5f⁵, and 5f⁶ states, as well as their occupation probabilities determined by x-ray spectroscopy (cf. Table 1), the fluctuating moment should be μ = 0.8 μ_B. We note that this intermediate coupling free-ion value only gives an upper limit because it neglects the possible influence of crystal fields and conduction electrons that may account for the difference observed here. Similarly, the DMFT calculation yields a fluctuating moment of μ = 0.82 μ_B [see eq. S16 anf fig. S5 and (11)], in good agreement with the experiment.

Figure 2 plots F(Q) obtained by energy-integrating both data sets in the range ±10 meV around E_sf. For comparison, we show the tabulated magnetic form factors for 5f⁴ and 5f⁵ configurations (20), assuming an intermediate coupling scheme (21). The 5f⁶ ground state is nonmagnetic, and its contribution to the δ-Pu magnetic form factor is therefore negligible (11). A 5f⁴ magnetic form factor (dashed red line) cannot explain our data, whereas a pure 5f⁵ magnetic form factor (solid red line) describes the data very well. However, both the experimental and theoretical average occupancy of the 5f⁵ configuration is far less than unity (see Table 1). Taking this into account, a weighted sum according to the 5f state occupation derived from RXES in Table 1 (dash-dotted red line) also reproduces the observed form factor. Finally, the form factor calculated via DMFT (blue solid line) that implicitly includes the 5f occupations is also in good agreement with the experiment and supports the conclusion that the ground state of δ-Pu is indeed a multivalence state.

Fig. 2. The magnetic form factor for δ-Pu.

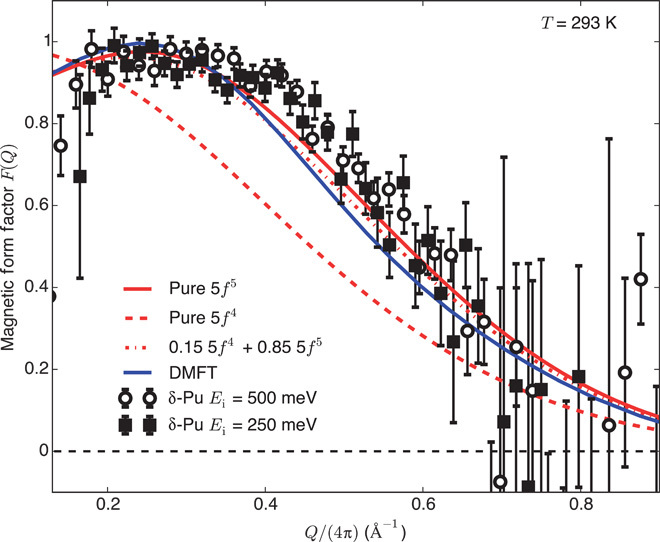
The black squares and open circles denote the magnetic form factor for δ-Pu as determined by our neutron spectroscopy experiment carried out at room temperature (T = 293 K) and with incident neutron energies E_i = 250 and 500 meV, respectively. The solid and dashed red lines are tabulated magnetic form factors for 5f⁴ and 5f⁵ electronic configurations in the intermediate coupling regime. The dash-dotted red line is a mix of both according to the 5f⁴ and 5f⁵ occupation as determined by RXES (see Table 1). The solid blue line was calculated via DMFT (11).

Using the sum rule for the dynamic magnetic susceptibility:

$${\mathrm{\chi }}^{\prime }(0)=\frac{1}{\mathrm{\pi }}{\displaystyle \int }\mathit{d}\mathrm{\omega }\frac{1}{\mathrm{\omega }}{\mathrm{\chi }}^{″}(\mathrm{\omega })$$

(11) we demonstrate that the magnetic properties of δ-Pu are consistently described by a valence-fluctuating ground state. Here, χ′(0) is the static magnetic susceptibility, which from magnetic susceptibility measurements is almost temperature-independent with a value of χ_Bulk = 5.3 × 10⁻⁴ cm³/mol at room temperature (22). Evaluating the sum rule for the dynamic susceptibility, our neutron scattering experiments yield ${\mathrm{\chi }}_{\text{Neutron}}^{{\mathit{f}}^4+{\mathit{f}}^5}$ = 0.8(2) × 10⁻⁴ cm³/mol, where we note that neutrons are insensitive to the temperature-independent Van-Vleck susceptibility ${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$ of the nonmagnetic 5f⁶ state. However, we estimate ${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$ = 3.1(15) × 10⁻⁴ cm³/mol from the magnetic susceptibility of the pure 5f⁶ state of Am, ${\mathrm{\chi }}_{\text{Am}}^{{\mathit{f}}^6}$ = 8.3 × 10⁻⁴ cm³/mol (23), which was scaled by the fractional 5f⁶ occupation by x-ray spectroscopy (Table 1). As demonstrated in Table 2, the sum of both contributions reproduces the measured static magnetic susceptibility of δ-Pu from (22) reasonably well. In this comparison, we have not included the small temperature-independent Pauli susceptibility of conduction electrons, which likely accounts for the small difference.

Table 2. The various contributions to the magnetic susceptibility of δ-Pu.

${\mathrm{\chi }}_{\text{Neutron}}^{{\mathit{f}}^4+{\mathit{f}}^5}$ denotes the magnetic susceptibility associated with the magnetic 5f⁴ and 5f⁵ states of δ-Pu at room temperature as determined by our neutron spectroscopy measurements. ${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$ gives the temperature-independent Van-Vleck contribution ${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$ of the nonmagnetic 5f⁶ that is estimated from the published magnetic susceptibility of Am (see the text). The error bar for ${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$ was estimated from the various values of the occupation of the 5f⁶ state of δ-Pu determined by different experiments (Table 1). The sum of both reproduces the static magnetic susceptibility χ_Bulk of δ-Pu as measured by magnetic susceptibility reasonably well (22). All quantities are given in units of 10⁻⁴ cm³/mol.

${\mathrm{\chi }}_{\text{Neutron}}^{{\mathit{f}}^4+{\mathit{f}}^5}$	${\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$	${\mathrm{\chi }}_{\text{Neutron}}^{{\mathit{f}}^4+{\mathit{f}}^5}+{\mathrm{\chi }}_{\mathrm{V}\mathrm{V}}^{{\mathit{f}}^6}$	χBulk
0.8(3)	3.1(15)	3.9(15)	5.3

DISCUSSION

In summary, the combination of our neutron spectroscopy and DMFT results unambiguously establishes that the magnetism in δ-Pu is not “missing,” but dynamic, and is driven by virtual valence fluctuations. Our measurements provide a straightforward interpretation of the microscopic origin of the large, Pauli-like magnetic susceptibility of δ-Pu and associated Sommerfeld coefficient. Several properties of δ-Pu have been successfully reproduced by phenomenological, so-called two-level models featuring ground states formed from a fixed admixture of two states (24). The experiments presented here, in combination with earlier core-hole spectroscopy (12) and RXES measurements (13), now define these “two levels” for the first time. Furthermore, because the various valence configurations imply distinct sizes of the Pu ion, the valence-fluctuating ground state of Pu also provides a natural explanation for its complex structural properties and, in particular, the large sensitivity of its volume to small changes in temperature, pressure, or doping. As this work has shown, DMFT (9, 11) has reached a level of sophistication and control that it can now anticipate the ground state and related properties of a material as complex as δ-Pu, and is poised to be a useful predictive tool for the design and understanding of complex, functional materials that are frequently characterized by similar electronic dichotomies.

MATERIALS AND METHODS

Neutron spectroscopy

We note that previous neutron experiments carried out on δ-Pu by Trouw et al. (25) reported a resonance-like feature at about 90 meV, in agreement with our study presented here. However, because of the strong neutron absorption of Pu and its frequent contamination with hydrogen that leads to strong spurious signals in the region of interest, as well as the special double-wall sample containers that are required for safety reasons and lead to increased background signals, neutron experiments on Pu are challenging, and it remains unclear whether this feature stemmed from spin fluctuations. We have designed both the experiment and analysis to overcome all of these issues as described in the following.

To avoid the high neutron absorption cross-section of most Pu isotopes [see table S1 in (11)], a δ-Pu sample with a total mass of 21.77 g [stabilized fcc structure with 3.5% atomic Ga, lattice parameter a = 4.608(1) Å, density ρ = 15.81 g/cm³] was prepared from 92.6% isotopically pure ²⁴²Pu (with less than 0.6% Pu-241), which is the least absorbing Pu isotope by more than an order of magnitude [see table S1 in (11)]. The exact isotopics of the measured samples are given in table S1 and result in a 1/e absorption length of 6 mm for thermal neutrons, thus allowing for a reasonably sized sample volume. In addition, the purity of this sample has been improved over previous samples used for neutron scattering (4, 25, 26) in a crucial way by removing hydrogen.

To remove hydrogen from the δ-Pu sample, it was placed in a Sieverts-type apparatus and heated in vacuum for 72 hours at 450°C, at which time the equilibrium hydrogen partial pressure indicated a hydrogen content of not more than 0.01 atomic % based on Sieverts law (27), and it was subsequently cooled to room temperature. After homogenization, the rod was axially bisected, and the samples were sent for metallography, density measurement, and nondestructive assay of isotopic composition. After these measurements and before final packaging, the samples were once again vacuum-homogenized at 450°C for an additional 72 hours, and hydrogen content was confirmed to be less than 0.01 atomic %. The absence of sharp features in any of the spectra recorded throughout this experiment demonstrates that the hydrogen removal was successful. We note that the sample stayed in the δ stability regime during the entire procedure and never went above 450°C.

The neutron spectroscopy measurements were performed at the ARCS (wide angular-range chopper spectrometer) instrument (28) at the Spallation Neutron Source operated at Oak Ridge National Laboratory (ORNL). A preliminary study was carried out at the Lujan Center at Los Alamos National Laboratory (LANL) using the PHAROS spectrometer. For safety and to avoid contamination, the sample was sealed in a double-wall Al can with indium seals using both screws and STYCAST 2850FT epoxy, which contained an atmosphere of ⁴He exchange gas. The sample is a polycrystalline rod of about 6-mm diameter and 51-mm length and was cut into two half-cylinders that were mounted side by side on the Al plate (thickness less than 0.5 mm) attached in the center of the inner Al can to make use of the entire beam cross section of ARCS. The flat side of the two half-cylinders was perpendicular to the incoming beam.

The ARCS instrument is a direct geometry neutron time-of-flight chopper spectrometer. The instrument was used with two different incident energies E_i, namely, 250 and 500 meV, resulting in energy resolutions at the elastic line of ΔE = 15 and 39 meV, respectively (full width at half-maximum, determined from vanadium standard measurements). We note that the inelastic resolution on the neutron energy loss side of the inelastic neutron scattering spectra is slightly improved, but as demonstrated in (28), this effect is only about 20% at the energy transfers of interest here (≈90 meV). To reduce the background from the double-wall Al can while maintaining the scattered intensity of the sample, the computer-controlled aperture upstream of the sample position was set to 10-mm width and 50-mm height. To isolate the spin fluctuations, a good estimate of the various background contributions, such as from the sample can, the phonon part of the inelastic spectrum, and multiple scattering, is required. For this experiment, this was solved by measuring an isostructural, nonmagnetic analog, as has been done similarly for other compounds such as CePd₃ (16) and Ce_1−xTh_x (29), where La analogs have been used. Here, we have used nonmagnetic Th with a total mass of 20.371 g that was arc-melted into a similar shape of two half-cylinders mounted in an identical container that was measured with the same incident energies and identical statistics. In addition, we have measured an identical empty double-wall Al can to determine the background contribution produced solely from the container. As we show in detail in the Supplementary Materials (11), the low momentum transfer neutron scattering data that contain the details about the dynamic magnetic susceptibility presented in Fig. 1 are independent of the details of the used background subtraction, in turn demonstrating the robustness of the presented results. All analyses presented in this article were carried out at room temperature.

Dynamical mean field theory

The theoretical method for computing the magnetic response of correlated solids is based on DMFT in combination with density functional theory (DMFT + DFT) (30). We use the implementation of this method in its charge self-consistent and all electron methodology, as developed in (31). The DFT part is based on the Wien2k package (32). In the DMFT + DFT method, the strong correlations on the Pu ion are described by the frequency and space-dependent potential, called self-energy ∑(r, r′, ω), which is added to the DFT Kohn-Sham Hamiltonian to describe the entanglement of the Pu atomic states with the itinerant spd electrons as well as the neighboring Pu atoms. The self-energy contains all Feynman diagrams local to the Pu ion and is defined through the quantum mechanical embedding in real space by the following equation:

$$\sum (\mathbf{r},{\mathbf{r}}^{\mathbf{\prime }},\mathrm{\omega })={\displaystyle \sum _{\mathrm{l}=3,{\text{mm}}^{\mathbf{\prime }}}}{\mathit{Y}}_{\mathrm{l},\mathrm{m}}(\widehat{\mathbf{r}}){\mathit{R}}_{\mathrm{l}}(\mathbf{r}){\displaystyle {\sum }_{\text{lm},{\text{lm}}^{\prime }}}(\mathrm{\omega }){\mathit{R}}_{\mathrm{l}}({\mathbf{r}}^{\mathbf{\prime }}){\mathit{Y}}_{\mathrm{l},{\mathrm{m}}^{\prime }}^{*}({\widehat{\mathbf{r}}}^{\mathbf{\prime }}),$$ (2)

where R_l(r) is the radial part of the solution of the Dirac equation inside the Pu muffin-tin sphere (using Kohn-Sham–like static self-consistent potential), linearized at the Fermi level. The components of the self-energy ${\displaystyle {\sum }_{\text{lm},{\text{lm}}^{\prime }}}$ are obtained by the solution of an auxiliary quantum impurity model, in which the impurity Green’s function G_impurity (ω) and impurity self-energy ∑_impurity (ω) must match the corresponding quantities in the solid, that is, ${\displaystyle {\sum }_{\text{lm},{\text{lm}}^{\prime }}}$ and ${\mathit{G}}_{\text{lm},{\text{ml}}^{\prime }}$, where the latter is given by

$${\mathit{G}}_{\text{lm},{\text{lm}}^{\prime }}(\mathrm{\omega })=\langle {\mathit{Y}}_{\text{lm}}{\mathit{R}}_{\mathrm{l}}|{(\mathrm{\omega }+\mathrm{\mu }+{\nabla }^2-{\mathit{V}}_{\mathrm{K}\mathrm{S}}(\mathbf{r})-\sum (\mathbf{r},{\mathbf{r}}^{\mathbf{\prime }}\mathrm{\omega }))}^{-1}|{\mathit{R}}_{\mathrm{l}}{\mathit{Y}}_{{\text{lm}}^{\prime }}\rangle .$$ (3)

The impurity model is solved by the numerically exact continuous time quantum Monte Carlo (CTQMC) method, as implemented in (33). Calculations are fully self-consistent in charge density, chemical potential and impurity levels, the lattice and impurity Green’s functions, hybridizations, and self-energies. The partially screened Coulomb repulsion on Pu atom is U = 4.5 eV (9, 34) and Hund’s coupling J = 0.512 eV. The simulations are performed at T = 232 K, and lattice constant 4.61 Å, which corresponds to the experimentally determined fcc structure of δ-Pu.

On the order of 500 DFT and 30 DMFT cycles are required for self-consistency using the highly parallel leadership supercomputing resources of Titan. Of the order of 10 million core hours were used for high-quality runs, which can be analytically continued to real frequencies with high confidence.

The magnetic susceptibility is computed in CTQMC by directly sampling the spin-spin correlation function in imaginary time defined by

$${\mathrm{\chi }}_{\mathrm{z}\mathrm{z}}(\mathit{i}\mathrm{\omega })={\int }_0^{\beta }{\mathit{e}}^{\mathit{i}\mathrm{\omega }\mathrm{\tau }}\langle {\mathit{M}}_{\mathrm{z}}(\mathrm{\tau }){\mathit{M}}_{\mathrm{z}}(0)\rangle .$$ (4)

where M_z = μ_B (L_z + 2S_z) is the magnetization on the Pu atom. The details of the algorithm are given in (33). The convergence of the magnetic susceptibility with the number of Monte Carlo moves is as fast as the convergence of Green’s function; hence, high-quality Matsubara data can be obtained. The real frequency susceptibility is obtained by analytic continuation using maximum entropy and Pade methods.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/6/e1500188/DC1

Fig. S1. A neutron powder diffraction profile of the δ-Pu sample enclosed in a double-wall Al can used for the experiments reported here is shown.

Fig. S2. Visual method of adjusting the analytically calculated self-shielding factor SSF_Pu for δ-Pu.

Fig. S3. Analytical method of adjusting the analytically calculated self-shielding factor SSF_Pu for δ-Pu.

Fig. S4. The dynamic magnetic susceptibility of δ-Pu measured via neutron spectroscopy for incident neutron energies of E_i = 500 meV (A) and 250 meV (B), respectively.

Fig. S5. Theoretical fluctuating magnetic moment of δ-Pu defined in eq. S16.

Fig. S6. Summary of the main results of our DMFT calculation.

Table S1. Isotopics and coherent and absorption neutron cross sections of the δ-Pu sample used for the experiment described in this report.

Table S2. Self-shielding factors SSF for the δ-Pu and Th samples for both used incident energies E_i = 250 and 500 meV obtained via eqs. S3 to S6.

Table S3. Results of the sum rule analysis for both the fluctuating magnetic moment 〈μ_z〉 (eq. S13) and the static susceptibility χ′(0) (eq. S14) are provided for incident energies E_i = 250 and 500 meV.

References (35–45)