Erratic pulsar behavior hints at new way of measuring the mass of stars.
Abstract
Pulsars are known for their superb timing precision, although glitches can interrupt the regular timing behavior when the stars are young. These glitches are thought to be caused by interactions between normal and superfluid matter in the crust of the star. However, glitching pulsars such as Vela have been shown to require a superfluid reservoir that greatly exceeds that available in the crust. We examine a model in which glitches tap the superfluid in the core. We test a variety of theoretical superfluid models against the most recent glitch data and find that only one model can successfully explain up to 45 years of observational data. We develop a new technique for combining radio and x-ray data to measure pulsar masses, thereby demonstrating how current and future telescopes can probe fundamental physics such as superfluidity near nuclear saturation.
INTRODUCTION
Pulsar glitches
Pulsars are rotating neutron stars born in the collapse and supernova explosion at the end of a massive star’s life. With a mass larger than that of the Sun and only about 25 km in diameter, neutron stars are primarily composed of neutron-rich matter near and above nuclear densities. Pulsars rotate at incredible speeds, with observed spin periods P ranging from 1.4 ms (1) to more than 1 s. These rotation periods are very stable, with some rivaling the precision of atomic clocks. An array of these distant high-precision clocks is being used in a global effort to detect gravitational waves from supermassive black holes at cosmic distances.
The precise timing behavior of many young pulsars is interrupted by sudden changes, so-called glitches, in their spin period. Pulsars emit beamed electromagnetic radiation (which is what allows us to detect a pulsar when its beam crosses our line of sight, like a lighthouse). This loss of energy comes at the expense of the pulsar’s rotational energy, causing the pulsar to spin more slowly over time (characterized by the time derivative of the spin rate , with Ω = 2π/P). However, during glitches, the pulsar spin rate suddenly increases over a very short time (<30 s) (2) and usually relaxes to its pre-glitch rate over a longer time (tens to hundreds of days). Examples of the accumulated effect of glitches on the spin rate of two pulsars, Vela (or PSR B0833−45) and PSR J0537−6910, are given in Fig. 1, where each step-like increase of spin rate is a glitch.
Fig. 1. Cumulative fractional change of pulsar spin frequency at glitches over time.
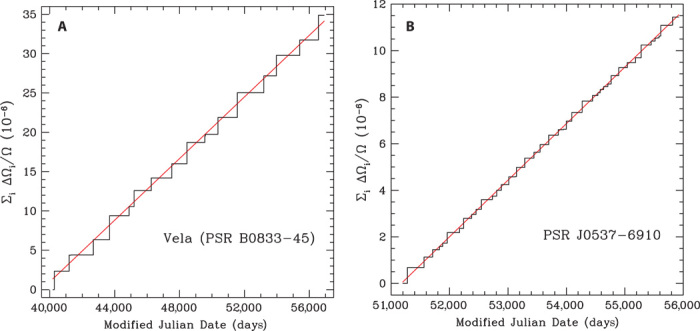
(A) Vela. (B) PSR J0537−6910. Glitch data for Vela are from (12), whereas data for PSR J0537−6910 are from Middleditch et al. (43) plus 22 new events found by Antonopoulou et al. (14). Straight lines are least-squares fit, with the average activity parameter 〈A〉 as the slope.
Glitches are believed to be the manifestation of a neutron superfluid in the inner crust of a pulsar. The structure of a neutron star can be divided into three regions: the outer crust, inner crust, and core. The outer crust is composed of a crystalline solid of normal matter at densities below neutron drip (at mass density ~4 × 1011 g cm−3). Above approximately half the nuclear saturation baryon density of nb ~ 0.16 fm−3, the core is predominantly composed of neutrons in a liquid state. Between the outer crust and core, the inner crust contains neutron-rich nuclei embedded in a sea of free neutrons. These free neutrons are expected to be in a superfluid state because the critical temperature Tc (below which neutrons become superfluid) is well above the typical temperature of pulsars (<109 K).
Superfluid in the neutron star crust
Unlike normal matter (for example, that in the outer crust), superfluid matter in the inner crust rotates by forming vortices whose areal density determines the spin rate of the superfluid. To decrease its spin rate, superfluid vortices must move so that the areal density decreases. In the inner crust of a neutron star, these vortices are usually pinned to the nuclei of normal matter (3). While the rest of the star slows down owing to electromagnetic energy loss, the neutron superfluid does not. As a result, this superfluid can act as a reservoir of angular momentum. Over many pulsar rotations, an increasing lag develops between the stellar spin rate and that of the neutron superfluid in the inner crust. When this lag exceeds a critical (but unknown) value, superfluid vortices unpin and transfer their angular momentum to the rest of the star, causing the stellar rotation rate to increase and producing what we observe as a glitch (3, 4). Link et al. (5) calculated both the minimum angular momentum needed to produce the glitches that are observed in seven pulsars and the crust moment of inertia predicted by theoretical models of neutron stars. They find that the theoretical moment of inertia matches that required by glitch observations, thus strongly supporting the above glitch model and providing key evidence for the superfluid component in the stellar crust. In particular, the superfluid reservoir must exceed the observable quantity G ≡ 2τc〈A〉, where is the pulsar characteristic age, 〈A〉 = (1/tobs)∑ΔΩ/Ω is the average activity parameter (6), and tobs is the time span over which the pulsar has been observed (years to decades in the cases studied here). The average activity 〈A〉 can be determined by the slope of a linear fit to glitches, as shown by the solid lines in Fig. 1, and results in G = 1.62 ± 0.03% for Vela and G = 0.875 ± 0.005% for PSR J0537−6910. These values of G should be compared to predictions of the crust moment of inertia relative to the total moment of inertia I of ≈ 3 to 5% at most [for the characteristic neutron star mass of 1.4 MSun; see, for example, Andersson et al. (7) and Piekarewicz et al. (8)], depending on the theoretical model of the nuclear equation of state (EOS). Furthermore, the regularity of large, similarly sized glitches from Vela and PSR J0537−6910 implies that glitches in these pulsars are tapping and essentially exhausting the entire superfluid reservoir rather than a small fraction of it.
Recent advances
Since the work of Link et al. (5), much progress has been made in understanding superfluidity in neutron star crusts. In particular, Chamel (9, 10) found that the effect of entrainment makes it very difficult to move superfluid neutrons relative to the crust lattice. As a result, Andersson et al. (7) and Chamel (11) found that the previous calculations of Link et al. (5) underestimate, by a factor of ≈4.3, the moment of inertia required by observed glitches and that the superfluid reservoir in the crust of neutron stars is insufficient to produce the observed size and frequency of glitches. For example, using the most up-to-date data (12–14), 19 glitches seen during 45 years of observing the Vela pulsar require a reservoir comprising 4.3 × 1.6% = 6.9% of the total moment of inertia, whereas 45 glitches seen during 13 years for PSR J0537−6910 require 4.3 × 0.9% = 3.9% of the total.
More recently, Piekarewicz et al. (8) and Steiner et al. (15) have shown that there is sufficient uncertainty in the theoretical nuclear EOS that determines the size of neutron star crusts for the crust to have enough moment of inertia to explain the glitches. Although possible, this argument does not take into account superfluidity, and more importantly, these authors (8, 15) note that their solution is in conflict with other observations. The proposed EOSs that meet the glitch requirement predict neutron star radii of ≈14 ± 0.5 km for typical neutron star masses of 1.2 to 2 MSun, which is in contrast to the observationally inferred radii of ≈11.8 ± 0.9 km (16) or even smaller (17). Here, we include a large number of more recent glitch data from (12), Antonopoulou et al. (14), and Yu et al. (18), and explore a solution proposed in Andersson et al. (7). In doing so, we find an unexpected and rather remarkable result.
RESULTS
Temperature dependence of superfluid
In the previous analyses (5, 7, 8, 11, 15), pulsar glitches are assumed to tap the angular momentum reservoir associated with superfluid neutrons in the inner crust of the star (although the temperature dependence of superfluidity is largely ignored). Therefore, by calculating the entire moment of inertia of the crust, it is possible to determine the maximum reservoir available for producing glitches, and this is found to be smaller than that needed to explain observed glitch activity (7, 11), unless the crust is unusually thick (8, 15). Here, we consider a superfluid reservoir that extends into the stellar core and account for the temperature dependence of superfluidity. Importantly, we use the latter in comparison with the observed temperature of pulsars. Figure 2 shows several example models of the critical temperature of neutron (singlet state) superfluidity as a function of nb for neutron stars built using the BSk20 EOS (19). The boundary between the crust (shaded region) and the core is at baryon density nb = 0.0854 fm−3 and is denoted by the vertical solid line. Because the correct nuclear EOS is unknown, we also consider the BSk21 EOS (19) and APR EOS (20). All three EOS models produce neutron stars with radius R ≈ 11 to 12.5 km, thus satisfying the observational constraint from (16), and maximum mass greater than the highest observed masses (21, 22). The superfluid models we use are parameterized fits to nuclear physics calculations; see Ho et al. (23) and references therein for details. For most superfluid models, the critical temperature, and hence allowed region for neutrons to become superfluid, is confined to the inner crust, that is, in the shaded region to the left of the vertical solid line. Therefore, pulsar glitches can only involve the moment of inertia of the inner crust if one of these superfluid models is the correct one. However, there are a few superfluid models that extend into the core, for example, the solid curve labeled SFB, which is the model from Schwenk et al. (24). For superfluid models such as the SFB model, if the temperature of a pulsar is low enough so that neutrons in the inner crust and outer core are superfluid, then glitches from the pulsar could involve additional moment of inertia from the core.
Fig. 2. Temperature dependence of neutron superfluid models as a function of baryon number density for the BSk20 nuclear equation of state.
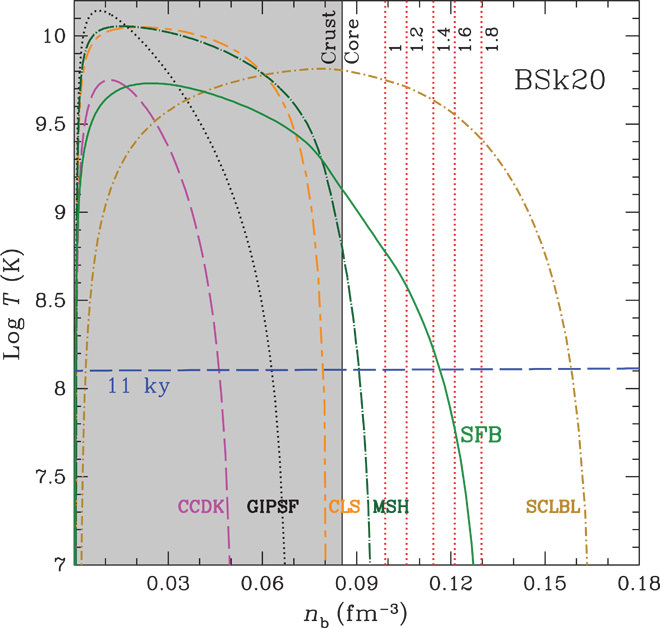
Thick curved lines are the superfluid critical temperature for the (labeled) models from (23). The vertical solid line indicates the separation between the crust (shaded region) and the core. Vertical dotted lines denote the density at which the superfluid moment of inertia (using the SFB superfluid model) is 1.6% of the total stellar moment of inertia for neutron stars of different mass (labeled in units of solar mass). The (nearly horizontal) dashed line is the temperature of a 1.4 MSun neutron star at an age of 11,000 years.
We compute the total and partial moments of inertia following the method described in Andersson et al. (7). Figure 2 shows our findings for the BSk20 EOS; BSk21 and APR EOSs produce qualitatively similar results. The vertical dotted lines in Fig. 2 indicate the density at which the moment of inertia of the superfluid (using the SFB superfluid model) exceeds G = 1.6% (from the Vela pulsar) for neutron stars of various masses. Low-mass neutron stars have a thicker crust than high-mass stars, and we see that a neutron superfluid confined to the crust can only provide a relative moment of inertia of 1.6% for neutron stars with a mass much less than 1 MSun for BSk20. All glitching pulsars with G ≈ 1% would have to be of low mass (<1 MSun) as well. For typical neutron star masses of 1.2 to 2 MSun (25), some small fraction of the core must contribute to the moment of inertia required by glitches seen in, for example, the Vela pulsar.
The next natural question is whether enough neutrons in this moment of inertia are actually superfluid, that is in Fig. 2, to the left of one of the vertical dotted lines and below the superfluid critical temperature Tc. To answer this question, we need to determine the interior temperature T(nb) of a neutron star and evaluate at what densities nb the inequality T < Tc is satisfied. This will vary for each pulsar, depending on its age and/or measured temperature; for example, the Vela pulsar is years old (26, 27) and has a surface temperature of 9.3 × 105 K (28), whereas PSR J0537−6910 only has an age determination of years (29, 30). Neutron stars are born in supernovae at very high temperatures, but they cool rapidly because of efficient emission of neutrinos. We perform neutron star cooling simulations using standard (“minimal”) neutrino emission processes (31, 32) to find the interior temperature at various ages; see Ho et al. (33) for details. Figure 2 plots the resulting temperature profile (at the age of the Vela pulsar; dashed line) for a 1.4 MSun neutron star built using the BSk20 EOS. The temperature profile is different for different masses but not drastically so, unless neutrino emission by (non-minimal) direct Urca processes occurs (see below). We find that, among nine superfluid models that span a wide range in parameter space [see Ho et al. (23) for references], only the SFB model provides a superfluid reservoir of the required level (with a maximum relative moment of inertia of 2.9% for an old and cold 1.4 MSun neutron star). For superfluid models that are confined to the crust, the reservoir is too small, whereas the reservoir is too large for models that extend much deeper into the core. The latter would be unable to explain the regularity of similar-sized glitches, which requires the reservoir to be completely exhausted in each event. The near intersection of the three lines [vertical dotted line for glitch requiring G = 1.6% at 1.4 MSun, solid line for the SFB model of superfluid critical temperature Tc, and horizontal dashed line for neutron star temperature T(nb) at age = 11,000 years] is one of our key findings: The mass of the Vela pulsar is near the characteristic value of 1.4 MSun, and the size and frequency of Vela’s observed glitches are a natural consequence of the superfluid moment of inertia available to it at its current age.
Pulsar mass from glitches
We summarize our results in Fig. 3, which shows the interior temperature T of a pulsar as a function of the value of G = 2τc〈A〉. These two quantities, G and T, are directly determined from observational data. The former comes from (radio or x-ray) observations of glitches and is best determined for pulsars that undergo regular large glitches. The latter is obtained either from the age of the pulsar [for example, by determining the age of an associated supernova remnant (SNR)] or by measuring/constraining the surface temperature of the pulsar through x-ray measurements (see Materials and Methods). The age gives the interior temperature via neutron star cooling simulations such as the ones conducted here, whereas the surface temperature is related to the interior temperature via well-known relationships (34), which depend on the composition of the outer layers of the star (taken to be iron here). Thus, for a given pulsar that has these two measurable quantities, this figure allows us to determine the pulsar’s mass. For example, using the BSk20 EOS, we find that Vela is a 1.51 ± 0.04 MSun neutron star and PSR J0537−6910 is a 1.83 ± 0.04 MSun neutron star. These two represent our two best cases because they have the smallest uncertainty in G and relatively small uncertainty in T (see Fig. 3 and Table 1).
Fig. 3. Neutron star mass from pulsar observables G and interior temperature T.
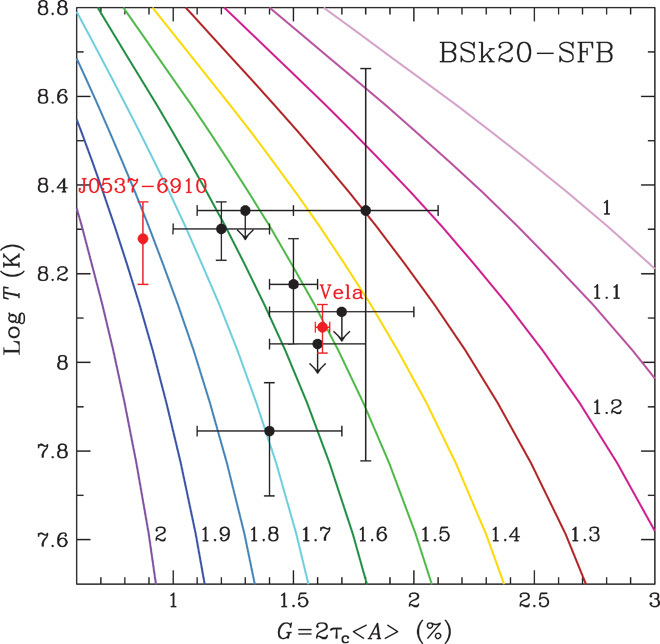
Data points are for pulsars with measured G from glitches and T from an age or surface temperature observation (see Table 1). Lines (labeled by neutron star mass, in units of solar mass) are the theoretical prediction for G and T using the BSk20 nuclear equation of state and SFB neutron superfluid models.
Table 1. Characteristics of glitching pulsars.
| PSR | τc (103 y) | 〈A〉 (10−9 d−1) | G (%) | Age (103 y) | Ref. | (106 K) | Ref. | T (108 K) |
| J0537−6910 | 4.93 | 2.43 ± 0.01 | 0.875 ± 0.005 | 1–5 | (29, 30) | 1.9 ± 0.4 | ||
| B0833−45 | 11.3 | 1.96 ± 0.04 | 1.62 ± 0.03 | 5.4–16 | (26, 27) | 0.93a | (28) | 1.2 ± 0.15 |
| B1046−58 | 20.4 | 1.1 ± 0.2 | 1.6 ± 0.2 | <1.4b | (44) | < 1.1 | ||
| B1338−62 | 12.1 | 1.7 ± 0.1 | 1.5 ± 0.1 | 3–30 | (45) | 1.5 ± 0.4 | ||
| B1706−44 | 17.8 | 1.1 ± 0.2 | 1.4 ± 0.3 | 5–18 | (46) | 0.5–0.8a | (47) | 0.7 ± 0.2 |
| B1757−24 | 15.5 | 1.5 ± 0.2 | 1.7 ± 0.3 | > 10 | (48, 49) | (50) | < 1.3 | |
| B1800−21 | 15.8 | 1.5 ± 0.2 | 1.8 ± 0.3 | 1–3b | (51) | |||
| B1823−13 | 21.5 | 0.8 ± 0.1 | 1.3 ± 0.2 | <2b | (52) | < 2.2 | ||
| 1E 1841−45 | 4.57 | 4 ± 1 | 1.2 ± 0.2 | 0.75–2.1 | (53) | 3b | (28) | 2 ± 0.3 |
aFrom an atmosphere spectral model.
bFrom a blackbody spectral model.
Figure 3 plots the data for other glitching pulsars (see also Tables 1 and 2). The nine sources shown are currently the best pulsars for our prescribed technique of measuring neutron star mass. They are selected on the basis of each undergoing several glitches that are approximately regularly spaced in time and similarly sized, so that a linear fit, such as the ones illustrated in Fig. 1, is a good characterization of their glitch behavior. Note that there are likely at least two types of glitches (18, 35), and glitching pulsars with G ≪ 1 would only be tapping a small portion of the superfluid moment of inertia (incidentally, this is the reason for excluding the Crab pulsar). Good candidates for this technique must also have an age or temperature constraint.
Table 2. Mass, radius, and total moment of inertia of glitching pulsars for three nuclear equation of state models.
| PSR | M (MSun) | R (km) | I (MSun km2) |
| BSk20 EOS | |||
| J0537−6910 | |||
| B0833−45 | |||
| B1046−58 | |||
| B1338−62 | |||
| B1706−44 | |||
| B1757−24 | |||
| B1800−21 | |||
| B1823−13 | |||
| 1E 1841−045 | |||
| BSk21 EOS | |||
| J0537−6910 | |||
| B0833−45 | |||
| B1046−58 | |||
| B1338−62 | |||
| B1706−44 | |||
| B1757−24 | |||
| B1800−21 | |||
| B1823−13 | ≥ 1.71 | ≤ 12.6 | ≥ 88.9 |
| 1E 1841−045 | |||
| APR EOS | |||
| J0537−6910 | |||
| B0833−45 | |||
| B1046−58 | |||
| B1338−62 | |||
| B1706−44 | |||
| B1757−24 | |||
| B1800−21 | |||
| B1823−13 | |||
| 1E 1841−045 | |||
CONCLUSION
We conclude by commenting on the nuclear EOS and superfluid models that are adopted and that lead to the results presented here. For the former, we focus on and describe the results for BSk20. The other two EOSs we consider, BSk21 and APR, yield qualitatively similar results as BSk20, except the mass of most pulsars is about 1.8 MSun, compared to 1.5 MSun for BSk20, and the mass of PSR J0537−6910 is >2 MSun (see Table 2). Such high mass pulsars (for BSk21 and APR) would cool to a much lower temperature than observed because fast (direct Urca) neutrino emission processes become operative above 1.59 MSun for BSk21 and above 1.96 MSun for APR. Note that direct Urca processes do not take place for any mass using BSk20. Uncertainty in the EOS is the primary contributor to the systematic error in our mass determinations. An indication of the effect of this uncertainty can be seen in Table 2: errors for M, R, and I arise from the errors in G and T (see Fig. 3), in contrast to the difference in a particular parameter for different EOS models. For neutron superfluidity, we concern ourselves only with a superfluid in the singlet state (1S0), which is likely present in the inner crust and possibly in a small fraction of the outer core of a neutron star. Deeper within the star, neutrons can be in a superfluid triplet state (3P2). The properties of this superfluid are much more uncertain. Recent measurements of the rapid cooling of a young neutron star in the Cassiopeia A supernova remnant have revealed the critical temperature of the triplet-state neutron superfluid (36, 37), although this finding is currently under debate (38, 39). The peak critical temperature of the triplet state is much lower than that of the singlet state, although there may be an overlap region, and the superfluid properties are unclear within this region.
The possibility of measuring the mass of isolated pulsars has not been previously demonstrated. To date, the most precise neutron star mass measurements are by radio timing of pulsars that are in a binary star system (25), for example, neutron stars with the highest measured mass of 1.97 ± 0.04 MSun (21) and 2.01 ± 0.04 MSun (22). The number of pulsars that are seen to glitch continues to increase (18, 35), along with ongoing discoveries of pulsars, including the binary system with PSR J2032+4127 (40), which could be used to test our method in the future. Our method of measuring neutron star masses can greatly increase the number of known masses, thereby allowing the determination of fundamental physics properties such as the nuclear EOS and superfluidity. Although there are currently relatively large systematic uncertainties, these will improve as our knowledge of the physics of dense matter improves. The novelty of our approach is the combination of pulsar glitch data and the temperature dependence of superfluidity. The method is especially promising with upcoming large astronomical observatories such as the Square Kilometer Array (SKA) in radio and Athena+ in x-rays. SKA could discover all the observable pulsars in the Galaxy, and we show that a program to monitor glitching pulsars could greatly transform the fields of neutron star and nuclear physics.
MATERIALS AND METHODS
Figure 3 and Table 1 present the data for the glitching pulsars studied in this work. Here, we explain how this information was determined. The average activity parameter 〈A〉 is obtained by a least-squares fit to the cumulative fractional change of pulsar spin frequency over time, examples of which are shown in Fig. 1. The errors for 〈A〉 given in Table 1 come directly from the fit to each set of pulsar glitches. We performed fits to four subsets of Vela glitches and compared the results to those obtained using the entire data set. We find that errors derived from using the subsets well represent the uncertainty arising from using fewer glitches due to lack of long-term information. Age is that of an SNR associated with the pulsar, except in the cases of PSR B1706−44 (where the association with SNR G343.1−2.3 is uncertain, so we use the SNR age for the lower limit and the characteristic age for the upper limit) and PSR B1757−24 (where the association with SNR G5.4−1.2 is uncertain, so we estimate a lower limit that is comparable to its characteristic age). Surface temperature is obtained from x-ray spectral constraint/measurement and is the redshifted value, that is, measured by a distant observer. Superscript “a” indicates that is from fitting the spectrum with a neutron star atmosphere model, whereas “b” indicates that is from fitting (or obtaining an upper limit) with a blackbody model; the latter generally overestimates surface temperature by a factor of ~1.5 (41).
Neutron stars are nearly isothermal after several hundred years (31, 32). Therefore, the temperature at the bottom of the neutron star envelope (at ~1010 g cm−3) is essentially the temperature in the deeper crust and core. To determine the interior temperature T from the age or surface temperature, we use the following procedure. If the pulsar only has an age determination, we perform neutron star cooling simulations (33) and extract the interior temperature at the appropriate age, with errors estimated from varying model parameters such as the mass. If the pulsar only has a surface temperature measurement, then we convert surface temperature into interior temperature using the relation given in, for example, Potekhin et al. (34), assuming an iron envelope composition (42). If the pulsar has both age and surface temperature measurements, then we use the age method described above and we verify that the inferred interior temperature produces a surface temperature that approximately matches the observed value. In the case of 1E 1841−045, this pulsar is a magnetar, and magnetars are unusually hot for their age [likely due to magnetic field decay and heating in the outer layers of the crust (33)]; because we are interested in the temperature near the crust-core boundary, we only use the age to determine T for 1E 1841−045.
Acknowledgments
We are grateful to A. Lyne and B. Stappers for unpublished radio data and L. Kuiper for X-ray ToAs of PSR J0537–6910. Funding: W.C.G.H., D.A., and N.A. acknowledge support from STFC in the UK. C.M.E. acknowledges support from FONDECYT (postdoctorado 3130152). D.A. acknowledges support from an NWO Aspasia grant (principal investigator: A. L. Watts) and the research networking programme NewCompStar (COST Action MP1304). Author contributions: W.C.G.H. contributed to developing the model, performed the model calculations, and wrote the manuscript. C.M.E. gathered and analyzed the data and contributed to writing the manuscript. D.A. gathered and analyzed the data and contributed to writing the manuscript. N.A. contributed to developing the model and writing the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data presented in this work are available upon request to C.M.E.
REFERENCES AND NOTES
- 1.Hessels J. W. T., Ransom S. M., Stairs I. H., Freire P. C. C., Kaspi V. M., Camilo F., A radio pulsar spinning at 716 Hz. Science 311 1901–1904 (2006). [DOI] [PubMed] [Google Scholar]
- 2.Dodson R., Lewis D., McCulloch P., Two decades of pulsar timing of Vela. Astrophys. SpaceSci. 308, 585–589 (2007). [Google Scholar]
- 3.Anderson P. W., Itoh N., Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 256, 25–27 (1975). [Google Scholar]
- 4.Baym G., Pethick C., Pines D., Ruderman M., Spin-up in neutron stars: The future of the Vela pulsar. Nature 224, 872–874 (1969). [Google Scholar]
- 5.Link B., Epstein R. I., Lattimer J. M., Pulsar constraints on neutron star structure and equation of state. Phys. Rev. Lett. 83, 3362–3365 (1999). [Google Scholar]
- 6.McKenna J., Lyne A. G., PSR1737–30 and period discontinuities in young pulsars. Nature 343, 349–350 (1990). [Google Scholar]
- 7.Andersson N., Glampedakis K., Ho W. C. G., Espinoza C. M., Pulsar glitches: The crust is not enough. Phys. Rev. Lett. 109, 241103 (2012). [DOI] [PubMed] [Google Scholar]
- 8.Piekarewicz J., Fattoyev F. J., Horowitz C. J., Pulsar glitches: The crust may be enough. Phys. Rev. C 90, 015803 (2014). [Google Scholar]
- 9.Chamel N., Band structure effects for dripped neutrons in neutron star crust. Nucl. Phys. A 747, 109–128 (2005). [Google Scholar]
- 10.Chamel N., Neutron conduction in the inner crust of a neutron star in the framework of the band theory of solids. Phys. Rev. C 85, 035801 (2012). [Google Scholar]
- 11.Chamel N., Crustal entrainment and pulsar glitches. Phys. Rev. Lett. 110, 011101 (2013). [DOI] [PubMed] [Google Scholar]
- 12. www.jb.man.ac.uk/pulsar/glitches.html
- 13.Kuiper L., Hermsen W., The soft γ-ray pulsar population: A high-energy overview. Mon. Not. R. Astron. Soc. 449, 3827–3866 (2015). [Google Scholar]
- 14.Antonopoulou D., Espinoza C. M., Kuiper L., Andersson N., in preparation. [Google Scholar]
- 15.Steiner A. W., Gandolfi S., Fattoyev F. J., Newton W. G., Using neutron star observations to determine crust thicknesses, moments of inertia, and tidal deformabilities. Phys. Rev. C 91, 015804 (2015). [Google Scholar]
- 16.Lattimer J. M., Steiner A. W., Neutron star masses and radii from quiescent low-mass x-ray binaries. Astrophys. J. 784, 123 (2014). [Google Scholar]
- 17.Guillot S., Servillat M., Webb N. A., Rutledge R. E., Measurement of the radius of neutron stars with high signal-to-noise quiescent low-mass X-ray binaries in globular clusters. Astrophys. J. 772, 7 (2013). [Google Scholar]
- 18.Yu M., Manchester R. N., Hobbs G., Johnston S., Kaspi V. M., Keith M., Lyne A. G., Qiao G. J., Ravi V., Sarkissian J. M., Shannon R., Xu R. X., Detection of 107 glitches in 36 southern pulsars. Mon. Not. R. Astron. Soc. 429, 688–724 (2013). [Google Scholar]
- 19.Potekhin A. Y., Fantina A. F., Chamel N., Pearson J. M., Goriely S., Analytical representations of unified equations of state for neutron-star matter. Astron. Astrophys. 560, A48 (2013). [Google Scholar]
- 20.Akmal A., Pandharipande V. R., Ravenhall D. G., Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828 (1998). [Google Scholar]
- 21.Demorest P. B., Pennucci T., Ransom S. M., Roberts M. S. E., Hessels J. W. T., A two-solar-mass neutron star measured using Shapiro delay. Nature 467, 1081–1083 (2010). [DOI] [PubMed] [Google Scholar]
- 22.Antoniadis J., Freire P. C. C., Wex N., Tauris T. M., Lynch R. S., van Kerkwijk M. H., Kramer M., Bassa C., Dhillon V. S., Driebe T., Hessels J. W. T., Kaspi V. M., Kondratiev V. I., Langer N., Marsh T. R., McLaughlin M. A., Pennucci T. T., Ransom S. M., Stairs I. H., van Leeuwen J., Verbiest J. P. W., Whelan D. G., A massive pulsar in a compact relativistic binary. Science 340, 1233232 (2013). [DOI] [PubMed] [Google Scholar]
- 23.Ho W. C. G., Elshamouty K. G., Heinke C. O., Potekhin A. Y., Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 91, 015806 (2015). [Google Scholar]
- 24.Schwenk A., Friman B., Brown G. E., Renormalization group approach to neutron matter: Quasiparticle interactions, superfluid gaps and the equation of state. Nucl. Phys. A 713, 191–216 (2003). [Google Scholar]
- 25.Lattimer J. M., Gen. Relativ. Gravit. 1713, 1–26 (2014). [Google Scholar]
- 26.Page D., Lattimer J. M., Prakash M., Steiner A. W., Neutrino emission from cooper pairs and minimal cooling of neutron stars. Astrophys. J. 707, 1131–1140 (2009). [Google Scholar]
- 27.Tsuruta S., Sadino J., Kobelski A., Teter M. A., Liebmann A. C., Takatsuka T., Nomoto K., Umeda H., Thermal evolution of hyperon-mixed neutron stars. Astrophys. J. 691, 621–632 (2009). [Google Scholar]
- 28.Viganò D., Rea N., Pons J. A., Perna R., Aguilera D. N., Miralles J. A., Unifying the observational diversity of isolated neutron stars via magneto-thermal evolution models. Mon. Not. R. Astron. Soc. 434, 123–141 (2013). [Google Scholar]
- 29.Wang Q. D., Gotthelf E. V., ROSAT and ASCA observations of the crab-like supernova remnant n157b in the large magellanic cloud. Astrophys. J. 494, 623–635 (1998). [Google Scholar]
- 30.Chen Y., Wang Q. D., Gotthelf E. V., Jiang B., Chu Y.-H., Gruendl R., Chandra ACIS Spectroscopy of N157B: A young composite supernova remnant in a superbubble. Astrophys. J. 651, 237–249 (2006). [Google Scholar]
- 31.Yakovlev D. G., Pethick C. J., Neutron star cooling. Annu. Rev. Astron. Astrophys. 42, 169–210 (2004). [Google Scholar]
- 32.Page D., Geppert U., Weber F., The cooling of compact stars. Nucl. Phys. A 777, 497–530 (2006). [Google Scholar]
- 33.Ho W. C. G., Glampedakis K., Andersson N., Magnetars: Super(ficially) hot and super(fluid) cool. Mon. Not. R. Astron. Soc. 422, 2632–2641 (2012). [Google Scholar]
- 34.Potekhin A. Y., Yakovlev D. G., Chabrier G., Gnedin O. Y., Thermal structure and cooling of superfluid neutron stars with accreted magnetized envelopes. Astrophys. J. 594, 404–418 (2003). [Google Scholar]
- 35.Espinoza C. M., Lyne A. G., Stappers B. W., Kramer M., A study of 315 glitches in the rotation of 102 pulsars. Mon. Not. R. Astron. Soc. 414, 1679–1704 (2011). [Google Scholar]
- 36.Page D., Prakash M., Lattimer J. M., Steiner A. W., Rapid cooling of the neutron star in Cassiopeia A triggered by neutron superfluidity in dense matter. Phys. Rev. Lett. 106, 081101 (2011). [DOI] [PubMed] [Google Scholar]
- 37.Shternin P. S., Yakovlev D. G., Heinke C. O., Ho W. C. G., Patnaude D. J., Cooling neutron star in the Cassiopeia A supernova remnant: Evidence for superfluidity in the core. Mon. Not. R. Astron. Soc. 412, L108–L112 (2011). [Google Scholar]
- 38.Elshamouty K. G., Heinke C. O., Sivakoff G. R., Ho W. C. G., Shternin P. S., Yakovlev D. G., Patnaude D. J., David L., Measuring the cooling of the neutron star in Cassiopeia A with all Chandra X-ray Observatory detectors. Astrophys. J. 777, 1–10 (2013). [Google Scholar]
- 39.Posselt B., Pavlov G. G., Suleimanov V., Kargaltsev O., New constraints on the cooling of the Central Compact Object in Cas A. Astrophys. J. 779, 186 (2013). [Google Scholar]
- 40.Lyne A. G., Stappers B. W., Keith M. J., Ray P. S., Kerr M., Camilo F., Johnson T. J., The binary nature of PSR J2032+4127. Mon. Not. R. Astron. Soc. 451, 581–587 (2015). [Google Scholar]
- 41.Potekhin A. Y., Atmospheres and radiating surfaces of neutron stars. Phys.-Uspekhi 57, 735–770 (2014). [Google Scholar]
- 42.Chang P., Bildsten L., Evolution of young neutron star envelopes. Astrophys. J. 605, 830–839 (2004). [Google Scholar]
- 43.Middleditch J., Marshall F. E., Wang Q. D., Gotthelf E. V., Zhang W., Predicting the starquakes in PSR J0537–6910. Astrophys. J. 652, 1531–1546 (2006). [Google Scholar]
- 44.Gonzalez M. E., Kaspi V. M., Pivovaroff M. J., Gaensler B. M., Chandra and XMM-Newton observations of the Vela-like pulsar B1046-58. Astrophys. J. 652, 569–575 (2006). [Google Scholar]
- 45.Caswell J. L., Kesteven M. J., Stewart R. T., Milne D. K., Haynes R. F., G308.8-0.1—An unusual supernova remnant containing a short-period pulsar, PSR J1341-6220. Astrophys. J. 399, L151–L153 (1992). [Google Scholar]
- 46.H.E.S.S. Collaboration, Detection of very-high-energy γ-ray emission from the vicinity of PSR B1706-44 and G343.1-2.3 with H.E.S.S. Astron. Astrophys. 528, A143 (2011). [Google Scholar]
- 47.McGowan K. E., Zane S., Cropper M., Kennea J. A., Córdova F. A., Ho C., Sasseen T., Vestrand W. T., XMM-Newton observations of PSR B1706–44. Astron. Astrophys. 600, 343–350 (2004). [Google Scholar]
- 48.Blazek J. A., Gaensler B. M., Chatterjee S., van der Swaluw E., Camilo F., Stappers B. W., The Duck Redux: An improved proper motion upper limit for the pulsar B1757-24 near the supernova remnant G5.4-1.2. Astrophys. J. 652, 1523–1530 (2006). [Google Scholar]
- 49.Zeiger B. R., Brisken W. F., Chatterjee S., Goss W. M., Proper motions of PSRs B1757–24 and B1951+32: Implications for ages and associations. Astrophys. J. 674, 271–277 (2008). [Google Scholar]
- 50.Kaspi V. M., Gotthelf E. V., Gaensler B. M., Lyutikov M., X-ray detection of pulsar PSR B1757-24 and its nebular tail. Astrophys. J. 562, L163–L166 (2001). [Google Scholar]
- 51.Kargaltsev O., Pavlov G. G., Garmire G. P., X-ray emission from PSR B1800–21, its wind nebula, and similar systems. Astrophys. J. 660, 1413–1423 (2007). [Google Scholar]
- 52.Pavlov G. G., Kargaltsev O., Brisken W. F., Chandra observation of PSR B1823–13 and its pulsar wind nebula. Astrophys. J. 675, 683–694 (2008). [Google Scholar]
- 53.Kumar H. S., Safi-Harb S., Slane P. O., Gotthelf E. V., Chandra and XMM-Newton study of the supernova remnant Kes 73 hosting the magnetar 1E 1841-045. Astrophys. J. 781, 41 (2014). [Google Scholar]


